Off-axis loads cause failure of the distal radius at lower magnitudes than axial loads: A finite element analysis

Abstract

Distal radius (Colles’) fractures are a common fall-related injury in older adults and frequently result in long-term pain and reduced ability to perform activities of daily living. Because the occurrence of a fracture during a fall depends on both the strength of the bone and upon the kinematics and kinetics of the impact itself, we sought to understand how changes in bone mineral density (BMD) and loading direction affect the fracture strength and fracture initiation location in the distal radius. A three-dimensional finite element model of the radius, scaphoid, and lunate was used to examine changes of ±2% and ±4% BMD, and both axial and physiologically relevant off-axis loads on the radius. Changes in BMD resulted in similar percent changes in fracture strength. However, modifying the applied load to include dorsal and lateral components (assuming a dorsal view of the wrist, rather than an anatomic view) resulted in a 47% decrease in fracture strength (axial failure load: 2752 N, off-axis: 1448 N). Loading direction also influenced the fracture initiation site. Axially loaded radii failed on the medial surface immediately proximal to the styloid process. In contrast, off-axis loads, containing dorsal and lateral components, caused failure on the dorsal–lateral surface. Because the radius appears to be very sensitive to loading direction, the results suggest that much of the variability in fracture strength seen in cadaver studies may be attributed to varying boundary conditions. The results further suggest that interventions focused on reducing the incidence of Colles’ fractures when falls onto the upper extremities are unavoidable may benefit from increasing the extent to which the radius is loaded along its axis.

1. Introduction

Distal radius (Colles’) fractures are a common injury in older women, and generally result from a fall onto an outstretched hand. While not life-threatening, these fractures cause significant impairment and are frequently associated with complications following healing, such as decreased grip strength and range of motion, wrist instability, contractures, carpal tunnel syndrome, and osteoarthritis (Colles’ Frx, 2006). Because Colles’ fractures usually occur during impact from a fall from standing height or lower and are considered low-energy fractures, diminished bone quality (i.e., osteopenia or osteoporosis) has been implicated as a risk factor for sustaining these and hip fractures (Doherty et al., 2001; Eastell et al., 2001; Finsen and Benum, 1987).

Whether and where a fracture of the radius occurs after a fall depends on the magnitude and direction of the impact force and upon the strength of the bone itself. A great deal of effort has been directed towards quantifying the impact mechanics that occur during forward-directed falls onto the hands (Chiu and Robinovitch, 1998; DeGoede and Ashton-Miller, 2003; DeGoede et al., 2002; Kim and Ashton-Miller, 2003; Lo et al., 2003; Robinovitch and Chiu, 1998). It is generally agreed that standing-height falls onto the hands can produce peak forces of around 2500–4000N (Chiu and Robinovitch, 1998), accompanied by rapid wrist extension (Reed-Troy and Grabiner, 2005). We recently quantified the kinematics and kinetics during simulated falls onto the hands and found that at the instant of peak force, the wrists were extended 46°±11° and ulnar deviated 4°±3°. At that instant, the direction of the resultant force relative to the radial axis had considerable dorsal and lateral components (Reed-Troy and Grabiner, 2005).

The failure strength of any bone depends on its density and upon its macro- and micro-architecture. Clinical interventions for osteoporosis have recently focused on improving bone density through pharmaceutical means such as anti-resorptive therapy (Baran, 2001). These generally result in a modest systemic increase in bone mineral density (BMD; 1–3%), accompanied by a dramatic decrease in remodeling activity. Finite element modeling studies of the hip in which local changes in bone material properties are simulated have shown that modest changes in bone density targeted to structurally relevant locations may cause larger changes in overall bone strength (Oden et al., 1999).

The load mechanics of the wrist are somewhat less well understood. Micro-finite element models of the distal radius have been used to examine the stress and strain distributions with the goals of predicting the failure loads (Pistoia et al., 2002, 2004), determining how load is transmitted through the bone, and identifying potential sites of fracture initiation (Ulrich et al., 1999). While these models have collectively helped to clarify the loading mechanics of the distal radius, they do not specifically address potentially important changes in impact mechanics.

Given that fracture initiation depends on both the strength of the bone and the loading to which it is subjected, we addressed two questions about fall-related fractures of the distal radius. First, how is fracture strength influenced by loading direction? And second, how do clinically achievable changes in bone mineral density influence the predicted fracture strength? A secondary goal was to identify the fracture initiation site and quantify the dependency of the site on loading direction. We developed and validated a three-dimensional finite element model to conduct this parametric study.

2. Methods

2.1. Model development

The right wrist of a 53-year-old female volunteer was imaged with computed tomography (GE LightSpeed QX, GE Healthcare, Chalfont St. Giles, UK), at a resolution of 0.455×0.455×1.25 mm/voxel. During the scan, the wrist was positioned at 57° flexion and 7° ulnar deviation, to simulate a realistic but extreme impact position. These values were one standard deviation above the mean flexion and ulnar deviation observed experimentally during falls onto the hands (Reed-Troy and Grabiner, 2005). Geometrical and density data for the radius, scaphoid, and lunate were extracted using custom-written software (Matlab 7.01) and a finite element model was built using ANSYS 10.0. Complex geometry of the ultradistal radius, scaphoid, and lunate prevented the use of hexahedral elements throughout. Instead, the final model consisted of 9415 8-node hexahedral (brick) elements in the proximal portion of the radius and 11,089 10-node tetrahedral elements for the ultradistal radius, cartilage, scaphoid, and lunate. Transitional pyramid elements were used at the interface.

Bone material properties were assigned to each element based on the average Hounsfield value (HU) for those voxels located in the immediate vicinity of the element. Material properties were assumed to be linear and isotropic and all bone was assigned a Poisson’s ratio (ν) of 0.4. A cut-off value of 672HU was assigned to distinguish cortical (HU>672) from cancellous (HU<672) bone. This value was determined visually by the investigator (KLT) and agrees well with published data (Aamodt et al., 1999). Density was assigned based on HU and was used to calculate elastic modulus using the following equations (Lotz et al., 1990; Snyder and Schneider, 1991; Wirtz et al., 2000):

$$\begin{array}{ll}\text{cortical}:\hfill & \rho =1.09+0.000445\times \text{HU},\hfill \\ \hfill & E=2065\times {\rho }^{3.09},\hfill \end{array}$$

$$\begin{array}{ll}\text{cancellous}:\hfill & \rho =0.0012\times \text{HU}+0.17,\hfill \\ \hfill & E=1904\times {\rho }^{1.64}.\hfill \end{array}$$

After the modulus was calculated for each element, the element was assigned one of 100 binned material definitions, the moduli of which ranged from 100MPa to 20.1 GPa in 200MPa increments.

A 2.5mm thick layer of cartilage was created by lofting the distal articular surface of the radius. Cartilage material properties were assigned based on the assumption that the model would simulate an impact during which the peak force occurs approximately 30 ms after initial contact (Chou et al., 2001; Reed-Troy and Grabiner, 2005). At this rapid loading rate, cartilage appears nearly incompressible (Stolz et al., 2004), thus ν=0.49 was assigned. Based on dynamic high-frequency compression studies, cartilage was assigned a stiffness of 48MPa (Park et al., 2004).

The ligaments that directly attached the radius, scaphoid, and lunate were included in the model as nonlinear springs. Each ligament included a quadratic toe-region and a linear elastic portion. Ligament connections, material properties, and pretension values are summarized in Table 1. Contact was modeled between the radius and scaphoid, radius and lunate, and lunate and scaphoid. The model was validated by comparing contact area and peak contact stress on the radius to published experimental data (Troy and Grabiner, 2006; Viegas and Patterson, 1997).

Table 1.

Ligament material properties (linear portion only) and attachment locations

Ligament	From	To	Linear stiffness (N/mm)
Radial collateral	Radius	Scaphoid	10
Scapholunate	Scaphoid	Lunate	95
Dorsal radiocarpal	Radius	Scaphoid and lunate	26
Palmar radiocarpal	Radius	Scaphoid and lunate	33

2.2. Parametric series

A total of 26 models were run in which bone density and loading direction were varied. In each model, a ramped 3000N load was applied to the radius through the centroids of the scaphoid (1800 N) and lunate (1200 N). The axial series consisted of all models to which an axial load was applied, described by a unit vector [0 0–1] in the [medial, dorsal, axial] directions. (A negative axial load indicates the force is directed from the wrist towards the elbow, and the coordinate system references a dorsal – as opposed to an anatomical – view of the radius) BMD was changed from its baseline value in either the cancellous bone only, the cortical bone only, or all bone of the radius, by −4%, −2%,+2%, or+4%. Combined with a model in which no change of BMD was simulated, this resulted in 13 total simulations. The off-axis series was identical to the axial series except that the loading direction was changed to simulate a worst-case off-axis load, described by a unit vector [−0.1385 0.3562–0.9241] in the [medial, dorsal, axial] directions. This vector, which was determined from experimentally collected kinematic data during simulated forward falls (Reed-Troy and Grabiner, 2005), was one standard deviation above the mean off-axis load.

2.3. Failure determination

For each simulation, the first and third principal stresses (s₁ and s₃) from each element were recorded during the ramped load, and element failure was determined using the Coulomb–Mohr criterion of (Keyak and Rossi, 2000):

$$\frac{s_1}{{\sigma }_{\text{ty}}}-\frac{s_3}{{\sigma }_{\text{cy}}}\ge 1,$$

where σ_ty and σ_cy are the material’s tensile and compressive yield stresses, respectively. Tensile and compressive yields were assigned to cortical and cancellous elements using the following equations (Rohl et al., 1991):

$$\begin{array}{l}\text{cortical}:{\sigma }_{\text{cy}}={\sigma }_{\text{ty}}=0.0154\times E(\text{MPa}),\\ \text{cancellous}:{\sigma }_{\text{cy}}={\sigma }_{\text{ty}}=0.011\times E(\text{MPa})\end{array}$$

After element failure was determined for a given load increment, a custom algorithm (Matlab 7.01) calculated the volume of the largest cluster of contiguous failed elements. A crack large enough to propagate was assumed to have developed when a cluster of elements with a volume exceeding 350, 400, or 450mm³ failed (Keyak et al., 1998). The centroid of the cluster was used to describe the fracture initiation site.

3. Results

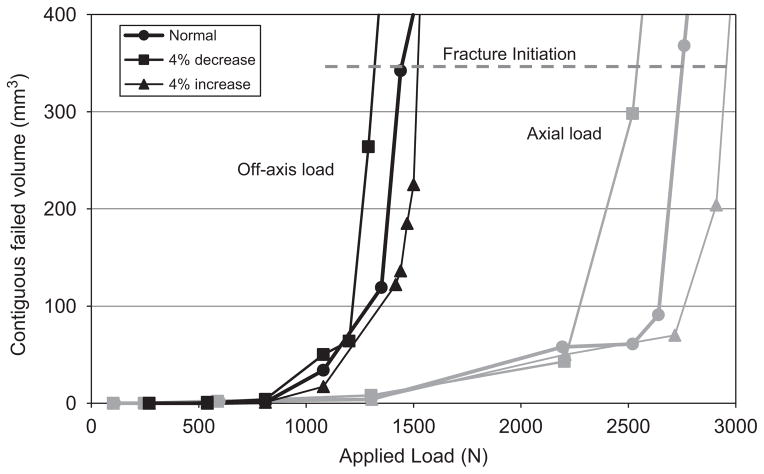
Loading direction had a strong influence on predicted fracture strength. For the unchanged (baseline) BMD model, an axial load caused fracture at 2752N (350mm³ failed elements) to 2830N (450mm³). In contrast, the off-axis load applied to the same unchanged BMD model predicted failure at 1448 and 1521N for 350 and 450mm³, respectively.

In all models, the volume of failed elements remained relatively constant as load increased until a critical point was reached, after which the failed volume increased rapidly (Fig. 1). Because of this, the predicted failure loads were relatively insensitive to whether clusters of 350, 400, or 450mm³ were used as fracture criteria. The remaining results and discussion will focus on those results obtained using 350mm³ as a fracture criterion, since this represents the most conservative estimate.

Fig. 1.

Applied load versus total contiguous volume of failed elements for the axial and off-axis series. Baseline and ±4% changes in BMD for all bone are shown. Fracture was assumed to occur when greater than 350mm³ failed.

Changes in BMD nonlinearly affected the predicted fracture strength for both series. In all cases a±2% change in cancellous or cortical BMD resulted in a −2.4% to +2.9% change in predicted fracture strength. However, a ±2% change in the entire model’s BMD resulted in a −8.4% to +4.6% change in fracture strength. The degree to which fracture strength increased with increasing BMD depended on both the type of bone in which BMD was changed and the direction of the applied load. Changes in cancellous bone made a larger contribution to fracture strength than did changes in cortical bone. The entire series data are summarized in Table 2.

Table 2.

Predicted fracture strengths (N) for the entire parametric series

		Bone mineral density
		−4%	−2%	Baseline	+2%	+4%
Cancellous	Axial	2576	2761	2752	2833	2929
	Off-axis	1401	1414	1448	1467	1716
Cortical	Axial	2754	2731	2752	2748	2718
	Off-axis	1346	1466	1448	1488	1527
All bone	Axial	2543	2522	2752	2881	2958
	Off-axis	1320	1389	1448	1515	1594

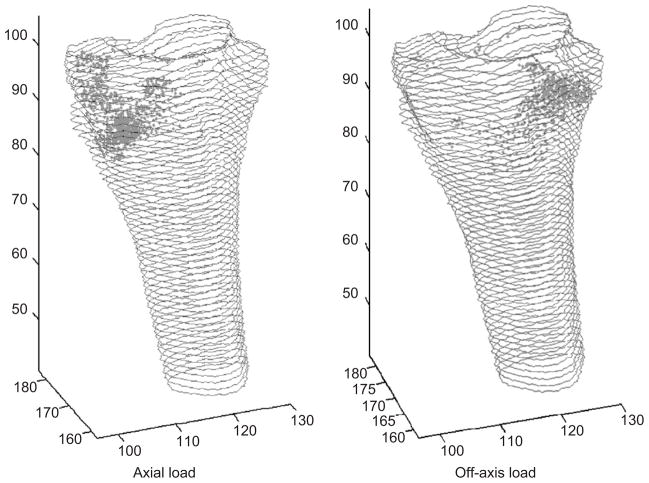
The fracture initiation site depended on the loading direction, but not upon changes in BMD. When an axial load was applied, failure occurred on the medial aspect of the ultradistal radius, directly proximal to the radial styloid process (Fig. 2, left). When an off-axis load was applied, failure first occurred on the dorsal aspect of the radius, directly proximal to where the lunate was located (Fig. 2, right). Loads with a significant dorsal component, such as those applied in the off-axis series, caused the scaphoid and lunate to shift towards the dorsal edge of the radial articular surface (Fig. 3). This motion, combined with the loading direction, led to increased compression of the dorsal surface of the radius compared to the volar surface. Additionally, tension of the volar ligaments connecting the scaphoid and lunate further contributed to the bending moment to which the radius was subjected.

Fig. 2.

Distribution of failed elements in the baseline cases at failure load of (a) axial series, (b) off-axis series.

Fig. 3.

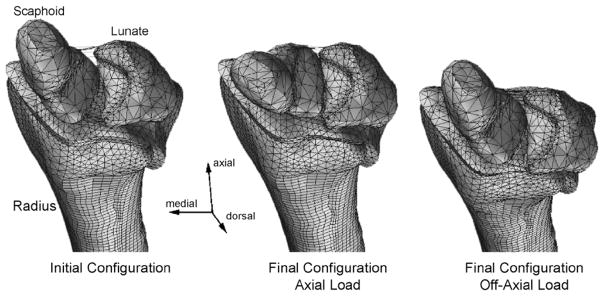
Radius, scaphoid, and lunate locations before (left) and after the axial (middle) and off-axis (right) loads.

4. Discussion

The questions we addressed in this study related to the dependence of predicted fracture load of the distal radius on loading direction and BMD. Based on the results we conclude that the direction of load applied to the radius has a strong influence on the fracture strength of the distal radius. The combination of bending and compression resulting from this off-axis load causes nearly a 50% decrease in the estimated strength of the radius. Because the majority of falls onto the hands probably result in offaxis peak loads (Reed-Troy and Grabiner, 2005), it is possible that estimates of the force required to initiate a fracture of the distal radius based on axial loading protocols may have been too large. Additionally, the apparent sensitivity of fracture strength to loading direction may partly explain why some falls result in fractures while others do not.

The magnitude of the predicted fracture loads we report, 1448–2830N, agrees well with the reported cadaveric fracture range of 1600–3400N (Augat et al., 1998; Muller et al., 2003; Pistoia et al., 2002). These studies each employed a different set of boundary conditions (loading direction and loading rate), many of which do not appear to have been based on experimental data. It is possible that differing boundary conditions in combination with biological variability may partially explain the wide range of fracture loads reported in the literature.

A noticeable effect of the off-axis loads was that the scaphoid and lunate shifted dorsally relative to the radius. As a result, the radius was compressed predominantly near the dorsal edge, the ligaments attached to the volar surface were loaded in tension, and the cancellous bone near the dorsal and lateral surface of the radius failed first. The model did not include active restraint of the carpal bones, such as would be provided through musculotendinous units. It is possible that during a fall, reflexive and/or voluntary co-activation of wrist flexors and extensors may further stabilize the carpal bones, reducing both the tension on the volar ligaments and the dorsal shift of the bones that occurred in the present simulation. If so, the model may have overestimated the degree to which such loads reduce the fracture strength of the radius. Stabilization of the wrist through muscular contraction may represent a viable means to reduce the effects of off-axis loading. Other possible ways to alter the radius loading patterns during a fall-related impact is by control of the upper extremities. Previous studies have shown that adjustments in landing kinematics, such as flexing the elbows, can reduce the peak impact force (DeGoede and Ashton-Miller, 2003). We have previously shown that changes in hand position relative to the body may influence the loading direction (Reed-Troy and Grabiner, 2005). If further confirmed, these landing strategies may represent a potential avenue for intervention.

Our model indicates that changes in BMD of 2–4% can modestly but meaningfully affect the predicted fracture load. Clinical evidence suggests that successful bisphosphonate therapy can reduce the incidence of hip fractures by up to 60% in severely osteoporotic individuals and to a substantially smaller extent in less osteoporotic patients (Masud and Giannini, 2003). Our results suggest that simply increasing BMD may not be sufficient to substantially increase fracture strength. However, the woman whose CT data were used to create the present model, though postmenopausal, had excellent BMD. The exact relationship between bisphosphonate-initiated increases in BMD and fracture risk is still not well understood (Watts et al., 2005). It has been suggested that bisphosphonates initiate changes in both bone density and in bone architecture (Day et al., 2004; Sato et al., 1996). Thus, it is possible that the present study underestimates the degree to which this type of intervention could influence fracture strength since continuum models cannot account for microstructural changes. Another possibility is that a majority of fractures occur due to forces that only barely exceed the fracture strength of the bone. In that case, even modest increases in bone strength such as those predicted in our model would contribute to the large reduction in fracture risk seen with clinical bisphosphonate use. A third possibility is that small increases in BMD may be sufficient to greatly improve fracture strength in severely osteoporotic individuals but not in people with reasonably healthy bones, in part because of the nonlinear relationship between BMD and failure stress.

Although anti-resorptive therapy may result in an overall increase in BMD, other methods may be more beneficial in improving fracture strength. For example, loading-initiated remodeling may both improve bone material properties (Beverly et al., 1989) and enhance bone architecture (Adami et al., 1999) to better resist applied forces. Local injections of growth factors have also been shown to initiate localized bone growth (Saito et al., 2003) and may significantly increase a bone’s fracture strength if appropriately placed. Determining which types of interventions may be most effective in improving fracture strength is an important future direction.

In summary, we have used a high resolution, three-dimensional contact finite element model to simulate impact forces on the distal radius and to predict fractures. From the present data we conclude that clinically achievable changes in BMD have a modest effect on fracture load. In contrast, loading direction appears to have a large effect on radius fracture load. Our model indicates that interventions to reduce the degree to which the wrist is loaded off axis may represent an avenue by which distal radius fractures can be prevented. Furthermore, reducing the degree to which the scaphoid and lunate shift dorsally relative to the radius during impact may help to increase the fracture load. Finally, enhancement of bone strength and/or architecture to specifically resist the types of loading seen during impact onto the hands, either through functional loading or pharmaceutical use, may reduce the likelihood of distal radius fracture in older women.