3D curvature of muscle fascicles in triceps surae

Abstract

Muscle fascicles curve along their length, with the curvatures occurring around regions of high intramuscular pressure, and are necessary for mechanical stability. Fascicles are typically considered to lie in fascicle planes that are the planes visualized during dissection or two-dimensional (2D) ultrasound scans. However, it has previously been predicted that fascicles must curve in three-dimensional (3D) and thus the fascicle planes may actually exist as 3D sheets. 3D fascicle curvatures have not been explored in human musculature. Furthermore, if the fascicles do not lie in 2D planes, then this has implications for architectural measures that are derived from 2D ultrasound scans. The purpose of this study was to quantify the 3D curvatures of the muscle fascicles and fascicle sheets within the triceps surae muscles and to test whether these curvatures varied among different contraction levels, muscle length, and regions within the muscle. Six male subjects were tested for three torque levels (0, 30, and 60% maximal voluntary contraction) and four ankle angles (−15, 0, 15, and 30° plantar flexion), and fascicles were imaged using 3D ultrasound techniques. The fascicle curvatures significantly increased at higher ankle torques and shorter muscle lengths. The fascicle sheet curvatures were of similar magnitude to the fascicle curvatures but did not vary between contractions. Fascicle curvatures were regionalized within each muscle with the curvature facing the deeper aponeuroses, and this indicates a greater intramuscular pressure in the deeper layers of muscles. Muscle architectural measures may be in error when using 2D images for complex geometries such as the soleus.

muscle fascicle curvature is an important architectural parameter related to the muscle function and is important to balance the pressures developed by the aponeuroses to maintain the mechanical stability of the muscle (20, 23, 32, 33). Muscle fascicles curve around regions of high intramuscular pressure and thus curve more at greater contraction levels (29–32, 35). Linear approximations of fascicles consider that their contribution to muscle force is the product of the fascicle force and the cosine of the angle of attachment to the aponeurosis (4, 27) and there would be no pressure differential across the fascicle. However, when the fascicles curve (31, 32), part of their tension contributes to the pressure development on the concave side of the curve (7).

Most experimental measures of fascicle properties have assumed the fascicles to be straight; both in animal studies where fascicles can be measured as the distance between sonomicrometry crystals implanted in the muscle (8, 14) and from noninvasive studies using ultrasound in humans where fascicles are commonly digitized by a point at their proximal and distal ends (12, 17, 22, 34). However, it has been known for many years that curved trajectories have a functional importance. Early work in axial muscle in fish suggested that the helical arrangement of the fast-twitch muscle fibers allowed them to shorten at a more uniform and slower velocity than if they were arranged parallel to the spine (2, 28), and it was subsequently shown that this allowed the muscle fibers to be used in a mechanically appropriate manner (2, 28).

Two-dimensional (2D) modeling studies of pennate muscle showed that muscle fascicles have to take on curved paths to establish mechanical stability within the muscle and also hinted that the curvature should extend into three dimensions (3D) (23, 31, 32). A number of studies have quantified curvature from 2D ultrasound images in humans (20, 21, 33, 35): it has been shown that 2D curvatures increase at higher contractile levels and shorter muscle lengths (19), and it has also been shown that fascicles can appear as S-shaped structures within these 2D images (20, 33). 2D ultrasound captures the muscle's architecture in the 2D scanning plane of the probe and cannot capture the 3D curving of the fascicles. Diffusion tension magnetic resonance imaging (DT-MRI) has been used to quantify the curvature values in passive tibialis anterior (5). A recent report on a MRI study showed that the fascicles within the cadaveric first dorsal interosseous followed a spiral trajectory (6, 10); however, the curvatures were not quantified in this study. 3D fascicles curvatures are an important feature of muscle structure but to date have not been quantified during active muscle contraction.

Fascicles curving in 3D may be contained in curved fascicle sheets rather than the 2D fascicle plane. Fascicle sheet curvature depends on the curvatures of the fascicles contained and the relative arrangement of the fascicles in the fascicle sheet. The relative arrangement of the fascicles may not change linearly with the fascicle curvature, making it important to quantify the fascicle sheet curvature independently from the fascicle curvature. The curved fascicle sheets have been reported in one study on the human vastus lateralis (29) but have not been quantified in the past.

The purpose of this study was to quantify 3D fascicle curvature across the whole muscle and fascicle sheet curvature in the transverse plane of the muscle at different muscle lengths and contractions levels.

METHODS

The curvatures of the fascicles and fascicle sheets were calculated from 3D grids of voxels (size 5 × 5 × 5 mm) obtained in previous studies, which contained information about the local fascicle orientation and fascicle sheet orientation (24–26).

Experimental design.

Triceps surae muscles of right leg were imaged from six male subjects (age 28.4 ± 6.2 yr, height 183.1 ± 8.9 cm, and mass 79.9 ± 20.1 kg; mean ± SD) during isometric plantarflexion contractions for a range of ankle angles (−15° dorsiflexion, 0, 15, and 30° plantarflexion) and torque levels [0, 30, and 60% maximum voluntary contraction (MVC)] at a fixed knee angle of 135°. A custom-made frame was used to perform the plantarflexion contractions in a water tank (24, 26). The frame had two parts, an adjustable foot plate to strap the right foot at a given fixed ankle angle and a leg support to support and strap the right thigh at a fixed knee angle throughout the experiment. The foot plate was connected to a strain gauge to obtain the ankle torque, and visual feedback for torque was provided to the subjects. The ankle torque data were collected at 2,000 Hz via a 16-bit A/D converter (USB-6210; National Instruments, Austin, TX) using a LabView software environment (National Instruments).

The scanning process was identical to that used in our previous studies (24, 26) with ultrasound images obtained using a linear ultrasound probe (Echoblaster; Telemed) recording at 20 Hz. The muscles of the lower leg were imaged using a sweeping motion of the ultrasound probe, and a grid was drawn over the skin surface before scanning to ensure the imaging of the whole lateral gastrocnemius (LG), medial gastrocnemius (MG), and soleus.

The scan times lasted for <2 min and resulted in ∼2,000 images. It is important to ensure uniform scanning of the muscle to generate reliable curvature maps in a short duration of time. It is difficult to maintain stable isometric torque levels for longer duration of times. The 2D information from the ultrasound images was combined with the 3D position and orientation of the ultrasound probe, obtained using an optical position sensor (Certus, Optotrak; NDI, Ontario, Canada) (26). Temporal synchronization of ultrasound images, torque data from the strain gauge, and position and orientation data from the optical sensor were achieved using a 5-V trigger signal generated by the ultrasound software (Echo Wave I; Telemed) at the start of the image acquisition.

Subjects gave their informed, written consent that followed the guidelines of, and was approved by, the Simon Fraser University's Office of Research Ethics policy on research using human subjects.

Determination of fascicle orientations and fascicle sheet orientations.

Images were processed using the methods described in our previous studies (24–26) to obtain the muscle fascicle orientation in 3D. In brief, 2D images obtained during the scanning process were filtered using multiscale vessel enhancement filtering followed by wavelet analysis to obtain the local 2D orientations of the muscle fascicles in each 2D ultrasound image (25). 2D orientations at every pixel in the image plane were combined with the 3D position and orientation of the ultrasound scanning plane to obtain the local 3D fascicle orientation corresponding to the respective pixels in 3D.

The muscle volume was divided into voxels of 5 × 5 × 5 mm³, and then a representative fascicle orientation was chosen for each voxel. The representative orientation in a voxel was obtained from the weighted mean of the orientations from all the pixels in that voxel (24, 26). The weights were based on the convolution values obtained from the wavelet analysis for a particular pixel and the distance of the pixel from the center of the voxel. The weight function for the convolution (w_c) and for the distance (w_d) were given by

$$w_{\text{c}}\left(x,y,z\right)=\text{Exp}\left\{-{\left[\frac{\text{conv}\left(x,y,z\right)}{{\text{conv}}_{\text{0}}}\right]}^2\right\}-1$$ (1)

$$w_{\text{d}}\left(x,y,z\right)=\text{Exp}\left\{-\left[{\left(x-x_0\right)}^2+{\left(y-y_0\right)}^2+{\left(z-z_0\right)}^2\right]/2{\sigma }^2\right\}$$ (2)

where conv is the convolution value at a particular pixel; conv₀ is the maximum convolution value over all the trials for a subject; {x, y, z} is the 3D location of the pixel center; {x₀, y₀, z₀} is the voxel center; and σ is the spread of an isotropic Gaussian distribution and was chosen to be 2.5 mm in this case (half-width of the isotropic voxel).

The orientations of fascicle sheets were represented by the normals to local regions within those sheets. Ultrasound images represent fascicle planes when the fascicles appear as long continuous curvilinear structures in an image (3, 13, 14, 16). An image with a continuous fascicular structure gives a high convolution number during the wavelet analysis (25). This quantity was used to select the fascicle plane orientation in each voxel (24, 26). Analogous to the fascicle orientation, the representative orientation for each voxel was obtained as the weighted mean of the orientation of the normals to the fascicle planes lying in that region, with the convolution value being the weighting factor.

Determination of muscle-based coordinate system.

Muscle architecture properties were represented in the muscle-based coordinate system (24) to compare between different trials and subjects. Three orthogonal axes x, y, and z were determined for the gastrocnemius muscles using eigenvalue decomposition of the points inside the muscle volume. The major axes correspond to the major anatomical axes of the muscle: the z-axis is the major (longitudinal) axis of the muscle, the y-axis lies across the width of the muscle (medial-lateral axis), and the x-axis lies across the depth (deep-superficial axis) of the muscle. The origin of the muscle coordinate system was set at the mean point in the muscle. Due to the semicylindrical shape of the soleus (1), a different coordinate system was used with its z-axis as the vector joining the mean coordinate of the knee joint centers with the mean coordinate of the distal muscle-tendon junction markers, the y-axis along the width of the muscle, and the x-axis along the depth of the muscle. The origin of the soleus was taken to be 60% of the total distance between the knee and the muscle tendon junction from the knee because this approximated the center of the muscle.

Determination of 3D fascicle curvature.

The trajectories of fascicle segments were tracked using the fiber assignment by continuous tracking (FACT) approach such that fascicle segments would be propagated on a continuous coordinate system (11, 18). Tracking started from the center p₀ of a particular voxel v₀ in the direction of the fascicle orientation at v₀ to obtain a point p₁ in voxel v₁ at a distance of 9 mm from p₀ (the point p₁ may not lie at the center of a voxel). At p₁, the tracking direction was changed to match the fascicle orientation in the voxel v₁ and the same procedure was repeated to obtain a third point p₂ in voxel v₂ (Fig. 1). These local trajectories were defined by the coordinates of the points p₀, p₁, and p₂ and were equivalent to 18 mm of length. The greatest distance between the centers of any two adjacent voxels was 8.67 mm, so the tracked segment length was chosen to be 9 mm to ensure that adjacent points were obtained in separate voxels. The voxel size was based on the size of the wavelets used to calculate the local orientations in the 2D image (25). Wavelet kernels were 39 × 39 pixels (equivalent to 6.09 × 6.09 mm); however, the intensity of the wavelets in the kernels fell to zero close to the edges (25), so the chosen voxel size of 5 × 5 × 5 mm was appropriate.

Fig. 1.

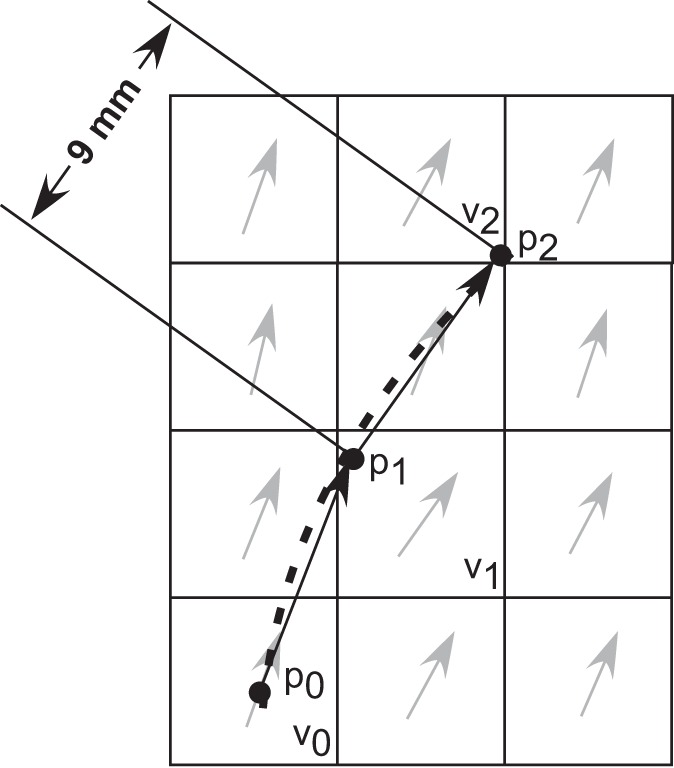
Two-dimensional (2D) representation of a tracked fascicle segment with the squares representing the voxels in the grid and arrows represent the fascicle orientation in the voxels. The tracking started at p_o in the orientation at v_o to obtain p₁ at a distance of 9 mm from p_o. p₂ Was obtained in the direction of orientation in v₁ and at a distance of 9 mm from p₁. The dotted line represents the 2nd degree fit function. The tracking was performed in a 3-dimensional (3D) grid, and the 2D drawing is for simplicity.

The coordinates of the points p₀, p₁, and p₂ were parameterized to create a second order parametric function in 3D, r(p). The curvature κ_c for the fascicle at the location p₁ in the middle of the tracked fascicle segment was calculated using the Frenet-Serret formula (30):

$${\kappa }_{\text{c}}\left(p\right)=\frac{\left|\dot{r}\left(p\right)\times \ddot{r}\left(p\right)\right|}{{\left|\dot{r}\left(p\right)\right|}^3}$$ (3)

where r(p) is a representation of the position vector of the fascicle trajectory in the Euclidean space as a function of pixel location [i.e., r(p) = {x(p), y(p), z(p)}] and ṙ(p) and $\ddot{r}\left(p\right)$ were the first and second derivatives of this function with respect to the arc-length parameter of the curve. The normal to the curve [N(p)] was obtained as

$$N\left(p\right)=\frac{\ddot{r}\left(p\right)}{\left|\dot{r}\left(p\right)\right|}$$ (4)

where N(p) is a 3D unit vector and was represented in spherical coordinates by its polar angle (β_c) and azimuthal angle (φ_c). β_c and φ_c show the direction where the concave side of the curve faces. β_c is the angle between N(p) and the long axis of the muscle, and φ_c is the angle in the cross-sectional plane of the muscle, relative to the medial-lateral axis of the muscle.

Intraclass correlation (ICC) was performed to assess the reliability of the results. For 1 trial a set of 602 ultrasound frames had originally been used to calculate the fascicle curvatures. Ten randomly selected subsets of images containing 552, 502, 452, 402, 352, 302, 252, 202, 152, and 102 images were additionally used to calculate the 3D curvatures. For each subset, the muscle voxel grid was constructed as for the original trial. The whole muscle volume was divided in 27 subregions with three equal divisions along the three axes of the muscle. The mean curvature was calculated in each region. The ICC coefficient was computed to compare all the subsets with the original set of 602 images using a crossed model (JMP Pro 10.00 Software, Cary, NC), with two factors, the image subset (as group) and the muscle region (as ID). The ICC coefficient was obtained for the group and the interaction between group and muscle region.

Determination of fascicle sheet curvature.

In 2D ultrasound and modeling studies, the fascicles are assumed to be arranged in planes (13, 15, 17, 19, 21–23, 31, 32). However, due to the shape of the muscle, the fascicles may not be arranged in planes, rather they may exist in curved sheets (29). The fascicle sheets are not anatomical features of the muscle but help to understand the arrangement of fascicles as a group in the muscle. The curvature of the fascicle sheet in the longitudinal plane of the muscle is reflected in the fascicle curvature. However, the curvature of the sheets in the transverse plane depends on the arrangement of the fascicles relative to each other rather than the fascicle curvature. To quantify this, the fascicle sheet curvature was obtained for a transverse plane through the muscle at the center of the belly (z = 0 in the muscle-based coordinate system). When a transverse section is taken through the muscle, it forms a 2D plane that intersects with the fascicle sheets. These intersections appear as lines in the plane (Fig. 2), with the lines being curved for curved fascicle sheets or straight for planar fascicle sheets.

Fig. 2.

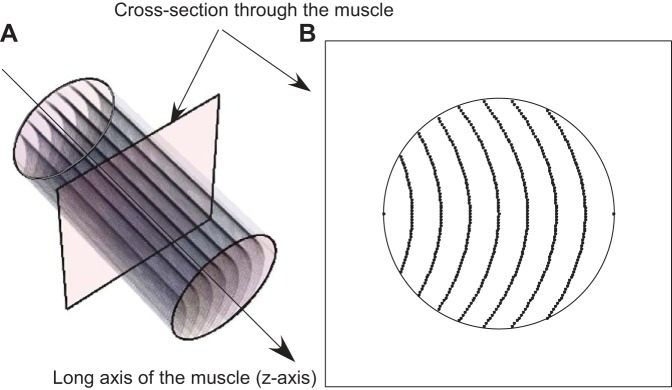
Schematic representation of curved fascicle sheets in a muscle (A) and a transverse plane containing edges of the fascicle sheets through the muscle (B).

The transverse plane through the muscle contained the position and orientation information of fascicle sheets contained in the local 3D voxels. However, there were not many voxels with their center location exactly lying on the z = 0 plane leading to insufficient points to track the boundaries of fascicle sheets. To resolve this problem, the orientation value at any point tracked (generally not at a voxel center) in the z = 0 plane was obtained as the weighted average of the orientations at the centers of neighboring voxels, with the weights (denoted w_d) chosen to be inversely proportional to the distance between voxel centers and the z = 0 plane. The Gaussian interpolation function used was same as Eq. 2, and the spread of the σ was chosen to be 0.7 mm.

The intersections of the fascicle sheets in the transverse plane (z = 0) were tracked using methods similar to those described for determining the fascicle sheet curvature. The edges of fascicle sheets were not long enough to obtain a considerable number of segments obtained by three-point tracking (as for fascicles) and were tracked until the aponeurosis was reached. The tracked points were obtained at a distance of 5 mm from the initial point in the direction of the local fascicle plane orientation at the initial point. The local orientation at each subsequent point was calculated as the weighted average of the orientation of neighboring voxels. To quantify the curvature of the fascicle sheets, seed points were selected halfway along the depth of the muscle (x = 0) and fascicle sheet intersections were tracked in both directions from the seed point towards the aponeuroses and the value of the curvature was reported at the middle of the tracked fascicle sheet. The magnitude and direction of the curvatures were calculated by using the Frenet-Serret formula. Since these measurements were made in 2D in the transverse plane, the fascicle sheet curvature was reported by its magnitude (κ_fsc) and azimuthal angle of the normal to the curve (φ_fsc). The azimuthal angle was calculated relative to the x-axis of the muscle-based coordinate system, i.e., the deep-superficial axis of the muscle.

Statistical analysis.

A least square model ANOVA was used to tests the effect of muscle region, ankle angle, and torque on the fascicle curvatures and fascicle sheet curvatures. Each muscle was divided into the following region to test the regionalization of the fascicle curvatures: three along the length of the muscle (z-axis): proximal, central, and distal; two along the depth of the muscle (x-axis): deep and superficial; and two along the width of the muscle (y-axis): medial and lateral (24). Fascicle curvatures and the polar and azimuthal angles of their normals were the dependent variables, and subject identity, muscle region (described in terms of length, depth and width of the muscle), ankle angle, and torque were independent variables. Subject identity was set as a nominal random factor and all other independent variables as ordinal fixed factors.

Fascicle sheet curvatures were obtained for the transverse plane at z = 0, and the transverse plane was divided into medial and lateral regions to test the regional differences in fascicle sheet curvature. Fascicle sheet curvature and azimuthal angle were the dependent variables, and subject identity (random), muscle region, ankle angle, and torque were factors. Subject identity was assigned random variable and all other independent variables as the fixed factors.

RESULTS

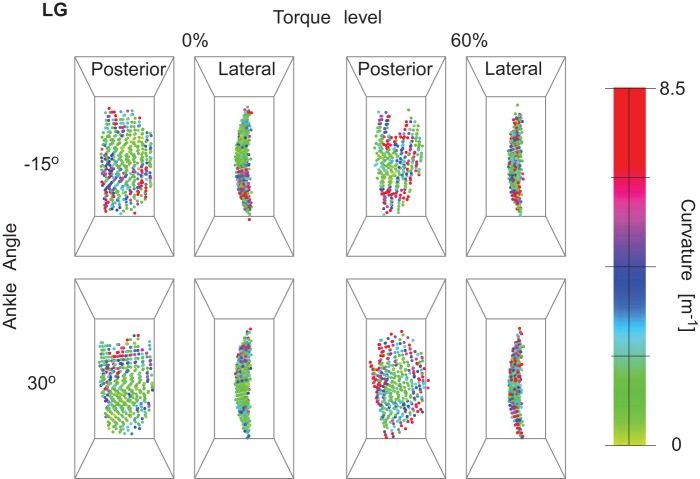
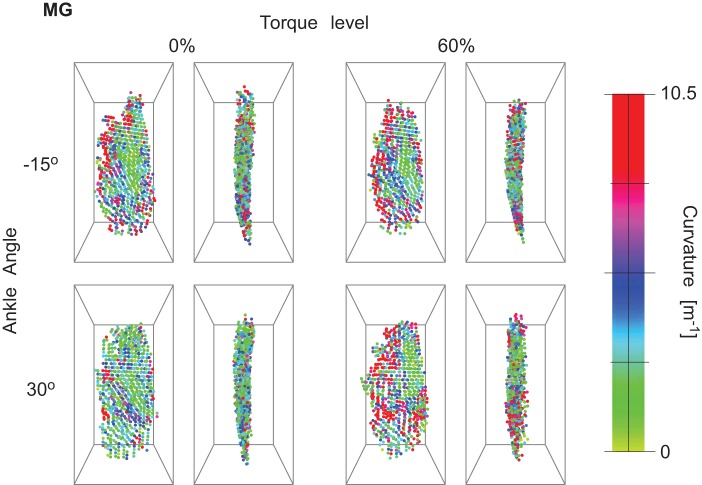
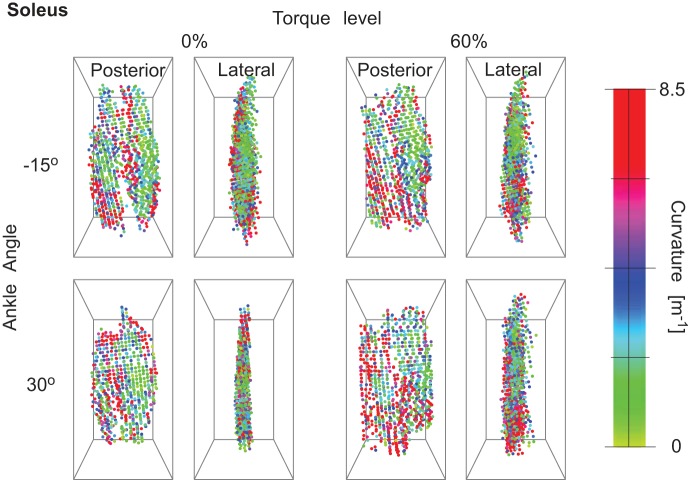
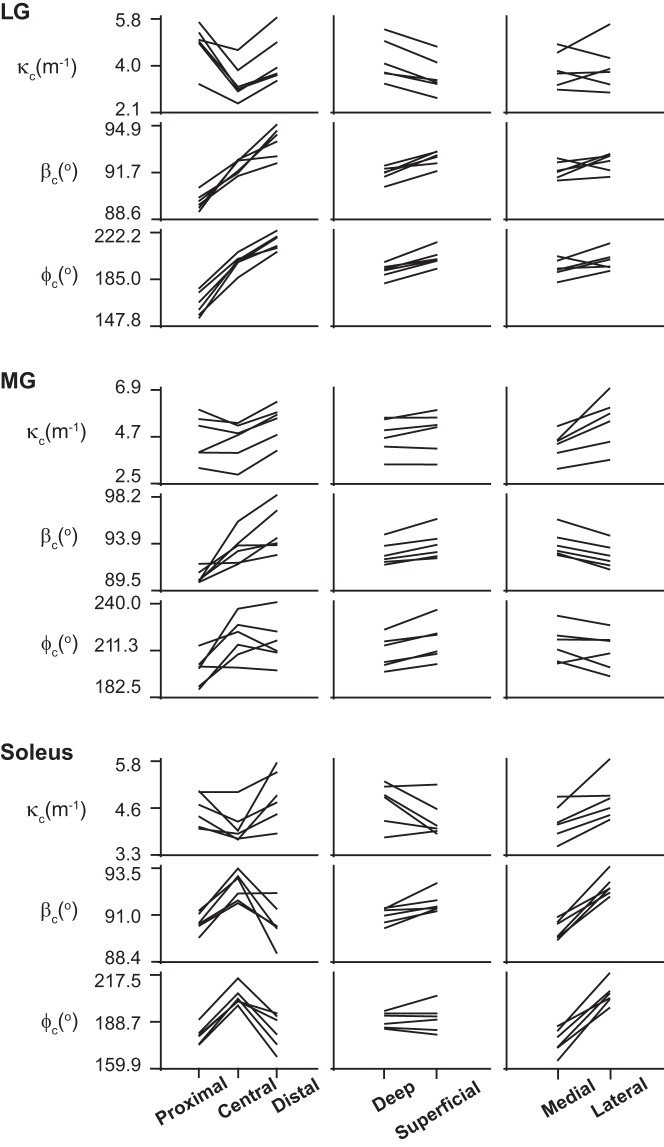
The fascicle curvatures and fascicle sheet curvatures were obtained for the triceps surae muscles at different ankle torques and ankle angles. Figures 3, 4, and 5 show the 3D grid from representative subjects from different viewpoints for the extreme ankle angles and torques used in the experiment. The figures show the regionalization of both magnitude and direction of the curvature in the three muscles along with these values depending on ankle torque and ankle angle. Fascicle curvatures were distributed nonuniformly in each of the three muscles (Fig. 6). The regional variations in β_c were small compared with those in variations in φ_c in all the three muscles. The β_c values were close to 90° indicating that the normals to the fascicle curves were nearly perpendicular to the long axis of the muscle.

Fig. 3.

Curvature magnitude in lateral gastrocnemius (LG) from posterior and lateral views for 1 representative subject. The images show the regionalization of curvature in the muscle and the change with torque and ankle angle.

Fig. 4.

Curvature magnitude in medial gastrocnemius (MG) from posterior and lateral views for 1 representative subject. The images show the regionalization of curvature in the muscle and the change with torque and ankle angle.

Fig. 5.

Curvature magnitude in soleus from posterior and lateral views for 1 representative subject. The images show the regionalization of curvature in the muscle and the change with torque and ankle angle.

Fig. 6.

Curvature magnitude and orientation in LG, MG, and soleus in all 6 participants in different regions of muscles. κ_c, fascicle curvature magnitude; β_c, direction of normal to curve in terms of polar angle; φ_c, direction of normal to curve in terms of azimuthal angle.

The mean (SD) values of the fascicle curvatures and fascicle sheet curvatures were obtained across six participants (see Tables 2 and 3).

Table 2.

Effect of ankle torque and ankle angle on muscle fascicle curvature

	κc, m−1			βc,°			φc,°
	0%	30%	60%	0%	30%	60%	0%	30%	60%
LG
−15°	2.92 (0.28)	3.78 (1.63)	3.66 (1.18)	93.24 (1.25)	90.75 (2.52)	91.19 (2.29)	206.41 (22.74)	196.1 (14.98)	182.66 (27.69)
0°	3.56 (0.91)	2.59 (0.45)	3.03 (0.63)	91.79 (2.68)	93.62 (2.2)	92.77 (2.62)	198.33 (28.28)	214.74 (7.62)	188.51 (19.7)
15°	3.38 (0.86)	3.67 (1.48)	3.19 (1.22)	92.25 (1.35)	92.45 (1.36)	93.27 (1.35)	209.16 (12.88)	190.62 (27.3)	215.67 (22.58)
30°	3.08 (0.63)	3.01 (1.36)	3.58 (1.27)	90.68 (1.29)	90.83 (2.88)	91.89 (2.66)	182.46 (23.64)	185.42 (29.05)	200.34 (26.11)
MG
−15°	4.53 (0.86)	4.04 (1.37)	4.51 (1.02)	92.83 (3.93)	93.51 (1.99)	93.21 (1.44)	213.44 (31.3)	215.27 (19.71)	205.26 (24.93)
0°	4.15 (0.77)	4.28 (1.28)	4.08 (0.63)	93.4 (1.89)	92.69 (2.18)	93.89 (2.2)	226.27 (28.61)	215.11 (14.43)	223.77 (19.85)
15°	4.55 (1.11)	4.42 (1.15)	5.38 (2.32)	92.76 (1.86)	93.24 (2.59)	93.58 (2.53)	215.6 (23.8)	231.59 (14.27)	210.64 (25.15)
30°	4.39 (1.21)	4.29 (1.54)	5.17 (1.63)	93.85 (2.25)	93.15 (2.68)	94.09 (2.05)	221.08 (16.88)	217.77 (21.5)	217.03 (26.9)
Soleus
−15°	4.48 (1.08)	4.21 (0.62)	4.25 (0.52)	93.58 (2.08)	93.24 (1.93)	92.92 (1.55)	215.03 (16.88)	209.35 (14.27)	202.29 (9.4)
0°	3.93 (0.39)	3.3 (0.6)	4.11 (1.19)	92.82 (2.06)	91.63 (1.61)	92.04 (1.5)	207.86 (13.96)	198.01 (13.42)	198.04 (17.2)
15°	4.34 (1.3)	3.81 (0.42)	4.21 (0.67)	92.65 (0.88)	93.95 (3.27)	92.72 (1.7)	206.39 (11.04)	215.54 (28.17)	213.23 (18.26)
30°	3.38 (0.94)	4.06 (0.74)	4.78 (1.22)	91.33 (1.15)	90.05 (2.92)	91.25 (1.15)	193.95 (16.62)	192.04 (19.2)	194.69 (13.06)

Values reported are mean (SD; n = 6 participants) of fascicle curvature magnitude (κ_c) and direction of normal to curve in terms of polar angle (β_c) and azimuthal angle (φ_c) from the central region of the muscle. LG, lateral gastrocnemius; MG, medial gastrocnemius.

Table 3.

Effect of region, ankle angle, and force on fascicle sheet curvature

	LG		MG		Soleus
	κfsc, m−1	βfsc,°	κfsc, m−1	βfsc,°	κfsc, m−1	βfsc,°
Medial	2.09 (0.80)	86.64 (2.30)	7.72 (2.18)	102.41 (7.64)	5.5 (3.07)	84.76 (4.39)
Lateral	3.54 (1.05)	88.39 (3.58)	3.64 (0.67)	105.00 (5.10)	7.25 (4.93)	92.61 (6.84)
−15°	2.50 (0.83)	86.11 (2.11)	5.23 (1.26)	110.52 (9.70)	6.74 (8.05)	90.73 (3.00)
0°	2.18 (0.67)	88.79 (2.24)	5.08 (1.21)	101.8 (13.10)	5.63 (3.72)	89.64 (4.46)
15°	2.78 (1.26)	87.71 (3.08)	6.01 (1.89)	101.31 (11.28)	6.39 (5.20)	88.63 (4.25)
30°	3.44 (1.12)	86.98 (4.81)	6.50 (0.99)	100.63 (5.10)	7.24 (9.52)	89.29 (7.86)
0%	2.72 (0.58)	88.88 (1.74)	5.54 (1.05)	105.35 (9.44)	6.05 (4.70)	89.56 (5.39)
30%	2.88 (0.74)	87.37 (2.54)	5.87 (1.13)	98.41 (6.04)	4.23 (2.39)	88.00 (9.57)
60%	2.57 (0.90)	86.34 (1.34)	5.75 (1.73)	107.53 (8.01)	9.65 (9.79)	91.26 (4.06)

Values reported are mean (SD; n = 6 participants values of fascicle sheet curvature magnitude (κ_fsc) and azimuthal angle (φ_fsc).

Fascicle curvature.

The results from reliability analysis for fascicle curvature using ICC analysis are shown in Table 1. The ICC coefficient without interaction terms was 1 for all the subsets; the ICC coefficient with interaction was >0.7 for image groups containing 352 images or more, indicating the reliability over subsampling of the images. The interaction between the muscle region and groups is because the voxels on the extreme ends of the muscle will be more susceptible to the subsampling of images.

Table 1.

ICC analysis for reliability of curvature magnitudes

Number of Images	ICC Without Interaction	ICC with Interactions
102	1	0.48
152	1	0.51
202	1	0.66
252	1	0.46
302	1	0.66
352	1	0.73
402	1	0.76
452	1	0.95
502	1	0.85
552	1	0.96

The intraclass correlation (ICC) values were obtained by performing a correlation analysis between the original set of 602 images and randomly subsampled set of images.

In LG, there was a significant effect (P < 0.01) of the ankle angle, torque level, and muscle region along the length and depth on κ_c, but there was no significant effect of the muscle depth. There was significant effect (P < 0.01) of ankle angle and all muscle regions on both β_c and φ_c, but the effect of torque level was not significant. The largest regional variations in curvature magnitude were along the length of the muscles and had a lower κ_c (3.50 m⁻¹) in the central region than the proximal (4.81 m⁻¹) and distal ends (4.34 m⁻¹). The φ_c values show that the curves were facing the medial side in the proximal (φ_c <180°) LG and the lateral side (φ_c >180°) in the distal LG (Table 2).

In MG, there was a significant effect (P < 0.01) of ankle angle, torque level, and muscle region along length, depth, and width on κ_c, β_c, and φ_c. In MG, the largest variations in κ_c were along the length and width of the muscle. κ_c increased from the medial to the lateral sides from 3.93 to 4.99 m⁻¹ and increased from proximal end (3.93 m⁻¹) to the distal end (4.66 m⁻¹) of muscle. φ_c was >180° across the whole muscle indicating that the curves were facing the lateral side (Table 2).

In soleus, there was a significant effect (P < 0.01) of ankle angle, torque level, and muscle region along length, depth, and width on κ_c and φ_c. There was a significant effect of ankle angle and muscle level on β_c, but the effect of torque level was not significant. In soleus, the largest variations in κ_c were along the length of the muscle. κ_c decreased slightly from the proximal end (4.60 m⁻¹) to the central region (4.26 m⁻¹) followed by an increase (4.50 m⁻¹) in the distal end of the muscle. The largest variations in φ_c were along the width of the muscle with 174.31° in the lateral side and 204.15° in the medial side, indicating that the curves were facing the medial side in the lateral side of the soleus and facing the lateral side in the medial side of the soleus (Table 2).

The curvatures increased with increase in ankle torque in all three muscles (Table 3). The general trend for ankle angles across the three muscles was a decrease in the κ_c with increase in ankle angle from −15 to 0° followed by an increase in κ_c at greater ankle angles (Table 3). β_c changed significantly but with very small magnitude (<1° in each muscle). The changes in φ_c with change in ankle angle and torque were small compared with that obtained across the muscle regions (Tables 2–3).

Fascicle sheet curvature.

The fascicle sheet curvatures were represented by curvature magnitude (κ_fsc) and direction (φ_fsc). There was a significant effect of muscle region and ankle angle on fascicle sheet curvatures (κ_fsc) in all three muscles. However, the effect of ankle torque was not significant.

In LG there was significant effect (P < 0.05) of muscle region and ankle angle on κ_fsc, but the torque level did not have a significant effect. There was a significant effect of muscle region on the φ_fsc but no effect of ankle angle and torque level. κ_fsc increased from the medial to the lateral side and increased with increase in ankle angle (Table 3). In MG, there was a significant effect (P < 0.05) of muscle region and ankle angle on κ_fsc, but the torque level did not have a significant effect. There was a significant effect (P < 0.05) of ankle angle and torque level on φ_fsc, but the effect of muscle region was not significant. κ_fsc decreased from the medial to the lateral side and increased with increase in ankle angle (Table 3). In soleus, the effect of ankle angle, torque level, and muscle region was not significant on κ_fsc. Muscle region had a significant effect on φ_fsc, but the effect of ankle angle and toque level was not significant.

DISCUSSION

This is the first time that the 3D fascicle curvatures and fascicle sheet curvatures have been quantified in a muscle contracting at different muscle lengths and torques. The ICC analysis performed over subsampled images confirmed reliability of the curvature magnitudes (Table 1). As indicated in the results for the ICC analysis, it is crucial to obtain a relatively dense set of ultrasound scans from the muscle volume to obtain reliable curvature values. Previous studies have quantified fascicle curvatures using manual (20) and automated methods (21, 33) in 2D with the values ranging from 0.5 m⁻¹ at rest up to 20 m⁻¹ during MVC. The curvature values reported in this study lie in the range of previously reported values.

The methods used to determine the 3D curvature in this study are similar to the ones used in our 2D study (21); however, these 3D curvatures are smaller than those reported for the 2D studies (21, 33). This difference occurs for a number of reasons: the 2D studies contracted to greater levels of effort (100% MVC) where greater intramuscular pressure and fascicle curvatures would be expected and, additionally, used externally applied compressive bandages that again increase the intramuscular pressure. Furthermore, the greatest curvatures reported from the 2D studies were measured from the superficial and deep layers of the muscle. The methods used for this 3D study involved 18-mm segments for the feature tracking. This 18-mm segment length was based on the voxel size (5 × 5 × 5 mm) in the 3D voxel grids, and the segment was extended between points that occurred in different voxels. The voxel size was, in turn, based on the wavelet kernel size (39 × 39 pixels equivalent to 6 × 6 mm) as described in our previous articles (25, 26). By contrast, the 2D studies (21, 33) were able to use shorter (7 mm) segment lengths for the feature tracking, based on the same 2D wavelet kernels, and so could determine fascicle curvatures closer to the aponeuroses where the curvatures were greatest (21, 33).

The resting curvature values from MG reported here (mean 4.15 ± 0.77 m⁻¹) are greater than those reported in a previous study that used manual digitization methods (mean 0.53 m⁻¹; Ref. 20). This may be because this previous study determined the curvature for one fascicle in each image and assumed a uniform curvature across the fascicle; however, our results show that the curvatures are regionalized in the muscles (Fig. 6 and Table 2). Manual methods calculate the curvatures from the middle of the muscles (20) where the curvatures are less than in the superficial and deep regions of the muscle (21, 33).

Fascicle curvature and intramuscular pressure.

Fascicle curvatures were regionalized in each of the three muscles and changed with muscle length and torque. In LG and soleus, the curvatures were lowest in the central region of the muscle with greater curvatures values at the peripheral ends while in MG the curvatures gradually increased from the proximal to the distal end of the muscle (Fig. 6 and Table 2). Intramuscular pressure depends on the fascicle curvature and tensile forces in the muscle fascicles. A curved fascicle generates a pressure difference between the convex and concave side with the pressure being greater on the concave side and the magnitude of the pressure differential increasing with the increase in the curvature (9, 31). Thus the fascicle curvature can be used to predict the changes in intramuscular pressure between different contraction states and the distribution of intramuscular pressure in a muscle.

Fascicle curvatures increase with increased contraction from 0 to 60% MVC (Table 3), indicating an increase in intramuscular pressure at greater contraction levels (29, 31). The orientations of the normals to the fascicle curves indicate a greater intramuscular pressure in the deeper regions of muscles, and this supports previous modeling studies (31, 32). There were no distinct medial-lateral differences in the orientation of the normals to the fascicle curves in the gastrocnemii muscles. By contrast, the soleus had the curves facing the midline sagittal plane of the muscle, leading to a region of greater intramuscular pressure. This greater intramuscular pressure may be around the median septum in soleus, dividing it into medial and lateral regions (1).

In LG, the concave side of the fascicles primarily faces the deep aponeurosis across the whole muscle resulting in a build up of pressure in the deeper regions of the muscle. Furthermore, the fascicle curvatures face the distal-medial region in the proximal region of the muscle and distal-lateral region in the central and distal regions, indicating higher intramuscular pressures towards the medial side in the proximal end and the lateral side in the distal end of the muscle. In MG, the concave side of the fascicles face the deep-lateral region of the muscle leading to a build of pressure in the deep-lateral corner of the muscle. In soleus, the concave sides of the fascicles face the deep-medial side in the lateral region of the muscle and the deep-lateral side in the medial region of the muscle, signifying the intramuscular greatest pressure in the deep-middle region of the muscle. Thus the results from this experimental study predict the greatest intramuscular pressures in the deeper layers of the triceps surae, and this supports predictions from 2D modeling studies (31, 32). The soleus has bipennate features with a median septum dividing it into medial and lateral regions (1). Modeling studies have predicted that bipennate muscles would have the greatest pressure around the central tendon of the muscle (31), and this supports our predictions of greater pressure in the middle region of the soleus.

Fascicle sheet curvature.

The fascicle sheets were curved, and the curvatures of the fascicle sheets in the transverse plane face the medial side of the muscle (values close to 90°; Table 3). There was a small increase in the fascicle curvatures with the increase in torque but this was not observed in the fascicle sheet curvatures. The increase in curvature of the fascicle sheets in the transverse plane indicates a change in the relative arrangement of the fascicles with increases in contraction level. The triceps surae muscles surround deeper muscles and bones that may constrain the increase in the fascicle sheet curvatures. The curved nature of the fascicle sheets that we have observed can alter the perceived values of fascicle curvatures that would be calculated in 2D studies.

Comparison with the 2D study on curvatures.

In 2D architectural studies, the curvatures can only be considered in the longitudinal plane of the muscle; however, it has been suggested in that in long muscles the curvatures are expected to be relatively small in the longitudinal plane but larger in the transverse planes (31). This 3D study has enabled us to detect details in the fascicle curvature that were not detectable from our previous 2D studies (33) and thus allows us to make more detailed interpretations of the results. S-shaped fascicles were reported from the 2D studies (33) with a positive curvature at the superficial regions (concave side facing the deep aponeurosis), negative curvature in the deep region (concave side facing the superficial aponeurosis), and relatively straight fascicles in the middle region of the muscle. If such S-shaped fascicles were curved in 3D, this would be reflected in the values of φ_c spanning different quadrants between the deep and superficial regions, but this was not the case (Table 2).

This difference from the 2D study can be explained by considering curved fascicles lying on a curved sheet as was found in this study. A 2D ultrasound image represents a section of a 3D entity in a 2D plane, and the local orientation of the 3D entity in the image plane is the orientation of the projection of the 3D entity in the 2D plane (24). To visualize this phenomenon, a curved line can be considered on a curved surface (Fig. 7) and viewed from different projection angles to compare with the 2D images (Fig. 8). In this case, only one fascicle was projected from different angles whereas in an actual image different regions of the image will contain projections of fascicles from different regions of the muscle.

Fig. 7.

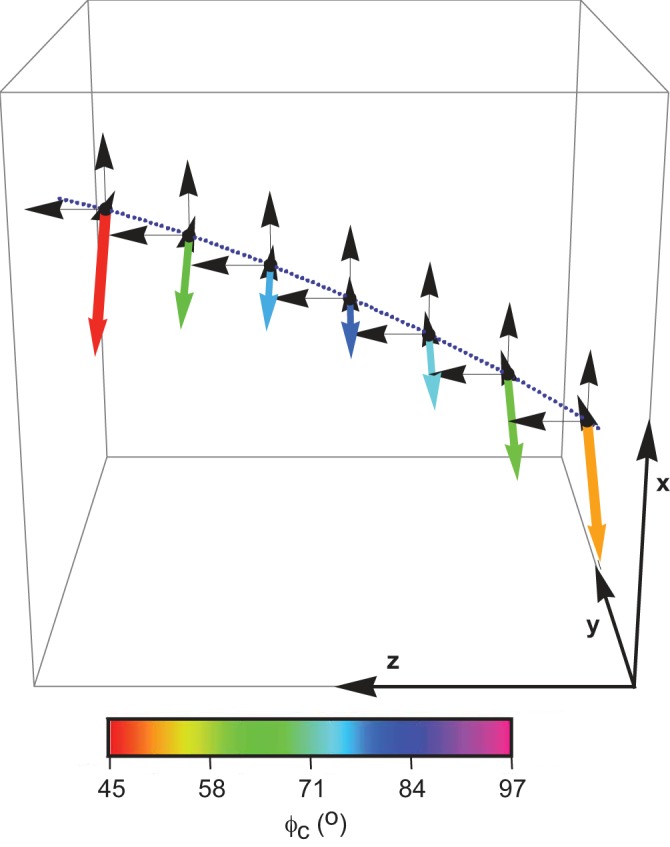
Schematic representation of the fascicle curvature in 3D. The path of the fascicle is shown by the blue dotted line. The curvature was represented by magnitude (represented by length of arrow) and azimuthal angle (represented by color of arrow). Polar angle (β_c) was constant in this case at 90°.

Fig. 8.

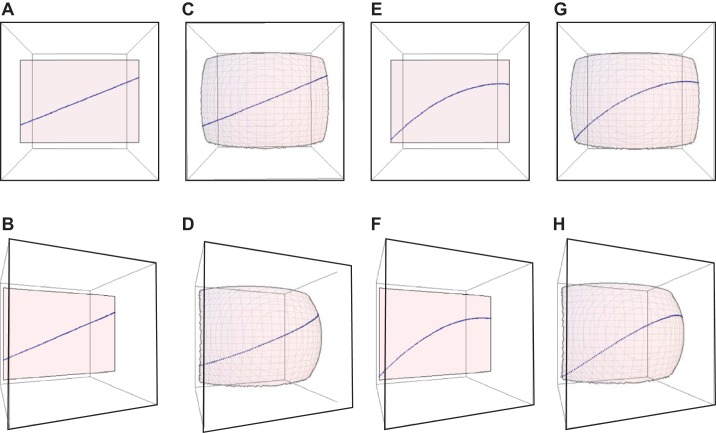
Visualization of a simulated straight fascicle on a planar sheet (A and B), a straight fascicle on a curved sheet (C and D), a curved fascicle on a planar sheet (E and F), and a curved fascicle on a curved sheet (G and H). Top row: representation of the front view. Bottom row: representation of a viewpoint rotated at an angle of 30°. The mean fascicle angle was 25° relative to the z-axis and mean curvature of 10 m⁻¹ for E–H, and fascicle sheet curvature was 15 m⁻¹ for C, D, G, and H and 0 m⁻¹ for A, B, E, and F.

Figure 8, A–H, was drawn for slightly exaggerated curvatures than the values obtained in this study to enhance the visualization and clearly demonstrates that the existence of curved fascicle sheets changes the perceived curvature of the fascicles based on the viewpoints of the muscle (Fig. 8). The viewpoints were changed to replicate the effect of rotating an ultrasound probe over the leg surface as is typically done to get a good muscle image (13, 17). Different curvatures would be visualized for a straight fascicle on a curved sheet from a rotated viewpoint compared with the front view (Fig. 8, C and D), and S-shaped fascicle projections can be visualized for a curved fascicle on a curved sheet (Fig. 8, G and H). Furthermore, the 2D study (33) reported an increase in the S shape of the fascicles at higher muscle forces; this may be attributed to the increasing curvature of the fascicles with increases in torque as seen in this study. The fascicles appear S shaped for curved fascicles from a rotated viewpoint but not for straight fascicles (Fig. 8, D and H). It should be considered that the curved fascicle sheets do not lie in a single plane, and hence, the ultrasound probe has to be aligned at different angles to obtain a good image of the fascicles: these different alignments would change the perceived values of curvature obtained in a 2D study. A 2D scan cannot capture the fascicle curvature due to the curved fascicle sheets, and hence, 2D measurement errors would be greater in muscles with higher values of fascicle sheet curvature.

Conclusions.

In conclusion, this study quantified the 3D fascicle curvature and fascicle sheet curvature in the triceps surae. Changes in the curvature agree with the changes in intramuscular pressure reported in the past studies. The fascicles are arranged in nonplanar sheets in the muscle. The 3D nature of the fascicle curvatures may affect the curvatures reported from 2D studies. The 3D fascicle curvatures and fascicle sheet curvatures are important parameters to understand the pressure development in the muscle that in turn affects the net function of the muscle and parameters involved in 3D muscle modeling.

GRANTS

This publication was supported by the National Sciences and Engineering Research Council of Canada and the National Center for Medical Rehabilitation Research of National Institute of Child Health and Human Development Grant T32-HD-064578. Its publications are solely the responsibility of the authors and do not necessarily represent the official views of the National Institutes of Health.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: M.R. and J.M.W. conception and design of research; M.R. performed experiments; M.R. analyzed data; M.R., G.H., and J.M.W. interpreted results of experiments; M.R., G.H., and J.M.W. prepared figures; M.R. and J.M.W. drafted manuscript; M.R., G.H., and J.M.W. edited and revised manuscript; M.R., G.H., and J.M.W. approved final version of manuscript.