Afferent inputs to cortical fast-spiking interneurons organize pyramidal cell network oscillations at high-gamma frequencies (60–200 Hz)

Abstract

High-gamma activity, ranging in frequency between ∼60 Hz and 200 Hz, has been observed in local field potential, electrocorticography, EEG and magnetoencephalography signals during cortical activation, in a variety of functional brain systems. The origin of these signals is yet unknown. Using computational modeling, we show that a cortical network model receiving thalamic input generates high-gamma responses comparable to those observed in local field potential recorded in monkey somatosensory cortex during vibrotactile stimulation. These high-gamma oscillations appear to be mediated mostly by an excited population of inhibitory fast-spiking interneurons firing at high-gamma frequencies and pacing excitatory regular-spiking pyramidal cells, which fire at lower rates but in phase with the population rhythm. The physiological correlates of high-gamma activity, in this model of local cortical circuits, appear to be similar to those proposed for hippocampal ripples generated by subsets of interneurons that regulate the discharge of principal cells.

there is abundant experimental evidence that functional activation of cortex is associated with increased EEG activity at frequencies in the so-called high-gamma range (60–200 Hz), and that non-phase-locked power augmentation in this frequency range can serve as a general-purpose index of task-related cortical processing (Crone et al. 2011). In human intracranial EEG, these responses have been observed in a variety of functional brain systems, including motor, somatosensory, auditory, visual, language, default mode network and memory systems (Crone et al. 2011; Lachaux et al. 2012). Additionally, responses with the same or very similar spectral features have also been observed in humans with magnetoencephalography (MEG) (e.g., Kaiser and Lutzenberger 2005) and even with scalp EEG (e.g., Darvas et al. 2010). At the other end of the spatial scale, recent animal studies have confirmed the presence of high-gamma responses in local field potential (LFP) recordings similar to those observed in human intracranial EEG (Belitski et al. 2008; Grenier et al. 2001; Liu and Newsome 2006; Ray et al. 2008a, 2008b; Ray and Maunsell 2011).

Despite the apparent ubiquity of high-gamma EEG responses and their practical utility for functional mapping and cognitive neurophysiology in humans, little is known about their neurophysiological bases. Recent studies (Ray et al. 2008a, 2008b) attempted to shed some light on this. The authors recorded single-unit and LFP activity from monkey somatosensory cortex while presenting vibrotactile stimulation to the finger. Time-frequency analysis of the LFP signals showed an increase in high-gamma power following stimulus onset. To further investigate the origin of high-gamma responses, a model of electrocorticography (ECoG) generators was postulated (Ray et al. 2008b). In that model, high-gamma power resulted from the temporal summation of sharp extracellular action potential waveforms having broadband power. However, it is traditionally assumed that LFP and ECoG activity mainly reflects synaptic potentials (Logothetis 2003; Mitzdorf 1985; Pesaran 2009). The contribution of different neuronal currents to high-frequency LFP has been investigated both in computer models and in vitro. Using detailed biophysical modelling, Schomburg et al. (2012) estimated that, during ripple oscillations in rat CA1, action potential currents contribute about 50% of the LFP signal power in the 140- to 200-Hz band. However, in vitro experimental studies have implicated synaptic currents rather than action potential currents as sources for LFP signals. Oren et al. (2010) investigated the current sources underlying cholinergically induced gamma LFP oscillations (30–100 Hz) in CA3 in vitro. Their conclusion was that the major contribution to LFP signals comes from pyramidal (PY) cell inhibitory postsynaptic currents (IPSCs), while action potential currents made a relatively small (<10%) contribution to the LFP. Similarly, Trevelyan (2009) observed a strong correspondence between IPSCs in PY cells and extracellular high frequency oscillations (80–500 Hz) in cortical slices. Based on significant cross-correlograms of the IPSCs vs. the extracellular signal, he concluded that PY cell IPSCs were the primary sources of high-frequency oscillations. Although action potential currents may contribute to LFP signals recorded from intracortical microelectrodes, they are much less likely to make any direct contribution to ECoG signals, or to EEG or MEG signals (Avitan et al. 2009; Nunez 1981; Schaul 1998). The mechanisms of most widespread neuroscientific interest and importance are arguably those that are responsible for high-gamma activity observed at all of these scales.

Another important, yet unanswered, question is what determines the frequency characteristics of high-gamma responses? A remarkable feature of these responses is their broadband spectral profiles, which have raised additional questions regarding their origin (Crone et al. 2011).

The aim of this study was to investigate the basic mechanisms generating high-gamma responses using a biologically based model of cortical networks. Many of the features of this model were designed to approximate the electrophysiological responses observed by Ray et al. (2008a, 2008b). Using this model, we show that a broadband high-gamma response to sensory activation of cortex is generated by a network-based mechanism mediated by the excited population of inhibitory (I) fast-spiking interneurons firing at high-gamma frequencies under strong excitatory input with a Poisson distribution in time.

MATERIALS AND METHODS

Experimental Data

Neural activity was recorded from SII cortex in two macaque monkeys (Macaca mulatta, one female, 4–6 kg) using platinum-iridium extracellular microelectrodes. A sinusoidal stimulus was delivered perpendicular to the skin surface through a probe on the distal pad of the second or third digits (D2 or D3) or on the palm by a vibratory stimulator. The stimulus was presented for 1 s, with an interstimulus interval of 1.2 s. Three different stimulus frequencies (50, 100, and 200 Hz) and four different amplitudes (in the ratio 1:2:5:10 and denoted by G1, G2, G5, and G10) were used, with 50 trials per frequency and amplitude combination. Stimuli were presented in pseudorandom order. Recorded signals were amplified and divided into two streams for the collection of LFP and spikes, respectively. One stream of the incoming signal was amplified (100×) and filtered (0.3–300 Hz, 6 dB/octave) and then sampled at 5 kHz. The second input stream was band-pass filtered (500–1,000 Hz) and amplified (10 to 100×), and spikes were isolated using a window amplitude discriminator. Only neurons for which the action potentials were well isolated from noise were selected for analysis. Detailed experimental procedure and analysis results are presented in Ray et al. (2008b). The experimental data presented in this study were obtained for vibrotactile stimulus frequency 50 Hz and have been kindly provided by Supratim Ray. All procedures and experimental protocols complied with the guidelines of the Johns Hopkins University Animal Care and Use Committee, which approved this study, and the National Institutes of Health Guide for the Care and Use of Laboratory Animals.

Time-Frequency Analysis

Time-frequency analysis was performed using the Matching Pursuit (MP) algorithm (Mallat and Zhang 1993). MP is an iterative procedure to decompose a signal as a linear combination of members of a specified family of functions g_n or “atoms”. They are usually chosen to be sine modulated Gaussians, i.e., “Gabor atoms”, because such functions give the best compromise between frequency and time resolution. In this algorithm, a large overcomplete dictionary of Gabor atoms is first created. In the first iteration, the atom g₀, which best describes the signal f(t), is chosen from the dictionary, and its projection onto the signal is subtracted from it. The procedure is repeated iteratively with the residual replacing the signal. Thus, during each of the subsequent iterations, the waveform g_n is matched to the signal residue Rⁿf that is left after subtracting the results of previous iterations. Time-frequency plots are obtained by calculating the Wigner-Ville distribution of individual atoms and taking the weighted sum.

LFP signals, originally recorded with a 5-kHz sampling rate, were down-sampled by a factor of 5, resulting in a sampling frequency of 1 kHz. Simulated signals, which had an original sampling rate of 10 kHz, were down-sampled by a factor of 10, also yielding a 1- kHz sampling frequency. The MP decomposition had a maximum time resolution of 1 ms and a maximum frequency resolution of 500/1,024 Hz, where 500 Hz is the Nyquist frequency after down-sampling. For each signal segment, we fitted 200 atoms, which allowed high-frequency atoms of lower energy to also be selected. The decomposition accounted for >99.9% of the signal energy.

In calculating average energy across trials (Fig. 1, B and D), we first computed the natural logarithms of single-trial energy, which is a standard procedure resulting in a more symmetric energy distribution and enhancement of low-energy components. Next, average energy was obtained by averaging log transformed energy over n trials (n = 50 for experimental data and n = 48 for simulated data). In Fig. 1, B and D, we computed the average change in energy relative to baseline. Baseline energy was computed as the time average of energy in the baseline period. The baseline period was 50–200 ms before stimulus onset for real data (Fig. 1B) and 350–500 ms for simulated data (Fig. 1D). Low-frequency components (<20 Hz) were stronger in simulated data than in experimental recordings. Gabor functions are symmetrical; hence the strong low-frequency atoms around the stimulus onset in the simulated data were extended in time and reached times before the stimulus onset. Therefore, for simulated signals, we calculated the reference period at times further away from stimulus onset. The change in energy relative to baseline was calculated as a difference between average energy after stimulus onset and energy in the reference period. In the MP analysis of real data, artifacts related to line noise were removed from the plots by excluding atoms around 60 Hz and its higher harmonics.

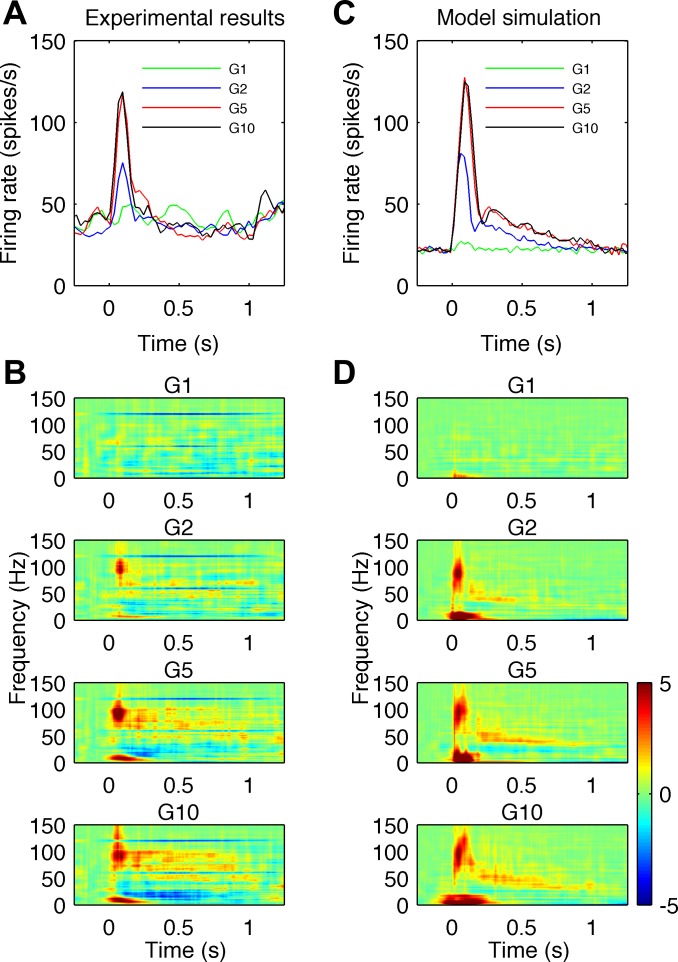
Fig. 1.

Comparison of high-gamma observed in vivo and simulated in the model during sensory stimulation for different stimulus amplitudes denoted G1, G2, G5 and G10. A and B: experimental results. C and D: model simulations. A: mean firing rate of the excited neurons shows an initial sharp peak followed by a slow decay. B: the different rows show the average time-frequency plots of power differences from baseline in local field potential (LFP) signals for different stimulus amplitudes. Maps for amplitudes G2 to G10 show an increase in power in the high-gamma frequency range (60–150 Hz) with dominant frequency ∼100 Hz in the early stimulus phase (50–200 ms) and increase in gamma and high-gamma frequencies (40–100 Hz) afterwards. A strong increase of power at low frequencies (<20 Hz) at stimulus onset and a decrease of power in the beta frequency range (10–30 Hz) after stimulus onset are also visible. C: mean firing rate across all cells in the model exhibit a similar time course to those observed experimentally. D: the time-frequency plots of simulated LFP signals exhibit similar changes in low (<20 Hz), beta, gamma and high-gamma frequency bands. Color bar showing relative energy scale in dimensionless dB units for B and D is shown on the right.

Cortical Network Model

In the present study, we used a modified version of a cortical network model previously described (Anderson et al. 2007, 2009; Franaszczuk et al. 2003; Kudela et al. 1997, 2003). Since the model was originally developed to study epileptic phenomena, we introduced necessary changes to adapt it to simulations of normal cortical sensory responses. The main difference concerned the connectivity of the network and not the single-cell properties. We also added external stimulation corresponding to sensory input from thalamocortical afferents.

The model consisted of two layers composed of either excitatory PY cells or I interneurons, with the ratio of PY to I cells 4:1. We simulated network sizes from 500 to 18,000 neurons. There were no noticeable effects of the network size on high-gamma responses. Thus the results are reported for a network size of 500 cells. Excitatory PY cells corresponded to regular spiking PY cells, while I cells corresponded to fast-spiking interneurons. Low-threshold spiking interneurons were not included, as they are believed to contribute to low-frequency rhythmogenesis (Fanselow et al. 2008; Vierling-Claassen et al. 2010). The neurons were modeled using single-compartment Hodgkin-Huxley type dynamics, modified by Av-Ron (1994). The regular spiking neuron model included a sodium current I_Na, a delayed rectifier potassium current I_K, a Ca-dependent potassium current I_K(Ca), a transient I_A current, and a leakage current I_L. The fast-spiking neuron model included the same set of currents, except for the Ca-dependent potassium current I_K(Ca). The parameters for the two different types of cells (regular spiking and fast spiking) are based on the modeling study of Anderson et al. (2007), where single-cell behavior is presented. The synaptic connections included excitatory AMPA and inhibitory GABA_A types of receptors. Postsynaptic currents were described by a double-exponential function and included transmission delays as in Anderson et al. (2007). The onset and decay times were t_o = 0.5 ms, t_d = 5 ms for excitatory postsynaptic current (EPSC) and t_o = 0.5 ms, t_d = 2 ms for IPSC, respectively. Synaptic conductance constants were g_syn^j = 0.0009 mS/cm² for EPSC and g_syn^j = 0.0014 mS/cm² for IPSC. Transmission delay is a delay between emergence of spike in the presynaptic neuron and beginning of current integration in the postsynaptic neuron. They include intrinsic synaptic delays, axonal conduction time and dendritic conduction time. Intrinsic synaptic delays are ∼0.4 ms (Eccles 1964), and axonal conduction velocities estimated in motor cortex are ∼1 m/s for short-range excitatory projection (Swadlow 1994) and ∼0.4 m/s for inhibitory projections (Kang et al. 1994). Delays due to dendritic conduction times are present mainly for excitatory connections. Thus we assumed transmission delays to have uniform distribution in postsynaptic cells in the range 0.5–1.5 ms.

The network connectivity was defined by the number of input connections, the synaptic conductances and the synaptic weights as in Anderson et al. (2007). Relative synaptic weights w_j were obtained by considering the reduction in size of the postsynaptic potential (PSP) due to distant synapsing in the dendritic arbor (Williams 2005; Williams and Stuart 2003). PY cells are assumed to synapse at 500 μm from the cell body, while basket cells make synapses close to soma. Relative mean weights for PY-PY, PY → I, I → PY, and I-I were 5, 20, −100, and −100, respectively. For each postsynaptic cell, synaptic weights had uniform distribution over the range 75% to 125% of the mean value.

Connectivity in our model was based on the available anatomical data from cat primary visual cortex (Binzegger et al. 2004) with some modifications. To our knowledge, for no other species or cortical area does such detailed data exist. The estimated numbers of synapses on one type of neuron formed by other neurons, in each cortical layer, are given in Fig. 7 of Binzegger et al. (2004). We used data from excitatory PY cells in cortical layer 2/3 (p2/3) and I basket cells in cortical layer 2/3 (b2/3) only. The reported numbers of convergent projections between respective cell types were as follows: between p2/3, 3,000–3,500; from p2/3 to b2/3, 1,500–2,500; from b2/3 to p2/3, 500–1,000; and between b2/3, 500–1,000. In our small network model we reduced, by a factor of 100, the number of synaptic connections, preserving the relative number of connections between each cell type, except the number of I (b2/3) to PY cells (p2/3) connections, which was increased from the derived 5–10 range up to 20. This increase was motivated by the fact that the power of high-gamma signals was dependent mainly on the inhibitory PSP currents generated by inputs from interneurons to PY cells. With this parameter setting, the power changes in the high-gamma range were more evident, allowing us to more easily examine the effects of other model parameters on these power changes. Thus, in the model, the numbers of connections each cell received from other cells were 30, 20, 20, and 5 for PY-PY, PY → I, I → PY, and I-I connections, respectively. For each connection type, we defined a neighborhood, i.e., a square array of cells from which cells could send outgoing connections to a given cell. The neighborhood size was 9 × 9 cells for each connection type and was always centered on a target cell. The consequence of this, for example, was that a single I cell received inputs from 20 different PY cells randomly selected from a square array of 81 cells, centered on the target I cell. The convergent and divergent projections in the model are illustrated in Fig. 2.

Fig. 2.

Schematic diagram of connectivity in the network model. The network consists of 400 pyramidal (PY) cells (top layer) and 100 inhibitory (I) interneurons (bottom layer). The network connectivity is defined by the number of convergent synaptic connections between different cell types. In the model, the number of inputs each cell receives from other cells is 30, 20, 20, and 5 for PY-PY, PY → I, I → PY and I-I connections, respectively. A and B: convergence, i.e., all input connections to single PY (A) and I cells (B). C and D: divergence, i.e., all outgoing connections from single PY (C) and I (D) cells.

The network heterogeneity of our model was captured by a spread of synaptic weights and transmission delays, but they were not the primary determinant of high-gamma energy. We also performed additional simulations to verify whether heterogeneity in single-cell properties could have led to an increase of the bandwidth of the high-gamma signals. These simulations of the network with leakage current synaptic conductance g_L and reversal potentials V_L uniformly distributed within 10% of their reference values did not produce any appreciable differences in the results.

Two types of inputs were present in the model. First, background input, representing activity from other cortical areas not included in the model and not activated by sensory stimulation, was modeled as a Poisson train of spikes arriving to each PY cell. The inputs to different cells were uncorrelated with each other. The average rate of the background input was 300 spikes/s, unless stated otherwise. Second, sensory inputs, representing input from thalamocortical afferents, were modeled as uncorrelated Poisson spike trains arriving to 50% of randomly selected PY and I cells. The conductance of thalamocortical sensory input synapses was three times larger in PY than in I cells as in the corticothalamic model of Destexhe et al. (1998). It has been estimated that the average number of thalamocortical synapses in a single cortical cell is about 100 (Binzegger et al. 2004). The investigated range of thalamocortical sensory input firing rates was between 100 and 12,000 spikes/s. This translates into firing rates of thalamocortical cells in the range of 1–120 spikes/s, which is in agreement with the reported firing rates of thalamocortical cells in the tonic firing mode (McCormick and Feeser 1990; Sherman 2001). In simulations of tactile stimulation, we took into account the rapidly adapting and slowly adapting responses of peripheral receptors. The time course of sensory input rate-simulating responses to tactile stimulation was described by sharp linear increase and decrease, followed by a slowly (exponentially) decaying response (see Fig. 3B). Such an input shape well approximated the responses of cortical neurons in monkey somatosensory cortex to step tactile stimulation (Pei et al. 2009; Ray et al. 2008a). The sensory inputs to cortex for different stimulus amplitudes G1, G2, G5, and G10 were not measured experimentally, and it is unknown how different stimulus intensities at the periphery would translate into sensory input properties at the cortical level. Based on the cortical firing rates shown in Fig. 1A, we assumed that, during a sharp increase in the firing rate of cortical neurons (0–90 ms), the increase in thalamocortical sensory input firing rate was linear in time and that the maximal input firing rate increased for increasing stimulus amplitudes. Additionally, we assumed a constant slope of the increase of the input firing rate for all stimulation strengths G1 to G10. In the late phase (180–1,000 ms) the firing rate decayed exponentially with an increasing decay time constant for increasing stimulation strength. Model output corresponding to microelectrode-recorded extracellular LFPs was assumed to correspond to average synaptic activity in PY cell layer. It was calculated as a sum of postsynaptic currents in PY cells, as in other point neuron models (e.g., Mazzoni et al. 2008). The simulations were run using custom software codeveloped by one the Authors (P. Franaszczuk). The model was implemented on a cluster of sixteen 32-bit, 1-GHz, ×86 architecture computers. One second of simulated time of 500 cells on each cluster node (i.e., 8,000 cells in total) took 2 s to run.

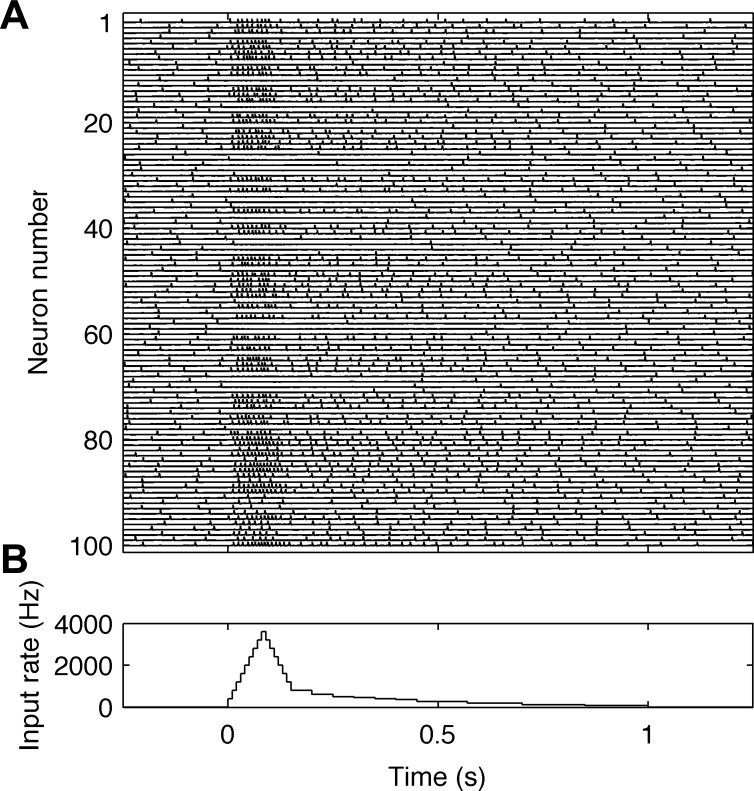
Fig. 3.

Behavior of neurons in the model during sensory stimulation. A: traces of the membrane potentials of 100 neurons. Neuron numbers from 1 to 80 correspond to PY regular spiking cells and from 81 to 100, to I fast spiking interneurons. B: the time course of average firing rates (in spikes/s) of simulated sensory inputs during vibrotactile stimulation.

RESULTS

High-Gamma Oscillations in Vivo and in the Model

Experimental results from monkey vibrotactile stimulation are shown in Fig. 1, A and B. The mean firing rate of the excited neurons (Fig. 1A) shows an initial sharp peak followed by a slow decay. The time-frequency plots of power change from baseline in LFP signals for four different stimulus amplitudes are shown in four rows in Fig. 1B. For the smallest stimulus amplitude G1, there is not much of a response. For increasing stimulus amplitudes from G2 to G10, the plots show progressively greater power increases in the high-gamma frequency ranges (60–150 Hz) and power decreases in the beta frequency range (15–30 Hz), after stimulus onset. A strong increase of power at low frequencies (<20 Hz) around the time of stimulus onset is also visible. For stimulation amplitudes G2 to G10, the dominant response frequency in the early stimulus phase (50–200 ms) appears to be constant at ∼100 Hz. In the late stimulus period (200–1,000 ms), there are power increases at frequencies 50–100 Hz, which are greater at higher stimulus amplitudes. Simulation results are shown in Fig. 1, C and D. The mean firing rate (Fig. 1C) across all cells exhibits temporal profile similar to the profile observed experimentally. In the time-frequency plots of simulated LFP responses (Fig. 1D), all main features seen in the experimental results are reproduced. The initial response has a dominant frequency at ∼100 Hz. This is followed by a power decrease at beta (15–30 Hz) frequencies and a power increase at gamma (>30 Hz) and high-gamma (60–150 Hz) frequencies. In the late stimulus period, the gamma and high-gamma responses are less evenly distributed over a broad frequency range than in the experimental results and are dominated by power at 50–80 Hz.

Temporal Dynamics of Neurons

To understand the simulation results shown in Fig. 1, C and D, it may be useful to follow the temporal dynamics of the simulated cortical neuronal network. Figure 3 shows a simulation of the membrane potentials of 100 cortical neurons, i.e., every fifth neuron in the network, during sensory stimulation via thalamocortical inputs. Neurons 1–80 correspond to PY regular spiking cells, while neurons 81–100 correspond to I fast spiking interneurons. The time course of sensory input firing rates is shown in Fig. 3B and corresponds to the maximal stimulation intensity. Before the onset of the stimulation, i.e., between −250 and 0 ms, the neurons fire with low firing rates at irregular intervals. During activation, the cortical neurons can be divided into three categories, depending on whether the firing rate of the individual cells increase (excited neurons), decrease (inhibited neurons) or are unaffected (not-driven neurons) by the stimulation, as observed in experimental recordings (Ray et al. 2008a). The increased firing of I and PY neurons observed in Fig. 3A generates postsynaptic currents that are responsible for high-gamma signals during stimulation, but the observed increase corresponds mainly to a transient fast-adapting responses, which may not be an optimal setting to clarify the mechanisms generating high-gamma activity. Adaptation at peripheral receptors transforms sensory stimulation of constant amplitude, applied at the periphery, into nonstationary, rising and decaying thalamocortical input to cortical cells (Kaas et al. 1984). This is why the experimental (Fig. 1, A and B) and corresponding simulation (Fig. 1, C and D, and Fig. 3) results are nonstationary. However, under some experimental conditions in which cortical network activation is more sustained, e.g., during language tasks, it may be possible to observe quasi-stationary high-gamma responses (Korzeniewska et al. 2011). Analysis of stationary network behavior is more useful in giving insight into the neuronal mechanisms playing a role in generating LFP oscillations. Therefore, we investigated stationary network behavior simulated with constant thalamocortical input. The mechanisms responsible for responses in beta, gamma and high-gamma frequencies are explained in detail based on these steady-state simulations.

Steady-State Simulations of Baseline Conditions

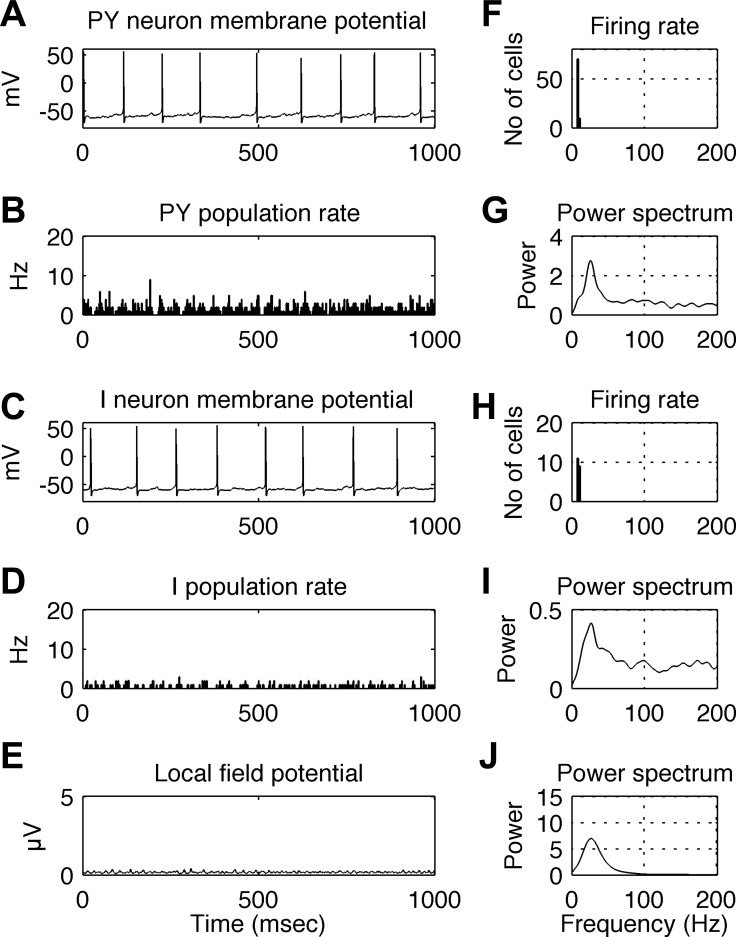
Conditions corresponding to the baseline period prior to stimulus onset were simulated with background input, modeled as a Poisson train of spikes with an average rate of 300 spikes/s, arriving to each and every PY cell. An example of the simulated network's behavior during 1 s is shown in Fig. 4. The five graphs in the left panel correspond to the membrane potential of a single PY cell (Fig. 4A), the instantaneous firing rate of the PY cell population (Fig. 4B), the membrane potential of a single I cell (Fig. 4C), the instantaneous firing rate of the I cell population (Fig. 4D) and the raw LFP signal (Fig. 4E). Here and in the next figure, population firing rates were calculated with a bin size of 2.5 ms. Five graphs in the right panel illustrate the simulation results: Fig. 4F shows the distribution of single neuron firing rates in the PY cell population; Fig. 4G shows the power spectrum of the time series of PY population firing rates (see Fig. 4B); Fig. 4H shows the distribution of single-neuron firing rates in the I cell population; Fig. 4I shows the power spectrum of the time series of I population firing rates (see Fig. 4D); and Fig. 4J shows the power spectrum of the LFP signal (see Fig. 4E). Both PY and I single-cell firing rates are about 10 spikes/s (Fig. 4, F and H), but the firing rates of both populations oscillate at a frequency of ∼25 Hz (Fig. 4, G and I). This is associated with an oscillation in the LFP signals at ∼25 Hz (Fig. 4J). It can be seen that, despite firing of individual cells at irregular intervals (Fig. 4, A and C), a coherent rhythm emerges in the network, manifesting as oscillations in population firing rates (Fig. 4, B, D, G, and I) and in the LFP signal (Fig. 4, E and J).

Fig. 4.

Behavior of the simulated network under baseline conditions. A: membrane potential of a single PY cell. B: instantaneous firing rate of the PY cell population. C: membrane potential of a single I cell. D: instantaneous firing rate of the I cell population. E: LFP signal generated by the model. F: distribution of single neuron firing rates in the PY cell population. G: power spectrum of the time series of PY population firing rates (as shown in B). H: distribution of single neuron firing rates in the I cell population. Note the smaller range in the y-axis relative to that of the plot in F is due to the 4:1 ratio of PY and I cells in the model. I: power spectrum of the time series of I population firing rates (as shown in D). J: power spectrum of the simulated LFP signal (as shown in E). Firing rates of both PY and I single cell are about 10 spikes/s, while the firing rates of both populations, as well as the associated LFP signal, oscillate at ∼25 Hz. In spite of the irregular firing of individual cells at a low rate, a coherent rhythm emerges at a higher frequency in the network, illustrated by peaks in the power spectra of population firing rates and LFP signals. In B and D, bin size is 2.5 ms.

Steady-State Simulation of Cortical Activation

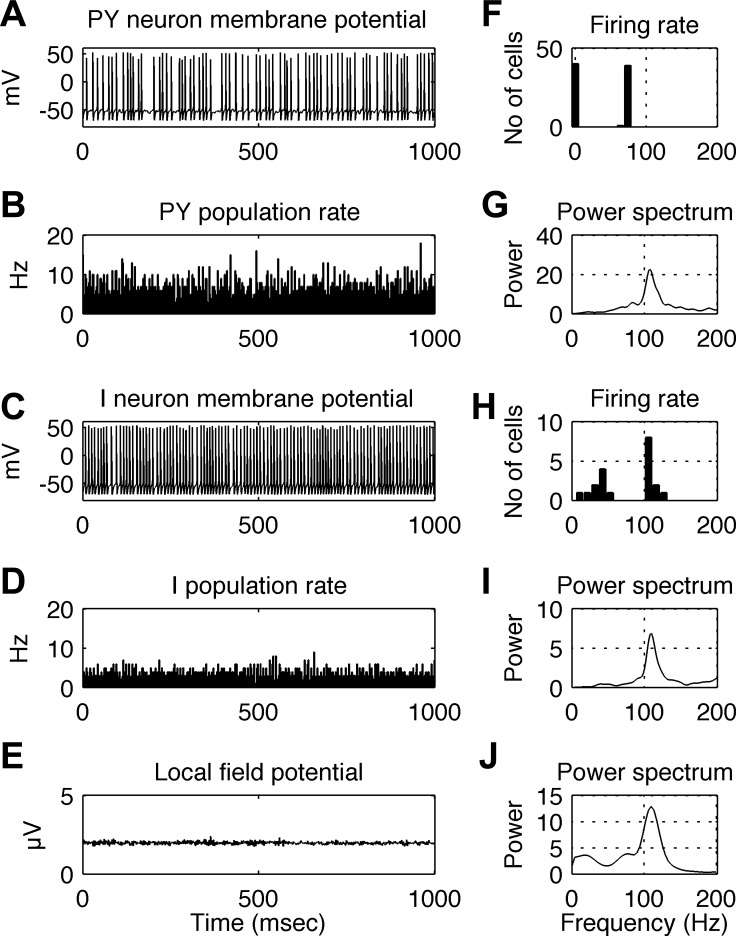
Steady-state cortical activation was simulated with both background input and sensory input present and having constant rates throughout the simulation. Such stationary conditions may correspond to the quasi-stationary responses in the late stimulus period shown in Fig. 1B (200–1,000 ms, plots G1 to G10). An example of the simulated network's behavior during stationary cortical activation for 1 s is shown in Fig. 5. The background input rate was 300 spikes/s, as in Fig. 4, and the input rate due to sensory stimulation was 3,000 spikes/s, delivered to 50% of the PY and I cells, selected randomly. The order of panels and graphs is the same as in Fig. 4. When receiving sensory stimulation, individual PY cells fire at irregular intervals at an average rate of ∼70 spikes/s (Fig. 5F), while the firing of individual I cells is more regular, with many firing at a rate of ∼110 spikes/s (Fig. 5H). The firing rates of both PY and I populations oscillate at a frequency of ∼110 Hz (Fig. 5, G and I), close to the firing frequency of individual I cells (Fig. 5H). The population rhythm is also reflected in LFP oscillations, having the same dominant frequency of ∼110 Hz (Fig. 5J). Note that, in the histograms of firing rates in Fig. 5, F and H, the PY cells with a firing rate of 0 (F) and the I cells with firing rates of 50 Hz and less (H) are cells that do not receive external sensory input (input was delivered to only 50% of the cells). I cells not receiving this input fire independently of each other at 50 Hz and below, resulting in a very small 40-Hz bump in the spectrum of the population firing rates (Fig. 5I). In contrast, the I cells receiving the external sensory input fire in synchrony at the population rhythm of 110 Hz, giving rise to a large peak in the spectrum. Because the LFP is modeled as the sum of all inhibitory PSPs and excitatory PSPs in PY cells, both I cell populations (with 40- to 50-Hz and 110-Hz firing rates) give rise to the LFP, but the synchronized population dominates (Fig. 5J).

Fig. 5.

Behavior of the simulated network during steady-state sensory stimulation at 3,000 spikes/s. A: membrane potential of a single PY cell. B: instantaneous firing rate of the PY cell population. C: membrane potential of a single I cell. D: instantaneous average firing rate of the I cell population. E: LFP signal. F: distribution of single neuron firing rates in the PY cell population. G: power spectrum of the time series of PY population firing rates (as shown in B). H: distribution of single neuron firing rates in the I cell population. I: power spectrum of the time series of I population firing rates (as shown in D). J: power spectrum of the simulated LFP signal (as shown in E). During high-gamma oscillations, PY cells fire at irregular intervals at a rate ∼70 spikes/s, while the firing of individual I cells is more regular at a rate of ∼110 spikes/s. The firing rates of both PY and I populations oscillate at ∼110 Hz, close to the frequency of single I cells. This may reflect synchronization of the firing of individual I and PY cells by the population rhythm. The population rhythm is also reflected in LFP oscillations, having the same dominant frequency of ∼110 Hz. In B and D, bin size is 2.5 ms.

Simulation of Baseline and Cortical Activation Conditions for a Range of Input Values

To better understand the mechanisms of the responses observed under baseline conditions and during cortical activation, we simulated network activity under steady-state conditions for a range of input values. Furthermore, we performed these simulations in the intact network and in modified networks where connections between the cells were selectively removed. In this way, we evaluated the influences of different types of connections on network behavior. The results are summarized in Fig. 6.

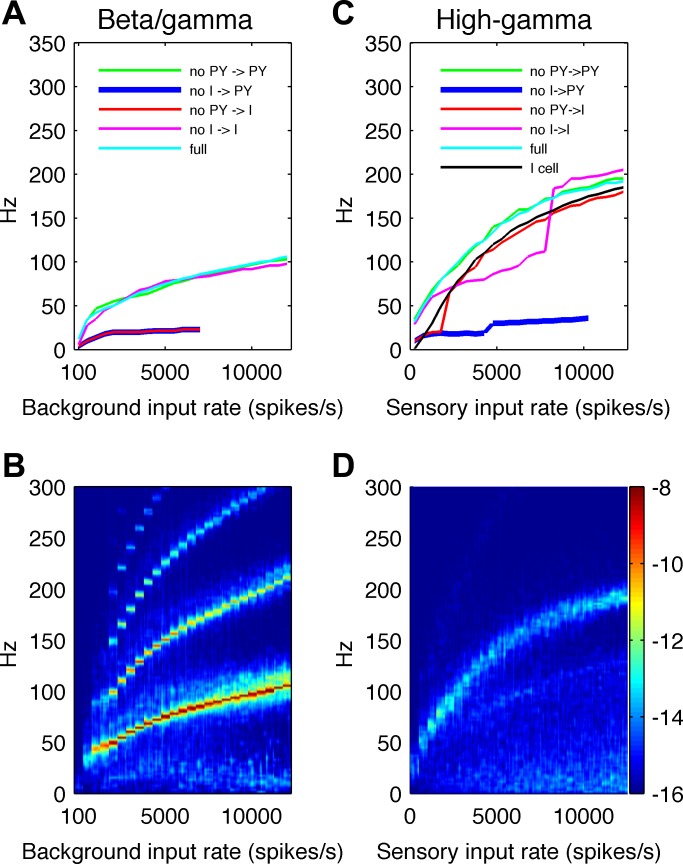
Fig. 6.

Analysis of steady-state baseline vs. activated conditions. A: the dominant frequency of the LFP signal under baseline conditions is plotted to show its dependence on background input levels and on different connection types between cells. As the background input level is increased from 100 spikes/s to 500 spikes/s and then in steps (23 total) of 500 spikes/s up to 12,000 spikes/s in a stepwise manner (every 1,000 ms), the dominant frequency of network activity gradually increases from ∼12 Hz to ∼100 Hz. Removing PY → I or I → PY connections abolishes these oscillations, indicating that the simulated rhythmic LFP activity is mediated by negative feedback loops between excitatory and inhibitory neurons. B: time-frequency plot of LFP signal energy generated under baseline conditions as background input values are systematically increased in a stepwise manner. For each input value, 250 ms of the time-frequency map are shown. For a large range of background input values, narrow-band oscillations with higher harmonics are present. Note that the 12-Hz peak generated with a background input of 100 spikes/s was smaller (fewer cells firing) and poorly seen in this plot at the scale used for the rest of the background input levels. C: under activated conditions, the dominant frequency of the LFP signal is shown for different sensory input values in the intact network (light blue line) and with connections between cells selectively removed. For the range of sensory input values, the intact network exhibits relatively broadband oscillations at frequencies increasing from ∼60 to ∼200 Hz. Removing I → PY connections abolishes these oscillations, suggesting that they are generated by the I cell population. D: time-frequency plot of LFP signals for different sensory input values, varied in a stepwise manner as in B. For each input value, 250 ms of the time-frequency map is shown. For a broad range of sensory input values, high-gamma responses are generated. Color bar showing logarithmic energy scale, in μV², for plots B and D, is shown on the right.

Baseline conditions.

To evaluate how network activity depends on the background input under baseline conditions, we simulated the LFP generated as background input rates were systematically increased from 100 spikes/s to 500 spikes/s and then, in steps (23 total) of 500 spikes/s, up to 12,000 spikes/s. For each value of the input rate, we simulated 1 s of activity. For each 1-s epoch, we performed a time-frequency decomposition and computed the power spectrum of the modeled LFP signal. The dominant frequency of the LFP signal for different input values in the intact network is shown in Fig. 6A (light blue line). The time-frequency map of the LFP signal for different input values is shown in Fig. 6B. For each input value, we used 250 ms of the time-frequency map to avoid border effects in the decomposition. As can be seen from Fig. 6B, the activity is relatively narrow band and exhibits higher harmonics. The dominant frequency of the network activity gradually increases, covering the frequency ranges typically associated with beta and gamma bands. At the highest (nonphysiological) input rates, this extends into the high-gamma range. We used the term beta/gamma oscillations to refer jointly to these rhythmic activities under baseline conditions.

We investigated how selectively removing different types of connections between cells affected network behavior under baseline conditions (Fig. 6A). Removing the PY-PY (green line) or I-I (magenta line) connections had little influence on the LFP frequency, while removing the PY → I (red line) or I → PY (blue line) connections abolished the beta/gamma oscillations and replaced them with lower frequency rhythms at around 15 Hz. This suggests that beta/gamma oscillations under baseline conditions in the model are primarily mediated by synaptic interactions between PY and I cells and are only weakly dependent on interactions within I and PY populations. The network frequency depends on both single-cell (integration of synaptic inputs, intrinsic ionic currents) and network properties (synaptic delays in disynaptic I-PY-I and multisynaptic, e.g., I-PY-PY-I, loops). Detailed analysis of the contribution of cellular and synaptic parameters to beta/gamma oscillations, however, was beyond the scope of this paper. Nevertheless, Fig. 6, A and B, shows that, for a broad range of input rates under baseline conditions, network oscillations have a narrow bandwidth and occur mainly below 100 Hz. Note that, although 12,000 spikes/s was used in this parameter sensitivity analysis, such high rates would not typically be encountered in the resting brain. Hence, these oscillations would rarely occur above 60 Hz. The narrow bandwidth and frequency range of these oscillations are not typical of the high-gamma responses that have been observed experimentally.

The weak low-frequency activity (<30 Hz) visible in Fig. 6B for increasing background input rates is a phenomenon dependent on PY cell properties and can be observed in a purely excitatory PY network. Under external input, individual PY cells cannot maintain a high discharge rate due to firing adaptation mediated by the hyperpolarizing I_K(Ca) current. Additionally, the PY-PY coupling leads to synchronous firing in the PY cells, which is followed by cessation of firing. Periods of fast spiking in PY cells and periods of silence occur at more or less regular intervals, which are determined by the recovery time from after-hyperpolarization. This activity is visible after disconnecting PY cells from I cells. As can be seen in Fig. 6A (red and blue line), the frequency of activity in the purely excitatory network, for low background input rates, is around 15 Hz. For higher rates, the PY network is dominated by input noise and does not exhibit a dominant frequency.

Cortical activation.

Analysis of network activity in the high-gamma range during sensory stimulation is shown in Fig. 6, C and D. The network activity (LFP) was simulated with the background input rate of 300 spikes/s and sensory stimulation input rates varying between 0 and 12,000 spikes/s in steps of 500 spikes/s (25 steps in total). For each value of the sensory input rate, we simulated 1 s of activity and computed the time-frequency spectra of the LFP signal (showing only the middle 250 ms to avoid border effects), as we had done for baseline conditions. In the intact network, the dominant frequency of the LFP signal for different sensory input values is shown in Fig. 6C (light blue line), while the corresponding time-frequency map of the LFP signal is shown in Fig. 6D. Over the range of sensory input values, the network exhibits activity at frequencies increasing from ∼60 to ∼200 Hz. The energy of this activity is less concentrated in the time-frequency spectrum, i.e., it is more broadband than the beta/gamma oscillations observed under baseline conditions, and its spectral characteristics are more consistent with experimentally observed high-gamma responses. Additionally, for increasing levels of sensory stimulation, there is a visible increase of power at lower frequencies, i.e., <30 Hz (Fig. 6D), which reflects the tendency of the purely excitatory network to fire at low frequencies, as described for the baseline conditions.

We also investigated how selectively removing different types of connections between cells affected network behavior during sensory stimulation (Fig. 6C). Blocking the PY-PY (green line), and PY → I (red line) connections had little influence on the peak frequency of LFP activity, while blocking the I → PY (blue line) connections abolished the activity in the high-gamma range. Note that the modeled LFP signals were measured from postsynaptic currents in PY cells only. Hence, the disappearance of rhythmic activity in the LFP when inputs to PY from I cells are removed, but not when other types of connections are removed, indicates that the modeled high-gamma activity critically depends on, and may be paced by, the I cells. The oscillation frequencies of single isolated I cells receiving excitatory Poisson input are also shown in Fig. 6C (black line). This shows that the firing frequencies of single I cells are comparable to, albeit slightly lower than, oscillations in the complete network. Single I cell oscillation frequencies closely follow the frequencies of network oscillations when PY → I connections are removed, i.e., when I cells do not receive recurrent excitatory input. These results suggest that the frequencies of high-gamma oscillations are mainly determined by the oscillation frequencies of I cells. However, the high-gamma EEG response is a network phenomenon because the activities of PY and I cells must be synchronized to generate measurable power at high-gamma frequencies in the LFP signal (visible in Fig. 6D). Due to the high divergence of connections from I to PY cells (Fig. 2D), a single I cell imposes inhibition on many PY cells. I-to-PY divergence and PY-PY (Fig. 2C) coupling allow synchronization between the temporal firing patterns of PY cells, which tend to fire together after being released from rhythmic inhibition at time windows determined by the I cell population rhythm. Synchronized recurrent excitation from PY to I cells, in turn, has a synchronizing effect on the I population. Mutually inhibitory connections between I cells do not appear to play a critical role in the high-gamma-generating mechanisms because high-gamma signals may still be generated without I-I connections present. After elimination of mutual inhibition (Fig. 6C, magenta line), the dominant LFP frequency is lower for lower input rates, and unchanged at higher input rates. This may reflect the influence of two different subpopulations of I cells. The first subpopulation (50% of all I cells) receives external sensory stimulation and oscillates at high-gamma frequencies as in the intact network. The second subpopulation does not receive external stimulation and oscillates at a lower frequency, as in Fig. 5H. This subpopulation appears to dominate network activity in the low (<8,000 spikes/s) range of sensory input rates. Only when sensory input is sufficiently strong does the higher frequency cluster dominate the network activity. The effects of these subpopulations of I cells may also be visible in the time-frequency plot (Fig. 6D) of intact network LFPs as a weak “branch” having lower power and situated below the stronger high-gamma “branch”. In the full network, the I-I connections may help to synchronize the majority of I cells such that the lower frequency cluster does not dominate the network's activity.

DISCUSSION

Mechanisms of High-Gamma Oscillations

The goal of this study was to use computational modeling to investigate the physiological mechanisms responsible for the high-gamma (60–200 Hz) power augmentation observed in LFPs recorded from somatosensory cortex in monkeys during finger vibrotactile stimulation (Ray et al. 2008a, 2008b). Based on the behavior of our computational model, we propose a new hypothesis: that oscillations in the high-gamma band observed during cortical activation are a network phenomenon in which high-gamma frequencies are primarily determined by the intrinsic firing properties of networks of fast-spiking cortical interneurons imposing rhythmic inhibition on PY cells. In different studies, oscillations in the high-gamma range have been reported, and the mechanism of their generation has been proposed. We discuss them below.

Miller et al. (2007, 2009) suggested that the power spectral density of brain potentials at high frequencies (80–500 Hz) can be described by a power law behavior which originates from input firing to neuronal populations, without a preferred time-scale. Accordingly, brain activation involving an increase in neuronal firing would contribute to a global upward shift in the power spectrum at all frequencies. Our model suggests that power increases at high-gamma frequencies are not densely concentrated in the spectrum but are, nevertheless, band-limited. The time-frequency plots of power changes shown in Ray et al. (2008a, Fig. 1B) do not give a definitive answer to whether high-gamma power increases are band-limited because the results are shown only up to 175 Hz. In spite of this limitation, however, the power changes do not appear to be uniform, but rather to be centered around a frequency of ∼100 Hz (see Fig. 1B, plots G2 to G10), similar to the experimental results that have been obtained in other functional brain domains (Korzeniewska et al. 2011, Fig. 10; Ray and Maunsell 2011, Figs. 1–3). A uniform upward shift of the power spectra, as proposed by Miller et al. (2009), cannot fully account for these experimental results. On the other hand, the two mechanisms are not mutually exclusive and could both contribute to the contour of experimentally observed spectral changes.

In the studies of Ray et al. (2008b) and Ray and Maunsell (2011), a hypothesis was put forward that high-gamma activity is related to spiking activity. This idea was based on the observations that high-gamma power in LFP signals was strongly correlated with the firing rate. Similar observations have been made by Manning et al. (2009). In the study of Ray et al. (2008b), a model of high-gamma activity was proposed in which ECoG potentials were modeled as a weighted sum of extracellular action potential waveforms (estimated by the spike-triggered average). The study showed that increases in the firing rate and in the synchrony between spikes could indeed lead to increased power in the high-gamma range. While the hypothesis that extracellular spike potentials contribute to high-gamma activity in LFP signals seems reasonable, there are some experimental observations that it cannot easily explain. 1) High-gamma activity has also been observed in EEG and MEG signals. Because extracellular synaptic potentials fall off much more slowly with distance than extracellular action potentials, spikes give negligible contribution to EEG and MEG signals (Nunez 1981). Therefore, it is likely that synaptic activity is also involved in the generation of high-gamma activity. 2) LFP energy spectra can have a high-gamma peak, which is shifted to the right as the firing rate is increased (Ray and Maunsell 2011, Figs. 1, F and I, 2A, and 3B). If the high-gamma activity in LFP signals originated solely from the summation of individual spike waveforms, a higher firing rate would increase the intensity of the high-gamma signals but not their frequency, because the spectral properties of individual spike waveforms are most likely invariant with respect to increases in firing rate. 3) Significant high-gamma activity power was observed even when firing rates were unchanged or reduced after stimulus onset (Ray et al. 2008a, Fig. 1) or were negligible (Ray and Maunsell 2011, Fig. 3). This could be explained by assuming that, in these cases, the high-gamma power came from spikes other than those recorded by the microelectrode. Nevertheless, in these examples, the correlation between the firing rate and gamma power does not hold. It shows that, due to experimental limitations (a microelectrode picks up potentials from a larger number of cells than those which give rise to spikes resolved from the background), conclusions based on correlations between these two variables cannot be taken with absolute confidence. Furthermore, Trevelyan (2009) observed strong correlations between synchronized inhibitory synaptic currents in PY cells and high-frequency activity (80–500 Hz) recorded by LFP electrodes in slices, supporting the physiological correlates of high-gamma activity suggested by the present model.

Our hypothesis regarding the neurophysiological mechanisms generating high-gamma oscillations appears to be similar to that of the mechanisms generating “ripples”, i.e., transient 80- to 200-Hz oscillations observed in the hippocampus in rats (Buzsáki et al. 1983, 1992; Csicsvari et al. 2000) and humans (Bragin et al. 1999). It was shown (Buzsáki et al. 1992; Ylinen et al. 1995) that, during ripple events, synchronously discharging CA3 PY cells activated both PY cells and interneurons in the CA1 area. During activation, PY cells discharged at a rate lower than the frequency of the population oscillation, but were phase locked to the population rhythm, while interneurons discharged at the population frequency. Based on these findings, it was proposed that rhythmic and coherent firing of interneurons was responsible for the timing of action potentials of CA1 PY cells during ripple events. Based on a timing analysis of presynaptic spikes in CA1 and CA3 areas and postsynaptic spikes in CA1 interneurons, it was suggested that the intrinsic properties of interneurons, rather than rhythmic excitatory drive, was the primary determinant of the frequency of the high-frequency population oscillation. The hypothesis that high-gamma oscillations are sensory-induced neocortical ripples, similar in physiological origin to the ripples of the hippocampus, was suggested by Edwards et al. (2005). However, it should be noted that hippocampal ripples are not sensory-evoked as they occur mainly during slow-wave sleep and quiet wakefulness (Buzsáki et al. 1992).

It is not yet clear whether gap junctions are necessary for the generation of cortical high-gamma activity, although their role in oscillations at gamma (30–70 Hz) and higher (>70 Hz) frequencies has been suggested (Traub et al. 2004). The current model suggests that synaptic interactions might be sufficient for the generation of cortical high-gamma activity, but it does not rule out a contribution from gap junctions either. It has been shown that gap junctions are specifically formed between neocortical interneurons (Galarreta and Hestrin 2001) and that electrical coupling among individual I cells promotes coherent spiking in response to uncorrelated Poisson excitation (Galarreta and Hestrin 1999). Therefore, gap junctional communication could provide an efficient way for synchronization among interneurons, which could in turn send synchronous input to PY cells and produce strong high-gamma responses.

Comparison with Other Models

Fast network oscillations in the 40- to 300-Hz range were investigated using a computational model of leaky integrate-and-fire neurons (Brunel and Wang 2003), and using subsequent developments of that model (Geisler et al. 2005; Mazzoni et al. 2008). In these models, activity at frequencies ∼200 Hz were observed in purely inhibitory networks with random Poisson input. When connections with PY cells were included, the network oscillation slowed down from 200 to ∼110 Hz. Despite a similar range of frequencies simulated in that model and in our study, the mechanisms seem to be distinct. In the models of Brunel and collaborators (2003), the oscillation was a network phenomenon depending on synaptic connections between I cells. During 110-Hz oscillations, both PY cells and interneurons generated irregular spikes at low mean rates (PY cells: <20 spikes/s, interneurons: ∼25 spikes/s). In our model, high-gamma oscillations were also network phenomena, but the mutually inhibitory connections were not essential for their generation. Additionally, firing rates during high-gamma oscillations in our model were much higher (PY cells ∼70 spikes/s, interneurons ∼100 spikes/s), which is closer to what has been observed in comparable experimental data (Ray et al. 2008a, Fig. 1A).

The Broad-Band Nature of High-Gamma Oscillations

There might be a number of reasons for the unusual broad-band spectral contours of experimentally observed high-gamma responses. High-gamma responses observed in frequency (Fourier transform) or time-frequency (Gabor transform) representations are usually short-lasting, which implies a large spread in their frequencies according to the Heisenberg uncertainty principle. Besides, signal power at high-gamma frequencies is usually relatively low, which often requires averaging across many trials to achieve a reliable estimate of its power spectrum. Intertrial variability, both in the timing and frequency of activation-related energy changes, is likely to contribute to broad-band responses. Using model simulations, it is possible to reduce intertrial variability and the transient behavior of high-gamma responses, and to investigate the bandwidth of high-gamma signals that are inherent to the mechanism of their generation. Under stationary conditions (i.e., constant mean rate of the Poisson input) and without intertrial variability, there is still a spread of frequencies in the output signal. This is likely due to the Poisson input, which is essentially a random process with a certain mean rate of spike occurrence. Fluctuating spike inputs to PY and I cells produce fluctuating spike outputs in these cells. In PY cells with firing adaptation, firing is quite irregular, giving rise to quite a broad frequency response. However, I cells, which do not exhibit spike frequency adaptation, are able to sustain repetitive, quasi-periodic firing when submitted to Poisson input of a sufficient rate. Thus the membrane properties of single I cells are responsible for their narrow frequency response. Additionally, synaptic connections between cells play a synchronizing role, further narrowing frequencies generated by the network. Finally, the frequency range observed in LFP signals is determined by a complex interplay between input fluctuations, individual PY and I cell characteristics, and the network architecture.

Model Predictions

The neuronal mechanisms that might lead to oscillations at high-gamma frequencies are not unique. Therefore, it is important that the model generates testable hypotheses. Only when model predictions are confirmed can one be confident that the mechanisms suggested by the model are likely to play a role in a real system. Our model generates a number of predictions, which should be testable.

Our model predicts that, during high-gamma oscillations, the excited cortical I interneurons of fast-spiking type should exhibit approximately regular discharges near the frequency of the population rhythm, similarly to what has been observed in vivo in hippocampal interneurons during ripple oscillations (Buzsáki et al. 1992; Ylinen et al. 1995). Regarding cortical interneurons, it has been shown in vitro (McCormick et al. 1985) and in vivo (Swadlow et al. 1998) that these cells are capable of generating nonadapting, high-frequency responses (∼300 Hz) to depolarizing current pulses (1–3 nA). These frequencies are higher than those reported for high-gamma oscillations and higher than the firing rates of interneurons in our model. However, responses to current injection are not equivalent to responses to fluctuating conductance inputs in vivo. Tateno and Robinson (2006) used in vitro conductance injection and investigated the behavior of regular-spiking neurons and fast-spiking I interneurons from layer 2/3 of somatosensory cortex during Poisson conductance input. For the 1- to 6-kHz range of Poisson input rates, the relationship between the firing frequency and the excitatory Poisson rate was logarithmic. The firing frequencies of I interneurons increased from 0 to 40 spikes/s, i.e., less than the reported firing rates during constant-current injection. Furthermore, the coefficient of variation, which is a measure of the local variation of interspike intervals, was lower for fast-spiking than for regular-spiking neurons, suggesting more regular periodic discharges in I cells.

The other prediction is that, under stationary conditions, higher firing rates of interneurons and PY cells should lead to high-gamma activity at higher frequencies (Fig. 6, C and D). This feature is already visible in Figs. 2A and 3B of Ray and Maunsell (2011). In the stationary phase (200–400 ms), the peak frequency of high-gamma oscillations exhibits a “shift to the right” for increasing values of the average firing rate. This phenomenon is also present on the time-frequency maps in Fig. 1B. It may be noticed that, in the quasi-stationary, late poststimulus period (250–1,000 ms after stimulus onset), the frequencies in the high-gamma range increase for increasing stimulation strengths from G2 to G10. However, it is less evident due to a time-frequency representation in which peak frequency locations are less discernible.

Functional Role

Our simulations suggest that, during high-gamma oscillations, neuronal interactions organize the firing of PY cells into precise temporal windows. PY cell populations with synchronized discharges are likely to exert more powerful influences on their targets than populations in which firing rates increase but cells fire incoherently. According to this view, stronger input signals would create higher firing frequencies and higher synchrony in the high-gamma range and a stronger effect on the next stage of cortical processing. Indeed, a strong correlation between stimulus intensity and high-gamma power has also been observed experimentally (Supplementary Fig. 3 in Ray et al. 2008b), which is in agreement with the present hypothesis.

GRANTS

This work was supported by National Institute of Neurological Disorders and Stroke Grant NS-40596. P. Suffczynski was partly sponsored by a fellowship from the Kosciuszko Foundation.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: P.S. performed experiments; P.S. analyzed data; P.S., N.E.C., and P.J.F. interpreted results of experiments; P.S. prepared figures; P.S. drafted manuscript; P.S., N.E.C., and P.J.F. edited and revised manuscript; P.S., N.E.C., and P.J.F. approved final version of manuscript; N.E.C. and P.J.F. conception and design of research.