Population interactions between parietal and primary motor cortices during reach

Abstract

Neural interactions between parietal area 2/5 and primary motor cortex (M1) were examined to determine the timing and behavioral correlates of cortico-cortical interactions. Neural activity in areas 2/5 and M1 was simultaneously recorded with 96-channel microelectrode arrays in three rhesus monkeys performing a center-out reach task. We introduce a new method to reveal parietal-motor interactions at a population level using partial spike-field coherence (PSFC) between ensembles of neurons in one area and a local field potential (LFP) in another. PSFC reflects the extent of phase locking between spike times and LFP, after removing the coherence between LFPs in the two areas. Spectral analysis of M1 LFP revealed three bands: low, medium, and high, differing in power between movement preparation and performance. We focus on PSFC in the 1–10 Hz band, in which coherence was strongest. PSFC was also present in the 10–40 Hz band during movement preparation in many channels but generally nonsignificant in the 60–200 Hz band. Ensemble PSFC revealed stronger interactions than single cell-LFP pairings. PSFC of area 2/5 ensembles with M1 LFP typically rose around movement onset and peaked ∼500 ms afterward. PSFC was typically stronger for subsets of area 2/5 neurons and M1 LFPs with similar directional bias than for those with opposite bias, indicating that area 2/5 contributes movement direction information. Together with linear prediction of M1 LFP by area 2/5 spiking, the ensemble-LFP pairing approach reveals interactions missed by single neuron-LFP pairing, demonstrating that cortico-cortical communication can be more readily observed at the ensemble level.

planning and performance of goal-directed arm reach requires the coordination of interconnected neuron populations across brain areas. Neurons in the arm area of primary motor cortex (M1) and more anterior parts of the posterior parietal cortex (area 2/5) are bidirectionally connected, and single-neuron studies show that they are engaged during reach planning and performance, with partially overlapping timing (Kalaska 1996). However, the temporal and spatial dynamics of parietal-frontal network communication during reach planning and performance are poorly understood. One difficulty in revealing computations that occur in area 2/5-M1 interactions with single-cell methods is that the interactions at this level are very weak (see Bullock et al. 1998; Shadmehr and Krakauer 2008). The growing availability of data recorded from ensembles of neurons in multiple, interconnected cortical areas provides an opportunity to examine cortico-cortical interactions at ensemble levels where collective dynamics of populations may be examined. However, there is a need for methods to examine larger-scale interactions in cortical networks, not only to reveal computations in parietal-frontal communication during reaching but also to identify general principles of network interactions in cortex.

Dorsal area 5 (5d; PE) is a parietal area dominated by kinesthetic input that, along with adjacent parts of area 2, is monosynaptically and bidirectionally connected with M1 (Jones et al. 1978; Strick and Kim 1978) and thus may be an important source of signals to generate or guide movement. Area 2/5 is thought to contribute information about movement kinematics to M1 during arm movement because 2/5 neurons show directionally tuned movement-related spiking activity (Kalaska et al. 1983; Mountcastle et al. 1975). However, most movement-related neurons located on the postcentral gyral surface, in the area 2/5 region, respond after movement onset, suggesting a role in processing sensory feedback (Ashe and Georgeopoulos 1994; Kalaska 1996) rather than planning or driving motor output. By contrast, cells deeper in the intraparietal sulcus, not directly connected with M1, show earlier changes (Cohen and Andersen 2002). Activity in 2/5 correlates with arm position and movement target during goal-directed reaching, and models of arm movement typically propose that 2/5 conveys a motor error signal, possibly related to errors of ongoing movement direction (Bullock et al. 1998; Graziano et al. 2000; Kalaska et al. 1997; Lacquaniti et al. 1995). These models are consistent with studies in humans showing that disrupting posterior parietal cortex function with transcranial magnetic stimulation (TMS) impairs the ability to correct arm movement trajectory when sensory information indicates that the plan for movement must be updated (Della-Maggiore et al. 2004; Desmurget et al. 1999).

Local field potentials (LFPs) in M1, which reflect currents flowing due to synaptic inputs among other signals (Mitzdorf 1985), are modulated in various spectral bands as movement is prepared and performed (Bansal et al. 2012; Donoghue et al. 1998; Murthy and Fetz 1996). In particular, a slow potential known as the motor event-related potential (mERP; Donchin et al. 2001; Gemba et al. 1981; Rickert et al. 2005; Sasaki and Gemba 1982) straddles movement onset. This potential may reflect the collective inputs from the areas that project to M1 as well as intrinsic activity. The overlap of the spiking in 2/5 with the late phase of the M1 mERP (Gemba et al. 1981; Rickert et al. 2005) may therefore represent input from area 2/5, especially related to feedback that ensues as movement begins.

Understanding the nature of 2/5-M1 communication is complex because of their reciprocal connections and temporal overlap of activity. Furthermore, the likelihood of detecting interactions is limited in pairwise recording of neuron spiking across connected zones because individual 2/5 and M1 neurons have widespread and individually weak intracortical connections; measuring the dynamics of such connections with dual single-neuron recording methods would be diminishingly small (Truccolo et al. 2010). To overcome this methodological limitation, partial spike-field coherence (PSFC) has been used to examine the relationship between the spiking of individual neurons in one area and LFP, as a measure of larger-scale interactions, in another. PSFC reflects primarily the degree of phase synchronization between spike times and LFP, after the coherence between the LFPs in areas 2/5 and M1 has been accounted for by “partialling” it out (Fries et al. 2001; Mitra and Bokil 2008; Pesaran et al. 2008). Using this approach, Pesaran et al. (2008) detected significant PSFC in 9% of 138 single neuron-LFP pairings between the spiking of single neurons in parietal area PRR and an LFP in dorsal premotor cortex of a monkey performing a center-out reaching task. These authors found significant PSFC in this small population at ∼15 Hz that was strongest around the time of onset of the targets for reach and during the reach performance.

Using a similar approach, Witham et al. (2007) measured spike-field coherence between single neurons in parietal areas 3a, 2, and 5 and a LFP in M1 of rhesus monkeys performing an index finger flexion task. This task required the monkey to move a lever to a target position with its index finger and maintain the lever on target for a hold period of 2 s. The authors found spike-field coherence in the beta range (∼17.5 Hz) during the hold period of the task; however, the strength of coherence was low (≤0.05, on average).

One shortcoming of this single cell-based approach is that synaptic currents recorded in the LFP emerge from population collective dynamics that are too weak to be detected statistically from the spiking of a single cell. To overcome methodological limitations in detecting circuit interactions, we developed an approach to evaluate the timing and strength of functional coupling between 2/5 and M1 at the ensemble scale by creating a new variant of PSFC. This approach uses the combined superimposed spike time series (SSTS) obtained from simultaneous recorded neural populations in one area and the LFP in another.

In the present study, we employed this ensemble-based method and used it to examine the collective dynamics of interaction between 2/5 and M1. We compared the PSFC detected by ensemble-LFP pairings to that detected by single neuron-LFP pairings. Data were based on recordings from 96-channel microelectrode arrays implanted in both M1 and area 2/5 of the three monkeys trained to perform reaching movements. Populations of simultaneously recorded neurons were used as the collective, superimposed spiking source to expose the aggregate ensemble influence and provide a larger number of events for statistical comparisons. We measured both the timing and the form of information contributed by area 2/5 to M1 LFPs and measured PSFC in three frequency bands: 1–10, 10–40, and 60–200 Hz. Additionally, we measured PSFC between neuron activity in area M1 and LFP in area 2/5 in these frequency bands to examine the bidirectionality of interactions.

Previous studies (Baker et al. 2003; Zeitler et al. 2006) have compared the spike-field coherence computed by the pairing of single neurons with LFP vs. the pairing of single-channel multiunit activity with LFP. Both studies found that multiunit-LFP pairings are associated with stronger spike-field coherence than single neuron-LFP pairings. However, the present study differs from these previous studies because our approach employs a “greedy” search algorithm to select only a subset of the single neurons in area 2/5 that contribute to the strength of PSFC, while excluding the neurons that do not contribute to PSFC. We find that the use of the greedy algorithm to select only a subset of area 2/5 cells yields stronger PSFC than the use of multiunit recordings containing the spike times for all events crossing a voltage threshold.

The final goal of our study was to evaluate the information provided by selected subsets of neurons. We specifically tested whether area 2/5 neurons with a directional bias similar to that of a particular M1 LFP channel are associated with stronger PSFC than area 2/5 neurons with opposite directional bias. Our results suggest that 2/5 contributes information about reach direction to M1 beginning after the onset of arm movement, consistent with a role for 2/5 neurons in providing sensory or central feedback of information related to the movement state of the limb. These results also bear upon the utility of this parietal region as a command signal source for human brain interface applications, which would need to be engaged in the absence of actual movement (Hochberg et al. 2012).

MATERIALS AND METHODS

Behavioral methods.

Three rhesus monkeys (Macaca mulatta; monkeys A, L, and P) were trained to perform a behavioral task involving unimanual center-out arm movements in response to visual cues. In each case, the monkey sat in a primate chair with its right arm on cushioned arm pads while holding a two-joint manipulandum (KINARM system; BKIN Technologies, Kingston, ON, Canada). The manipulandum was freely moveable in the horizontal plane. The shoulder joint was abducted at 85°, so that movements of the shoulder and elbow were in an approximately horizontal plane. The x and y hand (end point) position was sampled at a rate of 20 Hz (monkeys A and P) or 100 Hz (monkey L). Manipulandum end-point position controlled the two-dimensional motion of a cursor on a visual display system, which consisted of a 32 × 45-cm computer monitor (Samsung 213T, Seoul, South Korea) and a mirrored glass (28.5 × 50.5 cm) with ∼50% light transmittance arranged so that the animal viewed the visual stimuli reflected onto the mirrored glass. The computer monitor was suspended 141 cm above and parallel to the floor, facing downward. It projected the visual stimuli onto the mirrored glass surface centered 29 cm from the monkey's eye and tipped at a 41.3° angle.

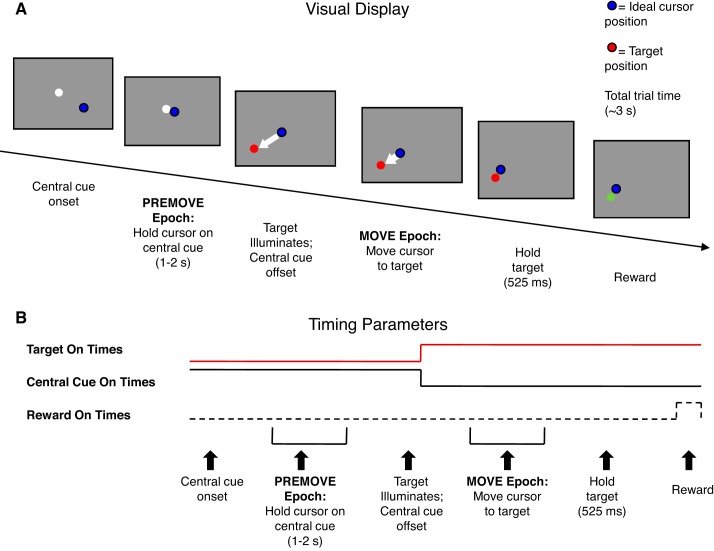
For monkeys A and P, each trial began with the appearance of a white circle (17-mm diameter/3.36° visual angle) at the center of the visual display (see Fig. 1). The animal had to acquire this cue with a feedback cursor (7-mm diameter/1.38° blue circle) that reported hand position based on the location of the end point of the arm manipulandum. After the hand was held at the central cue for 1–2 s (all times were pseudorandomly selected unless specified), a red target circle (17-mm diameter/3.36° diameter) appeared in one of eight equally spaced peripheral locations 4 cm from the center of the display. Target location was randomly selected on each trial, with equal probability. Upon the appearance of the target circle the central cue disappeared, and the animal had to initiate the reach within 1,400 ms, acquire the target within the next 1,400 ms, and then maintain the cursor on the target location for ≥525 ms. Correct trials were rewarded with 0.5 ml of fruit juice.

Fig. 1.

Schematic diagram of the center-out reaching task used in the present study. A: trial sequence as presented on the visual display. White dot, center hold position; blue dot, hand position; red dot, target position. B: trial timing. The center-hold PREMOVE epoch lasts 1–2 s, followed by the MOVE epoch, which is initiated by target illumination. After holding at the target for 525 ms, the target turns green and a reward is delivered. The target then disappears, followed immediately by reappearance of the central cue (white dot) to begin the next trial. Target On times are shown by the red line, Central Cue On times by the black line, and Reward On times by the dashed line. This figure shows the task completed by monkeys A and P; the task completed by monkey L had slight differences (see materials and methods).

Monkey L performed the same task, except for small differences in timing and stimulus parameters. These differences arose because the data for monkey L were originally obtained as part of a different study containing an additional noninterleaved experimental condition that is not reported here. For monkey L, the target and feedback circles were smaller and different colors. The target circle was purple with 9-mm/1.77° visual angle diameter. The feedback circle was blue-green with 7-mm/1.38° diameter. Hold times could be longer (pseudorandomly selected between 1 and 3 s), and the reach distance was slightly longer (4.25 cm from display center). For monkey L, the reach had to be completed within 1,000 ms and hold times were longer (1–2.5 s). Reward sizes were also smaller (0.15 ml of fruit juice).

We separated the recordings into pre- and post-movement onset periods for data analysis. For monkeys A and P, we averaged the arm movement speed over trials and computed jerk, the second derivative of average movement speed. We defined average movement reaction time (RT) as the time between central cue offset and the peak of the jerk during the rising phase of the average arm movement speed profile (Nagasaki 1989). For each trial in monkeys A and P, movement onset was defined as the time of central cue offset + average movement RT. For monkey L, we averaged the arm movement speed over trials and located the time point at which speed crossed a threshold of 0.75 cm/s. Movement onset was defined as time point of central cue offset + latency to this threshold crossing in the average arm movement speed profile.

Throughout this report, pre- and post-movement onset refer to the entire time period before and after the movement onset. We sampled from different intervals of the pre- and post-movement onset time periods to compute the spectra of the M1 LFPs. However, we also use the terms PREMOVE and MOVE to refer to the 1,000 ms preceding or following arm movement onset for the analysis of PSFC.

Eye position was monitored continuously with an infrared eye tracking system (Iscan, Burlington MA). For monkeys A and P, we used TG2 (custom software) to generate visual stimuli and control the behavioral experiment on a laboratory computer. For monkey L, we used TCL (http://www.tcl.tk/).

Electrophysiology.

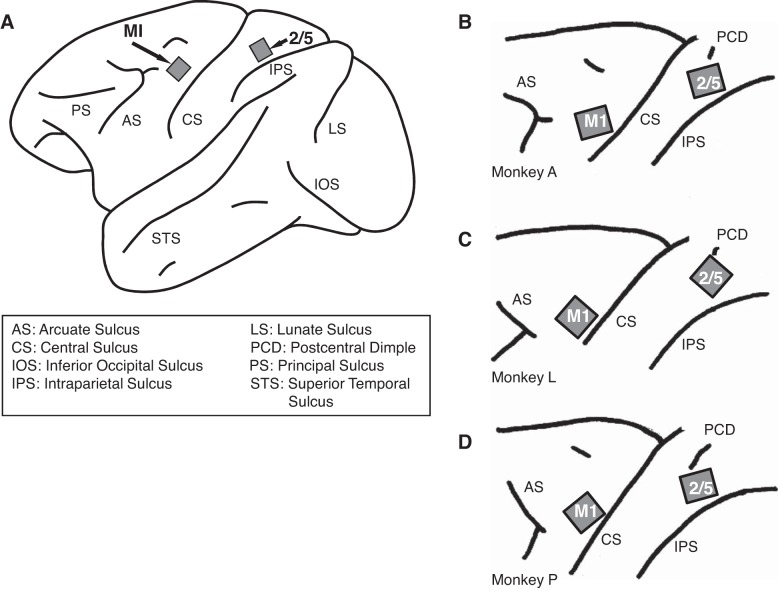
The details of the electrodes and implantation methods are described elsewhere (Suner et al. 2005). Briefly, two silicon-based microelectrode arrays (Blackrock Microsystems, Salt Lake City, UT) composed of 100 electrodes (1.0-mm length; 400-μm interelectrode separation, 96 wired to record) were implanted in M1 and area 2/5. One was implanted in the M1 arm area (see Kwan et al. 1978; Suner et al. 2005; Woolsey et al. 1952). This array was implanted on the precentral gyrus medial to a line extending from the genu of the arcuate sulcus posteriorly to the central sulcus and parallel to the sagittal fissure. The other array was implanted in parietal area 2/5 on the surface of the postcentral gyrus, immediately dorsal to the intraparietal sulcus and ventral to the superior postcentral dimple (see Fig. 2). All surgical, behavioral, and electrophysiological procedures were in compliance with the guidelines of the National Institutes of Health (NIH) and were approved by the Institutional Animal Care and Use Committee (IACUC) of Brown University.

Fig. 2.

Electrode implant sites. A: approximate locations of the microelectrode arrays in the monkeys' cortex. The M1 array is located in the arm area immediately in front of the central sulcus at the level of the principal sulcus and the arcuate genu. The 2/5 array is located immediately in front of the intraparietal sulcus (see materials and methods). B–D: locations of the microelectrode arrays in monkeys A, L, and P, respectively (Philip et al. 2013).

Signals from up to 96 electrodes were recorded from each array during each experimental session. The electrodes had impedance of 100 kΩ–1 MΩ at 1 kHz. All channels were initially analog-band-pass filtered between 0.3 Hz and 7.5 kHz and sampled digitally at 30 kHz per channel with a Cerebus acquisition system (Blackrock Microsystems). To isolate single-unit activity, we used a digital high-pass filter (cutoff at 0.3 kHz) and applied a voltage threshold to the filtered signal. For each channel, the waveform recorded during a window of 1.6-ms length starting 0.33 ms before the voltage crossed a threshold of 5 times the root mean square of 2 s of voltage measurements was saved to disk. Waveforms from each channel were sorted into separate single-unit spike trains with a density clustering algorithm (Vargas-Irwin and Donoghue 2007). All neurons included in the sample had a spike rate of ≥1.818 Hz during the first 1 s after movement onset. These spike rates were computed with partially overlapping 110-ms bins (10-ms overlap). To isolate the LFP recorded on each channel, the original broadband analog signal (0.3 Hz–7.5 kHz) was digitally filtered (low-pass cutoff at 500 Hz) and sampled at 1 kHz. Table 2 summarizes the number of single units and LFPs recorded in the seven recording sessions. Because neuron populations recorded change each day and it is difficult to ascertain which cells remain across sessions, data sets may include overlapping samples of neurons. We treated each data set as an independent neural population.

Table 2.

Summary of neuronal recordings by session

	Single Units in 2/5	Single Units in M1	LFP Channels in 2/5	LFP Channels in M1
Monkey A (4 sessions)
Number	110	389	166	179
% Directionally tuned	51.8	60.2	82.5	94.4
Monkey L (2 sessions)
Number	50	24	85	93
% Directionally tuned	46	83.3	84.7	89.2
Monkey P (1 session)
Number	64	29	45	42
% Directionally tuned	40.6	37.9	82.2	78.6

M1, primary motor cortex; 2/5, area 2/5; LFP, local field potential.

During each recording session, we recorded 48 LFP channels in M1 and 48 LFP channels in area 2/5 (every other electrode in the array was used). LFP channels were rejected from the data analysis if they were corrupted by electrical noise artifact, which may reflect broken connections. Such artifacts were evidenced by extreme values for voltage, outside the normal physiological range of a cortical LFP. To determine the range of acceptable values for LFP voltage, we computed a 95% confidence interval for LFP voltage as the 2.5th and 97.5th percentiles of all sorted LFP voltages recorded on all channels for each monkey. Channels in which >10% of the LFP voltages exceeded the 95% confidence interval were discarded.

Characterization of directional tuning.

For spiking activity recordings, the directional tuning was calculated as the center of mass, or vector average, of spike rate across all target directions in the 100-ms bin during the MOVE epoch that yielded the highest spike rate. These spike rates were calculated with nonoverlapping bins of 100-ms length. We chose to compute the preferred direction (PD) based on a short time window of neural activity because recent research shows that the directional tuning of cortical neurons in the motor system can show significant changes on a timescale of ∼100 ms (Rickert et al. 2009). For M1 LFP channels, we first band-pass filtered the LFP signal between 1 and 10 Hz with a finite impulse response filter with a Kaiser window. We then computed the center of mass of the mean of the squared LFP voltages during the MOVE epoch. For both spiking activity and LFP, the significance of directional tuning was evaluated by a Raleigh test.

Partial spike-field coherence.

We calculated the spike-field coherence between area 2/5 spikes and M1 LFP to examine putative input to M1 from 2/5. To remove the contribution of coherence between the LFPs recorded in the two areas and coherence between spikes and LFP recorded in 2/5, we used partial spike-field coherence (PSFC; see Pesaran et al. 2008). Here the time series of spikes recorded in 2/5 is denoted ΔN(t), the LFP recorded in M1 is denoted x(t), and the LFP recorded in 2/5 is denoted y(t).

Single-neuron spike times and LFP across the MOVE and PREMOVE periods (the 1 s defined above) were aligned to arm movement onset for each trial. Spike trains were treated as binary vectors. We subtracted the mean over the ensemble of trials from each time point on a trial-by-trial basis for both spike and LFP data (i.e., we subtracted the mean perievent time histogram) and then subtracted the trial's temporal mean from each time point in the trial.

We used nonparametric multitaper spectral estimation (Percival and Walden 1993; Thomson 1982) to perform the PSFC analysis separately for the PREMOVE and MOVE epochs. Power, cross-power, and coherency spectra were computed with the Chronux toolbox for MATLAB (Bokil et al. 2010). The PSFC was further computed with the following equation:

$$C_{X\Delta N|Y}\left(f\right)=\frac{\left|C_{X\Delta N}\left(f\right)-C_{XY}\left(f\right)C_{Y\Delta N}\left(f\right)\right|}{\sqrt{\left(1-{\left|C_{XY}\left(f\right)\right|}^2\right)\left(1-{\left|C_{Y\Delta N}\left(f\right)\right|}^2\right)}}$$ (1)

C_XΔN(f), the spike-field coherency between x(t), the LFP recorded in M1, and ΔN(t), the spiking activity of the neuron recorded in area 2/5, is given by

$$C_{X\Delta N}\left(f\right)=\frac{\langle \tilde{X}\left(f\right)\Delta \tilde{N}*\left(f\right)\rangle }{\sqrt{S_Y\left(f\right)S_{\Delta N}\left(f\right)}}$$ (2)

C_YΔN(f), the spike-field coherency between ΔN(t), the neuron recorded in 2/5, and y(t), the LFP recorded in 2/5, is given by an analogous equation. C_XY(f), the field-field coherency between x(t), the LFP recorded in M1, and y(t), the LFP recorded in area 2/5, is similarly given by

$$C_{XY}\left(f\right)=\frac{\langle \tilde{X}\left(f\right)\tilde{Y}*\left(f\right)\rangle }{\sqrt{S_x\left(f\right)S_Y\left(f\right)}}$$ (3)

where X̃(f) and ỹ(f) are the tapered Fourier transforms of x(t) and y(t), respectively. S_ΔN(f) is the power spectrum of ΔN(t), S_X(f) is the power spectrum of x(t), and S_Y(f) is the power spectrum of y(t); * denotes the complex conjugate, and <> denotes the average over trials and windowed Fourier transforms (see Pesaran et al. 2008). We used 5 tapers and a half-bandwidth of 3 Hz to compute the spectral estimate.

In addition to computing the PSFC between single-neuron spike trains and a particular channel's LFP, we also extended this measure to the case in which a population spike train is constructed by compounding or superimposing the spike train process (1-ms time resolution) of a subset of simultaneously recorded neurons. The goal of this new population PSFC, which is described in results, is to increase the sensitivity of the PSFC to detect cortico-cortical interactions by considering spikes of selected ensembles of single neurons. We additionally performed analogous calculations of PSFC for single neurons and neuron ensembles in area M1 and LFP in area 2/5 to examine the reciprocity of this interaction.

To compare unselected interactions, we computed the PSFC between multiunit activity (MUA) in area 2/5 and each M1 LFP channel. MUA was defined as all spiking events that crossed the initially recorded voltage threshold (see above). All channels included in the sample had a spike rate of ≥1.818 Hz during the first 1 s after movement onset. These spike rates were computed with partially overlapping 110-ms bins (10-ms overlap).

Greedy algorithm for PSFC.

We developed a novel procedure using a “greedy” algorithm to compute the PSFC separately for each LFP channel in M1 and the set of neurons in area 2/5. We performed multiple different versions of the greedy algorithm for each recording session. In one version, we selected the neurons that were associated with the strongest PSFC in the 1–10 Hz range using only data from the MOVE epoch. In a second version, we computed PSFC for the PREMOVE epoch selecting neurons that were associated with PSFC in the 10–40 Hz range. In a third version, we computed PSFC for the MOVE epoch selecting neurons that were associated with strongest PSFC in the 60–200 Hz range. In each version, we used data aggregated across all target locations. We used the MOVE epoch for the 1–10 Hz and 60–200 Hz ranges and the PREMOVE epoch for the 10–40 Hz range because our M1 LFP power spectral analysis (see results) showed that M1 LFP power was generally stronger during movement vs. premovement at frequencies <10 Hz and 60–200 Hz and stronger during premovement vs. movement in the 10–40 Hz range.

This greedy algorithm was performed for each M1 LFP channel. In general, the greedy approach is used to reduce the computational burden of an exhaustive search for the one set of neurons that produces the strongest PSFC. To be computationally more efficient, the one spiking unit with the strongest PSFC is found and then each unit is evaluated until the neuron that increases the PSFC is found. This process is continued until a maximum is reached. In other words, given an ensemble of n neurons, on the first iteration of the algorithm, PSFC was computed n times, by separately pairing each of the neurons recorded in area 2/5 with the LFP recorded in M1. The maximum of PSFC in the relevant frequency range was taken as the index of the strength of PSFC across all target directions. The spike times from the neuron that produced the strongest PSFC were then stored in a variable that we term the superimposed spike time series (SSTS).

On the second iteration, spike times from each of the remaining area 2/5 neurons were superimposed with the spike times contained in the SSTS. We then computed PSFC separately for the M1 LFP channel and each of these superimposed spike trains. We selected the neuron that yielded the strongest PSFC after superimposition with the neuron selected on the first iteration. On the nth iteration, the SSTS contained the superimposed spike trains for each of the n area 2/5 neurons.

To control for potential overfitting, we randomly divided the set of trials from a session into two equal-sized subsets: SUBSET 1 and SUBSET 2. We performed the greedy selection procedure as described above on SUBSET 1. We used the selected neurons from SUBSET 1 to create an SSTS composed of the selected ensemble's spiking activity from SUBSET 2. We stored the SSTS from SUBSET 2. Next, we performed the same greedy selection procedure, but now selecting neurons based on SUBSET 2 and constructing and storing the corresponding SSTS from SUBSET 1. The strength of the PSFC produced by the pairing of the M1 LFP and the SSTS typically increased for several iterations of the greedy algorithm, reached a maximum, and then decreased for the remaining iterations of the algorithm (see results) as additional neurons were added. The SSTS for all iterations up to and including the maximum is referred to as the SSTS_Contribute (SSTS_C). We computed the PSFC between the constructed SSTS_C (from SUBSET 1 and SUBSET 2) and their corresponding LFPs. In this way, one PSFC estimated for the entire set of trials was computed under a “twofold” cross-validation (with respect to the greedy neuron selection). We repeated this selection procedure for each of the 314 M1 LFP channels. We additionally performed this procedure for the pairing of 296 PE LFP channels with neuron activity in M1 to examine the reciprocity of the effect.

Statistical significance testing of differences in LFP power.

We compared the differences in M1 LFP power during the movement and premovement periods. We tested for differences in average LFP log power in the 1–3 Hz, 10–40 Hz, and 60–200 Hz frequency bands. To establish a significance level for differences between these two behavioral periods, we performed 1,000 random permutations of data from the movement vs. premovement periods, calculating the difference in average log power for each permutation.

The tests for differences in LFP power were performed on temporal segments different from those in the tests on PSFC. For the 1–3 Hz band, the M1 LFP spectrum related to movement was computed based on the voltages recorded from 250 ms before to 250 ms after movement onset. This was necessary because the mean-subtraction procedure (see above) removed the low-frequency increase in LFP power during arm movement, except during the period of ∼500 ms straddling movement onset. For the 10–40 Hz and 60–200 Hz bands, the spectrum was computed based on the voltages recorded during the first 500 ms after movement onset. We used this epoch for the 10–40 and 60–200 Hz ranges because movement-related changes in the LFP spectra occurred after movement onset in these frequency ranges. For all three frequency bands, we selected the period from 1,000 to 500 ms prior to movement onset as the premovement period.

We used 2 tapers and a half-bandwidth of 3 Hz for spectral estimates computed on data windows of 500-ms length. For the 60–200 Hz band, we removed all power estimates within +/− the half-bandwidth of 60 Hz and its harmonics to remove any influence of electrical line noise. We derived a P value for the difference in LFP power in each frequency band from the distribution of 1,000 permutation-based differences. This permutation test was two-tailed to assess the significance of either increases or decreases in spectral power averaged across frequencies in each band. For these two-tailed tests of the significance of LFP power differences, we used the approximate false discovery rate (FDR; Benjamini and Hochberg 1995) to correct the α-level for multiple tests across animals, sessions, channels, and frequency bands.

Statistical significance testing of PSFC.

To test the significance of PSFC, we applied a z-transformation to the PSFC for each neuron-LFP pairing according to the following equation (Jarvis and Mitra 2001):

$$\text{z}=\beta \left(q-\beta \right)$$ (4)

where

$$q=\sqrt{-\left(v-2\right)*\log (1-{\left|C\right|}^2)}.$$ (5)

β = 1.15, C is the value of PSFC, and v is the number of degrees of freedom given by the number of trials × the number of tapers. The purpose of the z-transformation is to transform the values of PSFC so that, under the null hypothesis, PSFC is distributed as a normal variate with a mean of 0 and variance equal to 1. We derived a P value for each channel for PSFC at its peak in the relevant frequency range by evaluating a standard normal cumulative density function at the z-scored value. We performed these significance tests for each single neuron-LFP pairing in the data set. We also performed analogous tests of the significance of PSFC associated with the pairing of SSTS_C-M1 LFP channel for the PREMOVE and MOVE periods. For each LFP channel, the SSTS_C for the PREMOVE and MOVE epochs were generated with the same set of neurons. In these tests of the significance of PSFC, we used the FDR procedure to correct the α-level for multiple tests across animals, sessions, channels, frequency bands, or behavioral epochs where appropriate. Unlike tests of the difference in average LFP log power in MOVE-PREMOVE, which are represented by a single number, it was necessary to correct across behavioral epochs for PSFC analyses because there are two behavioral epochs in these tests.

We performed Monte Carlo simulations using trial or spike shuffling to further test the significance of PSFC. Unless otherwise noted, each Monte Carlo simulation used 1,000 random permutations of condition labels to build a nonparametric distribution for each frequency. Statistical significance was evaluated for each frequency by comparing the PSFC from the unshuffled data against the nonparametric distribution.

The first permutation test was an additional test of the significance of PSFC at each frequency. We randomly permuted the trial order of the spike data with respect to the trial order of the LFP data and recomputed PSFC 1,000 times to yield a chance level for PSFC at each frequency. The purpose of this test was to determine whether PSFC could be explained by the concomitant change in area 2/5 spike rate and low-frequency modulation of the M1 LFP during the MOVE epoch. If PSFC for the unshuffled data is significant based on this chance-level distribution, then the PSFC must depend upon the precise alignment of spike times and LFP recorded on the same trial, not solely upon the presence of low-frequency movement-related changes in spike rate and LFP voltage.

Next, we tested whether the peak in PSFC in the range of 1–10 Hz from the MOVE epoch was significantly higher than the peak at the same frequency during PREMOVE. To do this, we randomly permuted the MOVE vs. PREMOVE condition labels to create a chance-level distribution for the difference between the peak in the 1–10 Hz PSFCs from the two randomly permuted groups. We compared the difference in peak PSFC in the 1–10 Hz range for the unshuffled data to the chance-level distribution to determine significance. We performed this test for all pairings of SSTS_C-LFP and pairings of single neuron-LFP.

Test for spatial clustering of neurons that produce spike-field coherence.

A spatial clustering analysis was used to test whether or not the neurons in area 2/5 that were associated with significant PSFC were grouped within area 2/5. To do this, we first selected those single neurons that produced significant PSFC in the 1–10 Hz range. We then used the coordinates (on the 10 × 10 array) of the electrodes on which these neurons were recorded to calculate a Euclidean distance matrix. We quantified the dispersion of the neurons as the sum of the distance matrix and used a permutation test to evaluate the significance of the sum of the distance matrix. To compute the nonparametric distribution for the permutation test, we generated random coordinates for a set of neurons the same size as the set of neurons that are associated with significant PSFC and used these randomly selected coordinates to compute a summed distance matrix. We tested the significance of spatial clustering by evaluating the value for the summed distance matrix in the real data against the nonparametric distribution.

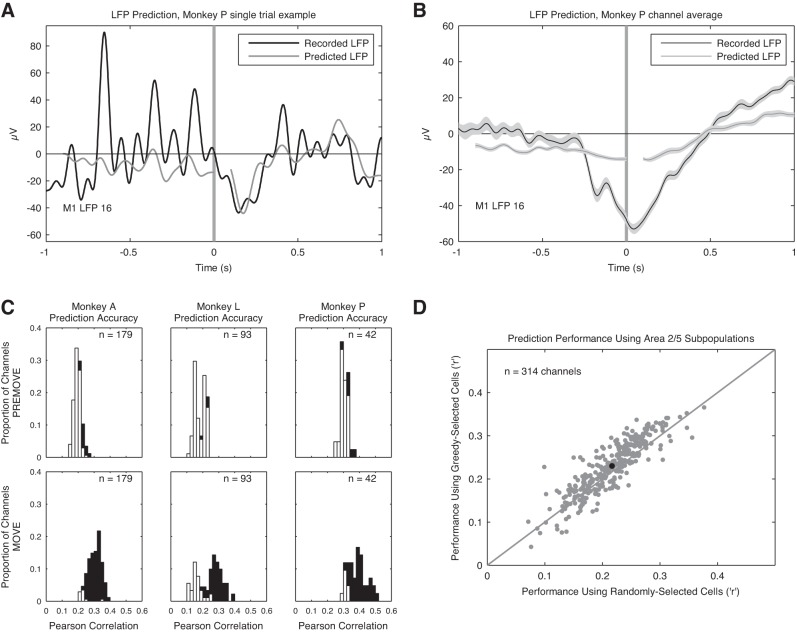
Spike-based LFP prediction.

We used “signal estimation theory” (Poor 1994) to predict the form of M1 LFPs associated with area 2/5 spikes (Gabbiani et al. 1996; Kreiman et al. 2000; Rasch et al. 2009; Warland et al. 1997). To do this, we found a bank of filters that were convolved with area 2/5 spike trains to elicit an estimate, x̂(t), of the M1 LFP signal to be predicted. We band-pass filtered the LFP signal between 1 and 10 Hz with a finite impulse response filter with a Kaiser window prior to computing predictions. As we were interested in the way recent area 2/5 spiking history affected M1 LFP amplitudes, we used 100-ms causal filters (which prevented us from predicting the first 100 ms of LFP data). The filters were represented as weighted sums of 10 temporal basis functions of the raised-cosine type, with log-scaling on the time axis (Pillow et al. 2008; Truccolo et al. 2010). Using basis functions reduced the number of parameters needed for estimation by an order of magnitude and conferred a degree of smoothness on the estimates. The estimate was then computed as

$$\widehat{x}\left(t\right)=\mu +{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{10}z{\left(t\right)}^i\cdot H_j^i}}$$ (6)

where z(t)ⁱ def is the history of a covariate spike train in [t − 0.1, t), Δt = 0.001 s, i = 1,…, n neurons. H_jⁱ = β_jⁱ f_jⁱ s.t. f_j is a raised cosine temporal basis function covering a 100-ms interval, and μ, β_j are scalars. The basis function coefficients, β_j, and a model constant, μ, were solved by least-squares regression.

We independently estimated LFPs from the pre- and post-movement onset periods recorded at each of the M1 channels for all seven sessions and combined data uniformly across trials of all eight reach directions. Fits were carried out under 10-fold cross-validation.

We report statistics on the Pearson correlation coefficient (r) and coefficient of determination (R²) between the predicted and recorded LFP data for each of the 314 channels across the 7 sessions. Hypothesis testing was performed only on r values for simplicity.

We used a Monte Carlo simulation to establish a chance level of prediction accuracy. To perform this simulation, the recorded LFPs were randomized trial by trial, and predictions were performed as before. This was repeated 500 times for each channel. To create the random surrogates, the phases of the Fourier coefficients of an LFP sample were reset to uniformly distributed random values (Schreiber and Schmitz 2000; Theiler et al. 1992). Such a surrogate, in theory, shares identical mean, variance, and power spectrum with the original signal. To avoid computational artifacts that could introduce novel frequencies, the surrogates were then low-pass filtered with a 10-Hz cutoff, using a sixth-order Butterworth filter (Mammen et al. 2009). To establish prediction accuracy significance for each channel, we calculated b, the proportion of accuracy values for the m random predictions that exceeded the actual coefficient, to find a P value. To avoid problems in using unbiased estimators of P in the context of permutation, we used the positively biased estimator (b + 1)/(m + 1) (Phipson and Smyth 2010). We used the FDR method, here defined as α(m + 1)/(2m), to correct α for multiple tests. To assess the overall hypothesis that the predictions did not arise from chance, we also combined the channel-specific P values, using Fisher's method. This P value was also compared to the FDR-corrected α-level.

A similar set of procedures was used for a second Monte Carlo simulation to establish whether the greedy selection procedure identified area 2/5 neurons that could predict M1 LFPs better than random samples of the area 2/5 population. Instead of phase-randomizing the LFPs to generate the Monte Carlo samples, we used randomly sampled subpopulations of area 2/5 neurons of the same size as the greedy-selected subpopulations. The size of this sample population was given by the size of the greedy-selected population for that channel.

RESULTS

Modulation of neural activity in M1 and 2/5 during reach.

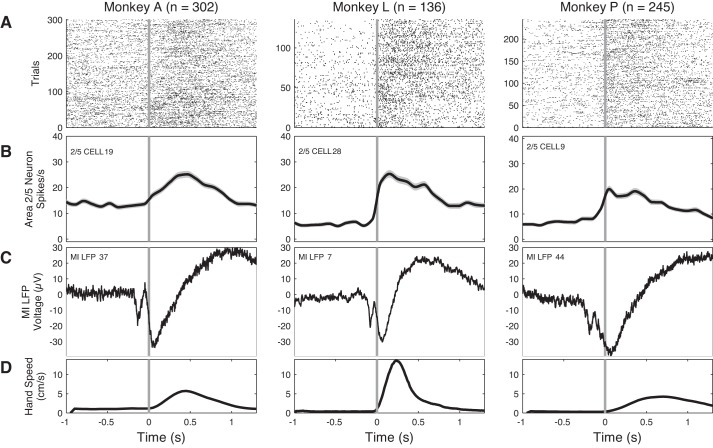
We report the results of seven experimental recording sessions: four sessions in monkey A, two in monkey L, and one in monkey P. The relationship between area 2/5 single-neuron activity, averaged M1 LFP activity for a single channel, and behavioral performance was similar across the three animals (Fig. 3). Monkeys showed about the same success rates (Table 1), although monkey L typically performed with a higher hand speed (Fig. 3D; also see Table 1). Results were comparable across the four sessions in monkey A and the two sessions in monkey L. Thus we summarize results across sessions for each monkey in Tables 1–10.

Fig. 3.

Relationship between neuron activity in 2/5 (A and B), local field potential (LFP) in M1 (C), and arm movement (D): examples of data collected in 1 session shown for monkey A (left), monkey L (center), and monkey P (right). A: raster displays of the firing of 3 single area 2/5 neurons on all trials recorded during 1 experimental session for each of the 3 monkeys, aligned on hand movement onset (time 0, vertical gray line). B: spike histogram from the neuron in A, averaged over trials in partially overlapping bins of 110 ms (10-ms overlap). This histogram was smoothed with interpolation. Number of trials is indicated by n at top. Note that firing rate changes occur near the time of movement onset. C: raw LFP amplitude from 1 LFP channel in M1, averaged over the same set of trials in A and B. D: hand speed (cm/s) averaged over the same trials. The 1,000 ms preceding 0 is the PREMOVE epoch, and the 1,000 ms subsequent to 0 is the MOVE epoch. Note that area 2/5 spiking begins very close to the onset of movement, while the negative field deflection in M1 begins ∼100–200 ms before movement. Also note that the M1 motor event-related potential (mERP) has a shorter overall duration with higher hand speed, which was generally true across channels.

Table 1.

Summary of behavioral data

	Monkey A (4 sessions)	Monkey L (2 sessions)	Monkey P (1 session)
Accuracy of reach to targets	73.4%	80.2%	67.7%
Mean hand speed, cm/s	3.49 ± 1.1	5.28 ± 0.51	3.04 ± 1.07
Time from central cue offset to target acquisition, s	1.16 ± 0.4	0.76 ± 0.11	1.31 ± 0.31

Table 10.

Partial spike-field coherence for pairing of neurons in area M1 with LFP in area 2/5

	Mean Strength of Peak PSFC During PREMOVE Area M1 Neuron-Area 2/5 LFP for Single Neuron-LFP Pairings	Mean Strength of Peak PSFC During PREMOVE Area M1 Neuron-Area 2/5 LFP for SSTSC-LFP Pairings	Mean Strength of Peak PSFC During MOVE Area M1 Neuron-Area 2/5 LFP for Single Neuron-LFP Pairings	Mean Strength of Peak PSFC During MOVE Area M1 Neuron-Area 2/5 LFP for SSTSC-LFP Pairings
Monkey A (4 sessions)
1–10 Hz	0.13 ± 0.03 (78/389)	0.13 ± 0.07 (50/166)	0.15 ± 0.05 (138/389)	0.2 ± 0.1 (107/166)
10–40 Hz	0.11 ± 0.02 (9/389)	0.12 ± 0.03 (42/166)	(0/389)	0.08 ± 0.01 (2/166)
60–200 Hz	(0/389)	0.07 ± 0.03 (2/166)	0.12 (1/389)	(0/166)
Monkey L (2 sessions)
1–10 Hz	0.16 ± 0.04 (2/24)	0.12 ± 0.03 (9/85)	0.15 ± 0.01 (2/24)	0.13 ± 0.05 (13/85)
10–40 Hz	(0/24)	(0/85)	(0/24)	(0/85)
60–200 Hz	(0/24)	(0/85)	(0/24)	(0/85)
Monkey P (1 session)
1–10 Hz	0.1 (1/29)	0.08 ± 0.02 (9/45)	0.15 ± 0.05 (16/29)	0.22 ± 0.07 (43/45)
10–40 Hz	0.14 ± 0.04 (13/29)	0.17 ± 0.06 (40/45)	0.12 ± 0.02 (4/29)	0.1 ± 0.03 (8/45)
60–200 Hz	(0/29)	(0/45)	(0/29)	(0/45)

Values are means ± SD; numbers in parentheses are the proportion of all pairings in which the peak PSFC was significantly greater than 0. α-Level was corrected for multiple tests (FDR method) across monkeys, sessions, channels, frequency bands, and epochs.

The responses of single area 2/5 neurons (Fig. 3, A and B) and LFPs (Fig. 3C) were similar across all three monkeys. Area 2/5 spiking typically increased at or after movement onset and was correlated with hand speed (Fig. 3D). Viewed in the time domain, the M1 mERP (Donchin et al. 2001; Gemba et al. 1981; Rickert et al. 2005) showed a biphasic downward peak that began a few hundred milliseconds before movement onset and then became positive-going after movement progressed (Fig. 3C). We defined a 1-s epoch for PREMOVE and MOVE for data analysis because all three animals required ∼1 s, on average, to complete the reach.

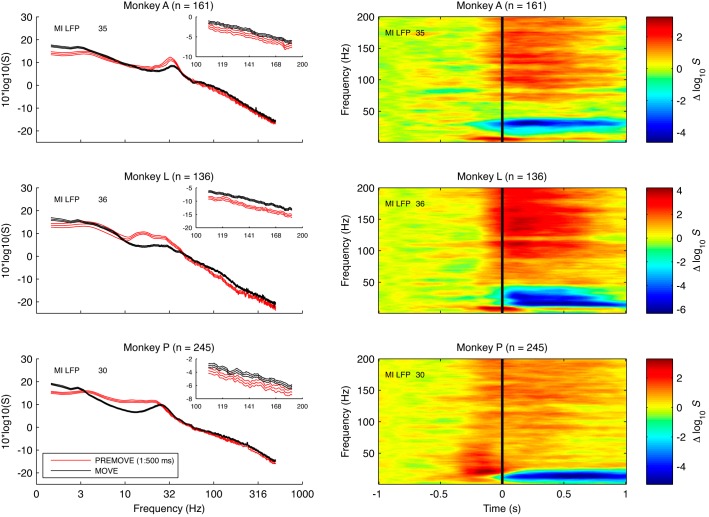
About half of area 2/5 neurons and nearly all M1 LFP channels were directionally tuned (Table 2, Fig. 4, Fig. 5). Three consistent features were evident in these LFP power spectra before and after movement onset (Fig. 6). First, LFP power in the range of ∼10–40 Hz (“beta range”) was elevated in the premovement period compared with the post-movement onset period, consistent with the drop in “fast oscillations” at movement onset previously reported for M1 (Donoghue et al. 1998). Second, LFP power in the range of ∼1–3 Hz was elevated during the post-movement onset period, consistent with the prominent mERP. Third, a small, very broad increase in LFP power was evident at highest frequencies (>60 Hz; gamma range) in the postmovement epoch. Thus, with movement, there was a characteristic decrease in the beta range and an increase in gamma and low-band LFP power (Table 3).

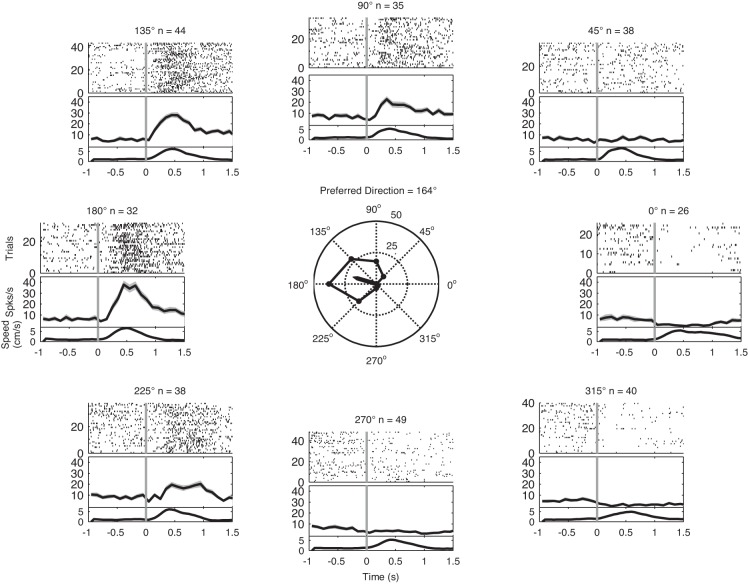
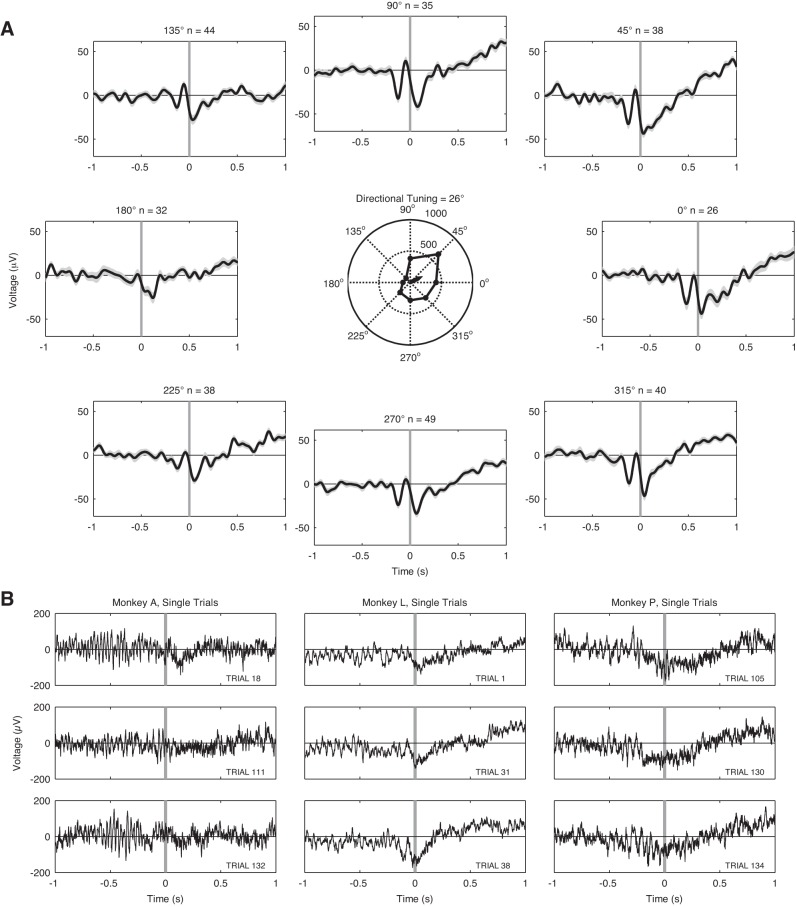
Fig. 4.

Representative, directionally tuned single neuron in area 2/5. Top of each subplot shows a raster of spike times occurring on each trial aligned on start of arm movement (vertical gray line). Middle of each plot shows the average spike rate in 100-ms bins; shaded gray lines indicate ±1 SE of average spike rate. Bottom of each plot shows averaged hand speed (cm/s). Arrow in polar plot (center) shows the preferred direction (PD) of this neuron during the MOVE epoch. Peak spiking for each target direction during movement is shown in the polygon. The inner circle indicates 25 spikes/s, and the outer circle indicates 50 spikes/s. As for other area 2/5 neurons, firing increases near or after the onset of movement.

Fig. 5.

A: M1 LFP voltages averaged over trials for each of the 8 target locations during 1 experimental session (monkey A). Numbers of trials are indicated by n above each subplot. LFP shown here was band-pass filtered between 1 and 10 Hz with a finite impulse response filter with a Kaiser window. Shaded gray lines indicate ±1 SE of the LFP voltages. Vertical gray line at time 0 indicates the start of arm movement. Arrow in polar plot (center) shows the PD of the LFP signal during the MOVE period (same conventions as Fig. 4). B: examples of LFP recorded on 3 individual trials of the experiment in each monkey. LFP shown here contains the full 0.3- to 500-Hz signal. Note that high-frequency (“gamma”) activity is associated with the MOVE epoch.

Fig. 6.

Left: representative power spectra of LFP recorded in M1. Each plot shows power spectra of 1 LFP recorded in M1 on 1 recording session for 500 ms of pre-movement onset (red) and post-movement onset (black) period from monkey A (top), monkey L (middle), and monkey P (bottom). Insets: spectra of LFP in the 100–200 Hz range. Note that LFP power (10–40 Hz) is greater for the pre- vs. post-movement onset periods. Also note a very broad increase in LFP power in the post-movement onset period at frequencies < 10 Hz and at high frequencies (see inset). Error bars are 95% confidence intervals (CIs) based on a jackknife procedure. A notch filter was used to remove line noise artifacts for this figure. Right: time-frequency spectrograms showing spectral modulation of representative LFP recorded in M1. The spectrograms were computed with a sliding window of 500 ms length, a step size of 10 ms, a half-bandwidth of 3 Hz, and 2 tapers. Each plot shows spectrogram for 1 LFP recorded in M1 on 1 recording session for ±1 s around movement onset from monkey A (top), monkey L (middle), and monkey P (bottom). Spectrograms show the change in log power relative to the average log power at each frequency during the first 500 ms of the pre-movement onset period. Number of trials is indicated by n. Note that LFP power (10–40 Hz) is greater for the pre-movement onset vs. post-movement onset periods. Also note increase in LFP power around the time of movement onset at frequencies < 10 Hz and a very broad increase at high frequencies > 60 Hz during the post-movement onset period.

Table 3.

Differences in M1 LFP power during pre- and post-movement onset periods

	1–3 Hz	10–40 Hz	60–200 Hz
Monkey A (4 sessions)
Pre-movement onset	0/179	179/179 (100%)	1/179 (0.6%)
Post-movement onset	137/179 (76.5%)	0/179	162/179 (90.5%)
Monkey L (2 sessions)
Pre-movement onset	0/93	92/93 (98.9%)	0/93
Post-movement onset	79/93 (84.9%)	0/93	92/93 (98.9%)
Monkey P (1 session)
Pre-movement onset	0/42	27/42 (64.3%)	0/42
Post-movement onset	3/42 (7.1%)	0/42	20/42 (47.6%)

Values indicate the proportion (%) of channels in which a significant increase in M1 LFP power occurred in each frequency band and epoch. Pre-movement onset is −1,000 to −500 ms before movement onset for all frequency bands. Post-movement onset is ±250 ms around movement onset for the 1–3 Hz band and 0 to 500 ms after movement onset for the 10–40 and 60–200 Hz bands. False discovery rate (FDR) correction of α-level was applied across animals, sessions, channels, and frequency bands.

Significant coherence between single-neuron spike trains in area 2/5 and LFP in M1.

To initially examine the functional interactions between area 2/5 spiking activity and M1 LFP, we computed the PSFC for the MOVE and PREMOVE epochs separately for each 2/5 neuron and a single M1 LFP channel. In general, PSFC for single neuron-LFP pairings was not common, although PSFC was more often significant during MOVE than PREMOVE (Table 4, Table 5). Across all three monkeys, there were 7/224 (3.13%) significant pairings during the PREMOVE epoch. The PSFC was significant in a larger fraction (51/224; 22.8%) of pairs during MOVE. These data indicate that coupling increases at movement onset. The strength and frequencies of the peak in PSFC in the 1–10 Hz range for each monkey are shown in Table 4.

Table 4.

Summary of strength and frequencies of peak PSFC in 1–10 Hz range for neuron-LFP pairings with significant PSFC

	Mean Frequency of Peak PSFC During PREMOVE, Hz	Mean Strength of Peak PSFC During PREMOVE	Mean Frequency of Peak PSFC During MOVE, Hz	Mean Strength of Peak PSFC During MOVE
Monkey A (4 sessions)
Single neuron-LFP pairings (1–10 Hz)	1.6 ± 0.3 (n = 6)	0.15 ± 0.01 (n = 6)	2.1 ± 0.6 (n = 44)	0.16 ± 0.06 (n = 44)
SSTSC-LFP pairings (1–10 Hz)	2.6 ± 1.7 (n = 79)	0.12 ± 0.04 (n = 79)	2.8 ± 1.1 (n = 153)	0.2 ± 0.08 (n = 153)
Monkey L (2 sessions)
Single neuron-LFP pairings (1–10 Hz)	(n = 0)	(n = 0)	1.7 ± 0.5 (n = 4)	0.19 ± 0.03 (n = 4)
SSTSC-LFP pairings (1–10 Hz)	(n = 0)	(n = 0)	1.6 ± 0.24 (n = 31)	0.14 ± 0.02 (n = 31)
Monkey P (1 session)
Single neuron-LFP pairings (1–10 Hz)	1.5 (n = 1)	0.13 (n = 1)	1.6 ± 0.3 (n = 3)	0.14 ± 0.03 (n = 3)
SSTSC-LFP pairings (1–10 Hz)	9.8 (n = 1)	0.07 (n = 1)	3.8 ± 1.8 (n = 24)	0.1 ± 0.03 (n = 24)

Values are means ± SD; n indicates number of pairings. These results were obtained with a temporal window of 1,000 ms, a half-bandwidth for spectral estimation of 3 Hz, and 5 dpss tapers. α-Level was corrected for multiple tests (FDR method) across animals, sessions, channels, bands, and behavioral epochs. PSFC, partial spike-field coherence; SSTS_C, SSTS_Contribute.

Table 5.

Significance of peak PSFC in 1–10 Hz range based on permutation test

	Permutation Test of Significance During PREMOVE	Permutation Test of Significance During MOVE	Permutation Test of PREMOVE vs. MOVE	Permutation Test of MOVE vs. PREMOVE
Monkey A (4 sessions)
Single neuron-LFP pairings (1–10 Hz)	56/110 (50.9%)	90/110 (81.8%)	5/110 (4.5%)	50/110 (45.5%)
SSTSC-LFP pairings (1–10 Hz)	154/179 (86%)	176/179 (98.3%)	6/179 (3.4%)	139/179 (77.7%)
Monkey L (2 sessions)
Single neuron-LFP pairings (1–10 Hz)	16/50 (32%)	21/50 (42%)	2/50 (4%)	9/50 (18%)
SSTSC-LFP pairings (1–10 Hz)	31/93 (33.3%)	60/93 (64.5%)	4/93 (4.3%)	30/93 (32.3%)
Monkey P (1 session)
Single neuron-LFP pairings (1–10 Hz)	24/64 (37.5%)	36/64 (56.3%)	5/64 (7.8%)	14/64 (21.9%)
SSTSC-LFP pairings (1–10 Hz)	31/42 (73.8%)	39/42 (92.9%)	6/42 (14.3%)	25/42 (59.5%)

First and second columns indicate the proportion of pairings (single neuron-LFP and SSTS_C-LFP) in which the peak of PSFC in the 1–10 Hz range was significantly larger than 0 (PREMOVE and MOVE epochs) according to a trial-permutation test. See materials and methods for details of the permutation test. These results indicate that significant PSFC in the 1–10 Hz range cannot be explained as an artifact resulting from the simultaneous change in area 2/5 spike rate and low-frequency modulation of the M1 LFP. Third and fourth columns give the proportion of pairings in which the 1–10 Hz peak during PREMOVE exceeded MOVE and the proportion of pairings in which the 1–10 Hz peak during MOVE exceeded PREMOVE, respectively. α-Level was corrected for multiple tests (FDR method) across animals, sessions, channels and epochs.

To address the concern that the PSFC for single neuron-LFP pairings could be explained by the concomitant increase in spike rate of area 2/5 neurons and the low-frequency mERP, we also conducted a permutation test as described in materials and methods. For the PREMOVE epoch PSFC in the 1–10 Hz range was greater than 0 (P < 0.05; FDR correction) in 96/224 (42.9%) of the pairings across all three monkeys, and for the MOVE epoch this PSFC was greater than 0 in 147/224 (65.6%) of the pairings across all monkeys (Table 5). This result indicates that PSFC in the range of 1–10 Hz depends on the coherence between area 2/5 spiking and M1 LFP on a trial-by-trial basis and cannot be explained as a by-product of the simultaneous increase in spike rate of area 2/5 cells and the low-frequency modulation of the M1 LFP alone.

Most pairings produced significantly stronger (P < 0.05; FDR correction) PSFC in the 1–10 Hz range during MOVE vs. PREMOVE. The maximum PSFC in the 1–10 Hz range was significantly larger during PREMOVE vs. MOVE in 12/224 (5.4%) of the pairings across all three monkeys. Conversely, the maximum PSFC in the 1–10 Hz range was significantly larger (P < 0.05; FDR correction) during MOVE vs. PREMOVE in 73/224 (32.6%) of the pairings (Table 5).

We also tested for PSFC between single neurons in area 2/5 and LFP in M1 in the beta (10–40 Hz) and gamma (60–200 Hz) frequency ranges. None of the single neuron-LFP pairings had significant PSFC in the 10–40 Hz range during either the PREMOVE or MOVE epoch. Similarly, in the 60–200 Hz (gamma) range, single neuron-LFP pairings show little coherence in either the PREMOVE or MOVE epochs (Table 6, Table 7).

Table 6.

Summary of strength and frequencies of peak PSFC in 10–40 Hz range for neuron-LFP pairings with significant PSFC

	Mean Frequency of Peak PSFC During PREMOVE, Hz	Mean Strength of Peak PSFC During PREMOVE	Mean Frequency of Peak PSFC During MOVE, Hz	Mean Strength of Peak PSFC During MOVE
Monkey A (4 sessions)
Single neuron-LFP pairings (10–40 Hz)	(n = 0)	(n = 0)	(n = 0)	(n = 0)
SSTSC-LFP pairings (10–40 Hz)	(n = 0)	(n = 0)	(n = 0)	(n = 0)
Monkey L (2 sessions)
Single neuron-LFP pairings (10–40 Hz)	(n = 0)	(n = 0)	(n = 0)	(n = 0)
SSTSC-LFP pairings (10–40 Hz)	19.9 ± 2 (n = 33)	0.14 ± 0.02 (n = 33)	(n = 0)	(n = 0)
Monkey P (1 session)
Single neuron-LFP pairings (10–40 Hz)	(n = 0)	(n = 0)	(n = 0)	(n = 0)
SSTSC-LFP pairings (10–40 Hz)	17.8 ± 7.4 (n = 15)	0.09 ± 0.03 (n = 15)	31 ± 4.2 (n = 4)	0.07 ± 0.02 (n = 4)

Values are means ± SD; n indicates number of pairings. PSFC for single neuron-LFP pairings does not reach significance in this frequency band. For the SSTS_C-LFP pairings, PSFC can be detected in 2 of 3 monkeys, especially during the PREMOVE epoch in the 10–40 Hz range. The greedy algorithm for the 10–40 Hz range selected for PSFC during the PREMOVE epoch. α-Level was corrected for multiple tests (FDR method) across monkeys, sessions, channels, frequency bands, and epochs.

Table 7.

Summary of strength and frequencies of peak PSFC in 60–200 Hz range for neuron-LFP pairings with significant PSFC

	Mean Frequency of Peak PSFC During PREMOVE, Hz	Mean Strength of Peak PSFC During PREMOVE	Mean Frequency of Peak PSFC During MOVE, Hz	Mean Strength of Peak PSFC During MOVE
Monkey A (4 sessions)
Single neuron-LFP pairings (60–200 Hz)	(n = 0)	(n = 0)	(n = 0)	(n = 0)
SSTSC-LFP pairings (60–200 Hz)	111.6 ± 46.6 (n = 2)	0.09 ± 0.02 (n = 2)	75.2 (n = 1)	0.1 (n = 1)
Monkey L (2 sessions)
Single neuron-LFP pairings (60–200 Hz)	(n = 0)	(n = 0)	(n = 0)	(n = 0)
SSTSC-LFP pairings (60–200 Hz)	118.2 ± 25.4 (n = 3)	0.12 ± 0.004 (n = 3)	141.8 ± 73.5 (n = 2)	0.11 ± 0.03 (n = 2)
Monkey P (1 session)
Single neuron-LFP pairings (60–200 Hz)	(n = 0)	(n = 0)	122.1 (n = 1)	0.1 (n = 1)
SSTSC-LFP pairings (60–200 Hz)	133.8 (n = 1)	0.07 (n = 1)	105 (n = 1)	0.08 (n = 1)

Values are means ± SD; n indicates number of pairings. PSFC for single neuron-LFP pairings and SSTS_C-LFP in this frequency range is rarely significant. α-Level was corrected for multiple tests (FDR method) across monkeys, sessions, channels, frequency bands, and epochs.

Single neurons associated with PSFC in the 1–10 Hz range showed spatial organization within area 2/5 in only one of the three monkeys, according to Euclidean distance test (see materials and methods). Single neurons associated with PSFC in the 1–10 Hz range in monkey P were significantly clustered in the center of the area 2/5 array, which was on the surface of the postcentral gyrus, ventral to the postcentral dimple.

To compute PSFC, the spike-field coherence between the area 2/5 neuron and the local area 2/5 LFP channels is factored out (Eq. 1). We report spike-field coherence for the pairing of area 2/5 neurons and area 2/5 LFP in Table 8. Additionally, we report spike-field coherence for the pairing of area 2/5 neurons and M1 LFP (without the removal of the local spike-field coherence) in Table 9.

Table 8.

Spike-field coherence for pairings of area 2/5 neurons and area 2/5 LFP

	Mean Strength of Peak SFC During PREMOVE Area 2/5 Neuron-Area 2/5 LFP for Single Neuron-LFP Pairings	Mean Strength of Peak SFC During PREMOVE Area 2/5 Neuron-Area 2/5 LFP for SSTSC-LFP Pairings	Mean Strength of Peak SFC During MOVE Area 2/5 Neuron-Area 2/5 LFP for Single Neuron-LFP Pairings	Mean Strength of Peak SFC During MOVE Area 2/5 Neuron-Area 2/5 LFP for SSTSC-LFP Pairings
Monkey A (4 sessions)
1–10 Hz	0.15 ± 0.04 (11/110)	0.18 ± 0.07 (167/179)	0.15 ± 0.05 (34/110)	0.26 ± 0.09 (178/179)
10–40 Hz	0.18 ± 0.06 (3/110)	0.1 ± 0.03 (36/179)	0.15 ± 0.02 (3/110)	0.1 ± 0.02 (36/179)
60–200 Hz	0.13 (1/110)	0.08 ± 0.02 (12/179)	(0/110)	0.11 ± 0.02 (16/179)
Monkey L (2 sessions)
1–10 Hz	0.17 (1/50)	0.12 ± 0.01 (5/93)	(0/50)	0.14 ± 0.04 (18/93)
10–40 Hz	(0/50)	0.12 ± 0.02 (48/93)	(0/50)	0.13 ± 0.02 (33/93)
60–200 Hz	(0/50)	0.14 ± 0.02 (6/93)	(0/50)	0.12 ± 0.02 (11/93)
Monkey P (1 session)
1–10 Hz	0.12 ± 0.02 (10/64)	0.15 ± 0.05 (39/42)	0.14 ± 0.02 (13/64)	0.16 ± 0.06 (38/42)
10–40 Hz	0.15 ± 0.05 (28/64)	0.24 ± 0.05 (42/42)	0.14 ± 0.04 (15/64)	0.2 ± 0.05 (42/42)
60–200 Hz	0.12 (1/64)	0.08 ± 0.02 (13/42)	0.11 ± 0.01 (2/64)	0.09 ± 0.02 (29/42)

Spike-field coherence (SFC) for the local area 2/5 recordings is partialled out to compute PSFC as in Eq. 1. Mean ± SD strength of these spike-field coherence values for all statistically significant pairings in each frequency band is shown. Numbers in parentheses are the proportion of all pairings in which the peak spike-field coherence was significantly greater than 0. α-Level was corrected for multiple tests (FDR method) across monkeys, sessions, channels, frequency bands, and epochs.

Table 9.

Spike-field coherence for pairing of neurons in area 2/5 with LFP in M1

	Mean Strength of Peak SFC During PREMOVE Area 2/5 Neuron-M1 LFP for Single Neuron-LFP Pairings	Mean Strength of Peak SFC During PREMOVE Area 2/5 Neuron-M1 LFP for SSTSC-LFP Pairings	Mean Strength of Peak SFC During MOVE Area 2/5 Neuron-M1 LFP for Single Neuron-LFP Pairings	Mean Strength of Peak SFC During MOVE Area 2/5 Neuron-M1 LFP for SSTSC-LFP Pairings
Monkey A (4 sessions)
1–10 Hz	0.14 ± 0.03 (7/110)	0.13 ± 0.04 (118/179)	0.17 ± 0.5 (48/110)	0.23 ± 0.08 (173/179)
10–40 Hz	(0/110)	0.13 (1/179)	(0/110)	(0/179)
60–200 Hz	(0/110)	0.09 ± 0.02 (4/179)	(0/110)	0.08 ± 0.02 (2/179)
Monkey L (2 sessions)
1–10 Hz	(0/50)	(0/93)	0.19 ± 0.04 (4/50)	0.14 ± 0.02 (38/93)
10–40 Hz	(0/50)	0.14 ± 0.02 (49/93)	(0/50)	(0/93)
60–200 Hz	(0/50)	0.12 ± 0.004 (3/93)	(0/50)	0.11 ± 0.03 (2/93)
Monkey P (1 session)
1–10 Hz	0.12 ± 0.01 (2/64)	0.07 ± 0.01 (2/42)	0.13 ± 0.03 (6/64)	0.1 ± 0.04 (26/42)
10–40 Hz	0.13 (1/64)	0.1 ± 0.03 (33/42)	0.12 ± 0.02 (2/64)	0.09 ± 0.02 (29/42)
60–200 Hz	(0/64)	0.07 (1/42)	0.11 (1/64)	0.08 (1/42)

Spike-field coherence (SFC) for the pairing of area 2/5 neurons with M1 LFP is partialled out to compute PSFC as in Eq. 1. Mean ± SD strength of these spike-field coherence values for all statistically significant pairings in each frequency band is shown. Numbers in parentheses are the proportion of all pairings in which the peak spike-field coherence was significantly greater than 0. α-Level was corrected for multiple tests (FDR method) across monkeys, sessions, channels, frequency bands, and epochs.

Significant coherence between superimposed spike trains of 2/5 neurons and M1 LFP.

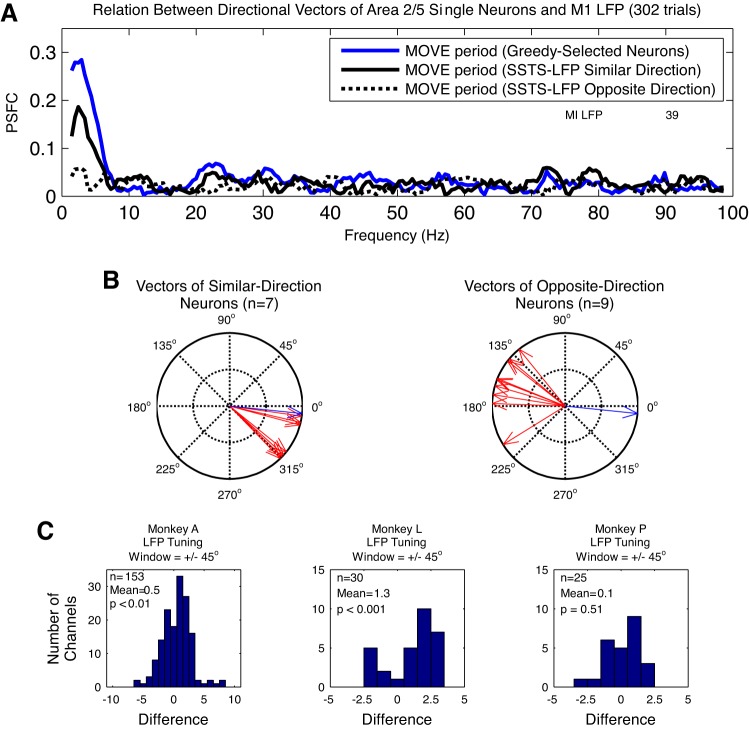
Because cortico-cortical interactions are typically pairwise weak, we attempted to increase the PSFC by combining the spike trains of multiple neurons in a superimposed point process. To create this ensemble level interaction, we use a greedy algorithm (see materials and methods); the nature of this approach is to first select the single neuron that provides the strongest PSFC and then select the next neuron that maximally increases the PSFC, until a peak is reached. This then identifies, in principle, a set of area 2/5 neurons subselected for their effect on M1. Figure 7 illustrates the iterative computation of PSFC for the combination of one M1 LFP channel and a set of area 2/5 neurons recorded for one session. Note that the maximum PSFC at frequencies below 10 Hz increases on successive iterations. Separate greedy algorithms were performed for the 1–10, 10–40, and 60–200 Hz ranges.

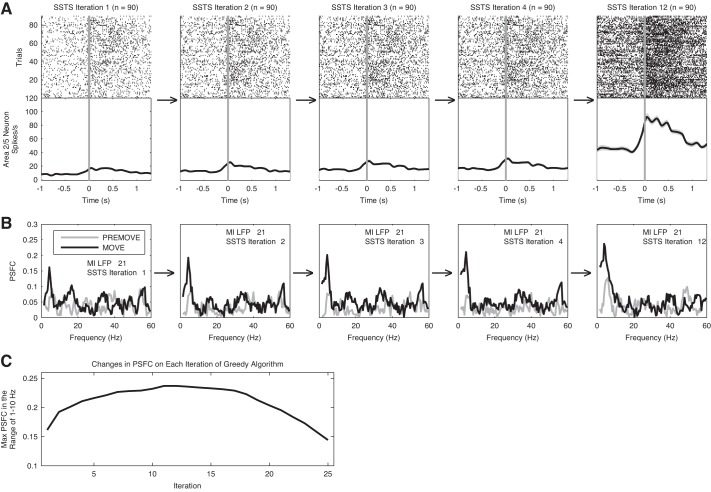
Fig. 7.

Computation of partial spike-field coherence (PSFC) by the greedy algorithm. This figure illustrates the iterative computation of PSFC in the 1–10 Hz range for the combination of 1 M1 LFP channel and the set of neurons recorded in area 2/5 on 1 recording session. Activity on only 1 of the 2 subsets of trials in the experiment used to perform cross-validation (see materials and methods) is shown. First plot in A shows the trial-by-trial raster of spike times and average spike rate of the 2/5 neuron that was selected on iteration 1 of the greedy algorithm for 1 LFP channel; first plot in B shows the PSFC calculated for this single neuron and LFP channel. PSFC for the PREMOVE period is shown in gray, and PSFC for the MOVE period is shown in black. Second plot in A shows the trial-by-trial raster of spike times for the superimposed spike time series (SSTS) on iteration 2 of the greedy algorithm. The SSTS on iteration 2 includes the superimposed set of spike times from the neurons that were selected on the first 2 iterations of the algorithm. Second plot in B shows the PSFC computed for this SSTS and the LFP channel. Third, fourth, and fifth plots in A and B show these results for iterations 3, 4, and 12 of the greedy algorithm. Note that the strength of coherence at frequencies < 10 Hz increases on successive iterations of the algorithm, as the spike times from additional neurons are included in the SSTS on each iteration. C: changes in the maximum PSFC in the 1–10 Hz range on each iteration of the algorithm. Note that the maximum PSFC increases across iterations, reaches a peak, and then decreases as new cells are added. Spikes for all neurons selected up to and including the neuron selected on the maximum iteration are included in the SSTS_Contribute (SSTS_C).

Although the number of possible choices is large, the maximum PSFC was reached with only a small subset of neurons. For the 1–10 Hz greedy algorithm, the algorithm reached its maximum in an average of 11, 7, and 19 iterations in monkeys A, L, and P, respectively.

There was one pairing of SSTS_C and M1 LFP channel for each of the M1 LFP channels used in the study. Including all such pairings across all three monkeys, the PSFC for the PREMOVE epoch in the range of 1–10 Hz was significant in 80/314 (25.5%) pairings. The 1–10 Hz PSFC for the MOVE epoch was significant in 208/314 (66.2%; Table 4).

We evaluated whether 1–10 Hz PSFC produced through greedy selection was a by-product of the simultaneous increase in area 2/5 spike rate and low-frequency change in M1 LFP. The results of this permutation test showed that PSFC in the 1–10 Hz range was significant in 216/314 (68.8%) of the pairings during the PREMOVE epoch and 275/314 (87.6%) of the pairings across all three monkeys during the MOVE epoch (Table 5). These results indicate that this PSFC cannot be explained as a by-product of the simultaneous increase in spike rate of the SSTS ensemble and the low-frequency modulation of the M1 LFP alone.

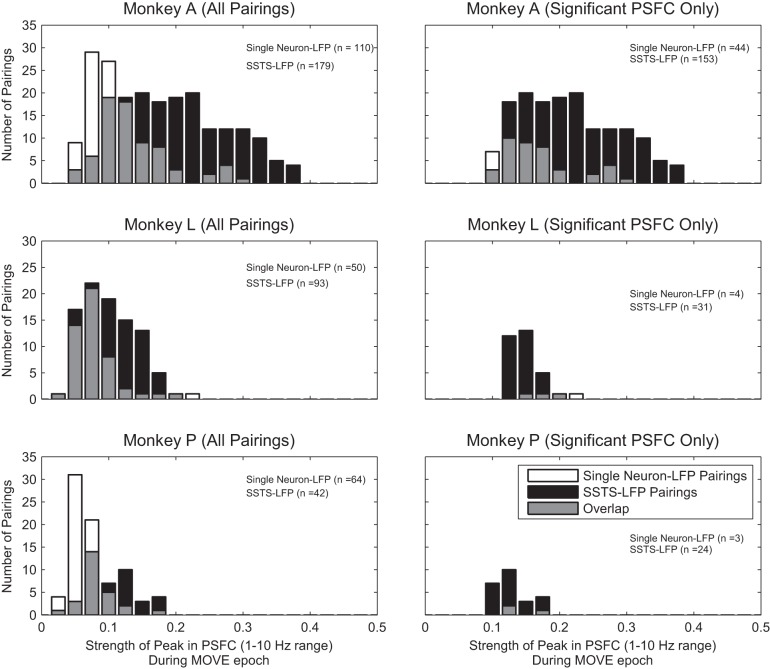
Comparisons of the ensemble to single-channel analysis showed that the greedy algorithm identified functional connectivity missed by single neuron-LFP pairing (Fig. 8). The pairing of SSTS_C-LFP yielded significantly stronger PSFC in the 1–10 Hz range than the pairing of single neuron-LFP in each monkey [monkey A: F(1,286.7) = 104.8, P < 0.001; monkey L: F(1,107.7) = 7, P < 0.01; monkey P: F(1,67.6) = 34.8, P < 0.001; 1-way ANOVA, Welch's method using z-transformed values].

Fig. 8.

Strength of PSFC in single neuron-LFP vs. SSTS_C-LFP pairings. Left: strength of PSFC at its peak in the 1–10 Hz range for all pairings of single neuron-LFP and all pairings of SSTS_C-LFP for each of the 3 monkeys. Right: strength of PSFC at its peak in the 1–10 Hz range for all pairings of single neuron-LFP and SSTS_C-LFP in which the PSFC is significantly greater than 0. Note that pairings of SSTS_C-LFP produce stronger PSFC than pairings of single neuron-LFP.

We also conducted control versions of the greedy algorithm that used the opposite epoch to select the neurons for inclusion in the ensemble (i.e., PREMOVE was used to select neurons for the 1–10 Hz range, MOVE was used to select neurons for the 10–40 Hz range, and PREMOVE was used to select neurons for the 60–200 Hz range). These control tests did not change our results qualitatively. In particular, they further supported the conclusion that 1–10 Hz PSFC is stronger during the MOVE epoch. Peak PSFC in the 1–10 Hz range for the PREMOVE epoch when PREMOVE was used to select neurons for superimposition was weaker, on average, than peak PSFC in the MOVE epoch when MOVE was used to select neurons. Average (±SD) peak PSFC across all channels for PREMOVE when that epoch was used for selection was 0.1 ± 0.04, 0.09 ± 0.03, and 0.08 ± 0.02, for monkeys A, L, and P, respectively. Conversely, average peak PSFC across all channels for MOVE when that epoch was used for selection was 0.2 ± 0.08, 0.1 ± 0.04, and 0.1 ± 0.04 for monkeys A, L, and P.

When examining the results of our greedy selection procedure, we found that there was a positive correlation between area 2/5 neuron MOVE epoch spike rate and ordinality of selection by the greedy algorithm in many channels. For the 1–10 Hz PSFC for the pairing of area 2/5 neurons with area M1 LFP, there was a positive correlation between MOVE epoch spike rate and ordinality of selection in 10.1%, 10.8%, and 54.8% of channels in monkeys A, L, and P, respectively. This correlation between neuron spike rate and ordinality of selection prevented us from identifying any relationship between the functional properties (e.g., directional tuning) of individual neurons and their tendency to increase or decrease the strength of PSFC. This positive correlation could have resulted from the fact that the spike-field coherence measure is biased—it tends to overestimate the population statistics for finite sample sizes (low-firing rate neuronal spike trains have fewer spikes/samples than higher-firing rate ones). However, it is important to note that neuronal activity with relatively low spike rate is not associated with stronger PSFC in general. The spike rates of the SSTS_C are generally much higher than those of single neurons, and PSFC associated with SSTS_C-LFP pairings is stronger, on average.

Time of peak coherence.

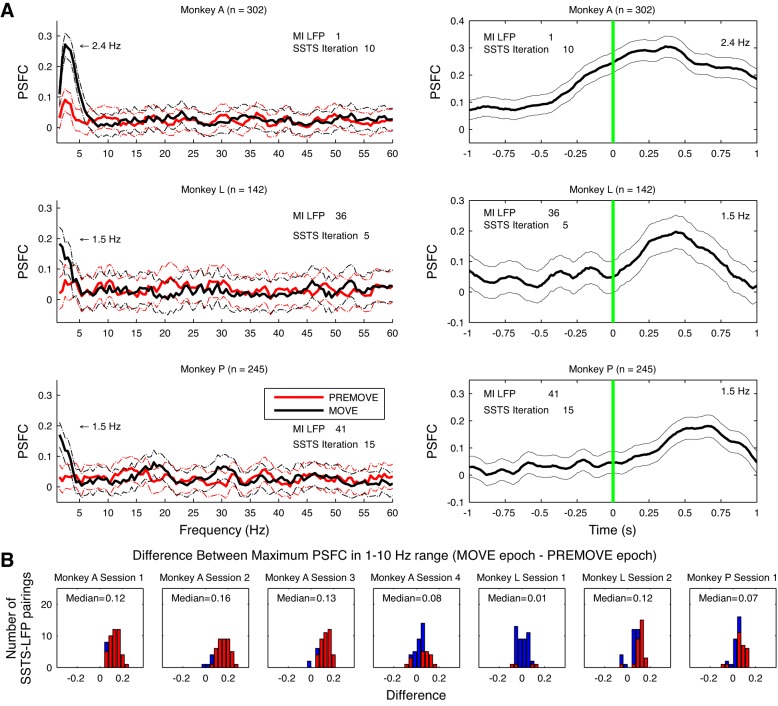
Across the three monkeys used in the study, most pairings of SSTS_C-LFP showed coherence between the neural population in 2/5 and M1 during arm reach (see Table 4). Figure 9 compares PSFC between movement and premovement epochs for all three monkeys. In these examples, PSFC increased in the range of 1–10 Hz during the MOVE epoch. Figure 9A, right, shows the changes in PSFC occurring across the time course of trials for the same pairings of data; PSFC for the frequency bin in which maximum PSFC occurred is shown in the figure. The average (±SD) time of maximal PSFC following movement onset was 398.5 ± 226.9 ms for monkey A, 273 ± 399.9 ms for monkey L, and 369.3 ± 249.6 ms for monkey P.

Fig. 9.

Summary of PSFC results. A, left: 1 example of PSFC for the pairing between 1 M1 LFP channel and its associated SSTS_C for monkeys A (top), L (middle), and P (bottom). In these examples for each monkey, PSFC increased during the MOVE vs. PREMOVE epochs at frequencies in the range of 1–10 Hz. Right: time-dependent changes in PSFC for the same SSTS_C-LFP pairings as on left. For these plots, PSFC was computed with a 1,000-ms sliding window (10-ms step size), a half-bandwidth of 3 Hz, and 5 tapers. Error bars on both left and right show a 95% CI for PSFC based on an arctangent transformation of PSFC values. Note that spike-field coherence rises around the time of movement onset and peaks ∼500 ms later. B: differences between the strength of PSFC at its peak in the 1–10 Hz range during the MOVE epoch and the strength of PSFC at its peak in the 1–10 Hz range during the PREMOVE epoch. Nonsignificant differences are in blue, and significant differences are in red. The false discovery rate (FDR) correction of α-level was applied across monkeys, sessions, channels, frequency bands, and epochs.

The PSFC between 2/5 and M1 typically increased significantly during arm movement compared with premovement holding. The maximum 1–10 Hz PSFC was significantly larger in the PREMOVE compared with the MOVE epoch in 16/314 (5.1%) of the pairings across all three monkeys. However, this PSFC was significantly larger during MOVE compared with PREMOVE in 194/314 (61.8%) of the channels across all three monkeys (Fig. 9B; Table 5).

Significant coherence in 10–40 and 60–200 Hz ranges.

Although coherence was generally weaker outside the low frequency band, we also tested for PSFC in the beta (10–40 Hz) and gamma (60–200 Hz) frequency ranges. Because the analysis of LFP power spectra (see above) showed that M1 LFP power is generally stronger prior to movement in the 10–40 Hz range, we performed greedy selection on the PREMOVE epoch for the greedy algorithm in this frequency range. For the 10–40 Hz range, PSFC for the PREMOVE epoch was significantly greater than 0 (P < 0.05; FDR correction) in 48/314 (15.3%) of the pairings. This effect was significant most often in monkey L and less often in monkey P and was not significant in monkey A (Table 6). For the data from the MOVE epoch, PSFC in the 10–40 Hz range was greater than 0 in a small minority of pairings (Table 6).

The results of the control version of the greedy algorithm that used the MOVE epoch to select neurons for the 10–40 Hz range supported the conclusion that 10–40 Hz PSFC is stronger during the PREMOVE epoch in two of the three monkeys. Average (±SD) peak PSFC across all channels for MOVE when that epoch was used for selection was 0.06 ± 0.02, 0.08 ± 0.01, and 0.07 ± 0.01 for monkeys A, L, and P, respectively. On the other hand, average peak PSFC across all channels for PREMOVE when that epoch was used for selection was 0.07 ± 0.02, 0.12 ± 0.02, and 0.09 ± 0.02 for monkeys A, L, and P.

For the 60–200 Hz range, we performed the greedy algorithm selecting on PSFC during the MOVE epoch. In this frequency range, PSFC for both the PREMOVE and MOVE epochs was significantly greater than 0 in <5% of pairings across the three monkeys (Table 7).

These results indicated that the greedy selection process allows for the detection of PSFC in the 10–40 Hz range in ∼15% of channels across all monkeys and in the 60–200 Hz range in very few channels. This is in contrast to the results of PSFC in the 1–10 Hz range, in which coherence was significant in most channels. The frequency of peak PSFC in these frequency ranges is shown in Tables 4 and 7. The selected ensemble approach allowed for the detection of significant PSFC in the 10–40 Hz range for SSTS-LFP pairings during PREMOVE in 33/93 (35.5%) channels in monkey L and 15/42 (35.7%) channels in monkey P, whereas no single neuron-LFP pairings had significant PSFC in the 10–40 Hz range during this epoch. This is evidence that the selected ensemble-LFP pairing method grants increased sensitivity to interaction between the two recording sites compared with single neuron-LFP pairings.

We do not focus our analysis on the 10–40 Hz frequency range because our study examines the relation between area 2/5 and M1 during movement, whereas coherence in the 10–40 Hz range is most strongly associated with the premovement epoch. Furthermore, PSFC in the 60–200 Hz range was generally nonsignificant. Thus we focused our study on the relation between area 2/5 spiking and M1 LFP in the 1–10 Hz range.

Coherence associated with selected ensemble vs. multiunit activity.

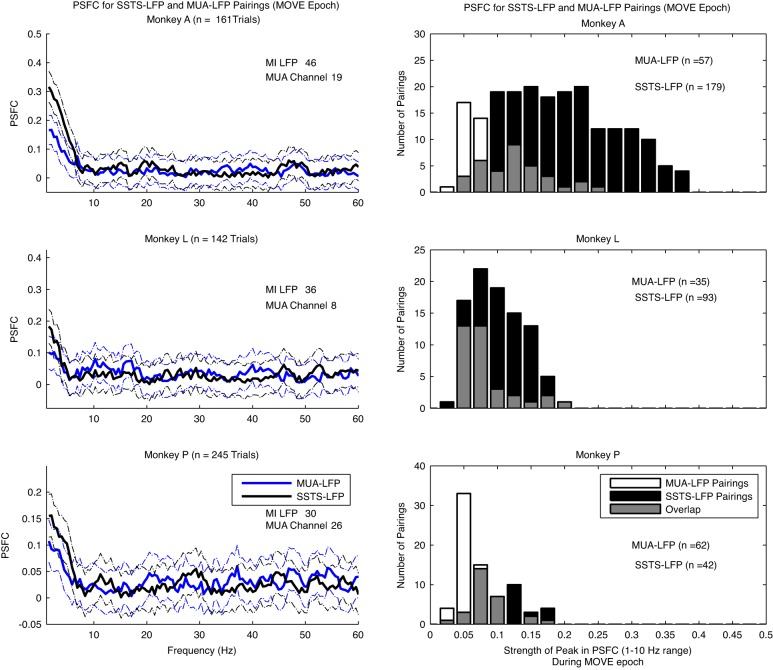
The effect of the SSTS_C-LFP comparisons may simply be the consequence of adding more units to the analysis. Both Baker et al. (2003) and Zeitler et al. (2006) showed that multiunit-LFP pairings yield stronger coherence than single neuron-LFP pairings. We therefore compared the 1–10 Hz PSFC in SSTS_C-LFP to the multiunit (MUA)-LFP pairings (Fig. 10). To evaluate the strength of PSFC produced by SSTS_C vs. MUA, we compared the peak of 1–10 Hz PSFC for all SSTS_C-LFP vs. all MUA-LFP pairings with a permutation test that evaluated the difference in the average strength of the peak of PSFC between the two conditions. On average, pairing of SSTS_C-LFP yielded 2.2, 1.3, and 1.7 times stronger PSFC in the 1–10 Hz range than pairing of MUA-LFP in monkeys A, L, and P, respectively (Fig. 10). The permutation test to compare PSFC in the 1–10 Hz range for SSTS_C-LFP vs. MUA-LFP was significant in each monkey (P < 0.01).

Fig. 10.

Comparison of PSFC calculated through the pairing of SSTS_C-LFP vs. multiunit-LFP (MUA-LFP). Left: an example of PSFC for the MOVE epoch computed by the pairing of 1 M1 LFP channel and its associated SSTS_C and PSFC computed by the pairing of the same M1 LFP channel with 1 channel of multiunit spike recording from area 2/5. An example is shown for each monkey. Error bars represent a 95% CI for PSFC based on an arctangent transformation of PSFC values. Note that the peak PSFC is in the 1–10 Hz range for both types of pairing, but the PSFC for the SSTS_C-LFP pairing is stronger. Right: strength of PSFC in the 1–10 Hz range for 1 representative channel of M1 LFP paired with all area 2/5 MUA channels from a single session vs. all pairings of SSTS_C-LFP for that monkey. An example of this comparison is shown for each monkey. On average, SSTS_C-LFP pairings yield stronger PSFC in each monkey.

The total number of spikes on all trials during the MOVE epoch was generally larger for SSTS compared with MUA channels. We tested whether the stronger 1–10 Hz PSFC for the SSTS-LFP pairings vs. the MUA-LFP pairings could be explained by the larger number of spikes in the SSTS vs. MUA. To do this, we selected a subset of trials for each channel of MUA and each SSTS such that the MUA and SSTS had at least 2,000 total spikes across all trials. There were 1,929, 234, and 1,596 MUA channels that met this criterion for monkeys A, L, and P, respectively. We randomly selected the minimum number of trials to collect this spiking activity. The average (±SD) number of trials of MUA data selected was 109 ± 58.8, 92 ± 31.1, and 130 ± 59.6 for monkeys A, L, and P, respectively. The average (±SD) total number of MUA spikes across all trials during the MOVE epoch was 2,020 ± 34.6, 2,014 ± 11.6, and 2,013 ± 11.1 for monkeys A, L, and P, respectively. For the SSTS data, the number of channels containing at least 2,000 total spikes across all trials was 179, 88, and 42 for monkeys A, L, and P, respectively. The average (±SD) number of SSTS trials selected was 26 ± 13.6, 59 ± 23.2, and 16 ± 7.2 for monkeys A, L, and P, respectively. The average (±SD) total number of SSTS spikes across all trials during the MOVE epoch was 2,050 ± 37.7, 2,023 ± 16.4, and 2,110 ± 93.4 for monkeys A, L, and P, respectively.

The truncated sets of trials of MUA and SSTS spiking activity were paired with their corresponding LFPs, and the PSFC was calculated for all such MUA-LFP and SSTS-LFP pairings. The permutation test to compare the average strength of PSFC for the two types of pairings indicated that the strength of 1–10 Hz PSFC for SSTS-LFP pairings was significantly larger than the strength of 1–10 Hz PSFC for MUA-LFP pairings for all three monkeys (P < 0.01), even when the total number of spikes between the two types pf signals was roughly equal. Thus the stronger 1–10 Hz PSFC for SSTS-LFP vs. MUA-LFP pairings cannot be explained by a larger number of spikes in the SSTS vs. MUA data.

In the 10–40 Hz range during the PREMOVE epoch, the SSTS_C-LFP pairings yielded stronger PSFC, on average, than the MUA-LFP pairings in two of the three monkeys (permutation test, P < 0.01). These were the same two monkeys (monkeys L and P) in which PSFC in the 10–40 Hz range was significantly larger than 0 in many channels (Table 6). In the 60–200 Hz range during the MOVE epoch, the difference in average strength of PSFC for SSTS-LFP vs. MUA-LFP was not significant in any of the three monkeys. Correspondingly, the strength of PSFC was generally not significant in any of the three monkeys (Table 7). These results show that the selective combination of a subset of area 2/5 neurons by the greedy algorithm reveals a stronger PSFC than the LFP-MUA coherence in the 1–10 and 10–40 Hz ranges.

An alternative explanation for the PSFC detected during the MOVE period of the task is that the PSFC may be explained by eye movements, because the animals were free to move their eyes throughout the experimental sessions. To examine this possibility, we used the signals from an infrared eye tracker to analyze eye position continuously for monkey L. On one subset of trials monkey L tended to perform a gaze shift from the center hold position to the reach target before initiating hand movement, and on another subset of trials the monkey performed the gaze shift after initiating the reach. The distance from central hold position to reach target was 8.29° visual angle. We plotted eye positions for the PREMOVE and MOVE epochs of the task and calculated the centroid of eye position during the MOVE epoch for each trial. We selected the subset of trials in which eye position remained within 3.51° visual angle (2 times the size of the target) from the centroid of eye positions throughout the entire MOVE epoch. On these trials, eye positions were considered stationary throughout the arm movement period. Eye position was stationary during the arm movement period in 12/136 trials in session 1 and 66/142 trials in session 2 in monkey L.

PSFC for the pairing of SSTS_C-LFP was significant (P < 0.05; FDR correction) in the range of 1–10 Hz in some channels in the subset of trials with eye movements during arm movement (10/93; 10.8%) and the subset of trials without eye movements (3/93; 3.2%) during arm movement across the two recording sessions in monkey L. An example of these results is shown in Fig. 11. The presence of significant PSFC in the absence of eye movement indicates that PSFC between spiking activity in 2/5 and LFP in M1 cannot be explained by eye movement alone.

Fig. 11.

Relationship between eye movement and PSFC. A, top: PSFC for PREMOVE and MOVE epochs for all trials recorded in 1 session with monkey L. Middle: PSFC for only the trials in which no eye movement occurred during the arm movement epoch of the trials. Bottom: PSFC for only the trials in which eye movements occurred during the movement epoch of the trials. All data shown are from the same pairing of SSTS_C-M1 LFP. Note that the peak in PSFC in the range of 1–10 Hz appears in each grouping of trials, indicating that PSFC does not depend on eye movement. B: eye positions recorded during PREMOVE (red) and MOVE (black) epochs. The animal moved its eyes freely during the behavioral task. Top: eye positions for trials classified as having no eye movement during the MOVE epoch. Bottom: data for trials classified as having eye movement during the MOVE epoch of the task. Inset: full range of eye positions recorded on all trials classified as having eye movement during the MOVE epoch.

To compute PSFC for the pairing of SSTS_C-LFP, the spike-field coherence between the area 2/5 SSTS_C and the local area 2/5 LFP channels is factored out (Eq. 1). We report spike-field coherence for the pairing of area 2/5 SSTS_C and area 2/5 LFP in Table 8. Additionally, we report the spike-field coherence for the pairing of area 2/5 SSTS_C and M1 LFP (without the removal of the local spike-field coherence) in Table 9.

Significant coherence between spike trains of M1 neurons and LFP in 2/5.

We additionally computed PSFC for the pairing of single neurons and ensembles of neurons in M1 with LFP recorded in area 2/5. While not a conceptual focus of our study, it was of interest to determine whether PSFC is associated with these pairings. The number of single neurons recorded in M1 is shown in Table 2. Similar to the pairing of area 2/5 neurons with M1 LFP, the PSFC for the pairing of M1 neurons with area 2/5 LFP was strongest in the 1–10 Hz range during the MOVE epoch. Across all three monkeys, there were 81/442 (18.3%) significant pairings in the 1–10 Hz range during the PREMOVE epoch (Table 10). The PSFC was significant in a larger fraction (156/442; 35.3%) of pairs in the 1–10 Hz range during MOVE. In the 10–40 Hz range, there were 22/442 (5%) significant pairings during the PREMOVE epoch and 4/442 (0.9%) significant pairs during the MOVE epoch. In the 60–200 Hz range, there were no significant pairings during the PREMOVE epoch and 1/442 (0.2%) significant pairing during the MOVE epoch (Table 10).

We also performed the greedy selection procedure for PSFC for the pairing of neuron activity in M1 and LFP in area 2/5. This greedy algorithm reached its maximum in an average of 18, 4, and 10 iterations in monkeys A, L, and P, respectively.

Across all three monkeys, the PSFC for the pairing of M1 SSTS-area 2/5 LFP for the PREMOVE epoch in the 1–10 Hz range was significant in 68/296 (23%) pairings (Table 10). For the MOVE epoch, the PSFC in the 1–10 Hz range was significant in 163/296 (55.1%) pairings across all three monkeys. The PSFC for the pairing of M1 SSTS-area 2/5 LFP for the PREMOVE epoch in the 10–40 Hz range was significant in 82/296 (27.7%) pairings. For the MOVE epoch, this PSFC was significant in 10/296 (3.4%) pairings across all three monkeys. For the 60–200 Hz range, PSFC for the PREMOVE epoch in the 60–200 Hz range was significant in 2/296 (0.7%) pairings. For the MOVE epoch, this PSFC was not significant in any of the pairings (Table 10).

The average (±SD) time of maximal PSFC in the 1–10 Hz range following movement onset was 373.3 ± 442.9 ms for monkey A, 458.8 ± 500.5 ms for monkey L, and 630.1 ± 219.7 ms for monkey P. These latencies were significantly longer than those for the area 2/5 SSTS_C-M1 LFP pairings in two of the three monkeys [1-way ANOVA; monkey A: F(1,343) = 0.45, P = 0.5; monkey L: F(1,176) = 7.5, P < 0.01; monkey P: F(1,85) = 26.8, P < 0.001]. The differences in latency to peak PSFC likely arose because the peak voltage of the late phase of the mERP in the M1 LFP typically occurred between 500 ms and 1.5 s after the start of movement (Fig. 3), whereas this peak was typically ∼500 ms to 1 s later in the PE LFP (not shown).

These results show that the strength, peak frequency, and behavioral conditionality of PSFC are similar for pairings of area 2/5 neurons-M1 LFP and area M1 neurons-area 2/5 LFP. These results likely reveal an influence of M1 neuron output on synaptic activity in area 2/5. However, we do not focus on this PSFC in the present study because our primary interest was to determine whether area 2/5 spiking provides reach-related input to M1 during the perimovement period.

Parietal cortex input to primary motor cortex during reach.

The timing of the relationship between spiking and the LFP can help reveal direction of information flow. We performed a temporal offset-shifting analysis (see Siapas et al. 2005) to examine the directionality of interaction between area 2/5 populations and M1 LFPs in the 1–10 Hz range. In the temporal offset-shifting procedure, an offset of 0 would indicate that the spike times and LFP are both aligned to movement onset. If PSFC between 2/5 and M1 is primarily driven by input from area 2/5 to M1, then the strongest PSFC should be elicited by SSTS_C-LFP pairings in which area 2/5 spike times are aligned to the future of the LFP signal in M1 (negative lags). Conversely, if the PSFC between area 2/5 and M1 is primarily driven by M1 input, the strongest PSFC could be elicited by SSTS_C-LFP pairings when area 2/5 spike times are aligned to the past LFP signal (positive lags). No offset would indicate that the PSFC is primarily driven by simultaneous common input to the two areas.

The temporal offset-shifting analysis revealed that the maximum PSFC was elicited at negative lags for all three monkeys. A representative example of this analysis for one recording session in monkey A is shown in Fig. 12. Note that the peak value of PSFC occurs at a lag of −50 ms (Fig. 12A), suggesting that neural activity in area 2/5 drove this coherence. Across all SSTS_C-LFP pairings for this session, the maximum values of PSFC generally occur at negative offsets (Fig. 12B). For the data shown in Fig. 12B, 38/42 significant peaks preceded and 3/42 peaks followed 0. A similar pattern and negative average offset was present in all three monkeys (mean ± SD of −45 ± 67.5 ms for monkey A, −34.4 ± 82 ms for monkey L, and −127.5 ± 107.9 ms for monkey P). The difference between the mean temporal offset at which the peak value of PSFC was achieved and 0 was significant (1-sample t-test, P < 0.05) for two of the three monkeys. This difference was not significant in monkey L [t(8) = −1.26, P = 0.24]. Although the mean peak offset for monkey L was consistent with that of monkey A, the number of channels with significant PSFC was fewer in monkey L, which may have contributed to a lack of sensitivity to this effect. The offsets at which peak PSFC occurred differed significantly between the three monkeys [1-way ANOVA, F(2,187) = 13.99, P < 0.001]. The offsets for peak PSFC were not different in monkey A vs. monkey L (multiple comparisons with Bonferroni adjustment), although those in monkey P were.

Fig. 12.

Timing relationship between area 2/5 spiking activity and M1 LFP: results for 1 representative recording session. A: peak of PSFC in the 1–10 Hz range computed as a function of temporal offset between the SSTS_C and LFP for 1 representative channel. For this analysis, PSFC was computed using 1 s of spiking and LFP data from the MOVE epoch, to allow for calculation of PSFC at offsets from −1,000 to +990 ms. Note that the peak value of PSFC is achieved at a temporal offset of −50 ms. B, top: the temporal offsets at which the maximum value of PSFC in the range of 1–10 Hz was achieved for all SSTS_C-LFP pairings in the recording session. Only offsets at which significant PSFC was detected are included in the histogram. For this analysis, statistical significance of PSFC at the peak frequency in the 1–10 Hz range was evaluated by finding a P value for the z-transformed PSFC at each frequency. The α-level for this test was adjusted by the FDR correction across monkeys, sessions, and channels. This corrected α-level was then divided by the number of offsets (200) to yield the final α-level for the test. Bottom: value of PSFC at its peak for each of the 200 temporal offsets for all channels in the recording session. Black circles indicate the offsets at which maximum statistically significant PSFC was detected, and white circles indicate the offsets at which maximum nonsignificant PSFC was detected.

Past spiking in parietal cortex predicts LFP in primary motor cortex.

Spike-field coherence and linear prediction are mathematically similar (Pesaran et al. 2008). However, spike-field coherence can describe only the relationship between a single vector of spike times and an LFP channel, while linear prediction of field potentials can be performed by independently weighting the contributions of an arbitrarily large number of spiking units. For this reason, it was not clear what prediction accuracy to expect given the PSFC results, and we reasoned that the ability of area 2/5 to accurately predict future M1 LFPs would show further support for the role of this parietal area during reach.

To predict M1 LFPs using area 2/5 spikes, we used a general linear model. The model inputs consisted of single-unit spiking activity from area 2/5 filtered through a bank of 10 time-causal raised cosine filters with different lags and periods (see materials and methods). The output was a weighted sum of the filter output across all area 2/5 neurons. The optimal weights on the filter outputs were solved by least squares. The two trial epochs (PREMOVE and MOVE) were predicted separately.

We found that past area 2/5 spiking history can be used to predict M1 field potentials with this method. Across all sessions, the average prediction accuracy was r = 0.20/R² = 0.05 and r = 0.29/R² = 0.11 for PREMOVE and MOVE, respectively (where r is the Pearson correlation and R² is the coefficient of determination). Furthermore, the prediction accuracy distribution across channels was significantly higher for the MOVE vs. PREMOVE epoch (Wilcoxon rank sum test, P < 0.001 in all animals), consistent with the PSFC results. The predictions even captured a significant portion of the LFP waveform shape for many single trials (Fig. 13A), and, when averaged over trials, they replicated the stereotypical shape of the M1 mERP, especially the component observed after movement onset (Fig. 13B).

Fig. 13.

Spike-based LFP prediction results. A: example of estimations (gray), for both epochs of a single trial in monkey P, compared with the recorded LFP (black). Because predictions were based on 100 ms of past spiking history, and to maintain a separation between the 2 epochs, only 900 ms of each epoch was predicted. B: average over all trials of the recorded (black) and estimated (gray) LFP for the same channel, showing that the predictions capture a portion of the post-movement onset mERP. C: estimation accuracy distributions for all channels (as given by the Pearson correlation), with each trial epoch plotted separately. These illustrate the improvement in prediction accuracy during the MOVE epoch. Channels for which prediction accuracy could not be explained by chance, α = 0.05, are shown in black. D: scatterplot comparing the distribution of prediction accuracy values for predictions based on the greedy-selected area 2/5 ensembles (SSTS_C) and those based on equally sized but randomly selected subpopulations: 500 random subpopulations were generated for each channel, and the median prediction performance is plotted here. For the majority (64%) of channels, the greedy-selected subpopulation outperformed the randomly selected subpopulations in predicting M1 LFPs.

Chance levels for our measurements of prediction accuracy were estimated via a Monte Carlo simulation using phase-randomized LFP surrogates (see materials and methods). Channels that individually outperformed chance are shown in black in Fig. 13C. The majority (82%) of channels were significant during MOVE, but this was true for only a small minority (12%) before movement onset. By combining the significance measures for each channel, we could reject the null hypothesis that the predictions could be explained by chance (P < 0.001, Fisher's method) for both epochs.

To confirm that the subset of area 2/5 neurons selected by the greedy algorithm to maximize PSFC plays a special role in the functional connectivity between area 2/5 and M1, we tested the ability of these subpopulations to predict M1 MOVE epoch LFPs on their own. The performance of these reduced predictions was, on average, 68% as good as the full-population predictions, even though in some cases only a small subpopulation was used. To assess the significance of this performance, we compared the greedy algorithm-based predictions to predictions using equally sized random subsets of area 2/5 neurons. For most channels (64%), the greedy algorithm-based prediction performance was better than the median of the performance of 500 randomly selected subpopulations (Fig. 13D). We used the empirical distribution of random subpopulation performance of each channel to generate P values for the greedy selection subpopulation performance, and by combining these P values we could easily rule out the null hypothesis that the greedy predictions could be explained by chance (P < 0.001, Fisher's method). Thus greedy selection found an area 2/5 subpopulation that outperformed random selection in predicting M1 LFPs.

Taken together, the results from the linear prediction model match those from our spike-field coherence analysis. First, both suggest increased functional connectivity during reach. Second, the success of past spiking history for prediction is consistent with the temporal asymmetry observed in the results from spike-field coherence. Finally, greedy selection produced a population that could be used to reconstruct M1 LFPs better than random selection, indicating that the greedy algorithm successfully identified functionally relevant subpopulations of area 2/5 neurons.

Relationship between directional bias of neuronal activity in area 2/5 and LFP in M1.

We next sought to determine whether the directional tuning of the M1 LFP after movement onset arose from a convergence of neurons in 2/5 with a similar directional bias. Thus we asked whether ensembles of area 2/5 neurons with the same directional bias as the M1 LFP produced the strongest PSFC among the set of recorded 2/5 neurons.

To address this question, we superimposed the spike times of all neurons whose directional vector (see materials and methods) during the MOVE epoch was ±45° of the M1 channel's LFP tuning. This SSTS was termed the SSTS_{Similar-Direction} (SSTS_SD). We then superimposed the spike times of all neurons whose directional vector was within ±45° of the opposite of that M1 channel's LFP tuning (i.e., within an interval from 135° to 225° from the tuning of the LFP). This superimposed spike train was termed the SSTS_{Opposite-Direction} (SSTS_OD). We included all recorded neurons whose direction vector fell within these intervals, whether or not their tuning was significant according to the Raleigh test. For each channel, we computed the difference between the maximum PSFC in the 1–10 Hz range for the SSTS_SD-LFP pairing vs. the maximum PSFC in the 1–10 Hz range for the SSTS_OD-LFP pairing. An example of this comparison for one channel in monkey A is shown in Fig. 14, A and B.

Fig. 14.

Relation between directional bias of area 2/5 single neurons and M1 LFP. A and B: example data from 1 channel in monkey A. A: PSFC for the pairing of SSTS_{Similar-Direction} (SSTS_SD)-LFP, SSTS_{Opposite-Direction} (SSTS_OD)-LFP, and SSTS_C-LFP. Note that the PSFC in the range of 1–10 Hz for the pairing of SSTS_C-LFP is the strongest overall, but the PSFC for the pairing of SSTS_SD-LFP exceeds that of the PSFC for the pairing of SSTS_OD-LFP. B: directional bias of each individual area 2/5 neuron entering the SSTS_SD (similar-direction neurons) and SSTS_OD (opposite-direction neurons) in red and directional tuning of the LFP during the MOVE period in blue. C: differences between peak PSFC in the 1–10 Hz range during the MOVE epoch for the SSTS_SD-LFP vs. SSTS_OD-LFP pairings for all 3 monkeys. Note that the distribution of differences is significantly higher than 0 for monkeys A and L and not monkey P with a window of ±45° for selection of area 2/5 neurons.

We conducted a one-sample t-test to determine whether the distribution of differences between maximum PSFC for the SSTS_SD-LFP pairing vs. the SSTS_OD-LFP pairing was significantly different from 0. To conduct this t-test, we used only channels for which the directional tuning of the M1 LFP during MOVE was significant (P < 0.05) according to a Raleigh test. Additionally, we used only channels for which the PSFC for the pairing of either the SSTS_SD-LFP or SSTS_OD-LFP was statistically significant in the range from 1 to 10 Hz (P < 0.05; FDR correction). We performed the subtraction on the z-transformed PSFC values (see materials and methods).

The data from each of the three monkeys indicated that area 2/5 neurons with directional vectors similar to the M1 LFP produced stronger PSFC than those with opposite directional vectors. Figure 14C shows histograms of the differences between peak PSFC for the pairing of SSTS_SD-LFP and peak PSFC for the pairing of SSTS_OD-LFP. For these examples, the means of the distribution of differences for monkeys A, L, and P are all positive (0.5, 1.3, and 0.2, respectively). The differences were centered significantly higher than 0 for monkeys A and L, but those for monkey P were not, perhaps as a methodological bias.

The relative absence of an effect for monkey P may have been due to the higher number of 2/5 neurons recorded per session in monkey P vs. monkeys A and L (64 for monkey P; mean of 27.5 and 25 for monkeys A and L, respectively). The number of neurons entering the ±45° LFP tuning window was generally much greater for monkey P than for monkeys A and L. Across LFP channels, the mean number of neurons entering the ±45° similar-direction neuron window was 6.6, 6.1, and 16.1 for monkeys A, L, and P, respectively. Across LFP channels, the mean number of neurons entering the opposite-direction window was 7.7, 6.7, and 17.8 for monkeys A, L, and P.

As described in the results of greedy selection, there was a relationship between the spike rate of the SSTS and the strength of PSFC, such that addition of neurons into the SSTS improves PSFC strength only up to a certain number of spikes, after which the measure of PSFC is hindered by inclusion of additional spiking activity. This may have resulted in a biased estimate of PSFC for monkey P compared with monkeys A and L, because the SSTS_SD and SSTS_OD had much greater spiking activity for monkey P than for the other monkeys. Thus the results from two of the three monkeys support the hypothesis that area 2/5 neurons input information related to the direction of arm movement to M1 after the onset of reach.

DISCUSSION

The present study demonstrates a behaviorally mediated, dynamic coherence between the spiking of a simultaneously recorded ensemble in parietal area 2/5 and the M1 LFP, revealed with a population spike-field coherence approach that can measure the strength and time course of the input from area 2/5 to M1. The PSFC revealed significant coherence during movement, rarely seen in single cells (∼23%), which occurred most strongly in the low frequency power band (1–10 Hz) M1 mERP. The method of combining the spiking activity of an ensemble of neurons also revealed a weaker, but significant spike-field coherence in the 10–40 Hz “beta” range during premovement. Our results also show how PSFC between an ensemble of neurons and LFP can be used to reveal the temporal interactions between cortical areas that may be useful to study other dynamic cortico-cortical network interactions. Our analyses revealed that a weak cortico-cortical influence from area 2/5 begins prior to movement onset and becomes stronger after movement onset. Finally, by subselecting ensembles, we provided evidence that area 2/5 contributes directional information to M1. Our findings further advance our understanding of the timing and forms of functional interactions of parietal-motor circuits.

Functional interactions between area 2/5 and M1.

We found significant PSFC with low and medium bands evident in the M1 power spectrum by comparing movement preparation to movement epochs. These bands coincide with well-known mERP and beta range activity that has been studied in M1 (O'Leary and Hatsopoulos 2006). Other bands have been identified in primary motor cortex (mu and alpha in humans; Gastaut and Bert 1954; Pfurtscheller and Lopes da Silva 1999) but were less clear in our data (Fig. 6). Because we could reliably see changes in these bands when comparing premovement to movement epochs, we focused on the effect of area 2/5 inputs to these changes. Overall, we found that the largest effect was on the mERP, with weaker and more unreliable effects on the midband. The mERP is thought to largely reflect synaptic currents that begin to appear before movement onset and persist afterward (Gemba et al. 1981). Our data show that area 2/5 only weakly contributes to the premovement phase and then becomes stronger as the limb moves. Our results are consistent with previous studies showing that movement-related changes in this part of parietal cortex lag behind those of M1 neurons by ∼50–100 ms, and that movement-related spiking increases in the 2/5 region occur after movement onset (Kalaska 1996; Kalaska et al. 1983). Thus our data indicate that synaptic input from area 2/5 neurons contributes to late phase of the M1 mERP.

Spike-field coherence in the midrange was detected during preparation, when beta oscillations are seen in both areas (Donoghue et al. 1998; MacKay and Mendonça 1995). This is consistent with the findings of Witham et al. (2007). This weak effect could suggest that parietal beta contributes in part to those oscillations in M1, or it could reveal a strong common input that is not adequately removed by our partialling method.

The M1 mERP is complex to interpret (Gemba et al. 1981). It is likely that it reflects the emergence of synchronous currents in M1 around movement onset. The short latency (∼50 ms) at which maximum PSFC is often elicited in the temporal offset-shifting procedure indicates that the portion of the mERP evolving after movement onset is produced by the well-established direct cortico-cortical projection from area 2/5 to M1 (Strick and Kim 1978). In addition, the disruption of corrective movements (Della-Maggiore et al. 2004; Desmurget et al. 1999) with TMS also implicates a 2/5-M1 interaction. However, common cortico-thalamic inputs might produce a similar effect. Thus a common input to the two areas with a delay on the order of tens of milliseconds in the branches to area 2/5 could not be distinguished by our approach. Anterior area 2/5 and M1 reach-related regions appear to have separate ventral thalamic tier inputs (Gharbawie et al. 2010), making the common input hypothesis less likely. However, on the basis of available data, we cannot conclusively eliminate the common input hypothesis. In addition, the reciprocal nature of connections between M1 and area 2/5 makes it difficult to conclude that any particular projection is solely responsible for the functional connectivity we observe.

The functional connectivity established with PSFC was replicated by using a linear prediction model to reconstruct M1 LFPs from area 2/5 spikes. The success of area 2/5 spiking history to predict the current state of M1 LFPs is consistent with the temporal asymmetry observed in the results from spike-field coherence. We also found that the subpopulation that produces strongest PSFC via greedy selection outperforms randomly selected subpopulations in predicting LFPs. However, the fact that the performance of the greedy-selected cells in predicting M1 LFPs did not match the performance of the entire area 2/5 population suggests that the prediction model is able to make use of population statistics beyond those captured by PSFC. Given this, further studies may explore prediction methods more closely, including analyzing the optimal filter weights fit by the model as a means of assessing the contribution of individual neurons. Closely related to these weights are the spike-triggered LFP averages, which can also give insight into the functional relationship between brain areas. All of these will be important tools for future multiarea population recording studies.

Area 2/5 contributes directional information to M1.

Using our PSFC method, we found that the strength of PSFC depended on reach direction in two of the three monkeys. That is, we found a greater PSFC when we compared the impact of neurons with directional bias similar to the M1 LFP compared to neurons with directional bias opposite to the M1 LFP. This result indicates that area 2/5 ensembles provide information about reach direction to M1 during arm movement, suggesting that subsets of intermingled neurons in area 2/5 dynamically link to M1 to influence the tuning of M1 neurons as movement progresses.

M1 neurons show a rotation of directional tuning after movement onset that may reflect the arrival of new information that changes the tuning of the neurons (Rickert et al. 2009). These observations suggest an ongoing evolution of direction information in area 2/5 as movement commences, but these previous studies fail to demonstrate that area 2/5 is the source of these directional rotations in M1. The fact that area 2/5 neurons and M1 LFP with similar directional bias are associated with stronger coherence suggests that area 2/5 generates at least part of the directional tuning of M1 neurons during movement and may account for changes in directional tuning over time (Rickert et al. 2009). Because spike-field coherence in the 1–10 Hz range between 2/5 and M1 is relatively absent until after movement begins, it appears that neurons in at least this part of 2/5 cannot account for directional tuning of M1 neurons until movement onset.

Methodological considerations.

Previous studies have compared the spike-field coherence computed by the pairing of single neurons with LFP vs. the pairing of single channel multiunit activity with LFP. Baker et al. (2003) computed the spike-field coherence between pyramidal tract neurons and LFP recorded in the primary motor cortex of monkeys performing a precision grip task. Baker et al. (2003), who focused their analysis on an epoch when the monkey held its arm in a stationary position, found spike-field coherence in the beta range (10–14, 17–31, and 34–44 Hz) that was statistically significant but weak (magnitude of coherence < 0.05). They produced a computational model of M1 pyramidal tract neurons and LFP and showed that the strength of spike-field coherence would increase if the spiking activity of a small population of neurons is used to compute the coherence instead of the activity of single neurons.

A similar spike-field coherence study compared single neuron- and multiunit-LFP coherence in macaque visual area V4 (Zeitler et al. 2006) during a visual fixation task. Zeitler et al. showed that the pairing of both single neuron-LFP and multiunit-LFP yielded significant spike-field coherence at ∼50 Hz. However, the strength of the peak in spike-field coherence increased from <0.1 for the single neuron-LFP pairing to >0.2 for the multiunit-LFP pairing, even when the number of spikes was equalized.

The superimposed ensemble approach introduced in the present study revealed substantially more interactions from area 2/5 to M1 compared with single cells or multiunit channels. The method of superimposition provided a clearer time course of interactions and revealed more aspects of the nature of the information communicated by the ensemble than was evident at the single-cell or multiunit channel level. Thus we see this selected ensemble-level PSFC method as a complementary approach to other available approaches to revealing interactions when populations of neurons can be simultaneously recorded.

While this method of calculating PSFC with a neuronal ensemble provides a means to evaluate the dynamics of interactions between cortical areas, it also has limitations. One important limitation of our study is the positive correlation between area 2/5 neuron spike rate and ordinality of selection by the greedy algorithm, which could have resulted from bias. As stated in results, spike-field coherence tends to overstate the population statistics for finite sample sizes. In our case low-firing rate neuronal spike trains have fewer spikes/samples than higher-firing rate spike trains, and thus because of bias effects these low-firing neurons may be selected on the earliest iterations (we also note, however, that the interaction of firing rates and spike-field coherence is more complex—in addition to bias, firing rates can contribute true effects in the spike-field coherence; e.g., Lepage et al. 2011). Because of this potential bias, we needed to employ a second approach to superimposing the spike times of ensembles of neurons—selecting neurons with either similar or opposite directional bias to the M1 LFP—to test whether PSFC strength depends on movement direction. PSFC associated with this method of selection was often statistically significant, and this technique revealed a relation between the directional bias of area 2/5 neurons and M1 LFP during the movement epoch.

Additionally, there are possible advantages to using single neuron-LFP pairings relative to the greedy selection method. For example, single neuron-LFP pairing provides a greater ability to explain the relationship between the functional properties of individual neurons (e.g., temporal structure of spike timing) and synaptic drive. Because of the bias toward neurons with lower spike rates inherent in the greedy selection, we cannot attribute the strength of PSFC for the SSTS_C-LFP pairings to the functional properties of the individual cells selected. However, the increased sensitivity provided by SSTS_C-LFP pairings allows us to detect long-range interactions that would likely be missed if only single neuron-LFP pairings were employed.

Future directions.

Our data indicate that area 2/5 delivers directional information to M1 after movement progresses. Previous studies have suggested that this input from area 2/5 neurons subserves error correction of movement trajectory (Bullock et al. 1998; Buneo and Andersen 2006; Kalaska 1988; Kalaska et al. 1983; Mulliken et al. 2008; Sabes 2000). Our data do not directly address this hypothesis. Tools such as optogenetics, which could manipulate area 2/5 input, are needed to demonstrate the necessity of 2/5 input to M1 to form or correct normal reach trajectories.

Our data confirm prior work that area 2/5 ensembles, as well as M1 LFP, contain movement direction-related information. These area 2/5 and M1 signals could be useful to create commands for brain-computer interfaces. Bansal et al. (2011, 2012) previously showed that multidimensional arm movements can be decoded from M1 mERPs. Although previous studies have indicated that the mERP has a peripheral origin (Deecke et al. 1976), the fact that low-frequency components of the LFP survive spinal cord transaction in humans (Hochberg et al. 2006) suggests that the mERP has contributions from a central origin, and could thus be used as a source of command signals.

GRANTS

We gratefully acknowledge the following sources of support: National Institutes of Health (NIH) Grants 5R01 NS-205074, 5R37 NS-205074, C06-16549-01A1, and 5K01 NS-057389; Rehabilitation R & D Service, Office of Research and Development, Department of Veterans Affairs (Merit Review Award A6779I and Senior Research Career Scientist Award B6459L). The contents do not necessarily represent the views of the Department of Veterans Affairs or the United States Government.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: D.L.M., N.G.R., A.B., W.T., and J.P.D. conception and design of research; D.L.M. and N.G.R. performed experiments; D.L.M., N.G.R., A.B., and W.T. analyzed data; D.L.M., A.B., W.T., and J.P.D. interpreted results of experiments; D.L.M. and A.B. prepared figures; D.L.M., A.B., and J.P.D. drafted manuscript; D.L.M., N.G.R., A.B., W.T., and J.P.D. edited and revised manuscript; D.L.M., N.G.R., A.B., W.T., and J.P.D. approved final version of manuscript.