Neural mechanisms of coarse-to-fine discrimination in the visual cortex

Abstract

Vision is a dynamic process that refines the spatial scale of analysis over time, as evidenced by a progressive improvement in the ability to detect and discriminate finer details. To understand coarse-to-fine discrimination, we studied the dynamics of spatial frequency (SF) response using reverse correlation in the primary visual cortex (V1) of the primate. In a majority of V1 cells studied, preferred SF either increased monotonically with time (group 1) or changed nonmonotonically, with an initial increase followed by a decrease (group 2). Monotonic shift in preferred SF occurred with or without an early suppression at low SFs. Late suppression at high SFs always accompanied nonmonotonic SF dynamics. Bayesian analysis showed that SF discrimination performance and best discriminable SF frequencies changed with time in different ways in the two groups of neurons. In group 1 neurons, SF discrimination performance peaked on both left and right flanks of the SF tuning curve at about the same time. In group 2 neurons, peak discrimination occurred on the right flank (high SFs) later than on the left flank (low SFs). Group 2 neurons were also better discriminators of high SFs. We examined the relationship between the time at which SF discrimination performance peaked on either flank of the SF tuning curve and the corresponding best discriminable SFs in both neuronal groups. This analysis showed that the population best discriminable SF increased with time in V1. These results suggest neural mechanisms for coarse-to-fine discrimination behavior and that this process originates in V1 or earlier.

to overcome ambiguities in two-dimensional representations of the visual scene, coarse spatial features can be extracted first and used to constrain analysis at local spatial scale (Marr 1982; Marr and Poggio 1979). Consistent with this algorithm, human psychophysical sensitivity to finer spatial details improves with time in visual tasks ranging from the recognition of objects, scenes, and letters to the detection and discrimination of line size, orientation, and stereoscopic depth (Hegde 2008). What neural mechanisms mediate these coarse-to-fine processes?

Magnocellular and parvocellular pathways in the retina and lateral geniculate nucleus are selective for low and high spatial frequencies (SFs), respectively (Casagrande and Xu 2004), and their response latencies increase with SF selectivity (Casagrande and Ichida 2002). Therefore, coarse-to-fine processing might originate in the lateral geniculate nucleus (Allen and Freeman 2006). In area V1, local circuits combine magno- and parvo-inputs (Callaway 1998; Sincich and Horton 2005). Reverse correlation methods, which offer good temporal resolution, have been used to investigate whether coarse-to-fine dynamics is preserved in V1 after this convergence. These investigations have shown that the preferred SF of V1 neurons increases with time (Bredfeldt and Ringach 2002; Malone et al. 2007; Mazer et al. 2002), receptive field (RF) sizes decrease with time (Malone et al. 2007), tuning for SF (Bredfeldt and Ringach 2002) and binocular disparity (Menz and Freeman 2003) becomes more selective with time, and cells preferring finer disparity ranges have longer response latencies (Menz and Freeman 2003). These findings are consistent with a progressive improvement in the psychophysical ability to detect, identify, and recognize fine spatial features with time.

In addition to the psychophysical ability to detect, identify, and recognize fine details, thresholds for discriminating fine changes in stimuli also improve with time (Westheimer 1991; Watt 1987). This fact is remarkable because mechanisms underlying fine discrimination are different from those that mediate detection, identification, and recognition of features. Psychophysics (Westheimer et al. 1976; Regan and Beverly 1985; Hol and Treue 2001; Jazayeri and Movshon 2007), modeling (Seung and Sompolinsky 1993), electrophysiology in anesthetized cats and monkeys (Bradley et al. 1985; Geisler and Albrecht 1997), and neurophysiology in awake, behaving monkeys (Vogels and Orban 1990; Purushothaman and Bradley 2005; Schoups et al. 2001; Gu et al. 2007; Chowdhury and DeAngelis 2008) have shown that stimuli best discriminated by a neuron are not near the peak of its tuning curve but fall in the flanks of the tuning curve where small changes to the stimulus yield the largest change in response. Moreover, the distributed population response of area MT neurons tuned to various directions of motion was measured in macaque monkeys performing a fine direction-discrimination task (Purushothaman and Bradley 2005). Analysis of this population response showed that activity fluctuations in neurons tuned near the flanks of this population distribution were significantly correlated with the monkey's behavioral choices (fine discrimination decisions). In contrast, activity fluctuations in neurons tuned near the peak of the population distribution were not significantly correlated with the monkey's choices. These results suggest that a neural population response is decoded in different ways for different tasks, in accordance with the amount of task-related information carried by each neuron (Purushothaman and Bradley 2005; Jazayeri and Movshon 2007). Therefore, the temporal dynamics of preferred SF, SF tuning width, and RF size measured in previous studies alone are not sufficient to account for the improvement in discrimination of finer details with time.

To understand neural mechanisms underlying coarse-to-fine discrimination, the temporal dynamics of SF discrimination thresholds (related to Fisher information for each flank of the SF tuning curve) must be measured with high temporal resolution. We have now done so in primate V1 neurons. Previous studies have documented a temporal shift in the preferred SF of some V1 neurons, consistent with nonseparable spatiotemporal RFs (Bredfeldt and Ringach 2002; Malone and Ringach 2008; Mazer et al. 2002). As the measurement of SF tuning with drifting gratings integrates responses over multiple grating cycles, the resultant tuning curves may be broader than the ones measured using a reverse correlation approach that allows for the estimation of tuning at an optimal temporal delay (Ringach et al. 2003; Nishimoto et al. 2005). In addition, the reverse correlation approach, when combined with multielectrode array measurement of neural responses, allows for efficient and simultaneous measurement of SF tuning functions at the optimal orientation for several cells (Nishimoto et al. 2005). For these reasons, we chose a subspace reverse correlation method over the traditional approach for estimating SF responses (Ringach et al. 1997a,b; Nishimoto et al. 2005).

For the above reasons, our hypothesis is that a coarse-to-fine discrimination mechanism, if it exists in area V1, will be one that manifests as an initial sharpening of the left flank of the SF tuning curve (increasing discrimination performance for low SFs) followed by a sharpening of the right flank. As the left flank is sharpened, the preferred SF could shift to higher SFs consistent with previous observations of coarse-to-fine tuning. The subsequent sharpening of the right flank could then result in a fine-to-coarse shifting of the preferred SFs, also as observed in some previous studies (e.g., Menz and Freeman 2003). Thus, in summary, we expected to find a coarse-to-fine sharpening of the flanks of the SF tuning curve concomitant with a coarse-to-fine-to-coarse shift in the preferred SF of the tuning curve.

MATERIALS AND METHODS

Subjects.

Three adult bush babies (Otolemur garnetti) of both sexes weighing 0.9–1.1 kg each were used in these experiments. All animals were handled according to the National Institutes of Health Guide for the Care and Use of Animals, under an approved protocol from the Vanderbilt University Animal Care and Use Committee (IACUC).

General procedures.

All experiments were conducted while the animals were under general anesthesia and paralysis. Anesthesia was induced with 2–4% isoflurane in O₂. Animals were given intramuscular dexamethasone to control edema (1 mg/kg); glycopyrrolate to control excessive pharyngeal, tracheal, and bronchial secretions (0.015 mg/kg); and Naxcel as an antibiotic (2.2 mg/kg). Two venous catheters were inserted. Body temperature was maintained near 37.5°C with a heating blanket and monitored using a rectal thermometer. Heart rate, inspired and expired CO₂, and ECG were continuously monitored. After tracheal intubation, animals were mounted in a stereotaxic apparatus and the anesthetic was switched to propofol (10 mg·kg⁻¹·h⁻¹). Neuromuscular blockade was induced with an intravenous injection of 1 mg/kg of pancuronium bromide, and animals were artificially ventilated with a mixture of 75% nitrous oxide, 23.5% oxygen, and 1.5% carbon dioxide that was delivered at a rate of 35–50 strokes/min in a volume sufficient to maintain the peak expired CO₂ at 3.5–4%. Paralysis was maintained with a continuous infusion of pancuronium bromide (1–2 mg·kg⁻¹·h⁻¹) in 5% dextrose lactated Ringer's solution. A 10-mm craniotomy was performed over primary visual cortex (V1) and the dura reflected. After craniotomy and durotomy, anesthesia was maintained with the nitrous oxide and propofol (4–7 mg·kg⁻¹·h⁻¹). Anesthetic levels were evaluated by observing heart rate, ECG, and CO₂ levels. Additional propofol was given as needed. Mydriasis and cycloplegia were induced with 1% atropine sulfate. Individually fitted gas-permeable contact lenses with 3-mm artificial pupils were used to render the retinae conjugate with the viewing screen at a 57-cm distance. In some cases, as indicated by direct retinoscopy, auxiliary spectacle lenses were added. Retinal landmarks [optic disk and area centralis (AC)] were projected onto the plotting screen using a fiber optic light source. The bright tapetum of the nocturnal bush babies allowed a clear image of the retina to be reflected on the screen. The clarity of the image of the retina also served as a good additional optical check to ensure that appropriate contact lens power was selected for each individual animal.

Recording and stimulation.

The 100-electrode Utah array (Cyberkinetics) was pneumatically inserted into area V1 to a depth of ∼600 μm. The locations of array in V1 and electrode tips in supragranular layers I–III were confirmed later by histological reconstruction of cytochrome oxidase (CO)-stained tissue sections (see Fig. 5). The array was secured and the craniotomy was covered with 1% agar. Signals on each electrode were band-pass filtered between 1 and 5 kHz with a 2nd-order Butterworth filter, the average noise level in this frequency band was estimated, and a threshold was set at 3–3.5 times the average noise level. Only those spikes that crossed this threshold were used to select a single neuron on each electrode for further analyses. In these experiments, about 5–40 neurons were obtained per implantation of the array.

Fig. 5.

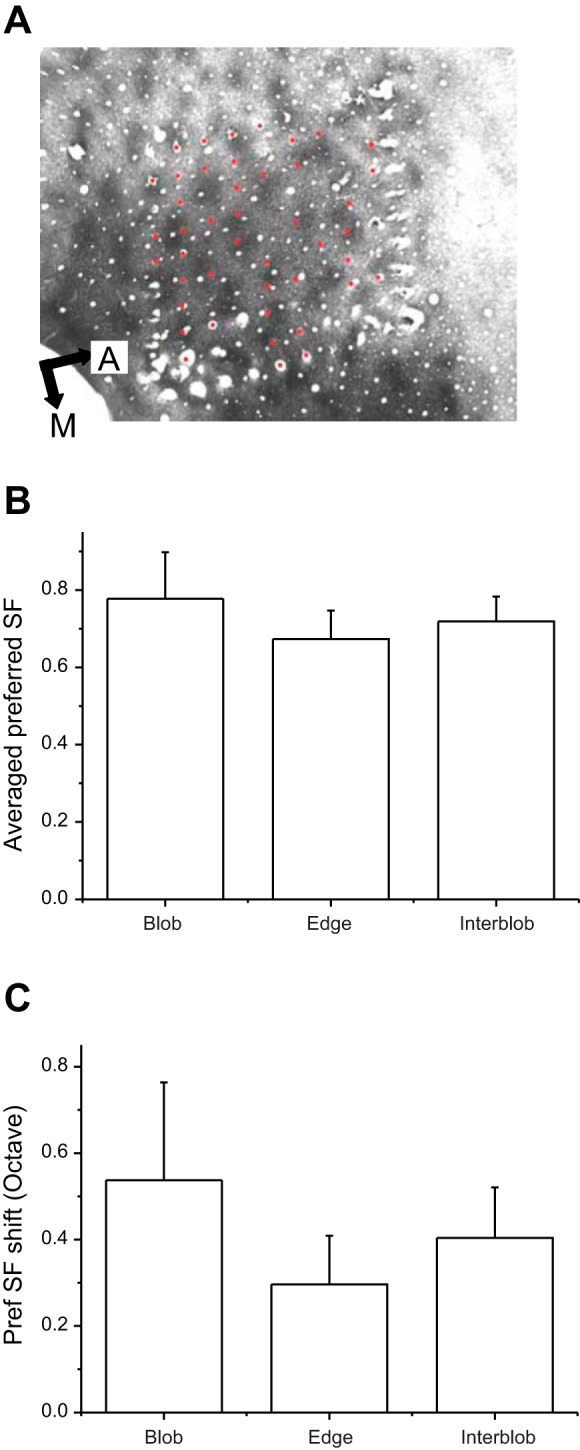
Cytochrome oxidase (CO) compartments and SF tuning properties. A: electrode positions (red dots) are shown superimposed on a CO-stained section of area V1. Positions of the red dots were determined by serial reconstructions of sections aligned using fiducial markers (A and M). The distribution of electrode locations relative to CO compartments was roughly uniform (see text). B: average preferred SF is shown separately for neurons in the 3 CO compartments. Error bars represent 1SE. C: average shift in the preferred SF is shown for neurons in the 3 CO compartments.

To accurately map RFs, we used a modified version of Bishop's plotting table method (Bishop et al. 1971). Optic disks and retinal blood vessels were back reflected with a fiber-optic light source and plotted on a tangent screen 57 cm in front of the eyes. AC was marked relative to the optical disk for each eye. Throughout the experiment, the positions of retinal landmarks were periodically checked for residual drifts of the paralyzed eyes. Stimuli such as moving lines, flashing lines, and flashing spots were created using a projector with analog controls and back projected onto the tangent screen. V1 RFs were then accurately hand mapped using these stimuli and plotted on the tangent screen along with retinal landmarks and the AC. With the use of a 45° mirror, the RFs, AC, and retinal landmarks were then precisely transferred to a CRT monitor on which experimental stimuli were presented.

To quantitatively define the preferred orientation for each neuron, we presented drifting sine wave gratings (SF = 0.5 cyc/°, temporal frequency = 2 Hz, contrast = 50% contrast, at 18 orientations from 10 to 180° at 10° increments) displayed on the full screen (21-in. monitor). These spatial and temporal frequency values were selected based on the average preferred values for V1 neurons from our previous study (DeBruyn et al. 1993). Visual stimuli were generated using WinVis (Neurometrics) library functions in MatLab (Mathworks). Stimuli were presented at a refresh rate of 100 Hz, with a mean luminance of ∼73 cd/m². Neural responses were Fourier transformed, and the ratio of the response at the stimulus frequency (F1) to the response at 0 Hz, with baseline response subtracted, was used to classify neurons as simple or complex (Skottum et al. 1991).

The temporal dynamics of SF tuning was determined using a reverse correlation method (Ringach et al. 1997a; Bredfeldt and Ringach 2002). High-contrast (50%) stationary sine wave gratings were presented in a virtual square window large enough to cover the RF center and surround each well-isolated cell (i.e., measurements were repeated for each cell with a distinctive RF location and size). Typically, the side of the square window was about 12°, approximately two to four times the diameter of the RF center, in agreement with previous studies (Ringach et al. 2003). This stimulus size was chosen to ensure that surround mechanisms, which appear to be largely responsible for suppression, were engaged (Ringach et al. 2003; see also Gillespie et al. 2001). In addition, stimuli covering only the RF center were too small compared with the ones used in psychophysical measurement of the temporal dynamics of discrimination thresholds, thus precluding a reasonable comparison of our results with psychophysics (Watt 1987; Westheimer 1991).

These stimuli were presented at eight different SFs (0.1, 0.2, 0.4, 0.6, 0.8, 1.1, 1.5, and 1.7 cyc/° in two cases and 0.1, 0.2, 0.4, 0.6, 0.8, 1.1, 1.5, and 2.0 cyc/° in the third case), five orientations (the 5 most-preferred orientations of the isolated cells), and eight phases (from 45° to 360° with 45° increments), randomly interleaved with blanks (grey screen of mean luminance, 8 blanks in each sequence of 328 stimuli presented) at the rate of 50 frames/s. To get a sufficient number of spikes to carry out reverse correlation analysis, each stimulus had to be presented about 500–700 times (Ringach et al. 1997a).

Experiments typically took 48–72 h depending on the number of well-isolated single cells obtained in each array implant. Once all required data were collected, the animal was perfused and brain fixed, blocked, and sectioned (see Histology).

Kernel estimation.

Spikes were reverse-correlated in 1-ms time steps with eight SFs, five orientations, and a blank. Spikes associated with the same SF but different phases were pooled together for this analysis. Here we report the temporal dynamics of SF selectivity only at the preferred orientation of the cell. Responses were quantified as the log likelihood A_n(f, t), at a given SF f and time t, as follows (Bredfeldt and Ringach 2002):

$$A_n\left(f,t\right)={\log }_{10}\left[\overline{A}(f,t)\right]={\log }_{10}\left[\raisebox{1ex}{$A(f,t)$}\!\left/ \!\raisebox{-1ex}{$A_0(t)$}\right.\right]$$ (1)

where A(f, t) is the estimated probability of appearance of a sine wave grating of SF f cyc/° in the t ms before a spike and A₀(t) is the estimated probability of appearance of a blank stimulus in the t ms before a spike. A positive A_n(f, t) corresponds to a facilitation of the neural response for the SF f cyc/° at time t ms over the response to the blank stimulus. A negative A_n(f, t) corresponds to a suppression of neural response for the SF f cyc/° at time t ms relative to the response to the blank stimulus. In a majority of the analyses, cubic smoothing splines were fit to the binned estimates of log likelihood ratio. Therefore, in what follows, A_n(f, t) is treated as a continuous function of f and t.

The signal-to noise ratio (SNR) of the estimated kernel was taken into account in all our analysis. The L₂-norm of the kernel with respect to the SF is defined as

$${\Phi }^2(t)={\displaystyle \int {\left|A_n(f,t)\right|}^{2}df}$$ (2)

The baseline noise level was estimated as the L₂-norm averaged over a range of long time delays (t > 200 ms) at which the spikes are uncorrelated with the stimuli (Bredfeldt and Ringach 2002; Malone et al. 2007; Ringach et al. 1997a). The beginning and the end of the range of time delays over which baseline noise level was estimated varied slightly (τ_ini = 200–220 ms and τ_fin = 220–240 ms, respectively) from cell-to-cell depending on when response completely decayed to baseline. Average noise level was estimated as

$$n^2=\frac{1}{{\tau }_{\text{fin}}-{\tau }_{\text{ini}}}{\displaystyle {\int }_{{\tau }_{\text{ini}}}^{{\tau }_{\text{fin}}}{\Phi }^2(t)dt}$$ (3)

The SNR was then estimated as a function of time by

$$\text{SNR}(t)=\frac{\Phi (t)}{n}$$ (4)

The average peak SNR across the population of cells used in all analyses in this study was 7.8. For each cell, only the time interval over which SNR(t) > 2 was used in the analysis. Within the time range over which SNR(t) >2, slices of the kernel A_n(f, t) were fit with cubic smoothing splines, derivatives were computed, and, as required, inflexion points or points of maxima and minima were solved (MATLAB; Mathworks). All parameters, including preferred SF, SF selectivity, slope of the tuning curve, response latency, peak amplitude, amplitude of peak suppression or facilitation, and time of peak suppression or facilitation, were estimated in this manner. The time at which SNR exceeded 2 initially was designated as the “response onset time,” τ_onset, and the time of decay of SNR back to 2 was designated as the “response offset time,” τ_final (Bredfeldt and Ringach 2002). Changes in SF tuning width [i.e., half-width at half-height (HWHH)] and preferred SF (f_p) were computed over the interval from τ_onset to τ_final. For example, the change in preferred SF, Δ f_p was computed in octaves as

$$\Delta f_p={\log }_2\left(\raisebox{1ex}{$f_p({\tau }_{\text{final}})$}\!\left/ \!\raisebox{-1ex}{$f_p({\tau }_{\text{onset}})$}\right.\right)$$ (5)

Estimation of slope.

The dynamic SF discrimination performance of neurons was estimated from the kernels A_n(f, t). Previous studies have used both the location of the peak slope of the tuning curve and the location of peak Fisher information as proxies for best discriminanda (Bradley et al. 1985; Seung and Sompolinsky 1993). We computed, compared, and used both measures in this study. To compute and correctly interpret the slope, we first noted that A(f, t) is the estimated probability that a sine wave grating of SF f cyc/° will evoke a spike in t ms. Multiplying this probability by constant rate gave the mean spike firing rate for each SF and time. Note also that A₀(t), its dividend in the log likelihood function, is independent of SF. Therefore, the slope of the function Ā(f, t) is equal to the slope of the neural response functions estimated in the traditional manner (e.g., as spike density functions) to within a scale factor. For our purposes, this slope was estimated as the partial derivative:

$$d_n(f,t)=\frac{\partial }{\partial f}\hspace{0.17em}\overline{A}(f,t)$$ (6)

Location of peak slope for a time slice was estimated by fitting smoothing cubic splines and determining the maxima, as stated above.

Estimation of Fisher information.

Fisher information is the inverse of the lower bound on the variance of unbiased estimators of a nonrandom parameter corrupted by random noise (p. 63–68, Van Trees 2001). As such, any unbiased estimator for which the variance equals the inverse of its Fisher information is a minimum variance, or efficient, estimator (p. 63–68, Van Trees 2001). Assuming discrimination of SFs involves the estimation of SF values (see the following section), the peak location of Fisher information might indicate the SFs that can be efficiently discriminated (Seung and Sompolinsky 1993). In addition, under certain assumptions, the probability of error in a two-alternative forced choice discrimination of two closely related stimuli is also inversely related to Fisher information (Seung and Sompolinsky 1993). In this sense, we computed and interpreted the dynamics of Fisher information as a proxy for how SF discrimination performance changes with SF and time. We assumed approximately Poisson statistics for the firing rate of V1 neurons. Therefore, for reasons described above, Ā(f, t) is a scaled Poisson variable and hence, a Poisson variable itself (albeit with a different variance; p. 123, Papoulis and Pillai 2002). We computed Fisher information as

$$F(f,t)=E\left[-\frac{{\partial }^2}{\partial f^2}\log \hspace{0.17em}\text{p}\left(\raisebox{1ex}{$r(f,t)$}\!\left/ \!\raisebox{-1ex}{$f$}\right.\right)\right]$$ (7)

where $p\left(\raisebox{1ex}{$r(f,t)$}\!\left/ \!\raisebox{-1ex}{$f$}\right.\right)$ is the conditional probability density of neural activity at a given SF and E[.] denotes expectation with respect to neural response r(f, t), with the mean response E[r(f, t)] = k Ā(f, t), where k is a constant. For Poisson statistics, this Fisher information is

$$F(f,t)=c\frac{{\left(\overline{A\prime }(f,t)\right)}^2}{\overline{A}(f,t)}$$ (8)

where c is a constant and A′ is the derivative with respect to f. This quantity was estimated from our data for all neurons.

Estimation of best discriminable SFs.

As briefly mentioned above, several assumptions are involved in inferring fine discrimination performance from the slope or Fisher information of the tuning curve. Some of these assumptions, such as an approximately linear relationship between mean and variance of firing rates as required for Poisson modeling, do not always hold true. Further, optimally discriminable stimulus parameters depend on a variety of factors not captured either by the slope or Fisher information, including the nonstationarity of baseline response (Van Trees 2001) and model assumptions used to relate neural responses to discrimination decisions (Seung and Sompolinsky 1993). Therefore, we also used a direct Bayesian approach to compute the SF discrimination performance from the kernel A_n(f, t) and estimated best discriminable SFs as the SFs at which this discrimination performance was maximal. The best discriminable SF on the left (low SF range) and right (high SF range) flanks of the SF tuning curve for each cell were separately estimated as follows. First, the directional derivatives of the kernel,

$$d_n(f,t)=\frac{\partial }{\partial f}\hspace{0.17em}\overline{A}(f,t)$$ (9)

were computed and used to determine the regions of rapid change in SF responses on the left and right flanks of the preferred SF. On the left flank, the derivative was positive and on the right, negative. On each flank, we chose a 1-octave range of SFs on either side of the peak slope location. Over this range, we estimated SF discrimination thresholds at several closely sampled points, as described in the following. For each sample SF point, a range of test SFs were chosen, reflecting a change of ± 0–100% in steps of 10%. Responses were modeled as Poisson variables and resampled from the distribution with the mean value A_n(f, t). For each test SF, a pair of response histograms was created, one for the test and one for the sample SF. With the use of the receiver operating characteristic method, the probability of correct discrimination was computed for each test SF, neurometric functions were fit, and SF discrimination thresholds were determined (Bradley et al. 1985; Purushothaman and Bradley 2005; Purushothaman et al. 2009). The sample SF with the lowest threshold on each flank was chosen as the best discriminable frequency.

Histology and alignment.

At the termination of each experiment, the animal was euthanized with an overdose of sodium pentobarbital (Nembutal) and perfused transcardially with a saline rinse followed by perfusion of a fixative containing 2% paraformaldehyde in 0.1 M phosphate buffer. The brain was removed and tissue encompassing V1 was dissected from the hemisphere and flattened overnight with weights in 30% sucrose buffer. This flattened piece of tissue containing V1 was then frozen and cut with the surface vasculature preserved in the first 100 um tangential section. The remaining sections were cut at 50 um. During cutting, three to four fiducial marks were made at the periphery of the tissue for later alignment of the sections. CO staining was done using methods described previously (Boyd and Matsubara 1996) to identify CO blobs and interblobs. Placement of the array in V1 was verified by reconstructing electrode locations with respect to CO blobs and interblobs. As V2 lacks the distinct blob-interblob geometry, this allowed us to confirm that our array sampled only V1 neurons in the experiments.

RESULTS

We studied a total of 87 neurons in layers 2/3 of area V1 from 3 bush babies (see materials and methods). We histologically verified, based on CO blob pattern, that the neurons were all located in area V1. Average eccentricity of the RFs was 4.3 ± 0.20° (means ± 1SE) from AC in the lower quadrant. Average diameter of the RFs was 3.6 ± 0.15° (means ± 1 SE). Using the ratio of the first harmonic to the mean firing rate in response to drifting gratings (F1/F0), we classified all 87 cells as complex (Skottun et al. 1991, but see Mechler and Ringach 2002). A majority of these cells (83/87, 95%) were band-pass tuned for SF, with an average preferred SF of 0.68 ± 0.03 cyc/° (means ± 1SE).

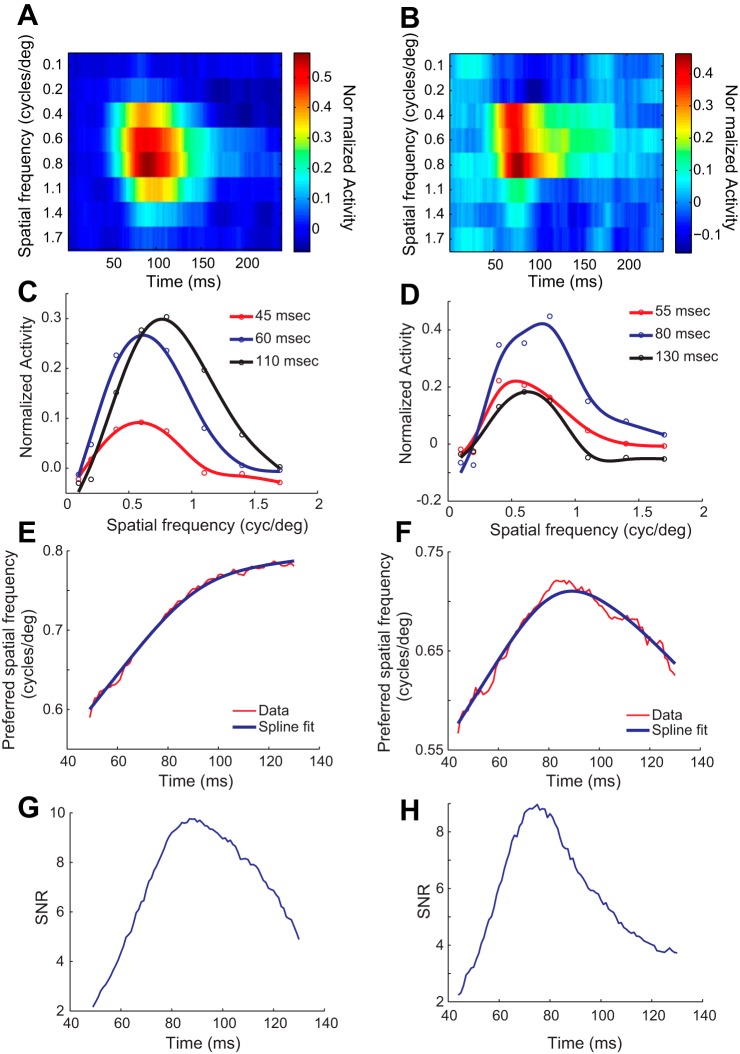
Neural responses were measured to a fast sequence of high contrast (50%) stationary sine wave gratings presented at different orientations, SFs, and spatial phases, intermixed with blank stimuli at the mean luminance (see materials and methods). The SF-time kernels (Eq. 1) were estimated from these responses using the reverse correlation approach. Typically, kernels showed significant responses developing around 40–50 ms after stimulus onset, peaking near the preferred SF around 60–80 ms and decaying to background levels around 120–150 ms (Fig. 1, A and B). Responses to higher SFs were delayed (onset ∼60–75 ms; Fig. 1A) with respect to those for lower SFs. Time slices showed SF tuning was band pass, with a clear preferred SF, at all times during which there was a significant response (Fig. 1, C and D).

Fig. 1.

Temporal dynamics of spatial frequency tuning. A: spatial frequency (SF) response kernel for a group 1 neuron is shown as a heat map. Response amplitude has been normalized so that baseline response is at 0 (cyan/blue). Activity-color scale bar is shown next to the figure. Darker blue regions show suppression of response below baseline, and colors trending towards deep red show enhancement over baseline response. Longer latency of response at higher SFs as well as greater amplitude and longer duration of response near preferred SFs are both obvious features. B: SF response kernel for a group 2 neuron. Dark blue showing suppression below baseline response is visible at low SFs around 75–100 ms and at high SFs around 100–150 ms. C and D: SF tuning curves shown at 3 times slices for the group 1 and group 2 neurons, respectively. Data (open circles) were fitted to smoothing cubic splines (continuous lines). E and F: preferred SF is shown as a function of time for the group 1 and group 2 neurons, respectively. Data (red) were fitted to smoothing cubic splines (blue lines). G and H: signal-to noise ratio (SNR) for the same 2 neurons remained well above 2 during the duration within which preferred SF data were further analyzed.

Dynamics of SF tuning.

A key finding was that there were two different patterns in the temporal evolution of the preferred SF of V1 neurons. In one group (group 1), the preferred SF increased monotonically with time and reached its highest value at the time the response decayed to background level (Fig. 1E). In the second group of neurons, group 2, the preferred SF evolved nonmonotonically with time, first increasing smoothly to a peak value and then decreasing (Fig. 1F). To ensure that this difference was not merely due to noisy measurements, we took two precautions. First, we considered for these tuning analyses only the time range of 30–130 ms within which all 87 neurons in our database showed robust response to stimuli. Second, within this interval, we quantified the SNR of the kernels using the method of Ringach and colleagues (Bredfeldt and Ringach 2002; Malone et al. 2007). Signal and noise were estimated as the L₂-norms of the kernel with respect to the SF averaged over the time interval during which spikes were strongly correlated and uncorrelated, respectively, with the stimuli (see materials and methods). Combining these two criteria, change in preferred SF was considered significant only over the interval in the time range 30–130 ms within which the signal was at least twice the noise level (Fig. 1, G and H).

We quantitatively classified the change in preferred SF as either monotonic or nonmonotonic by computing the percentage of time over which the preferred SF decreased after reaching its peak value within the criterion interval (i.e., 30–130 ms and SNR > 2). For example, for the neuron depicted in the Fig. 1, A, C, E and G, SNR increased to a peak value of 9.8 and decreased to 4.9 between 30 and 130 ms after “stimulus onset” (Fig. 1G). Within this period, the preferred SF continued to increase monotonically (Fig. 1E). Consequently, the percentage of time over which preferred SF decreased after reaching its peak value was 0%. For the neuron depicted in Fig. 1, B, D, F, and H, the SNR increased to a peak value of 9.0 and decreased to 3.7 (Fig. 1H). Over the same interval, the preferred SF increased to a peak and then declined smoothly (Fig. 1F). As a result, the slope of the preferred SF curve was negative over 47% of the interval. Allowing for neural variability and measurement noise, we classified cells that exhibited negative slope over 0–10% of the criterion interval as group 1 or “monotonic neurons,” and those with negative slope over more than 25% of the criterion interval as group 2 or “nonmonotonic.” With the use of this rule, 83/87 cells could be clearly classified. There were 51 cells in group 1 with negative slope over 2.2 ± 0.9% (means ± 1SE) of the criterion interval. Of these, 41 cells (80%) showed no negative slope at all (0% of the interval). Group 2 consisted of 32 cells that had negative slope over 40.0 ± 2.8% (means ± 1SE) of the criterion interval.

We further examined the net temporal changes in SF tuning width and preferred SF over the criterion interval (i.e., value at the end of the interval − value at the beginning of the interval) by comparing the two. Note that both groups of neurons showed a net positive change (i.e., increase) in the preferred SF over the criterion interval (see Fig. 1, E and F) although this change will be smaller for group 2 neurons. To facilitate comparison with previous studies, we plotted the changes both as simple differences in cycles by degrees (Fig. 2A) and in octaves (Fig. 2B). This comparison showed that HWHH of SF tuning decreased for both groups by 0.40 ± 0.07 cyc/° (means ± 1SD) while the preferred SF increased by 0.28 ± 0.16 cyc/° (mean ± 1SD). This amounted to a 0.34 octaves change in the HWHH and 0.62 octaves change in the preferred SF. Remarkably, these values are more similar to those reported for the macaque, another primate, than for the nocturnal mammal cat (Bredfeldt and Ringach 2002; Nishimoto et al. 2005). Furthermore, there was a fairly strong and significant relationship between the changes in SF selectivity and preferred SF as indicated by a linear regression analysis (R² = 0.58, F = 40, P = 0.0; Fig. 2A).

Fig. 2.

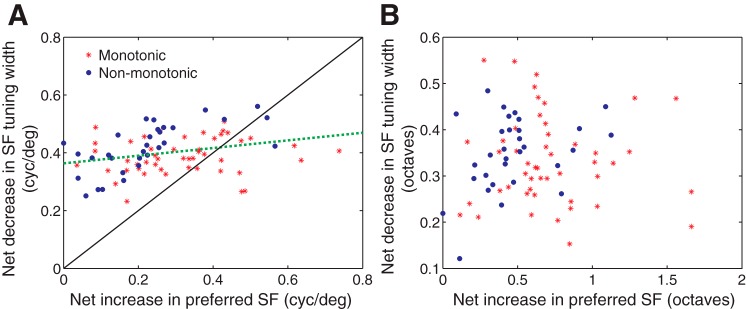
Relationship between changes in SF tuning width and preferred SF. A: change in SF tuning width is plotted against the net change in preferred SF for both group 1 (red) and group 2 (blue) cells over the criterion temporal interval. Regression line is shown in green (dotted). B: same data plotted in octaves. Color notation same as in A.

Dynamics of Fisher information.

As fine discrimination depends on the properties of the flanks of the tuning curve and not on its peak (Westheimer et al. 1976; Regan and Beverly 1985; Bradley et al. 1985; Vogels and Orban 1990; Seung and Sompolinsky 1993; Geisler and Albrecht 1997; Hol and Treue 2001; Purushothaman and Bradley 2005; Schoups et al. 2001; Gu, et al. 2007; Chowdhury and DeAngelis 2008), we examined in detail how the flanks of the SF response kernels evolved with time.

We computed two indirect measures of fine SF discrimination performance, the slope and the Fisher information of the kernel, as functions of time at all stimulus SF values (see materials and methods). The SF tuning curve was typically band pass in shape for a fixed time slice (e.g., compare Fig. 1C and Fig. 3C, left). Therefore, both slope and Fisher information reached extremum values on either side of the peak SF. In group 1 neurons, both slope and Fisher information reached their maximum values on the left flank, i.e., for SFs lower than the preferred SF (Fig. 3, C–E, left). In contrast, both slope and the Fisher information reached their highest values on the right flanks (i.e., at SFs above preferred SF) of group 2 neurons (Fig. 3, C–E, right). The average peak Fisher information on the left flank of the SF tuning curves for group 1 neurons (means ± 1SE = 1.52 ± 0.12; n = 51) and group 2 neurons (means ± 1SE = 1.45 ± 0.10; n = 32) was not significantly different from each other (Student t-test, P > 0.66, Fig. 4A). On the right flank of the SF tuning curves, the average peak Fisher information for group 1 neurons (means ± 1SE = 0.70 ± 0.05; n = 51) and group 2 neurons (means ± 1SE = 0.89 ± 0.07; n = 32) was significantly different from each other (Student t-test, P < 0.04; Fig. 4B). These results showed that both group 1 and group 2 neurons have similar discrimination abilities for low SFs (Fig. 4A) but group 2 neurons are better discriminators of high SFs (Fig. 4B). In group 1 neurons, the difference between the times at which Fisher information peaked on the two flanks of the SF tuning curve (median = −1.2 ms; interquartile range = 14.9 ms) was not significantly different from 0.0 (Wilcoxon signed rank test, P > 0.60; Fig. 4C). However, in group 2 neurons, this difference (median = −16.7 ms; interquartile range = 21.4) was significantly different from 0.0 (Wilcoxon signed rank test, P < 0.001; Fig. 4C).

Fig. 3.

Slope and Fisher information of SF tuning. A: SF response kernels for a group 1 (left) and 2 group 2 (middle and right) neurons. Same conventions as in Fig. 1. B: slope (first derivative along SF axis) of the SF response kernel is shown as a heat map for the group 1 (left) and group 2 (middle and right) neurons. Slope-color scale bar is shown next to the figure. Both dark blue and dark red show high rate-of-change of response with respect to SF, bluer and redder shades representing decrease and increase in activity, respectively, with increasing SF. C: temporal response profiles are shown at a low (red), medium (blue), and high (black) SFs for group 1 (left) and group 2 (middle and right) neurons. Longer latency at the highest SF is obvious in both neurons. A strong suppression of the response below baseline is clearly visible at the highest SF in the group 2 neuron. The suppression at the highest SF is greatest around 100 ms while the peak responses at the low and medium SFs occur near 50 ms. D: temporal profiles of the magnitude of the slope are shown at low (red) and high (black) SFs for the group 1 (left) and group 2 (middle and right) neurons. It is clear that the slope is of greater magnitude at lower SFs in the group 1 neuron and at higher SFs in the group 2 neuron. Note that the maximum magnitude of slope and Fisher information (e.g., 1.1 cyc/° in middle and 0.8 cyc/° at right) need not occur at the SF at which the response is suppressed (e.g., in C, 1.4 cyc/° in middle and 1.1 cyc/° in right). E: temporal profiles of Fisher information are shown for the same low (red) and high (black) SFs for the same group 1 (left) and group 2 (middle and right) neurons. Again it is clear that Fisher information is greatest at low SFs in the group 1 neuron and at high SFs in the group 2 neuron.

Fig. 4.

Temporal dynamics of spatial frequency discrimination. A: distribution of the maximum Fisher information on the left flank of the SF tuning curve (i.e., for SFs < preferred SF) for group 1 (“Monotonic,” red) and group 2 (“Nonmonotonic,” blue) neurons. The arrows indicate the mean values in corresponding colors. B: distribution of the maximum Fisher information on the right flank of the SF tuning curve (i.e., for SFs > preferred SF) for group 1 (“Monotonic,” red) and group 2 (“Nonmonotonic,” blue) neurons. The arrows indicate the mean values in corresponding colors. C: distribution of the difference between the times at which Fisher information peaked on the left and right flanks. These time difference distributions are shown for group 1 (red) and group 2 (blue) neurons. Because of the obvious skew in the shapes of these distributions, the arrows indicate median values for the 2 distributions. Nonparametric tests were used for analyzing these data (see results). D: final preferred SF is shown as a function of the total high-SF suppression strength for group 2 neurons. Data are shown in blue dots, regression line in red. Green and yellow circles correspond to the nonmonotonic neurons shown in Figs. 1 and 3, respectively. E: maximum Fisher information on the right flank of the SF tuning curve is shown as a function of the total high-SF suppression strength for group 2 neurons. Conventions are same as above. Green and yellow circles correspond to the nonmonotonic neurons shown in Figs. 1 and 3, respectively. Note, as stated above, that the time slices in Fig. 1 were taken arbitrary instants to clearly illustrate the slope changes while the Fisher information in D are estimates obtained from fitted curves (see materials and methods). F: overall best discriminable SF, estimated directly using Bayesian methods (see text), is plotted against the time of its occurrence for group 1 (“Monotonic,” red) and group 2 (“Nonmonotonic,” blue) neurons. Black like shows linear regression (see text for details).

Suppression at high SF.

What accounts for these differences between the two neuronal groups? The most noticeable difference in the SF kernels of group 1 and group 2 neurons was the presence of stronger suppression at high SFs, 1.1–1.7 cyc/°, during the later epochs of the response, 100–175 ms (compare Fig. 3, A and B, left, group 1 neuron, with right, group 2 neuron). We suspected this stronger suppression might have a greater influence in shaping the right flank (higher SFs) of tuning curve for group 2 neurons, consequently changing the dynamics of their SF response. We carried out two analyses to test this intuition. We quantified the total amount of suppression as the volume below the baseline response in the SF vs. time plot of activity at the suppressed high SFs (e.g., Fig. 3A, right). If the nonmonotonicity of preferred SF dynamics resulted from this suppression, then suppression strength must correlate with final preferred SF. Indeed, the regression of the final preferred SF against suppression strength (Fig. 4D) had a negative slope (95% confidence interval = [−0.011 −0.004]) that was statistically significant (R² = 0.42, F = 21.6, P < 0.0001, Var = 0.02). Furthermore, if the suppression were responsible for the sharpening of the right flank of the SF tuning curve, then suppression strength must correlate with the peak Fisher information for high SFs. Consistent with this hypothesis, we found that the regression of peak Fisher information for the right flank of SF tuning curve against suppression strength (Fig. 4E) had a positive slope (95% confidence interval = [0.003 0.016]) that was statistically significant (R² = 0.24, F = 9.6, P < 0.005, Var = 0.08).

Dynamics of SF discrimination.

Using receiver operating characteristic analysis, we estimated the best discriminable SF for each neuron in both groups (see materials and methods). These computations were repeated for all time slices over the previously chosen criterion time interval of response (i.e., 30–130 ms and SNR > 2). The sample SF at which discrimination probability was the greatest across SF and time was taken as the best discriminable SF for the neuron. In general, the best discriminable SFs for group 1 neurons (shown in red, Fig. 4F) were lower than for group 2 neurons (shown in blue, Fig. 4F), as expected from the above results (Fig. 3, D and E). When examined as a function of the time at which the probability of SF discrimination peaked, the best discriminable SF showed a statistically significant increasing trend (Fig. 4F; 95% confidence interval for the regression slope = [22.7 39.0]; R² = 0.30; F = 55.8; P < 0.00001; Var = 485). Thus, on the average, the best discrimination of higher SFs occurred later than the best discrimination of lower SFs.

Comparison of neurons in CO compartments.

We examined the relationship between SF tuning properties of V1 neurons and their locations with respect to CO blobs. We were able to clearly identify the CO compartments for 43 well-isolated neurons (Fig. 5A; see materials and methods; 3/43 were low-pass tuned for SF). By aligning the CO-stained section with the electrode marks (red dots in Fig. 5A), we performed serial reconstructions through the stacked sections (see Histology and alignment). Neurons recorded on the clearly identified and located electrodes were assigned to blobs, edges, or interblobs. Of the 43 cells, 11 were in blobs, 16 at the edge of blobs, and 16 in interblobs, suggesting that our cells were distributed randomly across compartments. There was no significant difference in the preferred SFs of neurons in the three CO compartments (Fig. 5B; ANOVA, P > 0.7). There was also no significant difference in the dynamics of SF tuning between the three neural populations (Fig. 5C; ANOVA, P > 0.54). However, because of the low number of cells in each compartment, we cautiously defer drawing conclusions about SF tuning properties of neurons in the different CO compartments from these data. We note that our previous study (DeBruyn et al. 1993) that specifically looked for differences in SF tuning properties found that, unlike in macaques, cells in CO blobs had significantly higher SF cutoffs than cells in interblobs. However, that study also had a small sample size.

DISCUSSION

Using reverse-correlation method, we studied the temporal dynamics of SF tuning in layers 2–3 of the primary visual cortex. We found that V1 neurons exhibited two types of SF dynamics. In group 1 neurons, the preferred SF increased monotonically. On the average, these neurons were better at discriminating lower SFs than higher SFs. Group 2 neurons had preferred SF that increased initially and then smoothly decreased. These latter neurons were better at discriminating higher SFs than lower SFs. When both populations of neurons were pooled together, best discrimination at higher SF occurred later in time, consistent with a coarse-to-fine trend in SF discrimination. The three properties that set group 2 neurons apart from group 1 neurons were the following: 1) nonmonotonic change in preferred SF, 2) better discrimination of higher SFs, and 3) longer time taken to reach best discrimination performance. These properties were correlated with the strength of late suppression near high SFs observed in group 2 neurons. Taken together with previous studies, these new results show that the dynamics of SF tuning of V1 neurons can account for both coarse-to-fine detection and discrimination.

The accuracy and advantages of subspace reverse correlation method over traditional tuning measurements have been well documented (Nishimoto et al. 2005). Previous studies of the dynamics of stimulus tuning in V1 have sometimes arrived at divergent results in different species. For example, some studies found dynamic changes in orientation tuning curves (Volgushev et al. 1995; Pei et al. 1994; Ringach et al. 1997a) but others found no significant changes (Celebrini et al. 1993; Mazer et al. 2002; Gillespie et al. 2001; Nishimoto et al. 2005; Müller et al. 2001). In contrast, there has been broad agreement that SF tuning changes with time (Bredfeldt and Ringach 2002; Mazer et al. 2002; Nishimoto et al. 2005). Our data show that in the prosimian primate bush baby, the HWHH of SF tuning in area V1 changes by 0.34 octaves and preferred SF shifts by 0.62 octaves. Bredfeldt and Ringach (2002) reported in the macaque a shift in preferred SF of about 0.62 octaves. Nishimoto et al. (2005) reported a shift in preferred SF of about 0.23 octaves in area 17 of cat. Thus there is remarkable similarity in SF tuning dynamics of primates even though the range of SF tuning and SF selectivity of the nocturnal prosimians are similar to those of the nocturnal mammal cat (see below).

Dynamics of SF tuning and coarse-to-fine processing: comparison of physiology and psychophysics.

In area V1 of rhesus monkeys, preferred SFs of neurons cover about 1 log unit, ranging from about 0.5 to about 45 cyc/° (De Valois et al. 1982). Psychophysical SF sensitivities of humans and rhesus monkeys are similar, also ranging from about 0.5 to 50 cyc/° (Harwerth and Smith 1985; De Valois et al. 1974). Human psychophysical data from adaptation and discrimination studies imply that sizes of spatial filters analyzing a stimulus shrink over time from about 4.5 to 45 cyc/° (Watt 1987; Wilson 1983; Watt and Morgan 1985). Thus coarse-to-fine mechanisms appear to operate in these species over a range that is consistent with both the range of psychophysically measured SF sensitivities and the range of preferred SF tuning of area V1 cells.

In the prosimian primate bush baby used in this study, behavioral and electrophysiological assessments show similar SF selectivity ranges, extending from about 0.1 to about 2 cyc/° and peaking around 0.2–0.4 cyc/° (DeBruyn et al. 1993; Bonds et al. 1987). Our data show (Fig. 4F) that the dynamic change in best discriminable SF for both group 1 and 2 neurons span from about 0.1 to about 2 cyc/°. It therefore appears that if there were a behaviorally measurable coarse-to-fine change in perceptual spatial filter in this species, it could be amply supported by the dynamic changes in the SF characteristics of V1 neurons in this species.

A final point of interest is that in cat, another nocturnal mammal whose behavioral and neural SF selectivity is similar to that of the bush baby (Nishimoto et al. 2005; DeBruyn et al. 1993), a temporal sweep of disparity frequency from about 0.1 to about 0.8 cyc/°has been identified as a correlate for coarse-to-fine depth computation (Menz and Freeman 2003; Ringach 2003).

Comparison of SF tuning in different species.

As mentioned above, bush baby V1 cells have lower average preferred SF than the macaque. A comparative review of macaque (diurnal primate), bush baby (nocturnal prosimian primate), and cat (nocturnal mammal) SF tuning data shows that our observation of a high propensity of band-pass tuning for SF in area V1 is consistent with previous results. Macaque foveal simple and complex cells have average preferred SFs of 3.5 and 5.1 cyc/°, respectively; parafoveal simple and complex cells have 2.2 and 3.2 cyc/°, respectively (De Valois et al. 1982). These are higher than the average preferred SFs in cats (simple = 0.8 cyc/°; complex = 0.93 cyc/°; Movshon et al. 1978) and in bush babies (simple= 0.54 cyc/°; complex = 0.7 cyc/°; Debruyn et al. 1993). The average SF tuning bandwidth, which has been shown in macaques to be inversely proportional to the average preferred SF (De Valois et al. 1982), is smaller in macaques (simple = 1.4 octaves; complex = 1.5 octaves; De Valois et al. 1982) than in bush babies (simple = 1.9 octaves; complex=2.8 octaves; Debruyn et al. 1993). De Valois et al. (1982, p. 551) also mention that while the distribution of SF bandwidth is quite broad, there are both sharply tuned (1–1.5 octaves) and broadly tuned cells (>2 octaves).

SF-specific suppression of V1 responses.

At least two previous studies have reported suppression of responses in cat striate cortical cells when an optimal sine wave grating (i.e., grating at optimal orientation and SF) is presented superimposed on another grating at a different SF (De Valois and Tootell 1983; Bauman and Bonds 1991). In both studies, suppression was observed at SFs both higher and lower than the optimum SF and was stronger in simple than complex cells. Nearly 90% of simple and 29% of complex cells were inhibited by a SF greater than the optimal SF of the neuron while only 8% of simple and 8% of complex cells were inhibited by a lower SF (De Valois and Tootell 1983). These results, showing that a preponderance of SF-specific suppression happens at higher SFs, are in contrast to the suppression reported mostly for lower SFs by previous reverse correlation studies (Bredfeldt and Ringach 2002; Malone and Ringach 2008). As we suggest above, suppression at higher SFs may occur beyond the duration over which responses were computed in these studies. SF-specific suppression is also suggested by the broadening of SF tuning observed in cat V1 following the administration of GABA (Vidyasagar and Mueller 1994). However, pharmacologically elicited excitatory responses of cat V1 cells were found unaffected by visual presentation of a single sine wave grating at nonoptimal SF (Ramoa et al. 1986). It is unclear whether the excitatory responses in the latter study are comparable to visually evoked responses.

Role of suppression in the tuning dynamics of V1 neurons.

Dynamical changes in stimulus tuning suggest the involvement of delayed suppression. Surround suppression, which is a ubiquitous property of visual cortical RFs, is known to be temporally delayed with respect to the center response (Allman et al. 1985; Gilbert 1992; Fitzpatrick 2000; Albright and Stoner 2002; Knierim and van Essen 1992; Zipser et al. 1996; Jones et al. 2001; Bair et al. 2003). Therefore, surround suppression has been suggested as a possible mechanism for the “sharpening” of the orientation tuning curve (Blakemore and Tobin 1972; Ringach et al. 1997a). Consistent with this idea is the suggestion by Gillespie et al. (2001) that stimuli restricted to the center of the RF do not dynamically change the orientation tuning of intracellular potential while stimuli spanning two to four times the RF center do (Ringach et al. 2003; but see Xing et al. 2005).

Further detailed analyses of orientation tuning characteristics as a function of time indicated 1) an early tuned excitation, 2) a delayed global (i.e., orientation independent) suppression, and 3) a delayed suppression tuned to the preferred orientation of the cell (Ringach et al. 2003). These measurements, made at the optimal SF of the cell, therefore suggest that the Fourier spectrum S(ω_x, ω_y, t) of the suppressive components for appropriately delayed values of t include 1) band-pass energy patches at the preferred orientation θ = tan⁻¹$\left(\raisebox{1ex}{${\omega }_x$}\!\left/ \!\raisebox{-1ex}{${\omega }_y$}\right.\right)$ corresponding to the tuned suppression and 2) circular band around ω_x² + ω_y² = ω² corresponding to the global (unturned) suppression.

Bredfeldt and Ringach (2002) specifically studied the dynamics of SF tuning at the preferred orientation of V1 cells and found delayed suppression at low SF that correlated with a monotonic shift of the preferred SF towards higher value. These dynamics are similar to the ones we describe for group 1 cells in this study. However, Bredfeldt and Ringach (2002) did not report nonmonotonic dynamics exhibited by group 2 cells in our study. There are many differences between their study and ours that could potentially account for this difference. First, they studied macaques while we studied bush babies and this species difference alone could be the reason for the different results. Second, in our study we used a more lenient criterion of SNR >2 to analyze response kernels over a longer duration (>100 ms). This allowed us to identify the late suppression at higher SFs (i.e., at SF > preferred SF of the cell). The correlation between this late suppression at high SFs and the shift of the preferred SF back towards lower values (i.e., group 2 cells) is a novel observation.

In a later study, Malone and Ringach (2008) measured the dynamics of tuning in the Fourier domain, thus assessing dynamical changes in response at a range of orientations and SFs simultaneously. Malone and Ringach (2008) primarily investigated the spectrotemporal separability of V1 responses. Nevertheless, late-developing suppression at high SFs similar to the one observed in our group 2 cells can be seen in some of their data (see Fig. 2F in Malone and Ringach 2008).

Finally, it should be noted that not all group 1 cells exhibit significant suppression at low SFs. In this respect, our results are consistent with those of Vreysen et al. (2012), who showed in the mouse visual cortex that a monotonic increase in preferred SF can occur without an accompanying suppression of responses at low SFs.

Size tuning.

Ringach and colleagues reported that in primate V1 neurons, width and length of the RF envelope as well as the carrier period decrease during the time-course of response (Malone et al. 2007). These results could account for monotonic change in the selectivity of SF tuning with time. However, in order for changes in RF size to account for the nonmonotonic shift in SF selectivity observed in group 2 neurons in our study, it is necessary for the RF size also to change nonmonotonically. In the current experiments, we directly measured the dynamics of SF selectivity using sinusoidal gratings. Therefore, we do not know if there were dynamic changes in RF size that were concomitant with the observed dynamics of SF tuning. Simultaneous measurement of both RF and SF tuning dynamics in future experiments is required to understand in detail this relationship, particularly the mechanisms of emergence of space-time inseparability in the responses of some V1 neurons.

Diversity of tuning properties of V1 neurons.

SF responses are quite diverse among V1 cells in both cats and monkeys (Frazor et al. 2004; Malone and Ringach 2008). Malone and Ringach (2008) reported that the temporal dynamics of V1 responses in the Fourier domain show substantial diversity. Some neurons have temporally separable spectral kernels but a significant number also exhibit inseparable dynamics. When responses are dominated by net enhancement/suppression, spectral kernels are separable. Inseparable kernels have both net enhancement and suppression. Malone and Ringach (2008) further found that cells with inseparable spectral kernels had longer temporal responses. We must note that even though previous studies of SF dynamics examined responses over ∼140 ms, significant responses in many cells appear to have been limited to within 100–120 ms (Bredfeldt and Ringach 2002). In contrast, group 2 cells in our study had extended responses, even up to 140 ms. It is therefore likely that group 2 cells are closely related to those with inseparable spectral kernels reported by Malone and Ringach (2008).

As described in materials and methods, a few cells (4/87 or 5%) could not be classified as belonging to group 1 or group 2 according to our quantitative criterion. Taken together with the diversity of SF tuning in V1 summarized above, this fact indicates that the two groups may not be categorical.

GRANTS

This work was supported by National Institutes of Health Grants R01-EY-01778, P30-EY-008126, T32-EY-07135, and P30-HD-15052.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: G.P., X.C., and V.A.C. conception and design of research; G.P., X.C., D.Y., and V.A.C. performed experiments; G.P., X.C., and V.A.C. interpreted results of experiments; G.P., X.C., and V.A.C. edited and revised manuscript; G.P., X.C., D.Y., and V.A.C. approved final version of manuscript; X.C., D.Y., and V.A.C. analyzed data; X.C. and V.A.C. prepared figures; X.C. and V.A.C. drafted manuscript.