An investigation of positive and inverted hemodynamic response functions across multiple visual areas

Abstract

Recent studies have demonstrated significant regional variability in the hemodynamic response function (HRF), highlighting the difficulty of correctly interpreting functional MRI (fMRI) data without proper modeling of the HRF. The focus of this study was to investigate the HRF variability within visual cortex. The HRF was estimated for a number of cortical visual areas by deconvolution of fMRI blood oxygenation level dependent (BOLD) responses to brief, large‐field visual stimulation. Significant HRF variation was found across visual areas V1, V2, V3, V4, VO‐1,2, V3AB, IPS‐0,1,2,3, LO‐1,2, and TO‐1,2. Additionally, a subpopulation of voxels was identified that exhibited an impulse response waveform that was similar, but not identical, to an inverted version of the commonly described and modeled positive HRF. These voxels were found within the retinotopic confines of the stimulus and were intermixed with those showing positive responses. The spatial distribution and variability of these HRFs suggest a vascular origin for the inverted waveforms. We suggest that the polarity of the HRF is a separate factor that is independent of the suppressive or activating nature of the underlying neuronal activity. Correctly modeling the polarity of the HRF allows one to recover an estimate of the underlying neuronal activity rather than discard the responses from these voxels on the assumption that they are artifactual. We demonstrate this approach on phase‐encoded retinotopic mapping data as an example of the benefits of accurately modeling the HRF during the analysis of fMRI data. Hum Brain Mapp 35:5550–5564, 2014. © 2014 Wiley Periodicals, Inc.

INTRODUCTION

The hemodynamic impulse response function, often simply referred to as the hemodynamic response function (HRF), is a fundamental property of the blood oxygenation level dependent (BOLD) functional magnetic resonance imaging (fMRI) response. For a sufficiently long input, the BOLD response can be estimated using a linear transform model that includes the HRF as an explicit component. This allows the fMRI time‐course to be predicted by convolving the time‐course of the neural response with the HRF and then adding noise [Boynton et al., 1996; Boynton et al., 2012]. This method for analyzing fMRI data was proposed in 1994 by Friston, and subsequent work has facilitated the evolution of fMRI paradigms from block designs to event‐related designs and from basic BOLD statistical parametric mapping to more sophisticated quantitative analyses [Boynton et al., 2012; Dale and Buckner, 1997; Friston et al., 1994]. For example, the linear transform model has recently found its place at the heart of methods for single voxel time‐course modeling [Dumoulin and Wandell, 2008; Zuiderbaan et al., 2012].

The growing sophistication of fMRI experiments and modeling has also stimulated interest in the underlying components of the BOLD response, especially the characteristics of the HRF and its variability. The HRF has been shown to vary significantly across subjects [Aguirre et al., 1998; Handwerker et al., 2004; Kim et al., 1997], across days [Neumann et al., 2003], and as a function of age [Jacobs et al., 2008]. Within‐brain, regional differences have also been shown in the hemodynamic response measured in rats [Pawela et al., 2008] as well as in humans [Birn et al., 2001; Buckner, 1998; Lee et al., 1995; Miezin et al., 2000; Soltysik et al., 2004].

The importance of accurately estimating or modeling the HRF and understanding its variability has been underscored by recent studies. In their influential paper on single voxel modeling of population receptive fields (pRFs), Dumoulin and Wandell emphasize that the HRF is “the most important non‐neural influence on the pRF size estimate [Dumoulin and Wandell, 2008].” Also, relatively minor mis‐specification of the HRF can result in a considerable loss of statistical power and can introduce bias. Such bias can inflate Type I error rates and cause inaccuracies in P‐values for common fMRI statistical analyses [Handwerker et al., 2004; Lindquist et al., 2009; Lindquist and Wager, 2007]. Network‐based analyses can also suffer from HRF variability. Simulations have shown that causal network analyses such as Granger causality and dynamic causal modeling can become unreliable under common levels of variation in the hemodynamic response [Handwerker et al., 2012; Smith et al., 2011]. Interregional differences in the HRF also pose a problem for functional connectivity analyses that rely on simple correlations at zero lag as variations in the HRF reduce the measured correlation between cortical regions irrespective of the underlying neural activity [Silver et al., 2010; Sun et al., 2004].

Studies on regional variation in the HRF have tended to focus on comparisons between regions that are functionally dissimilar (i.e., somatosensory vs. visual vs. motor). Here, we investigate regional variation of the HRF within a single modality. We show that significant differences do exist in the HRF when compared across visual areas. We also show that areas near one another based on common organizational frameworks such as visual area hierarchy [Felleman and Van Essen, 1991] and visual field map clustering [Wandell et al., 2005] tend to have HRFs most similar to one another. Finally, we describe a subset of cortical voxels that have “inverted” HRFs. These inverted HRFs are intermixed with those exhibiting positive responses and appear to be of vascular origin. Using a simple model, we demonstrate how the identification of these inverted responses can potentially help resolve some of the conflicting literature concerning the source of “negative BOLD responses” [Boorman et al., 2010; Devor et al., 2007; Harel et al., 2002; Kannurpatti and Biswal, 2004; Pasley et al., 2007; Shmuel et al., 2006; Smith et al., 2004]. We also discuss how the identification of these HRFs can be used to improve the analysis of a broad range of fMRI data. We provide a practical example using temporal phase‐encoded retinotopic mapping data [DeYoe et al., 1994; Engel, 2012; Engel et al., 1994]. To highlight the importance of this issue, we use both a simulation and empirical data to demonstrate how inverted HRFs affect the analysis of phase‐encoded fMRI data and show that correctly accounting for the polarity of each voxel's HRF can improve the resulting cortical maps.

MATERIAL AND METHODS

General Design

To estimate the HRF, subjects were asked to fixate the center of a visual display while a large field, flickering checkerboard was presented for 3 sec ON periods followed by a uniform gray field for 29 sec OFF periods. The ON/OFF sequence was repeated five times per fMRI scan (Fig. 1A). Theoretically to estimate an impulse response function an infinitely short stimulus is used. Practically, we set the ON phase to have a temporal duration of 3 sec to evoke a reasonably robust response while minimizing the stimulus duration. Also, previous research has shown that the BOLD response becomes significantly nonlinear for very short stimuli (less than 3 sec in primary visual cortex) [Birn et al., 2001; Soltysik et al., 2004] so we wanted to avoid such nonlinearities. The OFF phase had a duration of 29 sec to allow the response to return to baseline prior to the next ON period.

Figure 1.

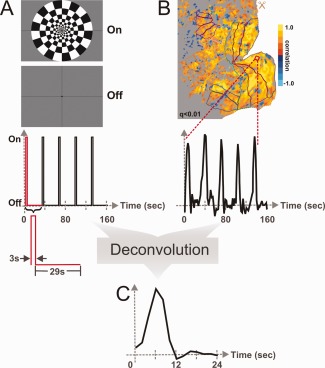
Experimental design used to estimate the HRF. (A) Visual stimulus and corresponding stimulus timing. (B) Cortical activation flat map and single voxel fMRI response. Colored outlines on map demarcate visual areas identified in Figure 2. (C) Single voxel HRF estimate.

Figure 1B illustrates the resulting fMRI BOLD activation as both a statistical parametric map and a single voxel fMRI time‐course. To acquire an estimate of each voxel's individual HRF, a deconvolution analysis was performed between the empirical fMRI time‐course and the stimulus timing waveform. The individual voxel HRF estimates were then used to compute and compare average responses across multiple visual areas demarcated using temporal phase‐encoded retinotopy data.

Experimental Subjects

Four male, right‐handed subjects (ages 25–61) with normal or corrected‐to‐normal vision and no history of neurological or psychiatric diseases participated in the experiments. Experiments were conducted with the written consent of each observer and were carried out in accordance with procedures approved by the Institutional Review Board of the Medical College of Wisconsin.

Visual Stimuli

Visual stimulation was presented by way of a custom, head‐coil mounted, back projection screen using the ViSaGe MKII visual stimulus generator by Cambridge Research to drive a BrainLogics BLMRDP‐A05 MR digital projector. The stimulus used to estimate HRFs (Fig. 1A) consisted of a counter‐phase flickering (8 Hz), black and white checkerboard extending to approximately 20° eccentricity with checks that scaled in size with eccentricity. The luminance of the black and white checks were 2.04 and 823 cd/m² respectively. The checkerboard alternated with a uniform gray field having a luminance of 173 cd/m². A fixation marker consisted of a small black dot at the center of the display flanked by thin black lines extending out to the edge of the display.

In addition to the HRF stimulus, temporal phase‐encoded retinotopy was performed [DeYoe et al., 1994; Engel et al., 1994] using expanding checkered rings and counterclockwise rotating wedges with a 40 sec expansion/rotation period. Ring size and expansion rate were roughly scaled to a 25% duty cycle. All other aspects of these stimuli (color, luminance, flicker frequency, visual field coverage) matched those of the HRF stimuli.

fMRI Paradigm

Functional MRI scans were acquired with an 8 sec BEFORE period, which was discarded due to magnetization transients. Functional runs were repeated five times, and the average of all five repetitions was subject to further analysis. After each functional run, the observer was asked for an alertness rating between 1 and 5 (1 being virtually asleep and 5 being awake and well‐focused on the task). This subjective measure was collected as a subject's state of alertness can impact the quality of the data and can be used as an inclusion criterion for analysis. It was not necessary to exclude any data from this study.

MRI Acquisition Parameters

The MRI experiments were carried out using a 3.0T GE Excite MRI scanner. fMRI data were collected with a gradient‐echo EPI pulse sequence having an effective TE of 30 ms, 2000 ms TR, 77 degree flip angle, 1 NEX, and acquisition matrices of 96 × 96 (Fourier interpolated to 128 × 128). The field of view (FOV) was 24 × 24 cm and 24 coronal slices with a slice thickness of 2.5 mm were acquired yielding a voxel size of 1.875 × 1.875 × 2.5 mm³. The volume of acquisition extended anteriorly from the occipital pole to beyond the parieto‐occipital sulcus. Sync pulses generated by the scanner were used to trigger the onset of the stimulus patterns. Whole brain, high‐resolution anatomical spoiled gradient recalled (SPGR) images were also collected for each MRI experiment. This was done using a TE of 3.9 ms, TR of 9.6 ms, 12 degree flip angle, and an acquisition matrix of 256 × 224 (Fourier interpolated to 256 × 256). The FOV was 24 cm, and 220 1.0 mm thick slices were acquired yielding voxel sizes of 0.938 × 0.938 × 1.0 mm³ that were resampled to 1.0 mm³.

Analysis Software

fMRI data analysis was performed using the AFNI/SUMA package (precompiled binary Linux OpenMP 64 bit: May 22, 2012) [Cox, 1996; Saad et al., 2004]. Surface models were created from high‐resolution SPGR images using Caret v5.64 [Van Essen et al., 2001]. The modeling of the hemodynamic responses and simulations were performed using MATLAB R2012b. Statistics were performed using IBM SPSS Statistics 19.0.

Preprocessing

Data preprocessing was performed for each subject in the following order: reconstruction, alignment and volume registration, averaging of time‐courses, removal of BEFORE periods. Alignment of the functional data with a skull‐stripped anatomical SPGR (created using AFNI's 3dSkullStrip) and volume registration was performed using AFNI's align_epi_anat.py script. We set up this script to transform the first functional dataset to match the anatomical SPGR and then transform all other functional datasets to be in alignment with the first EPI and the SPGR. This combines the alignment to the anatomical dataset and volume registration into a single transformation matrix. A weighted sinc interpolation (wsinc5) was used for the final interpolation. The time‐courses for all the repetitions of each functional task were then averaged together individually using ANFI's 3dMean, and the BEFORE periods containing magnetization transients were removed using AFNI's 3dTcat.

Identifying Active Voxels, HRF Deconvolution

As a first step, voxels activated by the large‐field HRF stimulus were identified by performing a correlation analysis [Bandettini et al., 1993] using AFNI's 3dfim+ between the empirical fMRI time‐course and a reference waveform created by convolving the HRF stimulus timing with the default “Cox special” canonical HRF model available in AFNI (http://afni.nimh.nih.gov/afni/doc/faq/17). The activation map was false discovery rate (FDR) corrected for multiple comparisons [Genovese et al., 2002] and only voxels with q‐values < 0.01 were used in further analyses.

In Step 2, HRF waveforms were estimated for each active voxel by deconvolution using a finite impulse response (FIR) model. To this end, we utilized AFNI's 3dDeconvolve algorithm, in which the measured signal is modeled as the convolution of the input stimulus with a FIR with the maximum length of the impulse response being determined by the user's input. We set the maximum length to 24 sec. Each individual HRF estimate (Fig. 1C) consisted of 13 time‐points sampled 2 sec apart. The sign of the correlation analysis from Step 1 was then used to classify HRFs as either positive (positive correlation) or inverted (negative correlation). No global mean correction was performed.

Visual Area Mapping and Regions of Interest

The phase‐encoded retinotopic mapping data were analyzed with AFNI's Hilbert Delay plugin [Saad et al., 2001], and the results were used to construct eccentricity and polar angle retinotopic maps displayed on cortical surface models. Data were only mapped to the surface to create the regions of interests (ROIs) and display data. All HRF analyses were done on the original volumetric data. The surface mesh used to define the ROIs and on which data were displayed was created using the center of the gray matter thickness. Voxels that were intersected by the surface normal were then assigned to the corresponding surface nodes.

The retinotopic maps were used to identify and define the boundaries of distinct cortical visual areas using criteria described by several labs [Amano et al., 2009; Arcaro et al., 2009; DeYoe et al., 1996; Engel et al., 1997; Hansen et al., 2007; Sereno et al., 1995; Sereno et al., 2001; Silver and Kastner, 2009; Swisher et al., 2007; Wandell et al., 2007; Wandell and Winawer, 2010]. Retinotopy data collected in the same session as the HRF data were used along with additional retinotopic datasets collected in separate sessions. Visual areas V1, V2, V3, V4, VO‐1, VO‐2, V3AB, IPS‐0, IPS‐1, IPS‐2, IPS‐3, LO‐1, LO‐2, TO‐1, and TO‐2 were identified for all subjects with the exception of IPS‐3, which could only be identified in 3 of 4 subjects. Figure 2 shows the layout of these visual areas for the left hemisphere of a single subject. On the left is a flat map representation of the cortex created by computationally cutting the three‐dimensional (3D) surface model on the right along the calcarine sulcus (Fig. 2, dashed line) and subsequently flattening the surface model until all surface mesh nodes were in the same 2D plane.

Figure 2.

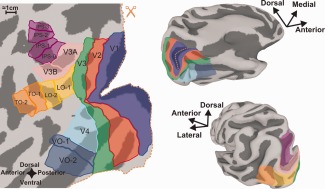
Visual areas and ROIs. (Left) Flat map of the left hemisphere with visual areas and ROIs demarcated. Areas combined into a single ROI share the same ROI color. (Right) Same hemisphere and ROIs but on an inflated surface. The top right is a ventral/medial view and the bottom right is a dorsal/lateral view. The occipital surface map was cut along the dotted line (scissors icon) to permit minimally distorted flattening.

Visual areas V1, V2, V3, and V4 each served as their own individual ROI. Ventral occipital regions VO‐1 and VO‐2 were combined into a single ventral occipital (VO) ROI. Similarly, areas V3A and V3B, intraparietal (IPS‐1,2,3), lateral occipital (LO‐1,2), and temporal occipital (TO‐1,2) regions were combined into single V3AB, IPS, LO, and TO ROIs respectively. The combined ROIs were needed to increase the number of samples in each ROI as higher order visual areas typically have smaller surface areas and are often less populated with active voxels than lower order visual areas. To assign visual area labels to the volumetric data we “shrank” and “expanded” the surface along the surface normals by 0.5 mm to create a pair of surfaces. This pair of surfaces was, then, used to map the visual area ROI labels into the volumetric domain using AFNI's 3dSurf2Vol function. The grid space was defined by the functional data and each voxel received only one ROI label (the most common value per voxel).

Comparing HRFs Across Visual Areas

The empirical HRFs for all active voxels were converted to percent signal change and then pooled by visual area ROI over all subjects. A two‐way MANOVA was performed to determine the effect, if any, of visual area ROI and subject on the empirical HRF estimates (characterized by a 13‐dimensional multivariate vector with each time point estimate of the HRF serving as a separate dimension within the vector). The overall similarity of the HRF across the visual area ROIs was explored by calculating the Mahalanobis distance between the HRF estimates for each pair of ROIs. The Mahalanobis distance relationships were visualized by constructing a dendrogram and pair‐wise distance matrix. The dendrogram shows HRF clustering based on similarity where the height of the line represents the Mahalanobis distance between connecting points. The pair‐wise distance matrix illustrates the Mahalanobis distance between each individual visual area with each of the other visual areas. All active voxels were also averaged across subjects per visual area ROI to yield group average HRF plots which served as input to a sum of two gamma functions model.

Modeling the HRF

The group average positive and inverted HRFs for each visual area ROI were fit by a sum of two gamma functions model using a constrained nonlinear optimization (a bounded version of MATLAB's fminsearch), that is, each HRF was modeled by:

$$y\left(t\right)={\text{gam}}_1\left(t\right)+{\text{gam}}_2\left(t\right)+C$$

where,

$${\text{gam}}_1(t)=\{\begin{array}{ll}{A}_1{\left(\frac{x(t)-{\partial }_1}{{\tau }_1}\right)}^2\frac{e^{-{\left(\frac{x(t)-{\delta }_1}{{\tau }_1}\right)}^2}}{{\tau }_1},& if\hspace{0.17em}x(t)\ge {\delta }_1\\ 0,& if\hspace{0.17em}x(t)<{\delta }_1\end{array}$$

$${\text{gam}}_2(t)=\{\begin{array}{ll}{A}_2{\left(\frac{x(t)-{\partial }_2}{{\tau }_2}\right)}^2\frac{e^{-{\left(\frac{x(t)-{\delta }_2}{{\tau }_2}\right)}^2}}{{\tau }_2},& if\hspace{0.17em}x(t)\ge {\delta }_2\\ 0,& if\hspace{0.17em}x(t)<{\delta }_2\end{array}$$

Using the parameters estimated by this optimization the time‐to‐onset ( ${\delta }_1$), time‐to‐peak, peak amplitude, and peak full‐width‐at‐half‐maximum (FWHM) for each ROI's group average HRF was determined. The sum of two gamma functions model was chosen to estimate these parameters based on its relative simplicity and ability to fit the most salient features of the HRF: the peak and post‐stimulus undershoot (or overshoot for the inverted HRF). Caution, however, must be taken when interpreting model‐estimated parameters as it has been shown that actual changes in one parameter can be mistaken for changes in others for nearly all models of BOLD hemodynamic responses [Lindquist et al., 2009; Lindquist and Wager, 2007]. The only difference between fitting the positive and inverted HRFs was that the sign of the amplitude variables, A1 and A2, were opposite in the two cases.

RESULTS

The empirically estimated HRFs varied significantly across individuals and across the nine retinotopically defined visual area ROIs. Furthermore, a subset of voxels in each visual area exhibited “inverted” HRFs. The set of time points defining the HRFs represented multidimensional vectors that were subjected to a two‐way MANOVA. Statistically significant main effects were found for visual area and subject as well as a significant interaction (P ≤ 0.001, all). This was true for both positive and inverted HRFs. Consistent with previous research, the variability across subjects was greater than that found across brain regions [Handwerker et al., 2004]. Here, the variance accounted for by subjects was approximately three times that accounted for by visual area for the positive HRFs (Pillai's trace from MANOVA for subject = 0.256, for visual area = 0.086). This did not hold for the inverted HRFs for which the variance accounted for by visual area was nearly equal to that accounted for by subject (Pillai's trace from MANOVA for subject = 0.177, for visual area = 0.178).

Figure 3 (A1 and B1) shows the group average HRFs for each visual area ROI along with the best fit provided by the sum of two gammas model (solid lines). To describe the differences in the empirical HRFs across areas, parameters from the sum of two gammas modeling of the average HRFs were used to estimate the time‐to‐onset ( ${\delta }_1$), time‐to‐peak, peak signal change, and the FWHM of the peak. The mean, minimum, and maximum values across visual area ROIs are shown in Table 1 along with the group average estimates for each individual visual area. This table shows that the mean values for most of the parameters are comparable between positive and inverted HRFs with the exception of the time‐to‐onset, which on average is 1.2 sec earlier for the positive HRF compared to the inverted HRFs. However, larger differences are associated with particular visual areas such as V3, V3AB, LO, and IPS. The range of values across areas shows more variability for the inverted responses for all characteristics except time‐to‐peak, which is nearly the same between HRF types. This greater degree of variability in the inverted HRFs can also be seen by visual inspection of the group average fits shown at the top of Figure 3.

Figure 3.

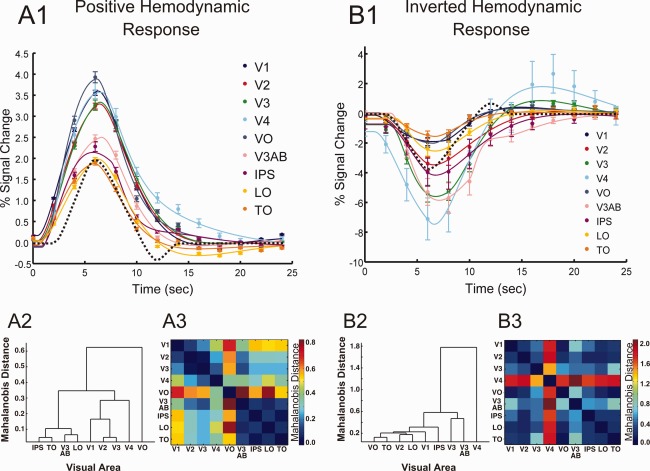
(A1, B1) Group average positive and inverted HRF estimates across visual areas. Solid lines: sum of two gammas model fits, error bars: +/− SEM, dashed lines: “Cox special” canonical model (arbitrarily scaled to half the maximum response measured). (A2, B2) Dendrograms of HRF Mahalanobis distances among visual areas. (A3, B3) Pair‐wise HRF Mahalanobis distance matrices. Color bar scaled to the maximum Mahalanobis distance between areas, which for positive HRFs was between VO and V3AB and for inverted HRFs was between V4 and V3AB.

Table 1.

Group average HRF characteristics across visual area ROIs for both positive and inverted HRFs

	Positive HRF			Inverted HRF
	Mean	Min	Max	Mean	Min	Max
Time‐to‐onset (s)	0.62	0.40	0.86	1.82	0.86	2.91
Time‐to‐peak (s)	6.3	5.8	6.5	6.7	6.5	7.1
Peak signal change (%)	2.91	1.87	3.89	−3.78	−1.56	−7.47
Peak FWHM (s)	6.31	5.85	6.90	6.52	5.20	8.85

		Time‐to‐onset (s)	Time‐to‐peak (s)	Peak signal change (%)	Peak FWHM (s)
V1	Positive	0.42	6.30	3.60	6.55
	Inverted	0.89	6.50	−1.90	6.55
V2	Positive	0.40	6.40	3.29	6.60
	Inverted	1.80	5.60	−3.47	8.85
V3	Positive	0.61	6.50	3.33	6.70
	Inverted	2.41	6.75	−5.60	6.45
V4	Positive	0.85	6.50	3.57	6.90
	Inverted	0.86	6.60	−7.47	6.45
VO	Positive	0.86	6.10	3.89	5.90
	Inverted	1.30	6.50	−2.02	5.20
V3AB	Positive	0.59	6.60	2.49	6.30
	Inverted	2.48	7.10	−5.86	6.55
IPS	Positive	0.83	5.80	2.14	6.10
	Inverted	2.05	6.75	−4.16	7.15
LO	Positive	0.67	6.30	1.98	5.85
	Inverted	2.91	6.70	−2.54	5.90
TO	Positive	0.40	5.90	1.88	5.95
	Inverted	1.75	6.70	−1.56	5.55

A positive and inverted version of AFNI's “Cox special” canonical model is included in Figure 3 for comparison (dashed lines). Although similar in overall shape there are differences between the canonical model and our group average HRFs. It appears that the “Cox special” has a later onset time and pronounced post‐stimulus under/overshoots, which are nearly absent in our HRFs. We did, however, see pronounced post‐stimulus activity similar to the canonical model in some individual subjects that did not survive the group averaging (data not shown).

Because the “Cox special” canonical HRF model was used in the correlation analysis by which we identified active voxels, one concern may be that our HRF estimates are biased toward responses similar to the canonical model. To address this issue definitively, we reanalyzed our data after including all additional voxels identified as responsive using the FIR model deconvolution results, which did not assume a specific response profile (Supporting Information Fig. S1). For positive HRFs the responses were nearly identical for all visual areas. For inverted HRFs, area V4 and to a lesser extent V3 showed some difference but this was primarily an amplitude reduction, not a change in shape. As the sample of inverted HRF voxels was much smaller than for positive HRFs, more variation is to be expected. It is worth noting that had we selected voxels based only on the FIR model results we would have excluded some voxels that were included in our original sample. The same would be true if we selected voxels based solely on their response to the retinotopic mapping stimuli, which independently stimulated the same extent of the visual field. None of these methods ensures the inclusion of all visually responsive voxels, but given the results of the additional analyses we are confident that the sample used in our analysis is representative of the responses in the various visual areas.

Differences and similarities in the HRFs across visual area ROIs were further explored by computing and comparing the Mahalanobis distance between the HRF estimates for each pair of ROIs. These relationships are illustrated in Figure 3 by way of a dendrogram (A2 and B2) and a pair‐wise matrix (A3 and B3) constructed using these distances. The dendrograms graphically illustrate HRF similarity relationships among visual areas whereas the distance matrices use color to represent specific Mahalanobis distances between pairs of areas. The dendrogram for the positive HRFs reveals an interesting relationship in that it appears that areas of visual cortex considered similar based on common organizational principles such as visual area hierarchy and visual field map clustering also show similar HRFs. There exists a distinct cluster comprised of lower‐order areas (V1, V2, V3) with V2 and V3 being most similar to one another. Considering the ventral regions (V4, VO), we see that V4 is most similar to the V1/V2/V3 cluster. VO, while being notably different from all other areas, is yet most similar to V4 (seen by inspection of the positive HRF pair‐wise distance matrix). The dorsal/lateral areas (V3AB, LO, IPS, TO) also cluster near one another. This hierarchical clustering of visual areas based on HRF similarities did not occur for the inverted HRFs. However, both the dendrogram and pair‐wise distance matrix show that the inverted HRF for area V4 is distinctly different from those of other visual areas (Fig. 3B2,3). Not only does the V4 inverted HRF show the maximum peak signal change (−7.5%), but it also has the earliest time‐to‐onset (0.86 sec.).

The inverted HRFs accounted for 6.32% of the total active voxels that responded to the large‐field visual stimulation. The inverted HRFs were found in all visual areas tested; the proportion of which are shown in Table 2. Figure 4 illustrates the cortical distribution of these HRFs. Typically, small clusters of inverted HRFs were distributed indiscriminately throughout each visual area ROI (Fig. 4, isolated blue spots). However, larger groups, particularly in ventral cortex are also evident (Fig. 4, arrows a–d). These larger clusters are in anatomical locations and arrangements likely to be associated with the transverse sinus or communicating veins. The small clusters of inverted HRFs within each ROI appeared to be randomly distributed with respect to retinotopic preference. This is illustrated in Figure 5A for area V1 where arrows a, b, and c point to inverted HRFs associated with foveal, mid‐eccentricity, and peripheral retinotopic locations respectively. Figure 5B shows that these inverted responses can be easily missed if even moderate spatial smoothing (3.5 mm spherical kernel) is performed on the original volumetric time‐course data. Such smoothing decreased the total percentage of voxels with inverted HRFs from 6.32 to 1.14%.

Table 2.

Proportion of voxels characterized by an inverted HRF

Visual area	V1	V2	V3	V4	VO	V3AB	IPS	LO	TO
# Active voxels	3803	3112	2577	697	1421	1640	1320	1384	969
% Inverted HRFs	3.96	5.64	7.07	7.80	7.25	7.97	7.24	6.74	8.32

Figure 4.

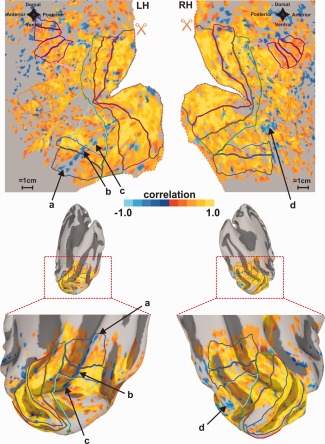
Spatial distribution of HRFs. Left and right hemispheres are shown for a single subject. Above are cortical flat maps and below are medial, posterior views of an inflated surface. Inverted HRFs are shown in blue. Arrows (a–d) denote large clusters of inverted HRFs likely to be associated with the transverse sinus and/or communicating veins. Maps were FDR corrected and thresholded with q < 0.01 using the correlation data. Visual area identification is the same as in Figure 2.

Figure 5.

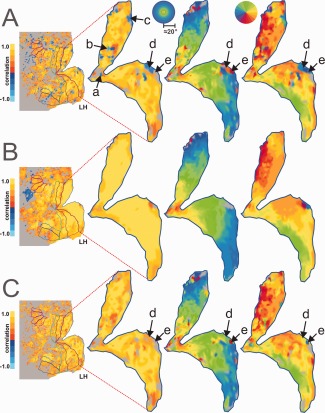
Cortical parametric maps for HRF, eccentricity, and polar angle mapping data for primary visual cortex, V1. The HRF maps are colored by correlation, and the retinotopic maps are colored by position in the visual field (phase delay). (A) Unsmoothed data. (B) Smoothed data (3.5 mm spherical kernel). (C) “Inversion corrected” data. Arrows a, b, c, and d point to regions exhibiting inverted HRFs. Arrow e points to a region that is likely characterized by an inverted HRF, but its response to the HRF stimulus does not reach statistical significance. All maps were FDR corrected and thresholded with q < 0.01 using the correlation data.

To examine the spatial stability of these inverted responses across visual stimuli other than the large field, flashed checkerboard pattern used to measure the HRFs, we inspected the responses at these locations to the phase‐encoded retinotopic mapping stimuli used to define the ROIs. In so doing, we found evidence that the responses at these locations were affected across both retinotopic mapping rings and wedges. A distinguishing feature of the retinotopic organization of visual cortex (especially lower visual areas) is local continuity. Regions near one another in visual cortex encode regions near one another in the visual field. But at locations where we found inverted HRFs, the fMRI retinotopy (measured independently) appeared to be inconsistent with the surrounding retinotopic pattern (Fig. 5A). For example at the location marked by arrow d (exhibiting an inverted HRF), the cortical eccentricity map appears to encode a visual field location near the fovea (red/orange) despite the surrounding cortex encoding mid‐eccentricity/peripheral locations (green/blue). Also, the cortical polar angle map shows that same region encoding the left horizontal meridian (blue) despite the surrounding cortex encoding the right horizontal meridian (yellow/orange). Not only are these responses inconsistent with the surrounding retinotopic pattern they are also inconsistent with the known mapping of primary visual cortex [Schira et al., 2007].

To investigate whether an inversion of the HRF alone could account for the degree of the errors seen in the cortical retinotopic maps, we implemented a simple model that treats the polarity of the HRF as a component independent of the underlying neuronal activity (Fig. 6) and applied that model to the temporal phase‐mapping analysis used to construct the retinotopic maps (Fig. 7). Figure 7A1,2 show two time‐courses obtained with a conventional rotating wedge stimulus. Without the baseline information (blue) provided by the additional HRF experiment, it is difficult to distinguish peaks from troughs in either time‐course. An exacting eye may note that periods of activation (peaks in A1, troughs in A2) are shorter than the baseline periods. But, this can vary since the duration of activation is dependent on the size of the pRF for each voxel [Dumoulin and Wandell, 2008; Smith et al., 2001; Tootell et al., 1997]. The penalty for such confusion is that phase‐encoded signals from voxels with inverted HRFs can be mistaken for signals that are shifted by 180° in phase. A simulation of this type of error is shown in Figure 7B,C. Two voxels with identical pRFs have identical neural responses to a rotating wedge stimulus. Yet, the phase analysis yields different delay values offset by 180° (Fig. 7, e _delay). The analysis would incorrectly assign diametrically opposed preferred locations to the two voxels. This is exactly what we see in our retinotopic maps at many of the locations exhibiting inverted HRFs (e.g., Fig. 5A, arrow d).

Figure 6.

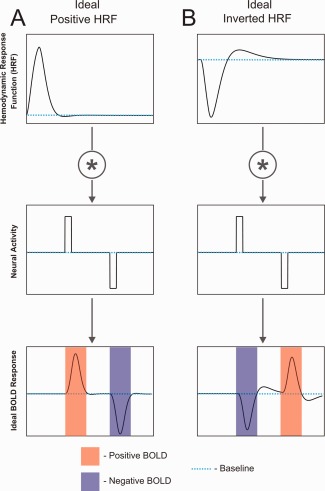
Conceptual relationships among positive and inverted HRFs, neural activity, and the BOLD response. (A) Positive HRF. (B) Inverted HRF. Note: both HRFs were taken from the sum of two gammas model fit for visual area V2.

Figure 7.

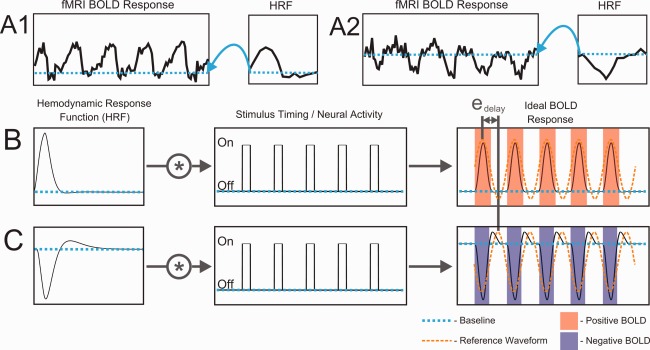
An example of the effect of inverted HRFs on fMRI analysis. (A) Empirical fMRI time‐courses from polar angle mapping in voxels with (A1) positive and (A2) inverted HRFs. (B,C) Simulation illustrating error in temporal phase‐mapping analysis caused by an inverted HRF. Ideal BOLD responses were predicted by convolving HRFs (B–positive, C–inverted) with identical stimulus timing waveforms. Stimulus timing was for a quarter‐field checkerboard wedge rotating about the center of gaze five times. Despite identical timing of neural activity, the apparent phase delay is shifted by e _delay for the voxel with an inverted HRF compared to that with a positive HRF.

A phase correction factor was then applied to voxels with inverted HRFs to compensate for the delay errors (Fig. 5C). To do this, we simply shifted the phases from the delay analysis by 180° for those voxels demonstrating inverted HRFs. As can be seen in Figure 5C, the region marked by arrow d is now consistent with both the surrounding retinotopic pattern and the known retinotopic mapping of the region. Directly adjacent to this region another arrow (e) points to an island of contrasting color that appears to have survived this correction procedure. This can be understood by inspection of the HRF experiment activation map (left of the retinotopy). This map shows no significant activation during the HRF experiment despite robust activation during the retinotopy task probably due to the shorter visual stimulation ON period used to estimate the HRF, and thus was not modified by the correction procedure.

DISCUSSION

Overall, the results of this study show that empirically measured HRFs vary significantly across human cortical visual areas. A subset of 6.32% of voxels exhibit “inverted” HRFs that have a waveform similar to an inverted version of the more common “positive” HRFs. The positive HRFs show a systematic relationship to the functional hierarchy of cortical visual areas [Felleman and Van Essen, 1991] in that areas which are hierarchically near one another exhibit similar HRFs. While each visual area contains inverted HRFs, they are more variable and do not show the same systematic relationship with visual hierarchy as the positive HRFs perhaps due to the smaller sample size and higher variability. The inverted HRFs typically occur in small clusters distributed throughout all visual areas although larger groupings were identified in ventral occipital cortex associated with likely vascular structures.

To understand these results we must consider the nature of the HRF. The HRF is a key component of a linear transform model expressing the relationship between a stimulus (or task) and the resulting fMRI signal (Fig. 8A). This transform is necessary because the fMRI signal does not directly reflect neural activity but, rather, activity‐induced changes in blood oxygenation within each voxel [Boynton et al., 1996; Friston et al., 1994]. The ideal HRF is a theoretical concept that was originally developed in fMRI studies to primarily encompass the effects of hemodynamic changes associated with neural activity. However, the BOLD response is known to physiologically originate from two responses to a neural event, one vascular‐hemodynamic and the other, metabolic (Fig. 8B) [Buxton, 2012; Buxton et al., 1998].

Figure 8.

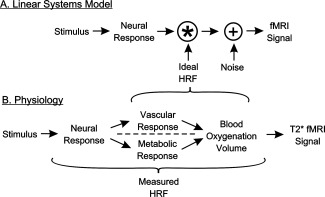
(A) HRF role in the linear systems model of the fMRI response. The stimulus evokes a neural response that is then convolved with the HRF to yield an fMRI signal, with the addition of noise at one or more points (shown here following the HRF convolution). (B) Physiological factors incorporated into the ideal versus the empirically measured HRF.

Hemodynamic and Metabolic Contributions to HRF Variability

It is clear that the “hemodynamic response function” reflects more than just hemodynamics. Any factor that influences the ratio and timing of the change in the hemodynamic response relative to the metabolic response will influence the measured BOLD signal and could contribute to variation in HRFs across visual areas. Although the degree to which the hemodynamic and metabolic processes are independent and the exact coupling of these responses to the underlying neuronal and astrocytic activity is currently under investigation [Lauritzen et al., 2012], it is clear that any metabolic and/or vascular differences that exist among visual areas are likely to affect each area's HRF. In particular, temporal characteristics of the HRF that vary across visual areas such as time‐to‐onset, time‐to‐peak, and peak width are likely to reflect differences in hemodynamic and/or metabolic factors due to the relatively slow timescale over which they operate (seconds).

Differences in blood vessel size across brain regions can significantly alter the hemodynamic response [Lee et al., 1995; Menon, 2012; Yu et al., 2012]. In this respect, it is important to note that cortical visual areas that are “close” within the visual system connectional hierarchy also tend to be physically close to each other within the brain. For example, V1, V2, and portions of V3 are contained in or near the medial aspect of the occipital lobe (cf Fig. 2). In contrast, the LO and TO areas are located on the lateral occipital surface. V4 and VO are located ventrally, whereas V3AB and IPS0–4 are located dorsally. Different cerebral arteries supply these different zones [Carpenter, 1976]. For example, the calcarine artery supplies medial occipital cortex while the middle cerebral artery supplies posterior and lateral occipital cortex. This suggests that the clustering seen in the positive HRF dendrogram may be due in part to a systematic spatial variation in vasculature that happens to correlate with the spatial layout of the functional hierarchy of the cortical visual system.

Neural Contributions to HRF Variability

In addition to hemodynamic and metabolic contributions, the HRF variability can also be affected by neural factors. Variation in the neurotransmitter profile has recently been shown to be related to the regional variability in the amplitude and shape of the HRF [Donahue et al., 2010; Muthukumaraswamy et al., 2009; Muthukumaraswamy et al., 2012]. Post‐mortem studies have also revealed variation in the number of neurotransmitter receptors across visual areas [Zilles et al., 2002]. Together this suggests a possible neural source for the HRF variation we see across visual areas.

In theory the ideal HRF and the neural response are independent, separable factors (Fig. 8A). In practice, however, it is not possible to measure the HRF in humans without it including some neuronal influences. Any empirical departure from this ideal neural signal will become incorporated into the HRF when it is estimated by deconvolution from the empirical fMRI response. For instance, variations in neural selectivity (color, motion, etc.), gain, or the effects of attention could cause the actual neural response for each visual area to vary from the modeled neural response. Similarly, the stimulus used to estimate the HRF is itself an important consideration. Ideally, the stimulus should evoke an identical response throughout all voxels in all visual areas. While this is not practically achievable, some neurons in most visual areas will respond to a high contrast, checkerboard (high‐contrast edges) flickering at a modest rate [Zeki, 1978]. Nevertheless, a checkerboard may be optimal for some voxels but suboptimal for others, potentially causing variations in response amplitude across visual areas or even from voxel to voxel. Such differences will then be incorporated into the HRF estimates. Indeed, we found that a characteristic distinguishing HRFs across visual areas was their peak amplitude (Fig. 3). This provides another factor that may account for the dendrogram results which showed meaningful clustering of positive HRF properties relative to the functional hierarchy of cortical visual areas [Felleman and Van Essen, 1991].

The inclusion of neuronal factors into the estimated HRFs potentially limits their generality. However, shifts in activation between functionally distinct neurons within a voxel or variations in timing at the millisecond level will be unimportant unless these factors translate into a gross change in net neural activity. Thus, while the HRFs measured in this study may not be accurate for all possible applications, they may be serviceable for a much wider range of conditions than just black and white checkerboards. At the very least, they are likely to be more accurate than using the fixed canonical HRFs provided by standard neuroimaging analysis packages, which ignore the significant HRF variations we observed across visual areas.

Source of the Inverted HRFs

As mentioned above, any factor that alters the balance between the hemodynamic and metabolic responses and/or their timing can alter the HRF and thus can potentially create an inverted waveform. As the hemodynamic response is typically thought to be the dominant factor, it is likely that the inversion originates from a hemodynamic effect rather than metabolic change. Inverted HRFs similar to those reported here have also been reported by Olman et al. who showed rather convincingly that they were of vascular origin [Olman et al., 2007]. As with the inverted responses analyzed here, those reported by Olman et al. were found intermixed with positive HRFs within the cortical representation of the stimulus. Also in line with our findings that the inverted HRFs were less consistent than the positive HRFs, Olman et al. found that their inverted HRFs were more variable than their positive HRFs.

A hemodynamic origin for inverted HRFs may also explain why the inverted HRF for V4 shown in Figure 3B is distinctly different from those of other areas. V4 has been notoriously difficult to image with fMRI due to a hemodynamic artifact created by the transverse sinus and possibly other communicating veins (i.e., the venous eclipse) [Winawer et al., 2010]. Winawer et al. contended that large‐field visual stimuli often evoke “counter‐phase” or “significantly delayed” responses in cortical regions adjacent to the transverse sinus and that such responses are associated with local Bo field inhomogeneities caused by the sinus. Bo field inhomogeneities tend to cause local shifts in the Lamor frequency and consequent off‐resonance signal loss. However, this does not account for the robust but opposite phase of the signals that Winawer reported for some subjects (e.g., Winawer; Fig. 4). We propose that, in addition to off‐resonance effects, the BOLD hemodynamic mechanism in this region may be characterized by an inverted HRF. Indeed the cortical maps shown in our Figure 4 show a strip of inverted HRFs in the left hemisphere (arrows a–c) and a large patch of inverted HRFs in the right hemisphere (arrow d) within a zone of ventral cortex similar to that referred to by Winawer et al. Thus, while we agree that the V4 “venous eclipse” (signal loss) is likely to be of hemodynamic origin, we suggest that the robust, phase shifted responses also observed in this region may reflect local alterations in the balance of hemodynamic and metabolic responses thereby producing an inverted HRF. In such case, it is possible that fMRI responses in this region may provide a more accurate rendition of the underlying neuronal activity than previously appreciated if the inverted HRF is taken into account in the analysis.

Although the evidence is consistent with a hemodynamic origin for the inverted HRFs, the exact mechanism remains unclear. One possibility is that a zone of strong neural activation could cause a local increase in blood flow that effectively “steals” blood from collateral vascular branches feeding adjacent or even distant brain areas. This can cause the BOLD signal to appear negatively correlated with (or even dissociated from) the underlying neuronal activity in those remote areas [Harel et al., 2002; Kannurpatti and Biswal, 2004]. Such a mechanism would be expected to produce an HRF with a similar but inverted form relative to nearby positive HRFs. Inverted fMRI responses have also been generated in visual cortex of monkeys under hypercapnic conditions [Zappe et al., 2008]. Zappe et al. suggested that hypercapnia caused vasodilation that raised the baseline cerebral blood flow to such an extent that it abolished the hemodynamic component of the BOLD signal in response to visual stimulation. Only the metabolic component remained so that the resultant inverted BOLD signal reflected only the increased metabolic rate of oxygen consumption (CMRO₂) and concomitant rise in deoxyhemoglogin content. Despite the response reflecting only the increased CMRO₂, the shape of the response was strikingly similar to a typical HRF, but inverted. Such results suggest that any factor that eliminates or greatly reduces the hemodynamic response could result in an inverted fMRI response to a stimulus that increases neural activity, as we have observed under normocapnia in the present study. This also suggests that if the inverted HRFs noted here primarily reflect the metabolic CMRO₂ response, then they should be preserved under hypercapnic conditions while formerly positive HRFs become inverted as well.

Negative BOLD Responses versus Inverted HRFs

One concern might be that the inverted HRFs we observed are associated with neurons whose activity was actually suppressed by our large field checkerboard stimulus. Previous studies have shown that some negative BOLD responses (NBRs) can reflect neural suppression and/or a decrease in neuronal activity [Boorman et al., 2010; Devor et al., 2007; Klingner et al., 2011; Pasley et al., 2007; Shmuel et al., 2006; Shmuel et al., 2002; Smith et al., 2004]. Such NBRs have been reported for visual checkerboard stimuli similar to ours [Saad et al., 2001; Shmuel et al., 2002]. However, the NBRs in these studies were recorded in voxels whose receptive fields appear to have been just outside the stimulated portion of the visual field within a zone where lateral inhibitory effects or vascular “steal” effects are likely. In this study, we deliberately restricted our analysis ROIs to include only those voxels with receptive fields inside the portion of the visual field stimulated by the flashed checkerboard pattern. This was done using detailed retinotopic mapping data collected independently from that used to measure the HRFs. By doing so, we strictly confined the analysis to the retinotopically coincident cortical zone associated with the stimulus to avoid contaminating it with voxels from the retinotopic zone outside the confines of the stimulus. Our assertion that the inverted responses are within the cortical activation field of the stimulus is integral to our interpretation of the responses as inverted and distinct from NBRs originating from neural suppression. While we cannot absolutely rule out the possibility that neural activity was somehow selectively suppressed within just the voxels at these loci, such a result would be contrary to known properties of both visual perception and neurophysiology.

Role of the Inverted HRF in Interpreting fMRI Studies

The relationships among stimulus timing, neural activity, the HRF, and the BOLD response are obviously complex. As summarized in Figure 6, if the polarity of the HRF is treated as an independent factor both types of HRFs are capable of producing positive and negative BOLD responses depending on the “polarity” of the underlying neural activity (activation vs. suppression). Note that without knowledge of the HRF, a NBR can be associated with either an increase or decrease in neuronal activity. While increased neural activity is typically associated with vasodilation and reduced neural activity with vasoconstriction, it has been shown that neuronal inhibition can occur without a change in the neuronal baseline firing rate and yet this inhibition is still accompanied by vasoconstriction and a NBR [Devor et al., 2007; Devor et al., 2005]. This fact does not change the specific relationships proposed in Figure 6, although it does call attention to additional neurovascular coupling complexities.

Inverted HRFs present a challenge for the interpretation of data acquired across a broad range of fMRI experiments. For example, voxels with inverted HRFs may be mistakenly interpreted as showing a decrease in neuronal activity when the underlying activity actually increases (Fig. 6). If such a voxel were used as the “seed” in a functional connectivity study, it would cause voxels with positive HRFs and correlated neuronal activity to appear anti‐correlated to the seed voxel. Similarly, temporal phase‐encoded fMRI data may be adversely affected. As shown in Figure 7B,C, inverted HRFs will cause phase errors of approximately 180°. Indeed, we found evidence of such inverted responses in our retinotopic mapping data at the time‐course level (Fig. 7A2) and in the cortical maps (Fig. 5A).

Correcting for Inverted HRFs

Figure 5 shows the effects of HRF‐related errors on cortical parametric maps constructed from the eccentricity and polar angle mapping data. Inverted HRF‐related artifacts are readily identified as islands of contrasting color in Figure 5A. Smoothing, of the volumetric time‐course data with a 3.5 mm spherical kernel prior to performing the phase delay analysis can reduce the influence of these inverted HRFs (Fig. 5B) but also removes legitimate retinotopic detail. An alternative to smoothing that avoids losing spatial detail is to correct for the inverted HRF (Fig. 5C). This can be accomplished by simply shifting the phase delay values by 180° for voxels with inverted HRFs. Obviously, this requires independent estimation of the HRF for each voxel as was done in this study. And, this will only be appropriate for cortical locations that can be assumed to have an activating BOLD response, such as those in this study that were within the topographic representation of the stimulus. This simple correction method will not be appropriate if the goal is to measure the amplitude of the response or more subtle differences in timing. In such cases, modeling the HRF completely for each voxel may be necessary. Despite these limitations, correcting for inverted HRFs improves the uniformity of cortical maps and suggests that a detailed accounting of HRF properties can recover fMRI information that might otherwise be discarded as artifactual [Olman et al. 2007; Winawer et al. 2010]. It also suggests that if the inversion reflects a blood steal effect then the region “stealing” the blood must be nearly adjacent to the inverted HRF voxel as this correction method would fail to improve the retinotopic maps if the stealing region encoded a different retinotopic location.

CONCLUSIONS

HRFs vary significantly across human subjects and across cortical visual areas V1, V2, V3, V4, VO, V3AB, IPS, LO, and TO. HRF amplitudes and timing tend to be similar for hierarchically similar visual areas, although this could reflect spatially correlated vascular anatomy as well as neural factors that influence empirically measured HRFs. A subset of voxels with inverted HRFs was found intermixed with positive HRFs in each visual area examined. The identification of the polarity of HRFs as a factor independent of the underlying neuronal activity resolves some of the confusion concerning the relationships between neural activity and fMRI responses. So‐called “negative BOLD responses” can be associated with either neural activation or neural suppression depending on the polarity of the HRF (inverted vs. positive, respectively). As fMRI experiments and analyses advance in complexity and precision, accurate estimation of single voxel HRFs becomes increasingly important. This is particularly true for rapid event‐related designs, temporal phase mapping, single voxel time‐course modeling, and network connectivity analyses.

Supporting information

Supplementary Information

Supplementary Information Figure 1.

Supplementary Information Figure Legend