Abstract
Ventricular growth is widely considered to be an important feature in the adverse progression of heart diseases, whereas reverse ventricular growth (or reverse remodeling) is often considered to be a favorable response to clinical intervention. In recent years, a number of theoretical models have been proposed to model the process of ventricular growth while little has been done to model its reverse. Based on the framework of volumetric strain-driven finite growth with a homeostatic equilibrium range for the elastic myofiber stretch, we propose here a reversible growth model capable of describing both ventricular growth and its reversal. We used this model to construct a semi-analytical solution based on an idealized cylindrical tube model, as well as numerical solutions based on a truncated ellipsoidal model and a human left ventricular model that was reconstructed from magnetic resonance images. We show that our model is able to predict key features in the end-diastolic pressure–volume relationship that were observed experimentally and clinically during ventricular growth and reverse growth. We also show that the residual stress fields generated as a result of differential growth in the cylindrical tube model are similar to those in other nonidentical models utilizing the same geometry.
Keywords: Remodeling, Reverse remodeling, Growth, End-diastolic pressure–volume relationship, Finite element method, Magnetic resonance imaging
1 Introduction
Maladaptive ventricular growth or remodeling1 is widely considered to be an important determinant of the clinical course of heart failure (Cohn et al. 2000). In its classical form, cardiac remodeling can be categorized into two different types: (1) concentric remodeling with a thickening of the ventricular wall that is induced by an overloading of pressure and (2) eccentric remodeling with a dilation of the ventricles that is induced by an overloading of volume (Grossman et al. 1975). These global geometrical changes in the form of concentric and eccentric remodeling of the heart ventricles are induced microscopically by the parallel and series addition of sarcomere units in the myocytes, respectively. Yet, these two forms of remodeling processes are not mutually exclusive and can coexist in other clinical events (e.g., after myocardial infarction) (Opie et al. 2006).
Several theoretical continuum models based on the concept of finite volume growth have recently been proposed to describe ventricular geometrical remodeling (Kroon et al. 2009; Göktepe et al. 2010 a,b; Rausch et al. 2011; Kerckhoffs et al. 2012). All these models were developed based upon the concept of the multiplicative decomposition of the deformation gradient tensor into a “growth” and an elastic component. This concept was first applied by Rodriguez et al. (1994) to model tissue growth and was originally developed by Lee (1969) in the context of finite plasticity. These ventricular growth models were developed with either ventricular myofiber stress as the stimulant of growth (as in Göktepe et al. (2010a,b) and Rausch et al. (2011) for modeling concentric remodeling) or with ventricular myofiber and/or myocrossfiber strain as the primary stimulant of growth (Kroon et al. 2009; Kerckhoffs et al. 2012).
Although a sizable number of theoretical models have been developed to model the process of ventricular remodeling and to predict the effects clinical treatments have on this process (Klepach et al. 2012), there are few (if any) theoretical models that describe its reversal. Due to the rapid advancement of clinical devices and treatments, reverse remodeling of the ventricles in the form of ventricular size normalization has been observed clinically after some interventions. These treatments include implantation of a left ventricular assist device (Burkhoff et al. 2006), mitral valve repairs (Brinke et al. 2010) and, more recently, bioinjection treatment using calcium-sodium-alginate hydrogel (Lee et al. 2013). All of these interventions have been associated with a reduction in ventricular loading due either to a reduction in hemodynamics loading (left ventricular assist devices and mitral valve repairs) or to the presence of mechanical support in the ventricular wall (bioinjection treatment). Besides clinical observations, experiments have also shown that ventricular remodeling as a result of aortocaval fistula (Gerdes et al. 1995) and aortic arch banding (Zhang et al. 2013) in the rat's heart can be reversed if these initiating stimuli were removed. As such, there is mounting evidence suggesting that a reversal of ventricular remodeling can occur after sufficient and prolonged unloading of the ventricles.
In this paper, we propose a theoretical constitutive model capable of describing both ventricular remodeling and its reversal. The focus here is on pathological ventricular remodeling and reverse remodeling, which is a subset of the broad subject of biological growth and remodeling (Taber 1995; Ambrosi et al. 2011). Our proposed model is based on the generic framework of volumetric strain-driven finite growth described by Göktepe et al. (2010b). The constitutive equations describing reversible ventricular remodeling are given in Sect. 2. In Sects. 3 and 4, we describe the problem formulations for a semi-analytical solution of reversible remodeling in a cylindrical tube model and the numerical solutions of reversible remodeling in more realistic left ventricular geometries (a truncated ellipsoidal model and a human left ventricular model that was reconstructed from magnetic resonance images), respectively. The results from these models are described in Sect. 5, where we show the effects of ventricular reverse remodeling (and remodeling) on end-diastolic pressure–volume relationship, as well as on the ventricular myofiber stress and strain fields. Finally, in Sect. 6, we discuss the compatibility of our results with clinically and experimentally observed features of ventricular reverse remodeling and remodeling.
2 Methods
2.1 Kinematics of growth and reversible growth
Following Rodriguez et al. (1994) and Göktepe et al. (2010b), we multiplicatively decomposed the deformation gradient F into an elastic part Fe and a growth part Fg, i.e.,
| (1) |
Given that the focus here is on the formulation of a reversible growth multiplier θ, we prescribed (without loss of generality) an isotropic growth tensor Fg that is parameterized by a scalar growth multiplier θ, i.e.,
| (2) |
where I is the identity tensor. We note that other forms of growth tensor have been proposed to describe eccentric hypertrophy, e.g., an anisotropic growth tensor Fg = I + (θ − 1) f0 ⊗ f0 (Göktepe et al. 2010b) and an isochoric growth tensor Fg = (θ) f0 ⊗ f0 +1/√θ(I −f0 ⊗ f0) (Klepach et al. 2012) with f0 denoting the myofiber direction. The purpose of using an isotropic growth tensor Fg here is to focus on the development of a growth multiplier θ.
Using the definition of an isotropic growth tensor Fg given in Eq. (2) and the multiplicative decomposition of the deformation gradient given in Eq. (1), the elastic deformation gradient tensor becomes
| (3) |
Correspondingly, the elastic part of the right Cauchy stretch tensor and Green-Lagrange elastic strain tensor are then:
| (4a) |
and
| (4b) |
respectively.
2.2 Elastic constitutive model
The elastic deformation of the myocardial tissue is described using a Fung-type transversely isotropic hyperelastic constitutive model with the following strain energy function (Guccione et al. 1991):
| (5a) |
where
| (5b) |
In Eq. (5), C, bf, bs and bfs are the material parameters and Eij with (i, j) ∊ (f, s, n) are the components of the Green-Lagrange strain tensor Ee, which correspond to the material coordinates in the fiber f, sheet s and sheet-normal n directions.
The incompressibility of the material is enforced by an augmented strain energy function Ŵ
| (6) |
where p is a hydrostatic pressure that functions as a Lagrange multiplier for the kinematic constraint det Fe = 1.
The resultant second Piola-Kirchkoff stress tensor is defined as
| (7) |
and the Cauchy stress tensor is
| (8) |
The Cauchy stress enters the equilibrium equation
| (9) |
where div denotes the divergence with respect to the deformed coordinates and body forces have been neglected.
2.3 Kinetics of growth
The constitutive model of a reversible growth multiplier is motivated by the strain-driven eccentric growth model proposed by Göktepe et al. (2010b):
| (10) |
In Eq. (10), the evolution of the growth multiplier depends on two scalar functions, namely, a rate limiting scalar function k(θ) and a growth driving function ϕ(λe) that depends on the elastic myofiber stretch λe.
Consistent with the hypothesis that excessive stretch of the myofiber beyond some homeostatic value λh2 can lead to growth and dilation of the ventricles (as in the case when the ventricle is “volume-overloaded”), the functions k(θ) and ϕ(λe) have the following forms when λe ≥ λh2:
| (11a) |
| (11b) |
Equation (11) is similar to the strain-driven eccentric growth model by Göktepe et al. (2010b). In this equation, γg, τg, θmax and θmin are the degree of nonlinearity of sarcomere deposition, a time-scale associated with tissue growth and the prescribed maximum and minimum permissible values of the growth multiplier θ, respectively. The stretching of the myofiber as a result of growth (or growth stretch) is . Correspondingly, the elastic myofiber stretch is . It is evident from Eq. (11) that growth terminates when either criterion θ = θmax or λe = λh2 is met.
The concept of a homeostatic target value of the myofiber stretch is consistent with the experimental results by Omens (1998), who suggested end-diastolic myofiber strain as the primary stimulus for myocardial growth in volume-overload hypertrophy (instead of end-diastolic stress). This concept is also consistent with the growth models of Kroon et al. (2009), Kerckhoffs (2012) and Taber (2001), although in the latter, myocardial stress (instead of strain) was postulated to be restored to a homeostatic value during growth.
2.4 Kinetics of reversible growth
In contrast to Göktepe et al. (2010b) where growth is irreversible, we hypothesize that cardiac growth is reversible in a way that the elastic myocardial stretch λe is always normalized to a homeostatic range λh1 ≤ λe ≤ λh2. Consequently, reverse growth occurs when the elastic myofiber stretch is less than the prescribed homeostatic myofiber stretch λh1. To model reversible growth, we propose the following functional forms for k(θ) and ϕ(λe) when λe ≤ λh1
| (12a) |
| (12b) |
Similar to Eq. (11), γrg and τrg in Eq. (12) are the degree of nonlinearity of sarcomere removal and a time-scale associated with reverse growth, respectively. We also note that reversal of growth terminates when either criterion: θ = θmin or λe = λh1 are met. In addition, the physical limit requires that θmin > 0.
Last, to ensure that growth does not occur within the homeostatic range of the elastic myofiber stretch, we prescribed ϕ = 0 when λh1 ≤ λe ≤ λh2.
3 Growth and reverse growth in a thick-walled cylindrical tube
To demonstrate the effects of our proposed constitutive model, we constructed a semi-analytical solution of an inflated thick-walled cylindrical tube undergoing reversible growth in response to changes in the hemodynamics load.
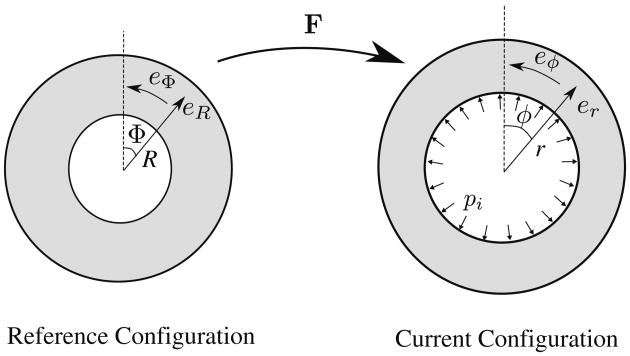
For a cylindrical tube undergoing homogeneous inflation (Fig. 1), the deformed radial position r is a function of only the initial radial position R, i.e., r(R) and the resultant deformation gradient tensor is:
Fig. 1. Inflation of cylindrical tube. The base vectors ez and eZ point out of the page.
| (13) |
We note the prescribed deformation does not include any shear deformation that may be present during actual passive filling of the left ventricle. The values of the undeformed inner radius Ri and outer radius Ro were prescribed to be 40 and 50 mm, respectively.
For an incompressible material, the deformation is isochoric and is subjected to the kinematic constraint det Fe = 1. Using Eqs. (3) and (13), this kinematic constraint reduces to
| (14) |
Integrating this kinematic constraint leads to:
| (15) |
The fiber direction in the cylindrical tube model was prescribed to be in the circumferential direction, i.e., (f, s, n) = (Φ, R, Z), and the material parameters of the Fung's law in Eq. (5) were given values C = 0.1 kPa, bf = 20, bs = 3 and bfs = 3.
The shear stresses σrz = σrθ = σϕz = 0 and the normal stresses σrr, σϕϕ, σzz are functions of only the radial position r when the cylindrical tube is inflated. Thus, the equilibrium Eq. (9) is reduced to a scalar equation:
| (16) |
With a prescribed internal pressure pi and zero external pressure, the boundary conditions at the tube inner and outer radius are
| (17a) |
| (17b) |
Integrating the equilibrium Eq. (16) and incorporating the boundary conditions lead to the following integral equation for the internal pressure,
| (18) |
Combining Eqs. (3)–(8) and (13), we can rewrite Eq.(18) in the following form,
| (19) |
However, integration of (19) requires knowledge of the dependency of r on R. This dependency is obtained through the integral form of the kinematic constraint in Eq. (15).
Equations (15) and (19), together with the kinetics of growth and reverse growth in Eqs. (10)–(12) form an initial value problem. We prescribed τg = τrg = 1s, yg = yrg = 1, λh1 = λh2 = 1.3, θmax = 2 and θmin = 1 for the parameters describing the kinetics of growth and reverse growth in the cylindrical tube model. We note that in doing so, we have assumed that the timescales of growth and reverse growth are similar. We believe that this is a reasonable assumption given that the experiments by Gerdes et al. (1995) showed that the myocytes length was normalized between the 2–12 week interval after reversal of an 4-week old aortocaval fistula that was created to induce eccentric hypertrophy in rats heart. The unknowns for this set of equations are the growth multiplier θ and the inner radius of the tube in the current configuration ri. Since the elastic fiber stretch λe is a function of the radial coordinate R in the undeformed configuration, the growth multiplier θ depends on the radial position and may vary across the thickness.
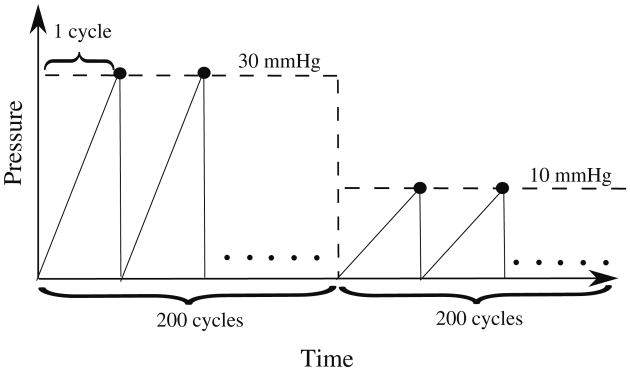
To mimic the hemodynamic loading of the heart, we prescribed a sawtooth time-periodic pressure–time curve for inner pressure pi (t) (Fig. 2).
Fig. 2. Prescribed cyclical hemodynamics load pi of the cylindrical tube model.
We assumed that the timescale for growth is significantly larger than the time scale for hemodynamic loading, which allows us to separate the time scales between growth and hemodynamics. As such, we locally update the growth multiplier θ using explicit-time integration only at the end of each loading cycle. Within each cycle, Eqs. (15) and (19), with θ treated as a constant, are recast into a nonlinear root finding problem for a scalar function defined as
| (20) |
Where
| (21) |
The explicit-time integration of Eq. (3) is implemented in MATLAB (The MathWorks, Inc) to solve the initial value problem. The MATLAB functions “fsolve” and “quad” are used to solve Eqs. (20) and (21), and evaluate the integrals, respectively.
4 Growth and reverse growth in realistic left ventricular geometries
After testing our model on an idealized cylindrical tube model, we applied our model to more realistic geometries of the left ventricle, namely, (1) a truncated ellipsoid model (ELLIPSOID) and (2) a normal human left ventricular model (HUMAN).
The construction of the HUMAN model is shown in Fig. 3. Specifically, the left ventricular epicardial and endocardial surfaces were reconstructed from magnetic resonance images (MRI) by manual segmentation using MeVisLab (MeVis Medical Solutions AG, Bremen, Germany) (Fig. 3a,b). A hexahedral mesh consisting of 3,456 trilinear elements was generated in the ventricular wall bounded by the epicardial and endocardial surfaces using the meshing software True-Grid (XYZ Scientific Application, Livermore, CA, USA) (Fig. 3c). Following Legrice et al. (1997), we prescribed a rule-based local myofiber orientation field in the ventricular wall, where the myofiber helix angle (measured with respect to the counterclockwise circumferential direction) varies linearly from −60° at the epicardial wall to 60° at the endocardial wall (see Fig. 3d). The same myofiber helix angle distribution was also prescribed to the ELLIPSOID model
Fig. 3.
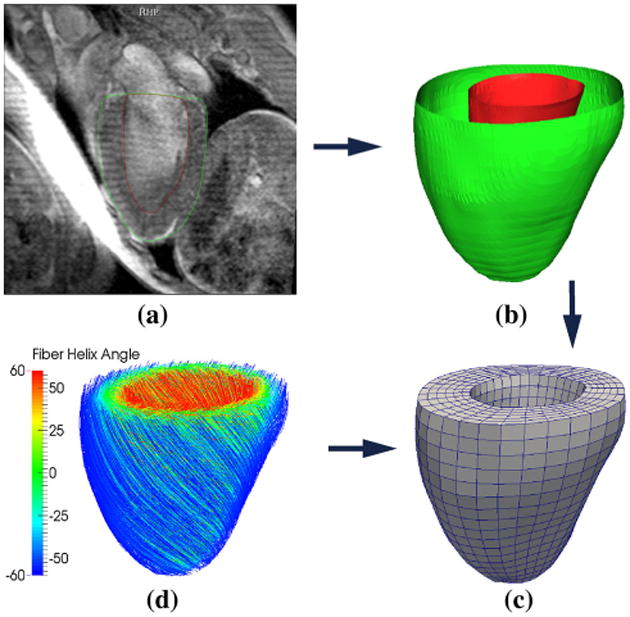
Construction of the HUMAN finite element model: (a) segmentation of the MRI, (b) reconstruction the endocardial (red) and epicardial (green), (c) construction of the finite element mesh and (d) assignment of rule-based myofiber orientation—streamlines follow fiber direction and are color coded with fiber helix angle
Similar to the cylindrical tube model, the elastic deformations in both models are described using Fung's constitutive equation given in Eq. (5). The material parameters are C = 0.195kPa, bf = 24.63, bs = 9.63 and bfs = 8.92, which correspond to the values defined in the human modeling study by Wenk et al. (2012). For the growth parameters, we chose τg = τrg = 1 s and γg = γrg = 1.
The homeostatic range of the elastic stretch at which neither growth nor reverse growth occurs λh1 ≥ λh2 was chosen as the range of elastic stretch in the HUMAN model when a nominal end-diastolic pressureP̄ = 10 mmHg was applied to the model's endocardial surface.
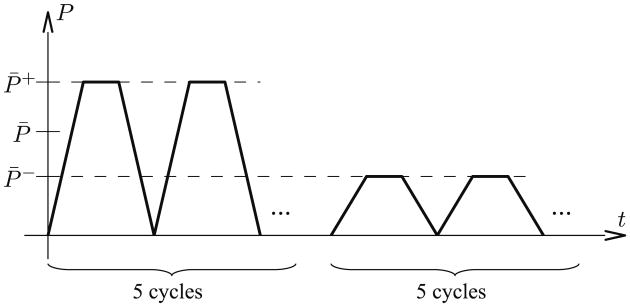
Figure 4 shows the prescribed pressure-time variation to simulate growth and reverse growth in both ELLIPSOID and HUMAN models. A cyclical high end-diastolic pressure P̄+ = 30 mmHg was applied successively to induce stretch-driven growth in both models. Thereafter, a low end-diastolic pressure P̄− = 1 mmHg and P̄− = 2 mmHg was applied cyclically to induce reverse growth in the ELLISPOID and HUMAN models, respectively.
Fig. 4.
Cyclical loading in the ELLISPOID and HUMAN models consisting of five high pressure cycles and five low pressure cycles. Every growth step lasts one characteristic time of the growth model
Similar to the idealized cylindrical tube model, we hypothesize that the timescale of a cardiac cycle and the timescales of growth or reverse growth are separable. This implies that we update the growth multiplier θ only at peak pressure in each cycle.
5 Results
5.1 Growth and reverse growth in a cylindrical tube
Figure 5 shows the evolution of the growth multiplier θ at the inner and outer surfaces Ri and Ro under the imposed hemodynamic pressure loading (Fig. 2). For the first 200 cycles at which the pressure pi was elevated, the growth multiplier θ increased monotonically at a decreasing rate and approached steady state with different values at the inner and outer surfaces of the tube. In the cylindrical tube model, the larger value of θ found at the inner wall is due to the larger fiber (circumferential) stretch found in the inner wall when compared to that at the outer wall. Because the steady-state values lay between the maximum and minimum permissible values of the growth multiplier, i.e., θmin = 1 and θmax = 2, the vanishing growth rates at steady state at both inner and outer surfaces are the outcome of λe → λh2 as the elastic stretch approached its homeostatic value. In a similar fashion, the growth multiplier θ decreased after 200 cycles in response to the reduced pressure pi, and approached a steady-state value as λe → λh1.
Fig. 5.
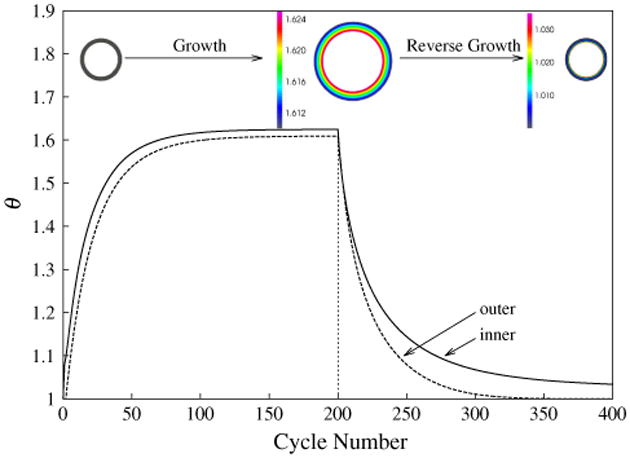
Growth multiplier θ at the inner and outer surfaces as a function of the cycle number. Cross section of the unloaded cylindrical tube are shown in the inset at cycles 0, 200 and 400. Color denotes growth multiplier θ in cycles 200 and 400
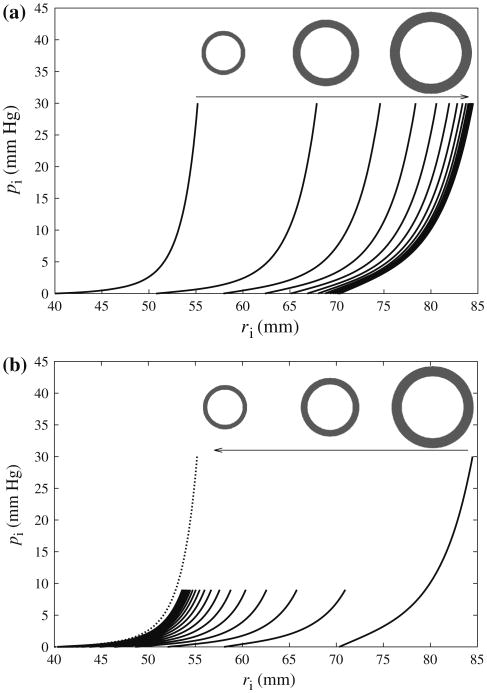
Figure 6 shows the effects of (a) growth and (b) reverse growth on the relationship between pressure pi and the tube internal radius ri. During growth, both the internal radius of the unloaded tube (i.e., ri at pi = 0) and the entire pi - ri relationship shifted to the right and asymptotically approached the first equilibrium state at which λe = λh2. During reverse growth, the inner radius and the pi - ri relationship shifted to the left and asymptotically approached the second equilibrium state at which λe = λh1.
Fig. 6.
Internal pressure pi versus inner radius ri at every 10th cycle in (a): cycles 1–200 during growth (inset: unloaded cylindrical cross section at cycles 1, 20, 200) and (b) cycles 200–400 during reverse growth (inset: unloaded cylindrical cross section at cycles 200, 220, 400). Dotted line: pi versus ri at first cycle
We note that the pi−ri relationship at the equilibrium state after reverse growth (N = 400) is different from the original one before the onset of growth, i.e., at cycle = 1 (dotted line). This is because of the existence of differential growth across the cylindrical tube wall. Therefore, residual stresses, i.e., internal stresses in the unloaded tube, were generated as a result.
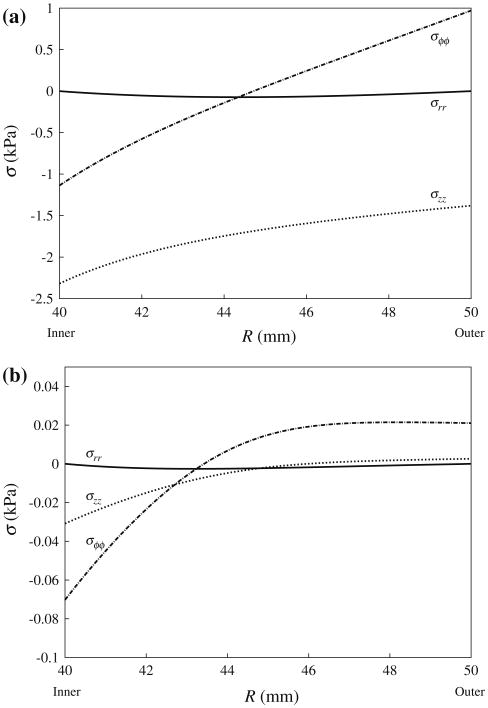
Figure 7 shows the variation of normal residual stresses σrr, σϕϕ and σzz across the tube wall at (a) the “fully grown” steady state, and at (b) the “fully shrunk” steady state. Although residual stresses in the “fully shrunk” steady state are substantially smaller than that in the “fully grown” steady state, they all share the same features. Specifically, the circumferential normal stress σϕϕ varies from negative at the inner wall indicating compression to positive at the outer wall indicating tension. By comparison, the longitudinal normal stress σzz is negative across the entire tube wall. A compressive σzz arises largely because the prescribed plane deformation of the model in Eq. (13) is not compatible with the isotropic growth deformation prescribed in Eq. (2). Therefore, in order to maintain the plane deformation prescribed in Eq. (13), the tube must be elastically compressed in its longitudinal direction when growth occurs. On the other hand, the normal radial stress σrr satisfies the boundary conditions in Eq. (17) with pi = 0 and is relatively small when compared to the other two stress components.
Fig. 7.
Residual normal stresses in the circumferential (σϕϕ), radial (σrr) and longitudinal (σzz) directions versus referential radial position R at the beginning of (a) cycle 201 and (b) cycle 400 with pi = 0
5.2 Growth and reverse growth in realistic left ventricular geometries
For the nominal pressure P̄ = 10 mmHg, the range of elastic stretch in the HUMAN model lay between the lower and upper limits of 1.05 and 1.15, respectively. These limits were used to set the homeostatic range of elastic stretch, i.e., λh1 = 1.05 and λh2 = 1.15 in the reversible growth constitutive law for both HUMAN and ELLIPSOID models (see Sects. 2.3 and 2.4).
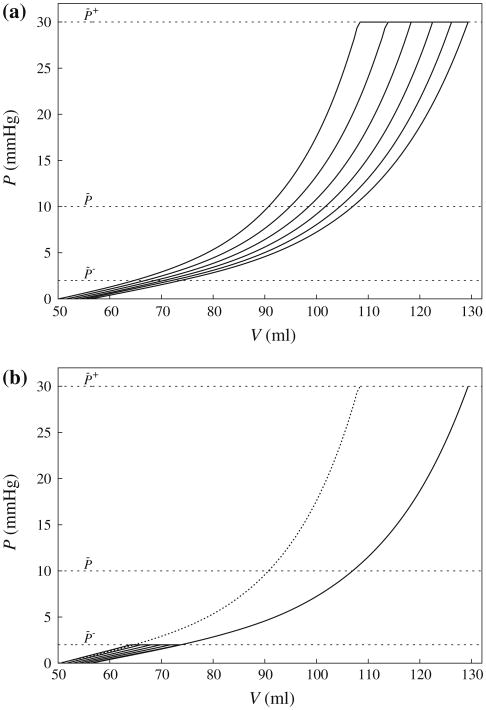
Figure 8 shows the pressure-volume relationship of the HUMAN model under the prescribed loading given in Fig. 4. The pressure–volume relationship of the ELLISPOID model behaved similarly to that of the HUMAN model and is not shown here. In the figure, the curves display similar features as the pressure–radius relationship of the idealized cylindrical tube model in Fig. 6, where the entire pressure–volume relationship shifted to the right under a high end-diastolic pressure loading of P̄+ = 30 mmHg (Fig. 8a), and shifted to the left under a low end-diastolic pressure of P̄− = 2 mmHg (Fig. 8b). Correspondingly, the unloaded LV cavity volume also increased and decreased (both by ∼5 ml) in response to the high and low end-diastolic pressure loading, respectively. Similar to the cylindrical tube model, the pressure–volume relationship in the final cycle of reverse growth is not identical to the initial one before the onset of growth although their unloaded left ventricular cavity volume are close to one another.
Fig. 8.
Evolution of the pressure–volume relationship of the HUMAN model during (a) growth and (b) reverse growth. The first and last cycle of the pressure–volume relationship in (a) is also shown in (b) as solid and dotted lines, respectively. Refer to text for definition of P̄−, P̄ and P̄+
Figure 9 shows the evolution of the left ventricular geometry color coded with the growth multiplier θ field as a result of growth and subsequent reverse growth in both ELLIPSOID and HUMAN models.
Fig. 9.
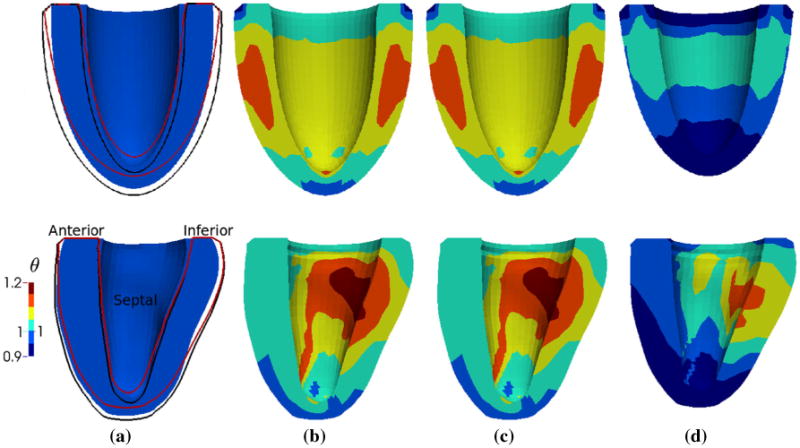
Evolution of the unloaded geometry and growth multiplier θ field of the ELLIPSOID (top) and HUMAN (bottom) models as a result of growth and reverse growth. Geometries are of the same scale in each model. Black and red line in (a) correspond to the geometry outline of (b) and (d), respectively. Note (b) and (c) are identical since no growth or reverse growth occurred between these 2 time points. a Before growth (Cycle 1). b After growth (Cycle 5). c Before reverse growth (Cycle 6). d After reverse growth (Cycle 10)
Both models increased in size with growth (Fig. 9b) that corresponded to a 20% increase in the left ventricular wall volume, and shrank longitudinally as a result of reverse growth (Fig. 9d) that corresponded to a recovery of the initial ventricular volume. In the ELLIPSOID model, growth is axisymmetric with larger growth occurring half-way between the apex and base at the ventricular mid-wall. Contrastingly, growth is largely heterogeneous in the HUMAN model where the endocardial (inner) wall exhibits larger growth when compared to the epicardial (outer) wall. This result is consistent with observations from the cylindrical tube model (see Fig. 5).
Similar features of growth can be found in the ELLIPSOID and HUMAN models. Specifically, the apical region in both models exhibits a little shrinkage (i.e., θ < 1) during growth (Fig. 9b) and more substantial shrinkage during reverse growth (Fig. 9d). This is in agreement with clinical observations during eccentric hypertrophic growth and implies that the apex is mechanically unloaded. The reduced apical stretch initiates negative growth or shrinkage in the apical region even during a global overload. Both models also became more spherical after growth. Defining the end-diastolic sphericity index as the maximum short-to-long-axis dimension ratio of the endocardial surface, the (ELLIPSOID, HUMAN) end-diastolic sphericity index was (0.70, 0.65) before growth, (0.71, 0.66) after growth and (0.70, 0.63) after reverse growth.
Figure 10 shows the evolution of the elastic myofiber stretch λe field as a result of growth and reverse growth in both ELLIPSOID and HUMAN models. The regional profiles of the elastic fiber stretch are similar to the respective profiles of the growth multiplier (Fig. 9) as elastic fiber stretch is the driving mechanism for growth. During growth and reverse growth, the elastic fiber stretch also became more homogeneous across the ventricular wall in both models. Specifically, the range of elastic fiber stretch (λe,min, λe,max) was reduced from (1.02, 1.22) to (1.04, 1.18) in the HUMAN model and from (1.04, 1.21) to (1.01, 1.18) in the ELLIPSOID model during growth (cycle 1–5). During reverse growth (cycle 6– 10), this range was reduced from (0.97, 1.08) to (1.01, 1.07) in the HUMAN model and from (0.92, 1.09) to (1.00, 1.07) in the ELLIPSOID model.
Fig. 10.
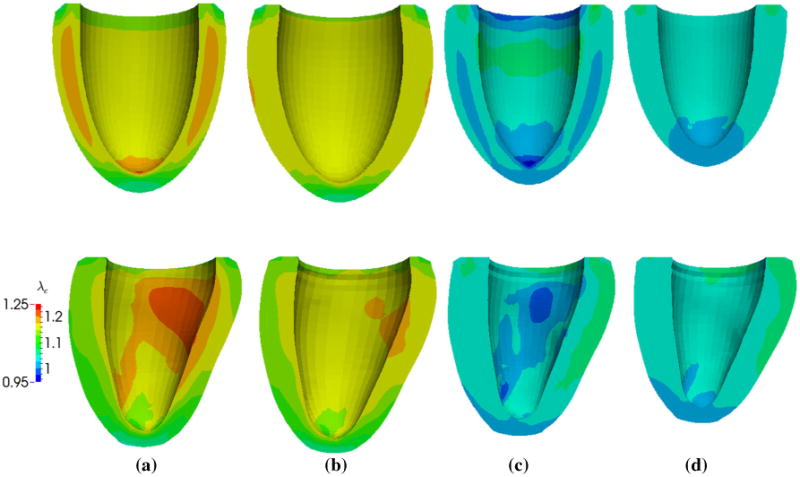
Evolution of elastic myofiber stretch λe in the ELLIPSOID (top) and HUMAN (bottom) models as a result of growth and its reversal. Geometries are of the same scale in each model. a Before growth (Cycle 1). b After growth (Cycle 5). c Before reverse growth (Cycle 6). d After reverse growth (Cycle 10)
6 Discussion
We have established a constitutive model for reversible growth based on the frameworks of irreversible stretch-driven growth by Göktepe et al. (2010b) and the multiplicative decomposition of deformation gradient into an elastic and “growth” component by Rodriguez et al. (1994). Specifically, we have established the first model with a homeostatic equilibrium range for soft tissue growth that is analogous to hard tissue growth in bone. This homeostatic equilibrium zone is often referred to as a “lazy” zone in bone (Frost 2003).
Using this constitutive model, we have constructed a semi-analytical solution based on an idealized cylindrical tube model and numerical solutions based on a truncated ellipsoidal left ventricular model as well as an MRI-reconstructed human left ventricular model. We showed that though common features exist between the ELLIPSOID and HUMAN models (e.g., negative growth or shrinkage at the apical regions), differences in the models' geometry can have a significant impact on the myofiber stretch distribution in the left ventricle, and consequentially, on the left ventricular growth distribution. The sensitivity of the myofiber stretch distribution to the left ventricular geometry exists even for the case of an axisymmetric left ventricle. As demonstrated by Choi et al. (2010), the myofiber strain distribution in a truncated ellipsoidal left ventricle varies depending on its sphericity. The myofiber stretch distribution in our ELLIPSOID model (Fig. 10) is consistent with that shown in Figure 5 of Choi et al. (2010).
Notwithstanding the fine-detail differences between the models' predictions of the left ventricular growth distribution, the models' predictions have been consistent at a larger scale. Specifically, all three models share the following predictions: (1) growth was induced by an increase in peak hemodynamic load that resulted in a rightward shift of the entire pressure–volume relationship (Fig. 6), (2) reverse growth was induced by a subsequent decrease in peak hemodynamic load that resulted in a leftward shift of the entire pressure–volume relationship (Fig. 8) and (3) differential growth-induced residual stresses in left ventricular wall. We now compare these three predictions of our models to the results of experimental studies.
6.1 Compatibility with experimental studies and clinical observations of ventricular remodeling
In terms of ventricular remodeling, the model predictions are consistent with the classical concept of eccentric hypertrophy arising from volume overload (e.g., mitral regurgitation). The global effects of an increase in preload associated with volume-overload hypertrophy are observed clinically in the form of a rightward shifting of the pressure– volume relationship (Gaasch and Meyer 2008), as well as an enlargement and increase in the sphericity of the heart (Cohn et al. 2000). Although the magnitude of growth in the HUMAN and ELLIPSOID models appears to be relatively small (because only 5 growth cycles were computed), especially when compared to hearts with end-stage dilated cardiomyopathy, our model predictions are consistent with all of these observations.
On the cellular level, myocytes in patients with ischemic cardiomyopathy were found to be lengthened through the serial addition of sarcomeres (Gerdes et al. 1992). Though end-diastolic myofiber stress was originally proposed as the growth stimulant during volume overload by Grossman et al. (1975), recent evidence from the experiments by Omens (1998) has pointed to end-diastolic myofiber strain as the growth stimulant. Specifically, Omens (1998) showed that the end-diastolic myofiber strain in rats induced with volume overload was normalized by 6 weeks during volume-overload hypertrophy whereas end-diastolic myofiber stress remained elevated during this time period. These experimental results form the basis for the construction of our model.
6.2 Compatibility with experimental studies and clinical observations of ventricular reverse remodeling
In contrast to myocardial growth and remodeling, which has been the subject of intense mathematical model development (Göktepe et al. 2010b; Kerckhoffs et al. 2012; Kroon et al. 2009), there are few, if any, mathematical models that describe the reverse of growth and remodeling. However, the phenomenon of reverse growth has increasingly been observed both experimentally and clinically. These observations form the basis of our proposed constitutive model for reversible strain-driven growth.
The original concept of reverse remodeling was spawned by the effects of left ventricular assist devices in normalizing end-diastolic pressure–volume relationship in patients with end-stage cardiomyopathy (Levin et al. 1995) that have been frequently observed in clinical practice (Burkhoff et al. 2006; Drakos et al. 2007; Ambardekar and Buttrick 2011). In particular, prolonged unloading of the left ventricular pressure (and volume) after left ventricular assist device implantation (Figure 1 in Burkhoff et al. (2006)) led to two key global features, namely, a decrease in left ventricular volume and a concurrent leftward shift in the end-diastolic pressure– volume relationship (Figure 2 in Levin et al. (1995)). These two clinical observations are consistent with our model prediction (Figs. 6 and 8).
Microscopically, reverse remodeling after left ventricular assist device implantation was accompanied by a decrease in myocyte size (Figure 2 in Madigan et al. (2001)). In the experiment by Gerdes et al. (1995), reversal of eccentric hypertrophic growth in rats was attributed to the removal of sarcomeres because the measured sarcomere length (∼1.90 μm) remained unchanged even though the myocyte length decreased after growth was reversed.
The mechanism behind reverse remodeling is likely a decrease in hemodynamics load—the basis of our model— as evidenced by a number of experiments, e.g., (Gerdes et al. 1995) and (Zhang et al. 2013). Moreover, reverse remodeling was also observed in clinical interventions other than the left ventricular assist device, which are associated with a reduction in ventricular loading. For example, a significant reduction in the left ventricular size (up to 50 %) was observed in patients who underwent bioinjection treatment with Algiysl-LVR, a calcium-sodium-alginate hydrogel proprietary to Lonestar Heart, Inc (Lee et al. 2013). This treatment was associated with a decrease in end-diastolic myofiber stress (Wenk et al. 2011) and a leftward shift in end-diastolic pressure–volume relationship (Wall et al. 2006). Reverse geometrical remodeling of the left ventricle was also observed after mitral valve repair, which decreases preload (Brinke et al. 2010). Given that the experiment by Omens (1998) strongly suggests an elevated elastic myofiber strain as the stimulant of ventricular remodeling, it is also very plausible that the reverse holds, i.e., a reduction in elastic myofiber strain initiates reverse ventricular remodeling.
6.3 Compatibility with experimental studies and clinical observations on growth-induced residual stress
Since non-homogeneous growth generates incompatibility that must be accommodated elastically, differential growth in the left ventricle in response to a non-homogeneous strain field will generate residual stresses, i.e., stresses in the unloaded state. The residual stress fields generated through our constitutive model in the idealized cylindrical model at maximal growth (Fig. 7) are consistent with other models utilizing the same cylindrical geometry (Rodriguez et al. 1994; Guccione et al. 1991). In Guccione et al. (1991), the residual stress field was the result from prescribing a “cut” cylindrical model as a stress-free reference configuration whereas in Rodriguez et al. (1994), the residual stress field was the result of stress-modulated differential growth. Consistent with these models, the circumferential stress varies transmurally from compressive (at the endocardial wall) to tensile (at the epicardial wall). In fact, the HUMAN model also exhibits such a transmural variation of circumferential stress (see Supplementary Material) that is consistent with that found in the mouse left ventricle (Omens et al. 2003). We also showed that our model predicts an increase in residual stresses during ventricular remodeling and a subsequent decrease in residual stresses during reverse ventricular remodeling (Fig. 7).
The effects of pathological and physiological remodeling on residual stress and strain have been studied widely in the arteries. For example, Fung and Liu (1989) showed that the residual strain in rat artery changes as a result of hypertrophy, whereas Wells and Walter (2010) showed that the residual strain in bovine aorta increases during fetal development. Unlike in arteries, the effects of pathological ventricular remodeling and reverse remodeling on residual stress and strain are still unclear given the paucity of experiments that studied these effects. To the best of our knowledge, there are few studies on the effects of residual stresses and strain due to ventricular remodeling. Some of these include the study by Omens et al. (1998) on the aging rat heart (i.e., physiological remodeling), by Taber and Chabert (2002) on the developing embryonic chick heart and by Weis et al. (2000) on extracellular matrix remodeling in mouse models. In Omens et al. (1998), the opening angle of the left ventricular equatorial ring after a radial cut was found to decrease during aging, while in Taber and Chabert (2002), the opening angle in the embryonic chick heart was found to decrease as a result of pressure overload. It is not entirely clear whether the reduction in opening angle in the experiment by Omens et al. (1998) was accompanied by a change in tissue stiffness, as besides differential growth, a change in tissue stiffness will also have an effect on the opening angle (Taber and Chabert 2002). The impact on the opening angle as a result of a change in tissue stiffness can be illustrated by considering a hypothetical case in which the tissue becomes infinitely compliant (i.e., have zero stiffness) during ventricular remodeling. In this limiting state, the left ventricle will be in a “stress-free” state even with finite growth and correspondingly, the opening angle will be zero. As such, future experiments to test our model prediction on the effects on residual stresses and strain due to ventricular remodeling and reverse remodeling should separate the effects arising from differential growth and a change in material properties.
6.4 Limitations of the model
Our proposed model of reversible growth and remodeling has the following limitations. First, we have neglected the effects on myocardial material properties due to remodeling and reverse remodeling. In the experiments by Omens (1998), volume-overload ventricular remodeling in rats was found to be associated with an increase in the mechanical stiffness of the myocardial tissues. A change in mechanical properties would not only have a confounding effect on the residual strain measured using the “opening angle” of radially cut slices of the left ventricle (as expounded in the previous paragraph), but also on the end-diastolic pressure–volume relationship. Specifically, a concurrent change in the mechanical stiffness of the myocardial tissues during the remodeling and reverse remodeling processes may affect the ability of the left ventricle to reach a steady state in our model.
Second, our model (as with other existing volumetric growth models) cannot distinguish a change in the number of myocytes (i.e., hyperplasia or dysplasia) from a change in cell size (i.e., hypertrophy or atrophy) (Taber 2001).
Third, we have not considered the effects of systolic contraction in our model as we hypothesized that the maximal fiber stretch occurs only at end-of-diastole. While this hypothesis is reasonable in normal hearts, it may not be true in abnormal hearts. For example, strain abnormality during systole was observed in human hearts with myocardial infarction (Rutz et al. 2008).
7 Conclusions
In conclusion, we have established a reversible strain-driven growth model and have shown that the proposed model can qualitatively reproduce a number of experimental and clinical observations of ventricular remodeling and reverse remodeling. Specifically, we have shown that our model prediction on the effects of end-diastolic pressure–volume relationship due to growth and reverse growth are compatible with clinical and experimental observations. We have also shown that our model predictions on the residual stress fields in an idealized cylindrical model are similar to those in other nonidentical models, namely, a model with stress-modulated growth and a model using a longitudinally cut cylinder as a stress-free configuration. The key limitation of our proposed growth model is that it does not take into account changes in the mechanical properties that may have occurred during both remodeling and reverse remodeling. We believe that such changes would have an effect on the ability of the heart ventricle to reach a steady state in our model.
Acknowledgments
This work was supported by NIH Grants R01-HL-077921 and R01-HL-118627 (J.M. Guccione); K25-NS058573-05 (G. Acevedo-Bolton); NSF Grants 0952021 and 1233054 (E. Kuhl); and Marie Curie international outgoing fellowship within the 7th European Community Framework Program (M. Genet). We thank the reviewers for their valuable comments, which have helped us improve the presentation.
Footnotes
In this paper, we used the words “growth” and “remodeling” interchangeably although other authors have used “growth” and “remodeling” to specifically describe a change in mass and properties, respectively.
Contributor Information
L. C. Lee, Email: lclee@egr.msu.edu, likchuan.lee@ucsfmedctr.org, Department of Mechanical Engineering, Michigan State University, 2445 Engineering Building, East Lansing, MI 48824-1226, USA.
M. Genet, Email: Martin.Genet@ucsfmedctr.org, Department of Surgery, School of Medicine, University of California at San Francisco, San Francisco, CA 94143, USA.
G. Acevedo-Bolton, Email: Gabriel.Acevedo-Bolton@ucsf.edu, Department of Radiology and Biomedical Imaging, School, of Medicine, University of California at San Francisco, San Francisco, CA 94143, USA.
K. Ordovas, Email: Karen.Ordovas@ucsf.edu, Department of Radiology and Biomedical Imaging, School, of Medicine, University of California at San Francisco, San Francisco, CA 94143, USA.
J. M. Guccione, Email: Julius.Guccione@ucsfmedctr.org, Department of Surgery, School of Medicine, University of California at San Francisco, San Francisco, CA 94143, USA.
E. Kuhl, Email: ekuhl@stanford.edu, Departments of Mechanical Engineering, Bioengineering, and Cardiothoracic Surgery, Stanford University, Stanford, CA 94305-4040, USA.
References
- Ambardekar AV, Buttrick PM. Reverse remodeling with left ventricular assist devices: a review of clinical, cellular, and molecular effects. Circ Hear Fail. 2011;4(2):33–224. doi: 10.1161/CIRCHEARTFAILURE.110.959684. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ambrosi D, Ateshian GA, Arruda EM, Cowin SC, Dumais J, Goriely A, Holzapfel GA, Humphrey JD, Kemkemer R, Kuhl E, Olberding JE, Taber LA, Garikipati K. Perspectives on biological growth and remodeling. J Mech Phys Solid. 2011;59(4):863–883. doi: 10.1016/j.jmps.2010.12.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brinke EA, Klautz RJ, Tulner SA, Verwey HF, Bax JJ, Delgado V, Holman ER, Schalij MJ, van der Wall EE, Braun J, Versteegh MI, Dion RA, Steendijk P. Clinical and functional effects of restrictive mitral annuloplasty at midterm follow-up in heart failure patients. Ann Thorac Surg. 2010;90(6):1913–1920. doi: 10.1016/j.athoracsur.2010.08.010. [DOI] [PubMed] [Google Scholar]
- Burkhoff D, Klotz S, Mancini DM. LVAD-induced reverse remodeling: basic and clinical implications for myocardial recovery. J Card Fail. 2006;12(3):227–239. doi: 10.1016/j.cardfail.2005.10.012. [DOI] [PubMed] [Google Scholar]
- Choi HF, D'hooge J, Rademakers FE, Claus P. Influence of left-ventricular shape on passive filling properties and end-diastolic fiber stress and strain. J Biomech. 2010;43(9):1745–1753. doi: 10.1016/j.jbiomech.2010.02.022. [DOI] [PubMed] [Google Scholar]
- Cohn JN, Ferrari R, Sharpe N. Cardiac remodeling concepts and clinical implications: a consensus paper from an international forum on cardiac remodeling. J Am Coll Cardiol. 2000;35(3):569–582. doi: 10.1016/s0735-1097(99)00630-0. [DOI] [PubMed] [Google Scholar]
- Drakos SG, Terrovitis JV, Anastasiou-Nana MI, Nanas JN. Reverse remodeling during long-term mechanical unloading of the left ventricle. J Mol Cell Cardiol. 2007;43(3):231–242. doi: 10.1016/j.yjmcc.2007.05.020. [DOI] [PubMed] [Google Scholar]
- Frost HM. Bone's mechanostat: a 2003 update. Anat Rec A Discov Mol Cell Evol Biol. 2003;275(2):1081–1101. doi: 10.1002/ar.a.10119. [DOI] [PubMed] [Google Scholar]
- Fung Y, Liu S. Change of residual strains in arteries due to hypertrophy caused by aortic constriction. Circ Res. 1989;65(5):1340–1349. doi: 10.1161/01.res.65.5.1340. [DOI] [PubMed] [Google Scholar]
- Gaasch WH, Meyer TE. Left ventricular response to mitral regurgitation: implications for management. Circulation. 2008;118(22):2298–303. doi: 10.1161/CIRCULATIONAHA.107.755942. [DOI] [PubMed] [Google Scholar]
- Gerdes AM, Clark LC, Capasso JM. Regression of cardiac hypertrophy after closing an aortocaval fistula in rats. Am J Physiol. 1995;268(6 Pt 2):51–H2345. doi: 10.1152/ajpheart.1995.268.6.H2345. [DOI] [PubMed] [Google Scholar]
- Gerdes AM, Kellerman SE, Moore JA, Muffly KE, Clark LC, Reaves PY, Malec KB, McKeown PP, Schocken DD. Structural remodeling of cardiac myocytes in patients with ischemic cardiomyopathy. Circulation. 1992;86(2):426–430. doi: 10.1161/01.cir.86.2.426. [DOI] [PubMed] [Google Scholar]
- Göktepe S, Abilez OJ, Kuhl E. A generic approach towards finite growth with examples of athlete's heart, cardiac dilation, and cardiac wall thickening. J Mech Phys Solids. 2010a;58(10):1661–1680. [Google Scholar]
- Göktepe S, Abilez OJ, Parker KK, Kuhl E. A multiscale model for eccentric and concentric cardiac growth through sarcomerogenesis. J Theor Biol. 2010b;265(3):42–433. doi: 10.1016/j.jtbi.2010.04.023. [DOI] [PubMed] [Google Scholar]
- Grossman W, Jones D, McLaurin LP. Wall stress and patterns of hypertrophy in the human left ventricle. J Clin Invest. 1975;56(1):56–64. doi: 10.1172/JCI108079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guccione JM, McCulloch AD, Waldman LK. Passive material properties of intact ventricular myocardium determined from a cylindrical model. J Biomech Eng. 1991;113(1):42–55. doi: 10.1115/1.2894084. [DOI] [PubMed] [Google Scholar]
- Kerckhoffs RCP. Computational modeling of cardiac growth in the post-natal rat with a strain-based growth law. J Biomech. 2012;45(5):865–871. doi: 10.1016/j.jbiomech.2011.11.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kerckhoffs RCP, Omens J, McCulloch AD. A single strain-based growth law predicts concentric and eccentric cardiac growth during pressure and volume overload. Mech Res Commun. 2012;42:40–50. doi: 10.1016/j.mechrescom.2011.11.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klepach D, Lee LC, Wenk JF, Ratcliffe MB, Zohdi TI, Navia Ja, Kassab GS, Kuhl E, Guccione JM. Growth and remodeling of the left ventricle: a case study of myocardial infarction and surgical ventricular restoration. Mech Res Commun. 2012;42:134–141. doi: 10.1016/j.mechrescom.2012.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kroon W, Delhaas T, Arts T, Bovendeerd P. Computational modeling of volumetric soft tissue growth: application to the cardiac left ventricle. Biomech Model Mechanobiol. 2009;8(4):301–309. doi: 10.1007/s10237-008-0136-z. [DOI] [PubMed] [Google Scholar]
- Lee EH. Elastic-plastic deformation at finite strains. J Appl Mech. 1969;36(1):1–6. [Google Scholar]
- Lee LC, Wall ST, Klepach D, Ge L, Zhang Z, Lee RJ, Hinson A, Gorman JH, Gorman RC, Guccione JM. Algisyl-LVR with coronary artery bypass grafting reduces left ventricular wall stress and improves function in the failing human heart. Int J Cardiol. 2013;168(3):2022–2028. doi: 10.1016/j.ijcard.2013.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Legrice IJ, Hunter PJ, Smaill BH. Laminar structure of the heart: a mathematical model. Am J Physiol. 1997;272(5 Pt 2):76–H2466. doi: 10.1152/ajpheart.1997.272.5.H2466. [DOI] [PubMed] [Google Scholar]
- Levin H, Oz M, Chen J, Packer M, Rose E, Burkhoff D. Reversal of chronic ventricular dilation in patients with end-stage cardiomyopathy by prolonged mechanical unloading. Circulation. 1995;91(11):2717–2720. doi: 10.1161/01.cir.91.11.2717. [DOI] [PubMed] [Google Scholar]
- Madigan JD, Barbone A, Choudhri AF, Morales DL, Cai B, Oz MC, Burkhoff D. Time course of reverse remodeling of the left ventricle during support with a left ventricular assist device. J Thorac Cardiovasc Surg. 2001;121(5):902–908. doi: 10.1067/mtc.2001.112632. [DOI] [PubMed] [Google Scholar]
- Omens JH. Stress and strain as regulators of myocardial growth. Prog Biophys Mol Biol. 1998;69(2–3):559–572. doi: 10.1016/s0079-6107(98)00025-x. [DOI] [PubMed] [Google Scholar]
- Omens JH, McCulloch AD, Criscione JC. Complex distributions of residual stress and strain in the mouse left ventricle: experimental and theoretical models. Biomech Model Mechanobiol. 2003;1(4):267–277. doi: 10.1007/s10237-002-0021-0. [DOI] [PubMed] [Google Scholar]
- Omens JH, Vaplon SM, Fazeli B, Mcculloch AD. Left ventricular geometric remodeling and residual stress in the rat heart. J Biomech Eng. 1998;120:715–719. doi: 10.1115/1.2834884. [DOI] [PubMed] [Google Scholar]
- Opie LH, Commerford PJ, Gersh BJ, Pfeffer MA. Controversies in cardiology. Lancet. 2006;367(9519):1315. author reply 1315–6. [Google Scholar]
- Rausch MK, Dam A, Göktepe S, Abilez OJ, Kuhl E. Computational modeling of growth: systemic and pulmonary hypertension in the heart. Biomech Model Mechanobiol. 2011;10(6):799–811. doi: 10.1007/s10237-010-0275-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rodriguez EK, Hoger A, Mcculloch AD. Stress-dependent finite growth in soft elastic tissues. J Biomech. 1994;27(4):455–467. doi: 10.1016/0021-9290(94)90021-3. [DOI] [PubMed] [Google Scholar]
- Rutz AK, Ryf S, Plein S, Boesiger P, Kozerke S. Accelerated whole-heart 3D CSPAMM for myocardial motion quantification. Magn Reson Med. 2008;59(4):755–763. doi: 10.1002/mrm.21363. [DOI] [PubMed] [Google Scholar]
- Taber LA. Biomechanics of growth, remodeling, and morphogenesis. Appl Mech Rev. 1995;48(8):487–545. [Google Scholar]
- Taber LA. Biomechanics of cardiovascular development. Annu Rev Biomed Eng. 2001;3:1–25. doi: 10.1146/annurev.bioeng.3.1.1. [DOI] [PubMed] [Google Scholar]
- Taber LA, Chabert S. Theoretical and experimental study of growth and remodeling in the developing heart. Biomech Model Mechanobiol. 2002;1(1):29–43. doi: 10.1007/s10237-002-0002-3. [DOI] [PubMed] [Google Scholar]
- Wall ST, Walker JC, Healy KE, Ratcliffe MB, Guccione JM. Theoretical impact of the injection of material into the myocardium: a finite element model simulation. Circulation. 2006;114(24):2627–35. doi: 10.1161/CIRCULATIONAHA.106.657270. [DOI] [PubMed] [Google Scholar]
- Weis SM, Emery JL, Becker KD, McBride DJ, Omens JH, McCulloch aD. Myocardial mechanics and collagen structure in the osteogenesis imperfecta murine (oim) Circ Res. 2000;87(8):663–669. doi: 10.1161/01.res.87.8.663. [DOI] [PubMed] [Google Scholar]
- Wells SM, Walter EJ. Changes in the mechanical properties and residual strain of elastic tissue in the developing fetal aorta. Ann Biomed Eng. 2010;38(2):345–356. doi: 10.1007/s10439-009-9825-8. [DOI] [PubMed] [Google Scholar]
- Wenk JF, Eslami P, Zhang Z, Xu C, Kuhl E, Gorman JH, Robb JD, Ratcliffe MB, Gorman RC, Guccione JM. A novel method for quantifying the in-vivo mechanical effect of material injected into a myocardial infarction. Ann Thorac Surg. 2011;92(3):935–941. doi: 10.1016/j.athoracsur.2011.04.089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wenk JF, Klepach D, Lee LC, Zhang Z, Ge L, Tseng EE, Martin A, Kozerke S, Gorman JH, Gorman RC, Guccione JM. First evidence of depressed contractility in the border zone of a human myocardial infarction. Ann Thorac Surg. 2012;93(4):1188–1193. doi: 10.1016/j.athoracsur.2011.12.066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang X, Javan H, Ms LL, Ms AS, Bs RZ, Deng Y, Selzman CH. A modified murine model for the study of reverse cardiac remodelling. Exp Clin Cardiol. 2013;18(2):115–117. [PMC free article] [PubMed] [Google Scholar]