Intrinsic Islet Heterogeneity and Gap Junction Coupling Determine Spatiotemporal Ca²⁺ Wave Dynamics

Abstract

Insulin is released from the islets of Langerhans in discrete pulses that are linked to synchronized oscillations of intracellular free calcium ([Ca²⁺]_i). Associated with each synchronized oscillation is a propagating calcium wave mediated by Connexin36 (Cx36) gap junctions. A computational islet model predicted that waves emerge due to heterogeneity in β-cell function throughout the islet. To test this, we applied defined patterns of glucose stimulation across the islet using a microfluidic device and measured how these perturbations affect calcium wave propagation. We further investigated how gap junction coupling regulates spatiotemporal [Ca²⁺]_i dynamics in the face of heterogeneous glucose stimulation. Calcium waves were found to originate in regions of the islet having elevated excitability, and this heterogeneity is an intrinsic property of islet β-cells. The extent of [Ca²⁺]_i elevation across the islet in the presence of heterogeneity is gap-junction dependent, which reveals a glucose dependence of gap junction coupling. To better describe these observations, we had to modify the computational islet model to consider the electrochemical gradient between neighboring β-cells. These results reveal how the spatiotemporal [Ca²⁺]_i dynamics of the islet depend on β-cell heterogeneity and cell-cell coupling, and are important for understanding the regulation of coordinated insulin release across the islet.

Introduction

The islets of Langerhans are multicellular micro-organs that release insulin and glucagon to regulate blood glucose levels. After an elevation in blood glucose, a series of metabolic and electrical events regulate insulin release from β-cells. These include glucose metabolism to elevate cellular ATP levels, membrane depolarization after closure of ATP-sensitive potassium (K_ATP) channels, activation of L-type Ca²⁺ channels to elevate intracellular free calcium ([Ca²⁺]_i), and triggering of insulin granule exocytosis. Membrane depolarization and [Ca²⁺]_i are highly dynamic, with regular oscillations observed in the islet at elevated glucose levels (1).

β-cells within the islet are extensively coupled (2) via a number of mechanisms (3–5). Electrical coupling via connexin36 (Cx36) gap junctions coordinates oscillations in membrane potential and [Ca²⁺]_i at elevated glucose levels (3,6), and suppresses spontaneous [Ca²⁺]_i elevations at low glucose (3,5). The coordinated oscillations in electrical activity lead to pulsatile insulin release, which can enhance insulin action and is disrupted in patients with type 2 diabetes (7,8). Importantly, a disruption of the coordination of [Ca²⁺]_i oscillations after a loss of Cx36 gap junctions disrupts pulsatile insulin and glucose homeostasis (9). Similarly, in islets from mouse models of diabetes, the coordination of [Ca²⁺]_i oscillations (10) and gap junction coupling (11) is disrupted. Therefore, the coupling of islet electrical dynamics via gap junction channels is a necessary factor in the overall function of the islet and hence in the regulation of glucose homeostasis.

Propagating calcium waves are associated with the coordination of [Ca²⁺]_i oscillations (6,12). The propagation of these waves is highly dependent on the level of electrical coupling, and we previously quantified the relationship between wave velocity and gap junction conductance (6). Calcium waves consistently originated from a certain region in the islet, which was accurately described in our islet mathematical model. To reproduce wave propagation dynamics and its gap junction dependence, β-cell heterogeneity was required. When dissociated from the islet, β-cells show irregular and widely varying patterns of [Ca²⁺]_i oscillations and [Ca²⁺]_i responses (13), and factors such as glucose metabolism (14) and insulin release are also variable (15,16). Heterogeneity in [Ca²⁺]_i oscillations and responses is similarly observed in intact islets lacking gap junction coupling. Thus, it was predicted that calcium waves originate in a subregion of the islet that contains a higher proportion of excitable cells due to β-cell heterogeneity. The gap junction coupling of heterogeneous β-cells has been shown to be important to normalize the electrical response to glucose (17). Therefore, a combination of electrical coupling and β-cell heterogeneity may also be important to regulate the overall spatiotemporal [Ca²⁺]_i dynamics of the islet, including propagating calcium waves.

Here, we further investigated the spatiotemporal [Ca²⁺]_i dynamics and the role of β-cell heterogeneity and coupling. We introduced patterns of glucose stimulation across the islet using a microfluidic flow device to test how these defined perturbations affect the overall spatiotemporal dynamics. First, we tested whether the origin of the calcium waves is determined by a defined pattern of heterogeneity, and whether there is an intrinsic spatial heterogeneity of β-cell activity that regulates calcium wave propagation. Second, we tested how electrical coupling determines the extent of calcium wave propagation in the face of β-cell heterogeneity. In each case, we compared experimental results with the predictions of a multicellular computational model of islet electrical activity.

Materials and Methods

Animal care and islet isolation

All experiments were performed in compliance with relevant laws and institutional guidelines and were approved by the Vanderbilt University Institutional Animal Care and Use Committee. Generation of Cx36-LacZ knockout mice (Cx36^−/−) was described previously (18). Islets were isolated according to established protocols (19) from the pancreata of 12- to 24-week-old male mice. After pancreas dissection, collagenase digestion, and islet isolation, the islets were maintained in RPMI medium (plus 10% fetal bovine serum, 11 mM glucose, 100 U/ml penicillin, 100 μg/ml streptomycin) at 37°C under humidified 5% CO₂ for 24–48 h before imaging.

Electrophysiology

Measurements of β-cell junctional conductance were performed as previously described (20). Isolated islets were perfused with an extracellular solution (115 mM NaCl, 5 mM KCl, 3 mM CaCl₂, 2 mM MgCl₂, 10 mM HEPES, 2 mM glucose, pH 7.2). Membrane potentials and currents were monitored using the perforated-patch method (13). Pipettes were filled with an intracellular solution (11.8 mM NaCl, 28.4 mM K₂SO₄, 63.7 mM KCl, 1 mM MgCl₂, 20.8 mM HEPES, 0.5 mM EGTA, pH 7.2, plus 0.1 mg/ml amphotericin-B). After a GΩ seal was obtained on a patched β-cell, extracellular solution containing 100 μM tolbutamide was applied to generate changes in the membrane potential. The membrane potential was recorded in current-clamp mode and then the coupling current was measured in voltage-clamp mode at a holding potential of −65 mV. An extracellular solution containing 100 μM tolbutamide with 11 mM or 20 mM glucose was then applied. The coupling conductance (g_coup) at each glucose level was determined by the change in coupling current (ΔI_coup) divided by the change in membrane potential (ΔV).

Microfluidic devices

The gradient-generating microfluidic device used here was based on the two-channel design originally described by Rocheleau et al. (21). A positive-relief master was made via a direct milling procedure in which a negative-relief master was first milled into machinable wax using a programmable milling machine with a 1.0 μm precision end mill, and a positive-relief master was formed from the negative-relief master using two-part urethane epoxy (Master Dyna-Cast Fast-Cast urethane, Freeman, Avon, OH). Polydimethylsiloxane devices were fabricated as described previously (22). A two-part elastomer (Sylgard 184, Dow Corning, Midland, MI) was allowed to cure on the positive-relief master and irreversibly bonded to 1.5 coverglass, and input ports were connected to Tygon tubing (Cole-Palmer, Vernon Hills, IL).

Fluorescence microscopy

All imaging experiments were performed according to published procedures (17,23). To measure [Ca²⁺]_i dynamics, isolated islets were loaded for 1.5 h with 4 μM Fluo4-AM (Invitrogen, Carlsbad, CA) at room temperature in imaging solution (125 mM NaCl, 5.7 mM KCl, 2.5 mM CaCl₂, 1.2 mM MgCl₂, 10 mM HEPES, 2 mM glucose; 0.1% bovine serum albumin, pH 7.4) and equilibrated at 37°C for 10 min. The islets were imaged in the microfluidic flow device (maintained at 37°C) on an LSM5Live microscope (Zeiss, Jena, Germany) with a 20× 0.8NA Fluar objective, using a 488 nm diode laser for Fluo4 excitation and a 495–555 nm band-pass filter to detect fluorescence emission. A series of images were acquired 15 min after the application of each glucose pattern for a period of 2 min.

To measure NAD(P)H autofluorescence, islets were imaged on an LSM510-Meta confocal microscope (Zeiss) using a 710 nm mode-locked Ti:Sapphire laser (Chameleon; Coherent, Santa Clara, CA) for two-photon excitation, and 380–500 nm band-pass filter (Chroma, Rockingham, VT) to detect fluorescence emission. All microscope and laser settings were kept constant between experiments. The NAD(P)H intensity was averaged across the islet perpendicular to the glucose gradient and normalized to the mean NAD(P)H intensity at low (2 mM) glucose.

Image analysis

All experimentally measured and computer-modeled [Ca²⁺]_i dynamics were analyzed in MATLAB (The MathWorks, Natick, MA) and Image Examiner (Zeiss) according to published procedures (6). Briefly, a cross-correlation of the time course for each image pixel or modeled cell was taken against a time course from a reference cell in the islet. The time index for the peak cross-correlation value represents the relative time at which [Ca²⁺]_i elevates, and a map of this time index reveals the propagation of the wave from start to end (Fig. S1 in the Supporting Material). To calculate the wave speed, the spatial separation between the start and end of the wave was divided by the temporal separation. The wave direction was calculated visually from the map of time-index values. The wave direction was measured for each [Ca²⁺]_i oscillation, and waves were considered consistent if they propagated within a 90° arc. The [Ca²⁺]_i elevation was calculated from the difference in time-averaged [Ca²⁺]_i before and after glucose elevation, excluding transient effects. Upon a modeled glucose gradient, the distance of [Ca²⁺]_i propagation was calculated by the distance at which [Ca²⁺]_i elevations decreased to 50% of that at 11 mM glucose.

Computer modeling

The computational model is based on a coupled Hodgkin-Huxley model (24) that was modified to include improved glucose metabolism and β-cell heterogeneity for examination of calcium waves (6). The membrane potential (V) of a single, uncoupled β cell is a function of the total transmembrane current:

$$-C\frac{d{V}_i}{dt}=I_{K\left(V\right)}+I_{Ca\left(V\right)}+I_{K\left(ATP\right)}+I_{K\left(Ca\right)}$$ (1)

The kinetics of each transmembrane current is described in Benninger et al. (6) and references therein. Within the modeled islet, the membrane potential in the ith β-cell surrounded by j adjacent β-cells is

$$-C\frac{d{V}_i}{dt}=I_i+\sum _j{g}_{coup}^{\left(i,j\right)}\left(V_i-V_j\right)$$ (2)

where g^(i,j)_coup is the coupling conductance between cells i and j. The islet is modeled as a 10 × 10 × 10 islet cube such that the index j represents coupling to three to six adjacent cells (depending on position). The total coupling conductance of a β-cell is the sum of the conductance g^(i,j)_coup over j to all surrounding β-cells.

The K_ATP channel current I_K(ATP) is dependent on the ADP and ATP concentrations, the open channel conductance, and the membrane potential:

$$I_{K\left(ATP\right)}=o_{\infty }\left(ATP,ADP\right)g_{K\left(ATP\right)}\left(V-V_K\right)$$ (3)

$$\frac{dADP}{dt}=k_a^{-1}\left(ATP-ADP{e}^{\mathbf{r}\left(1-\frac{Ca}{r_1}\right)}\right)$$ (4)

where o_∞(ATP,ADP) represents the proportion of open K_ATP channels as a function of ATP and ADP levels (25). The metabolic flux through citric-acid-cycle metabolism that increases the cellular ATP/ADP ratio is described by the parameter r, which varies linearly with glucose concentration. The maximal r (1.3, equivalent to 11 mM glucose) was empirically determined to produce oscillations similar to those generated by an islet at uniform 11 mM glucose concentration. Ca is the intracellular free-calcium concentration ([Ca²⁺]_i) and k_a and r₁ are constants. We focus on electrical coupling of fast [Ca²⁺]_i oscillations after a step elevation from low (2 mM) to high (11 mM) glucose, and exclude terms describing metabolic feedback (25). β-cell and gap junction heterogeneity is represented by introducing random variation into the metabolic flux (r) and the gap junction conductance (g^(i,j)_coup) for each cell according to a Gaussian distribution with values below zero discarded (6). Multiple islets were modeled using different random number seeds.

An alternative model describing gap junction coupling was modified from that described by Kitagawa et al. (26). This model is based on the GHK approximation, where the difference in ionic concentrations between each cell and the difference in membrane potential between each cell are considered. As Na⁺ currents are neglected, only Ca²⁺ and K⁺ ions are considered. Equation 2 is modified to

$$-C\frac{d{V}_i}{dt}=I_i+\sum _j\frac{u_K{z}_{K}F{S}_G}{d_G}{N}_G^{\left(i,j\right)}\left(V_i-V_j\right)\left(\frac{K_i-K_j{e}^{-a{z}_{K}F\left(v_i-v_j\right)/RT}}{1-e^{-a{z}_{K}F\left(v_i-v_j\right)/RT}}\right)+\sum _j\frac{u_{Ca}{z}_{Ca}F{S}_G}{d_G}{N}_G^{\left(i,j\right)}\left(V_i-V_j\right)\left(\frac{C{a}_i-C{a}_j{e}^{-a{z}_{Ca}F\left(v_i-v_j\right)/RT}}{1-e^{-a{z}_{Ca}F\left(v_i-v_j\right)/RT}}\right)$$ (5)

where K_i is the intracellular potassium concentration ([K⁺]) and a, z_K, z_Ca, u_K, u_Ca, and F are constants. S_G and d_G approximate the area and length of the gap junction channel. N_G^(i,j) is the number of open channels between cells i,j. [K⁺] and [Ca²⁺]_i are determined by

$$\frac{d{K}_i}{dt}=-\left(\alpha I_{K\left(V\right)}+\alpha I_{K\left(ATP\right)}+\alpha I_{K\left(Ca\right)}-\alpha I_{coup\left(K\right)}+\alpha I_{K\left(in\right)}\right)$$ (6)

$$\frac{dC{a}_i}{dt}=f_c\left[-\left(\alpha I_{Ca\left(V\right)}-\alpha I_{coup\left(Ca\right)}+k_{PMCA}C{a}_i\right)+p_{leak}\left(C{a}_{ER}-C{a}_i\right)-k_{SERCA}C{a}_i\right]$$ (7)

where f_c, α, k_SERCA, p_leak, and k_PMCA are constants involved in [Ca²⁺]_i handling (6). In the steady state, to maintain ionic concentrations and membrane potential, inward K⁺ current is approximated as equal to inward voltage-gated Ca²⁺ current: $-I_{Ca\left(V\right)}=I_{K\left(in\right)}\cdot I_{coup\left(K\right)}$ and $I_{coup\left(Ca\right)}$ are the coupling currents mediated by K⁺ or Ca²⁺ ions, defined within the first and second summations of Eq. 5. To maintain consistency and facilitate comparisons between the original model (Eq. 2) and the revised model (Eq. 5) of gap junction coupling, N_G^(i,j) is set such that when two cells have equal ionic concentrations, Eq. 5 reduces to Eq. 2 with an equivalent g_coup, as in (26):

$$I_{coup\left(Ca\right)}+I_{coup\left(K\right)}=g_{coup}\left(V_i-V_j\right)$$ (8)

A list of all the parameters used in the model and their values is included in Table S1.

Results

Calcium wave propagation direction related to heterogeneity in the modeled islet

We previously observed propagating calcium waves in isolated pancreatic islets and in a multicellular islet model (6). Data showing how the observed spatiotemporal [Ca²⁺]_i dynamics are described by the islet model are summarized in Fig. S1. A similar range of wave velocities was measured in each case (30–160 μm/s vs. 60–150 μm/s, respectively) and the majority of waves propagated in a consistent direction (81% ± 3% and 92% ± 6%, respectively).

Heterogeneity between β-cells in the model was required to reproduce the observed spatiotemporal [Ca²⁺]_i dynamics (6,27). We introduced heterogeneity in glucose metabolism (r) as experimentally measured (14). To examine how cellular heterogeneity regulates calcium wave propagation, we examined the spatial distribution of heterogeneity using the computational model (with Eq. 2 describing gap junction coupling). Cells that coincided with the point at which the calcium wave originated had a higher glucose metabolism (high r) (Fig. 1, A and B). When the modeled cells were electrically isolated from the islet, those cells that were near the start of the wave showed elevated [Ca²⁺]_i and faster oscillations compared with cells at the end of the wave (Fig. 1 C), indicating enhanced excitability (see red traces). Over a number of modeled islets, the cells in the region where the wave originated had an average r parameter significantly larger than the islet average (1.77 ± 0.07 compared with 1.31 ± 0.01; Fig. 1 D), with the earliest cell showing the highest r (2.14 ± 0.14). In contrast, cells where the wave terminated had an r parameter similar to the islet average (1.26 ± 0.04 compared with 1.31 ± 0.01; Fig. 1 D). Waves propagated with a faster velocity when the excitability was more uniform across the propagation path between the start and end of the wave (Fig. 1 E).

Figure 1.

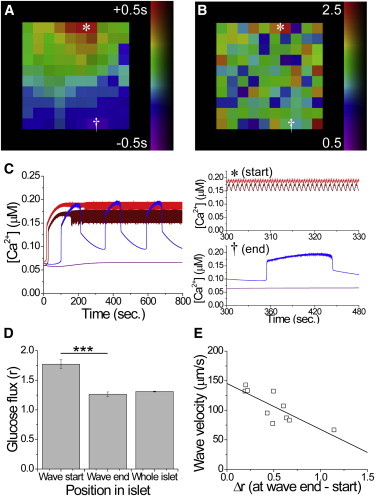
The computational islet model predicts that heterogeneity correlates with calcium wave propagation. (A) Representative phase map of the surface of a modeled islet, showing the temporal progression of wave propagation. (B) Map of the metabolic flux (r) at the surface in panel A. ^∗ and † indicate the start and end of a wave, respectively. (C) Representative time courses of [Ca²⁺]_i in cells corresponding to the start (^∗red) and end († blue) of the wave, indicated in A and B, when electrically isolated from the modeled islet. (D) Mean (± SEM) metabolic flux (r) in cells averaged over the start and end of the wave (n = 3–8 cells per region) and over the whole islet. (E) Correlation between the calcium wave velocity and the difference in glucose metabolic flux (Δr) between the start and end of the wave. The solid line indicates a linear fit. Equation 2 describes gap junction coupling. Data in D and E were averaged over 10 modeled islets. ^∗∗∗ indicates significant difference comparing each group indicated (p < 0.001, Student’s t-test). To see this figure in color, go online.

Due to heterogeneity, several β-cells distributed throughout the modeled islet could have high excitability (Fig. 1 B). Waves preferentially originated from cells with high r located at the side of the islet (∼90% modeled islets), with no islet exhibiting waves originating from the interior. In the cubic islet structure, waves did not originate preferentially from corners (∼10% modeled islets). We examined the probability of highly excitable cells being distributed close together at the edge of the modeled islet (Fig. S2). At the edge, ∼90% of modeled islets had a region of high average r (r > 1.77), ∼90% had two highly excitable cells (r > 2.14) neighboring each other, and ∼80% had multiple highly excitable cells ([Ca²⁺]_i oscillation period ≤1 s) clustered together. Therefore, in the islet model, calcium waves originated in a subset of cells with elevated excitability, which in this case was due to random heterogeneity in glucose metabolism.

Testing the role of heterogeneity and excitability in determining the wave direction

The data presented above suggest that calcium waves originate in areas of the islet where β-cells have elevated excitability. These local regions of elevated excitability arise due to random heterogeneity of β-cell electrical activity (5,6,13) and would not be readily observed in islets under normal conditions due to gap junctions coordinating [Ca²⁺]_i elevations (6,28). Thus, locally elevated excitability may be an intrinsic property of the islet and determine the origin of the calcium waves. To test this prediction, we introduced a local elevation in excitability using a previously developed two-channel microfluidic device (21). This device allowed glucose to stimulate different sides of the islet (Fig. 2 A) to elevate glucose metabolism in a specific region as measured by the NAD(P)H responses (Fig. 2 B, pattern ii or iii).

Figure 2.

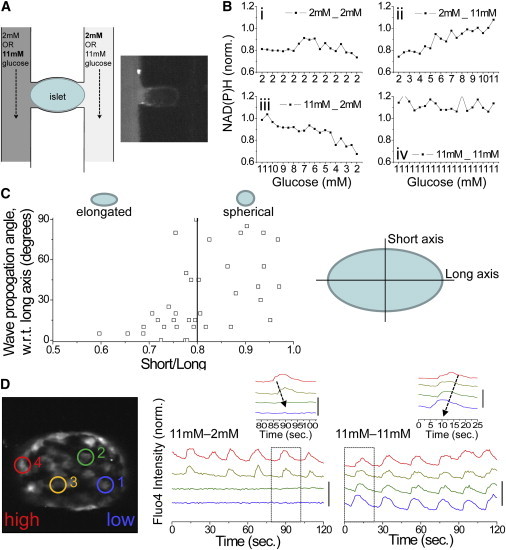
Testing the dependence of calcium wave propagation on islet heterogeneity via a glucose gradient. (A) Schematic of the islet and microfluidic device used. Inset shows Rhodamine B applied to a single channel, indicating no cross-talk. (B) Normalized (norm.) NAD(P)H response, indicating glucose metabolic flux across the islet under each glucose stimulation pattern used. The x axis indicates the estimated glucose. (C) Calcium wave direction with respect to the long axis of the islet, plotted as a function of islet elongation (short axis length/long axis length, where short/long = 1 represents a spherical islet). The solid line delineates islets with a long axis 25% greater than the short axis. (D) Representative time courses of [Ca²⁺]_i at positions indicated in the islet under a glucose gradient (11mM-2mM) and uniform elevated glucose (11mM-11mM). Inset: close-up of a single pulse, indicating the propagation of a calcium wave under each condition. Time courses are offset for clarity; vertical bar indicates a 50% increase in fluorescence. To see this figure in color, go online.

When glucose was uniformly elevated, calcium waves preferentially propagated along the long axis of elongated islets (long axis 25% greater than short axis) in 81% ± 9% of islets (Fig. 2 C). This was not observed in close-to-spherical islets. By utilizing elongated islets and the gradient-generating microfluidic device, the experiment reduces to a single dimension where we can test whether waves preferentially propagate toward or away from the region of elevated glucose. Fig. 2 D displays example time courses of [Ca²⁺]_i under a gradient of glucose (Fig. 2 B, pattern ii). As observed previously (21), only part of the islet showed synchronized oscillations. However, in the majority of cases, calcium waves propagated away from the side of the islet stimulated with elevated glucose (Figs. 2 D and 3 A). Thus, we could generate a region of elevated glucose metabolism to test our prediction regarding the origin of calcium wave propagation.

Figure 3.

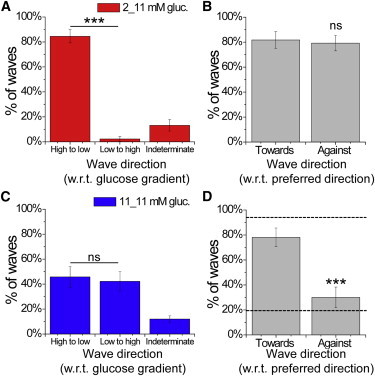
Experimental dependence of calcium wave propagation direction on intrinsic islet heterogeneity and applied heterogeneity. (A) Proportion of calcium waves that propagate with respect to an applied glucose gradient originating from the side at elevated glucose (high to low) or the side at low glucose (low to high), or in an unrelated direction (indeterminate). (B) Proportion of calcium waves under a glucose gradient that propagate with respect to the preferred wave direction at uniform glucose levels, where the gradient is applied toward or against the preferred direction. (C) Proportion of calcium waves under uniform elevated glucose that propagate with respect to a previously applied glucose gradient, as in A. (D) Proportion of calcium waves under uniform elevated glucose that propagate with respect to the preferred wave direction, where a gradient is previously applied toward or against the preferred direction. The dashed line indicates that the direction is solely determined by intrinsic cellular heterogeneity. Data in A and B were averaged over 22 islets. Data in C and D were averaged over 16 islets. ^∗∗∗ indicates significant difference comparing the indicated groups (p < 0.001 Student’s t-test). ns, no significant difference (p > 0.05). To see this figure in color, go online.

Heterogeneity in excitability determines the wave direction

In the majority of cases, calcium waves propagated from the side of the islet stimulated with elevated glucose, with minimal numbers propagating against this gradient (Fig. 3 A). To quantify the robustness of a locally elevated glucose metabolism in determining the wave direction, we reversed the direction of the glucose gradient and applied elevated glucose to the opposite side of the islet (Fig. 2 B). If the preferred wave direction under uniform glucose (pattern iv) originated from the region previously exposed to elevated glucose (pattern ii), we measured whether the direction of propagation was reversed by applying a glucose gradient in the opposite direction (pattern iii). In the majority of cases, the preferred wave direction could be switched (Fig. 3 B). There was no difference with respect to the direction of the applied glucose gradient (i.e., comparing patterns ii and iii). Thus, elevated glucose applied to a region of the islet can fully determine the origin and direction of calcium wave propagation.

After a gradient of glucose stimulation, a uniform elevation of glucose stimulation was applied (Fig. 2 B, pattern iv following pattern ii). This resulted in synchronized [Ca²⁺]_i oscillations with calcium waves propagating in a consistent direction (80.4% ± 4.2%), similar to what was seen with uniform elevated glucose (Fig. S1). In the example shown in Fig. 2 D, under uniform elevated glucose, the preferred calcium wave direction switched and originated in the region that was previously at low glucose. On average, there was no difference in the preferred wave direction with respect to the side previously stimulated by elevated glucose (Fig. 3 C). This suggests that under uniform stimulation, the calcium wave direction is not determined or biased by the prior heterogeneity in glucose stimulation (in this case, a gradient).

We next quantified how the robustness of the wave direction under uniform glucose is intrinsic to the islet and independent of the previous glucose gradient. If the preferred wave direction under uniform glucose (Fig. 2 B, pattern iv following pattern ii) originated from the region previously exposed to elevated glucose, we tested whether the direction could be reversed at uniform glucose levels after the application of a glucose gradient in the opposite direction (Fig. 2 B, pattern iv following pattern iii). We found that only in a small minority of cases could the preferred wave direction be switched (Fig. 3 D), similar to our finding that a minority of waves did not propagate in a consistent direction under normal uniform elevated glucose (Fig. S1). In the majority of cases, the waves propagated in a direction independent of the previous glucose gradient, with a consistency similar to that observed under normal uniform elevated glucose. The direction in which glucose was initially applied to generate a glucose gradient (i.e., in the left or right channel) did not cause any significant bias with respect to the subsequent preferred wave direction (Fig. S3). These data further show that the preferred calcium wave direction appears to be intrinsic to the islet.

Modeling the wave direction under a glucose gradient

We found experimentally that the calcium waves could not be altered by a previous heterogeneity (gradient) of glucose, in agreement with our prediction. To confirm and quantify the model prediction for a glucose gradient, we reproduced the experimental conditions described above using our islet model (with Eq. 2 describing gap junction coupling). We generated a gradient of glucose metabolism (r), applied a uniform level of glucose metabolism, and then measured the direction of calcium wave propagation in each case. We then switched the gradient direction across the islet.

Fig. 4 A displays example time courses of [Ca²⁺]_i under a gradient of glucose metabolism (pattern ii). As observed experimentally, only part of the modeled islet showed synchronized oscillations. In all cases, calcium waves propagated away from the side of the islet stimulated with elevated glucose metabolism (Fig. 4, A and B). The robustness of locally elevated glucose metabolism to determine the wave direction is similar to our experimental results, which showed that all calcium waves switched direction (Fig. 4 C). Under a subsequent uniform elevation of glucose metabolism, calcium waves propagated in a consistent direction (84.1% ± 6.1%) similar to that seen under conditions of normal uniform elevated glucose metabolism (Fig. S1). In the example shown in Fig. 4 A, upon uniform glucose metabolism, the calcium wave originated in the region that had previously experienced elevated glucose metabolism, i.e., the preferred wave direction was maintained. On average, we observed no difference in the preferred wave direction with respect to the side previously exposed to elevated glucose metabolism (Fig. 4 D). Similarly, the robustness to which the preferred wave direction under uniform glucose is intrinsic to the islet and independent of a previous glucose gradient is similar to our experimental results, which showed that the majority of waves did not switch direction (Fig. 4 E). The order in which the gradient was applied (left or right) did not induce any bias in the wave direction (Fig. S3). Thus, the computational model describes the experimental data (Fig. 3), suggesting that intrinsic heterogeneity in β-cell excitability is sufficient to determine calcium wave propagation direction independently of prior conditions.

Figure 4.

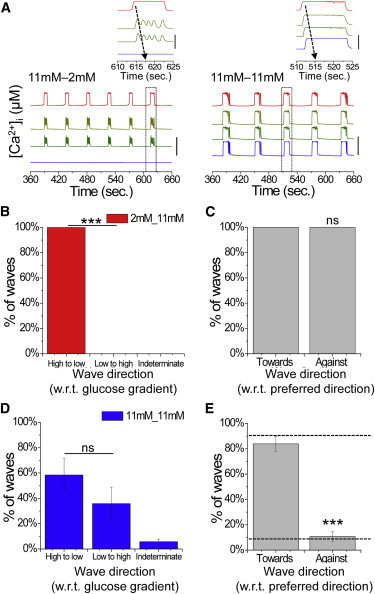
Computational model dependence of calcium wave propagation direction on islet heterogeneity. (A) Representative time courses of [Ca²⁺]_i at positions across the modeled islet under a gradient of glucose metabolism (11mM-2mM) and uniform elevated glucose metabolism (11mM-11mM). Inset: close-up of a single pulse, indicating the propagation of a calcium wave under each condition. Time courses are offset for clarity; vertical bar indicates a change of 0.1 μM. (B) Proportion of calcium waves that propagate with respect to an applied glucose metabolism gradient originating from the side at elevated glucose metabolism (high to low) or the side at low glucose metabolism (low to high), or in an unrelated direction (indeterminate). (C) Proportion of calcium waves under a gradient that propagate with respect to the preferred wave direction at uniform glucose metabolism, where the gradient is applied toward or against the preferred direction. (D) Proportion of calcium waves under uniform glucose metabolism that propagate in directions with respect to a previous gradient, as in B. (E) Proportion of calcium waves under uniform glucose metabolism that propagate with respect to the preferred wave direction, where a gradient is previously applied toward or against the preferred direction. The dashed line indicates that the direction is solely determined by intrinsic cellular heterogeneity. Equation 2 describes gap junction coupling. Data in B–E were averaged over 10 modeled islets. ^∗∗∗ indicates significant difference comparing the indicated experimental groups (p < 0.001, Student’s t-test). ns, no significant difference (p > 0.05). To see this figure in color, go online.

Gap junction regulation of wave propagation across a glucose gradient

Under a gradient of glucose stimulation, the calcium wave halted approximately halfway across the islet (Fig. 2 D), with a sharp transition between the coordinated pulsatile [Ca²⁺]_i and quiescent [Ca²⁺]_i (Fig. S4). Although gap junction coupling is important to mediate calcium wave propagation, gap junctions also mediate a suppression of spontaneous [Ca²⁺]_i elevations at low glucose. The sharp transition was proposed to arise from a balance of these two processes (21).

To test this, we measured [Ca²⁺]_i in Cx36^−/− islets where β-cells lack electrical coupling. Cx36^−/− islets show heterogeneous behavior similar to that seen in dissociated β-cell preparations, indicating that gap junctions mediate a suppression of activity via coupling of excitable and inexcitable cells (5). Under a glucose gradient, uncoordinated [Ca²⁺]_i oscillations were observed partially across the islet (Fig. 5 A). Under subsequent uniform elevated glucose, those cells that were inactive became active, yielding similar [Ca²⁺]_i oscillations as in Cx36^−/− islets under uniform elevated glucose (6). In wild-type (WT) islets, [Ca²⁺]_i oscillations and propagating waves occurred across ∼40% of the islet, which is equivalent to a glucose level of ∼7.4 mM (Fig. 5 B), consistent with previous observations (21). In Cx36^−/− islets, uncoordinated [Ca²⁺]_i oscillations occurred significantly farther across the islet, halting at a position corresponding to a glucose level of ∼4.9 mM (Fig. 5 B). Therefore, gap junction coupling halts [Ca²⁺]_i oscillations and propagating waves under a glucose gradient, with reduced coupling allowing [Ca²⁺]_i to propagate farther into the islet.

Figure 5.

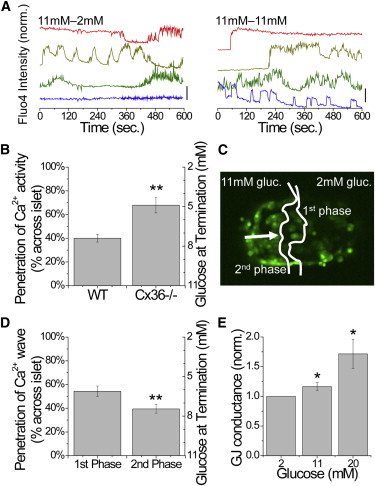
Gap junction dependence of [Ca²⁺]_i under a glucose gradient. (A) Representative time courses of [Ca²⁺]_i across a Cx36^−/− islet under a glucose gradient (11mM-2mM) and uniform elevated glucose (11mM-11mM). Time courses are offset for clarity; vertical bar indicates a 50% increase in fluorescence. (B) Mean (± SEM) distance across the islet, with equivalent glucose levels, at which [Ca²⁺]_i oscillations propagate in WT islets and Cx36^−/− islets. (C) Representative islet indicating the extent to which the initial [Ca²⁺]_i elevation (first phase) and the subsequent calcium waves (second phase) propagate. (D) Mean (± SEM) distance across the islet, with equivalent glucose levels, at which each phase of [Ca²⁺]_i elevation propagates. ^∗∗ indicates significant difference comparing each group in B and D as indicated (p < 0.01, Student’s t-test). (E) Coupling conductance as a function of glucose, normalized to the conductance at 2 mM glucose. ^∗ indicates significant elevation (p < 0.05). To see this figure in color, go online.

Interestingly, as a glucose gradient was established in WT islets, the initial first-phase elevation of [Ca²⁺]_i propagated farther (54% ± 4%) than the subsequent second-phase calcium waves (40% ± 4%; Fig. 5, C and D). As the propagation distance is gap junction dependent, this suggests that glucose elevates the coupling conductance to further halt calcium wave propagation. This is supported by measurements of the coupling conductance in a patched β-cell, where the conductance increased by 17% ± 4% as glucose was elevated from 2 to 11 mM glucose (1.06 ± 0.05 to 1.23 ± 0.04 nS), and by 83% ± 32% as glucose was elevated from 2 to 20 mM glucose (Fig. 5 E). These results are consistent with gap junction coupling regulating the extent of wave propagation across the islet in the presence of a glucose gradient.

Modeling calcium activity across the islet under a glucose gradient

The multicellular islet model can describe the dependence of calcium wave propagation on β-cell heterogeneity. We next tested whether it could describe the [Ca²⁺]_i response upon applied β-cell heterogeneity and variation in gap junction coupling. Previous studies have not been able to fully describe the islet [Ca²⁺]_i dynamics after a glucose gradient (29). The above experimental measurements demonstrate a sharp transition between coordinated activity and quiescence occurring over one to two cells (Fig. S4) (21). In the islet model (with Eq. 2 describing gap junction coupling), a sharp transition in [Ca²⁺]_i was well described upon a gradient in glucose metabolism (Fig. 6 A).

Figure 6.

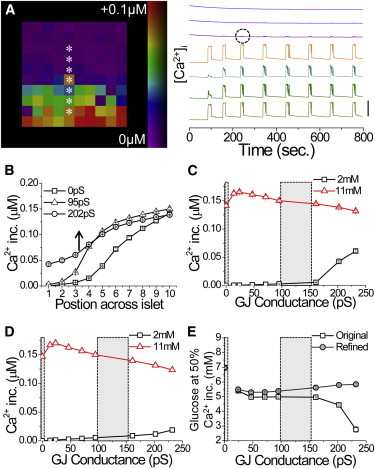
Modeling the dependence of the [Ca²⁺]_i response on gap junction coupling under a glucose gradient. (A) Map of [Ca²⁺]_i elevation upon a gradient of glucose metabolism, with [Ca²⁺]_i time courses from cells indicated by ^∗. Time courses are offset for clarity; vertical bar indicates a change of 0.1 μM. Excitation bleed-through is circled. (B) Mean [Ca²⁺]_i response across the islet for different levels of gap junction conductance (mean values indicated). (C) Mean [Ca²⁺]_i response as a function of gap junction conductance, at positions across the islet equivalent to the glucose concentrations indicated. (D) Mean [Ca²⁺]_i response as a function of gap junction conductance as in D, for the model accounting for the gap junction electrochemical gradient. (E) Equivalent glucose concentration at which the [Ca²⁺]_i response is 50% of the maximum, as a function of gap junction conductance for the original model (original) and improved model (refined). In C–E, areas in gray correspond to Cx36^−/− and WT gap junction conductance values. A–C and E utilize Eq. 2, and D and E utilize Eq. 5 to describe gap junction coupling. To see this figure in color, go online.

Above, in the presence of gap junction coupling, the wave propagation retracted to halt at higher levels of glucose compared with the absence of gap junction coupling. In the model, increasing gap junction coupling caused the wave to propagate progressively farther into the islet and led to elevated [Ca²⁺]_i at the side of the islet at 2 mM glucose (Fig. 6, B and C). This is in contrast to experimental measurements. Therefore, adding purely electrical coupling between β-cells does not describe the [Ca²⁺]_i response accurately under spatially varying β-cell heterogeneity (glucose gradient), and shows a propagation of stimulated activity instead of a suppression of activity.

To better describe the experimental measurements, we included an electrochemical gradient across the gap junction (26), rather than a purely electrical gradient (with Eq. 5 now describing gap junction coupling). Thus, gap-junction-mediated Ca²⁺ and K⁺ currents also depend on the respective [Ca²⁺]_i and [K⁺] gradients. [K⁺] changes upon elevated glucose were very small (<0.01%), but given the high intracellular concentration (∼100 mM), the differences between cells were still substantial. With this modification, calcium wave propagation velocity and consistency were maintained (Fig. S5). Under uniform glucose metabolism, waves still originated from regions of increased r (Fig. S5), and the r in regions where the waves ended was not significantly different from the islet average. Increasing gap junction conductance maintained low [Ca²⁺]_i at the side of the islet at 2 mM glucose while slightly decreasing [Ca²⁺]_i at the positions equivalent to elevated (>7 mM) glucose (Fig. 6 D). As a result, [Ca²⁺]_i oscillations propagated less into the islet compared with the original islet model (Fig. 6 E). Calcium waves halted at progressively higher glucose levels as gap junction conductance increased (Fig. 6 E), as suggested by experimental results. This is in contrast to the original islet model, in which calcium waves propagated farther into the islet to halt at lower glucose levels as gap junction conductance increased. However, at very low coupling conductances, [Ca²⁺]_i oscillations propagated less into the islet, in disagreement with experimental measurements. Therefore, although electrochemical gradients are not required to describe propagating waves under uniform glucose stimulation, accounting for electrochemical gradients across the gap junction allowed the islet model to better describe the dependence of [Ca²⁺]_i on gap junction coupling under a spatially varying heterogeneity (glucose gradient).

Discussion

Coupled electrical dynamics triggered by elevated glucose metabolism are a key feature of pancreatic islet function. Gap junction coupling is important for the regulation of islet electrical activity, insulin secretion, and glucose homeostasis (3,5). Previously, we described the coupled islet electrical dynamics and their dependence on gap junction coupling with computational models (6), which generated specific testable predictions. In this study, we tested these predictions to examine how the coupled electrical dynamics are regulated in the islet in the face of β-cell heterogeneity. In doing so, we further refined our multicellular islet model to better describe the regulation of electrical dynamics in the islet in quantitative detail over a wide range of experimental perturbations.

Elevated excitability determines the calcium wave origin

We predicted that calcium waves emerge from subregions of the islet that have elevated excitability and propagate via gap junctions across the islet. To test this prediction, we utilized microfluidic technology to locally elevate glucose metabolism and excitability, and determined how this affected the generation of propagating calcium waves (Fig. 2). We found that locally elevated excitability could determine the origin of the calcium wave, and that the origin of calcium waves was an intrinsic property of the islet (Fig. 3). This was in quantitative agreement with a computational model of this perturbation experiment (Fig. 4), verifying our prediction.

These results can explain why calcium waves propagate in a consistent direction, suggesting that their origin corresponds to a set of cells with elevated excitability. This also suggests that these excitable cells form a so-called pacemaker region of the islet that controls the electrical dynamics across the whole islet. Our data do not suggest a specialized pacemaker region, but rather a region determined randomly by the distribution of excitable β-cells within the islet, as applied in our multicellular model. β-cells isolated from the islet (13) or electrically uncoupled by a deletion of Cx36 (6) are heterogeneous, showing different [Ca²⁺]_i oscillation patterns and responses to elevated glucose. To reproduce realistic calcium wave velocities, this heterogeneity is required in the modeled islet (6,27). We examined the random distributions of highly excitable cells and found that the proportion of modeled islets with a cluster of highly excitable cells or an area of high excitability at the edge of the islet (80–90%; Fig. S2) was similar to the probability of waves propagating with a consistent direction in experimental measurements (78–85%; Figs. 2 C, 3 D, and S1C) and modeled islets (84–92%; Figs. 4 E and S1C). Therefore, the simplest explanation is that the pacemaker region arises due to the random distribution of excitability. However, we cannot exclude the possibility that distributions of excitability may arise during islet development or as a result of proximity to other islet cells that modulate excitability.

Our model also demonstrates that calcium waves consistently arise from β-cells at the edge of the islet. Although experimental data suggest that this occurs (Figs. 2 and 3), we are unable to image β-cells within the intact islet to demonstrate this unequivocally. However, a recent study using pancreas slice preparations demonstrated that membrane potential and calcium waves do originate at the islet edge (30), consistent with the presence of a randomized pacemaker region as predicted by our model.

In this study, we only considered heterogeneity in glucose metabolism, similar to that measured in previous experimental studies (14). This was sufficient to describe the observed [Ca²⁺]_i dynamics; however, heterogeneity in other factors, such as K_ATP channel expression, could also be present (5). Although the factor(s) underlying the variability in uncoupled β-cells remains to be fully determined, the approaches used here may prove valuable for examining the impact of heterogeneous cell pollutions within the intact coupled islet.

Describing spatial variation in β-cell electrical activity

After an applied glucose gradient, we observed a sharp transition between an area of coordinated [Ca²⁺]_i oscillations and an area of quiescent [Ca²⁺]_i (21). The transition occurred at a position equivalent to ∼7.4 mM glucose, which is the level at which islets start to show synchronous [Ca²⁺]_i oscillations. The transition showed a dependence on gap junction coupling, such that [Ca²⁺]_i oscillations propagated farther (albeit uncoordinatedly) in islets lacking gap junction coupling. This is consistent with the lower level of glucose at which spontaneous [Ca²⁺]_i occurs in Cx36^−/− islets and dissociated β-cells (5). It is likely that the absence of a coupled hyperpolarizing current from less active β-cells allows more excitable cells to show spontaneous [Ca²⁺]_i (5). Thus, upon a glucose gradient, gap junctions limit the propagation of calcium waves into regions of low glucose and low excitability by coupling hyperpolarizing current from cells in this region toward the more active cells near the transition.

The relationship between wave propagation distance and coupling conductance can also explain the variability in the wave propagation distance with time. Gap junction conductance elevates with increasing glucose (Fig. 5), which would limit the wave propagation distance. The initial first-phase calcium wave propagates farther into the islet, which is consistent with a lower coupling conductance than during the second phase propagation. This suggests that the time course for glucose modulating gap junction coupling is of the order of several minutes, consistent with previous studies that indicated a glucose dependence of gap junction coupling (31).

Previous studies utilizing computational modeling have been unable to describe the sharp transition observed upon a glucose gradient, as well as the dependence of this transition on gap junction conductance (29). Therefore, we still do not precisely understand how gap junctions couple electrical activity in the presence of spatially heterogeneous excitability. Our results reproduce the sharp transition observed experimentally, occurring over one or two cells (Figs. 6 and S4). Therefore, the heterogeneity in β-cell excitability and electrical coupling conductance is an important factor in how β-cells coordinate [Ca²⁺]_i oscillations and waves under spatially heterogeneous stimulation (32). However, this level of modeling is still insufficient to reproduce the gap junction dependence we experimentally measure. To describe the increased [Ca²⁺]_i propagation distance as gap junction coupling is reduced, the coupling term in the model requires an electrochemical gradient.

Inclusion of the electrochemical gradient across gap junctions better describes the suppression and limited propagation of calcium waves. Less excitable cells in the low-glucose region have lower [Ca²⁺]_i, higher [K⁺], and lower V_m compared with the more excitable cells at the transition. For these less excitable cells, the electrochemical gradient increases K⁺ outflux via gap junctions due to the higher [K⁺], but increases Ca²⁺ influx via gap junctions due to the lower [Ca²⁺]_i. These changes respectively hyperpolarize or depolarize the cells, which halt or enhance calcium wave propagation. Our results therefore suggest that the K⁺ electrochemical gradient has a greater impact in halting wave propagation. Although the relative changes in [K⁺] are very low, the resting [K⁺] levels are high; therefore, even very small changes likely affect the gap junction current and halt wave propagation into the low-glucose region. Such effects likely play a role in gap junction coupling upon large spatial variations in stimulation or cellular excitability.

Recent studies have provided alternative insights into gap-junction-mediated suppression of excitable cells, including a description of the gap junction suppression of [Ca²⁺]_i resulting from K_ATP channel loss-of-function mutations (33). In addition, other currents may be missing from the model that might better reproduce experimental measurements, such as those that better describe β-cell activity under nonstimulatory conditions. However, we find that a recent, more complete ion channel model (34,35) yields similar results upon a glucose gradient (M.J.Westacott and R.K.P.Benninger, unpublished data). In addition, we still observe a discrepancy in the model at zero coupling conductance, where reduced activity is observed. However, we do not include any stochastic effects in the model, since their inclusion has been shown to elevate [Ca²⁺] in β-cells (36). Therefore, heterogeneity in cellular activity and coupling is sufficient to describe islet spatiotemporal dynamics under normal physiological conditions. However, under perturbations that impose a spatial varying heterogeneity in cellular activity that exceeds physiological variations, a modified description of gap junction coupling (as we show here) or another factor is required.

Physiological relevance

Our results also provide further insight into the physiological function of the islet. One finding from this study is that a randomly determined pacemaker region controls the origin of calcium waves. Although this pacemaker region may change over time, it may significantly impact the control of islet oscillations. Upon a single-sided glucose stimulation, we (Fig. 2) and others (21) found that the oscillation period is similar to that under uniform stimulation. This suggests that the region with increased excitability at 11 mM glucose determines the [Ca²⁺]_i oscillation period for the rest of the islet that is stimulated. Therefore, factors that preferentially modulate more excitable cells at elevated glucose may have a disproportionate effect on the overall islet dynamics and response. This may be important when considering that immature β-cells have an altered glucose threshold for insulin secretion (37), and these occur with varying numbers in the adult islet (38), which may change under certain physiological or pathophysiological conditions.

We also found that the gap junction coupling conductance is glucose dependent, with elevated glucose increasing the coupling conductance. This increases the coordination of electrical activity within the islet, which would speed up calcium wave propagation and better synchronize [Ca²⁺]_i oscillations and pulsatile insulin release. This is similar to recent work showing that GLP1 better synchronizes [Ca²⁺]_i oscillations (39). In other systems, Cx36 gap junctions are regulated by multiple factors (40,41); however, this regulation is poorly understood within the islet. Further, with the inclusion of an electrochemical gradient across the gap junctions, the coupling current is [Ca²⁺]_i and [K⁺] dependent. As discussed above, even very small changes in cytosolic [K⁺] may play a significant role in affecting the suppressive effect of gap junctions across the islet.

Conclusions

In summary, we have shown that calcium wave propagation in the islet is determined by a subset of excitable cells, which can be overcome by stimulating a subregion with elevated glucose. This behavior can be described using a coupled β-cell model that requires random heterogeneity in β-cell excitability and coupling. The response to a spatial varying pattern of excitability and its dependence on gap junction coupling can only be described computationally by including a description of an electrochemical gradient in coupling. This better describes the coupled spatiotemporal [Ca²⁺]_i dynamics, which are important for regulating the dynamics of insulin release, and provides insight into how subsets of cells may disproportionately impact overall islet function.