Mechanics of Individual Keratin Bundles in Living Cells

Abstract

Along with microtubules and microfilaments, intermediate filaments are a major component of the eukaryotic cytoskeleton and play a key role in cell mechanics. In cells, keratin intermediate filaments form networks of bundles that are sparser in structure and have lower connectivity than, for example, actin networks. Because of this, bending and buckling play an important role in these networks. Buckling events, which occur due to compressive intracellular forces and cross-talk between the keratin network and other cytoskeletal components, are measured here in situ. By applying a mechanical model for the bundled filaments, we can access the mechanical properties of both the keratin bundles themselves and the surrounding cytosol. Bundling is characterized by a coupling parameter that describes the strength of the linkage between the individual filaments within a bundle. Our findings suggest that coupling between the filaments is mostly complete, although it becomes weaker for thicker bundles, with some relative movement allowed.

Introduction

The cytoskeleton of eukaryotes consists of microtubules, actin filaments, and intermediate filaments (IFs) along with associated binding proteins and motor proteins (1). It is believed that among these filamentous proteins, IFs provide resilience against mechanical forces and ensure cellular integrity. Whereas actin and tubulin proteins are highly conserved between different cell types and different organisms, IFs vary from cell type to cell type and are thought to reflect different mechanical properties (2). Mechanical resistance is particularly important for epithelial cells, which are constantly exposed to forces and stresses. In these cells, keratins are the primary type of IFs. In vitro experiments have shed light on the mechanical properties of keratin intermediate filaments (KIFs). For example, 10-nm-diameter KIFs adsorbed on a substrate and investigated using electron microscopy (EM) have a persistence length in the range between 0.30 and 0.48 μm in the absence or presence of magnesium ions, respectively (3), and keratin gels, like other biopolymer networks, show strain stiffening (4). Further studies have revealed that IFs are highly extensible, up to a factor of about 3 (5,6).

In cells, KIFs tend to form networks of bundles, in contrast to, e.g., vimentin, which forms more fine-meshed, highly connected networks. This aspect has also been addressed in in vitro experiments, and it has been shown that KIF bundling can be initiated and influenced by the addition of salts. In vivo, however, keratin-associated proteins add further regulating functions (7–9).

In contrast to in vitro experiments, probing the mechanical properties of specific proteins and structures in living cells is more challenging. This is due to the higher complexity and the large number of interactions present in a cell. Nevertheless, previous studies have revealed that in vivo KIFs form complex networks of bundles that enhance the mechanical stability of the cell (10,11). Recent experiments show that keratin networks play a key role in epithelial cell integrity and stiffness. For example, atomic force microscopy (AFM) and magnetic tweezers experiments have revealed that keratin-deficient cells are much softer than wild-type cells (12). Along the very same lines, keratin-knockout cells have a deformability that is ∼60% higher than deformability reported for cells with an intact keratin network (13).

Whereas the studies mentioned investigated the mechanical properties of whole cells depending on an intracellular keratin network, little is known about the mechanical properties of the bundles that make up the networks themselves. Here, we address this question by studying buckling events of keratin (K8/K18) bundles in living cells. We thus obtain information about the mechanical properties of the individual bundles in their natural environment, the surrounding cytoplasm. In the applied model we account for the distinct architecture of the bundles and the coupling between individual filaments.

Materials and Methods

Cell culture

The SK8/18-2 cell line, which was derived from human adrenal cortex carcinoma SW-13 cells (ATCC CCL-105) and then stably transfected to express fluorescent human keratin hybrids (HK8-CFP and HK18-YPF) (10,14,15), was kindly provided by Rudolf Leube (Rheinisch-Westfälische Technische Hochschule, Aachen, Germany). Cells were seeded on culture dishes in high-glucose (4.5 g/L) Dulbecco’s modified Eagle’s medium (PAA Laboratories, Pasching, Austria) supplemented with 10% fetal calf serum (Life Technologies, Carlsbad, CA) and 100 U/mL penicillin and 0.1 mg/mL streptomycin (Sigma-Aldrich, St. Louis, MO). The cells were maintained at 37°C in a water-saturated atmosphere at 5% CO₂.

Live cell microscopy

Time-lapse movies of living cells were acquired using an Olympus (Hamburg, Germany) IX81 FV1000 confocal microscope equipped with a 100×, 1.4 NA oil immersion objective. During the experiment, the cells were kept in cell culture medium at 37°C in a water-saturated atmosphere at 5% CO₂ using a top-stage incubation chamber (INUG2E-ONICS, Tokai Hit, Shizuoka-ken, Japan).

Electron microscopy

SK8/18-2 cells were fixed by adding to the culture medium 2× concentrated fixative (8% formaldehyde, 5% glutaraldehyde in 0.1 M phosphate buffer, pH 7.3). After removal of the supernatant after 5 min, the fixation was continued with 4% formaldehyde and 2.5% glutaraldehyde in 0.1 M phosphate buffer, pH 7.3 for at least 4 h. The cells were then postfixed in 1% OsO₄ (Science Services, Munich, Germany) in 0.1 M phosphate buffer and embedded in Epon (Serva, Heidelberg, Germany) after dehydration with ethanol and en bloc staining with 1.5% uranyl acetate (Merck, Darmstadt, Germany) and 1.5% tungstophosphoric acid (Merck) in 70% ethanol. Ultrathin sections of cultured cells were cut parallel to the substrate using an Ultracut S Ultramicrotome (Leica, Vienna, Austria) and stained with an aqueous solution of 4% uranyl acetate followed by lead citrate (16). Sections were analyzed with a LEO EM912 Omega (Zeiss, Oberkochen, Germany), and digital micrographs were obtained with an on-axis 2048 × 2048-CCD camera (TRS, Moorenweis, Germany).

Determination of bundle diameters

The raw confocal microscopy images (Fig. 1 a) were convoluted with a Gaussian filter to reduce noise. In a subsequent step, the images were binarized and the keratin structure was thinned to a one-pixel line using MATLAB algorithms. Fig. 1 b shows the filtered image together with the calculated spline fit to the one-pixel line and marked positions where the curvature has local maxima. We then extracted the intensity profiles of lines perpendicular to the spline curve and fitted Gaussian functions to these profiles. The result is shown in Fig. 1 c, where the red bars correspond to the full widths at half-maximum (FWHMs) and the yellow circles mark the maxima of the Gaussians. The same procedure was followed for fluorescent beads of similar and known diameters to calculate a correction term (offset between the real diameter and the apparent diameter in the fluorescence images) for the point-spread function in the fluorescent images. The subtractive correction term was finally used to obtain the actual bundle widths.

Figure 1.

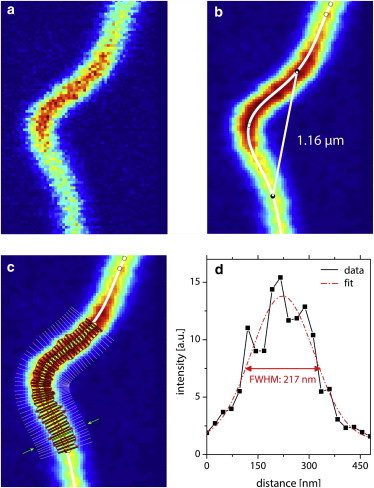
Determination of bundle diameters. The raw confocal image of a buckling event (a) was filtered with a Gaussian function (b) to reduce noise and was then processed to obtain a spline fit, which was then used to determine the buckling wavelength (see details in text). In a subsequent step, we extracted intensity profiles along lines perpendicular to the spline curve and fitted Gaussians to them. (c) Red bars correspond to the FWHMs of each Gaussian fit, with centers located at the yellow circles. (d) As an example, we show one of those fits, which corresponds to the bar indicated by the green arrows in c. To see this figure in color, go online.

Results

When a compressive force is applied along the long axis of an elastic rod, Euler buckling occurs and the rod is bent into one arc extending over its full length, as shown in Fig. 2 a, I and II (17). If the rod is embedded in an elastic matrix, the buckling wavelength, λ, decreases (Fig. 2 a, III) (18). The change in buckling wavelength in the presence of a constraining surrounding matrix can be understood by considering the additional energy consumption needed for the deformation of the elastic matrix. As a consequence, it is energetically favorable for the rod to buckle with a shorter wavelength. For a description of such constrained Euler buckling, the bending and compression energy of the rod and the elastic deformation energy of the surrounding matrix are taken into account. By solving the energy equation, Brangwynne et al. found that the buckling wavelength is given by λ = 2π (κ/α)^1/4, where κ represents the bending rigidity of the rod and $\alpha =4\pi G/\text{ln}\left(l/a\right)$ is a measure for the shear modulus, G, of the environment, where G = E_SM/(2(1 + ν)) is defined by the elastic modulus of the surrounding medium, E_SM, and Poisson’s ratio, ν. Here, l is the characteristic length scale of the buckling and a is of the order of the rod radius (18). Refined models have been developed that treat the surrounding matrix as a viscous or viscoelastic material (19,20). The model was further enhanced by allowing for nonlinear mechanical properties of the environment and explicit longitudinal coupling between the rod and the medium (21). This work shows that the buckling wavelength itself, which is the quantity we measure in our experiments, is not influenced by these additional contributions.

Figure 2.

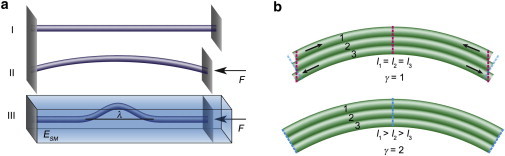
(a) An elastic rod buckles when it is compressed along its long axis by a force F (I and II). This leads to Euler buckling, where the arc extends over the whole length of the rod (II). The buckling behavior changes when the rod is surrounded by an elastic material (III). The resulting wavelength, λ, depends on the shear modulus of the surrounding matrix, G, and the persistence length of the rod, L_P. (b) This model is also applicable when the rod consists of several subrods that are able to slide against each other to a certain degree. Shown are the two limiting cases: completely uncoupled subrods (γ = 1) that can move and keep their initial length (upper), and fully coupled subrods (γ = 2), which have to adjust their length when the whole rod is bent (lower). To see this figure in color, go online.

Brangwynne et al. observed and described buckling events in intracellular microtubules (18,22), which are hollow cylinders formed from tubulin subunits. In a similar way, in time-lapse movies of KIFs, we observe buckling events (see Movie S1 in the Supporting Material), which are caused by intracellular compressive forces. In this case, the rods have a substructure consisting of individual filaments. We therefore extend the model and account for the unknown degree of coupling of the filaments. The bending rigidity of a semiflexible rod is linked to the persistence length, L_P, via κ = L_Pk_BT, which can also be expressed in terms of the elastic modulus of the rod, E, and the area moment of inertia, I, by κ = EI. In bundles of filaments, the persistence length of the bundle, L_PB, is related to the persistence length of an individual filament, L_PF, by L_PB = L_PFN^γ. Here, N represents the number of filaments, and the coupling parameter, γ, can range between 1 (no coupling) and 2 (complete coupling) (23). That is, in the limit of no coupling it is implied that individual filaments are allowed to slide with respect to each other (Fig. 2 b), and the persistence length of the bundle is a sum of the persistence lengths of all contributing filaments, $L_{\text{PB}}={\sum }_{i=1}^N{L}_{\text{PF},i}=N{L}_{\text{PF}}$. In the limit of full coupling, all filaments in a bundle act together as a unit, so that the persistence length is expressed by the radius of the bundle, R_B: $L_{\text{PB}}=\frac{\kappa }{k_{\text{B}}T}=\frac{E{I}_{\text{B}}}{k_{\text{B}}T}=\frac{E\frac{\pi }{4}{R}_{\text{B}}^4}{k_{\text{B}}T}$. The cross-sectional area of the bundle, in turn, is connected to the area of a single filament, $\pi R_{\text{B}}^2=N\pi R_{\text{F}}^2$, yielding L_PB = N²L_PF. For intermediate coupling, the persistence length of the bundle ranges between these two limits (γ ∈ [1,2]).

Combining the equations above, we obtain

$$\lambda =2\pi {\left(\frac{N^{\gamma }{L}_{\text{PF}}{k}_{\text{B}}T}{\alpha }\right)}^{1/4},$$ (1)

and can separate the coupling parameter γ from the elasticity of the surrounding matrix and the filament persistence length L_PF:

$$\begin{array}{l}\text{ln}\left({\lambda }^{\ast }\right)=\frac{1}{4}\gamma \text{ln}\left(N\right)+\text{const},\hfill \\ \text{const}=\frac{1}{4}\text{ln}\left(L_{\text{PF}}^{\ast }{k}_{\text{B}}^{\ast }{T}^{\ast }\right)+\text{ln}\left(2\pi \right)-\frac{1}{4}\text{ln}\left({\alpha }^{\ast }\right),\hfill \end{array}$$ (2)

where asterisks indicate dimensionless parameters (e.g., λ^∗ = λ/λ₀, λ₀ = 1 m).

With this adapted model, we evaluate our experimental data of buckling events in KIF bundles inside living cells, an example of which is shown in Fig. 3, a and b, and an animated version of which can be found in the Supporting Material (Movies S1 and S2). In Eq. 1, L_PF and α are material parameters known from the literature, λ and N are derived from the experiments, and the coupling parameter γ can subsequently be determined. To ensure reproducibility, we automatically evaluate the buckling wavelength, λ, of the manually identified buckling events using MATLAB scripts. Here, one-pixel lines of the keratin bundles are extracted from binarized images and fitted by a spline function. The wavelength λ is determined as the distance between the maxima in curvature of the spline. Buckling is a result of compressive forces, and it is therefore essential to omit bending events that are caused, e.g., by pulling forces from our analysis. To this end, we identify buckling as occurrences, where the network shows local compression and the contour of the bent bundle has three distinct turning points (Fig. 2 a). By contrast, we exclude data where the curvature remains unchanged over the length of the bundle. In addition, we focus on buckling events occurring at a certain distance from other bundles to minimize potential cross-influences. The resulting measured buckling wavelengths lie between 0.75 and 1.75 μm (see Fig. 3 c).

Figure 3.

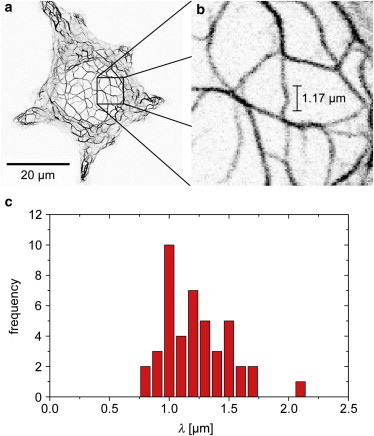
(a and b) An inverted fluorescence confocal microscope image of an SK8/18-2 cell showing a buckling event (a), which is shown in greater detail (b). (c) The average buckling wavelength of keratin bundles is 1.22 μm. To see this figure in color, go online.

The number of filaments in a bundle, N, is derived from the diameter of the bundle combined with the spatial ordering of the KIFs inside a bundle, assuming a circular shape of the bundle’s cross section. Estimating the filament diameter from the fluorescence images is not straightforward, since we cannot directly image objects that are smaller than the point-spread function of the setup. However, we can calibrate this shift in size caused by the convolution with the point-spread function by applying the same imaging procedure to 100-nm-diameter fluorescent beads, i.e., in the same size range as the bundle diameters. The FWHM is determined by Gaussians fitted to intensity profiles perpendicular to the original spline fit. The measured bundle diameters are corrected by the deviation between the FWHM of the beads and the known bead diameter. We include bundles with diameters between 40 and 130 nm in the analysis presented here.

The relative organization of the filaments, and in particular the interfilament distance within a bundle, is determined from transmission electron microscopy (TEM) images of sections through the cell, as shown in Fig. 4. The distance between the KIFs inside a bundle is estimated by assuming a hexagonal ordering of the filaments and averaging several line scans perpendicular to the long axis of the bundle in images of longitudinal cross sections (Fig. 4 a). As the exact orientation of the bundle within the slice (in particular the rotation about the long axis) is unknown, our result of 12.2 nm slightly overestimates the real distance. In a similar way, when determining the lattice distance in perpendicular cross sections (Fig. 4 b), we measure a distance of ∼14 nm, probably due to a slight cut angle relative to the bundle axis. In addition, we cannot exclude a loosening of the ion-mediated KIF packing inside a bundle during EM-preparation. Nevertheless, we find our results in good agreement with previous studies that have revealed a median filament distance of 11 nm in cryo-TEM images for stratum corneum keratin structures, which are also ordered on a hexagonal lattice (24). From the estimated bundle diameter, we determine the number, N, of individual filaments in the bundle.

Figure 4.

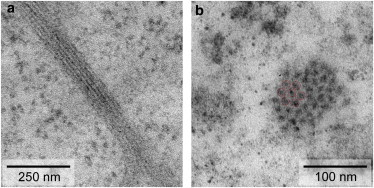
Examples of TEM images of keratin bundles in SK8/18-2 cells. (a) Longitudinal slice. The average distance between the individual filaments is 12.2 nm. (b) Cross section of a KIF bundle showing hexagonal lattice ordering. To see this figure in color, go online.

The persistence length, L_PF, of individual filaments has been investigated in in vitro experiments. Atomic force microscopy (AFM) and EM reveal a value for L_PF in the range 0.30–0.48 μm (3). It should be noted that the persistence length depends on the ionic environment, a factor that is difficult to control in the cell. Moreover, due to filament-substrate interactions, the persistence length measurement for adsorbed filaments using EM or AFM tends to be underestimated compared to the real persistence length in solution; a factor of 2 has been found for vimentin (25). Here, we therefore assume an equilibrium persistence length of 0.78 μm, which is in good agreement with recent results of ∼0.65 μm found in high frequency rheology experiments (26). According to Eq. 2, the exact value for L_PF influences the intercept of the curve only weakly. When changing the L_PF from 0.78 μm to 0.65 μm, the intercept of the curve decreases by <0.05. The characteristic length scales for the calculation of α are experimentally determined as the average buckling wavelength of l = 〈λ〉 = 1.22 μm (see Fig. 3 c) and the average bundle diameter, 〈2a〉 = 81 nm.

In Fig. 5, the buckling wavelength, λ, is plotted against the number of filaments, N, inside the bundle for 44 buckling events in 16 cells (black squares). Here, each data point represents an individual bundle. As the cells are heterogeneous, and the environmental conditions encountered by each bundle therefore may differ quite considerably, we abstain from fitting the data points directly. Instead, we include theoretical curves according to Eq. 2 in the plot to represent different degrees of coupling between the individual filaments as given by γ. Here, the elastic modulus of the cytoplasm, E_SM, is set to 1.5 kPa (12,27) and the Poisson’s ratio is assumed to be 0.5, corresponding to no volumetric changes. In addition, we indicate the range of E_SM = 0.75–2.5 kPa (Fig. 5, red, green, and blue regions) to account for the wide range of values found in the literature. All measured values lie in the expected order of magnitude, which is quite astonishing given the complex situation in the cell and the simplicity of the model applied. Of the data points, 93% suggest a coupling parameter of 1.5 or above. Note that the thicker bundles are less strongly coupled than the thinner ones.

Figure 5.

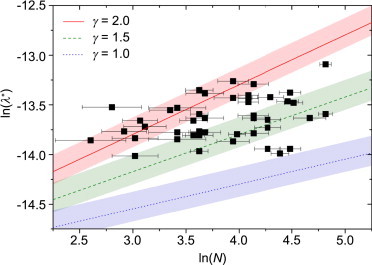
Buckling wavelength, λ, plotted against the number, N, of filaments in a bundle. Lines for different coupling parameters, γ, are depicted. Their intercepts are defined by the persistence length of one filament (L_PF = 0.78 μm) and the elastic modulus of the surrounding matrix (E_SM = 1.5 kPa). The range between 0.75 and 2.5 kPa is shown by the colored regions around the coupling-parameter lines. Error bars for N correspond to an error of 5 nm in bundle thickness. To see this figure in color, go online.

Discussion

The rather high values of the coupling parameter show that the linkage between the individual keratin filaments inside a bundle is strong. As a consequence, the ability of the filaments to shift against each other is limited, although it exists. Note that some values exceed the theoretical limit of γ = 2. This behavior can be explained by taking into account that the elastic modulus of the cytoplasm is inhomogeneous throughout the cell. Hence, data points that would suggest a coupling parameter >2 in Fig. 5 may be explained by a surrounding matrix that is locally softer than average.

The strong cross-linking between individual KIFs may be mediated by electrostatic interactions via ions or by bundling proteins. As discussed in a recent review (28), electrostatic interactions mediated by ions between charged biopolymers, like intermediate filaments, can lead not only to bundling, but also to numerous other morphologies, such as network or lamellar phase formation. The effects vary depending on the type of polymer, polymer length and stiffness, the surface distribution of the charges on the biopolymer, and the ion concentrations. For bundling, in particular, the ion concentration needs to exceed a critical level. Interestingly, this critical level is strongly dependent on the valence of the ion, but hardly influenced by the structure of the ion or by the type of the biopolymer. In the case of KIFs, experimental evidence for the bundling effect of monovalent and divalent ions, e.g., 1 mM Mg²⁺, has been provided by several groups (7–9,29,30). Furthermore, Pawelzyk et al. recently suggested that hydrophobic amino acid clusters in keratins play a key role in the formation of filament bundles (26). However, other studies, which favor protein-mediated interactions, suggest that intermediate-filament-associated proteins such as filaggrin have the ability to bundle keratin (31,32).

Additional proteins that influence the bundling behavior have been identified in vivo. Thus, it has been shown that epiplakin plays a role in regulating KIF dynamics and stabilization under stress (33). Furthermore, plectin affects the keratin network organization and the bundle thickness. In this respect, it was revealed that in plectin-deficient keratinocytes, the bundle thickness is increased, probably due to collapse of finer filament bundles (34). By contrast, in wild-type keratinocytes, bundle collapse is inhibited by the formation of stabilizing orthogonal bridges between filament bundles, which finally results in reduced bundle thickness. Our data show that for thicker bundles the coupling parameter is systematically smaller than for thinner ones (see Fig. 5). This decrease in coupling for thicker bundles may be related to a reduced protein involvement in stabilizing filament-filament cross-links in large bundles. Also, it is likely that thicker bundles are structurally less well ordered and thus less strongly coupled. Alternatively, in cases where larger bundles originate from the collapse of finer bundles, there are only a few contact points between the collapsed finer bundles, which also leads to reduced average coupling.

It has also been shown that the mechanical properties of keratin structures are influenced by their state of phosphorylation, which in turn may affect buckling. For example, the keratin subunit exchange rate depends on the phosphorylation state of keratin (35). Furthermore, an increased phosphorylation leads to the formation of thicker bundles (36). In this study, we do not mechanically stress the cells, and we therefore assume no (pronounced) influence of phosphorylation. Phosphorylation and subunit exchange can, however, facilitate buckling behavior, as they may lead to a local weakening of the bundle, making it easier for the bundle to bend at these particular sites (37).

In analogy to the wormlike-chain model (38), the so-called wormlike-bundle model was introduced and applied to actin bundles and microtubules (39,40), taking into account the elastic properties of both the filaments and the cross-links. The authors found that the competition between the mechanical contributions of filaments and cross-links is influenced by the specific architecture of the respective systems; it is thus not straightforward to apply their models to our experiments. However, independent of the molecular structure, bundle bending mechanics are governed by a competition between the energy required to extend single filaments and the energy required to shear the cross-links between the filaments in a bundle. Very consistent with their model, we find that in the case of KIFs, which are orders of magnitude more extendable than actin filaments and microtubules (5,6), it is energetically more favorable to stretch individual filaments in a bundle than to loosen or extend the cross-links, as depicted in the lower sketch in Fig. 2 b.

To summarize, the relatively strong linkage between the KIFs in most bundles is likely the result of a combination of ionic conditions and keratin-associated proteins. The tight cross-linking, which leads to enhanced stiffness of the bundles, supports the idea that the keratin network is important for the integrity of the cell. This aspect is emphasized when calculating the persistence length of a bundle, L_PB. Assuming a coupling parameter of 1.5–2, L_PB is on the order of 1 mm for an average bundle, thus similar to what is found for individual microtubules. The relevance of KIF bundles for the structural integrity of the cell is further emphasized when looking at buckling events in cells exposed to external (shear) forces. We previously showed that upon application of shear stress, the dynamics of the keratin network is reduced on a timescale of minutes (41). This phenomenon has been quantified by comparing the trajectories of individual network nodes or by cross-correlating frames of the time-lapse movies. Thus, we hypothesized that the reduced dynamics hint to a stiffening of the cell, which is thereby protected against potentially harmful external forces. When comparing buckling events of the KIF bundles between nonsheared and sheared cells (0.14 Pa wall shear stress applied using microfluidic methods), we find a reduction of the buckling wavelength by 14% and a smaller number of buckling events within the same amount of data (see Fig. S1). This can be understood by a closer look at the influence of an increased stiffness of the surrounding matrix. Equation 1 shows that an increased value of α leads to a decreased buckling wavelength, λ. The critical force that has to be overcome for a buckling event to occur is given by f_crit = 2(ακ)^1/2 (18) and thus increases with increasing matrix stiffness. Hence, our findings strongly support the concept that one of the important functions of keratin is to provide the cell with resilience against external stresses.

In conclusion, we analyze the mechanical properties of individual keratin bundles in living cells, their natural environment. Thus, we link in vitro experiments on purified protein to cell studies that consider the cell as a whole. By measuring buckling events in the cells, we characterize the internal architecture and the stiffness, or persistence length, of the bundles as well as the elastic properties of the surrounding matrix. We find that the coupling between the individual 10-nm-diameter filaments is strong and allows little relative movement, which is in nice agreement with the finding that IFs are extremely extendable. However, thicker bundles are less strongly coupled, and this finding could be related to there being a maximum diameter to which the bundles grow in cells. Our results demonstrate the importance of keratin bundles and networks for cell mechanics. It should be noted that due to the comparatively low connectivity of the bundles, the structure of bundle networks is completely different from, e.g., actin networks in cells.

Supporting Material

Movie S1. Buckling event in an SW13 cell (two alternating frames)

The cell was stably transfected with CFP/YFP keratin K8/K18. Shown is the inverted gray scale. The time difference between the two alternating frames is 2 s. The scale is 0.053 μm/pixel. The buckling event is highlighted (box).