Abstract
How many of the structural and functional properties of proteins are inherent? Computer simulations provide a powerful tool to address this question. A series of studies on QS, quasi-spherical, compact polypeptides which lack any secondary structure; ART, artificial, proteins comprised of compact homopolypeptides with protein-like secondary structure; and PDB, native, single domain proteins shows that essentially all native global folds, pockets and protein-protein interfaces are in the ART library. This suggests that many protein properties are inherent and that evolution is involved in fine-tuning. The completeness of the space of ligand binding pockets and protein-protein interfaces suggests that promiscuous interactions are intrinsic to proteins and that the capacity to perform the biochemistry of life at low level does not require evolution. If so, this has profound consequences for the origin of life.
Keywords: Completeness of the space of single domain protein structures; ligand binding sites and protein-protein interfaces; origin of protein biochemical function, protein-ligand interactions; promiscuous interactions
Introduction
Proteins are remarkable biological machines that carry out a myriad of functions ranging from enzymatic catalysis to cellular regulation and control[1]. For proteins to perform their function, they have to adopt a specific three-dimensional structure, the native conformation, and they then often bind small molecules in cavities or ligand binding sites or to other proteins or macromolecules. Such intermolecular interactions require specific geometric surfaces and constellations of amino acid residues. When one looks at the remarkable complexity of protein structures and their attendant molecular functions, one cannot but wonder how many of these features are the result of the inherent physical properties of proteins without selection and how many reflect selection due to evolution. In other words what is the relative balance of physics and evolution in dictating protein structure and function?
Consider two limiting models of how protein structure and function could have arisen: The “inherent structure & functionality model” asserts that to a first approximation the majority of the structural and molecular functions of proteins result from their intrinsic physical chemical properties[2], which evolution exploits and amplifies. In such a model, the global fold, ligand binding cavities and protein-protein interfaces seen in wild type proteins were already present in proteins that had not undergone the purifying process of evolution. In this model, the random background probability for structure and function is quite high. In stark contrast, in the “acquired structure &functionality model”, most proteins were objects without ligand binding pockets, protein-protein interfaces and perhaps lacked significant structural similarity to contemporary proteins. Evolution selected for function on a very tiny minority of protein structures by creating pockets and protein-protein interfaces. The inherent structure &functionality model by providing a significant nonzero background probability on which evolutionary selection operates suggests that proteins engage in a large variety of biochemical functions. These weak, inherent intermolecular interactions should be highly promiscuous and would act like biochemical noise that is difficult, if not impossible, to eliminate. In contrast, the acquired functionality model implies that selection for function is difficult and rare; if so, promiscuous interactions could be readily eliminated.
To test which picture is likely more correct, one must entirely eliminate evolutionary selection and see what structural and functional features such random polypeptides share with native proteins. Protein design is a way of experimentally achieving this objective. Recent work of Hecht et al provides support for the inherent structure & functionality model[3]. On binary patterning of six polar and five nonpolar residues, they created a combinatorial library of designed 4-helix bundle proteins expressed in E. coli that were not selected for any function[3]. They then screened the resulting sequences for a variety of functions including heme binding, peroxidase, and lipase activities. The majority bound heme, with a sizeable fraction showing activity in all assays. This suggests that protein scan exhibit rudimentary activity even without functional selection. It is also consistent with the idea[4] that “primitive enzymes possessed a broad range of specificity” that would allow an early cell to carry out the biochemistry of life. Despite preconceived notions to the contrary, even contemporary enzymes routinely catalyze other, sometimes barely related, chemical reactions[5]. Such extrinsic functions could evolve without interfering with the original catalytic activity[6]. Similarly, Tawfik et al argue that enzyme catalytic promiscuity has always been present[5c, 5d]. Consistent with the notion that biochemical function is an inherent feature of proteins, protein design studies often find the desired low-level function after a remarkably small number of generations[7].
While protein structure, sequence and function are not fully separable, it is conceptually convenient to examine the nature of the space of protein structures and what factors give rise to native like ligand binding sites and protein-protein interfaces. One of the salient and fundamental features of protein structures is that they often adopt regular secondary structure, with roughly 60% of their residues located in helices or β-stands[8]; such structures satisfy the requirement that many of their hydrogen bonds are intramolecular and reflect the fact that the free energy cost of not being hydrogen bonded is high. Another geometric feature of proteins is that they are compact, with almost crystal like packing densities[2a]. A key question is how many structural and functional features of proteins arise simply from packing a polypeptide into a dense sphere?
Another question is how complete is the space of observed single domain protein structures? Is there anything special about the global protein structures observed in nature? Does the global chain topology of native like proteins emerge simply from dense packing, does it require the presence of secondary structure or does it require strong selection due to evolution, with native like structures having a very low inherent probability that is only amplified when the forces of evolutionary selection act? Again, one needs reference systems where the effects of evolution are absent. Furthermore, to address these questions, given a structural entity, whether it be the global fold of a protein, a ligand binding site or a protein-protein interface, a structural comparison metric that assesses the structural similarity of the compared pair of structures relative to random and algorithms that can perform the necessary structural alignment are needed. We address these issues below.
While experimental studies have been suggestive, computational studies can play a significant role. They offer the advantages of being comprehensive and could allow us to tease out which features of protein structures/sequences likely give rise to which functional properties. Consider three types of protein libraries[2, 9]: “PDB”, real, single domain protein structures found in the Protein Data Bank[10]; “ART”, computationally generated, compact homopolypeptide, artificial, structures with protein-like secondary structure; and quasi-spherical, “QS”, random polypeptide structures packed in the same average spherical volume as proteins but lacking backbone secondary structure and hydrogen bonding. ART polyleucine protein structures are generated by selecting the secondary structure patterns based on that found on the PDB and then generating a manifold of compact structures using the TASSER structure prediction algorithm[11]. QS proteins[2a] were generated by considering a sphere whose radius is that expected for a protein of the same number of residues, then randomly packing balls of diameter, 3.8 Å, in that sphere subject to excluded volume restraints, generating a connected chain by minimizing the overall contour length by solving the traveling salesman problem, and finally, rebuilding full atom polyleucine conformations using PULCRA[12]. For both QS and ART proteins, the sequence composition was randomly generated based on the average composition of the PDB. A genetic algorithm then selects the specific sequence that optimizes the sequence for stability in the given fold using a variety of potentials[13]. Examples of ART and QS structures are provided in Figure 1.
Figure 1.
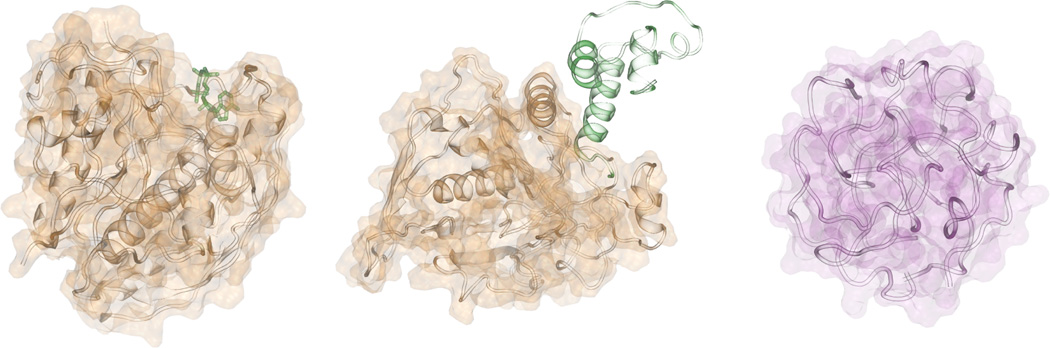
Illustrations of an artificial structure (brown) and quasi-spherical structure (red). Artificial structures exhibit pocket-like shapes for small-molecule binding (left) and planar surfaces for protein-protein interactions (middle).
By comparing the properties of the PDB with those of ART and QS proteins where there is no evolutionary selection, we examine what is required to generate native like global folds, small molecule ligand binding sites, protein-protein interfaces, as well as the relationship between pocket or protein interface geometry and global protein structure, and whether sequences that are computationally selected to stabilize the fold of interest exhibit native like patterns of amino acid conservation in ligand binding pockets. Thus, conclusions about the role of physics in dictating protein structure and molecular function emerge from the consonance of the structure properties of native proteins with those in either the ART or QS proteins. As will be shown, some features of native proteins are present in the QS structures, but far more features emerge in ART structures when secondary structure is included. Thus, many features of native like proteins are nothing special, but in order to demonstrate that this is the case, one needs appropriate metrics of similarity for global protein folds, ligand binding pockets and protein-protein interfaces. We turn to this issue next.
Methods for the structural alignment of global protein structures
To ascertain whether a pair of proteins are structurally similar, a comparison metric is needed[14]. Such metrics include the root mean square deviation, RMSD, of the coordinates (generally of Cαs) and the GDT_TS score[15]. However, the statistical significance of these two metrics depends on the length of the structures being compared. For example, is a RMSD of 6 Å associated with a 50 residue alignment statistically more significant than an RMSD of 3 Å associated with a 10 residue alignment[16]? To address this, the TM-score, provided by the TM-align structural alignment algorithm, whose statistical significance is alignment length independent[17]was developed[18]. The TM-score is given by
| (1) |
where LQ is the number of residues in the target protein (the protein of interest), and is the average distance between a pair of residues in the best structural alignment of a randomly related pair of protein structures. The TM-score lies in the range [0, 1], with a TM-score =1.0 for identical structures. The most probable TM-score of randomly related protein structures is 0.15, with the average best TM-score of 0.30[17]. Two proteins are structurally related if they share a TM-score ≥ 0.40 (P-value of 3.4 × 10−5[18c]).In extensive benchmarking over a number of years, this has proven to a useful threshold for building a target structure on a template, given that the majority if not all of the secondary structural elements of the core are preserved at this value[9a, 19].An improved version of TM-align[17], fr-TM-align[18b] generates alignments with a 9% higher TM-score than TM-align, with 7% more residues aligned. fr-TM-align shows the most improvement in the 0.3–0.5 TM-score regime, where the improvement is up to 0.15 TM-score units. This is the regime where significant alignments might be missed using the original TM-align algorithm[18c]. We next turn to the corresponding approach for the structural alignment of ligand binding pockets.
Algorithms for the comparison of protein ligand binding pockets
Ligand-binding sites on protein surfaces, where direct physical contacts occur between small-molecule ligands and proteins, are often found in concave structures or “pockets”[20]. Thus, they can be detected using geometric criteria. For example, SURFNET uses sphere-filling[21], while POCKET[22] and LIGSITE[23] are grid-based, as is CAVITATOR[24], a much less sensitive approach to structural fluctuations than LIGSITE, while CAST employs Delaunay triangulation and α-shape theory[25].Then, after applying a given pocket detection algorithm to the PDB, the resulting large number pocket structures allows for a comprehensive analysis of ligand-binding pockets[26]. In practice, small-molecule ligands can bind to pockets in proteins whose global structural is dissimilar. What do such pockets have in common? Global structural comparison is often inadequate, and methods for local structural comparison dedicated to the geometric and/or physicochemical features of the protein pockets are required. Among these, a heuristic maximum clique finding algorithm has been implemented in Cavbase[27], IsoCleft[28], and SOIPPA[29]. Another approach employed by Site Engine is geometric hashing[30]. Other methods do not use atoms to represent a pocket; rather spherical harmonics[31] or 3D Zernike descriptors[32]are employed. While these reduced descriptors are fast, a detailed alignment is not provided. As was the case for global structural alignments[15], many scoring functions for measuring pocket similarity are dependent on pocket size and do not estimate the statistical significance of their similarity score[27–31]. This is an issue when one performs comparisons on the entire PDB[33].
To address statistical significance, APoc was developed[24]. Given a template and a target pocket, APoc evaluates their Pocket Similarity score (PS-score), which reflects the similarity in their backbone geometries, side-chain orientations, and the chemical similarities between the aligned pocket residues. The length of a pocket is the number of pocket residue Cα atoms. Suppose an alignment is obtained between a query (target) of length LQ and a template of length LT. The PS-score is
| (2a) |
| (2b) |
| (2c) |
| (2d) |
Here, the number of aligned residue pairs is Na, the distance in Å between the Cα atoms of the ith aligned residue pair is di, and the empirical scaling factor d0 ≡ 0.70(LQ − 5)1/4 − 0.2. pi measures the directional similarity between two Cα to Cβ vectors in the two pockets, which span an angle θi at the ith alignment position of two non-Glycine residues. ri measures the chemical similarity of the two aligned amino acids. if the two amino acids belong to the same group (I–VIII) defined as: I (LVIMC), II (AG), III (ST), IV (P), V (FYW), VI (EDNQ), VII (KR), VIII (H)[26d], and 0 otherwise. ensures that the mean score of two aligned random pockets is length independent. Similar to the TM-score, a heuristic iterative extension algorithm is employed to calculate the PS-score[34]. Identical pocket structures have a PS-score of 1.0, and the statistical significance of the PS-score is estimated by comparing millions of randomly selected pocket pairs[24]. PS-scores ≥0.38 are statistically significant with a P-value <0.03.This value appears to be the lower boundary of PS-scores among pockets from the same protein super families.
Algorithms for the comparison of protein-protein interfaces
If one wishes to characterize the nature of protein-protein interactions, it makes sense to directly focus on the protein-protein interface where such interactions occur. The most straightforward approach utilizes individual protein structure alignments and defines interaction modes by the orientation of the proteins in the complex and/or their interface overlap[35]. This is reasonable when the structures of individual proteins do not change significantly on association and when the isolated protein alignments produce a good interface alignment; often, this is not the case. A second strategy generates a global structural alignment of the entire protein complex[36]. This approach does not differentiate between the structural similarity of the interface and non-interface regions. Depending on the relative size of the proteins in the complex, a significant similarity score need not mean that two complexes have similar interaction modes. Thus, a dedicated method for comparing protein-protein interfaces is needed. An early approach employed geometric hashing[37]. More recent methods compare physical chemical interactions, non-covalent interactions, or contact maps as in I2I-SiteEngine[38], Galinter[39], and CMAPi[40]. None of these approaches provide an assessment of the statistical significance of interface similarity, and all were tested on quite small data sets.
To address these limitations, iAlign was developed[41]. Using the same notation as in Eq. 2, the IS-score is derived from the TM-score and is given by
| (3a) |
| (3b) |
The contact overlap factor fi ≡ (ci/ai + ci/bi)/2, where ai and bi are the numbers of interfacial contacts of the template and of the query interface at the ith position of the alignment, respectively, and ci is the number of overlapped interfacial contacts at the same position. s0 ≡ 0.18 – 0.35/LQ0.3 makes the IS-score length-independent. The IS-score ranges from 0 to 1, with identical structures having a score of 1.0. IS-scores >0.19 are statistically significant when only sequential alignment is allowed and >0.25 when non-sequential alignment is also permitted. In this review, we discuss results when the non-sequential alignment mode is enabled. Over 90% of biologically related protein complexes (formed by protomers from the same protein super family respectively) share an IS-score above these thresholds.
Likely completeness of the space of single domain protein structures
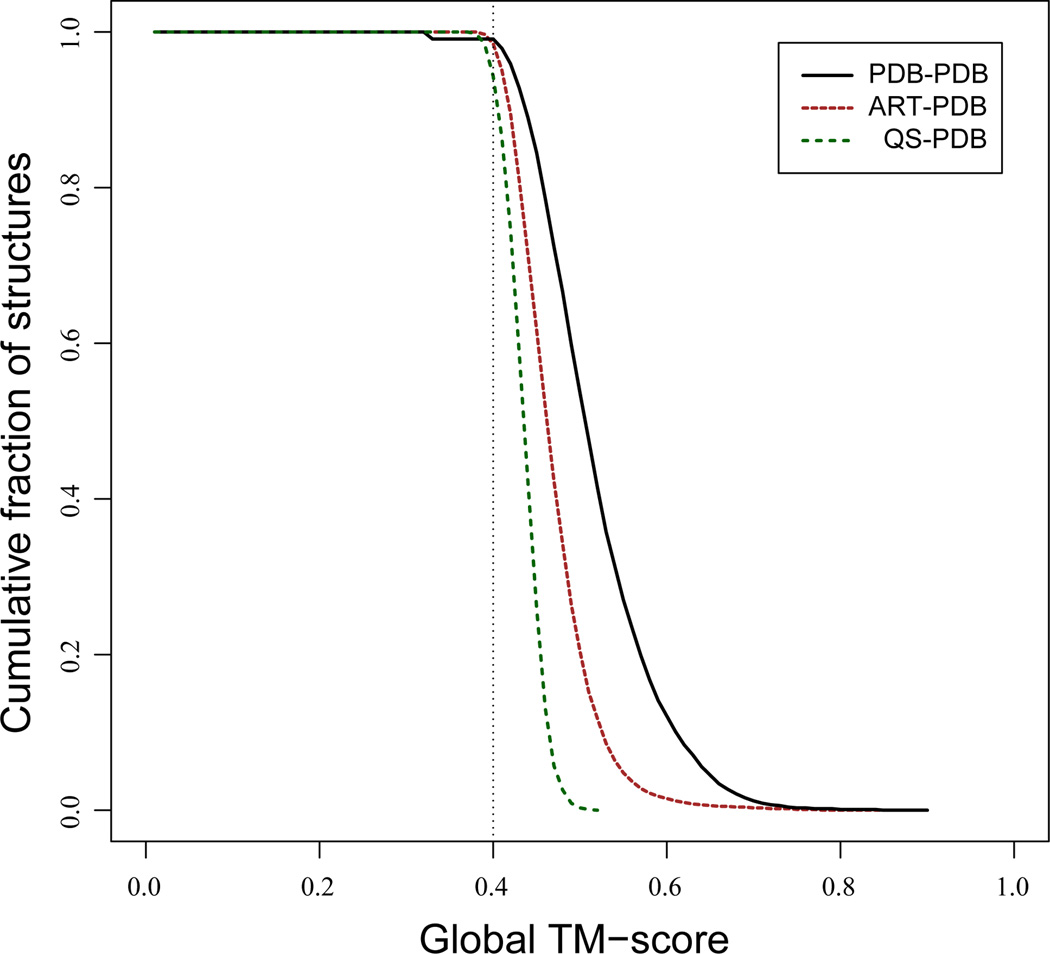
For ART and QS protein structures up to 250 residues in length, structural alignments using TM-align to the corresponding full set of PDB template structures and to the subset of PDB structures up to250 residues in length, PDB250were done[2a]. In Figure 2, the cumulative fraction of proteins whose TM-score ≥ abscissa is shown for QS, ART structures to the corresponding full set of PDB templates. Despite that fact that they entirely lack secondary structure, 94% of QS structures have a structurally related protein (TM-score ≥0.4) in the PDB with a mean TM-score=0.43. This just reflects the fact that one is looking at the spatial arrangement of geometric objects. Conversely, for the PDB250 set, 71% of native structures have a significant structural alignment to QS structures. However, if we consider the chain smoothed versions of both PDB250 (where local structural fluctuations are averaged out), then 94% of the QS templates have a TM-score to the smoothed native structure ≥0.40, with a mean TM-score of 0.42[19]. Moreover, if we use these QS templates and refine them using the TASSER structure prediction algorithm[42], the mean TM-score of the resulting model is 0.71, with 98% of the targets having a TM-score ≥0.40. (The remaining 2% arise because the closest structure to native is not top ranked, but is in a lower ranked cluster; nevertheless the structures in this cluster also have a TM-score ≥0.40[19, 43]).
Figure 2.
Demonstration that the space of single domain protein structures is likely complete. Cumulative fraction of ART, QS and PDB250 target proteins aligned to PDB templates that have a best TM-score ≥ abscissa. For the comparison of PDB250 to the full PDB, templates whose sequence identity to the target is >3% are excluded.
Turning to the ART compact homopolypeptide library, 99% of targets have a significant template match to the full PDB, with a mean TM-score of 0.47. PDB250 structural alignments to the ART300 structure library (ART proteins up to 300 residues in length) have almost identical behavior as the ART250 library does to PDB300 (native proteins up to 300 residues in length). Finally, we consider structure alignments of real protein structures in PDB250 to other PDB structures, subject to the constraint that the sequence identity between the target-template pair is ≤ 3%. This reduces the evolutionary similarities between the pairs of aligned proteins. 90% of PDB250 proteins find a structurally similar partner among members of PDB300, with an average TM-score of 0.46. Thus, in the limit of little, if any, detectible evolutionary relationship between target and templates, the structural space of real single domain proteins and ART structures are very similar. The conclusion that the single domain library of protein structures is likely complete is provided by the comparison of PDB to ART and QS structures and not to the PDB structures among themselves.
On the basis of the above, we conclude that the space of protein structures is strongly dictated by the requirement of dense packing of locally semi stiff chains, does not require backbone hydrogen bonding and is most likely complete. In other words, the structures adopted by proteins are an inherent feature of densely packed, quasi-spherical objects comprised of residues with excluded volume but no regular secondary structure. Once secondary structure is allowed, the local geometric fidelity to real structures improves as does the global structural similarity, but this is a minor effect. Thus, native like global structures are typical compact polymers.
Internal packing and ligand binding pockets
The relationship of the accessible surface area (ASA) and molecular volume (MV) calculated for the ART structures are very similar to PDB structures (Figure 3A)[2a]. In contrast, QS structures have less solvent-accessible surface, with the ASA/MV relation shifted slightly towards ideal spheres. Thus, the packing of the interior of QS structures is denser than in PDB or ART structures. Consistent with this, the average QS pocket size is much smaller than in ART or PDB structures. This is clearly shown in Figure 3B where the average number of grid points assigned by LIGSITE[44] to the largest and second largest pockets in the set of PDB, ART and QS structures are shown. The size of the largest (2nd largest) pockets in PDB and ART structures is very similar: 95 (38) and 89 (24) grid points, respectively. QS structures have very small cavities; the average size of the largest (2nd largest) pocket is only 32 (23) grid points. The pockets in the QS structure are too tiny to bind typical small molecule, organic ligands. On the other hand, hydrogen-bonded ART structures, that contain rigid secondary structure elements, have pockets of appropriate volume.
Figure 3.
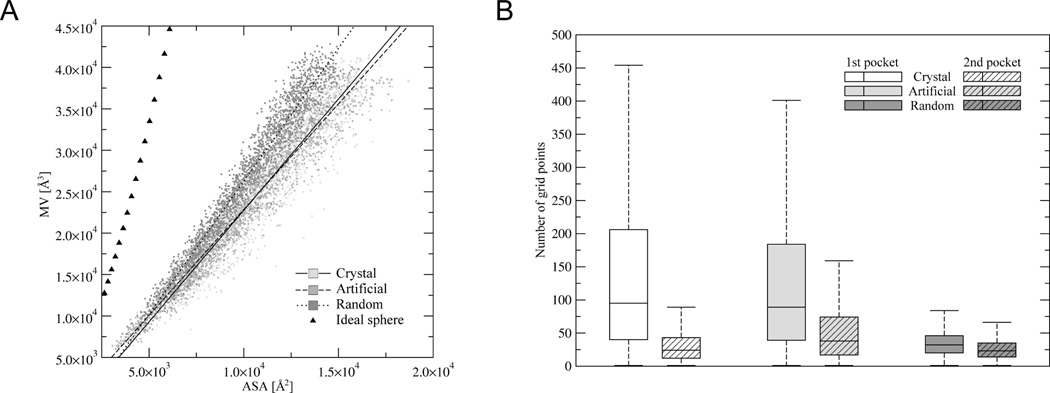
Comparison of the packing density and cavity size for QS, ART and PDB250 proteins compared to ideal spheres (triangles). (A). Accessible surface area (ASA) vs. molecular volume (MV) for ART, QS and PDB250 proteins compared to ideal spheres (triangles). (B). Distribution of the number of grid points assigned to the largest (1st) and the second largest (2nd) pockets.
While ART proteins have cavities of requisite volume, the key issue is whether the shapes of the pockets in the ART and PDB structures are similar. To explore the dependence of the ART results on the potential used to evaluate stability, sequences whose stability is determined by burial, secondary structure and residue based pair preferences (ART), or just by burial and secondary structure preferences in “no-pr”[2a] were generated; all qualitative and many quantitative results are independent of the potential. Key questions examined were the number of statistically distinct ligand binding pockets, the completeness of the space of pockets, the coupling of pocket geometry and global fold similarity and the extent of pocket sequence conservation in evolutionarily unrelated proteins[13]. We turn to these issues next.
Likely completeness of the space of ligand binding pockets
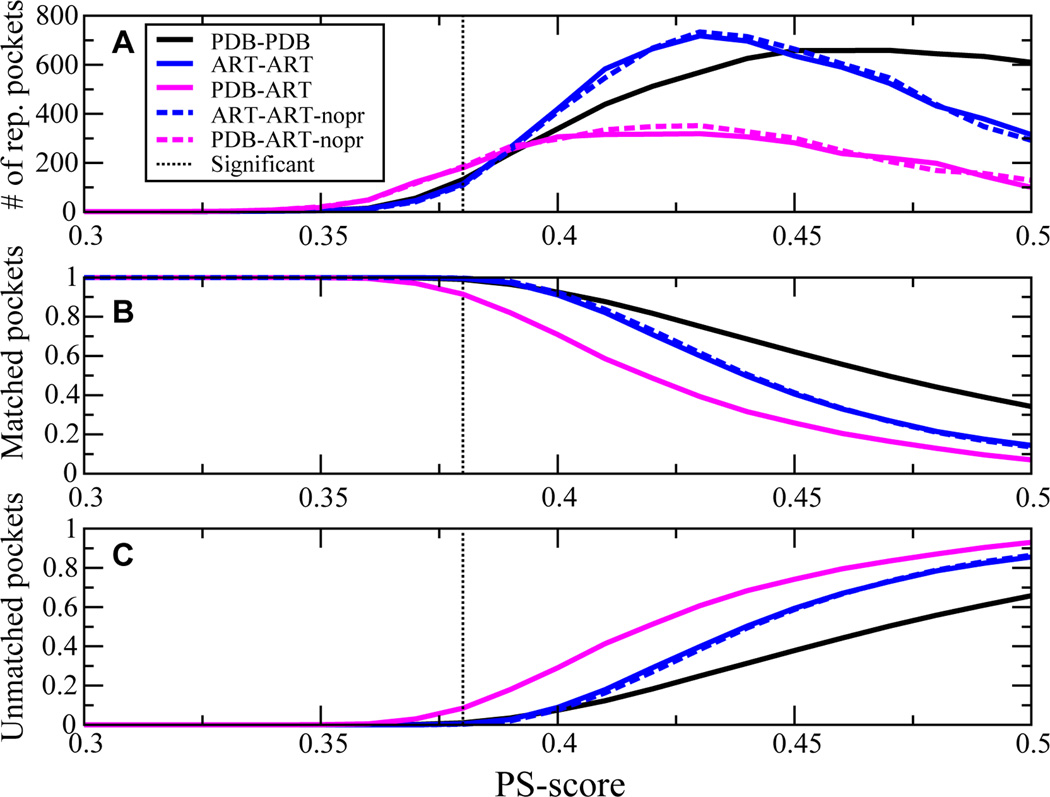
If the number of distinct ligand binding pockets that share significant sequence conservation were small, then similar ligand-protein interactions should occur across different protein folds. This would concomitantly rationalize the large number of off-target drug interactions[45] but would also imply that endogenous metabolite-protein interactions are likely quite promiscuous. In Figure 4,for a representative set of native, single domain proteins, the PDB250 set, and the corresponding ART protein library, the number of representative distinct pockets, the fraction of target pockets that match these representative pockets (i.e. having at least one matching pocket), and the fraction of unmatched pockets versus PS-score are shown. For a PS-score threshold of 0.38, a small number of pockets, 132 (180), in the PDB (ART) pocket library cover 99.0% (91.5%) of the space of PDB pockets. PDB-PDB and PDB-ART pockets behave similarly to ART-ART structures that require 114 pockets to cover 99.5% of all pockets. A few large pockets cover the space of many small pockets. At a PS-score of 0.40, as shown in Figure 4B, 92.5% (91.1%) of PDB (ART) pockets match one of the 339 (420) representative PDB (ART) structures. Of course, as in Figure 4C, the number of unmatched pockets increases with increasing PS-score, viz. as the two pockets become structurally more similar. A comparably small number of pockets is also found when we restrict ourselves to known ligand binding sites (defined by residues contacting small molecule ligands) that typically comprise a subset of the corresponding pocket structures[46].
Figure 4.
Demonstration that the space of ligand binding pockets is likely complete.(A) At a given PS-score, the number of representative, distinct pocket structures in the pocket template library that match pockets in the given target library. (B) At the specified PS-score, fraction of pockets in the target library matched to representative pocket templates. (C) Fraction of target pockets that do not match any other pocket structure in the pocket template library at the specified PS-score. Solid (dashed) lines are protein sequences selected for global stability in ART structures generated using burial, secondary structure and with (without) pair potentials.
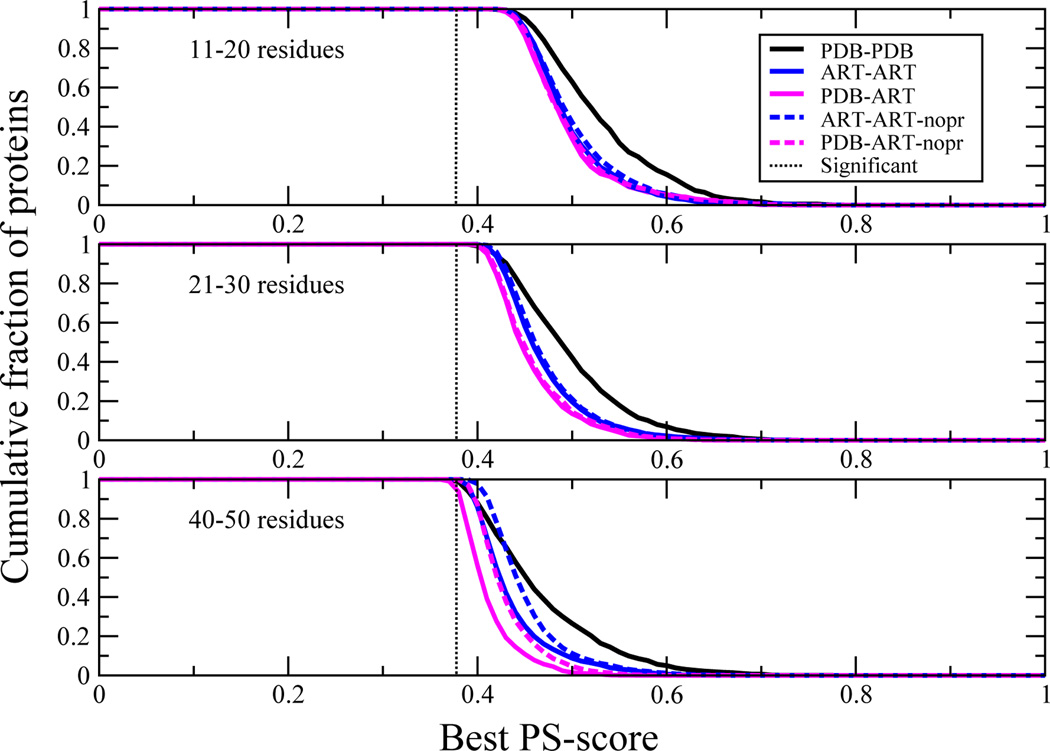
How similar are the best matching pockets in the various structural libraries? Figure 5 shows the distribution of best PS-scores of pairs of pockets between native proteins, between ART proteins and when PDB proteins are compared to ART templates. Clearly, almost all native ligand-binding pockets have a statistically significant match to a pocket in the ART library. Thus, evolutionary selection is not required to generate native like ligand binding pockets; rather, they are a geometric effect arising from defects in secondary structural element packing.
Figure 5.
Demonstration that all pockets can find a statistically significant match to other pockets in the various pocket libraries. For different size pockets, cumulative fraction of proteins whose best PS-score to a pocket in the given structural library ≥ the PS-score on the abscissa. The dotted black line indicates the PS-score for a significantly related pair of pockets (P < 0.03).
Relationship of global structural similarity and ligand binding pocket similarity
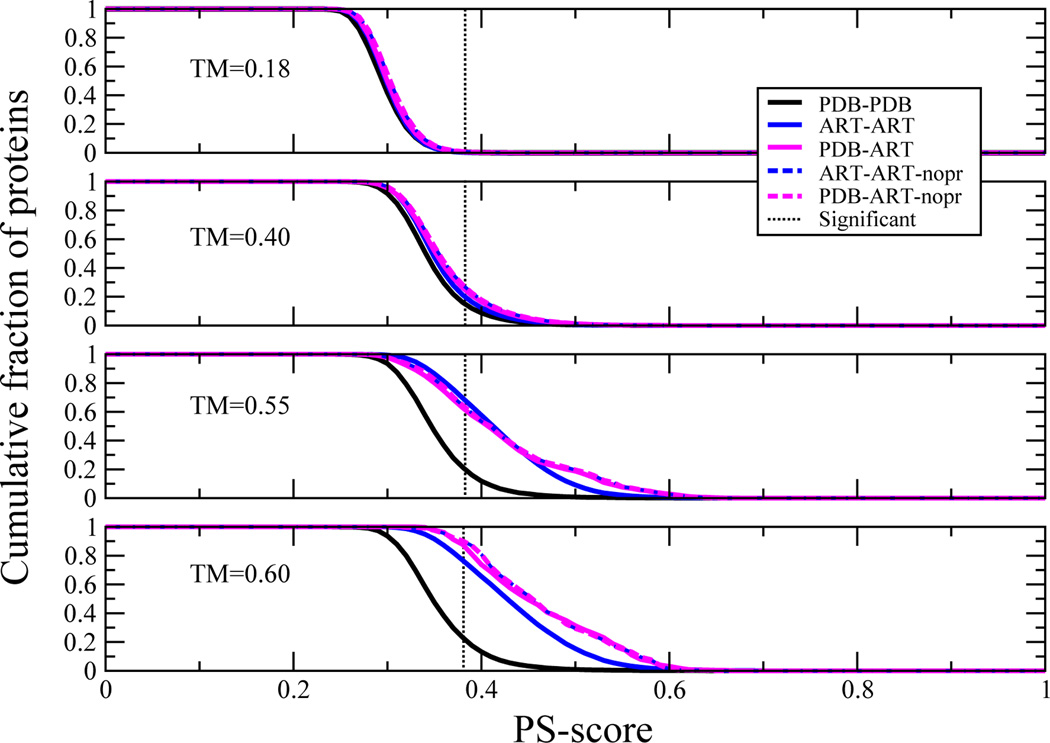
Often, global similarity between a pair of protein structuresis assumed to imply functional similarity[47]. Furthermore, the coincidence of structurally similar pockets in globally similar proteins is often assumed to imply an evolutionary relationship. However as implied by the limited number of distinct protein pockets, this need not be the case. Consider the results of Figure 6, where, for the largest pocket in the protein of interest, the cumulative fraction of proteins whose best PS-score to a pocket in a protein in the library of interest is ≥ the abscissa for a given structural similarity as assessed by the global TM-score is shown. Most pockets are dissimilar in structurally unrelated proteins, (TM-score=0.18); yet, even here,~0.5% of their pockets are structurally similar. For globally similar proteins at a TM-score=0.40, ~16% of all three types of compared structures (PDB-PDB, PDB-ART, ART-ART) have similar pockets. For structurally very similar proteins (TM-scores of 0.55 and 0.60) pairs of PDB-PDB proteins have significant pocket matches in ~22% of cases. Thus, structural similarity does not automatically imply pocket similarity; rather for the majority it is likely that their pockets are dissimilar. Moreover since there are significant matches to structurally similar pockets in both the PDB-ART and ART-ART libraries, having a significant pocket match need not imply any evolutionary relationship.
Figure 6.
Demonstration that that structural similarity does not enforce pocket similarity. For fixed TM-score, the cumulative fraction of proteins whose best match PS-score is ≥ abscissa. The PS-score for a significantly related pair of pockets is indicated in the dotted black line.
It is somewhat surprising that the ART-ART and PDB-ART pairs have a larger fraction of significant pocket structural matches for globally similar structures (those with TM-scores >0.4) than native pairs. Perhaps evolution acts to increase the specificity of particular ligands for a given protein by making pockets in globally similar structures more dissimilar than would be expected for the random background. Finally, a similar analysis of the extent of global similarity for a given extent of pocket similarity led to the conclusion that similar pockets can occur in proteins of completely different global structures and dissimilar pockets can occur in proteins with the same global structures, with similar variation seen in the PDB-PDB and ART-ART structural libraries[13].
Relationship of pocket residue conservation to evolution
To tease out inherent from evolutionary effects on the sequence conservation of pocket residues, in Figure 7, the fraction of proteins that have a given number of pocket residues conserved at structurally aligned positions in the pocket as a function of PS-score are shown. Up to a PS-score of 0.5, the sequence conservation behaviors of PDB-PDB, PDB-ART and ART-ART sets of pockets are very similar. Residue conservation at given pocket positions does not demand that the pair of pockets be evolutionarily related. On comparing PDB-PDB and PDB-ART pocket pairs, ALA, VAL, ILE, LEU, and GLU residues are conserved to a similar extent, independent of pocket structural similarity. ARG (SER) becomes more (less) conserved as the pocket similarity increases. Thus, ART proteins recapitulate the native residue conservation results, suggesting that the degree of sequence conservation in pockets is at least partly driven by the selection for thermodynamic stability and the geometric properties of the given residues.
Figure 7.
Extent of sequence conservation in pockets. For 31–40 residue pockets, at a given PS-score the fraction of proteins with a given number of conserved residues at structurally aligned positions. The background for randomly related pockets is given by the black dotted line.
Comparison of protein-protein interfaces in native, QS and ART structures
Having considered the case of ligand binding pockets, we next explore the structural properties of another type of structure associated with intermolecular interactions, namely protein-protein interactions.
Similar protein-protein interfaces occur in native proteins of different global fold
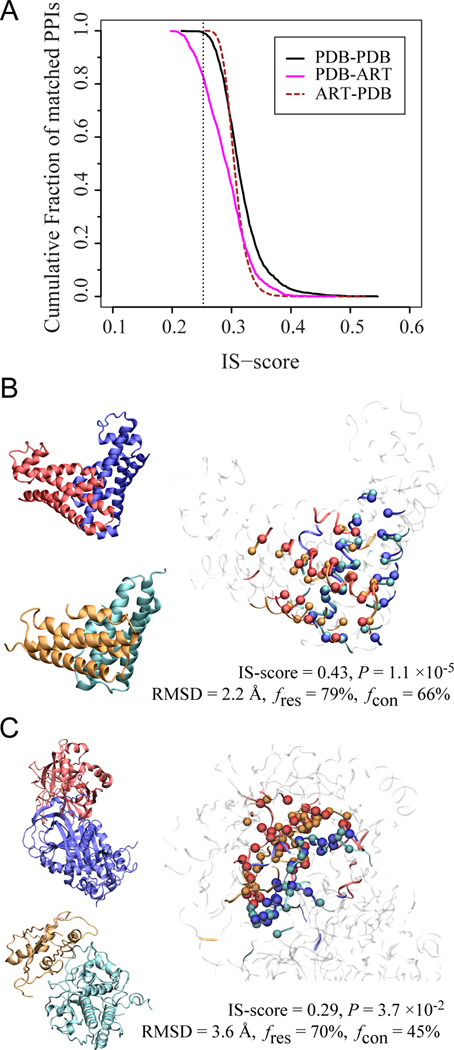
Before focusing on protein-protein interfaces in ART or QS structures, one must characterize native interfaces. A non-redundant set of 1,519 experimentally determined protein-protein complexes[48] were selected, where native protein-protein interfaces contain no more than 150 residues; this set of 1,374 representative interfaces was named PDB150inter[49]. To explore if structurally similar interfaces can occur in proteins lacking global similarity, the interface cannot belong to proteins of the same SCOP fold, cannot have significant sequence similarity (PSI-BLAST E-value > 1[50]), or similar monomeric structure (TM-score < 0.4[17]). On evaluating interface similarity by the IS-score of Eq. 3[41a], Figure 8 shows the statistics of closest interface matches. The mean IS-score is 0.317 compared to 0.207 for the best random interface alignments. ~88% of native interfaces find a match with a significant score (P-value < 0.05. These results suggest that one can find a structurally similar interface for the vast majority of native interfaces even when it is formed by monomers with unrelated global structures.
Figure 8.
Demonstration that the space of protein-protein interfaces is likely complete.(A) Distribution of the closest match between protein-protein interfaces found in the PDB and those generated artificially. The dotted line is located at a significant IS-score 0.25. (B&C) Two examples of matches found for PDB (blue/red) in the artificial complex structures cyan/orange. In each panel, the left snapshots show the individual monomers; the right snapshot shows the optimal interface alignment reported by iAlign; the Cα atoms of aligned residues are shown in a Van der Waals representation, and the non-interface regions are dimmed.
Do QS and ART structures have planar surface patches?
Since most native protein-protein interfaces are flat[49], can QS or ART structures provide a planar surface patch of requisite size? To address this, the most planar surface patch within a solvent accessible area of 1000 Å2 (a typical interface area per protein in a protein complex[51]) in a set of QS, ART and PDB structures was examined[2a]; while the planarity of ART and PDB structures was similar, QS proteins behaved differently; planarity is defined as the RMSD of the Cα atoms of the best-fit surfaces were much less planar. About 67/47% of the native/ART patches have very low curvature, with absolute values< 0.01 Å−1. In contrast, a mere 32% of QS structures satisfy this threshold. These results indicate QS structures are less likely to have a surface patch whose geometry is suitable for protein-protein interactions.
Do QS and ART structures form native-like protein-protein interfaces when there are structurally similar to monomers in native dimeric complexes
Putative dimeric complexes were built by superimposing QS or ART structures onto their corresponding aligned monomers (with TM-score>0.4) from native dimers. All-against-all alignments of 1,988 QS and 30,000 ART structures were examined[52]. On removing structures with steric clashes, the remaining putative protein-protein interfaces were compared to the real, native protein-protein interface of the corresponding dimeric template. On searching through roughly 12.6 trillion QS-native structure pairs, just a single spherical complex structure had a significant IS-score at P-value < 1×10−3. In contrast, at this same threshold, 51,096 pairs were found among only 192 million ART-native structure pairs. The chance of finding a putative, structurally native-like interface with a significant IS-score at P = 1×10−3 is 2.8×10−4, about four million times higher than for QS structures. Thus, because QS structures lackquasi-planar interfaces they are essentially incapable of having protein-protein interactions, whereas ART structures can.
Are native and ART protein-protein interfaces structurally similar?
The above analysis was restricted to possible interfaces belonging to native proteins whose monomeric structure matched that of a known dimer. We now examine what happens when we ignore monomer structural similarity.Figure 8A shows the statistics of closest interface matches among ART interfaces for each native interface of PDB150inter. The mean of IS-score is 0.291, slightly lower than the mean of 0.317 from comparison among native interfaces. About 83% of native interfaces find an ART interface match with a significant score (P-value < 0.05). Thus, most native interfaces have a counterpart in the ART library. Next, we examine if one can find a similar native interface for each artificial interface? Figure 8A also shows the statistics of 20,000 pairs of closest interface matches. The mean IS-score is 0.308; about 89% of artificial interfaces have a native interface counterpart with a significant score (P-value < 0.05).These results are comparable to those for native interface comparisons, suggesting that most artificial protein-protein interfaces have a native counterpart already deposited in the PDB. Finally, Figures 8B & C show examples of ART and PDB dimers that share both monomeric fold similarity and significant interface similarity.
Estimate of the Number of Distinct Dimer Structures
The fact that most native interfaces are in the library of artificial interfaces and most artificial interfaces are in the library of native interfaces suggests that the library of interfaces is close to complete. There are about 1,000 types of interfaces after complete linkage clustering (at an IS-score P-value of 0.001). Based on previous work[17], there are about 2,000 statistically distinct monomeric protein structures below 200 residues. From the clusters obtained from docking simulations, we estimate that there are on average about 30 representative interaction modes (IS-score P-value < 0.05) between each pair of ART protein folds. Thus, there are ~60 million possible statistically distinct quaternary dimeric structures. This suggests that the library of solved dimeric structures is far from complete. Of course, this estimate ignores evolutionary selection, which likely dramatically reduces the number of dimeric structures utilized by nature.
Distribution of ligand binding pockets adjacent to protein-protein interfaces
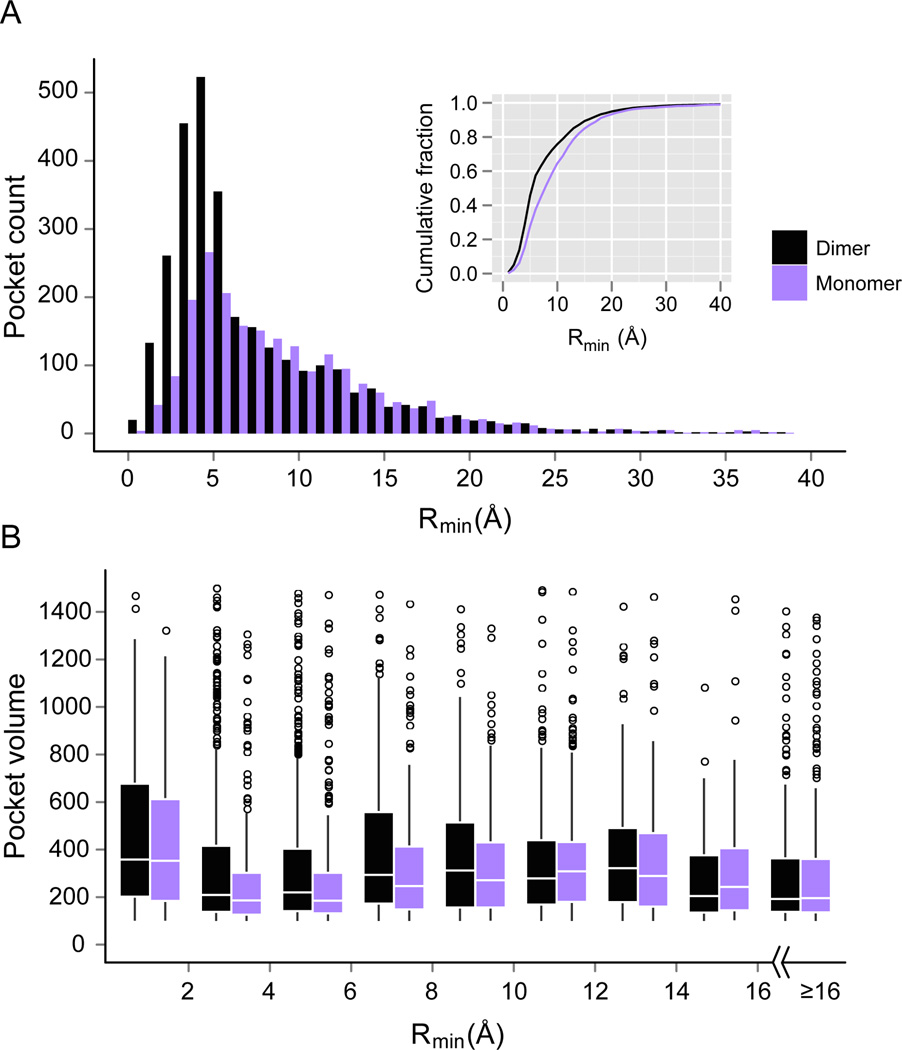
What is the structural relationship between ligand binding pockets and protein-protein interfaces, if any? One might imagine that as a pair of convex surfaces associate they could form a pocket adjacent to their binding interface. In fact, many interfacial residues are partially exposed, i.e., they are “rim” residues[51]. Do these rim residues contribute to both protein-ligand and protein-protein interactions? To address these questions, a comprehensive analysis of the distribution of pockets around protein-protein inter faces was performed[53]. To characterize the distance between a detected pocket and a protein interface, Rmin, the minimum of all distances between the center of mass of the pocket and heavy atoms of protein-protein interfacial residues was calculated. As shown in Figure 9A, the maximum in the Rmin distribution is 5 Å, with about 57% of pockets within a Rmin of 6 Å. Thus, most pockets that could bind ligands are adjacent to protein-protein interfaces. To determine whether these pockets are formed on protein association, we separated all protein complexes into individual monomers and repeated the same pocket detection procedure. 30% fewer pockets are detected. As shown in Figure 9B, formation of the complex yields more and larger pockets; the mean pocket volume within a Rmin=6 Å is 418 grid points in dimers and 293 in monomers.
Figure 9.
Distribution of ligand pockets around protein-protein interfaces in dimers and monomers. (A) Histograms of number of pockets versus their distance from the protein interface. The width of the distance bins is 1Å. Inset shows the cumulative fraction of pockets at different distances. (B) Box plots of pocket volume (in grid points) in different distance bins from the protein interface. The width of distance bins is set at 2Å, except that the last bin includes all pockets with Rmin ≥ 16 Å. The boxes range from the 25th to 75th percentiles, and whiskers extend to a distance of up to 1.5 times the interquartile range. The white line locates the median. Outliers are indicated by hollow spheres.
Distribution of ligands in protein complexes
Next, the preference for small molecule ligands to bind to pockets adjacent to protein interfaces was examined. The dataset contained 741 protein complexes with at least one ligand, with a total of 2,255 ligands bound. Among all bound ligands, 54% contact at least one side of the protein interface and 35% contact both sides. If we consider the ligand closest to the interface, then71% and 52% bind one and both sides respectively. Next, ρ, the ratio of buried surface area of a bound ligand due to contacts with protein interfacial residues versus all protein surface residues in the complex was calculated. Analysis of the closest ligands contacting both sides of protein interface yields a mean ρ of 0.52; i.e. on average about half of a ligand’sburied surface area is due to interactions with interfacial residues. Finally, in order to avoid possible size effects of proteins, we compared protein-protein interfaces with random protein surfaces of the same solvent accessible area taken from the same complex. Protein-protein interfaces are statistically significantly closer to their bound ligands (P-value < 2.2×10−16) and make contacts to about 23% more ligands than randomly selected protein surfaces.
Distribution of ligands in two-domain proteins
Many monomeric proteins contain multiple domains. Except for their covalent linkage, domain-domain and protein-protein interfaces are quite similar. As such, packing around domain interfaces creates pockets that would also be expected to form ligand binding sites. Thus, an analysis of the ligand distribution around domain interfaces in 1,416 representative two-domain protein structures was performed[53]. Among all multi-domain proteins that interact with at least one ligand, 77% have at least one ligand contacting at least one side of the domain interface, and 64% interact with at least one ligand contacting both sides of the interface. In contrast, in dimeric proteins, 52% bind to at least one ligand at both sides of the interface. Compared to a randomly selected surface patch of the same surface area accessible to solvent, the domain interface region is favored by ligands. Random surfaces give median Rmin values of 7.1 Å, in contrast to much smaller values of 3.6 Å by protein interfaces. Similarly, random surfaces make a smaller contribution to the ligand surfaces. On average, the difference in ρ values is 12% by domain-domain interfaces, significantly higher compared to random surfaces (P < 2.2×10−16).
Location of pockets in ART dimers
We hypothesize that pockets suitable for ligand binding around protein interfaces could arise from random protein-protein interactions with a cavity arising from the juxtaposition of two convex surfaces. To test this, 363 ART protein complexes from a previous study were selected[49]. Each corresponds to one of 363 native protein complexes with a bound ligand (not necessarily located at the protein interface), such that each ART/native pair has a weak but statistically significant interface structure match with a mean IS-score of 0.29 and a P-value < 0.05 for 89% of the pairs. We then examined the set of pockets closet to the protein interface. In total, the number of pockets/dimer for native and ART dimers,1.58 versus 1.50, respectively, is very similar. The median/mean of pocket and interface distance Rmin is 4.0/4.1 Å for native pockets vs.3.8/3.9 Å for ART pockets. The median volume of native pockets is 234, almost the same as 238 for artificial pockets. However, native dimers have a higher frequency of large pockets > 1000, resulting in a larger mean size (402) than (345) of artificial pockets. The mean sizes are 311/302 for native/artificial pockets, after removing 24/20 pockets larger than 1000 grid points. Thus, the similar size pockets generated in ART protein docking arise mainly from geometric effects. Finally, on comparing native and ART pockets using APoc[24], we find that interfacial native and ART pockets have a statistically significant match to the pockets found in single domain proteins. This observation further reinforces the idea that the library of ligand binding pockets is complete.
Summary and Outlook
Comparison of the structural and sequence based properties of native proteins with QS and ART proteins, allows us to dissect the relative roles of the inherent physical properties of proteins from selection due to evolution. While QS proteins are merely dense collections of residues, remarkably, they have essentially all of the global structures seen in native globular proteins and vice versa. This strongly suggests that the space of single domain protein structures is likely complete and merely arises from the packing of polypeptide backbones into a compact structure. If so, then there are on the order of 2000 distinct single domain, global folds. However, QS structures are devoid of regular hydrogen bonded secondary structures. The absence of secondary structure has a number of profound consequences. The pockets in QS proteins are too small for organic molecules to fit. Moreover, being quasi-spherical, they lack the planar interfaces needed to engage in protein-protein interactions. Thus, the absence of hydrogen bonded secondary structures generates model proteins whose inability to bind small molecule ligands or other proteins is very nonnative. Thus, QS proteins, while they reproduce the global fold, share little else in common with native proteins.
When hydrogen bonding is turned on, as in the ART structures, the resulting ensemble of structures and sequences are remarkably like native proteins. The presence of secondary structural elements increases the local structural fidelity of ART proteins to native proteins, but with regard to the completeness of the space of global protein structures, this is merely fine-tuning. However, the functional consequences are far more dramatic. Now, defects in packing secondary structural elements create native like pockets whose volume is quite close to that in native proteins. ART sequences selected for stability reproduce the extent of sequence conservation seen in native ligand binding pockets. Furthermore, essentially all native pockets are found in the ART pocket library and vice versa. Thus, the library of ligand binding pockets is likely complete and remarkably small (less than 1000 pockets, depending on the criteria applied[13, 46]). Combined with the fact that similar pockets occur across many different types of protein structures with similar patterns of amino acid conservation, we conclude that ligand-binding promiscuity is likely an inherent feature resulting from the geometric and physical-chemical properties of proteins. This promiscuity implies that the notion of one molecule-one protein target that underlies some drug discovery approaches is likely incorrect, a conclusion consistent with recent studies[45, 54]. Moreover, within a cell, a given endogenous ligand likely interacts at low level with multiple proteins that may have different global structures.
Turning to the nature of the structural space of protein-protein interfaces, most native interfaces are found in the library of randomly docked ART structures, once again implying that the space of protein-protein interfaces is likely close to complete. The only interfaces that are missed are either those that involve domain swapping or involve non-compact monomeric structures. The number of distinct protein-protein interfaces is on the order of 1000, which, when recognizing that the average number of possible interfacial regions per monomer is about 30, suggests that there are on ~ 60 million structurally distinct dimers possible.
One of the remarkable conclusions of the series of studies reviewed here[2a, 9a, 13, 19, 24, 46, 53, 55] is just how many features of native proteins are reproduced without any evolutionary selection whatsoever. The coincidence of global folds, ligand binding sites and protein-protein interaction sites in native and ART structures shows that these metrics cannot be used to infer an evolutionary relationship between proteins. Indeed, one finds ART ligand binding pockets selected on the basis of global thermodynamic stability whose pattern of amino conservation mimics native proteins. Moreover, ART sequences also behave very much like native proteins in terms of which protein structures are thread able and which are not. This suggests that many of the standard criteria used to infer an evolutionary relationship between proteins might be incorrect. To date, the only reliable way we have found to infer an evolutionary relationship is when the pair of proteins is connected by a series of intermediate protein sequences, all sharing quite high sequence identity.
On the basis of the above, there is very strong evidence that the inherent structural and functional model rationalizes many of the observed properties of native proteins. At first glance, the structural and functional properties of native proteins examined here seem quite special; however, they are inherent to polypeptides, with the random probability for native like protein structure and function much higher than previously believed. Background biochemical noise reflective of a soup of functions is likely omnipresent, with evolution acting to optimize these inherent functions. Thus, with regards to the role of physics and evolution in dictating protein structure and function, we conclude that physics plays a dominant role, with evolutionary selection involved in essential fine-tuning. On the one hand, this produces robustness; yet, it makes cellular regulation and control more difficult. How nature achieves the collective behavior needed for living cells is not fully understood. But the present work strongly suggests that proteins are primed to engage in low-level biochemical function; if so, this has profound implications both for the origin of and ubiquity of life in the universe.
ACKNOWLEDGMENTS
This research was supported in part by grant Nos. GM-48835 and GM-37408 of the NIH Institute of General Medical Sciences.
Biographies
Jeffrey Skolnick is Director of the Center for the Study of Systems Biology at Georgia Tech. His research in Computational Systems Biology focuses on the development of algorithms and their application to proteomes for the prediction of protein structure and function, small molecule ligand-protein interactions with applications to drug discovery and drug repurposing, and fundamental studies on the interplay between physics and evolution in determining protein structure and function, with applications to the possible origin of life. He has also developed approaches for the prediction of protein-protein and protein-DNA interactions. Most recently, he has undertaken molecular based simulations designed to explore the basic physical principles underlying molecular motions in a cell.
Mu Gao is Research Scientist at the Center for the Study of Systems Biology at Georgia Tech. He obtained his Ph.D. in physics from University of Illinois at Urbana-Champaign. His primary research interests are in the development of computational approaches for studying the structure, function, and dynamics of proteins and nucleotides, and their applications for a better understanding of biological systems and rational drug design.
Hongyi Zhou is Research Scientist at the Center for the Study of Systems Biology at Georgia Tech. His research focuses on developing methods for protein structure and function prediction using physical and evolutionary principles; applying structure and function predictions for drug and target discovery, and simulating the mechanism/pathways of protein folding.
References
- 1.Alberts B. Molecular biology of the cell. 5th ed. New York: Garland Science; 2008. [Google Scholar]
- 2.a) Brylinski M, Gao M, Skolnick J. Physical chemistry chemical physics: PCCP. 2011;13:17044–17055. doi: 10.1039/c1cp21140d. [DOI] [PMC free article] [PubMed] [Google Scholar]; b) Gao M, Skolnick J. Proc. Natl. Acad. Sci. USA. 2012;109:3784–3789. doi: 10.1073/pnas.1117768109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Patel SC, Bradley LH, Jinadasa SP, Hecht MH. Protein Sci. 2009;18:1388–1400. doi: 10.1002/pro.147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Jensen RA. Annual review of microbiology. 1976;30:409–425. doi: 10.1146/annurev.mi.30.100176.002205. [DOI] [PubMed] [Google Scholar]
- 5.a) Khersonsky O, Malitsky S, Rogachev I, Tawfik DS. Biochemistry. 2011;50:2683–2690. doi: 10.1021/bi101763c. [DOI] [PubMed] [Google Scholar]; b) Tawfik DS. Nature chemical biology. 2010;6:692–696. doi: 10.1038/nchembio.441. [DOI] [PubMed] [Google Scholar]; c) Khersonsky O, Tawfik DS. Annual review of biochemistry. 2010;79:471–505. doi: 10.1146/annurev-biochem-030409-143718. [DOI] [PubMed] [Google Scholar]; d) Khersonsky O, Roodveldt C, Tawfik DS. Current opinion in chemical biology. 2006;10:498–508. doi: 10.1016/j.cbpa.2006.08.011. [DOI] [PubMed] [Google Scholar]
- 6.a) Khersonsky O, Kiss G, Rothlisberger D, Dym O, Albeck S, Houk KN, Baker D, Tawfik DS. Proceedings of the National Academy of Sciences of the United States of America. 2012;109:10358–10363. doi: 10.1073/pnas.1121063109. [DOI] [PMC free article] [PubMed] [Google Scholar]; b) Ben-David M, Elias M, Filippi JJ, Dunach E, Silman I, Sussman JL, Tawfik DS. Journal of molecular biology. 2012;418:181–196. doi: 10.1016/j.jmb.2012.02.042. [DOI] [PubMed] [Google Scholar]; c) Bar-Even A, Noor E, Savir Y, Liebermeister W, Davidi D, Tawfik DS, Milo R. Biochemistry. 2011;50:4402–4410. doi: 10.1021/bi2002289. [DOI] [PubMed] [Google Scholar]
- 7.a) Jurgens C, Strom A, Wegener D, Hettwer S, Wilmanns M, Sterner R. Proceedings of the National Academy of Sciences of the United States of America. 2000;97:9925–9930. doi: 10.1073/pnas.160255397. [DOI] [PMC free article] [PubMed] [Google Scholar]; b) Song G, Lazar GA, Kortemme T, Shimaoka M, Desjarlais JR, Baker D, Springer TA. The Journal of biological chemistry. 2006;281:5042–5049. doi: 10.1074/jbc.M510454200. [DOI] [PMC free article] [PubMed] [Google Scholar]; c) Pande J, Szewczyk MM, Grover AK. Biotechnology advances. 2010;28:849–858. doi: 10.1016/j.biotechadv.2010.07.004. [DOI] [PubMed] [Google Scholar]
- 8.Frishman D, Argos P. Proteins. 1995;23:566–579. doi: 10.1002/prot.340230412. [DOI] [PubMed] [Google Scholar]
- 9.a) Skolnick J, Arakaki AK, Lee SY, Brylinski M. Proceedings of the National Academy of Sciences of the United States of America. 2009;106:15690–15695. doi: 10.1073/pnas.0907683106. [DOI] [PMC free article] [PubMed] [Google Scholar]; b) Skolnick J, Zhou HY, Brylinski M. J. Phys. Chem. B. 2012;116:6654–6664. doi: 10.1021/jp211052j. [DOI] [PMC free article] [PubMed] [Google Scholar]; c) Hildebrand A, Remmert M, Biegert A, Soding J. Proteins. 2009;77(Suppl 9):128–132. doi: 10.1002/prot.22499. [DOI] [PubMed] [Google Scholar]
- 10.Berman H, Henrick K, Nakamura H, Markley JL. Nucleic Acids Res. 2007;35:D301–D303. doi: 10.1093/nar/gkl971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Zhou H, Skolnick J. Proteins. 2011 [Google Scholar]
- 12.Rotkiewicz P, Skolnick J. Journal of computational chemistry. 2008;29:1460–1465. doi: 10.1002/jcc.20906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Skolnick J, Gao M. Proceedings of the National Academy of Sciences of the United States of America. 2013;110:9344–9349. doi: 10.1073/pnas.1300011110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wrabl JO, Grishin NV. Journal of computational biology : a journal of computational molecular cell biology. 2008;15:317–355. doi: 10.1089/cmb.2007.0161. [DOI] [PubMed] [Google Scholar]
- 15.Zemla A, Venclovas C, Moult J, Fidelis K. Proteins. 1999;(Suppl 3):22–29. doi: 10.1002/(sici)1097-0134(1999)37:3+<22::aid-prot5>3.3.co;2-n. [DOI] [PubMed] [Google Scholar]
- 16.Zhang Y, Skolnick J. Proteins. 2004;57:702–710. doi: 10.1002/prot.20264. [DOI] [PubMed] [Google Scholar]
- 17.Zhang Y, Skolnick J. Nucleic Acids Res. 2005;33:2302–2309. doi: 10.1093/nar/gki524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.a) Zhang Y, Skolnick J. Proceedings of the National Academy of Sciences of the United States of America. 2005;102:1029–1034. doi: 10.1073/pnas.0407152101. [DOI] [PMC free article] [PubMed] [Google Scholar]; b) Pandit SB, Skolnick J. BMC bioinformatics. 2008;9:531. doi: 10.1186/1471-2105-9-531. [DOI] [PMC free article] [PubMed] [Google Scholar]; c) Xu J, Zhang Y. Bioinformatics. 2010;26:889–895. doi: 10.1093/bioinformatics/btq066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Skolnick J, Zhou H, Brylinski M. The journal of physical chemistry. B. 2012 doi: 10.1021/jp211052j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.a) Laskowski RA, Luscombe NM, Swindells MB, Thornton JM. Protein Sci. 1996;5:2438–2452. doi: 10.1002/pro.5560051206. [DOI] [PMC free article] [PubMed] [Google Scholar]; b) Liang J, Edelsbrunner H, Woodward C. Protein Sci. 1998;7:1884–1897. doi: 10.1002/pro.5560070905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Laskowski RA. J. Mol. Graphics. 1995;13:323–330. doi: 10.1016/0263-7855(95)00073-9. [DOI] [PubMed] [Google Scholar]
- 22.Levitt DG, Banaszak LJ. J. Mol. Graphics. 1992;10:229–234. doi: 10.1016/0263-7855(92)80074-n. [DOI] [PubMed] [Google Scholar]
- 23.Huang BD, Schroeder M. BMC Struct. Biol. 2006;6 doi: 10.1186/1472-6807-6-19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Gao M, Skolnick J. Bioinformatics. 2013;29:597–604. doi: 10.1093/bioinformatics/btt024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Binkowski TA, Naghibzadeh S, Liang J. Nucleic Acids Res. 2003;31:3352–3355. doi: 10.1093/nar/gkg512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.a) Gold ND, Jackson RM. J. Mol. Biol. 2006;355:1112–1124. doi: 10.1016/j.jmb.2005.11.044. [DOI] [PubMed] [Google Scholar]; b) Kahraman A, Morris RJ, Laskowski RA, Thornton JM. J. Mol. Biol. 2007;368:283–301. doi: 10.1016/j.jmb.2007.01.086. [DOI] [PubMed] [Google Scholar]; c) Minai R, Matsuo Y, Onuki H, Hirota H. Proteins: Struct. Funct. Bioinform. 2008;72:367–381. doi: 10.1002/prot.21933. [DOI] [PubMed] [Google Scholar]; d) Zhang ZD, Grigorov MG. Proteins-Structure Function and Bioinformatics. 2006;62:470–478. [Google Scholar]
- 27.Schmitt S, Kuhn D, Klebe G. J. Mol. Biol. 2002;323:387–406. doi: 10.1016/s0022-2836(02)00811-2. [DOI] [PubMed] [Google Scholar]
- 28.Najmanovich R, Kurbatova N, Thornton J. Bioinformatics. 2008;24:I105–I111. doi: 10.1093/bioinformatics/btn263. [DOI] [PubMed] [Google Scholar]
- 29.Xie L, Bourne PE. Proc. Natl. Acad. Sci. USA. 2008;105:5441–5446. doi: 10.1073/pnas.0704422105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Shulman-Peleg A, Nussinov R, Wolfson HJ. J. Mol. Biol. 2004;339:607–633. doi: 10.1016/j.jmb.2004.04.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Morris RJ, Najmanovich RJ, Kahraman A, Thornton JM. Bioinformatics. 2005;21:2347–2355. doi: 10.1093/bioinformatics/bti337. [DOI] [PubMed] [Google Scholar]
- 32.Chikhi R, Sael L, Kihara D. Proteins-Structure Function and Bioinformatics. 2010;78:2007–2028. doi: 10.1002/prot.22715. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Davies JR, Jackson RM, Mardia KV, Taylor CC. Bioinformatics. 2007;23:3001–3008. doi: 10.1093/bioinformatics/btm470. [DOI] [PubMed] [Google Scholar]
- 34.Zhang Y, Skolnick J. Proteins: Struct. Funct. Bioinform. 2004;57:702–710. doi: 10.1002/prot.20264. [DOI] [PubMed] [Google Scholar]
- 35.a) Aloy P, Ceulemans H, Stark A, Russell RB. J. Mol. Biol. 2003;332:989–998. doi: 10.1016/j.jmb.2003.07.006. [DOI] [PubMed] [Google Scholar]; b) Kim WK, Henschel A, Winter C, Schroeder M. PLoS Comp. Biol. 2006;2:1151–1164. doi: 10.1371/journal.pcbi.0020124. [DOI] [PMC free article] [PubMed] [Google Scholar]; c) Shoemaker BA, Panchenko AR, Bryant SH. Protein Sci. 2006;15:352–361. doi: 10.1110/ps.051760806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Mukherjee S, Zhang Y. Nucleic Acids Res. 2009;37:e83. doi: 10.1093/nar/gkp318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Tsai CJ, Lin SL, Wolfson HJ, Nussinov R. J. Mol. Biol. 1996;260:604–620. doi: 10.1006/jmbi.1996.0424. [DOI] [PubMed] [Google Scholar]
- 38.Shulman-Peleg A, Mintz S, Nussinov R, Wolfson HJ. In: Algorithms in Bioinformatics. Jonassen IKJ, editor. Vol. 3240. Berlin: Springer-Verlag; 2004. pp. 194–205. [Google Scholar]
- 39.Zhu H, Sommer I, Lengauer T, Domingues FS. PLoS One. 2008;3:e1926. doi: 10.1371/journal.pone.0001926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Pulim V, Berger B, Bienkowska J. Bioinformatics. 2008;24:2324–2328. doi: 10.1093/bioinformatics/btn432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.a) Gao M, Skolnick J. Bioinformatics. 2010;26:2259–2265. doi: 10.1093/bioinformatics/btq404. [DOI] [PMC free article] [PubMed] [Google Scholar]; b) Gao M, Skolnick J. Proteins-Structure Function and Bioinformatics. 2011;79:1623–1634. doi: 10.1002/prot.22987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Zhang Y, Skolnick J. Proceedings of the National Academy of Sciences of the United States of America. 2004;101:7594–7599. doi: 10.1073/pnas.0305695101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Zhang Y, Skolnick J. Journal of computational chemistry. 2004;25:865–871. doi: 10.1002/jcc.20011. [DOI] [PubMed] [Google Scholar]
- 44.a) Hendlich M, Rippmann F, Barnickel G. J Mol Graph Model. 1997;15:359–363. 389. doi: 10.1016/s1093-3263(98)00002-3. [DOI] [PubMed] [Google Scholar]; b) Huang B, Schroeder M. BMC Struct Biol. 2006;6:19. doi: 10.1186/1472-6807-6-19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.von Eichborn J, Murgueitio MS, Dunkel M, Koerner S, Bourne PE, Preissner R. Nucleic acids research. 2011;39:D1060–D1066. doi: 10.1093/nar/gkq1037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Gao M, Skolnick J. PLoS computational biology. 2013;9:e1003302. doi: 10.1371/journal.pcbi.1003302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.a) Petrey D, Fischer M, Honig B. Proceedings of the National Academy of Sciences of the United States of America. 2009;106:17377–17382. doi: 10.1073/pnas.0907971106. [DOI] [PMC free article] [PubMed] [Google Scholar]; b) Brylinski M, Skolnick J. Proteins. 2010;78:118–134. doi: 10.1002/prot.22566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Murzin AG, Brenner SE, Hubbard T, Chothia C. Journal of molecular biology. 1995;247:536–540. doi: 10.1006/jmbi.1995.0159. [DOI] [PubMed] [Google Scholar]
- 49.Gao M, Skolnick J. Proceedings of the National Academy of Sciences of the United States of America. 2010;107:22517–22522. doi: 10.1073/pnas.1012820107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Altschul SF, Madden TL, Schaffer AA, Zhang JH, Zhang Z, Miller W, Lipman DJ. Nucleic Acids Res. 1997;25:3389–3402. doi: 10.1093/nar/25.17.3389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Janin J, Bahadur RP, Chakrabarti P. Q. Rev. Biophys. 2008;41:133–180. doi: 10.1017/S0033583508004708. [DOI] [PubMed] [Google Scholar]
- 52.Lee SY, Skolnick J. Biophysical Journal. 2010;99:3066–3075. doi: 10.1016/j.bpj.2010.09.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Gao M, Skolnick J. Proceedings of the National Academy of Sciences of the United States of America. 2012;109:3784–3789. doi: 10.1073/pnas.1117768109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.a) Lim E, Pon A, Djoumbou Y, Knox C, Shrivastava S, Guo AC, Neveu V, Wishart DS. Nucleic Acids Res. 2010;38:D781–D786. doi: 10.1093/nar/gkp934. [DOI] [PMC free article] [PubMed] [Google Scholar]; b) Sturm N, Desaphy J, Quinn RJ, Rognan D, Kellenberger E. J Chem Inf Model. 2012;52:2410–2421. doi: 10.1021/ci300196g. [DOI] [PubMed] [Google Scholar]
- 55.Zhang Y, Hubner IA, Arakaki AK, Shakhnovich E, Skolnick J. Proceedings of the National Academy of Sciences of the United States of America. 2006;103:2605–2610. doi: 10.1073/pnas.0509379103. [DOI] [PMC free article] [PubMed] [Google Scholar]