3D Traction Stresses Activate Protease-Dependent Invasion of Cancer Cells

Abstract

Cell invasion and migration that occurs, for example, in cancer metastasis is rooted in the ability of cells to navigate through varying levels of physical constraint exerted by the extracellular matrix. Cancer cells can invade matrices in either a protease-independent or a protease-dependent manner. An emerging critical component that influences the mode of cell invasion is the traction stresses generated by the cells in response to the physicostructural properties of the extracellular matrix. In this study, we have developed a reference-free quantitative assay for measuring three-dimensional (3D) traction stresses generated by cells during the initial stages of invasion into matrices exerting varying levels of mechanical resistance. Our results show that as cells encounter higher mechanical resistance, a larger fraction of them shift to protease-mediated invasion, and this process begins at lower values of cell invasion depth. On the other hand, the compressive stress generated by the cells at the onset of protease-mediated invasion is found to be independent of matrix stiffness, suggesting that 3D traction stress is a key factor in triggering protease-mediated cancer cell invasion. At low 3D compressive traction stresses, cells utilize bleb formation to indent the matrix in a protease independent manner. However, at higher stress values, cells utilize invadopodia-like structures to mediate protease-dependent invasion into the 3D matrix. The critical value of compressive traction stress at the transition from a protease-independent to a protease-dependent mode of invasion is found to be ∼165 Pa.

Introduction

Metastatic dissemination of cancer cells is a key contributor to >90% of cancer-related mortality (1). Though metastasis involves multiple steps, the ability of cancer cells to break through the basement membrane and traverse through the extracellular matrix (ECM) is a crucial manifestation of cancer malignancy. Recent studies suggest that cancer cells can invade matrices in either a protease-independent or a protease-dependent manner. An emerging critical component that influences the mode of cell invasion is the physical properties of the ECM, which include porosity, alignment, and stiffness (2–12). For instance, cells encapsulated in a loosely cross-linked collagen network have been shown to migrate without the use of matrix metalloproteinases (MMPs) in a protease-independent manner by adopting an amoeboid phenotype and employing actomyosin-generated forces to squeeze through the pores and channels of the ECM network (2–7). Conversely, cells utilize protease-mediated degradation to navigate through dense ECM networks lacking such pore structures (7–11,13).

It is widely established that the mechanical properties of the tissues are drastically altered in the vicinity of solid tumors such as breast cancer as the disease progresses (14). The changes in the mechanical and structural environment of the tumor have been shown to contribute to dissemination and enhanced migration of cancer cells. Results from Leventhal et al. have demonstrated the prevalent effect of collagen cross-linking-mediated stiffening of the matrix on cancer cell dissemination (15,16). The mechanical and structural changes of the environment could significantly affect the cellular traction force of the residing cancer cells, which is a key regulator of migration (15). Chavrier and colleagues have shown that the contractility of the rear part of the cell promotes migration and invasion of MDA-MB-231 cells in a Matrigel network (6). In a similar way, studies have shown that contractile forces contribute to glycosylphosphatidylinositol-anchored receptor-CD24-facilitated cancer cell invasion (17). The increased invasiveness could also be attributed to traction-stress-mediated invadopodia formation (12). Studies have also reported significant differences in mechanical properties of the cells with their metastatic competence (18).

The aforementioned studies clearly demonstrate the pivotal role played by the physical properties of the ECM in promoting invasion and migration of cancer cells. In this study, we quantify the interdependence between the initiation of cancer cell invasion into 3D matrices and the mechanical resistance of the matrix to cell penetration. To this end, using MDA-MB-231 cells as a model system, we developed a quantitative single-cell invasion assay and determined the role of cell-generated three-dimensional (3D) traction stresses in driving cancer cell invasion and protease activity.

Materials and Methods

Cell culture

MBA-MD-231 (ATCC, Manassas, VA) cells were expanded in growth medium (GM) comprised of high glucose Dulbecco’s modified Eagle’s medium (Life Technologies, Carlsbad, CA), 10% fetal bovine serum (Hyclone, Logan, UT), 2 mM L-glutamine (Life Technologies), and 50 units/mL of penicillin/streptomycin (Life Technologies). The cells were maintained at 37°C and 5% CO₂.

Fabrication of Matrigel networks tethered to glass

To tether the Matrigel networks, glass-bottom dishes (Fluorodishes, World Precision Instruments, Sarasota, FL) were activated to react with amine groups of the Matrigel network. To activate the glass surfaces, 2.5 M NaOH was added for 30 min to remove impurities from the glass surface (19). The glass-bottom dishes were then rinsed with distilled water, dried, and reacted with 3-aminopropyl-trimethoxysilane (Sigma, St. Louis, MO) for 7 min. The treated dishes were then washed with distilled water, dried, and reacted with 0.5% glutaraldehyde (GA) (Electron Microscopy Sciences, Hatfield, PA) for 40 min. The activated surfaces were rinsed thoroughly and kept in distilled water for an additional 30 min. All of the above reactions were carried out at room temperature. The activated glass-bottom dishes were used immediately.

The Matrigel networks were formed according to the manufacturer’s instructions. Briefly, frozen Matrigel (cat. no. 354234, lot no. 30133, BD Biosciences, San Jose, CA) solutions were thawed overnight on ice at 4°C. Fluorescent particles with a nominal diameter of 200 nm (Fluospheres, Life Technologies; max excitation at 660 nm and max emission at 680 nm) were dispersed in the Matrigel solution to achieve a final concentration of 2% (v/v). After mixing thoroughly, 18.75 μL of the solution was quickly transferred to the activated glass-bottom dish and spread over a circular region of ∼15 mm in diameter. The solution was then spun using a Spin Coater KW-4A (Chemat Scientific, Northridge, CA) at room temperature for 1 min at 600, 800, 1100, and 1300 RPM to thin the Matrigel solution to create networks of thicknesses (T) 30, 20, 10, and 6 ± 2.5 μm, respectively, without altering the Matrigel concentration. The spun Matrigels were incubated at 37°C for 6 min to complete gelation before the addition of phosphate-buffer saline solution (PBS). After 15 min of incubation in PBS, the Matrigel was ultraviolet-sterilized for 30 min before replacing the PBS with GM. The thicknesses of the equilibrated Matrigels were determined using a spinning-disk confocal microscope (UltraView Vox Spinning Disk Confocal, Perkin Elmer, Waltham, MA). The difference in the vertical position at which the fluorescent beads were in focus at the top and bottom of the gel was designated as the thickness of the gel. Both the surface and the bottom of the Matrigels were imaged at multiple locations to determine the gel thickness. Fig. S1 in the Supporting Material shows the X-Y and X-Z cross-sectional images of Matrigel networks of varying thickness. The dishes were then incubated in medium at 37°C and 5% CO₂ overnight prior to cell seeding.

Cell invasion and imaging

The invasion of MDA-MB-231 cells into the Matrigel network was determined by using a quantitative single-cell invasion assay. MDA-MB-231 cells were plated onto the Matrigel networks tethered to the glass-bottom dishes at a density of 6000 cells/cm² in GM with serum or OptiMEM (OM) (Life Technologies) for serum-free conditions. The cells were allowed to invade into the Matrigel for 1, 2, and 4 h. Individual cells were imaged, and their corresponding stage positions were marked. For each location, differential interference contrast was used to acquire an image of the cell and fluorescence image stacks of the matrix embedded with fluorescent particles. The z-slice spacing was set as 200 nm and the z-range was chosen to encompass 3 μm above the surface of the Matrigel to 3 μm below the maximum penetration depth of the cells. Previously marked stage positions were reimaged after the removal of the invading cells. A total of n > 160 cells were used and analyzed.

Removal of cells after cell invasion

The invading cells were removed using a cell-dissolving solution, as described elsewhere (20). The cell-dissolving solution was made by mixing NH₄OH and Triton X-100 in PBS to achieve a final solution containing 20 mM NH₄OH and 3% w/v Triton X-100. To remove the cells, 1 mL of the culture medium was removed from the 2 mL total volume before adding 0.5 mL of the cell-dissolving solution. To this, 2 mL of PBS was added before removing 3 mL of the above mixture followed by a further addition of 2 mL of PBS. The continuous washing with PBS was used to neutralize the drastic changes in pH due to the cell-dissolving solution (Fig. S2 A). The effect of the cell removal process on swelling and/or shrinking of the Matrigel network was determined as described in the Supporting Material (Fig. S2, B–E). The removal of cells was also confirmed through bright-field images and staining for F-actin. (Fig. S3).

Mechanical yielding of Matrigel networks

A series of experiments were carried out to determine the mechanical yielding of Matrigel used in this study, as described in the Supporting Material).

MT1-MMP FRET analysis

Cells were plated into 24-well plates, cultured in GM, and allowed to reach 80% confluence before transfection. The cells were transfected with MT1-MMP fluorescence resonance energy transfer (FRET) biosensor plasmid using Fugene HD Transfection Reagent (Promega, Madison, WI) 2 days before the experiments. For transfection, each well containing cells was exposed to 1.7 μL of Fugene transfection reagent mixed with 25 μL of OM containing 1.1 μg of the DNA plasmid. Before plating the cells, 50 μg/mL of fibronectin (Sigma) diluted in PBS was coated onto glass surfaces or 30-μm-thick Matrigels for 1.5 h at 37°C. Untreated cells or cells treated overnight with the MMP inhibitor GM6001 (50 μM) were plated on either glass or Matrigel surfaces. Images were collected 4 h postplating using a Zeiss Axiovert inverted microscope equipped with a 100× objective (1.4 NA) and a cooled charge-coupled device camera (Cascade 512B, Photometrics, Tucson, AZ) using the MetaFluor 6.2 software (Universal Imaging, Bedford Hills, NY). The parameters of dichroic mirrors and excitation and emission filters for different fluorescence proteins were described previously (21). In brief, the MT1-MMP biosensor was excited at 420 ± 20 nm, and the emissions were collected at 475 ± 40 nm or 535 ± 25 nm for enhanced cyan fluorescent protein or FRET images, respectively. Quantification of the ratio of enhanced cyan fluorescent protein signal to FRET (FRET ratio) signal was performed using our MATLAB-based software fluocell (22,23). A higher FRET ratio indicates increased activity and/or presence of MT1-MMP on the cell surface.

Zymography and fluorogenic peptide assay

Secreted proteases were detected using zymography and fluorogenic peptide assays. A detailed description is provided in the Supporting Material.

Immunofluorescence staining and imaging

MDA-MB-231 cells were plated onto Matrigel at a seeding density of 6000 cells/cm² and allowed to invade the matrix for over 2 h. To stain cells generating steep indentations (ϕ_3D > 10°), Matrigels with the invading cells were fixed in 4% paraformaldehyde for 10 min, washed in PBS, and incubated in a blocking buffer containing 3% bovine serum albumin and 0.25% triton X-100 in PBS for 30 min. The fixed cells were incubated with primary antibodies such as Alexa Fluor 488-conjugated Phalloidin (Life Technologies), anti-Cortactin p80/85 antibody (Millipore), and/or anti-MT1-MMP (cat. No. Ab38970, Abcam, Cambridge, MA) diluted 1:100 in the blocking buffer for 1 h at room temperature. The samples were washed extensively in PBS before adding Alexa Fluor 568-conjugated secondary antibody diluted (1:250) in the blocking buffer for 1 h. The samples were washed in PBS and were imaged immediately.

For cells generating flat indentations (ϕ_3D < 10°), GA-mediated fixing of the cells was found to provide the best results. The cells were plated at a density of 20,000 cells/cm² and were allowed to invade for 15 min before fixation with 0.1% w/v GA in PBS for 1 min. The higher cell density was used to ensure that enough cells invaded the matrix during the short time span. The samples were subsequently washed in PBS and permeabilized with blocking buffer for 30 min. After removing the blocking buffer, the GA-treated samples were incubated in 0.1% w/v sodium borohydride in PBS to neutralize unreacted aldehyde moieties for 30 min to quench the autofluoresence. Sodium borohydride was subsequently removed, and the samples were washed in PBS before incubation with primary and secondary antibodies.

All experiments were carried out independently at least three times, beyond the replicates used in each experiment.

Method Development

Quantitative cell invasion assay

We have developed a quantitative single-cell invasion assay that can quantify the traction stresses and accompanying matrix deformations as the cancer cells migrate into the matrix. The cell invasion assay utilized an ECM network, Matrigel, tethered onto glass and embedded with fluorescent particles to track the progressive matrix deformation as MDA-MB-231 cells invade the matrix as single cells (Fig. 1 A) (see text in the Supporting Material and Fig. S4 for characterization of the Matrigel networks). We choose Matrigel because of its tight network microstructure (mesh size ≤20 nm); absence of large network pores and channels will eliminate the possibility of cells squeezing through the network (24,25).

Figure 1.

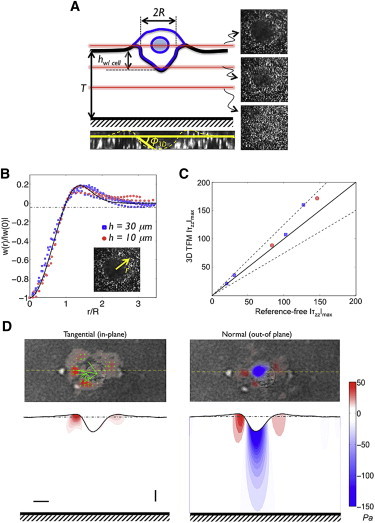
Quantitative single-cell invasion assay. (A) Schematic representation of a cancer cell (MDA-MB-231) invading a Matrigel network embedded with 200 nm fluorescent beads and tethered onto glass. Experimentally obtained confocal z-stack images are shown. The red lines illustrate the confocal sectioning along the vertical axis of the invading cells. h_w/cell and R denote the depth and radius, respectively, of matrix indentation during cell invasion. T is the thickness of the Matrigel. ϕ_3D is the indentation angle, defined as ϕ_3D = tan⁻¹(h_w/cell/R). (B) Indentation profiles generated by invading cells along the radial direction (inset) are shown in blue squares and red circles for cells in 30-μm- (n = 4) and 10-μm-thick (n = 2) Matrigels, respectively. The black line is a semiempirical fit, which shows an agreement between the experimental data and the model and satisfies mechanical equilibrium. The y axis indicates the normal deformation at various radial locations, w(r), normalized to the deformation at the center of the indentation, w(0). (C) Maximum compressive stresses exerted by the cells depicted in B, obtained using our novel reference-free TFM method (x axis) and the 3DTFM method of del Alamo et al. (26) (y axis). The solid line represents x = y (zero error), and the dashed lines represent y = 0.75× and y = 1.25×. (D) Tangential and normal traction stresses of MDA-MB-231 cells elastically deforming a 30-μm-thick Matrigel obtained using 3DTFM. Upper images display the traction stresses on the free surface of the gel (i.e., the xy plane) superimposed on the differential interference contrast cell image. The lower images display the measured traction stresses and deformation profile on the vertical section of the gel (i.e., the xz plane), corresponding to the yellow dashed lines in the upper images, showing the propagation of normal stresses into the gel. The color bar represents the magnitude of the stresses, and the green arrows indicate the direction and magnitude of the tangential stresses. Horizontal and vertical scale bars are 5 and 1 μm, respectively. To see this figure in color, go online.

Confocal-image quantification of the profile of matrix indentation caused by the invading cells

MDA-MB-231 cells were allowed to invade the Matrigel network and the process was imaged using a confocal microscope to detect the accompanying matrix deformation. The image stacks corresponding to cell invasion were analyzed using a custom MATLAB code to quantify the depth of matrix indentation caused by the cells H_i(x,y), the maximum indentation depth caused by the cells h_{w/ cell}, the indentation depth after cell removal, h_{w/o cell}, and the radius of indentation, R (Fig. S5). First, each z-slice of the stacks was normalized with the average image intensity of the whole z-stack. A Sobel edge detection filter was applied to each slice in the stack to detect and count the number of in-focus pixels as a function of z (Fig. S5, blue line). The slice with the maximum z-change of in-focus pixels is set as the top surface of the matrix and used as a reference to obtain the indentation profile, h_{w/ cell}, h_{w/o cell}, and R. For each image slice, we calculated the in-plane Euclidean distance transform, which yielded the minimum distance to an in-focus pixel in that z-slice. Because cell indentation pushed the beads downward and out of focus (Fig. S5, inset, or Fig. 1 A), the maximum value of the Euclidean distance in the whole z-stack was defined as R (Fig. S5, green circles). On the other hand, the z-slice at which the Euclidean distance reached its floor was designated as the bottom of the cell. The z-distance between the top and bottom slices provided h_{w/ cell}. After cell removal, the previously marked positions of the cells (i.e., before their removal) were reimaged to determine h_{w/o cell}.

The quantities h_{w/ cell} and h_{w/o cell}, provide unique information about the nature of matrix deformation due to cell invasion—elastic versus permanent. The extent of permanent matrix deformation caused by the invading cells was quantified by the ratio of maximum indentation depths before and after removing the cells, γ = h_{w/o cell} divided by h_w/ cell. A value of γ = 0 indicates elastic recovery, whereas γ ≠ 0 suggests permanent deformation of the matrix due to structural changes during cell invasion. The deformation of the matrix was further quantified using the angle of 3D indentation, calculated as ϕ_3D = tan⁻¹(h_{w/ cell}/R), where R is the radius of matrix deformation (Fig. 1 A). The angle ϕ_3D quantifies whether the matrix deformation created by the cell is flat (ϕ_3D ≈ 0) or steep (ϕ_3D ≈ 90°). Representative indentation profiles of the Matrigel network with varying thickness during cell invasion are shown in Fig. 1 B.

To eliminate the interference of postplating time on degree of permanent deformation of the matrix, we have determined ϕ_3D values for different postplating times (1, 2, and 4 h). Our results indicate that a subset of cells imaged at different postplating times attain similar ϕ_3D values. Therefore, to rule out the possibility of these cells exhibiting a different extent of matrix degradation as a function of time, the γ values for cells at similar ϕ_3D values but different plating times were plotted (Fig. S6). The effect of time on the degree of permanent deformation was negligible, since the γ values for cells analyzed at different postplating times were statistically insignificant.

Calculation of 3D traction stresses during cell invasion

To calculate 3D traction stresses such as those shown in Fig. 1 D, we acquired time-lapse z-stack images of cells invading the Matrigel. The cells were removed before the matrix was permanently deformed, and 3D Fourier traction force microscopy (3DTFM) methods described in detail elsewhere (26,27) were used to determine the stresses generated by the cells. The lack of degradation of the Matrigel was experimentally confirmed by the lack of vertical surface indentation after cell removal. Corresponding images of the undeformed matrix were used as a reference state to obtain the matrix 3D deformation of each z-stack. Imposing these measurements as boundary conditions and zero displacements at the bottom of the matrix tethered to glass, we obtained the exact analytical solution to the equation of elastic equilibrium for a homogeneous and isotropic 3D body:

$$\nabla \left(\nabla ·\overrightarrow{u}\right)+\left(1-2\sigma \right){\nabla }^2\overrightarrow{u}=0$$ (1)

The solution to this equation provided the full 3D strain tensor in the whole Matrigel network, which was plugged into Hooke's law to calculate the traction stresses. An important feature of this solution is that it takes into account the finite thickness of the gel (26,27). The Poisson’s ratio of the Matrigel network was approximated to be 0.495, and the elastic modulus was measured as 400 Pa. (see Supporting Material text, Fig. S4).

Reference-free estimation of normal traction stresses during cell invasion

Standard 3DTFM methods, such as that used to plot Fig. 1 D, require imaging the network in an undeformed condition to use it as a zero-stress reference (26,28–31). This can be achieved by either tracking single particles or, as done in our study, by applying image correlation techniques (32,33). However, if cells switch from protease-independent to protease-dependent invasion, the network may experience permanent remodeling and it may not be in an undeformed reference condition after cell removal. This also imposes stringent experimental requirements that an unperturbed zero-stress reference state needs to be imaged for each cell before the invasion process. To circumvent these limitations and to determine the threshold traction stress at which the invading cells switch from a protease-independent to a protease-dependent mode, we developed a reference-free method that does not require imaging the undeformed condition to measure the compressive traction stresses generated by the cells. This method models the measured indentation profiles generated by the invading cells as

$$H\left(x,y\right)=h_{w/cell}\left(\frac{r^6}{6{\lambda }^6}-1\right)e^{-\frac{r^2}{{\lambda }^2}},$$ (2)

where $r=\sqrt{x^2+y^2}$ is the distance to the indentation center. The parameters h_{w/ cell} and R were determined experimentally, and λ = 0.74R was fixed by imposing w(R) = 0. The functional dependence of this model profile was chosen to conform to the following experimental observations and physical considerations: 1), the vertical deformation caused by the cell is negative (i.e., downward) under the cell center and positive around the cell periphery (Fig. 1); 2), the vertical deformation decays to zero away from the cell periphery; and 3), the cell is in mechanical equilibrium. The model is plotted in Fig. 1 B together with measurements of matrix deformation in the normal direction for several cells showing good agreement with experimental data regardless of the matrix thickness.

For each cell, the normal traction stresses were computed using Eq. 2 for the normal deformation profile and zero tangential deformation in the 3DTFM equations (26). In particular, we focused on the maximum negative value of the normal traction stresses,τ_zz(0), which is found at the lowest point of the indentation, because this value indicates the pushing force exerted by the cell to penetrate into the matrix. Fig. 1 C compares the value of τ_zz(0) obtained with this reference-free method with that obtained using the full 3DTFM method of del Alamo et al. for a small group of cells to which both methods were applied (26). The results show good agreement between the two methods, although the reference-free method slightly under estimates τ_zz(0) (mean error = 11%) due to the averaging involved in the fitting procedure used to obtain h_{w/ cell} and R. This approach is further justified because the normal traction stresses are much higher than the tangential ones for the invading cells, and the tangential stresses are zero under the central region of the cell where the normal stresses are maximal (Fig. 1 D). This reference-free approach facilitates high-throughput and quantitative analyses of individual cells with varying indentation profiles. Our calculation of normal stresses is flexible regarding the shape of H(x,y), which could be easily replaced by any other profile. It should be noted that a Hertz model could not be used for this purpose, as the cells not only pushed into the matrix but also pulled away from it (Fig. 1 B) to satisfy the mechanical equilibrium condition.

Estimation of apparent Young’s modulus encountered by the invading cells

Because the Matrigel networks are anchored to the underlying glass, which is significantly stiffer compared to the Matrigel network, and because compressive traction stresses penetrate deep into the gel (Fig. 1 D), the apparent Young’s modulus encountered by the cells has been shown to increase as the thickness of the matrix decreases to a value comparable to cell size (26). To quantify the apparent Young’s modulus (E_app) encountered by each invading cell, we multiplied the nominal Young’s modulus of the Matrigel (E = 400 Pa) by the ratio of the measured normal traction stresses considering the finite thickness of the matrix to the stresses calculated for a matrix of infinite thickness (26):

$$E_{\text{app}}=E\frac{{\tau }_{zz}\left(h\right)}{{\tau }_{zz}\left(\infty \right)}.$$

Results and Discussion

Invasion of MDA-MB-231 cells into Matrigel networks

By employing the quantitative cell invasion assay, we have determined the invasion of MDA-MB-231 cells into a Matrigel network of 30 μm thickness tethered onto glass. The 3DTFM analyses of the invading cells suggest that to invade downward into Matrigel, the cell pulled away from the matrix at several locations along its periphery while pushing against the matrix under its center (see Fig. 1 D). Because all forces must be in equilibrium, as cell inertia is negligible, this leads to a significant amplification of the pushing stresses (by a factor of >3, as in Fig. 1 D), a mechanism that we call stress focusing. These normal traction stresses (τ_zz) were also found to be much higher than the tangential ones ($\sqrt{{\tau }_{zx}^2+{\tau }_{zy}^2}$), suggesting that the invading cells were actively burrowing through the matrix using mechanical force. Because pushing traction stresses penetrate much deeper into the matrix than pulling and shearing traction stresses, it could be possible that cells utilize this type of force to sense the mechanical resistance exerted by the matrix (Fig. 1 D and Movie S1).

The cell invasion analyses demonstrate that as the cells invade deeper into a 30-μm-thick matrix, they create steeper matrix deformations, leading to an increase in ϕ_3D and h_w/ cell (Fig. 2 A). The cells exerting these large deformations (ϕ_3D ≥20° and h_{w/ cell} > 5 μm) resulted in permanent matrix deformations (Fig. 2B). On the contrary, for small deformations (ϕ_3D ≤ 10° and h_{w/ cell} ∼2 μm), the cells deformed the matrix elastically and the Matrigel recovered its undeformed state after cell removal. Permanent deformation due to pure mechanical yielding of the matrix in response to cellular traction stresses was ruled out, because the Matrigel did not undergo permanent deformation when subjected to pure mechanical loads >200 Pa—a value higher than the maximum traction stress measured at the transition from elastic to permanent matrix deformation (see text in the Supporting Material and Figs. S7 and S8) (34). Thus, the permanent deformations observed during cell invasion for large matrix indentations were due to proteolytic degradation of the Matrigel network.

Figure 2.

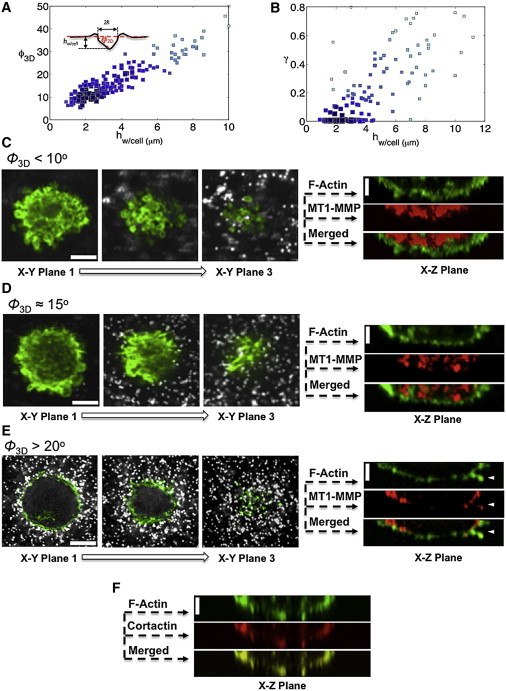
Invasion of MDA-MB-231 cells into 30-μm-thick Matrigel networks. (A) Scatter plot of the increase in the indentation angle, ϕ_3D, as the cells invade into the Matrigel network. Each symbol corresponds to one cell. The size and color of the symbols are proportional to the density of data points such that large, dark symbols indicate highly frequent occurrences. (Inset) Schematic of matrix indentation generated by the invading cells. (B) Corresponding scatter plot showing the extent of permanent matrix deformation caused by the invading cells, γ, as a function of invasion depth, h_w/cell. As in A, each symbol corresponds to one cell and large, dark symbols indicate highly frequent observations. (C–E) Confocal z-slice images of the invading cells as a function of ϕ_3D. (Left) Images in the xy plane showing the F-actin staining (green) and beads (white) within the network. (Right) Section in the xz plane of the corresponding xy image stacks for F-actin (green) and MT1-MMP (red). At ϕ_3D ≤ 10°, plasma membrane blebbing was observed (xy plane 1–3), whereas MT1-MMP was located in the cytoplasm (xz plane). At ϕ_3D ∼ 15°, the extent of blebbing diminished and MT1-MMP was again detected within the cytoplasm. At ϕ_3D ≥ 20°, actin-rich invadopodia-like protrusions filled with MT1-MMP were observed at the cellular cortex (arrowheads). (F) Colocalization of F-actin and cortactin confirms invadopodia formation. Scale bars (both horizontal and vertical), 10 μm. To see this figure in color, go online.

This transition from elastic to permanent matrix deformation as the cells invade deeper into the matrix suggests a switch from a protease-independent to a protease-dependent mode of invasion. To further understand the cellular responses associated with different modes of invasion, we examined the changes in F-actin and MT1-MMP, a key MMP involved in MDA-MB-231 invasion (2,35) for the population of cells that elastically and permanently deformed the 30-μm-thick matrix. Immunofluorescent staining for F-actin revealed plasma membrane blebbing, which preceded the invasion of cells into the Matrigel and persisted until a ϕ_3D of ∼15° and h_{w/ cell} of ∼3 μm were reached. The majority of these blebs were found at the leading edge of the cell, whereas the MT1-MMPs were clustered within the cytoplasm (Fig. 2, C and D, and Movie S2). The absence of MT1-MMP on the cell periphery for small matrix deformations was confirmed by low levels of MT1-MMP FRET signal, comparable to those for cells treated with the broad-spectrum MMP inhibitor GM6001 (Fig. 3 A, left and center, and Fig. 3 B). The matrix-mediated bleb formation was also observed in cultures containing no serum, thus eliminating the contribution of serum components to this phenomenon (Fig. S9).

Figure 3.

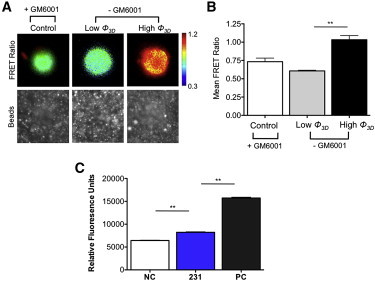
Protease activity during invasion of MDA-MB-231 cells into 30-μm-thick Matrigel networks. Cells were transfected with the MT1-MMP FRET biosensor to detect the activity of MT1-MMP at the cell surface. High FRET ratio indicates active MTI-MMPs at the cell surface. (A) MT1-MMP activity map for cells invading 30-μm -thick Matrigel for low (ϕ_3D < 10°) and high (ϕ_3D > 20°) angles of 3D indentation. The MMP inhibitor GM6001 was used as a control (left). (B) The mean FRET ratios for the cells shown in A. These ratios were found to be significantly lower for cells at low ϕ_3D than for those at high ϕ_3D. ^∗∗p < 0.05, calculated using Student’s t-test (n > 12). (C) Fluorogenic peptide assay for broad-spectrum secreted proteases measured at 405 nm wavelength is shown for negative controls (NC), 231, and positive controls (PC). Negative controls indicate growth medium collected from acellular Matrigel, and positive controls indicate growth medium collected from acellular Matrigel containing bovine collagenase IV, whereas 231 indicates medium collected from Matrigel networks with invading MDA-MB-231 cells (ϕ_3D > 20°). ^∗∗p < 0.005, calculated based on one-way analysis of variance followed by the Bonferroni posttest (n = 3). Error bars indicate the mean ± SD. To see this figure in color, go online.

Conversely, for large matrix deformations (ϕ_3D > 20° and h_{w/ cell} > 4 μm), blebbing was no longer observed and the MT1-MMP was relocalized from the cytoplasm to the plasma membrane. These cells with round morphology exhibited invadopodia-like protrusions enriched with actin fibers, cortactin, and MT1-MMP at the leading edge (Fig. 2, E and F and Movie S3) (36–39). Although cortactin was located all along the protruded structures, MTI-MMP was located at the base of the invadopodia in discrete locations. At the onset of permanent matrix deformation, the invading cells showed the coexistence of bleb and invadopodia-like structures (Fig. S10). A recent study by Bergert et al. has shown that migrating cells exhibit bleb-to-lamellipodium transition in response to changes in actomyosin contractility (40). Giri et al. reported that cells use dendritic protrusions to deform the surrounding matrix (41). The relocalization of MTI-MMP to the cell membrane and MT1-MMP activation with large matrix deformation was further confirmed by FRET analyses using MT1-MMP biosensors (Fig. 3, A and B) (42). We also observed the presence of secreted MMPs and their activity by zymography and by monitoring the cleavage of MMP-sensitive fluorogenic peptides (Fig. 3 C and Fig. S11).

Effect of mechanical resistance on invasion of MDA-MB-231 cells

To decouple the role of traction stresses in triggering protease activity from the influence of other parameters, such as steepness and depth of the matrix indentation, we examined the invasion of MDA-MB-231 cells into Matrigel networks that exert varying levels of mechanical resistance, keeping the network composition and interfacial properties constant. Matrigel networks with similar interfacial properties but varying effective rigidity were created by adjusting the overall thickness of the gels to approximately T = 10, 20, and 30 ± 2.5 μm. This quantitative approach allows a unique way to vary the mechanical resistance in a controlled manner without altering the network composition and matrix surface properties across the experiments, thus eliminating the effect of matrix interfacial properties on cell functions (43,44).

As the thickness of the gels decreased, the apparent Young’s modulus encountered by the cells increased and a higher fraction of cells deformed the matrix permanently (Fig. 4 A, first and second graphs). Cells on thinner gels elicited permanent matrix deformation at smaller matrix deformations and shallower indentation angles (Fig. 4 A, third and fourth graphs), suggesting that neither h_{w/ cell} nor ϕ_3D were decisive factors in triggering proteolytic ECM degradation. The critical values of h_{w/ cell}, ϕ_3D, and normal traction stress at the transition between protease-independent and protease-dependent invasion were determined by averaging data from cells with 0.05 < γ < 0.2, which had barely degraded the ECM. Contrary to h_{w/ cell} and ϕ_3D, the critical value of normal traction stresses (i.e., the pushing traction forces) at the transition between elastic and permanent matrix deformation, |τ_zz,(0)|_crit, was found to be independent of gel thickness and around 165 ± 20 Pa (Figs. 4 A, fifth graph, and Fig. S12). Because the normal traction stresses were calculated assuming elastic deformation (γ = 0), our prediction of τ_{zz, crit}, could possibly overestimate the true traction stresses at the onset of proteolytic matrix degradation. Nevertheless, it should be noted that the small error associated with this approach (5–20%) is lower than the statistical noise in the measurements (the standard deviation in the plot is ≈33% of the mean), and it does not introduce a bias when considering different matrix thickness.

Figure 4.

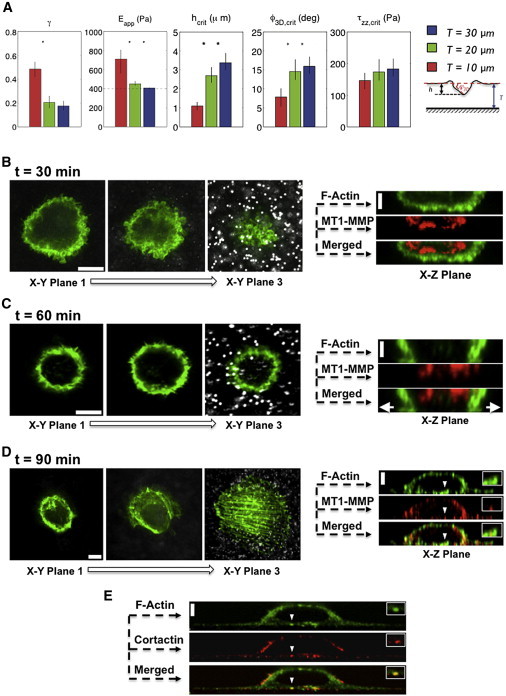
Effect of mechanical resistance on the invasion of MDA-MB-231 cells into Matrigel networks. (A) The leftmost graph shows the average value of permanent deformation for cells invading Matrigel networks of thickness T = 10 (red), 20 (green), and 30 μm (blue). The second graph shows the apparent elastic modulus of the Matrigel encountered by the cells for each gel thickness, E_app. The nominal elastic modulus of the gel is 400 Pa. Higher values of E_app of thinner gels reflect an increase in gel stiffness caused by the proximity of the rigid glass coverslip. The last three graphs show the h_crit, ϕ_3D,crit, and τ_zz,crit for cells invading Matrigel networks of varying thickness calculated in the range γ = 0.05–0.2. Values of h_crit, and ϕ_3D,crit increase with mechanical resistance while the compressive traction stresses at which the cells switch from elastic to permanent deformation of the matrix,τ_zz,crit, remain constant. Stars denote statistically significant differences among groups using the Kruskal-Wallis nonparametric analysis of variance (^★p < 0.005; ^∗p < 0.05). Error bars indicate the 5% confidence interval of the mean (n = 73, 88, and 161 for T = 10, 20, and 30 μm respectively). (B–D) Confocal images of cells invading a 6-μm-thick Matrigel network at ϕ_3D ≤ 5° with varying postplating time (30–90 min). At left are three xy images showing F-actin staining (green) and beads (white) within the network, and at right are the corresponding xz sections showing F-actin (green) and MT1-MMP (red) staining. At t = 30 min, plasma membrane blebbing was observed in cells similar to invasion into 30-μm-thick Matrigel (xy plane 1–3). MT1-MMP was detected within the cytoplasm (xz plane). At t = 60 min, the blebs were found to divert along the Matrigel surface, as indicated by arrowheads (xy plane 1–3). MT1-MMP was again detected within the cytoplasm (xz plane). At t = 90 min, cells adopted a spread morphology with the appearance of actin stress fibers at the basal domain of the cell (xy plane 1–3). The MT1-MMP translocated to the cellular periphery (xz plane). (E) The presence of invadopodia is observed through colocalization of cortactin and F-actin at discrete locations. (Insets in the xz-plane images (D and E)) Magnification of the location of invadopodia formation indicated by white arrowheads. Scale bars (both horizontal and vertical), 10 μm. To see this figure in color, go online.

We also examined the bleb-to-invadopodia transition for cells invading a thinner Matrigel exhibiting very small matrix deformations. Similar to the case for the 30-μm-thick matrix, bleb formation was observed before any substantial deformation of the matrix was detected whereas MT1-MMPs remained within the cytoplasm (Fig. 4 B). As cells continued the invasion process, blebbing was deflected along the cell-matrix interface whereas MT1-MMP still remained in the cytoplasm (Fig. 4 C). This suggests that the blebs were unable to push forward in the normal direction, where they encountered a higher mechanical resistance due to the influence of the glass at the bottom of the gel. As the cells spread farther on the Matrigel surface, the blebbing disappeared, actin stress fibers formed at the basal domain of the cells, and invadopodia-like protrusions were localized with cortactin and MTI-MMP (Fig. 4, D and E). These findings further confirm that invadopodia enriched with MT1-MMP form at low matrix deformation when the mechanical resistance is increased.

Together, these findings identify traction stresses as a key determinant in triggering protease-dependent cancer cell invasion into 3D matrices. This is in accordance with recent studies that suggest that mechanical forces play a role in extracellular proteolysis (8,12,13,45). Although other extracellular matrix properties, such as pore size and fibrillar structure(s), were not addressed, the findings from this study can be easily extended to unravelling the effect of these ECM properties on cancer cell invasion. The physical characteristics of the ECM provide different levels of mechanical resistance, and thereby cell-generated traction stresses, to trigger protease-mediated invasion and migration. For instance, in networks with large pores, cells can migrate through the matrix with minimal resistance and thus would be in a state below the threshold of traction forces (7). On the other hand, the alignment of the fibrillar structure of the ECM mediated by the cells increases the mechanical tension in the extracellular network and promotes proteolysis (8). Furthermore, the anisotropic alignment of 3D cellular traction stresses has been correlated with cancer cell invasiveness (30). The interplay between traction stresses and ECM remodeling could also vary dynamically, as the cell could adapt its protease-dependent invasive phenotype to the time-evolving resistance resulting from matrix degradation. Future development of quantitative force microscopy assays that consider inhomogeneity and anisotropy of the ECM, as well as its time-evolving material properties, will provide further insight into the interplay between traction stresses and protease-dependent cancer cell invasion into 3D matrices.

Conclusion

In summary, the results reported here demonstrate the role of 3D traction stresses in regulating the mode with which cancer cells invade ECM networks to contribute to cancer metastasis. We showed that invading cells pull away from the matrix at several locations while compressing the matrix at only one site, thus enabling a stress-focusing mechanism that amplifies the compressive load applied to the matrix and conceivably promotes invasion. At low compressive stresses, the cells indent the matrix in a protease-independent manner using bleb formation. However, at compressive traction stresses >∼165 Pa, the cells invade in a protease-dependent manner, utilizing invadopodia-like structures where MT1-MMP activity on the cell surface is high. Identification of such quantitative approaches not only could advance our understanding of the interdependence of cell mechanics and ECM proteolysis in dissemination of cancer but could also aid in identifying new pathways that might be targeted to develop therapies to treat cancer metastasis.

Supporting Citations

References (46–48) appear in the Supporting Material.