Scanning X-Ray Nanodiffraction on Dictyostelium discoideum

Abstract

We have performed scanning x-ray nanobeam diffraction experiments on single cells of the amoeba Dictyostelium discoideum. Cells have been investigated in 1), freeze-dried, 2), frozen-hydrated (vitrified), and 3), initially alive states. The spatially resolved small-angle x-ray scattering signal shows characteristic streaklike patterns in reciprocal space, which we attribute to fiber bundles of the actomyosin network. From the intensity distributions, an anisotropy parameter can be derived that indicates pronounced local variations within the cell. In addition to nanobeam small-angle x-ray scattering, we have evaluated the x-ray differential phase contrast in view of the projected electron density. Different experimental aspects of the x-ray experiment, sample preparation, and data analysis are discussed. Finally, the x-ray results are correlated with optical microscopy (differential phase contrast and confocal microscopy of mutant strains with fluorescently labeled actin and myosin II), which have been carried out in live and fixed states, including optical microscopy under cryogenic conditions.

Introduction

Directed movements of cells involve rearrangements in the cytoskeleton that determine cell shape dynamics. An understanding of the physics and biology underlying these processes requires a quantitative description from the molecular to the mesoscopic scale, including predictive models that relate, for example, the observed dynamics at the leading edge of the cell to the intracellular signaling processes (1). For experimental validation, advanced techniques with high spatial and (if possible) adequate temporal resolution are needed. Representative for a multitude of eukaryotic cellular migration modes, directed amoeboid cell motion can yield basic insights (2–4).

For example, the migratory social amoeba Dictyostelium discoideum has been established as a genetically fully controlled model system (4–6). Upon immersion in buffer, D. discoideum cells enter a starvation cycle during which they are chemotactically tracking sources of the signaling molecule cAMP (7) and reach a maximum motility after ∼6 h. The chemotactic migration is accompanied and enabled by a reorganization of cytoskeletal biopolymers in the cell cortex. As is well known, the active movement of eukaryotes is promoted by controlled polymerization and depolymerization actin fiber bundles (8). One essential feature of cell migration is pseudopod formation, where the cell membrane is locally pushed outwards (treadmilling (9–11)) by actin polymerization. Alongside the pseudopodiae, at the cellrear, a network of actin, together with myosin-II motor proteins, is involved in contractile retraction (12). Although much is known about the underlying actin network and its reaction dynamics, the detailed structure of actin fiber bundles and its rearrangement during migration is still elusive.

Actin filaments can form ordered bundles, which have been investigated in vitro by confocal fluorescence and small-angle x-ray diffraction (SAXS) (13,14). High-resolution micrographs of actin networks in cells are available by cryogenic electron transmission microscopy (15,16), but at the price of invasive sample preparation, which can be accompanied by staining, cutting, and/or dehydration artifacts. Contrarily, x-rays are compatible with hydrated environments and can easily penetrate the entire cell. Cellular diffraction, which is a relatively new technique (17–19), can overcome the restrictions associated with conventional SAXS, apart from extending x-ray structure analysis from the in vitro to the in vivo level. By nanofocused x-ray diffraction on a precisely controlled region of the cell, one can overcome the loss of information inherent in the spatial and orientational averaging that is associated with conventional SAXS (20).

Beyond analysis in reciprocal space, coherent diffractive x-ray imaging (CDI) has emerged in recent years as a novel method capable of visualizing the electron density in two or three dimensions (by tomographic extension). Unstained and unsliced biological cells can be investigated by this method (17,21–25). To date, however, CDI has always been limited to moderate resolution, not reaching the resolution of typical diffraction experiments on soft matter samples. For this reason, combining high-resolution diffraction patterns with moderate resolution in real space (17–19) is a promising strategy. Unstained living cells are clearly the goal for this approach, inasmuch as standard procedures, such as fixation with formaldehyde, have already been shown to influence the structure (19); however, it is also true that a fixed state (chemically or cryogenically) is a necessary intermediate step.

Here we perform cellular nanodiffraction to study the actin network in D. discoideum. The density of the actin cortex and fiber orientation, as well as mean spacing, elastic anisotropy, and cross-linking density, are properties of the cytoskeleton that are defined by a local average on length scales of 10–1000 nm (26,27). These properties can therefore be well probed by diffraction with a beam of equivalent size. By analysis of the recorded diffraction patterns, Fourier components corresponding to smaller structures than the beam size become accessible, averaged locally over a controlled area in the cell. Nanodiffraction thereby gives information similar to a SAXS experiment with two important differences: 1), the scattering volume is scaled down by up to 7–10 orders of magnitude, enabling an association with local structure; and 2), anisotropy of the SAXS pattern is not averaged out, enabling more general structural models.

Conceptually, the nanodiffraction approach is simple and robust. The sample holder or chamber with fixed or live cells (here D. discoideum AX2) is scanned through the focus of a synchrotron beam, resulting in a two-dimensional image with a pixel size given by the scan increments p_x/p_y, e.g., in the range of 100–500 nm with each pixel encoding a diffraction observable o. This can be, for example, the phase shift (proportional to the projected density), the ion concentration from fluorescence yield, the SAXS intensity integrated over the entire far-field pattern (dark-field), or other structural parameters derived from the full two-dimensional diffraction pattern, such as actin fiber bundle orientation and spacing. Beyond the scalar value o, for each pixel a fully quantitative far-field diffraction pattern is available at much higher signal/noise than typically in CDI, because oversampling and coherence constraints can be relaxed.

A major challenge of the technique is the proper definition of the beam preparation: small spot size and high flux density has to be combined with a clean diffraction signal with low tails/background and with a suitable working distance (focal length). To this end, we have previously designed and commissioned the nanofocus coherent diffraction endstation Göttingen instrument for nano-imaging with x-rays (GINIX) at the P10 beamline of the PETRA III storage ring (DESY, Hamburg, Germany). It is equipped with a high gain Kirkpatrick-Baez (KB) mirror system, enhanced with additional beam cleaning optics (soft apertures), and provides a dedicated sample environment for handling for biological samples, including an online optical microscopy and cryogenic sample environment (under commissioning).

Fig. 1 illustrates the experimental setup, including the diffraction geometry, typical diffraction patterns, and contrast modes.

Figure 1.

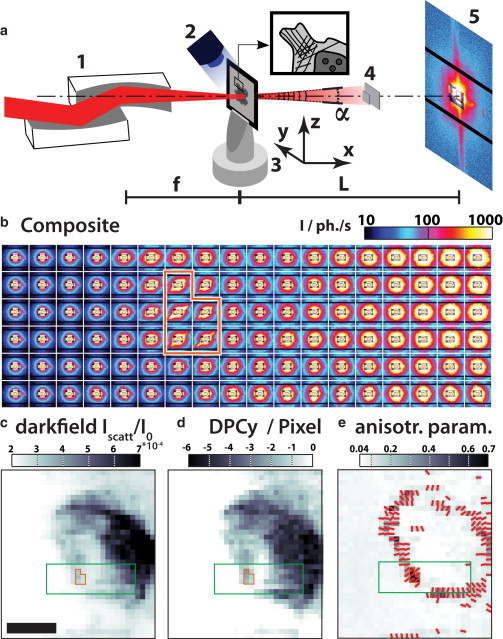
(a) Sketch of SAXS setup used at the GINIX with 1), a pair of Kirkpatrick-Baez-mirrors, 2), the cryostream, 3), the sample on the goniometer base positioned at the focal distance f = 200 mm from the second mirror, 4), the semitransparent beamstops in the flight tube (not shown), and 5), the Pilatus 300 K detector (Dectris) at the distance L = 5.29 m. (b) Collage of the far-field intensity distributions arranged according to where the beam impinged the cell. This subset corresponds to the green rectangle in panels c–e, and its orange region corresponds to the one in panels c–e. All far-field images are oriented as seen with the beam, i.e., left is the positive y direction and up is the positive z direction (as referred to the axes in panel a). A single diffraction pattern was obtained with a dwell time of 0.1 s. Adjacent diffraction patterns were recorded 500 nm apart, the scalebar in panel c represents 5 μm. (c–e) Quantified maps from the same dataset: (c) The dark-field map color encodes the scattered intensity with respect to the primary intensity of the scan. A cell can be identified by more intense scattering. (d) The differential phase contrast in horizontal direction, calculated from the deviation of the center of mass in the diffraction pattern. (e) Anisotropy coefficient as described in Fig. 5: Highly oriented intensity distributions in the far-field occur on the rim of the cell; the orientations of the patterns shown are standing perpendicular to the cell cortex, indicating structures in the cell with a high orientation parallel to the cell cortex. To see this figure in color, go online.

Fig. 1 a shows the schematic of the GINIX. The sample is placed on a motorized scanning stage and positioned in the focus of two KB mirrors. The far-field intensity distribution is captured by a pixel detector. By raster-scanning the sample, one far-field pattern per sample position is acquired.

A subset of such a measurement is shown in Fig. 1 b by arranging the raw data according to the corresponding sample position. The cellular diffraction patterns show two different signatures: isotropic scattering patterns mainly from the cellular interior, and highly anisotropic streaklike patterns at the periphery. Quantified maps are calculated from these datasets, as follows:

The dark-field given in Fig. 1 c represents the integrated scattered intensity, i.e., number of scattered photons normalized to the photons in the primary beam.

Variations in the center of mass of the primary beam result from the local gradient in the projected density of the sample; Fig. 1 d shows the vertical component that is denoted by differential phase contrast in y (DPCy).

In addition to the common dark-field and DPC contrast modes, we introduce an azimuthal anisotropy parameter S, which is high for far-fields with strong variations in the azimuthal intensity distribution and low for isotropic scattering patterns; this is shown in Fig. 1 e.

Nanodiffraction is easiest performed on freeze-dried cells attached to a thin foil (17,18) with no constraints concerning special sample environments or x-ray compatible chambers (28). However, the freeze-drying process is invasive, and in the dehydrated state, the structure preservation is poor. Hence, chemically fixed and hydrated, cryogenically fixed, or even live cells are the preferred state in view of more relevant structural results. For this work we have included nanodiffraction maps of D. discoideum cells recorded in four different states: 1), freeze-dried, 2), chemically fixed, 3), frozen-hydrated (vitrified), and 4), (initially) alive cells. For State 3, cells were kept under cryogenic conditions to preserve structure and to minimize radiation damage. In this state, the highest dose can be applied and thus, the highest resolution can be expected. Nanodiffraction in this cryogenic state is therefore the focus of this work, but comparison to the other states is also an important aspect.

In Materials and Methods, the different preparation protocols and sample environments are detailed along with the setup and instrumental parameters of the scanning nanodiffraction experiments. As we then show in Analysis of Cell Diffraction Patterns, the diffraction signal for D. discoideum cells is surprisingly strong and shows characteristic features. Particularly strong diffraction signals were observed at the cellular boundary in the form of distinct angular streaks. With the automated identification and analysis of the anisotropic diffraction patterns, as enabled by a specially devised Streak Finder algorithm (presented in its own section), we can map out the spatial distribution of the signal (see Results in Real Space), which can be attributed to a highly ordered fiber network of actomyosin complexes. The article closes with Summary, Conclusion, and Outlook, with remarks on additional steps needed to fully exploit the structural information by model building.

Materials and Methods

Preparation of cells

We used D. discoideum of the axenic D. discoideum line AX2-214 with a green fluorescent protein (GFP) fused to the LimE-protein (29), a component of the Arp2/3-complex, which acts as a selective marker for filamentous actin polymerization (30). Thus, the actin components of the cytoskeleton, i.e., pseudopodia and the actin myosin cortex, can be visualized by fluorescence microscopy of a second set of samples. The second cell line, shown later in Fig. 8 c, is derived from the same stem, but the LimE-protein carries a monomeric RFP, and a GFP is fused to the myosin-II motor proteins.

Figure 8.

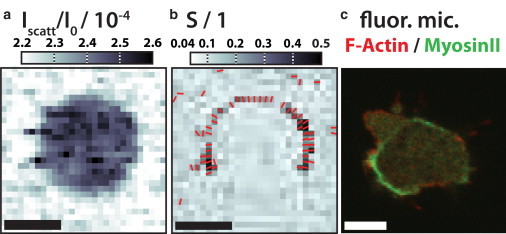
Maps of the (a) dark-field and (b) anisotropy parameter of a frozen hydrated D. discoideum measured at the GINIX with a dwell time of 0.1 s at I₀ = 1.1 × 10¹¹ ph./s. The scale bars denote 5 μm. (c) Fluorescence micrograph of a D. discoideum cell (AX2 wild-type with LimE-mRFP and myosin-II-GFP label scanned sequentially line by line) moving towards to top right imaged with an IX81 Confocal Laser Scanning Microscope (Olympus, Melville, NY). A pseudopodium (Top left) is identified by the high actin concentration. The rear end, facing the lower-left corner, shows a high concentration of myosin II. This is typical for the contractile actomyosin arc at the rear end of cells during attachment-retraction cycle. We often find that the oriented signal of this network shows one or more weak spots, resulting in a C-shape, as can be seen in panel b. To see this figure in color, go online.

Frozen hydrated cells were prepared on silicon nitride (Si₃N₄) membranes (Silson, Northampton, UK) and vitrified via a grid plunger (model GP2; Leica Microsystems GmbH, Wetzlar, Germany (31,32)). A drop of the cell suspension is gently pipetted onto the membrane and the cells are allowed to adhere (see Fig. S1 a in the Supporting Material). As soon as the cells show a state of high motility, as detected by optical microscopy (Observer Z1; Carl Zeiss, Oberkochen, Germany), the membrane is transferred to the humidity preparation chamber of the grid plunger. The fast cooling rate ensures vitrification of the water inside the cells.

Freeze-dried cells were prepared from frozen hydrated cells, using a home-built freeze drier.

Chemically fixed cells were prepared using living, motile cells on a substrate under phosphate-buffered saline (PBS). The PBS is then carefully replaced with a fixation solution of 4% formaldehyde. The fixation solution is left for 15 min before the substrate is gently rinsed and afterwards stored under pure PBS again. Fixed cells are stored at 4°C.

Living cells were measured in x-ray compatible microfluidic devices (ibidi, Munich, Germany). The channel is defined by a 5-mm-wide and 50-mm-long slit in the spacer. Silicon nitride windows are fitted into the channel floor and top to reduce background scattering. A sketch and photograph of the chamber taken during experiments is shown in Fig. S1 d, with the chamber outlined in red.

Further details on the preparation are given in the Supporting Material.

X-ray nanodiffraction experiment

X-ray measurements were performed at the endstation GINIX (26,33), at the P10 beamline of the synchrotron radiation source PETRA III (DESY Photon Science, Hamburg, Germany) (Fig. 1 a). A photon energy beam of E_λ = 7.9 keV was focused by a pair of elliptically shaped KB mirrors to 326 nm(h) × 392 nm(v) (full width at half-maximum), with a total photon flux of I₀ = 1.1 × 10¹¹ ph./s, as measured with the photon-counting pixel detector Pilatus 300 K (Dectris, Baden, Switzerland). This detector was positioned 5.29 m behind the sample itself, which had been placed in the focal plane of the KB. A tantalum aperture was used to suppress the pronounced streaks of typical KB far-fields, which can contaminate the diffraction patterns of the sample. As sketched in Fig. 1 a, two motorized semitransparent beamstops (34) installed in the detector’s evacuated flight tube are employed to attenuate the direct (primary) beam.

An xyz piezo stage was used to scan the samples in the beam with typical step sizes of 250 nm to 2 μm. Depending on the scan, typical dwell times were between 0.05 and 0.5 s. At each position, a full diffraction pattern is recorded. An inline optical microscope, positioned directly behind the sample, is used to identify the region of interest (ROI) on the sample and position it with respect to the beam (see Fig. S1 e). To protect the sample from radiation damage, a 100 K environment is provided by a N₂ cryostream (Oxford Cryosystems, Oxford, UK), as sketched in Fig. 1 a. Further details are given in the Supporting Material.

Analysis of Cell Diffraction Patterns

Next, we address the analysis of the diffraction patterns in reciprocal space. We distinguish the azimuthally averaged signal I_cell(q_r) as a function of momentum transfer

$$q_r=\sqrt{q_y^2+q_z^2},$$

where q_y and q_z denote the horizontal and vertical components of the momentum transfer in Cartesian coordinates. These coordinates are used to describe diffraction signals summed over all pixels in the cell. The two-dimensional pattern I(q_r,χ_s), used for a single diffraction pattern, can show anisotropic features reflecting the local orientation in the sample (compare the data shown in Figs. 2 and 3, respectively). To represent the signal averaged over the ROI and the azimuthal angle χ_s (Fig. 3 a), we use masking schemes to regroup and sum diffraction patterns, e.g., to generate representative average background and average (regional) cell signals, similar to Weinhausen et al. (19).

Figure 2.

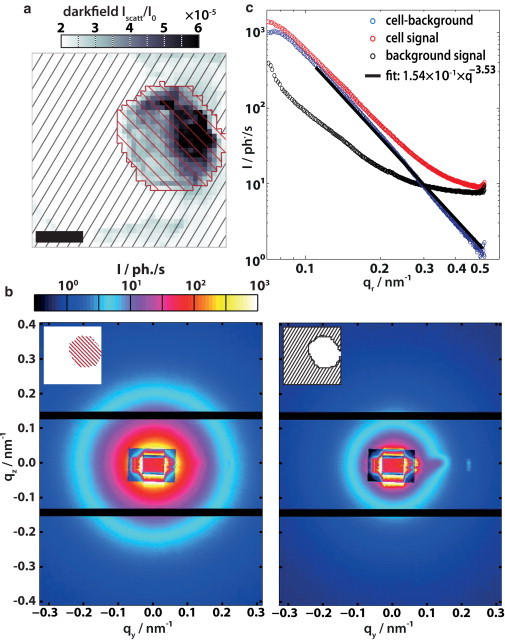
(a) Based on a scans dark-field map, two subsets of pixels are defined, those with scattering from the cell (hatched in red) and the surrounding ones (hatched in black). (b) The diffraction pattern of these subsets are averaged separately for the (left) cell and (right) background region. (c) Azimuthal averaging yields (red and black) two curves I(q_r) for the subsets. The cell signal is corrected for background effects by subtraction of the background signal. The resulting blue curve can be fitted with a power-law function, thus characterizing the curve with a single exponent. To see this figure in color, go online.

Figure 3.

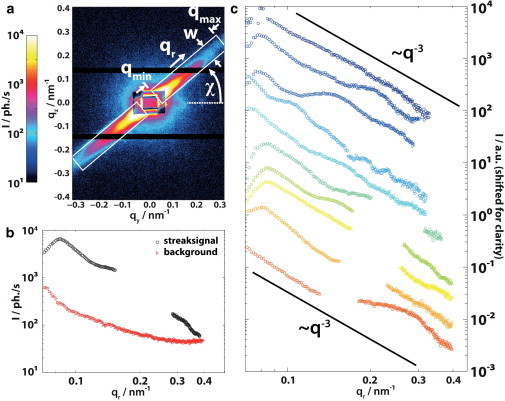
Comparison of the I(q_r) profiles in streaky diffraction patterns. (a) Typical example for anisotropic scattering patterns. The streak intensity profile is read out by averaging the intensity perpendicular to the streak. The readout region is defined by the azimuthal angle χ_s, the inner q_min and outer q_max scattering vector q_r and the width perpendicular to the streak w. The remaining part of the detector image is used for background correction by averaging along constant radii over the azimuthal angle. (b) Resulting streak and background signal from panel a. A gap in the data corresponds to the dead regions of the detector. The difference I_streak(q_r) – I_background(q_r) represents the intensity distribution in the streak pattern. (c) Profiles I(q_r) of different streak patterns measured on the same cell. The plots are shifted for clarity and a power-law decay ∝ q⁻³ is drawn as a guide to the eye. To see this figure in color, go online.

Averaged I_cell(q_r) from entire cells

The diffraction patterns of a given scan are first grouped into those obtained from pixels inside and those from pixels outside. This information is readily available from a dark-field map (Fig. 2 a), where the outline of the cell is marked by a line, based on the high cellular SAXS intensity. The diffraction patterns from inside and outside the cell are then averaged separately, as illustrated in Fig. 2 b, showing (left) the cellular signal and (right) the background with residual scattering due to chamber, windows, air scattering, amorphous ice, or water. The average is over all data points in the cell regardless of the local anisotropy observed at the periphery of the cell. In the background signal, a residual scattering contribution from KB tails is discerned to the right of the center, indicating some imperfection in the upstream cleaning optics (apertures). Finally, an azimuthal average over the angle χ_s results in a radial intensity decay I(q_r) for background and cell, respectively (Fig. 2 c). Subtraction of the background curve yields the background-corrected averaged scattering signal from the cell I_cell(q_r). Two conclusions can be drawn immediately:

• 1.The SAXS signal of the cells is substantially higher than the background, i.e., it can be recorded for up to three orders of magnitude in intensity, reaching the background level at q_r ≃ 0.5 nm⁻¹, which corresponds to a resolution of Δ_RS ≃ 6.3 nm. This resolution in reciprocal space must be distinguished from the real-space resolution Δ_STXM of the scanning transmission x-ray microscopy (STXM) maps given by the beam size or step size.
• 2.Compared to conventional SAXS from macroscopic suspensions or solutions, the background subtraction can be performed without any free parameters. Whereas variations such as between a capillary with sample and one without sample, or one with self-absorption in the sample, in most cases require scaling of signal to noise, the nano-SAXS curves are in perfect registry, reflecting the uniform and identical background on these length scales.

The averaged cellular scattering curves I_cell(q_r) do not show any peaks or modulations. Instead, they show a monotonic decay, which is well described by a power-law function, resulting in a characteristic exponent that can be extracted from a least-square fit. The corresponding graphs can be regarded as a spectral power density of the cell, measured here in the native state without staining or slicing. This power-law decay is in agreement with previous nano-SAXS studies on bacteria (17) and on eukaryotic cells (18,19). Note that in Weinhausen et al. (19), where the signal was mainly attributed to overexpressed intermediate filaments, two power-law regimes were observed; however, here, D. discoideum seems to be well described by a single exponent. Many cells are analyzed and the corresponding exponents will be compared further below for the different preparation states (see Fig. 7 c, later).

Figure 7.

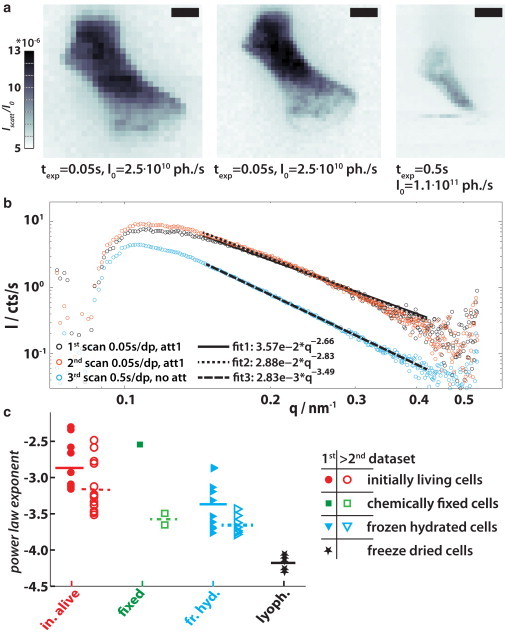
Experiments on initially living cells and comparison of preparation protocols. (a) Dark-field maps of three consecutive scans on an initially living D. discoideum cell in a microfluidic chamber. The scale bars denote 5 μm and the color axis is adjusted equally. The first and second scans are done with short exposure times and a reduced primary intensity of I₀ = 0.23 × I₀. All three dark-fields show slightly different intensity values, which becomes clearer in (b) background-corrected scattering signal I_cell(q_r) from the cell in panel a. The second measurement (orange curve) mainly coincides with the first scan’s data (in black), but intensity and the fitted exponent decrease significantly toward the long third scan (blue). (c) To compare the influence of preparation methods and measurements on the results, this scheme was applied to many measured cells, namely samples with initially alive cells, with formaldehyde-fixed cells, with cells that were frozen-hydrated (plunge-frozen), and with cells that were plunge-frozen and additionally freeze-dried. (Solid symbols) Scans on cells that have not encountered the dose of a fine scan (like shown in panel a, unless open symbols are used). (Small lines) Average value for one set of points; (solid lines) for solid symbols; and (dashed lines) open symbols. To see this figure in color, go online.

Streak profiles

In several pixels of the cell, in particular at the cellular boundary, highly anisotropic diffraction patterns have been observed. These anisotropic patterns typically show a single streak extending over the entire detector (Fig. 3 a). The streak width corresponds to the width of the central beam. This pattern indicates a fiber- or rodlike scattering object, with the fiber axis perpendicular to the streak.

We proceeded by extracting the fiber orientation and performing an empirical analysis of the intensity decay I(q_r), to provide a basis for future analysis that would include model fitting, once additional reference data become available. To this end, we first define the ROI around the streak, assessing the orientation angle χ_s of the streak, a lower q_min and upper q_max bound for q_r, and a width w in the direction perpendicular to the streak, and plotted it as a function of q_r (black curve in Fig. 3 b). The dead regions of the detector (between the three modules) cause missing values in the streak profiles. The position of the gaps varies according to the orientation χ_s of the streak (Fig. 3 c). Background signal is determined from averaging the remaining diffraction patterns along the azimuthal angle χ_s (red curve in Fig. 3 b). Fig. 3 c shows typical profiles after background subtraction, each from different locations within the same cell, as recorded during the same raster scan. The modulations in the streak profiles indicate positional order in the oriented (fiber) structures. Note the diversity of modulations, which could be caused either by local variation in the structure or rotations of the same structure around the fiber axis. The signal of a single fiber is probably too weak to be observed, but a fiber bundle of actin may possibly explain the observed data.

As a first attempt to parameterize and model this fiber diffraction pattern, one can first proceed as in standard conventional SAXS. In the coordinate system X,Y,Z attached to the fiber bundle with fiber axis Z, and reciprocal space coordinates Q_z and Q_||: = (Q_x² + Q_Y²)^0.5, the fiber symmetry (i.e., azimuthal isotropy of the single filament) results in the usual factorization into a single filament form factor F. It has a structure factor SF(Q_||,Q_Z), which reflects the azimuthal plane positions R_j of all 1 ≤ j ≤ N filaments in the bundle

$$I\left(\mathbf{Q}\right):={\left|F\left(Q_z,Q_{\parallel }\right)SF\left(Q_X,Q_Y\right)\right|}^2={\left|F\left(Q_z,Q_{\parallel }\right)\sum _j^N\text{exp}\left(ı{\mathbf{R}}_{\mathbf{j}}\cdot {\mathbf{Q}}_{\parallel }\right)\right|}^2.$$ (1)

For simplicity, the actin filaments can be modeled as Gaussian cylinders,

$$F\left(Q_z,Q_{\parallel }\right)=\frac{1}{\sqrt{2\pi }{L}_P}\text{exp}\left(-0.5Q_Z^2{L}_P^2\right)2J_0\left(R{Q}_{\parallel }\right)/\left(R{Q}_{\parallel }\right),$$ (2)

with L_p a parameter associated with the persistence length, i.e., characterizing the effective length of the filament, and R associated with the radius. The model could be extended to more sophisticated models, taking into account the structure of actin including its helicity—which is based on either coarse-grained representations of electron density (35) or a fully atomistic model. As detailed in the Supporting Material, the intensity distribution in the reciprocal plane probed by the two-dimensional detector I(q_y,q_z) (corresponding to an equidistant grid in small angle approximation) can then be calculated based on a rotational variable transformation involving a rotation angle φ around the fiber axis Z, a tilt angle ϑ of the fiber axis with respect to the optical axis x, and a rotation corresponding to the streak angle χ_s. Hence, the parameters R, L_p, φ, ϑ, and χ along with the filament positions R_j specify the diffraction pattern.

For illustration, typical streak profiles obtained in this simplistic model are shown in Fig. 4, which mainly served to illustrate the diversity of the diffraction streaks obtained and the dependence on the fiber angles. Aside from the fiber orientation angles, information about the structure of these bundles is particularly contained in the modulation of the intensity decay in the direction perpendicular to the fiber axis, i.e., the streak profile I(q_r) on the detector. Finally, in a nanodiffraction experiment, an important further step is necessary. To account for the finite-size illumination and its deviation from a perfect plane wave, the final intensity pattern of a nanodiffraction experiment I_nd is only obtained after a convolution with the probing wavefront P, i.e., $I_{nd}={|(SF\times F)\ast P|}^2$. This last step is responsible for the visible replication of a relatively square far-field pattern of the KB in the diffraction beam. However, the approach sketched above was still found to be intractable without further reference data of in vitro cross-linked actin fibers, in view of the large configurational space corresponding to the R_j, and compared to the diversity of experimental patterns observed in the cells.

Figure 4.

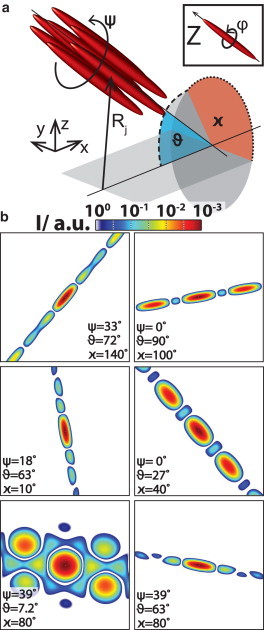
(a) Sketch of an arbitrarily defined fiber bundle consisting of seven filaments arranged in a hexagonal lattice. The angle ϑ and the azimuthal angle χ describe the orientation of the fiber bundle. Together with the bundle rotation angle ψ, which is defined in the bundles coordinate system, they determine the far-field diffraction pattern of a given set of filaments. The filaments are defined by their position R_j and have an individual angle φ, defined in the filaments’ coordinate system. (b) Simulated diffraction patterns calculated from seven rods. The rods are aligned in a hexagonal lattice. We show six different configurations of the angles ψ, ϑ, and χ, the angle φ does not influence the result due to the rotational symmetry of the single rods. For small ϑ, here ϑ = 7.2°, the hexagonal rod lattice leads to side maxima whereas the far-field intensity distribution appears streak like for all others ϑ∈[27°–90°]. It is easy to see, that the orientation of the far-field intensity distributions can be interpreted directly with regard of the fiber orientation χ. To see this figure in color, go online.

The Streak Finder

Anisotropy or orientation in diffraction patterns cannot be inferred from standard STXM contrasts (dark-field, DPC). But even without quantification, some pattern evidence is clearly visible in the very accessible composite maps, such as those of Fig. 1 b. Therefore, we introduce an anisotropy parameter S to quantify the orientation and correlate it to the standard contrast maps, as already given in Fig. 1, c–e.

To determine the anisotropy of the azimuthal distribution, the diffraction pattern is transformed from Cartesian to polar coordinates with the primary beam q_r = 0 as the center, leading to a representation I(q_r,χ), as shown in Fig. 5 b. The average over χ,

$${\langle I\left(q_r,\chi \right)\rangle }_{\chi }=\frac{1}{2\pi }{\int }_0^{2\pi }I\left(q_r,\chi \right)\text{d}\chi ,$$

is used to normalize the intensity distribution along q_r and obtain a weighted intensity distribution

$$I_w\left(q_r,\chi \right)=\frac{I\left(q_r,\chi \right)}{{\langle I\left(q_r,\chi \right)\rangle }_{\chi }}.$$ (3)

As a result, the contribution of the streak signal at large q_r is emphasized (Fig. 5 c). A relative azimuthal intensity distribution I_rel is then calculated from I_w according to

$$I_{\text{rel}}\left(\chi \right)={\int }_{q_{\text{min}}}^{q_{\text{max}}}{I}_w\left(q_r,\chi \right)\text{d}{q}_r.$$ (4)

In the next step, we apply the discrete Fourier transform function FFT to I_rel(χ):

$$FFT\left(k\right):=\sum _{n_{\chi }=0}^{N-1}{I}_{\text{rel}}\left(n_{\chi }\right)\cdot \text{exp}\left(\frac{-2\pi ı}{N}k{n}_{\chi }\right),0\le k\le N-1.$$ (5)

Finally, the anisotropy parameter S is defined as the sum of the first six even-components of the discrete Fourier transform, normalized to the zero-order component

$$S=\frac{1}{\left|\left|FFT\left(0\right)\right|\right|}\sum _{k=1}^6\Vert FFT\left(2k\right)\Vert .$$ (6)

The entire data reduction scheme and algorithm is illustrated in Fig. 5 by means of Fig. 5 a, as an anisotropic diffraction pattern. After the coordinate transformation, the q_r window is chosen in view of the beamstop shadow (i.e., the lower limit) and the detector corners (i.e., the upper limit; see hatched regions in Fig. 5 b). Fig. 5 c shows I_w(q_r,χ) of the chosen q_r region; note that the weighted intensity is increased at large q_r with respect to small q_r. The relative intensity profile I_rel(χ) of the anisotropic pattern, and for comparison an isotropic scattering pattern, is shown in Fig. 5 d. Finally, in Fig. 5 e, the corresponding discrete Fourier transform with its (in the case of the oriented diffraction signal) characteristically amplified even components is shown. From Fig. 5 d, the orientation can easily be determined and used to draw a small orientation indicator in the pixels with high S.

Figure 5.

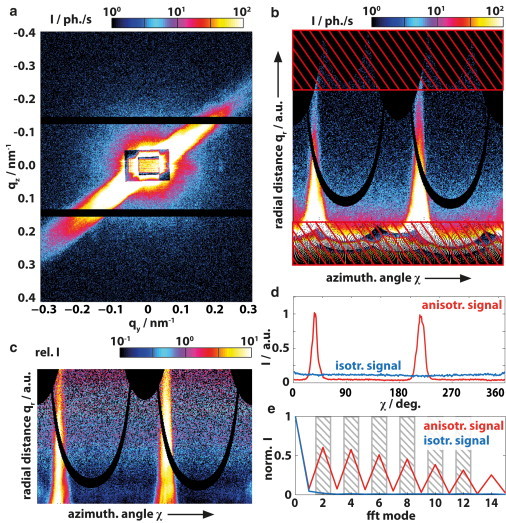
Illustration of the MATLAB software routine (The MathWorks, Natick, MA) that calculates the order parameter S. (a) The diffraction pattern is initially rescaled with a polar-to-Cartesian-coordinate transformation. (b) Regions with very small or large scattering vectors q_r are omitted (hatched region). (c) Reweighting along the radial (q_r) axis, according to Eq. 3. Integration of the signal along the former radial direction results in (d) an azimuthal profile. (Red curve) Curve for the example in panels a–c with the two peaks; for comparison, a profile obtained from an isotropic diffraction pattern measured on a cell is shown (blue). The orientation of the streak is determined by smoothing the profile and taking the maximum position. (e) The first even components of the Fourier transform are significantly increased for streaky far-field diffraction patterns as compared to isotropic patterns. The sum over the second, fourth, sixth,…twelfth component of the normalized Fourier transform serves as a parameter for the occurrence of streaks in the diffraction patterns. To see this figure in color, go online.

Diffraction patterns with streaklike intensity distributions have values of S ≈ 1 and even above. Intensity distributions that seem isotropic are typically found at around S ≤ 0.1. The procedure does not require a thresholding parameter as used in Weinhausen et al. (18); it better discriminates thin streaks than previous definitions (36) by considering higher-order-Fourier components. It yields a dimensionless anisotropy parameter S, which is similar but not (yet) identical to an order parameter, because S ≥ 1 is allowed. The algorithm has proved to be robust and has been shown to work well on different experimental settings (beamlines) and biological systems (cell types).

Results in Real Space

Characterization of cryogenic samples

Three different scans on frozen-hydrated D. discoideum cells are shown in Fig. 6 using dark-field and DPCy contrast, complemented by the anisotropy parameter S. All cells are clearly visible in dark-field and DPCy, as is the cell contour in the Streak Finder maps. The cell body can be recognized from its stronger scattering in the dark-field, and a stronger primary beam deviation in the DPCy contrast. The relative scattering intensity (dark-field) ranges from I/I₀ = [2 – 7] × 10⁻⁵. The DPCy maps color-encode the deflection of the primary beam on the detector in the unit detector pixels with typical ranges of 1.5–7 pixels. Due to the position of the semitransparent beamstop, it is not possible to accurately measure the position of the primary beam (see Section S5 of the Supporting Material). These values therefore have to be interpreted as a relative value rather than an absolute measurement. The color range of S varies for the measurements shown and lies in the range of S = [0.04 – 0.4] for Fig. 6 f and S = [0.04 – 2.0] for the dataset shown in Fig. 6 i, in which the anisotropic scattering patterns even dominate the corresponding dark-field map Fig. 6 g. Despite the variation of S between different datasets, anisotropic scattering occurs predominantly on the cell perimeter with the orientation perpendicular to it.

Figure 6.

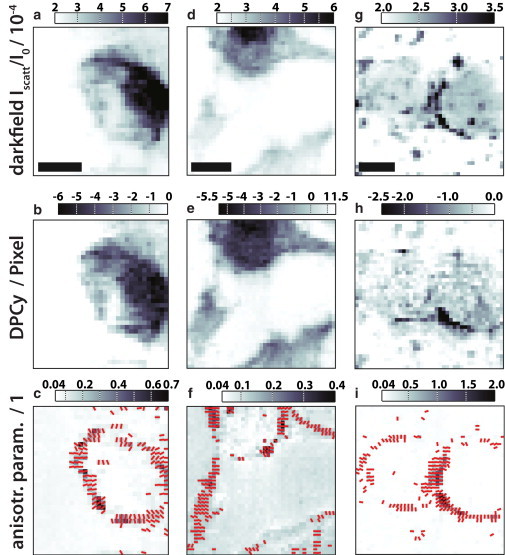
Comparison of three different scans (columns) on cryogenic hydrated cells in three different contrast modes (rows). All measurements were performed at GINIX with I₀ = 1.1 × 10¹¹ ph./s and 0.1 s exposure per data point. The scale bars denote 5 μm. (a–c) Typical case often found for single cells where the cell body shows up in dark-field and differential phase contrast (y component: DPCy). Anisotropic diffraction patterns are occurring close to the cell cortex and are standing perpendicular to it. (d–f) Cell with additional elongated structures, which show streaks perpendicular to its elongation direction. (g–i) Two adjacent cells show a comparable behavior to the single cells in panels a–f, but with particularly pronounced streaks occurring at the cell-cell contact region. To see this figure in color, go online.

Experiments on initially living cells

Scattering experiments were performed on living cells of D. discoideum using the x-ray-compatible microfluidic chambers described in Materials and Methods. Fig. 7 a shows the dark-field maps for three datasets scanned subsequently on the same cell to address the interaction of the beam with the sample due to beam damage. The first two raster scans were performed with the shortest possible dwell time of 0.05 s and the attenuated beam I_att = 0.23 × I₀ = 2.5 × 10¹⁰ ph./s. The third scan was performed with the full primary intensity I₀ = 1.1 × 10¹¹ ph./s and long dwell times of 0.5 s. Slight changes are already visible between the first two scans, inasmuch as the scattering intensity increases a little. These are characterized via the background-corrected averaged scattering signal from the cell I_cell(q_r), as explained before in Fig. 2. The first two datasets coincide except for the region of small q_r (see Fig. 7 b) whereas the last one drops significantly in intensity. Further, the exponent γ of a power-law decay F(γ) ∝ q_r^γ fitted to an inset 0.11 nm⁻¹ ≤ q_r ≤ 0.42 nm⁻¹ decreases, here from γ = −2.66 via −2.83 to −3.49, which we find to be characteristic for beam damage during repeated exposures.

Comparison of preparation protocols and beam damage

Many comparable datasets have thus been analyzed and classified by their power-law exponent. All datasets with reasonable signal/noise are represented by their power-law exponent in Fig. 7 c, where they are sorted by their preparation method and dose history. Solid symbols represent scans that were not exposed to more than a search scan (as can be seen in Fig. S1 e, right image). Successive detailed scans are represented by open symbols. Small horizontal lines show the mean value for each subset.

Datasets from initially living cells that were scanned for the first time have not endured any search scans (inasmuch as the cells migrate too quickly for this method), and can act as a reference for all preparations. The power-law exponent is largest in these scans, although the datasets show a wide spreading. The datasets on initially living and frozen-hydrated samples show a strong tendency to a steeper power-law decay from the first to subsequent scans, indicating beam damage. The cryopreparation also shows a shift in the exponent as compared to the initially living cells, an indication that cell microstructure has actually been altered (opposite to what is commonly believed (31,32)) throughout the preparation process. As expected, the intensively processed lyophilized samples show the smallest exponent and vary significantly from all other preparation techniques. Chemically fixed cells have been shown recently to differ from their native state (19), but more statistics is needed here to comment on it.

Summary, Conclusion, and Outlook

Toward a more detailed understanding of cytoskeleton structure and rearrangement during cellular migration, we have applied and refined an experimental approach based on cellular nanodiffraction. This article includes the optimized beam preparation, automated diffraction analysis based on algorithmic feature identification, adequate sample preparation, and sample handling procedures. In particular, cryogenic coherent x-ray diffraction was implemented by a dedicated sample preparation and environment. This enables measurements under hydrated conditions and at high signal levels. To this end, rapid plunging of cells in ultracold liquids has been used for structure-preserving vitrification, followed by sample transfer into a cryogenic jet at the beamline and optical control using in situ and cryogenic microscopy.

A full vacuum cryogenic sample environment seems not to be required in all cases, and both nanodiffraction and ptychographic coherent diffractive imaging techniques (data not shown), which have more stringent stability requirements, can be performed on cryogenically vitrified cells, using a convenient commercial cryogenic jet system. At the same time, first experiments on (initially) alive cells have indicated that it is possible to probe live structure in isolated diffraction shots during chemotactic locomotion.

As shown here, the emerging techniques of x-ray nanodiffraction can thus be applied to resolve structural features in the cell on length scales in the range of 1–200 nm, at a resolution intermediate between typical length scales of the organelle and the molecular constituents. We have found persistent elongated anisotropic diffraction signals in D. discoideum (termed “diffraction streaks” in this work) at the periphery of the cell. This signal was attributed to fiber bundles oriented parallel to the cell cortex. Such signal has been observed at more than one instrument (37) and with different instrumental settings (photon energy, focusing optics, accumulation time, sample preparation), which confirms that this feature is an intrinsic structural property. From automated analysis of the scanning diffraction data, an isotropy parameter was defined, yielding the local actin orientation. We attribute these ordered regions to actin/myosin bundles, based on the ringlike morphology of the anisotropy regions in the x-ray micrographs, which are very similar to the arclike regions of enhanced myosin-II/actin concentration at the cell cortex (double mutants with fluorescent myosin and actin) observed with fluorescence microscopy (contractile rings).

The interpretation of the diffraction signal as given here is supported by the comparison to fluorescence microscopy (shown in Fig. 8). In Fig. 8 a, the dark-field map of a D. discoideum cell is shown with Fig. 8 b, its Streak Finder map. The arc of anisotropic diffraction patterns is characteristic for the cells we investigated. Fig. 8 c shows a two-channel fluorescence map (from confocal microscopy) of a D. discoideum where filamentous actin is labeled in red and myosin II motor proteins are labeled in green. The image is one of a whole sequence, during which the cell moved to the top right. While the filamentous actin is dominating in the pseudopodiae like the one facing the top left, the myosin II concentration is highest at the rear end of the cell where the contraction of an actomyosin network is known to take place (12).

Notwithstanding the positive outcome of the method development and proof-of-concept, we also want to briefly comment on the remaining challenges. Still lacking, in view of a more complete exploitation of the structural results, is a quantitative modeling of the diffraction signal in terms of fiber bundle parameters (geometry, spacing, number of filaments). Therefore, the goals of visualizing mesh sizes, fiber orientation, cross-link distribution, and assembly of bundles in the actin network of the cytoskeleton, have not yet been reached. However, the experiments carried out so far have clearly demonstrated that the methods applied will be able to yield structural information at a higher resolution than in classical light microscopy and without the staining and slicing constraints typical for electron microscopy. In addition to the cellular diffraction, and with the goal of better dissecting the nature of the anisotropic diffraction signal, we are now complementing the cellular diffraction by scanning-nanobeam diffraction analysis on in vitro, cross-linked actin suspensions.

We also plan to combine coherent imaging and nanobeam diffraction of biological cells. By simple experimental parameters (slit opening in front of KB, detectors, beamstop, defocus position) one can switch between a setting optimized for a high-resolution diffraction, and a setting optimized for coherent imaging, on the same cell. Compared to a standard nanodiffraction experiment, the following advantages apply for a combined approach:

• 1.The illuminating beam (probe function) and corresponding interaction volume can be deduced quantitatively from ptychographic inversion instead of simple knife-edge scans.
• 2.Correlative microscopy images of projected density and diffraction observables are obtained.
• 3.One can easily and quickly determine where exactly the beam is positioned on the cell with a full field (defocus) image with minimum dose, before more scanning diffraction maps with higher radiation dose are recorded.

Supporting Citations

References (38–40) appear in the Supporting Material.