Dual Biochemical Oscillators May Control Cellular Reversals in Myxococcus xanthus

Abstract

Myxococcus xanthus is a Gram-negative, soil-dwelling bacterium that glides on surfaces, reversing direction approximately once every 6 min. Motility in M. xanthus is governed by the Che-like Frz pathway and the Ras-like Mgl pathway, which together cause the cell to oscillate back and forth. Previously, Igoshin et al. (2004) suggested that the cellular oscillations are caused by cyclic changes in concentration of active Frz proteins that govern motility. In this study, we present a computational model that integrates both the Frz and Mgl pathways, and whose downstream components can be read as motor activity governing cellular reversals. This model faithfully reproduces wildtype and mutant behaviors by simulating individual protein knockouts. In addition, the model can be used to examine the impact of contact stimuli on cellular reversals. The basic model construction relies on the presence of two nested feedback circuits, which prompted us to reexamine the behavior of M. xanthus cells. We performed experiments to test the model, and this cell analysis challenges previous assumptions of 30 to 60 min reversal periods in frzCD, frzF, frzE, and frzZ mutants. We demonstrate that this average reversal period is an artifact of the method employed to record reversal data, and that in the absence of signal from the Frz pathway, Mgl components can occasionally reverse the cell near wildtype periodicity, but frz- cells are otherwise in a long nonoscillating state.

Introduction

M. xanthus is a soil-dwelling, delta proteobacterium with a unique form of motility in which cells glide on solid surfaces and periodically reverse direction (1–5). M. xanthus cells move at the extraordinarily slow rate of ∼ 1 μm/min, yet the direction of cell movement is highly regulated and changes through a switch in cell polarity with a period of ∼ 6 min (1–3,5–8). This unique behavior serves, in part, to mediate their predatory life style, as M. xanthus cells that encounter prey will fastidiously reverse until the available prey cells are all lysed (6–11). Surface-based gliding motility in M. xanthus is governed by a combination of homologs to one of the best-studied bacterial signaling circuits, the Che-like Frz pathway, and one of the best studied eukaryotic paradigms for cell signaling, the Ras-like Mgl pathway (9–12). It is still unclear why this organism requires a signal transduction system that is so much more complex than Escherichia coli (E. coli). However, these two pathways work synergistically to regulate cell movement and behavior (9,12–17) and provide an intriguing example of how disparate signal transduction pathways integrate in vivo. The fascinating combination of Che-like and Ras-like molecular control of M. xanthus cell polarity, as well as the availability of quantitative data from numerous studies on the behavior of M. xanthus signaling mutants, make this organism an excellent candidate for mathematical modeling so as to better understand signal transduction and cell motility.

To date, there have been many models of M. xanthus behavior, which have been helpful for untangling the nature of rippling behavior (9,13,15–19), fruiting body formation (2,19,20), sporulation (9,16,20,21), cell-cell contacts (8,16,21–24), and mechanical models for individual cell motility (9,22–24). Igoshin et al. first proposed the Frizilator model of cyclic protein activation controlling reversal behavior of individual cells (9). Wu et al. (17,25,26) constructed a model of both swarm behavior and some cellular reversal periods that showed a link between reversal frequency and efficient swarm migration. Cell shape, flexibility, velocity, and cell-cell interactions have all been analyzed for their impact on models of behavior and multicellular development (8,26,27), In this study, we present a model of cell behavior that revisits the cyclic activation model by incorporating relatively novel ideas about intracellular biochemical components (e.g., Mgl GTPase activity) and how they may affect cellular reversals (25,26,28).

Cell movement is mediated by two distinct motility systems (A- and S-motility), with overlapping function. Recent breakthroughs indicate that M. xanthus gliding A-motility involves distributed sites of cell traction that start at the leading cell pole but span the entire length and distort the cell envelope to push the cell forward (27,29–31). In S-motility, cells deploy Type IV pili from the leading pole and subsequently retract the pili, pulling themselves forward (3,5,30,31). Both motility systems require the Mgl pathway to demark the leading and lagging cell pole, creating a signaling hierarchy from Frz to Mgl to the S- and A-motor proteins.

Regulation of cell movement in M. xanthus is similar, yet distinct from chemotactic swimming behavior of E. coli cells (3,5,32). M. xanthus uses distributed clusters of cytoplasmic receptor FrzCD along the length of the cell to transmit extracellular signals via protein-protein interactions to FrzE (a Che-A homolog); FrzCD activity is modulated by the methylation activity of FrzF (a CheR homolog) and the demethylation activity of FrzG (a CheB homolog). FrzE then phosphorylates FrzZ, (a CheY homolog), which diffuses through the cell to act on the Ras-like Mgl system (12,32,33). Rather than changing the rotation state of a single flagellum such as E. coli does, M. xanthus regulates the polarity of its cell body. Regulation of cell polarity requires the Ras-like Mgl proteins (12,34,35). Ras-like proteins are small GTP-binding switch proteins; the hydrolysis reaction of a phosphate group is catalyzed by a GTP hydrolysis activating protein (GAP) and the exchange of GDP for GTP is sometimes catalyzed by a guanine nucleotide exchange factor (GEF). In M. xanthus, MglA is a Ras-like protein and MglB is its cognate GAP. Ras proteins are often critical for regulation of cytoskeletal restructuring in eukaryotic cells, facilitating amoeboid movement (28,35,36). The role of Ras-like proteins in bacteria is less understood, but there is evidence for roles in organelle localization in several bacterial systems (3,28,37). Previous studies in M. xanthus suggest that the Ras-like Mgl system is governed by signals from the Che-like Frz pathway, allowing cell polarity to be controlled by a Che system (1–5). Recent studies on this dual signal transduction circuit indicate that 1), MglA activity occurs at the leading cell pole, 2), FrzZ may interact directly with MglB, and 3), FrzZ∼P localizes at the leading cell pole (1–3,5–8).

Although there are more steps in the M. xanthus signaling cascade than in E. coli signaling, this system provides the cell with the ability to coordinate two motility systems with a single spatial output. Previous models have examined Frz only, so we lack a comprehensive model that maps out signal flow from the distributed FrzCD receptors through Frz and Mgl components to the gliding motors. It is well known that feedback of downstream proteins onto upstream proteins in a signaling cascade can result in a self-sustained oscillating pattern of cyclic protein activations and deactivations (6–11). The feedback loops present in Che-like and Ras-like pathways make them both examples of cellular oscillators. Igoshin et al. first demonstrated that M. xanthus signaling activity could be modeled mathematically so as to better understand the Frz signaling circuit (9–12); they found that the pathway constituted a reversal clock they named the “Frizilator.” Indeed, the period of cell polarity reversals in M. xanthus has been found to vary within a window from 6 to 14 min depending on the strain, the type of surface, and cell-cell signaling (9,12–17). In this study, we incorporate recent findings on Frz and Mgl pathways into a mathematical model (Fig. 1) that faithfully depicts behavior not only of unperturbed wildtype cells, but also of mutant phenotypes and the effects of cell contact-based stimulation. We show that two levels of feedback can create a cycle of activity for proteins in the Frz and Mgl systems that cascades downstream, causing oscillations in the motor system, which results in physical oscillations of the bacterium in space through changes in cell polarity. This model of nested feedback explains the fast-reversing behavior of mglB mutants and predicts that reversal-deficient strains do not show evidence of a slower clock. Indeed, our experimental data supports the idea that both the Frz and Mgl pathways are oscillating molecular clocks that function synchronously.

Figure 1.

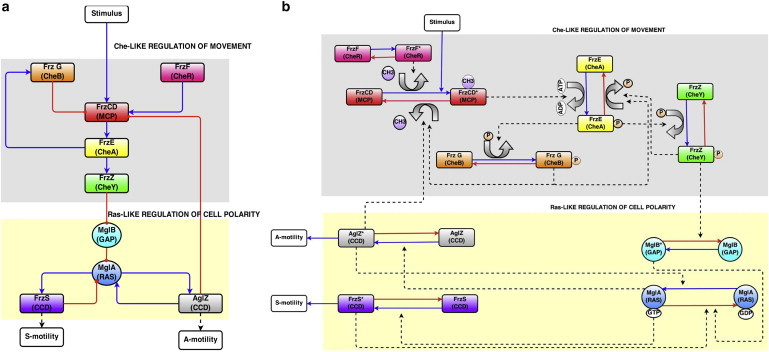
Oscillatory model for regulation of motility in M. xanthus. M. xanthus Frz and Mgl proteins can be depicted as either (a) as a simple circuit diagram or (b) a network diagram of biochemical interactions. The pathway requires the Che-like Frz proteins, and the Ras-like GTPase Mgl for regulating motility. Unlike E. coli, there are no random reorienting tumbles; in M. xanthus the entire cell polarity switches, causing the cell to retread its path. Our model is based on the following steps: An external stimulus (not required) causes a conformational change in the FrzCD receptor that stimulates autokinase activity of FrzE. Phosphotransfer from FrzE∼P to FrzZ causes a dissociation of FrzZ∼P from FrzE. FrzZ∼P disrupts the MglB-MglA complex at the leading pole releasing MglA. A new polarity is established by MglA, which interacts with the coiled coil domain proteins AglZ and FrzS to regulate motor activity of the two motility systems at the leading pole. FrzF methyltransferase activity and feedback from FrzG onto FrzCD adapt the system. Feedback from AglZ to FrzCD, and from the motors on to MglA form a dual oscillation cycle. To see this figure in color, go online.

Materials and Methods

Constructing the computational model

All equations and graphs were first created using Berkeley Madonna version 8.4, a differential equation modeling program (available at BerkeleyMadonna.com, Berkeley, CA). Once the equations and parameters were finalized (Table S4 in the Supporting Material), the data was exported to GraphPad Prism version 6 (GraphPad Software, Inc., La Jolla, CA), which we used to produce our graphs. Fig. 1 was produced using the web-based diagram editor draw.io (Jgraph, Ltd., London, England).

Strains and growth conditions

All strains of M. xanthus were routinely grown aerobically in CYE medium (Campos et al., 1978) at 32°C. For microscopic analysis of motility, 1.5% CYE agar-coated slides were used. Strain names used here correspond to the following strain IDs and original publications: DZ2 (9,13,15–19), DZ4480 FrzCD, and DZ4487 FrzCD^C (2,19,20).

Cell analysis

Midlog phase M. xanthus cells were diluted to 10⁸ cells/ml, and 5 μl of the cell suspension spotted on agar-coated slides. After 2 h incubation at 32°C to allow for motility to begin, cells were analyzed by light or fluorescence microscopy. For fluorescence microscopy, image acquisition was performed on a DV Elite microscope setup (Applied Precision) equipped with a CCD camera (CoolSnap HQ, Photometrics), and using solid-state illumination at 461/489 nm (GFP). Time-lapse capture was performed for up to an hour at 15 to 60 s intervals. Faster captures were performed to ensure that using 60 s intervals did not miss cell reversals. Most captures were 20 min, with longer experiments performed to reanalyze reversals in hypo-reversing strains. Cell behavioral analysis was performed using ImageJ software. All observations reported are based on three or more independent microscopy experiments.

Mathematical model construction

The math model of protein activity was constructed using Berkeley Madonna software, v.8.4 based on current data gathered from previous studies of the proteins required for behavioral control in M. xanthus. The nature of the interaction (excitatory or inhibitory) between each protein was also based on documented or hypothesized interactions described in the literature. See Table S1 and descriptions of the individual differential equations below as well as Table S4 for a list of parameters.

The fractions of methylated FrzCD, phosphorylated FrzG, activated FrzF, phosphorylated FrzE, phosphorylated FrzZ, activated MglB, GTP-bound MglA, activated AglZ, and activated FrzS are given by the following generic equation:

$$protein=\frac{\left[protei{n}^{\ast }\right]}{\left[protei{n}^{\ast }\right]+\left[protein\right]},$$ (1)

where FrzCD, FrzE, FrzZ, MglB, MglA, AglZ, and FrzS are each substituted for the word protein in their own equation and ^∗ indicates the activated state of that protein. For instance, the fraction of activated FrzF is given by the following:

$$FrzF=\frac{\left[Frz{F}^{\ast }\right]}{\left[Frz{F}^{\ast }\right]+\left[FrzF\right]}$$ (2)

Using these fractions, differential equations can be used to track the changes in the fractions over time using either Michaelis-Menten kinetics or first-order in/activation terms (9,16,20,21). The velocity (k) of each component (relative to the concentration of the implicated protein) of a given reaction depends on the maximum velocity attainable (kmax), the Michaelis constant (K_m), and the relative concentration of the two forms of that component. For certain reactions (those in which the exact nature of the in/activation components are not known), we used first-order in/activation to capture the basal in/activation rate. Note that k_F and k_R denote the velocity of the first-order forward and reverse reactions respectively. We found it necessary to use autocatalysis kinetics for the reverse reaction of the S’ equation; we initially tried using first-order kinetics but were unable to produce all of the behaviors discussed in this paper with a single parameter set.

The reaction rate equations are of the form $produc{t}^{\prime }=\frac{k_{cat}\left[enzyme\right]}{K_m+\left[substrate\right]}\left[substrate\right]$ or $k_{FR}\left[substrate\right]$:

$$F^{\prime }=k_{FF}\left[1-F\right]-k_{FR}\left[F\right]$$ (3)

$$G^{\prime }=\frac{k_{GF}^{\mathit{max}}\left[E\right]}{K_{GF}+\left[1-G\right]}\left[1-G\right]-k_{GR}\left[G\right],$$ (4)

where the E in the first term is indicative of the feedback of FrzE-P onto FrzG predicted because of homologous feedback between CheA and CheB in E. coli (8,16,21–24). The feedback of FrzE onto FrzG can be removed without affecting the fundamental oscillatory reversal behaviors of the model.

$$C{D}^{\prime }=\frac{k_{CDF}^{\mathit{max}}\left[F\right]}{K_{CDF}+\left[1-CD\right]}\left[1-CD\right]-\frac{k_{CDR}^{\mathit{max}}\left[G+AglZ\right]}{K_{CDR}+\left[CD\right]}\left[CD\right],$$ (5)

where the F and G in the first and second terms, respectively, represents the methylation and demethylation of FrzCD by FrzF and FrzG (9,22–24). The AglZ in the second term reflects the fact that FrzCD interacts with AglZ in a way that serves to modulate the inhibition of the Frz system on cellular reversals (9,17,38).

$$E^{\prime }=\frac{k_{EF}^{\mathit{max}}\left[CD\right]}{K_{EF}+\left[1-E\right]}\left[1-E\right]-\frac{k_{EF}^{\mathit{max}}\left[Z+G\right]}{K_{ER}+\left[E\right]}\left[E\right],$$ (6)

where the CD in the first term reflects the FrzE requirement of activated FrzCD for its own activation (17,25,26). The Z in the second term reflects FrzE phosphorylation of FrzZ, whereas the G in the second term reflects FrzE phosphorylation of FrzG (8,26,27).

$$Z^{\prime }=\frac{k_{ZF}^{\mathit{max}}\left[E\right]}{K_{ZF}+\left[1-Z\right]}\left[1-Z\right]-k_{ZR}\left[Z\right],$$ (7)

where the E in the first term reflects the FrzZ requirement of phosphorylated FrzE for its own phosphorylation (27,29–31).

$$Mgl{B}^{\prime }=k_{MglBF}\left[1-MglB\right]-\frac{k_{MglBR}^{\mathit{max}}\left[Z\right]}{K_{MglBR}+\left[MglB\right]}\left[MglB\right],$$ (8)

where the Z in the second term reflects the fact that MglB is hypothesized to be inhibited by FrzZ (3,5,30,31).

$$Mgl{A}^{\prime }=\frac{k_{MglBF}^{\mathit{max}}\left[Mot+AglZ\right]}{K_{MglAF}+\left[1-MglA\right]}\left[1-MglA\right]-\frac{k_{MglAR}^{\mathit{max}}\left[MglB+S\right]}{K_{MglAR}+\left[MglA\right]}\left[MglA\right],$$ (9)

where the MglB in the second term reflects fact that MglB acts as a GAP for MglA (3,5,32). The AglZ and FrzS in the first and second terms, respectively, reflect the hypothesized feedback of these proteins onto MglA. The Mot in the first term represents an unknown input (perhaps from the motility organelles) and can be used to induce irregular oscillations (extrinsic to the oscillation clock modeled here) seen in the FrzE and FrzZ knockouts; it is described further in the explanation to Eq. 16 and the discussion.

$$Agl{Z}^{\prime }=\frac{k_{AglZF}^{\mathit{max}}\left[MglA\right]}{K_{AglZF}+\left[1-AglZ\right]}\left[1-AglZ\right]-k_{AglZR}\left[AglZ\right],$$ (10)

where the MglA in the first term reflects AglZ requirement of activated MglA for its own activation (12,32,33).

$$Frz{S}^{\prime }=\frac{k_{SF}^{\mathit{max}}\left[MglA\right]}{K_{SF}+\left[1-FrzS\right]}\left[1-FrzS\right]-\frac{k_{SR}^{\mathit{max}}\left[1-FrzS\right]}{K_{SR}+\left[FrzS\right]}\left[FrzS\right],$$ (11)

where the MglA in the first term reflects FrzS requirement of activated MglA for its own activation (12,34,35).

We assume that the total concentration of the modeled proteins remains constant over the timescale that we are interested in; that is, we are assume protein transcription, translation, and degradation are negligible. We also make the quasi-steady-state assumption, which requires that enzyme-substrate complexes reach steady-state significantly earlier than do the products. We assume noncooperativity. We recognize that Michaelis-Menten kinetics uses an irreversible step in the generation of product but note that when using Michaelis-Menten kinetics instead of mass action kinetics for detailed balance, the numerical solutions are virtually indistinguishable (28,35,36). To ensure that our model did not violate detailed balance at equilibrium, we set the system of differential equations to zero and verified that indeed all quantities are conserved. It is recognized that as more biochemical data is acquired, it may be found that some of the mechanisms described in this study may not be governed by Michaelis-Menten kinetics (or for that matter, first-order or autocatalysis kinetics terms). However, the Michaelis-Menten formalism used provides a phenomenological way to express that the activity of a given protein varies in steep, abrupt manner as a function of the level of the protein that controls it in the pathway (3,28,37). Given that Michaelis-Menten equations may not be appropriate for each protein, it is important to mention that this model is also functional if the components are written using Hill Equations, where the velocity component for each reaction is given by the following:

$$k_{proteinF}=\frac{k_{proteinF}^{\mathit{max}}}{K_{dproteinF}+{\left(1-protein\right)}^n}$$ (12)

$$k_{proteinR}=\frac{k_{proteinR}^{\mathit{max}}}{K_{dproteinR}+protei{n}^n}.$$ (13)

Whereas in Eqs. 4 through 11, we assume that all Michaelis constants = 0.005 M, in Eqs. 12 and 13, we assume that all dissociation constants = 0.005 M. We also assume that the Hill coefficients = 1. Finally, in applying Hill equations, we assume that the rate of substrate-enzyme formation is much greater than the rate of its decomposition.

Next we describe a variable, Mot, which could add back the irregular oscillations in FrzE and FrzZ knockouts. It should be noted that these oscillations would not come from the internal feedback systems described previously. Stim is the size of the stimulus. H(t) is a unit step function (a Heaviside function), where H(t < 0) = 0 and H(t > 0) = 1. t_0x is the start of the pulse, for example, any nonnegative real number multiple of a random digit between 0 and 100, and Δt_x is the duration, for example, 0.5 min.

$$\text{Mot}=\{\begin{array}{ll}Stim\times \left[H\left(t-t_{0x}\right)-H\left(t-t_{0x}-\Delta t_x\right)\right]\hfill & ifMglB=1\hfill \\ 0.2\hfill & ifMglB\mathrm{\ne }1\hfill \end{array}$$ (14)

Protein knockouts can be modeled by setting the differential equation and the initial condition for that protein to 0. Additionally, the nested feedback loops can be separated from each other by removing the feedback term(s) denoting the impact of a downstream component (e.g., AglZ) on an upstream component (e.g., FrzCD) from the upstream component's differential equation (e.g., equation [5]).

A unit step function (or multiple unit step functions) can also be used to model the protein cascade that is thought to result from cell to cell contacts (8,9). In reality, extracellular signal is transduced to FrzCD by unknown proteins but the model simplifies this and only provides for the spike in activated FrzCD. Again, H(t) is a unit step function where H(t < 0) = 0 and H(t > 0) = 1. t_0step is the start of the extracellular stimulus and Δt_step is the duration:

$${\text{k}}_{CDF}^{\mathit{max}}={\text{k}}_1+{\text{k}}_2\times \left[\text{H}\left(\text{t}-{\text{t}}_{0step}\right)-\text{H}\left(\text{t}-{\text{t}}_{0step}-\Delta {\text{t}}_{step}\right)\right].$$ (15)

In the absence of stimuli, k₂ = 0 and the equation reduces down to ${\text{k}}_{CDF}^{\mathit{max}}={\mathrm{k}}_1$; but in the presence of stimuli, k₂ > 0. Note that multiple stimuli can be modeled by adding multiple Heaviside functions in the bracket.

The sequential order of protein activity can be obtained by looking at a single oscillation cycle for all proteins and plotting the time at which each protein starts to become activated by the protein before it. This method can also be used to look at the effect a contact stimulus has on the time between protein activations.

Reversals are fairly robust over a range of parameters. Michaelis constants are robust over orders of magnitude. Initial conditions, which are necessarily between 0 and 1, are not important for the model’s behavior at all. Most of the maximum velocity constants can be increased by several-fold without disrupting the fundamental oscillatory behavior of the model system. Some of the maximum velocity constants for either forward or reverse protein activations (e.g., the rate of concentration decrease for MglB) are less robust because these values must remain higher or lower than the maximum velocities for the reverse or forward reactions of the same protein (e.g., the rate of concentration increase for MglB), or else within a certain percentage of the other maximum velocity, to keep the relative concentrations of those proteins from being pegged at 0 or 1. However, these parameters can take on a wide range of values (several-fold difference) if the other velocity constant for the same variable is also modified so that the overall relationship between a given protein’s forward reaction and reverse reaction is maintained. The size of a Mot stimulus (given by Stim) affects model behavior, as small values produce no change in behavior and large values cause a termination of cellular reversals; the value of Stim we use for a Mot stimulus in a FrzCD mutant yields the longest reversal period for this parameter set. The robustness of the parameter set signifies that despite a lack of empirical data on the rate constants used in this model, and the inevitable presence of biochemical signaling noise inside all cells, the structure of the model works well for predicting reversals.

Results

M. xanthus gliding behavior requires discrete oscillation control

There is a great deal of data on the behavior of M. xanthus cells that we used to determine mathematical functions for each protein essential to the regulation of motility. We began by considering the model described by Igoshin et al., which first described the oscillatory behavior of this signal transduction circuit, but removed components that have since been found to be superfluous to motility (e.g., CsgA, FruA) and added components now recognized to be essential (e.g., FrzZ, MglA, MglB). Our model is summarized by the diagram shown in Fig. 1 a, which shows the overall organization of Che-like and Ras-like signaling components. For further detail, see the network diagram in Fig. 1 b and the list of equations in Table S1. In addition, we rigorously reexamined M. xanthus cell behavior as we developed the model (Fig. 2). M. xanthus gliding occurs in both individuals (A-motility) and groups (S-motility), with individual movement used to assay reversal behavior (Fig. 2 a and b). M. xanthus cell reversals cause cells to retread their previous path (Fig. 2 b), whereas cell flexibility provides some randomness to surface movement. Incubating cells on agar-coated slides and tracking the leading cell pole of individual cells, allowed for the observation that wildtype strain DZ2 cells move in zigzag patterns (Fig. 2 c) with reversals corresponding to a change in leading pole position occurring on average ∼ 7 min (Fig. 2 d). In contrast, behavioral mutants such as hyper-reversing frzCDc cells are trapped by their rapid reversal rate of ∼ 3 min (Fig. 2 c and e). Hypo-reversing frzCD cells move in elongated paths, with rare cell reversals (Fig. 2 c and f). The behavior of wildtype cells therefore moderates two behavioral extremes and highlights the importance of the biochemical oscillator that regulates the frequency of reversal behavior.

Figure 2.

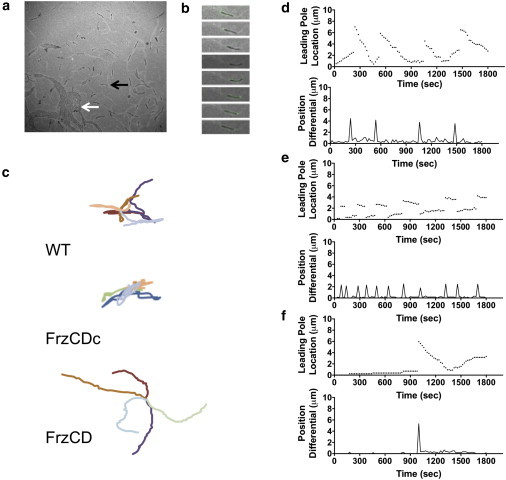
Analysis of oscillating cell behavior of M. xanthus gliding. (a) Incubation of M. xanthus cells on an agar pad shows the gliding behavior of cells, which move as individuals (black arrow) or coalesce into groups (white arrow). (b) The movement of individual cells is characterized by periodic cell reversals that correspond with the reorganization of several motility proteins including the lagging pole localization of MglB-GFP shown here. To analyze oscillatory behavior, > 50 cells were tracked for 60 min on CYE agar-coated slides. (c) Cell tracks for five cells each of wildtype strain DZ2, hyper-reversing frzCDc, and hypo-reversing frzCD cells show the resulting behavior of various signaling states. The wildtype state shows both movement in to new areas and retreading of a previous track. Hyper-reversing frzCDc cells primarily retread the same small area. Hypo-reversing frzCD cells move out into new areas without retreading. (d–f) Tracking of the leading pole position (above) and plotting of the position differential (below) shows the oscillation attributable to cell reversals for (d) wildtype strain DZ2, (e) hyper-reversing frzCDc, and (f) hypo-reversing frzCD cells. To see this figure in color, go online.

Modeling the activity of Frz proteins

Graphical solutions of the mathematical model of the Frz and Mgl signaling cascades were used to depict the spatial oscillations of wildtype M. xanthus (Fig. 3); the parameters and equation sets can be found in the methods section. Our approach was based on previous work by Gonze and Goldbeter (9,14) and Igoshin et al. (3,9), where protein concentrations are represented as the fraction of a protein in its active state over the total concentration of that protein in the cell. By looking at the activity of the two most downstream proteins—FrzS, which regulates S-motility, and AglZ, which regulates A-motility—motor activity, and thus cell motility, can be predicted. Cell polarity can also be predicted under the assumption that once polarity has been established, changes in activity state will correlate with changes in cell polarity. The period of oscillations for active-state AglZ and FrzS is ∼ 6 min, which is in line with the reported reversal period for wildtype M. xanthus cells (Fig. 3).

Figure 3.

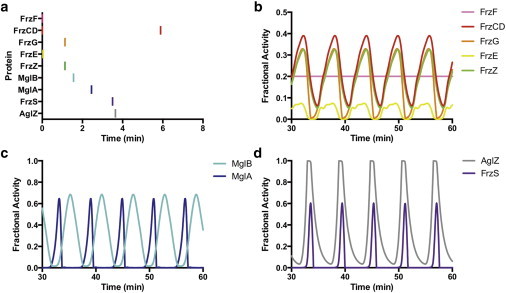
Oscillatory model for regulation of motility in M. xanthus. This model depicts relative protein activities in the absence of an extracellular signal. (a) The sequential order of cyclic protein activity in this model beginning with FrzCD. (b) Activity of FrzCD (red) then FrzE (yellow) lead to the activation of FrzZ (green) and FrzG (orange) with FrzZ the most downstream component of the Frz pathway. (c) The Mgl components also show oscillatory activity. The peak of MglA activity (dark blue) corresponds to when MglA is changing cell poles, whereas the broad peak of MglB activity (light blue) corresponds to when the major cluster of MglB is localized to the lagging pole and the cell is moving forward. (d) Activity of AglZ (gray) and FrzS (purple), which regulate the A- and S-motility systems, respectively, are coordinated with activity corresponding to when the proteins are changing cell poles with each ∼ 6 min oscillation. To see this figure in color, go online.

Fig. 3 a depicts the overall order of protein activation that occurs between the Frz, Mgl, and motor pathways. This order is consistent with what is expected based on what is known of Che-like and Ras-like signaling pathways. This figure shows one oscillation cycle starting and ending with activity of FrzCD. The Frz components are all slightly out of phase with each other, as would be expected for a hierarchical signaling cascade similar to the E. coli Che system. Large gaps in the timing of protein activations occur within the Mgl pathway, between the Mgl pathway and the motors, and between AglZ and a new FrzCD activation. We predict the delayed activations are because of relocalization of the proteins to new poles of the cell.

The Frz pathway is represented in the model by five major components, the receptor FrzCD, the kinase FrzE, the response regulator FrzZ, and the adaptation components FrzF and FrzG (Fig. 3 b). Receptor activity is transmitted via protein-protein interactions to the kinase FrzE, which autophosphorylates and then transfers phosphoryl groups to FrzZ. The increase in activated FrzZ∼P protein triggers the downstream Mgl pathway.

Modeling the activity of Mgl proteins

Mgl is predicted to receive a signal to switch from the upstream Frz pathway, though the exact nature of this interaction has still yet to be determined experimentally (1,3,39). Fig. 3 c shows the oscillating active concentrations of the Mgl proteins. MglA resides at the leading cell pole and is required to establish the direction of cell movement (1,3,39). MglB has been shown to act as a GAP protein on the Ras-like MglA, and has an asymmetric bipolar localization with a stronger signal at the lagging cell pole (3,5). Thus, the GAP activity of MglB prevents accumulation of active MglA at the lagging cell pole during cell movement (3,40). RomR has been suggested to act downstream of FrzZ, and proven to affect MglA and MglB localization patterns (39); because the function of RomR has yet to be determined, we do not include it in this model but note that its inclusion between the Frz system and the Mgl system is compatible with the model presented in this work. A rapid change in signaling state then occurs when Mgl receives an inhibitory signal from the Frz pathway, modeled here as FrzZ acting on MglB, but the impact is the same if FrzZ signals to MglA, or to both proteins. The Frz signal is expected to target the lagging cell pole (soon to be the new leading pole) and cause migration of both Mgl proteins through the cell to the opposite pole (5,39,40). Thus, the activity of MglA and MglB in Fig. 3 c corresponds to when they are most active in terms of localization change and impact on cell polarity. This model is consistent with previous predictions that translocating MglA is in the GTP bound state (38–41).

Motor activity can be inferred from the activity of FrzS and AglZ, which correspond to the S- and A- motors, respectively (Fig. 3 d). These proteins both localize predominantly to the leading cell pole, and change their location in the cell with each reversal of cell direction (27,38,41,42). Activity of FrzS and AglZ is observed to be synchronized, with a brief period of activity corresponding to cellular reversals, followed by a longer period of inactivity corresponding to cell migration. Note that this model does not take into account the poorly understood interaction of FrzS and AglZ with their respective motility organelles (24,27,42), and that the active state for these two proteins refers to when they are dynamically relocalized, which could be because of intrinsic active/inactive states or because of the action of other proteins. Models of force generation by Type IV pili and A-motility have been described elsewhere (24,38).

Dual oscillator activity of Frz and Mgl proteins

The oscillating protein concentrations seen in Fig. 3 are the result of a two-tiered self-contained feedback system. Each tier of feedback retains oscillatory character when separated from the other tier (Fig. S2) and both are required for full functionality of the model. The first level of feedback involves the known interaction of AglZ with the N-terminus of FrzCD (38,43); it creates an oscillation in the activity of the Frz proteins that cascades downstream. Fig. S2 a depicts a severance of the larger feedback loop (AglZ onto FrzCD) and results in a compressed oscillation period (∼ 2.4 min). The second level occurs within the Mgl pathway, and we propose a mechanism where MglA receives feedback from downstream components (e.g., AglZ and FrzS). Fig. S2 b depicts a severance of the smaller feedback loop of motility systems onto MglA and results in a slightly elongated oscillation period (∼ 6.1 min), as compared with the wildtype period. This feedback is proposed based on several behavioral observations that conditions that promote S-motility inhibit reversals whereas conditions that promote A-motility stimulate reversals (3,8,44), although the specific mechanism we model here is only hypothetical. The combination of these dual oscillators is essential for the model’s description of mutant behavior phenotypes (see below). The oscillations from the first feedback system serve as a molecular master clock to which the Mgl oscillations are tuned. The frequencies of the disconnected feedback loops vary depending on the parameter set used, but typically remained < 10 min and never approached 30 min (the reported period of Frz mutants—see below).

Application of the activity model to mutant behavior phenotypes

Previous mathematical models for M. xanthus behavior also showed oscillatory behavior that matches an idealized wildtype cell, but did not simulate mutant behaviors. An exception to this is a model by Hendrata and Yang (3,43), which simulates two mutant aggregation phenotypes but does not simulate mutant reversal phenotypes. Thus, we sought to incorporate protein knockouts into the model and assess if they reproduce known mutant reversal phenotypes. A comparison of Fig. 3 with Fig. 4 shows the difference between wildtype behavior and the knockout behavior produced by the model. Note that single gene knockouts of FrzCD and FrzF (Fig. 4 a) both result in a nonreversing phenotype. FrzG knockout produces a phenotype with a higher frequency of oscillation than wildtype of roughly once per 3.5 min (Fig. 4 b). Further examination of the model reveals that any knockout that severs communication between the Frz and Mgl systems (e.g., FrzCD, FrzE, FrzZ knockouts) results in MglB over activation (its fractional activity eventually saturates at 1), causing MglA to be maximally inhibited and trapped at the leading cell pole.

Figure 4.

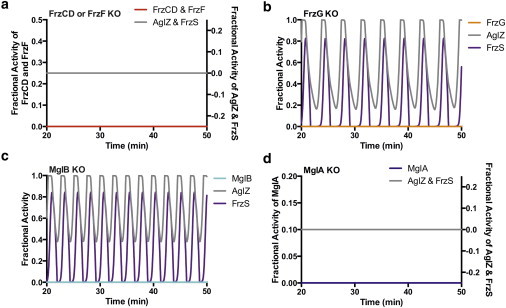
Knockout model for behavior of M. xanthus mutant cell lines. The model is optimized to accurately depict cell behavior consistent with known mutant phenotypes by setting activity for a given protein to zero. (a) Both FrzCD and FrzF knockout simulations cause loss of FrzS and AglZ activity indicating the entire pathway is disrupted, resulting in FrzS and AglZ remaining trapped at one cell pole and constitutive cell motility in one direction. (b) FrzG knockout simulation causes a hyper-reversing phenotype, in which cellular reversals increase to roughly once per 3.5 min. (c) Knockout of MglB causes hyper-activity of MglA, and therefore FrzS and AglZ, leading to rapid cell reversals, which matches the mglB hyper-reversing mutant phenotype of ∼ 2.5 min. (d) Knockout of MglA, however, results in rapid shutdown of any FrzS or AglZ activity and a nonmotile phenotype, which matches observed phenotypes. To see this figure in color, go online.

MglB knockouts (Fig. 4 c) result in rapid reversals because of the loss of GAP activity by MglB on MglA. Loss of MglB activity results in a constitutive active state for A-motility, combined with a lack cell polarity regulation (3). Because MglB is predicted to be cyclically suppressed by Frz signaling, termination of MglB activity means the Frz system is no longer capable of suppressing Mgl, and cellular reversals increase to roughly a 2.5 min frequency. In contrast, MglA knockouts (Fig. 4 d) result in no cellular reversals. This is because MglA is critical in transmitting the reversal signal to the motor proteins AglZ and FrzS; in the case of MglA, this is expected to affect motor activity and motor localization, rendering the cell nonmotile (3,45,46). Some reports observe mglA mutants are actually oscillating very quickly in place, which supports the idea of unlocalized motors unable to propel the cell forward (2–4,46). Thus, no reversals here refers to no reversals resulting from interactions between the Frz, Mgl, or motor systems, which effectively renders these mutants nonmotile. These four phenotypes of the modeled FrzCD, FrzF, FrzG, MglB, and MglA knockouts match the phenotypes of actual knockout strains reported previously (2,3,17), as well as those presented in this work.

Distinguishing between average reversal period and reversal windows

In our model, some knockouts abolish oscillation, whereas others speed up the reversal clock. There are numerous reports, however, indicating that Frz mutants such as frzZ should not totally abolish the clock, but rather should slow it down, resulting in a slower oscillation cycle than wildtype (2,17). 30 to 60 min reversal periods of Frz knockouts are often reported. However, motility assays are often conducted by observing many cells for a relatively short period of time (e.g., 10 min) with the average number of reversals in the population multiplied by a constant to achieve the average time between reversals per cell (2,9). The discrepancy between our model’s output for the reversal frequency of FrzZ mutants and previously reported findings prompted us to observe cells for a longer period of time to determine if these frz mutants retard the reversal clock to the expected 30 min mean, or abolish the clock as in our model (Fig. 5).

Figure 5.

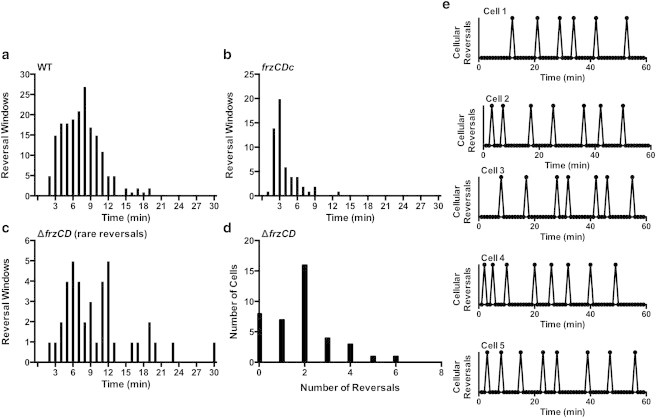
Examination of the reversal window in M. xanthus cells. Reversal period is the average obtained from counting the number of reversals observed per cell over time. Reversal window is the amount of time elapsed between two observed reversals. The model does not predict the long reversal windows of 30 to 60 min reported for FrzCD mutants, which prompted a reexamination of the reversal window (a–c, e) and period (d) in M. xanthus cells. Cell behavior was tracked in 1 hr blocks and the reversal window measured, i.e., the amount of time elapsed between each observed cell reversal. Note that the timescale for (a–c) only goes up to 30 min because no cells were observed to display reversal windows above this length. (a) Wildtype DZ2 cells show the expected average of 7 min between reversals but with a wide variance between 3 to 11 min, whereas (b) hyper-reversing frzCDc cells have a peak reversal of 3 min and reduced variance. (c) Although rare, reversals are observed in the hypo-reversing ΔfrzCD strain and the average reversal window of ΔfrzCD cells shows a peak at 6 min and a 2nd peak at 12 min. (d) The total number of reversals in ΔfrzCD cells ranged from 0 to 6, with many ΔfrzCD cells observed to move for 60 min with zero or one reversal, such that reversals appear to be suppressed, rather than slowed. (e) Reversal measurements are provided for five individual wildtype cells, showing that variance in reversal window is observed at the level of the individual cell.

Tracking of wildtype and frz mutant cells over 60 min allowed us to examine reversal behavior more thoroughly. We observed wildtype cells to reverse after an average of 8 min (Fig. 5 a). In contrast, hyper reversing frzCDc cells reversed after an average of 3 min (Fig. 5 b). In both cases, a wide distribution of outliers was observed as well. Tracking of 50 individual frzCD cells for 60 min resulted in 74 total cell reversals observed across a total of 1886 min, for a final average reversal period of 25 min (Fig. 5 c). This average fits with previous reports. However, cell-by-cell analysis indicates that individual cells reversed anywhere from zero to six times during observation, with a mode = 2 (Fig. 5 d). Indeed, in cells that reverse more than once we analyzed the time elapsed between reversals and found that the reversal window is most commonly between 6 to 12 min in frzCD cells (Fig. 5 c). The much longer population average of 25 min comes from the large number of cells that did not reverse (8 of 50) or only reversed once (7 of 50). Restated, this means that each frzCD cell has a small chance of reversing, and when a FrzCD cell reversed twice, we did not observe a 30 min delay between reversals, but instead observed that the window between reversals was closer to that of wildtype cells. Similar behavior was observed in other Frz mutants (FrzE, FrzZ, FrzF) (data not shown). Thus, the 25 min average is not representative of a cell clock with a slower oscillation state.

Further analysis of individual wildtype cells was performed to distinguish between variance at the individual and population levels (Fig. 5 e). The reversal patterns of five unique cells are shown, all of which show a large variance in reversal windows ranging from 3 to 12 min, whereas the average reversal frequency is 6.1 to 8.8 for these five cells. Note that there is no evidence for the presence of two distinct populations of cells (one having a small window and the other a large window). Based on our observation of frzCD mutant cells and observations of other mutant cell lines of the Frz signaling cascade, we conclude that the 30 to 60 min average reversal periods of frzE, frzCD, and frzF mutants are not representative of slowed molecular clocks. Thus, our analysis of reversal window indicates that the Frz reversal clock is indeed broken rather than slowed, as depicted in the model.

Addition of external stimuli to the activity model

Although our model depicts a perfect oscillation of activity, in reality cell behavior is much more complex. Although internal noise can in part explain the wide variation in reversal frequency, the data available would indicate that the system is either very noisy, or exquisitely sensitive to surface cues. Our equations can also be used to model reversal behavior in response to external stimuli (see Figs. 6 and S3). The model contains a relative refractory period and a sensitive period, consistent with previous predictions of variations in the sensitivity of the system to external stimuli (4,13,47). A stimulus on FrzCD causes a spike in FrzCD activity, which cascades through the Frz and Mgl systems to the motor proteins, where it ultimately causes faster reversals (Fig. 6 a). It is important to note that, as with previous models, the extent to which an external stimulus speeds up cellular reversals is dependent both on its relative strength and on when it occurs during the FrzCD oscillation cycle (9,15).

Figure 6.

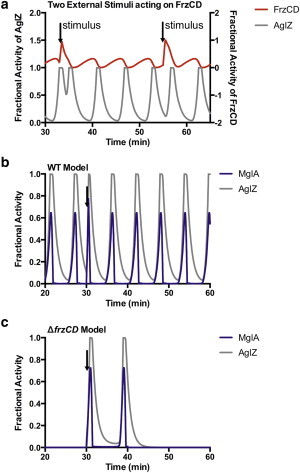
Modeling external stimuli impact on behavior in M. xanthus. The irregular pattern of cellular reversals seen in Fig. 5 prompted us to consider the effects of stimuli on cell behavior. (a) Impact of stimuli (arrows) on FrzCD results in a change in the output timing of cell reversals, through monitoring AglZ activity. The change in timing depends on the refractory period (Supplement S4). The first stimulus occurs during the sensitive period and results in a ∼ 2 min period between reversals, whereas the second occurs during a relative refractory period and results in a ∼ 4 min period between reversals. (b,c) Impact of stimuli on Mgl (via Mot) acting below the level of the Frz system. (b) Shows a stimulus from Mot in the wildtype model, which is similar to an external stimulus acting on FrzCD. Here the reversal time after the stimulus is ∼ 3.3 min. (b) Plot showing the effect of a stimulus from Mot in a FrzCD mutant model, that causes two cellular reversals ∼ 8.1 min apart before returning to a prolonged nonoscillating state. To see this figure in color, go online.

Although this can explain the variation in behavior observed in wildtype cells, it is more difficult to explain the behavior of ΔfrzCD cells that move primarily in a nonreversing state, but occasionally reverse with timing similar to wildtype. The mutant frz- phenotypes lead us to consider that this activity could be mediated through a non-Frz stimulus on the Mgl pathway, modeled here as a stimulus from the motors (Mot variable). In the wildtype model this causes a faster reversal window—similar to a stimulus on FrzCD (Fig. 6 b). But in an frzCD mutant model, a stimulus on Mgl can result in a transient reversal or reversals similar to what was observed with frzCD cells (Fig. 6 c). The modeled stimulus shown causes a reversal window of 8.1 min, followed by a return to a prolonged, nonreversing state. Stimuli on FrzCD and Mgl are need not be mutually exclusive and the wide variation observed in individual cell behavior could be inclusive of both, with our results suggesting that the Mot stimulus can explain reversals in frz- strains as well.

Discussion

Signal transduction pathways are critical for transforming extracellular stimuli into intracellular signals that modify existing cellular processes and thereby allow cells to sense and respond to their environment. There are many examples of oscillatory clocks that respond to extracellular stimuli to regulate cell behavior, ranging from [Ca²⁺] oscillations in response to IP₃ stimulation to cAMP oscillations mediated by Ras2-GTP (48,49). Computer modeling of these systems is necessary because the complexity of the feedback and number of proteins in the cascade makes it very difficult to elucidate cellular behavior using bench-top experiments alone.

Isolated M. xanthus cells oscillate when gliding on surfaces, switching the leading and lagging cell poles. Both Che-like and Ras-like signaling are used together to regulate this oscillation of cell polarity and motility. By regulating the frequency of oscillation, M. xanthus cells can switch between wandering behavior (low reversal frequency) and homing in on a single location (high frequency) triggered by contact sensation through FrzCD. For a slow-moving, surface-bound soil microbe, staying close to a good nutrient source of prey can be achieved by regulating oscillation frequency. The model here describes this behavior through a proposed internal feedback system (motors->MglA) within a larger internal feedback loop (AglZ->FrzCD). Each of these two feedback systems can create regular oscillations in the model without the other. A plausible explanation for why there would be two oscillators rather than a single oscillator is that it allows for two levels of regulation. An alternative explanation is that it may allow for better coordination of the two synergistic motility systems. This proposed mechanism will need to be confirmed through genetic and biochemical studies, but our analysis of frz mutant behavior indicates that oscillations occur in the absence of the Frz pathway.

We have also shown that the description of 30 to 60 min reversal periods in frz mutants is an artifact of the method previously used to observe them. Instead, cell reversals in Frz knockouts are either completely inhibited, or they show an oscillation pattern similar to wildtype. This result shows 1), that the Frz and Mgl systems are tuned to a similar frequency and 2), predicts that the Mgl system may have a secondary function, possibly in sensing motor feedback. The idea of a nested Mgl oscillator within a larger Frz-Mgl oscillator has been previously proposed by Wu et al. (17). However, there are key differences between the predictions derived from their model and ours. Wu et al. hypothesize that MglA and MglB are solely responsible for the nested oscillator, whereas we predict that interactions between MglA and motor proteins are responsible for the nested oscillations. Based on the presence of irregular reversals in the cell data, we propose that a secondary signal acts on MglA (or AglZ) and incorporate this phenomenon into the model through the variable Mot (included in Eq. 9). More importantly, they implicate the nested oscillation in the 30 min reversal periods, previously associated with FrzCD, F, E, and Z mutants. Our evidence indicates the 30 min average reversal period does not reflect cell behavior and that the nested oscillation period is ∼ 2.5 min, corresponding to the reversal frequency of MglB mutants. It is interesting to note that the modeled Mgl system can operate independently (Fig. S2), indicating that motor feedback may in some circumstances stimulate cell reversal—perhaps in the absence of a dynamic signal from the Frz system (Fig. S2 b). These ideas will require further testing, but double mutants such as frzCD-aglZ have previously been observed to show hyper reversals (38), supporting the idea that cells can receive a reversal stimulus in the absence of Frz. For now, we note that a pulse of activity in Mot can trigger a cellular reversal in the model in the absence of an Frz signal.

Our model was created using Michaelis-Menten kinetics to describe each step in the Frz-Mgl-motor signaling cascade, but Hill equations can also be used to model zero-order ultra-sensitivity (37). Furthermore, as the biochemistry of the system is better elucidated, we expect that future models will need to incorporate collision and localization modeling to fully account for all of the intricacies of signal transduction. For instance, the AglZ feedback onto FrzCD provides the basis for one oscillatory loop, yet still there is much to learn about how these proteins interact and how signal is transduced between them (38). In addition to this major feedback, we model MglA receiving minor positive and negative feedback from AglZ and FrzS respectively. We do this to propose one possible explanation for why mglB mutants oscillate despite being disconnected from the oscillating Frz system. It should be noted that we observed similar oscillatory behaviors in models with alternative combinations of feedback between MglA, AglZ, and FrzS. A further clarification of the interaction between MglA, and the motor complexes will be necessary. For now, AglZ and FrzS are used as a proxy, because the exact mechanism of engaging the motors is poorly understood. An additional regulator, RomR, that is essential for targeting of Mgl proteins to the cell poles may also be involved in this dynamic, but needs further study (1,50). Moreover, the connection between the Frz system and the Mgl system is still actively being debated: whether FrzZ interacts with MglB directly, via RomR, or with MglA, is not known, but all of these possibilities are in line with the fundamental nature of the model (3,5,39). Thus, we propose this model, not as the definitive mechanism of protein interactions, but as a way to showcase the fact that nested feedback circuits can account for wildtype and mutant behaviors. Further examination of the interactions between the regulatory pathways of Frz, Mgl, and the motor proteins, will better elucidate how these cells translate signals into motion.

Supporting Citations

References (51–54) appear in the Supporting Material.