Adaptive randomized phase II design for biomarker threshold selection and independent evaluation

Abstract

Background

Frequently a biomarker capable of defining a patient population with enhanced response to an experimental agent is not fully validated with a known threshold at the start of a phase II trial. When such candidate predictive markers are evaluated and/or validated retrospectively, over-accrual of patients less likely to benefit from the regimen may result, leading to underpowered analyses or sub-optimal patient care.

Purpose

We propose an adaptive randomized phase II study design incorporating prospective biomarker threshold identification (or non-identification), possible early futility stopping, potential mid-trial accrual restriction to marker-positive subjects, and final marker and treatment evaluation in the patient population identified as most likely to benefit.

Methods

An interim analysis is used to determine whether an initially unselected trial should stop early for futility, continue without a promising marker, or adapt accrual and resize (up to a pre-determined maximum) according to a promising biomarker. Final efficacy analyses are performed in the target population identified at the interim as most likely to benefit from the experimental regimen. Simulation studies demonstrate control of false-positive error rates, power, reduced average sample size, and other favorable aspects.

Results

The design performs well at identifying a truly predictive biomarker at interim analysis, and subsequently restricting accrual to patients most likely to benefit from the experimental treatment. Type I and type II error rates are adequately controlled by restricting the range of marker prevalence via the candidate thresholds, and by careful consideration of the timing of interim analysis.

Conclusions

In situations where identification and validation of a naturally continuous biomarker are desired within a randomized phase II trial, the design presented herein offers a potential solution.

Introduction

Development of targeted therapies is accelerating in response to widespread identification of hypothesized biomarkers. Of particular interest are candidate predictive markers believed to be related to the efficacy of an experimental treatment under study, where co-primary aims of a phase II trial may be determination of the marker's predictive value and identification of the marker-related subpopulation most likely to benefit. Before a new biomarker can be used to guide treatment decisions and patient care, however, a lengthy process from marker identification to validation must occur. For quantitative biomarkers (e.g., circulating levels of a target), a threshold to distinguish marker-low from marker-high patients may additionally be required. This process becomes inefficient when individual steps are accomplished in a post-hoc manner using data from multiple and potentially disparate sources, and results may be biased or confounded if marker identification and marker evaluation studies are performed separately or without a prospective framework.

Existing biomarker-based adaptive designs are either not truly adaptive (in the sense that adaptations are applied retrospectively), or rely on a dichotomous marker or previously defined marker threshold. Freidlin and Simon (2005) proposed a two-stage “adaptive signature design”, where a set of genes sufficiently predictive of treatment efficacy among patients enrolled during the first stage of a phase III trial are subsequently used to classify the remaining patients as “sensitive” or “not sensitive” in the second stage (1). This design, which was subsequently expanded to incorporate cross-validation (2), does not restrict accrual based on interim results, and thus is not truly adaptive in the sense that adaptations are not applied during the course of the trial. Other proposed “retrospective-adaptive” designs (3-5) similarly do not affect treatment of patients on-study, though one such design by Jiang, Freidlin, and Simon (2009) does include retrospective identification of a continuous marker threshold (4). Of those existing truly adaptive designs (i.e., allowing for interim changes or restrictions to accrual to marker-defined subpopulations), most assume that dichotomizing thresholds for marker(s) of interest have already been established (6-11).

Here, we propose a novel phase II biomarker-based design that prospectively integrates four key desired features: (I) an interim analysis for continuous biomarker threshold selection (or non-selection); (II) possible futility stopping in either the overall or marker-defined populations; (III) potential restriction of accrual to the marker-based population of patients who, based on preliminary data, are most likely to benefit from the experimental treatment; and (IV) fully-powered final analyses in the population identified as benefitting at interim, where these analyses are based on an independent set of marker-positive patients in the event a promising marker exists. At the interim analysis, a pre-specified candidate biomarker is evaluated for its ability to predict the treatment effect, and if sufficiently promising, a threshold is chosen to distinguish marker-negative from marker-positive subjects. Depending both on the presence/ absence of a predictive biomarker and marker subgroup-specific/ overall performance, the trial may stop for futility, continue accrual to both marker groups, or restrict accrual to the marker-positive group. In the event a promising biomarker is identified at the interim analysis, the design includes subsequent final evaluation of the marker in an independent set of patients from the target subpopulation of interest.

Methods

Application context

Throughout, we describe our design in the context of our experience developing an actual randomized phase II trial to include biomarker identification and subsequent independent evaluation. This oncology trial—now ongoing—was originally planned as a simple randomized phase II design with retrospective evaluation of candidate biomarkers. In this framework, the design called for a maximum accrual of 160 patients randomized to an experimental arm versus placebo in a 2:1 ratio, which provided 80% power to detect a hazard ratio (HR) of 0.60 based on 107 progression-free survival (PFS) events with a one-sided type I error rate of α =0.05. During study development, investigators identified a candidate predictive biomarker; that is, a marker with the potential to identify a subgroup of patients who would achieve substantial benefit from therapy. A modified design was desired, to include prospective assessment of the continuous, serum-based baseline marker for prediction of treatment benefit, and further, to identify a threshold for classification of patients into positive (treatment responsive) versus negative (treatment resistant) marker status. Also desired were interim futility stopping rules in both the overall and biomarker-defined populations, and possible interim accrual restriction and final treatment evaluation in the preliminarily identified “treatment-responsive” or biomarker-positive population.

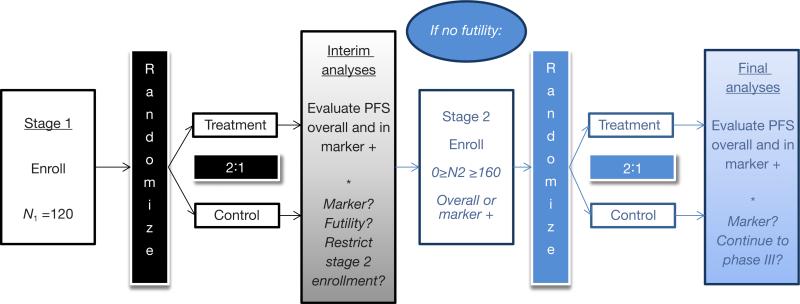
Below, we describe details of the final design solution in terms of the algorithm we used for its implementation. Here, primary interest lies in a time-related endpoint (PFS), where a single interim check incorporates a series of analyses for predictive marker evaluation, cut-point selection, futility, and possible restriction of accrual. A design overview and schema are presented in Figure 1. In specific application to this study, we performed interim and final analyses with the numerical settings and thresholds as described in the algorithm below, but note that particular study characteristics (e.g., primary endpoint, randomization ratio, and timing of interim analyses) may be easily generalized to extend the design to other settings. A discussion intended to guide selection of these trial-specific design quantities follows presentation of the algorithm, to facilitate the reader's implementation of the design in future contexts.

Figure 1.

Adaptive design schema.

Study algorithm and analyses

We assume existence of a single continuous marker, possibly predictive of treatment effect, but with unknown distribution in the study population. Based on the sponsor's prior experience with the marker and preliminary data, possible dichotomizations of the marker are considered that result in marker(-positive) prevalence in the range of 25% to 75%. In the event the marker is unrelated to treatment effect in the interim analyses, the sponsor wishes to limit enrollment to the originally planned 160 patients. However, if the marker demonstrates sufficient association with the treatment effect in the interim analyses, the sponsor is willing to enroll up to an additional 160 patients to confirm efficacy in the tentatively identified benefit population (overall or marker-positive). We note that the timing of the interim analyses was chosen in simulations to provide the minimum acceptable power for the treatment-by-biomarker interaction and efficacy tests described in the algorithm below. Additional practical details are provided in the subsequent discussion.

Step 1: interim analyses for marker identification

After N₁ =120 stage I patients (80 on the treatment arm, 40 on placebo) are enrolled and followed for at least eight weeks, interim analyses will be performed. At that time, possible cut-points of the candidate biomarker are explored, restricted to those cut-points that result in a 25% to 75% marker prevalence. A series of Cox proportional hazards (PH) regression models are fit across a reasonably fine grid of possible cut-points for the biomarker. Each Cox model treats (possibly right-censored) PFS as the outcome, and treatment assignment, dichotomous biomarker status, and treatment-by-biomarker interaction effect as covariates. The cut-point associated with the strongest interaction effect (potentially after smoothing of these effects over neighboring cut-points) is used in subsequent interim analyses, and potentially in the test for subpopulation benefit in final analyses, assuming the interaction effect is associated with significance p ≤ P_int. Thus, at the conclusion of the stage I enrollment and interim analysis, we establish two scenarios:

Scenario 1: promising biomarker. A promising biomarker is considered to have been identified when, according to the best-identified cutpoint, the interaction P-value is less than or equal to P_int and the treatment demonstrates greater benefit in the biomarker-high group relative to the marker-low group.

Scenario 2: no promising biomarker. No promising biomarker is considered to have been identified when, according to the best-identified cutpoint, the interaction P-value is greater than P_int or the treatment demonstrates greater benefit in the biomarker-low group relative to the marker-high group.

In practice, P_int is chosen via simulation to optimize the design's operating characteristics (e.g., desired power or type I error), given practical constraints such as stage I sample size, distribution of the primary study endpoint, anticipated or targeted clinical benefit, and level of censoring for a time-to-event endpoint. According to Scenarios 1 and 2 defined above, the following additional analyses will be performed.

Scenario 1: test for the treatment effect in subgroups. If the biomarker is promising for prediction of treatment effect (Scenario 1), then log-rank tests for the superiority of treatment versus placebo are performed within each marker subgroup defined by the newly-selected cut-point. Cox PH models are also used to compute the HR in the marker-high and marker-low patients, HR_L and HR_H respectively, for treatment versus placebo.

Scenario 2: test for overall treatment effect. If no promising biomarker exists at stage I (Scenario 2), a log-rank test for the superiority of the treatment arm versus placebo is performed using data from all (biomarker low and high) stage I patients. A Cox PH model is used to compute the interim HR of treatment versus placebo in terms of overall PFS.

Step 2: stage I futility stopping rules

Immediately following the interim analyses for stage I patients, futility stopping may be invoked according to Scenarios 1 and 2 defined in Step 1.

Scenario 1: promising biomarker. If the biomarker is promising for prediction of differential treatment effect, futility is separately evaluated within marker-low and marker-high subgroups as follows: if the one-sided P-values from both subgroups’ log-rank tests for superiority are greater than P_fut (approximately corresponding to a HR greater than HR_fut), the trial terminates for futility. If the one-sided P-value is greater than P_fut for marker low but not marker high patients, accrual to stage II will continue only in marker high patients, as described in Step 3.

Scenario 2: no promising biomarker. If the biomarker is not promising for prediction of differential treatment effect, futility is evaluated as follows: if the P-value associated with the overall log-rank test for superiority is greater than P_fut (approximately corresponding to a HR greater than HR_fut), the trial terminates for futility. Similar to P_int, the futility stopping boundary P_fut is chosen via simulation to optimize the operating characteristics of the design for a given application.

Step 3: stage II accrual restrictions and trial resizing

If the study is not stopped for futility based on the interim analyses and decision rules described in Step 2, an additional N₂ patients are accrued in stage II, taking into account sponsor-defined enrollment caps on total enrollment and marker-low enrollment, given by N_cap and, respectively. In practice, N_cap and $N_{cap}^L$ are chosen jointly by the sponsor and statistical team, such that the design operating characteristics (i.e., power and type I error) may be optimized for the specific study objectives and resource constraints. For our trial, we set N_cap =280 and $N_{cap}^L$ and proceed with accrual and corresponding primary endpoint analyses according to Scenarios 1 and 2, where special subcases of Scenario 1 (A and B) are defined below.

Scenario 1A: promising biomarker, restricted accrual. If the biomarker is identified as promising at interim Step 1 (Scenario 1), but subgroup analysis of marker-low patients (Step 2) shows that treatment provides no meaningful benefit relative to placebo in terms of PFS by the futility threshold P_fut, accrual to stage II proceeds only in the marker-high group. Henceforth, we refer to this scenario as Scenario 1A or “restricted accrual.” In this case, stage II sample size is N₂ =160 marker-high patients, to achieve 80% power to detect HR_H =0.60 for treatment versus placebo with 1-sided α =0.05 based on 107 PFS events. Under this scenario, the total trial size is N = N₁+N₂ =280 combined (120 stage I +160 stage II) patients, such that N = N_cap.

Scenario 1B: promising biomarker, unrestricted accrual. If the biomarker is identified as promising at interim Step 1 (Scenario 1), and corresponding subgroup analysis of marker-low patients (Step 2) shows that treatment may still hold promise versus placebo in terms of PFS by the futility threshold P_fut, accrual to stage II continues to both biomarker groups, but in accordance with $N_{cap}^L=90$ total marker-low patients in the trial. If $N_{cap}^L$ has already been reached at the time of interim analysis, stage II accrual continues only to the marker-high group. Regardless of whether $N_{cap}^L$ is already reached at interim, we refer to this scenario as Scenario 1B or “unrestricted accrual.” In this case, sample size for stage II is based on achieving 160 total (stage I and stage II) marker-high patients, to provide 80% power to detect HR_H =0.60 for treatment versus placebo with 1-sided α =0.05 after 107 PFS events have occurred in the marker-high group. Under this scenario, the total trial size N = N₁+N₂ falls between 214 and 250 combined (120 stage I +94 to 130 stage II) patients, depending on marker prevalence falling between 25% and 75%, such that N < N_cap.

Scenario 2: no promising biomarker. If in the Step 1 analysis the biomarker is not promising for prediction of treatment effect, the trial is not resized, and accrual to stage II continues to all patients regardless of biomarker status. In this case, the final analysis of treatment versus placebo ignores the biomarker and follows the original design; i.e., an additional N₂ =40 patients are enrolled regardless of biomarker status in stage II, to yield a total trial size of N = N₁+N₂ =160 patients to detect HR =0.60 for PFS with at least 80% power and 5% one-sided type I error after 107 events have occurred. After the trial's conclusion, retrospective exploratory analyses of the biomarker (or other potential biomarkers) may be performed.

Step 4: final efficacy testing in the biomarker-based benefit population

Final tests for efficacy are performed in either the marker-high (Scenario 1A or 1B) or overall (Scenario 2) benefit population as follows.

Scenario 1A: promising biomarker, restricted accrual. If a promising marker is identified at the interim analysis and stage II accrual is restricted to the marker-high group (Scenario 1A), the primary difference in PFS between treatment and placebo is tested using a log-rank test with stage II marker-high patients only. This is to preserve independence of the (marker unrestricted) stage I patients that were used to identify the marker effect from the (marker-restricted) stage II patients to be used to confirm efficacy in patients defined by the marker. This case, interim testing of stage I patients results in a permanent change to the trial's population of interest for testing efficacy where marker-low patients are no longer considered for enrollment. To address this lack of exchangeability of stage I and II patients, only stage II marker-high patients are used in the final log-rank test for efficacy, while stage I patients are not used in the primary efficacy analysis. The decision rule considers the treatment promising in the marker-high subpopulation if the P-value associated with a one-sided log-rank test is p ≤ P_eff in favor of treatment.

Scenario 1B: promising biomarker, unrestricted accrual. If a promising marker is identified at the interim analysis but stage II accrual is unrestricted (Scenario 1B), a treatment versus placebo difference in PFS within the marker-high subgroup is tested using stage I and II patients, as stage I and stage II patients were enrolled from the same (marker-unrestricted) population. While it is true that the primary treatment effect will be tested in the marker-high population at the trial's conclusion, reuse of stage I patients in the final analyses is justified as stage I and stage II patients are exchangeable; specifically, interim testing of stage I patients has not changed the population of patients (both marker-high and marker-low) enrolled to the trial. In this case, the treatment is considered promising in the marker-high subpopulation if the P-value associated with a one-sided log-rank test is p ≤ P_eff in favor of treatment. As an independent test of the biomarker under scenario 1B, a log-rank test using only stage II marker-high patients may be performed.

Scenario 2: no promising biomarker. If the biomarker was not promising at the interim analysis and accrual was limited to the 160 originally-planned patients, then treatment will be considered promising overall if the p-value associated with a one-sided log-rank test is p ≤ P_eff in favor of treatment. As exploratory analyses, additional biomarker explorations and subgroup analyses may be performed.

Design evaluation approach

A simulation study was performed to investigate the operating characteristics of the design. Throughout, settings and assumptions were chosen to reflect the particular oncology study for which the design was created.

All simulation scenarios were performed with 10,000 iterations (hypothetical trials), with interim analyses performed after eight weeks follow-up on the 120^th patient enrolled. Trials for which futility was not reached at the interim analysis were allowed to enroll up to a financially dictated, sponsor-defined cap N_cap =280 total patients, with a marker-low enrollment cap of $N_{cap}^L=90$ patients ensuring an adequate number of marker-high patients are enrolled to power the stage II analyses. Throughout, we assume uniform accrual at the rate of four patients per week, exponentially-distributed PFS, and a median PFS of eight weeks for the control arm, regardless of biomarker status. Patients were randomized in a 2:1 ratio to experimental versus control treatments, respectively.

Throughout, we fix P_int =0.50, P_fut =0.60, and P_eff =0.10 to maximize overall power, given the possibilities of low marker prevalence and imperfect interim marker identification. Other values of these thresholds were considered via simulation (results not shown), and for a given new application of this design, possible adjustments should be studied accordingly. We constructed simulation scenarios using three different values of biomarker prevalence, representing relatively extreme levels of prevalence (25% and 75%) as well as moderate prevalence (50%). Within each of these levels, we vary both the HR in the marker-low subgroup (HR_L) and the HR in the marker-high subgroup (HR_H), considering a sequence of cases where HR_L ≥ HR_H.

Results

Simulation-based operating characteristics for the proposed design are presented by marker prevalence and hypothesized marker subgroup-specific HRs in Table 1. In the null case (HR_L = HR_H =1), the type I error rate (concluding the experimental treatment is efficacious when it is not, with or without a biomarker) is controlled at 12.1% or less for our specific choice of design parameters. This rate was deemed acceptable by the sponsor of our motivating study. In practice, design thresholds should be modified to achieve the specific desired type I target. Among the same scenarios, futility stopping after the initial 120 patients occurred in 29.6% of cases for low marker prevalence, and at higher rates for higher prevalence. When the control arm was slightly inferior, false positive results were obtained in a maximum of 8.1% of cases across prevalence levels with HR_L =1.2 and HR_H =1, and a maximum of 2.1% of cases with HR_L = HR_H =1.2. Under these same scenarios and regardless of prevalence, futility stopping rates were at least 37.5% and 55.7%, respectively, and reached as high as 65.3%.

Table 1.

In each section of the table, mutually exclusive special cases such as “Marker” and “No marker” are indented and presented with plain text, while primary parent outcomes of interest are presented in bold text. Rates in parentheses are conditional on biomarker detection at interim analysis

Average/percent	HRL =1.2 HRH =1.2	HRL =1.2 HRH =1.0	HRL =1.0 HRH =1.0	HRL =1.0 HRH =0.8	HRL =1.0 HRH =0.6
25% marker prevalence
Trial size	166	187	176	198	224
Interim marker	26.3%	39.2%	25.8%	42.4%	63.5%
Restricted accrual	21.4%	31.5%	15.8%	24.3%	32.2%
Interim futility	55.7%	41.2%	29.6%	18.2%	7.7%
No marker	53.6%	39.4%	29.3%	17.9%	7.6%
Marker	2.1%	1.8%	0.3%	0.3%	0.1%
Final efficacy	1.7% (2.3%)	6.4% (12.0%)	12.1% (16.3%)	30.9% (51.7%)	67.0% (91.8%)
No marker	1.1%	1.7%	7.9%	9.0%	8.7%
Marker	0.6%	4.7%	4.2%	21.9%	58.3%
Final marker	0.5% (1.9%)	3.8% (9.7%)	2.6% (10.1%)	17.2% (40.6%)	54.0% (85.1%)
50% marker prevalence
Trial size	159	186	175	201	232
Interim marker	25.2%	40.1%	26.2%	43.5%	69.1%
Restricted accrual	17.8%	31.5%	18.4%	27.9%	35.4%
Interim futility	59.7%	37.9%	31.0%	13.8%	2.5%
No marker	53.8%	33.6%	29.0%	12.8%	2.3%
Marker	5.9%	4.3%	2.0%	1.0%	0.2%
Final efficacy	2.1% (2.8%)	7.6% (12.0%)	12.0% (15.6%)	36.1% (52.9%)	78.9% (93.3%)
No marker	1.4%	2.8%	7.9%	13.1%	14.4%
Marker	0.7%	4.8%	4.1%	23.0%	64.5%
Final marker	0.5% (2.0%)	3.6% (9.0%)	2.4% (9.2%)	16.4% (37.7%)	55.0% (80.0%)
75% marker prevalence
Trial size	151	181	171	200	228
Interim marker	25.5%	38.4%	25.1%	40.7%	63.4%
Restricted accrual	13.8%	28.0%	18.4%	29.4%	37.7%
Interim futility	65.3%	37.5%	34.0%	10.7%	1.0%
No marker	54.2%	29.8%	30.2%	9.2%	0.9%
Marker	11.1%	7.7%	3.8%	1.5%	0.1%
Final efficacy	1.8% (2.0%)	8.1% (10.7%)	11.2% (13.9%)	39.1% (50.4%)	85.2% (92.6%)
No marker	1.3%	4.0%	7.7%	18.6%	26.5%
Marker	0.5%	4.1%	3.5%	20.5%	58.7%
Final marker	0.3% (1.2%)	3.0% (7.8%)	2.2% (8.8%)	14.8% (36.4%)	46.7% (73.7%)

Among scenarios with no treatment effect for marker-low patients but a beneficial effect for marker-high patients (HR_L =1 and HR_H <1), overall power increases with marker prevalence, as expected. For example, with HR_L =1 and HR_H =0.60 (the latter being the targeted treatment effect), overall power (defined as a significant result overall or within the marker-high subgroup) is 67.0% for 25% marker prevalence, 78.9% for 50% prevalence, and 85.2% for 75% marker prevalence. We note that power is highly dependent upon successful identification of the true predictive marker at the time of interim analysis. Specifically for the case of HR_L =1 and HR_H =0.60, the probability of reaching a positive trial result given successful interim marker identification (“conditional” power) is 91.8% to 93.3% across possible values of marker prevalence. This critical identification of a truly predictive marker depends not only on marker prevalence and magnitude of the effects, where HR =0.60 was the largest effect reasonably expected by the sponsor, but also on timing of the interim analysis. Where the total sample size is large enough to justify a later interim analysis, or where larger treatment effects than HR =0.60 might reasonably be expected (simulations not shown), the power to detect a truly predictive marker at the time of interim analysis will be increased.

Among the scenarios considered along the continuum from no biomarker (HR_L = HR_H =1) to best-case biomarker (HR_L =1 and HR_H = 0.60), the chance of identifying a biomarker at the interim analysis ranged from 26.2% to 69.1% with 50% marker prevalence. Though greater differentiation of the no marker and promising marker cases would certainly be desired, in simulations, these probabilities of false positive and successful marker detection could not be further separated without modifying one of two design factors: an increase in the targeted differential treatment effect between marker-based subgroups (which was not deemed plausible in our case), or an increase in the maximum trial size (also constrained), which in turn allows a later interim analysis based on a greater number of events. Under our best-case marker scenario (HR_L =1 and HR_H =0.60), given marker identification at interim, the conditional rate of marker validation ranged from 73.7% to 85.1% across levels of marker prevalence. These rates were deemed acceptable by the sponsor; see Section 4 for additional discussion of the power of treatment-by-marker interaction tests.

Discussion

Practical considerations

We note that the final version of our design presented in Section 2 is the result of a number of iterative decisions, beginning with initial modifications made to an original, biomarker-free design with 160 patients. In the original design, an interim analysis was planned after the first 80 patients. In simulation studies, however, this stage I sample size was identified as too small to detect a meaningful predictive biomarker using treatment-by-marker interaction tests; thus, the decision was made to postpone the interim analysis until after 120 patients were enrolled and followed. With this timing, false-positive marker identification was controlled to approximately 25% across prevalence levels for the null case, and an interim marker identification rate of 69% was observed under the best-case marker scenario considered for this specific application (HR_L =1 and HR_H =0.60). These rates were deemed acceptable by the sponsor, given the maximum allowed sample size and interim timing constraints. In particular, the sponsor was motivated by the fact that liberal identification of a marker at interim analysis would be balanced by stringent confirmation of the marker's predictive value at the time of final analysis.

It should be noted that prevalences (cutpoints) outside of the range of 25% to 75%, while plausible in some settings, might result in dramatically reduced power at the time of marker detection at the interim analysis. In this case, there may be less enthusiasm for use of this design. Indeed, the post-interim performance of this design is conditional upon successful identification of truly predictive biomarkers, and to a lesser degree, successfully concluding at the interim analysis when a biomarker indeed does not exist. While performing an earlier interim analysis for futility might yield (on average) a smaller trial, an earlier interim analysis would also yield less power to detect a truly predictive biomarker or early overall efficacy. In application of this design, timing of interim analyses for efficacy and futility should be studied via simulation against the corresponding trade-offs.

A 2:1 randomization ratio was utilized in our motivating study, specifically to motivate accrual given the required possibility of randomization to a placebo control arm. Data and Safety Monitoring Board (DSMB) surveillance was in place to ensure patient safety as greater than half of enrolled patients received an active experimental agent with possible associated toxicities. In other applications of this design, straightforward 1:1 randomization may be sufficient. In this case, all other things being unchanged, a smaller sample size will be required for 1:1 randomization, or higher power will be achievable with the same sample size. A smaller sample size or greater power to detect treatment and interaction effects may also result in settings where treatment effects larger than HR =0.60 are considered possible to observe. In our study, larger effects were deemed highly unlikely by the sponsor and investigators and were thus not studied in simulations. Given the early stage of drug development this trial was intended to address and the relatively small sample size, early stopping rules for efficacy were not considered.

Our design also assumes a continuous marker such that the experimental treatment is hypothesized to work better for marker-high patients than marker-low patients. That is, a larger treatment effect among marker-low patients than marker-high patients would not be of interest in our setting, but may be possible in others. From our point of view, if a marker is so new (having not been previously studied, at least retrospectively, in earlier trials) or lacking in scientific rationale such that the sponsor does not have a clear idea of the anticipated (marker high versus marker low) direction of benefit, we would caution against use of a marker-based design altogether—especially adaptive designs such as ours where the trial conduct may change based on preliminary results. For comparison against a general one-stage randomized design with no biomarker, the results presented in Section 3 may be compared against the operating characteristics of the original, biomarker-free design described in the first paragraph of Section 2.1.

Implementation

To facilitate adaptation of our proposed design to a new trial setting where a candidate predictive biomarker exists, we suggest the following algorithm. First, the sponsor and study statistician(s) should jointly determine a value of N_cap beyond which the objectives of the trial would be too costly to pursue, where the statistician's role is to convey feasibility of the design under a range of enrollment limits. Given a plausible N_cap, a study-relevant randomization ratio (e.g., 1:1 versus 2:1), a reasonable range of differential treatment effects (e.g., HRs) within each marker-defined subgroup, and desired levels of power and type I error, the statistician then determines via simulation the optimal stage I sample size N₁, such that the interim analysis occurs after an adequate subset of those patients experience the primary event of interest (e.g., PFS). We suggest tentatively setting N₁ = N*/2, where N* is the total sample size required to power a biomarker-free design with the same operating characteristics, and then increasing N₁ to find the value associated with the optimal interim biomarker detection rates allowed by both N_cap under the best-case marker scenario (HR_H < HR_L =1) and reasonable values of marker prevalence. The stage II sample size N₂ is then chosen by adequately powering the final analysis in the marker-positive benefit population under Scenario 1A, subject to constraints given by N_cap, the best-case HR_H, and the desired type I error α. As in our motivating study, it may be necessary to impose a limit $N_{cap}^L$ on the total number of marker-low patients enrolled under Scenario 1B. In practice, this value should be chosen such that a sufficient amount of stage II accrual is reserved for the marker-high patients required to power the final analysis. While our application intentionally uses a smaller N₂ under Scenario 1B (unrestricted accrual) than under Scenario 1A (restricted accrual), such that N is guaranteed to be less than N_cap for the former scenario, it may be important in certain applications to continue observing the effect of experimental treatment on as many marker-low patients as allowed by N_cap; e.g., when these patients show a non-negligible response to treatment (Scenario 1B). Jointly in simulation studies, the statistician should consider the operating characteristics as a function of marker prevalence, such that minimum and maximum values of the threshold distinguishing marker-positive from marker-negative patients may be prospectively defined. The R program used to design our motivating study and conduct simulations is available from the first author upon request.

Limitations

Some limitations not already mentioned and inherent to our proposed design, and biomarker designs in general, should be noted. First, we perform dichotomization of a continuous biomarker, to achieve the simplicity and interpretability similar to the dichotomous marker assumptions present in most existing biomarker design literature. In some cases, maintaining a marker as continuous in the interaction modeling process may be more appropriate. On a related note, we acknowledge an often-cited limitation of interaction testing, namely that the power to detect a treatment-by-marker interaction may be low relative to the power to detect a treatment effect using the same sample size. Nonetheless, rather than perform an overall test for treatment benefit followed by a test within a marker-defined subgroup in the event the overall test is negative, as is common in the marker design literature, we utilized a formal treatment-by-marker interaction test within a Cox model at the interim analysis to check for early evidence of a marker-treatment-outcome relationship. We maintained this test specifically to address the question of whether the marker is truly predictive in nature, as opposed to merely prognostic, which may actually be the case if a treatment effect is weak in the overall population but strong in a marker positive subgroup. Another limitation generally common to multi-stage classical designs is that variability inherent to the interim and final analyses are not comprehensively addressed in a formal manner, e.g., via Bayesian posterior distributions with accompanying decision rules, though we note that this will be an area of future exploration. Lastly, we acknowledge that in practice, limited sponsor resources may restrict the total sample size to an extent that may impact the design's performance or make its use impractical relative to other existing designs. Despite these limitations, which elicit important topics for further research, we expect the prospective and adaptive biomarker-based design presented here to prove both efficient and practical for phase II screening of targeted therapies and companion biomarker diagnostics for subsequent study in phase III trials.

Conclusions

The prospective biomarker-based design to evaluate a time-related endpoint (e.g., PFS) presented herein provides a potentially powerful and useful tool in the situation where limited information exists regarding the predictive ability of an exploratory, continuous biomarker. This design could easily be modified to address alternative endpoints, such as tumor response within a pre-specified time period. Making timely use of available patient data, the design yields a candidate marker threshold, identifies the population (overall or marker-based) most likely to benefit from the experimental treatment, and subsequently optimizes enrollment for members of this population. Prospectively including predictive biomarker identification within a phase II study of a novel experimental treatment will not only significantly shorten development timelines by removing the second phase II study required for biomarker validation, but also reduce the population required for a selected phase III trial, compared with a trial in which an unselected population is studied. Through integration of a panel of important phase II objectives—biomarker threshold selection (or non-selection), determination of overall or subgroup-specific futility, possible accrual restriction to the hypothesized treatment benefit population, and timely independent marker evaluation in patients from the same trial—this design allows flexible specification of parameters to suit sponsor interests and objectives, while also encouraging efficient and ethical use of patient resources.