Potential for large outbreaks of Ebola virus disease

Highlights

• •We revisited data from the first known Ebola outbreak in Zaire in 1976.
• •Using a mathematical model, we estimated transmission rates in different settings.
• •Analysis suggests the person-to-person R0 was 1.34 (95% CI: 0.92–2.11).
• •Epidemiological conditions in 1976 could have generated a larger outbreak.

Abstract

Outbreaks of Ebola virus can cause substantial morbidity and mortality in affected regions. The largest outbreak of Ebola to date is currently underway in West Africa, with 3944 cases reported as of 5th September 2014. To develop a better understanding of Ebola transmission dynamics, we revisited data from the first known Ebola outbreak, which occurred in 1976 in Zaire (now Democratic Republic of Congo). By fitting a mathematical model to time series stratified by disease onset, outcome and source of infection, we were able to estimate several epidemiological quantities that have previously proved challenging to measure, including the contribution of hospital and community infection to transmission. We found evidence that transmission decreased considerably before the closure of the hospital, suggesting that the decline of the outbreak was most likely the result of changes in host behaviour. Our analysis suggests that the person-to-person reproduction number was 1.34 (95% CI: 0.92–2.11) in the early part of the outbreak. Using stochastic simulations we demonstrate that the same epidemiological conditions that were present in 1976 could have generated a large outbreak purely by chance. At the same time, the relatively high person-to-person basic reproduction number suggests that Ebola would have been difficult to control through hospital-based infection control measures alone.

Introduction

There have been more than twenty-five known outbreaks of Ebola virus disease in Africa since the disease was first identified in Zaire (now Democratic Republic of Congo) in 1976 (Centers for Disease Control and Prevention, 2014). Five ebolavirus strains have been identified in total, the most virulent of which appears to be the Ebola Zaire variant (EBOV); it was responsible for over a dozen outbreaks between 1976 and 2008, with overall case fatality rate of 79% (95% CI: 0.76–0.81) (Centers for Disease Control and Prevention, 2014; Breman et al., 1978; Formenty et al., 2003; Georges et al., 1999; Heymann et al., 1980; Khan et al., 1999; Leroy et al., 2004; Nkoghe et al., 2011; Pattyn, 1978; Report of an International Commission, 1978). Transmission occurs as a result of direct contact with the body fluids of infected individuals, and is unlikely to occur during the incubation period (Breman et al., 1978; Dowell et al., 1999). In March 2014, a new outbreak of EBOV was identified in West Africa. Cases were reported first in Guinea (Baize et al., 2014), then in Liberia, Sierra Leone, Nigeria and Senegal. The outbreak is the largest to date: as of 5th September 2014, 3944 cases have been reported by the World Health Organisation, and 1759 deaths (World Health Organisation, 2014). Unlike previous outbreaks, which were centred on rural communities, infections have also been detected in large urban areas in 2014. It is therefore crucial to develop a better understanding of the transmission dynamics of EBOV, and the implications it could have for control measures.

There have been a number of modelling studies of Ebola, which have focused on two historical outbreaks (Table 1). For the 1995 outbreak in Democratic Republic of Congo, estimates of the basic reproduction number have ranged from 1.4 to 3.7 (Chowell et al., 2004; Ferrari et al., 2005; Legrand et al., 2007; Lekone and Finkenstädt, 2006; Ndanguza et al., 2013; White and Pagano, 2008); for the 2000/1 outbreak in Uganda, estimates span 1.3–2.7 (Chowell et al., 2004; Ferrari et al., 2005; Legrand et al., 2007; McKinley et al., 2009). These studies fitted models of varying complexity to time series with date of disease onset and/or death. However, in both outbreaks, hospital-based infection played a substantial role in transmission (Borchert et al., 2011; Khan et al., 1999; Francesconi et al., 2003). As the data were not stratified by likely source of infection, it was not possible to identify the relative contribution of different transmission routes to the reproduction number. It therefore remains unclear to what extent person-to-person transmission contributed to past Ebola outbreaks, and how community and hospital-specific control measures influenced the reproduction number in each setting.

Table 1.

Previously published estimates of basic reproduction number, R₀, for Ebola.

Location	Date	R0	95% CI (if given)	Reference
DRC	1995	1.83		Chowell et al. (2004)
		3.65	3.05–4.33	Ferrari et al. (2005)
		2.7	1.9–2.8	Legrand et al. (2007)
		1.38		Lekone and Finkenstädt (2006)
		2.22	1.9–2.73	Ndanguza et al. (2013)
		1.93	1.74–2.78	White and Pagano (2008)
Uganda	2000/1	1.34		Chowell et al. (2004)
		1.79	1.52–2.30	Ferrari et al. (2005)
		2.7	2.5–4.1	Legrand et al. (2007)

To gain further insights into the dynamics of Ebola, we revisited case data from the first known EBOV outbreak in 1976. These data included information on the likely source of infection, as well as date of onset and outcome. We used a transmission model to infer the basic reproduction number in different settings, and assessed the contribution of hospital and community infection to disease transmission. Having characterised the dynamics of EBOV, we used stochastic simulations to investigate alternative outcomes that could have been generated with the same epidemiological conditions present in 1976, and assessed the potential for a large outbreak of the disease. Finally, we discuss the implications of our results for other Ebola outbreaks.

Methods

Data

Between August and November 1976, there were 318 reported cases of Ebola in the Yandongi collectivity of Zaire, with 280 deaths. The outbreak was centred around the Yambuku Mission Hospital. With only five syringes issued each day, exposure to contaminated syringes and needles during routine outpatient visits was a common route of transmission; infected hosts then returned to their villages, and in some cases infected others in the community (Breman et al., 1978).

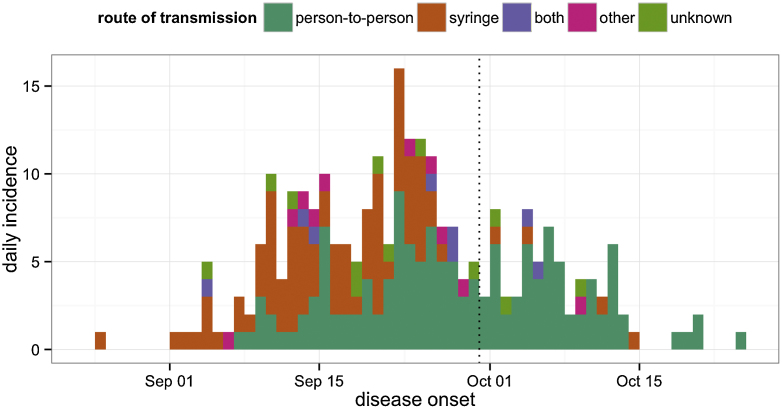
In our analysis, we used a line list of 262 cases, taken from the original epidemiological investigations (Breman et al., 1978; Report of an International Commission, 1978). The data (Supplementary File S1) reported: date of disease onset; outcome (death/recovery); date of outcome; and likely source of transmission (syringe during outpatient visit/person-to-person transmission/both/other). The progression of the outbreak is shown in Fig. 1. Of the reported 262 cases, 250 had a likely source of infection recorded and 8 dates of onset and outcome were missing (Table S1). We used the line list to compile four daily time series: onset of disease following hospital infection via syringe (87 cases in total); onset of disease following person-to-person infection (140 cases in total); reported deaths (248 cases in total); and reported recoveries (11 cases in total).

Fig. 1.

Daily incidence time series of Ebola virus disease onsets in 1976. Cases are coloured by route of transmission, as reported by the epidemiological investigation team (Breman et al., 1978). ‘Both’ indicates infections that could have come from syringe or person-to-person transmission; ‘other’ denotes alternative infection routes (mainly congenital). The dotted line corresponds to the hospital closure date (30th September). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Model

We used a compartmental model of infection to analyse the temporal dynamics of Ebola (Legrand et al., 2007). The model structure is outlined in Fig. 2. We assumed that individuals start off susceptible to infection (S). Upon infection they enter an incubation period (E), then become symptomatic and infectious in the community (I). We therefore assume that the latent and incubation periods are equivalent. After this point, they either: enter a recovered state (R); remain infectious and go into hospital (H); or die and remain infectious (D) until buried (B). Following hospitalisation, infectious hosts also move either into the recovered or dead compartment.

Fig. 2.

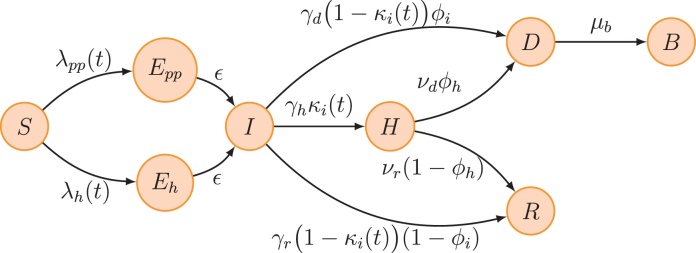
Schematic of model structure. Individuals start off susceptible to infection (S). Upon infection they enter an incubation period (E), then at symptom onset they become infectious in the community (I). After this point, they either: enter a recovered state (R); remain infectious and go into hospital (H); or die and remain infectious (D) until buried (B). Hospitalised infectives also move either into the recovered or dead compartment. Finally, the E compartment is split according to the route of transmission in order to keep track whether a case was infected via contaminated syringes at the hospital (E_h) or by person-to-person contact (E_pp) with either an infective in the community or a dead but not buried case. The forces of infection for the two transmission processes are λ_h(t) = β_h(t)H/N and λ_pp(t) = (β_i(t)I + β_d(t)D)/N, where β_h(t), β_i(t) and β_d(t) are the time-varying transmission rates given by Eq. (1). Other parameters are as follows: ϵ, inverse of the mean incubation period; γ_h, γ_d and γ_r, inverse of the mean duration from symptom onset to hospitalization, death and recovery respectively; ν_d and ν_r, inverse of the mean duration from hospitalization to death and recovery respectively (see Eq. (7)); μ_b, inverse of the mean duration from death to burial; κ_i(t) is computed to ensure that the overall hospitalisation rate is equal to κ until hospital closure (see Eq. (5)); ϕ_i and ϕ_h are computed to ensure that the overall case–fatality ratio is equal to ϕ (see Eq. (4)). Parameter values and prior assumptions can be found in Table 2. The model was simulated by integrating the set (3) of ordinary differential equations using the SSM library (Dureau et al., 2013).

We assumed susceptible hosts in the community could become infected in three different ways: person-to-person transmission from an infectious host in the community, at rate β_i(t), or from a dead but not buried patient during a traditional funeral ceremony, at rate β_d(t); or hospital transmission via syringe during outpatient visits, at rate β_h(t).

There was evidence that hospital and person-to-person transmission declined over the course of the 1976 outbreak. Epidemiological reports note that the community stopped coming to the outpatient department as they associated the epidemic with the Yambuku Mission Hospital, which eventually was closed on 30th September. Also, as time went on the population became very suspicious and did not touch the corpses anymore, not even to bury them (Breman et al., 1978). We therefore used time-dependent smooth decreasing functions for β_i(t), β_d(t) and β_h(t) (Chowell et al., 2004; Lekone and Finkenstädt, 2006; Ndanguza et al., 2013):

$$\begin{array}{cc}\hfill {\beta }_i(t)& ={\beta }_i(1-{\delta }_{\mathrm{pp}}\sigma (t,{\alpha }_{\mathrm{pp}},{\tau }_{\mathrm{pp}}))\hfill \\ \hfill {\beta }_d(t)& ={\beta }_d(1-{\delta }_{\mathrm{pp}}\sigma (t,{\alpha }_{\mathrm{pp}},{\tau }_{\mathrm{pp}}))\hfill \\ \hfill {\beta }_h(t)& ={\beta }_h(1-\sigma (t,{\alpha }_h,{\tau }_h))1_{t<T_h}\hfill \\ \hfill & \hfill \end{array}$$ (1)

where $1_{t<T_h}$ is the indicator function and σ is the following sigmoid function:

$$\sigma (t,\alpha ,\tau )=\frac{1}{1+exp(-\alpha (t-\tau ))}.$$ (2)

As t grew large, we assumed that β_i(t) and β_d(t) approached values equal to a proportion δ_pp of their initial values. We also assumed that no further hospital transmission occurred after the hospital closed on 30 September (i.e. β_d(t) = 0), and that no new cases entered the H compartment after this point.

Using our estimates of β_i(0), β_d(0) and β_h(0), we were able to calculate the basic reproduction number, R₀, defined as the average number of secondary cases produced by a typical infectious host at the onset of the outbreak (i.e., in a completely susceptible population), see details in Text S3. At the start of the outbreak, the reproduction number, R(t), defined as the average number of secondary cases produced by a typical infectious host at time t, was equal to R₀; as the outbreak progressed, R(t) could vary depending on the values of β_i(t), β_d(t) and β_h(t), as well as through depletion of susceptibles.

The full model was as follows (for brevity, the time dependencies of state variables are omitted):

$$\begin{array}{cc}\hfill \frac{\mathrm{d}S}{\mathrm{d}t}& =-({\beta }_i(t)I+{\beta }_h(t)H+{\beta }_d(t)D)\frac{S}{N}\hfill \\ \hfill \frac{\mathrm{d}{E}_{\mathrm{pp}}}{\mathrm{d}t}& =({\beta }_i(t)I+{\beta }_d(t)D)\frac{S}{N}-ϵE_{\mathrm{pp}}\hfill \\ \hfill \frac{\mathrm{d}{E}_h}{\mathrm{d}t}& ={\beta }_h(t)H\frac{S}{N}-ϵE_h\hfill \\ \hfill \frac{\mathrm{d}I}{\mathrm{d}t}& =ϵ(E_{\mathrm{pp}}+E_h)-{\mathrm{\Gamma }}_i(t)I\hfill \\ \hfill \frac{\mathrm{d}H}{\mathrm{d}t}& ={\gamma }_h{\kappa }_i(t)I-({\varphi }_h{\nu }_d+(1-{\varphi }_h){\nu }_r)H\hfill \\ \hfill \frac{\mathrm{d}D}{\mathrm{d}t}& ={\gamma }_d(1-{\kappa }_i(t)){\varphi }_{i}I+{\nu }_d{\varphi }_{h}H-{\mu }_{b}D\hfill \\ \hfill \frac{\mathrm{d}R}{\mathrm{d}t}& ={\gamma }_r(1-{\kappa }_i(t))(1-{\varphi }_i)I+{\nu }_r(1-{\varphi }_h)H\hfill \\ \hfill \frac{\mathrm{d}B}{\mathrm{d}t}& ={\mu }_{b}D\hfill \\ \hfill & \hfill \end{array}$$ (3)

Parameters are summarised in Table 2. We used flat priors for case–fatality ratio and transmission-related parameters. We also used additional epidemiological information not in our time series (Supplementary File S2; (Breman et al., 1978; Report of an International Commission, 1978; Khan et al., 1999; Nkoghe et al., 2011; Okware et al., 2002)) to inform strong prior distributions for: proportion of cases reported; proportion of cases hospitalised; incubation period; time from onset to hospitalization, death and recovery. A strong prior centred around 24 h was used for the time from death to burial of individuals (Isaacson et al., 1978; Sureau et al., 1978). We fixed the initially susceptible population size at 60,000, as this was the number of people for which the Yambuku Mission Hospital served as principal point of care (Report of an International Commission, 1978). We assumed that the index case was introduced in the H compartment at a time T₀, which was also estimated. Indeed, the first reported case (25th August) was infected via a syringe and there is evidence that an unknown man came to the hospital with Ebola-like symptoms shortly before that date (Breman et al., 1978).

Table 2.

Parameter definitions and corresponding estimates. Prior distributions used during model fitting are also shown.

Parameter	Description	Prior	Estimates: median (95% CI)
N	Population size	Fixed	60, 000
T0	Date of introduction of index case to H compartment	$\mathcal{U}$[August 05–August 25]	August 24 (August 21–August 24)
Th	Date of hospital closure	Fixed	September 30
ρonset	Proportion of onsets reported	$\mathcal{N}(0.71,0.05)$	0.70 (0.62–0.79)
ρd	Proportion of death reported	$\mathcal{N}(0.89,0.05)$	0.89 (0.80–0.97)
ρr	Proportion of recovery reported	$\mathcal{N}(0.29,0.05)$	0.28 (0.19–0.39)
κ	Proportion of cases hospitalised until hospital closure	$\mathcal{N}(0.17,0.05)$	0.21 (0.14–0.30)
ϕ	Case–fatality ratio	$\mathcal{U}$[0–1]	0.88 (0.80–0.94)
1/ϵ	Incubation period (days)	$\mathcal{N}(6,0.1)$	5.99 (5.80–6.18)
1/γh	Mean time from onset to hospitalisation (days)	$\mathcal{N}(3,0.1)$	3.00 (2.81–3.20)
1/γd	Mean time from onset to death (days)	$\mathcal{N}(7.5,0.1)$	7.49 (7.30–7.69)
1/γr	Mean time from onset to recovery (days)	$\mathcal{N}(10,0.1)$	10.00 (9.80–10.19)
1/μb	Mean time from death to burial (days)	$\mathcal{N}(1,0.1)$	0.99 (0.80–1.18)
βi	Transmission rate in the community at the onset of the epidemic	$\mathcal{U}$[0–100]	0.10 (0.01–0.20)
βd	Transmission rate during traditional burial at the onset of the epidemic	$\mathcal{U}$[0–100]	0.78 (0.08–2.00)
αpp	Shape of the change of person-to-person contact behaviour in community and during traditional burial	$\mathcal{U}$[0–5]	0.30 (0.14–4.17)
τpp	Midpoint date for the change of person-to-person contact behaviour	$\mathcal{U}$[August 25–October 14]	September 27 (September 20–October 03)
δpp	Reduction of the person-to-person transmission rate following change of contact behaviour (%)	$\mathcal{U}$[0–100]	98.00 (90.00–100.00)
βh	Transmission rate in hospital at the onset of the epidemic	$\mathcal{U}$[0–100]	3.24 (2.36–4.43)
αh	Shape of the change of hospital seeking behaviour from outpatients	$\mathcal{U}$[0–5]	2.29 (0.49–4.85)
τh	Midpoint date for the change of hospital seeking behaviour	$\mathcal{U}$[August 25–September 30]	September 17 (September 14–September 19)

As the model included multiple transitions between compartments, we needed to define certain parameters carefully. To ensure that the overall case–fatality ratio was equal to ϕ, we defined ϕ_i and ϕ_h as follows:

$$\begin{array}{cc}\hfill {\varphi }_i& =\frac{\varphi {\gamma }_r}{\varphi {\gamma }_r+(1-\varphi ){\gamma }_d}\hfill \\ \hfill {\varphi }_h& =\frac{\varphi {\nu }_r}{\varphi {\nu }_r+(1-\varphi ){\nu }_d}.\hfill \\ \hfill & \hfill \end{array}$$ (4)

Similarly, κ_i(t) was computed to ensure that the overall hospitalisation rate was equal to κ until hospital closure:

$${\kappa }_i(t)=\frac{\kappa ({\gamma }_r(1-{\varphi }_i)+{\varphi }_i{\gamma }_d)}{\kappa ({\gamma }_r(1-{\varphi }_i)+{\varphi }_i{\gamma }_d)+(1-\kappa ){\gamma }_h}{1}_{t<T_h}.$$ (5)

Finally, Γ_i(t) denotes the total rate of exit from the I compartment:

$${\mathrm{\Gamma }}_i(t)={\gamma }_h{\kappa }_i(t)+{\gamma }_d(1-{\kappa }_i(t)){\varphi }_i+{\gamma }_r(1-{\kappa }_i(t))(1-{\varphi }_i),$$ (6)

and ν_d and ν_r are the inverse of the mean time from hospitalisation to death and recovery respectively:

$$\begin{array}{cc}\hfill {\nu }_d& =\frac{{\gamma }_d{\gamma }_h}{{\gamma }_h-{\gamma }_d}\hfill \\ \hfill {\nu }_r& =\frac{{\gamma }_r{\gamma }_h}{{\gamma }_h-{\gamma }_r}.\hfill \\ \hfill & \hfill \end{array}$$ (7)

Inference

To compare the model output with observed data, we calculated the incidences corresponding to the four time series on each day:

$$\begin{array}{cc}\hfill \mathrm{\Delta }{I}_{\mathrm{pp}}(t)& ={\int }_t^{t+1}ϵE_{\mathrm{pp}}\mathrm{d}t\hfill \\ \hfill \mathrm{\Delta }{I}_h(t)& ={\int }_t^{t+1}ϵE_h\mathrm{d}t\hfill \\ \hfill \mathrm{\Delta }D(t)& ={\int }_t^{t+1}({\gamma }_d(1-{\kappa }_i(t)){\varphi }_{i}I+{\nu }_d{\varphi }_{h}H)\mathrm{d}t\hfill \\ \hfill \mathrm{\Delta }R(t)& ={\int }_t^{t+1}({\gamma }_r(1-{\kappa }_i(t))(1-{\varphi }_i)I+{\nu }_r(1-{\varphi }_h)H)\mathrm{d}t\hfill \\ \hfill & \hfill \end{array}$$ (8)

We assumed that onset (i.e. ΔI_pp(t), ΔI_h(t)), death (ΔD(t)) and recovery (ΔR(t)) data were reported according to Poisson processes with constant reporting rates ρ_onset, ρ_d and ρ_r respectively. We allowed for three potentially different reporting rates because (i) not all cases had reported onsets; (ii) 30 of the 262 were reported with both, other or unknown source of infection rather than person-to-person or syringe. These cases were therefore included in the outcome time series but not in the onset one; and (iii) only 11 of 38 (29%) recovery cases versus 248 of 280 (89%) death cases were reported.

The probability of observing y_pp(t) new onsets resulting from person-to-person transmission on day t, for a given parameter set θ (summarised in Table 2) was therefore as follows:

$$L_{\mathrm{pp}}(y_{\mathrm{pp}}(t)|\theta )=\frac{{[{\rho }_{\mathrm{onset}}\mathrm{\Delta }{I}_{\mathrm{pp}}(t)]}^{y_{\mathrm{pp}}(t)}{e}^{-{\rho }_{\mathrm{onset}}\mathrm{\Delta }{I}_{\mathrm{pp}}(t)}}{y_{\mathrm{pp}}(t)!}.$$ (9)

Similar expressions (L_h, L_D and L_R) were derived for the other incidence data and combined into the likelihood function:

$$L(y_{\mathrm{pp}},y_h,y_D,y_R|\theta )=\prod _{t=1}^{72}\prod _{k\in \{\mathrm{pp},h,D,R\}}{L}_k(y_k(t)|\theta )$$ (10)

We used a Bayesian framework to fit the model to all four time series simultaneously and make inference on the parameter set θ. Given the likelihood function L and the chosen prior distribution of the parameters, the posterior distribution is known up to a normalising constant. Markov chain Monte Carlo methods construct Markov chains whose stationary distribution is the distribution of interest, when it cannot be directly simulated. We used the SSM library (Dureau et al., 2013), which implements an adaptive Metropolis–Hastings algorithm (Roberts and Rosenthal, 2009) to generate sequences of draws from the posterior distribution of the parameters. We refer to Text S1 for more details. To test the accuracy of our inference framework, we fitted the model to observed data, generated a set of simulated time series from our fitted model, then estimated the parameters from the simulated data; our inference framework was able to recover the parameters in question (Text S2, Table S2 and Figs. S2–S5).

Results

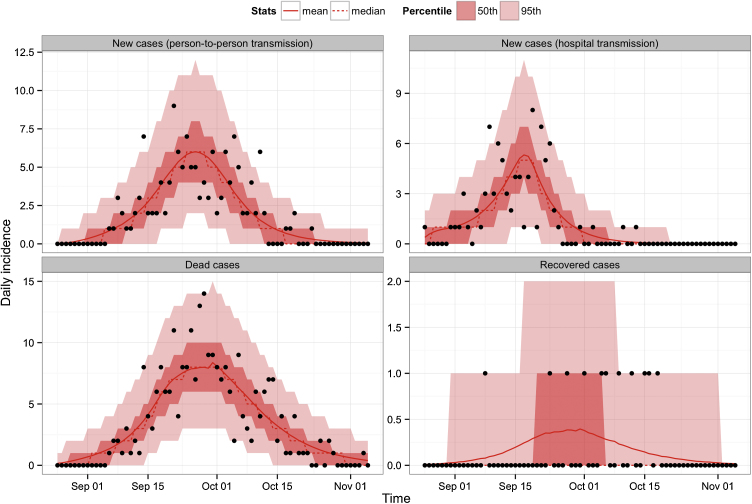
Our model was able to capture the dynamics of Ebola virus disease, including infections resulting from exposure to contaminated syringes and person-to-person transmission, and the timing of outcomes (Fig. 3). By fitting to multiple time series, we were able to jointly estimate a number of key epidemiological parameters (Table 2 and Fig. S1). Using these estimates, we calculated the contribution of person-to-person transmission (via infection from living and dead hosts in the community) and hospital-based transmission (via contaminated syringe) to the overall basic reproduction number, R₀ (see Text S3). We found that the overall R₀ was 4.71 (95% CI: 3.92–5.66) at the onset of the epidemic. Most of this number was the result of hospital-based transmission, although we found evidence that the person-to-person basic reproduction number was above 1 (Table 3).

Fig. 3.

Comparison of our fitted model and observed daily incidence time series (black dots) reconstructed from the line list of Ebola cases in Zaire in 1976. The mean and median fits are represented by solid and dashed red lines respectively. The dark and light red shaded areas correspond to the 50% and 95% credible intervals. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Table 3.

Estimates of the basic reproduction number, R₀, split into different component transmission routes.

Parameter	Route of transmission	Estimates: median (95% CI)
R0h	Hospital via syringe	3.32 (2.53–4.34)
R0pp	Person-to-person (in community and during funeral)	1.34 (0.92–2.11)
R0	Overall	4.71 (3.92–5.66)

Person-to-person transmission was separated into two components in the model: infections occurring while the case was alive and those occurring after death (i.e. before the patient had been buried). This meant fitting both transmission rates β_i and β_d. However, due to limited data on these specific transmission routes, the relative contribution to infection from living and dead patients in the community was not fully identifiable (see Text S1). When we fitted both transmission rates independently, the contributions from community and funeral cases to R₀ were highly correlated (Fig. S6). As it was not possible to identify the contribution from community and funeral infection to person-to-person transmission, we therefore gathered the two measurements together into a single person-to-person basic reproduction number, denoted R_0pp, which could be estimated from the available data.

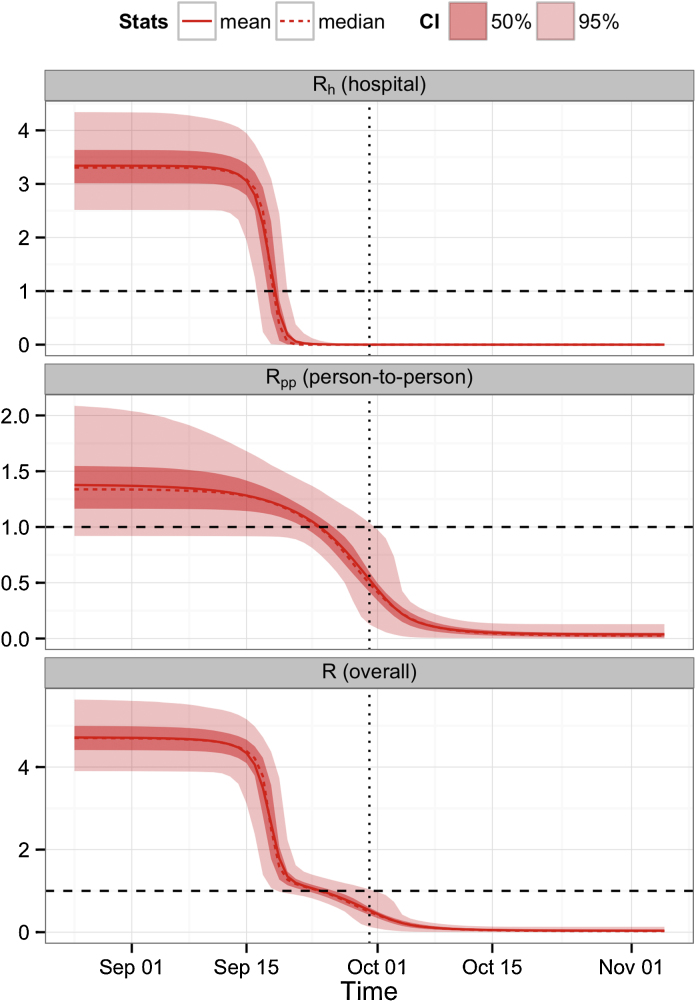
As the epidemic progressed, we found that the overall reproduction number decreased due to changes in the contact rate within the community and within the hospital. Splitting the overall reproduction number into its person-to-person and hospital components, we found that although hospital transmission was dominant during the early stages of the epidemic, it had dropped significantly by mid September (Fig. 4). Our results suggest the hospital reproduction number R_h was below 1 well before the hospital closed on the 30 of September. Moreover, we found that hospital closure alone could not explain the observed data; when changes in person-to-person and hospital-based transmission were excluded, the model performed significantly worse (Table S3). We estimated that the drop in person-to-person transmission occurred later and less sharply than the reduction in exposure to contaminated syringes. However, the reduction in person-to-person transmission was still enough to drive the overall reproduction number below 1 by the end of September. Overall, these results are consistent with the observations reported by the epidemiological investigation team (Breman et al., 1978).

Fig. 4.

Drop in the reproduction number (R(t)) owing to change of behaviour in community contacts and visit of outpatients to the hospital. The overall R (lower panel) can be split into an hospital (upper panel) and person-to-person (middle panel) component. The dashed line indicates the epidemic threshold (R = 1) and the dotted line corresponds to the hospital closure (30th September). Solid, dashed and shaded red lines/area as in Fig. 3. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

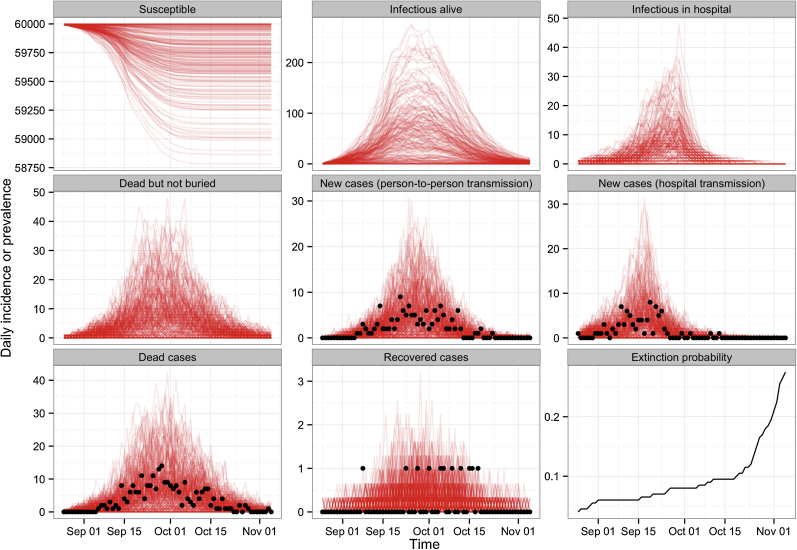
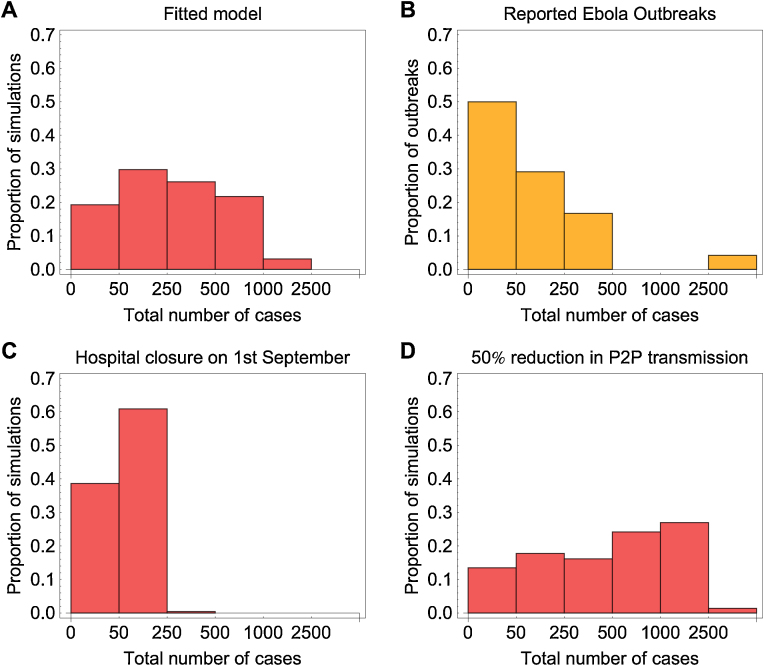
To examine the possible range of dynamics for an outbreak with the same characteristics as the one observed in the 1976 Yambuku outbreak, we ran 10,000 stochastic simulations of our model under the maximum a posteriori probability estimates of the parameters (Fig. 5). We found that although most simulated epidemics were of similar size to the one in 1976, major outbreaks could also occur. Although only 3% of simulations resulted in a major outbreak (i.e. more than 1000 cases), the cumulated number of cases could reach up to several thousands in the worst-case scenario (Fig. 6A). In the context of the 1976 epidemic, such a major outbreak could have arisen if – by chance – a sufficiently high number of infections had occurred before the change of community contact and hospital seeking behaviours.

Fig. 5.

Potential alternative trajectories of an Ebola outbreak in Yambuku. Ten thousand stochastic simulations were run with parameter values taken from the maximum a posteriori probability estimate (for readability only the first 200 are plotted). For comparison, data are plotted as black dotted points.

Fig. 6.

Distribution of Ebola outbreak sizes in different scenarios. (A) Outbreak size distribution from 10,000 stochastic simulations using the maximum a posteriori probability estimate. (B) Distribution of number of cases reported in Ebola outbreaks in Africa from 1976 to present. (C) Outbreak size distribution from 10,000 stochastic simulations when hospital is closed 7 days after the date of the first onset (i.e. 1st September). All other parameters remain the same. (D) Outbreak size distribution from 10,000 stochastic simulations when person-to-person transmission is reduced by 50% rather than 98%. The final category includes all outbreaks with more than 2500 cases.

To understand how different control measures could affect outbreak size, we also considered several alternative scenarios in our simulation study. First, we set the hospital closure date in the model to be 7 days after the onset date of the first case in the line list i.e. on 1st September rather than 30th. Although early closure resulted in fewer cases, with no outbreaks generating more than 1000 cases, there were still occasionally outbreaks consisting of several hundred cases (Fig. 6C). Next, we examined the effect of a smaller reduction in person-to-person transmission, assuming that the hospital reduction remained the same. We found that if the person-to-person transmission rate was reduced by 50% – rather than 98% as in our median estimates – transmission could persist longer in the community, and hence 28% of simulations resulted in an outbreak of at least 1000 cases (Fig. 6D). The number of reported cases in historical Ebola outbreaks has varied greatly, from a few infections to more than 3500 (Fig. 6B); our results suggest that such variability might be expected given the transmission dynamics of Ebola.

To explore the possibility of a large outbreak occurring without the large contribution from hospital transmission, we also considered a model with only person-to-person transmission (i.e. R_0h = 0). We assumed that the index case started in the community (I compartment). In the absence of control measures, we found that 35% of outbreaks resulted in more than 1000 cases.

As well as allowing us to model setting-specific transmission, the line list made it possible to directly calculate the case–fatality ratio (CFR) in different settings. We found that the probability of survival varied depending on route of transmission. The overall CFR – defined as the proportion of cases that died – across the 262 cases in our line list was 251/262 = 0.96 (binomial 95% CI: 0.93–0.98). The CFR for cases that resulted from person-to-person transmission was 0.92 (0.87–0.96); in contrast, the CFR for cases that were exposed via a contaminated syringe was 1.00 (0.96–1.00). Note that these empirical CFR estimates are based on a subset of 262 of the 318 reported cases in the Yambuku outbreak, for whom individual data were available. The CFR based on all 318 reported cases was 280/318 = 0.88 (95% CI: 0.86–0.92) (Breman et al., 1978).

Discussion

Using a model of Ebola virus transmission, we examined the role of different transmission routes during the 1976 outbreak in DRC. We found that the basic reproduction number (R₀) associated with hospital transmission was significantly above one. Our analysis also suggests that the person-to-person reproduction number R_pp could have been above 1 for the early part of the outbreak. This has profound implications: it suggests that a large outbreak (involving thousands of cases) could have happened even without changing any epidemiological conditions. We estimated the probability of such a large outbreak (>1000 cases) to be around 3%. This means that given the same initial conditions, Ebola outbreaks would have been occasionally been large, just by chance. Moreover, a relatively high person-to-person transmission component (R_0pp ≈ 1) implied that the 1976 epidemic would have been difficult to control via hospital-based infection control measures alone. If the reduction in community transmission had been smaller, or infection had been seeded into a number of different communities, the outbreak could have continued for some time.

Our results also suggest that changes in behaviour caused a significant reduction in both hospital-to-community and within-community transmission. Although Yambuku Mission hospital closed on the 30th September, we found that the reduction in transmission occurred well before this point, most likely from susceptible hosts having less contact with infected patients, and making fewer routine outpatient visits to the hospital (Breman et al., 1978). As well as contributing to transmission, infections from syringes also appeared to have a higher case fatality ratio (CFR) than person-to-person infections. This could have been the result of a larger viral inoculum during contact with a contaminated syringe. With more data on transmission events – including chains of person-to-person infection – it would be possible to further investigate the role of exposure in the natural history of Ebola infection.

Even with four time series, it was not possible to robustly distinguish between person-to-person transmission resulting from contact with community cases and funeral attendance. Additional case data, such as dates on which patients took care of an infected case or attended a funeral ceremony could allow us to disentangle the relative role of these two routes of community transmission. However, it is plausible that individuals had similar contact rates with infected and dead patients. Epidemiological investigations in 1976 found that 86% of hosts infected from person-to-person transmission reported prior contact with alive Ebola patients; the same proportion reported attending the funeral of an infected case (Breman et al., 1978). Assuming similar transmissibility for both types of contact, this would be equivalent to setting β_i = β_d in our model.

There are some additional limitations to the model. First, we assumed that hosts mixed randomly both in the community and hospital. This was a reasonable assumption given that we stratified the data by route of transmission and outcome. However, there was evidence that certain groups, such as women aged 15–29, were more likely to attend clinics at Yambuku Mission Hospital in 1976 and hence be exposed to syringes (Report of an International Commission, 1978). To model the dynamics of the infection at a finer resolution, for instance by comparing model outputs to age-stratified case data, it would be necessary to account for such heterogeneity. We also assumed that occurrence of reported cases was Poisson distributed, and the proportion reported did not vary over time or by location. This might be plausible when cases occur in a relatively short outbreak in a small geographic region, but during outbreaks that span a much larger geographic area and persist for several months, reporting could change with time and vary between different settings. Moreover, if the dynamics of Ebola were to be modelled in real-time, it would be important to account for potential delays in reporting of cases and outcomes.

In our stochastic scenario analysis we also assumed that timing and magnitude of changes in transmission rate were independent of epidemic size. Our simulations that used parameters from the fitted model (Fig. 6A) therefore assumed that identification and control of the infection would not have occurred quicker if more individuals had been infected earlier. However, we tested the sensitivity of our results to timing of hospital closure by assuming that the hospital closed one week after the first case (Fig. 6C); we also explored the effects of a smaller change in magnitude in person-to-person risk (Fig. 66D). Ideally, it would be possible to define a functional relationship between incidence and changes in transmission rate (Funk et al., 2009). However, this relationship is likely to be complex and setting-specific: in 1976, behavioural changes reduced transmission (Breman et al., 1978); in other Ebola outbreaks, large amounts of infection have increased fear and mistrust in the community, which might also have increased transmission (Borchert et al., 2011; World Health Organisation, 2014).

The modelling tools illustrated here could easily be adapted for other Ebola outbreaks, and highlight the benefits of having data on likely source of infection and time of onset, hospitalisation and outcome for each patient. Previous Ebola modelling studies have examined the 1995 outbreak in Kikwit, DRC (Chowell et al., 2004; Ferrari et al., 2005; Legrand et al., 2007; Lekone and Finkenstädt, 2006; White and Pagano, 2008; McKinley et al., 2009; Ndanguza et al., 2013), and the 2000/1 outbreak in Uganda (Chowell et al., 2004; Ferrari et al., 2005; Legrand et al., 2007). As in Yambuku in 1976, hospital-based transmission played a substantial role in both outbreaks (Khan et al., 1999; Francesconi et al., 2003). However, modelling studies so far have incorporated time series for onset and/or death only, which meant that it was not possible to robustly infer the role of different routes of infection, such as the contribution of hospital and community transmission. In contrast, by fitting a transmission model to time series stratified by transmission route, we were able to estimate the contribution of different sources of infection to the dynamics of the epidemic.

We estimated that the overall R₀ was 4.71 (95% CI: 3.92–5.66) for the 1976 Yambuku outbreak. This is high compared to estimates of R₀ in the 1995 and 2000/1 outbreaks, which ranged from 1.34–3.65 (Table 1). However, our analysis suggests that most of the R₀ in 1976 consisted of transmission via syringe; the person-to-person basic reproduction number was 1.34 (0.92–2.11). Given data on likely source of infection in 1995 and 2000/1, it would be possible to establish whether person-to-person transmission contributed a similar amount to overall transmission during these outbreaks.

Our estimate of a person-to-person basic reproduction number R_0pp ≈ 1 in 1976 suggests that Ebola would have been capable of generating a wide range of outbreak sizes in the absence of any extrinsic variation in epidemiological conditions. This implies that effective reduction in person-to-person transmission was crucial in reducing the potential size of the outbreak; stochastic simulations suggest Ebola could still have generated a large number of cases if hospital transmission was absent in 1976. Measures to reduce person-to-person transmission – including isolation of patients, follow-up surveillance of their contacts, and education to curtail infection in the community – are therefore likely to form a crucial part of the response to Ebola outbreaks (Borchert et al., 2011; Khan et al., 1999; Okware et al., 2002).

As well as variation in social and cultural factors between different regions, the stochastic nature of Ebola outbreaks means that inference to other settings must be done with caution. Our analysis concentrates on a single outbreak of 318 cases, rather than a set of past Ebola outbreaks, which have ranged from a small number of cases to several thousand (Fig. 6B). Analyses of data from a large number of historical outbreaks simultaneously would help reduce this stochastic uncertainty and allow comparative studies to be performed. By making the line listing of the 1976 outbreak available (Supplementary File S1), we hope to stimulate such work. Comparative studies could potentially shed further light on which underlying factors contribute to the differences in outcome of Ebola outbreaks, and which control measures are likely to be most effective.

Appendix B. Supplementary Data

The following are the supplementary data to this article: