Computational analysis of three-dimensional epithelial morphogenesis using vertex models

Abstract

The folding of epithelial sheets, accompanied by cell shape changes and rearrangements, gives rise to three-dimensional structures during development. Recently, some aspects of epithelial morphogenesis have been modeled using vertex models, in which each cell is approximated by a polygon; however, these models have been largely confined to two dimensions. Here, we describe an adaptation of these models in which the classical two-dimensional vertex model is embedded in three dimensions. This modification allows for the construction of complex three-dimensional shapes from simple sheets of cells. We describe algorithmic, computational, and biophysical aspects of our model, with the view that it may be useful for formulating and testing hypotheses regarding the mechanical forces underlying a wide range of morphogenetic processes.

Introduction

A common mode of metazoan development involves organizing cells into monolayers or sheets, and using these sheets to form structures with higher complexity; such sheets of cells are called epithelia. Cells within an epithelium are characterized by polarity along an axis defining the apical and basal side of the cell. The cells adhere to each other at their lateral surfaces and thus form a sheet; see Figure 1. Epithelial sheets and the processes by which they form complex morphological structures play key roles in evolution and development. Epithelial tissue is the most highly conserved tissue in multicellular animals. The mechanical integrity of epithelia compartmentalized early animals, allowing food to be captured and digested extracellularly in an enclosed space, and permitting the construction of complex, three-dimensional organs [1–3]. Due to the highly organized structure of epithelia, large-scale tissue shape changes, such as folding or bending, can be achieved by controlling the activities of individual cells. Such morphogenetic processes, often termed epithelial folding, are involved in a variety of important developmental processes, such as formation of the ventral furrow in Drosophila and the neural tube in vertebrates [4–6].

Figure 1. Descriptions of epithelia.

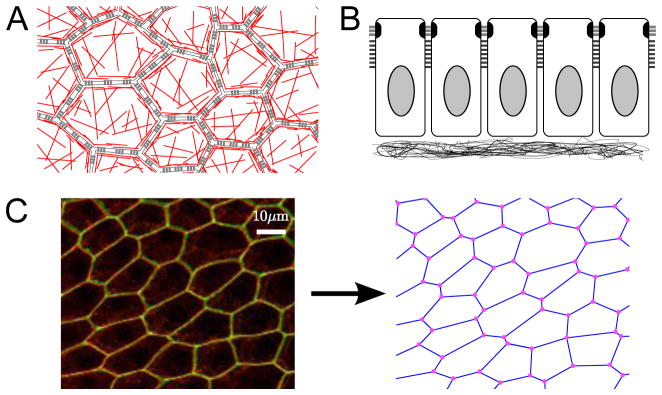
A. Schematic of epithelium viewed from the apical side; cells adhere to each other laterally via adherens junctions (gray bars); within a cell, there is a cortical ring of actin around the perimeter as well as a meshwork of actin throughout the apical side (red lines). B. Schematic side view of a Drosophila epithelium. The apical side points up; cells adhere to each other laterally via adherens junctions (gray bars) and septate junctions (black bars); cell are attached on their basal side to a basement membrane. C. Follicle cell epithelium of Drosophila, visualized as the maximum projection of a confocal z-stack. E-cadherin (red) marks the subapical adherens junctions, while neuroglian (green) marks the septate junctions, which are located slightly basal to the adherens junctions. This epithelium is abstracted in the vertex model where cells are represented by polygons, with lateral membranes abstracted as bonds, and junctions of three or more cells abstracted as points.

Epithelia share many properties with other disordered cellular materials such as foams and granular materials. For example, it has been discovered that cell positioning and sorting can be driven largely by the relative surface adhesion strengths of neighboring cells [7–10], which are phenomenologically equivalent to negative surface tension. As a result of such similarities, authors in these fields frequently borrow from each other’s approaches. A variety of models have been constructed to describe cellular materials, ranging from those describing cells as spheres with distance-dependent interaction forces [11,12], to those that include detailed geometry and shape of the cells but generally lack an explicit representation of realistic forces, such as cellular automata models and cellular Potts models [13], to models that take into account both cell shape and explicit forces describing interactions among cells [14–19]. We have chosen to implement a vertex model, which captures a somewhat simplified cell geometry but explicitly describes realistic forces such as surface tension and pressure.

Vertex models (see Figure 1) represent an epithelium as a set of polygonal cells that can be assigned an energy based on geometry, typically designed to represent the cohesive forces from adhesion molecules, elasticities due to active actin-myosin networks, and effective elasticities that serve to constrain cell volumes. In a variety of biological [20–23] and non-biological [24,25] applications, the dynamics are largely driven by surface tension and pressure. Additionally, discrete rearrangements of vertex connectivity are prescribed to simulate common empirically observed cellular rearrangements. The vertex model gives a simple framework under which forces may be combined with geometry to phenomenologically describe the physics of cellular structures.

In previous work, vertex models of epithelia have been mostly confined to two dimensions. In many cases of epithelial morphogenesis, however, it appears that a two-dimensional nonuniform spatial pattern of gene expression results in a nonuniform pattern of cell properties that helps transform a 2d sheet into a 3d structure. Motivated by work on dorsal appendage formation in Drosophila [26], we have extended a previously described vertex model by embedding it in three dimensions. Using results from this model, we propose that the generation of 3D structures from flat epithelia might in some cases be driven not by differences in mechanical properties along the apical-basal axis as generally hypothesized [27], but from mechanical buckling to due to in-plane stresses. The purpose of this paper is to discuss the main aspects of our model formulation, computational implementation, and analysis of simulations.

Results

In this section, we will give four examples of biological applications of our vertex model. First, we will consider how in-plane tensions can cause buckling of a 2d sheet embedded in 3d. Second, we carefully follow a single intercalation event and discuss the energetics of canonical cell rearrangements. In the final two examples, we examine how including both buckling and cell rearrangements in the same model allows for generation of complex morphologies, and discuss biological applications.

The energy function for vertex models that we will use is:

$$E=\sum _{\alpha }\left(a_{\alpha }{\left(A_{\alpha }-A_{\alpha }^0\right)}^2+b_{\alpha }{L}_{\alpha }^2\right)+\sum _{\langle ij\rangle }{\sigma }_{ij}{l}_{ij}+\sum _{\langle \alpha \beta \rangle }{c}_{\alpha \beta }\left(-{\widehat{\mathbf{A}}}_{\alpha }·{\widehat{\mathbf{A}}}_{\beta }+1\right).$$ (1)

The variables in this equation are described in detail in the Models section, along with a description of the calculations of these terms in 3d, expressions for force derived from the energy function, and details of implementation. Here, we briefly reiterate that the first term corresponds to area elasticity of each cell, the second term corresponds to perimeter elasticity of each cell, the third term corresponds to line tension along individual membrane edges of the epithelium, and the fourth term is a curvature term penalizing out-of-plane bending, which is non-zero only in 3d. Energy functions including the first three terms have been widely used in 2d models of epithelia [20, 21, 23, 28]; the fourth term is commonly used in other types of models to describe bending of thin membranes [29].

The implementation of our model described here calculates forces from the energy function and assumes overdamping to evolve the system in time. This approach, which has been also used by other authors [30], allows the model to describe overdamped dynamics explicitly through equations of motion. An important advantage over the Monte Carlo and similar methods is the ability of the model to incorporate time-dependent processes, for example, temporally regulated developmental signals or transport processes.

Analysis of buckling: from 2d to 3d

In our first set of examples, we demonstrate how non-uniform spatial patterning of parameters corresponding to individual cell properties can initiate 3d morphogenesis. It is widely known that compression within the two-dimensional plane of a physical sheet, for example due to inhomogeneities in the material, is linearly unstable with respect to any perturbations in the z direction, and the sheet will buckle much in the way that a blade of grass would become wrinkled if the thickness were non-uniform [31,32]. Therefore, we wanted to establish how our vertex model behaves when subjected to similar spatially non-uniform forces.

First, we consider a model for a myosin cable enclosing a patch of cells, motivated by the myosin cables observed in Drosophila follicle cell appendage and trachea formation [26, 33]. We model the tissue as a rectangular sheet of cells, fixed at the boundaries, and uniformly patterned with parameter values a_α = a, b_α = b, and σ_ij = σ for all cells α and β and edges 〈ij〉 with the exception of the edges surrounding a smaller patch of cells. For these edges, which represent the myosin cable, a larger σ_ij = Tσ is assigned with T > 1 (see Figure 2A). Using these parameter specifications, we solve for equilibrium configurations of the sheet and obtain the critical values of T for which the sheet buckles.

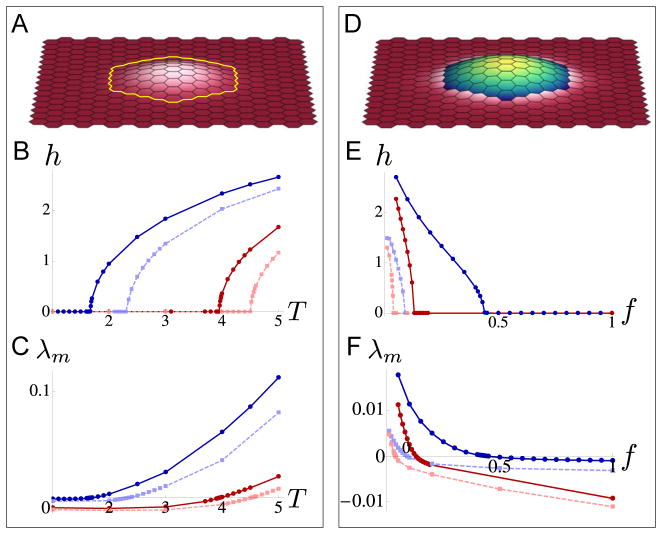
Figure 2. Out-of-plane buckling of a patch of cells.

A–C. Equilibrium configurations and plots for a simulated system in which a patch of cells is surrounded by a “cable” of high line tension. Dimensionless parameter values were a_α = 1, b_α = 0.1, σ_ij = 1, and $A_{\alpha }^0=3\sqrt{3}/2$ for all cells α and bonds 〈ij〉 except for the bonds indicated by the yellow line whose tensions were σ_ij = T, varied in parts B and C. A. Resulting equilibrium configuration for T = 2 with the simulation domain fixed to its equilibrium size (also see Movie S1). B. The maximum height h of the cells in the patch as a function of T. Dark blue solid line shows h for a system fixed to its equilibrium size with c_αβ = 0; dark red solid line shows h for a system fixed to approximately 1.04 times its equilibrium size (a “stretched” system, as described in the main text) with c_αβ = 0; light blue dotted line shows h for a system fixed to its equilibrium size with c_αβ = 0.03; and light red dotted line shows h for the “stretched” system with c_αβ = 0.03. C. The maximum λ_m of the real part of the eigenvalues of the Jacobian of the 3d system for the flat (z component equal to 0), but not necessarily stable, equilibrium state as a function of T. The transition of λ_m from negative to positive corresponds to the emergence of non-flat stable equilibria for the four situations described in part B (color schemes are also similar). D–F. Equilibrium configurations and plots for a simulated system in which there is increased stiffness and tension throughout a patch of cells compared to surrounding cells. Dimensionless parameter values were a_α = 1, b_α = 0.1, σ_ij = 1, and $A_{\alpha }^0=3\sqrt{3}/2$ for all cells α and bonds 〈ij〉 within the patch of blue cells, and a_α = f, b_α = 0.1f, σ_ij = f, and $A_{\alpha }^0=3\sqrt{3}/2$ for all cells α and bonds 〈ij〉 in the pink cells; the bonds between blue and pink cells were assigned to σ_ij = 1; the factor f is varied in parts E and F. D. Resulting equilibrium configuration for f = 0.2 with the simulation domain fixed to its equilibrium size (also see Movie S2). E. The maximum height h of the cells in the patch as a function of f; the four lines correspond to the four situations described in part B. F. Similarly to part C, we plot the maximum λ_m of the real part of the eigenvalues of the Jacobian of the 3d system for the flat equilibrium state. Again, the transition of λ_m from negative to positive corresponds to the emergence of non-flat stable equilibria.

We obtain the equilibrium states and plot their maximum heights for four different cases, to illustrate the effects of boundary conditions and bending energy on model results (Figure 2B:). First, with the boundary of the sheet fixed to its equilibrium size as calculated in the Models section, we examine the effect of incorporating a bending parameter by setting it either to c_αβ = 0 or c_αβ = 0.03 (dark blue and light blue lines). In both cases, the small patch of cells buckles out-of-plane for large enough values of T, as illustrated in Figure 2A and Movie S1; as expected; the critical value of T is larger when c_αβ > 0 as opposed to c_αβ = 0. Next, we consider similar cases, except that the boundary of the entire model tissue is “stretched” by being fixed to approximately 1.04 times its equilibrium size; as before, the bending parameter is set to either c_αβ = 0 or c_αβ = 0.03 (dark red and light red lines). Note that this stretched epithelium example may be relevant in biological situations where an epithelium is under constant external force from certain geometric constraints, for example the follicular epithelium that is stretched over an oocyte in Drosophila egg chambers [26, 34, 35]. As one might intuitively expect, the critical value of T at which the buckling transition occurs is larger for the “stretched” systems compared to the unstretched systems.

To formally show that the out-of-plane motion seen in Figure 2 reflects true buckling, we also performed linear stability analysis of the buckling transition. Figure 2C indicates the maximum real part λ_m of the eigenvalues of the Jacobian for the equilibrium state of the system confined to 2d geometry for the four respective situations; the value λ_m crosses from negative to positive as a function of T when the flat equilibrium configuration loses stability, as typical in cases of buckling instabilities due to compression. Note that near the buckling transition, equilibrium states are not bistable; that is, either a flat or a buckled state, but not both, is stable for a given set of parameters.

Next we consider a related set of examples, representing situations in which there is increased myosin activity throughout a patch of cells. This may be biologically relevant in cases such as in Drosophila ventral furrow invagination, where a meshwork of actin and myosin distributed across the apical surface of the epithelium appears to cause the required cell shape changes [36]. We model this situation as a similar rectangular sheet of cells, where cells in the small patch have vertex model parameter values a_α = a, b_α = b, and σ_ij = σ for all cells α and edges 〈ij〉 within the patch, while outside the patch, parameter values for cells and edges are suppressed by a factor f < 1 to be a_α = fa, b_α = fb, and σ_ij = fσ, and edges on the boundary of the patch are chosen to have tension values σ (see Figure 2D). As a function of f, we test this set of parameter values for the same variations in stretch and bending as described in the previous example; the results for maximum height of the patch are plotted with the same color schemes in Figure 2E. For small enough values of f, the patch of cells buckles out of plane as illustrated in Figure 2D and Movie S2. Again, changes in the critical value of f at which buckling occurs agree with intuition, in that more compliant cells are needed around the patch to cause out-of-plane buckling when there is already overall tension in the system or when the system is averse to bending. Results from linear stability analysis (Figure 2F) confirm that out-of-plane bending in these scenarios is again due to a buckling instability. Taken together, our results here show that two different spatial patterns of mechanical properties can be employed to yield similar qualitative configurations, a buckled patch of cells.

Cell rearrangements in the Vertex model: analysis of intercalation and resolution of T1 junctions

Vertex models typically specifiy not only energy-driven time-evolution, as described above, but also a set of discrete moves or rearrangements that may occur when vertices approach each other. Previous work has established a canonical set of rearrangements that can be used to represent cell neighbor exchange (also called cell intercalation), cell death, and cell division [21, 23]. In this section, we examine the two types of rearrangements (Figure 3A) that are incorporated into our model in subsequent examples: intercalation, and vertex “merging”, which other authors [37] have used to simulate rosette formation.

Figure 3. Schematics of discrete rearrangements.

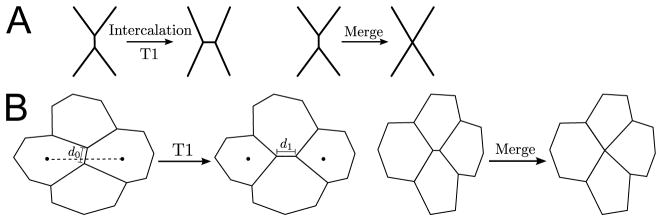
A. Cell intercalation and vertex merging are indicated. B. T1 transitions and merging in the context of cells are illustrated. In our implementation of T1 junctions, we set the new orientation of the intercalating bond to be parallel to the vector connecting the centers of the two cells that are finally separated after the T1 transition (dotted line); we set the new midpoint of the intercalated bond identical to the old midpoint (open circle), and we set the new length to 2.2 times the old length, i.e. d₁ = 2.2d₀.

Biologically, intercalation reflects the ability of cells to move past one another in a plane. For example, in processes such as germband extension, cells need to move past one another to allow for global changes in tissue shape and dimension [38, 39]. Cell intercalation can arise passively as the tissue is stretched by external forces or be actively generated [40]. In the language of the vertex model, cell intercalation necessarily involves the formation of T1 junctions. A T1 junction forms when an edge between two cells shrinks to length 0, and the two vertices involved become effectively one vertex belonging to four cells (a “4-vertex”). The T1 junction is “resolved” when the 4-vertex becomes two new 3-vertices, where the edge joining the two new 3-vertices forms an interface between two cells that originally did not border each other.

Our particular implementation is illustrated and described in Figure 3B. The threshold edge length for implementing a T1 transition should be chosen to be a minimum distance to ensure that two vertices do not arrive at the same position within the next time step. Specifically, we chose this threshold length to be twice the line tension of the edge multiplied by the mobility constant η and by the size of the adaptive time step during which the transition is implemented. However, the implementation may be chosen in a variety of ways as long as the choices allow for smooth numerical propagation of equations.

To illustrate how intercalation can affect the energy of a system, we analyze a large, nearly uniform 2d system (approximately 16 by 19 cells) with a single high tension bond near the center. Figure 4 shows plots of energy and force evolution of this system during a single cell rearrangement event. The higher tension bond is assigned the parameter value σ_ij = 3 if the bond is formed horizontally, that is, in its intial configuration where it is an edge shared between upper and lower cells (shaded gray). Whenever the bond is instead vertical (forming an edge between left and right cells), it is assigned parameter value σ_ij = 1. Below, we explore the total energy E (minus the energy of a completely uniformly patterned cell array) for the system as a function of time t for various prescribed dynamics (Figure 4, Movies S3–S6). We also examine the magnitude of the total concatenated force |F| as a scalar indicator of resultant force and its discontinuities, where the concatenated force F is defined as a large vector whose components are dE/dx_i where x_i is one coordinate degree of freedom.

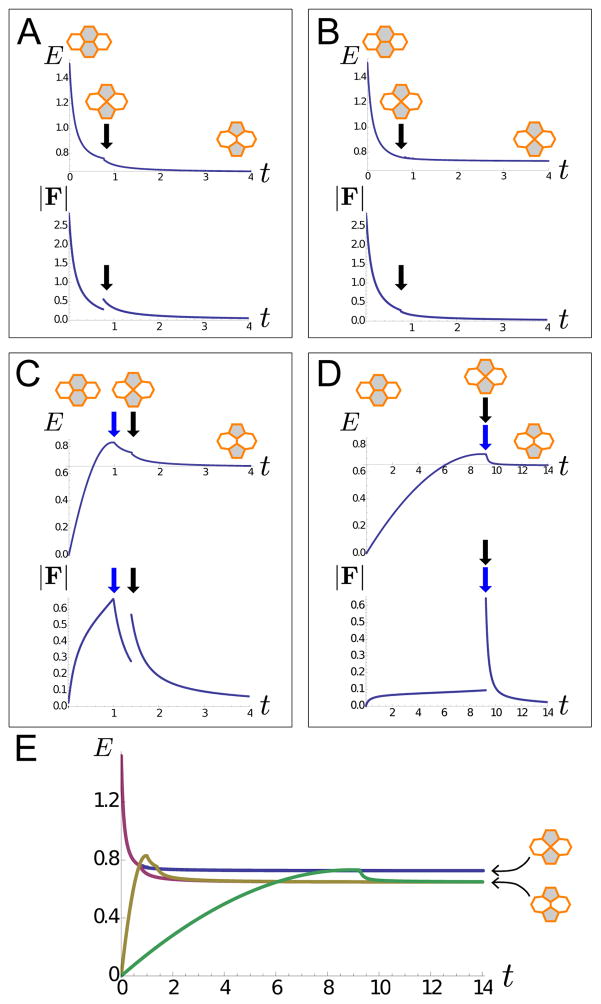
Figure 4. Analysis of a single intercalation event.

A single intercalation event in a domain of 313 uniformly patterned cells, fixed to its equilibrium size at the boundaries. All parameters in the simulation, except for at the highlighted bond, have dimensionless values a_α = 1, b_α = 0.1, σ_ij = 1, and $A_{\alpha }^0=3\sqrt{3}/2$; fixed boundary conditions are implemented. For the highlighted, intercalating bond, σ_ij = 3 if the bond is formed between gray cells, and σ_ij = 1 if the bond is formed between white cells. A–D. Plots of the system’s energy E, with the energy of uniformly patterned domain subtracted out, and magnitude of total concatenated force vector F as functions of time t for various dynamics. Small insets indicate configurations of the intercalating bond as a guide to the plots. A. The highlighted bond is set to have tension σ_ij = 3 at time t = 0. The energy E of the system decreases monotonically until a T1 junction is formed (black arrow), at which time a discrete intercalation event occurs; here, E exhibits a kink and |F| exhibits a jump (Movie S3). B. Same situation as part A, but the T1 junction is not allowed to resolve. In this case, E decreases until the formation of the T1 junction (black arrow), but continues to decrease without a kink, and |F| does not exhibit a discontinuity (Movie S4). C. The highlighted bond is set to have tension σ_ij = 1 at time t = 0 with σ_ij set to linearly increase to σ_ij = 3 at time t = 1. Energy E of the system increases during the time that σ_ij is increased; at time t = 1 (blue arrow), E starts to decrease; at t ≈ 1.4 (black arrow), an intercalation event occurs, and E exhibits a kink. The magnitude of force |F| exhibits a jump at the intercalation event at t ≈ 1.4 but does not exhibit a jump at t = 1 (Movie S5). D. Same situation as part C, but σ_ij increases from 1 to 3 over the time t = 0 to t = 10. In this case, the intercalation event occurs before time t = 10; there is a kink in E and a discontinuity in |F| at time t ≈ 9.2 (blue and black arrows) (Movie S6). E. Energies in parts A–D plotted together with case A (purple), case B (blue), case C (yellow), and case D (green), such that it is apparent that the system allowing for intercalations in cases A, C, and D find mechanical equilibria at a lower energy than case B. The energy in cases A, C, and D all exhibit a kink at the energy value of the T1 junction (4-vertex) formation.

First, we consider the simple case in which the highlighted bond is set to have tension σ_ij = 3 at time t = 0, see figure 4A and Movie S3. The energy E of this system decreases monotonically until a T1 junction is formed (black arrow), at which time a discrete intercalation event occurs. At the moment of intercalaton, E exhibits a kink, while |F| exhibits a discontinuity or jump; after this, E decreases both smoothly and monotonically and approaches a constant value at time t → ∈. For comparison, we next considered a similar situation in which we disallow intercalations and instead require that T1 junctions result in merged 4-vertices; see figure 4B and Movie S4. In this case, E decreases monotonically until the formation of the 4-vertex (black arrow) as before, but then continues to decrease monotonically without a kink, since no discontinuous topological change is made, and approaches a slightly higher constant value at time t → ∈ than for the intercalating case. Furthermore, in the merging case, |F| does not exhibit a discontinuity as it did in the intercalating case.

Next, we consider two related simple cases in which vertex model parameter values can vary over time. Specifically, we consider the same array of cells, where tension of the highlighted bond is set to σ_ij = 1 at time t = 0, then linearly increases until σ_ij = 3. This increase in σ_ij is imposed either quickly, reaching σ_ij = 3 at time t = 1 (Figure 4C and Movie S5), or slowly, reaching σ_ij = 3 at time t = 10 (figure 4D and Movie S6). There are several points about these different cases that may be useful to observe. First, it is apparent that implementations allowing for intercalation (cases A, C, and D) find mechanical equilibria of lower energy than implementations (case B) that do not allow for T1 junction resolution (Figure 4E). Also, the energy E generally remains continuous at the formation of T1 junctions but exhibits a kink; this reflects the discrete change in forces acting on the vertices after rewiring the vertex connectivity. Finally, as demonstrated in figures 4C–D, when parameters are allowed to vary during a time interval, for example by depending explicitly on time as in this example, or by depending on space as illustrated in later examples, the energy of a system can increase over that interval.

Alternative implementation of T1 junctions

In some cases, a T1 junction may form repeatedly if the configurations resulting from different resolutions of the junction are very similar energetically, or if the 4-vertex is temporarily stable. In order to resolve such “stubborn” T1 junctions without significantly slowing down the propagation of the equations of motion, which uses adaptive time-stepping, we introduce a particular stochastic implementation of T1 junction resolution that is discussed more in the Supplementary Materials and Figure S1. We note although that the dynamics of edge contraction may look quite different when noise is added (compare Movie S7 and Movie S8), the final changes in cell neighbor relationships are generally comparable when using either method. Since cell edge fluctuations seen in our stochastic simulations bear resemblance to those observed in vivo in some Drosophila mutants [41], it appears that systematically explored noise parameters that may realistically simulate biological fluctuations may be a future direction for research. For our purposes, however, we have simply chosen noise parameters that helped with computational performance. We further expect that the relative efficiency of implementing the model with versus without noise may vary due to the specific details of the system.

Applications of the vertex model in 3d

Until this point, we have separately illustrated how non-uniform spatial patterning of parameters can lead to buckling, or to intercalation. This raises the question of what effect spatially patterned parameters would have in a model that includes both three-dimensional freedom of movement and cell rearrangements. Answers to this question may be important in understanding how 3d structures form from epithelial sheets. For example, myosin cables have been observed in a variety of developmental contexts, where they appear to serve a variety of functions, such as forming or maintaining straight compartment boundaries, driving tissue elongation through cell rearrangements, or inducing tissue buckling. At this point, however, it remains unclear what factors determine which of these possible outcomes is realized in any particular circumstance [42]. Here, we show how our model may be used to address these issues in the context of intrinsically 3d phenomena by presenting two simple examples, one with relevance to follicle cell appendage formation, and the other to invagination or budding phenomena.

Appendage formation and discussion of energy and active force

Previously, we used a version of the model described here to investigate appendage formation in the follicle cell epithelium of the Drosophila egg [26]. Here, we present a smaller version of a similarly patterned epithelium to provide a more clear view of the mechanisms underlying ordered intercalation in this system (Figure 5A); the parameters are described in detail in the figure legend. Importantly, the edges along the “outer cable” of the patch of cells (red line in Figure 5A) have line tensions that are position-dependent. Namely, T_o = 1.4 + 2e^−ϕ2/200, where ϕ, in degrees, is the angle from the central vertical line. This means that as the red edges move closer to the central vertical line, the assigned value of the line tension parameter increases. This corresponds to energy being added to the system through active force generation (biologically, for example, by myosin activity and use of ATP), similarly to the increasing energies in Figure 4C–D.

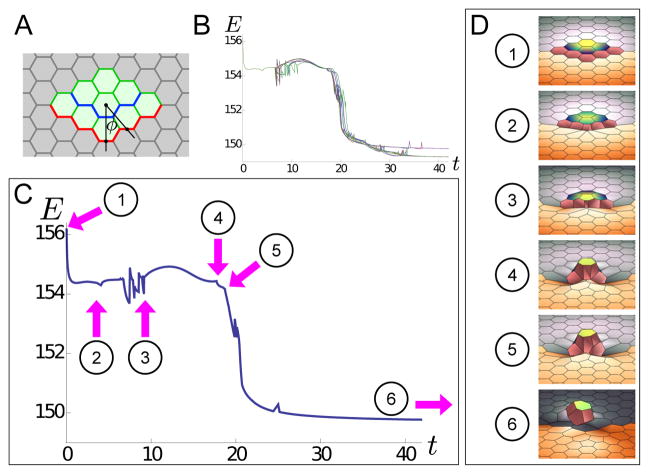
Figure 5. Energy profile for a small appendage formation.

A. Tissue patterning for small appendage simulation: the light green cells have a_α = a = 1 and b_α = b = 0.1; the light gray cells have a_α = 0.1a and b_α = 0.1b; green edges have σ_ij = σ = 1; gray edges have σ_ij = 0.1σ; blue edges has σ = 1.4σ = 1.4, and red edges as position-dependent tension T_o(ϕ) = 1.4 + 2e^−ϕ2/200, where ϕ, in degrees, is the angle from the central vertical line. All cells have c_alphaβ = 0. B. When we pattern a sheet of cells according to part A, vertex model dynamics lead to the formation of a small appendage. Stages of appendage formation are marked on the plot of total system energy E as a function of time t. Here are plots of 12 energy profiles for small appendage formation, shown together. The profiles are slightly different due to the implementation of noise; however, they share many of the same features. C–D. Annotated example of an the energy profile from part B, with characteristic features labelled. 1–2: Period in which no intercalations occur, but the tissue changes shape. This includes cells changing shape to conform to the high tension cable at the pink line (contributing to energy decrease) as well as moving towards the middle of the tissue (contributing to energy increase); whether energy at an instant has net increase or decrease is a matter of which contribution is bigger at a particular instant; the same smooth feature is seen between points 3 and 4. 2. First intercalation occurs. 2–3. Several intercalations occur in which orange cells rearrange, including intercalations that require multiple attempts to resolve. 3–4. Period in which no intercalations occur, but the tissue changes shape significantly. This includes appendage cells moving significantly out of plane (contributing to energy decrease) as well as moving towards the middle of the tissue (contributing to energy increase). 4. Appendage cell right of central line intercalates and looses contact with orange cells. 5. Appendage cell left of central intercalates and losses contact with orange cells. For both points 4 and 5, there is a significant kink in E. 5–6. Non-appendage cells rearrange. 6. Final configuration of appendage cells.

In this example, we follow the energy profile of the system as the appendage is formed from a near-flat sheet (Figure 5B–C and Movie S13). Initially, the energy drops smoothly since decreases in energy due to cell shape-changes are greater than increases in energy from edges moving closer to the central line (frames 1–2 in Figure 5C–D). Next, several rearrangements occur, including ones involving repeated formations of T1 junctions that are resolved with noise, as discussed in Figure S1 (frames 2–3 in Figure 5C–D). Following that, there is a period of no intercalations in which cells move significantly out-of-plane (contributing to decreasing energy) as well as move toward the central line (contributing to increasing energy); here, the energy goes up and down smoothly depending on which of these contributions is greater (frames 3–4 in Figure 5C–D). Finally, in frames 4 and 5 of Figure 5C–D, intercalations occur in which two appendage cells (to the right and left of the central appendage cell respectively), lose contact with the orange cells and therefore lose the high tension edge. This causes kinks in the energy plot, much like the kinks in Figure 4A, C–D. The final configuration of a small appendage is in frame 6 of Figure 5C–D. Due to the numerical noise introduced in the simulations, different iterations of the same simulation produce different plots of energy as a function of time. However, the general features of these different iterations are very similar, as indicated by the energies of 12 different iterations all plotted together as a function of time in Figure 5B.

Budding: multiple intercalations at the edge of a patch of cells

In the example above, active forces appear to play an important role, raising the question of whether active forces are required to generate complex 3d structures. To address this question, we decided to examine a simpler model. This model is motivated by the spatial pattern of myosin in Drosophila tracheal pits [33], a highly-studied example of budding, which is a common form of morphogenesis in branched tissues. We consider a model with parameters that combine the features of Figure 2A and B; a visual representation of the parameter patterning is shown in Figure 6A. More specifically, we consider a patterned domain in which cells within a patch of the domain have model parameters that are a factor of 1/f larger than cells outside the patch, with f ≤ 1, and also such that a “cable” of high line tension runs between any patch and non-patch cells. The edges forming the boundary of the patch, or the cable, are assigned line tension values T + ΔT, with ΔT a random number selected initially (and re-selected after intercalation events) from a uniform distribution between −0.15T and 0.15T in order to break symmetry. We start simulations with an initial configuration of cells in which vertices have a small non-zero z component and repeat several times to control for effects of choosing particular sets of ΔT’s. The reason the initial configuration includes some non-zero z components is that buckling relies on an instability of the flat state to infinitesimally small perturbations. Therefore, to obtain a buckled state in a simulation, small z-perturbations must be introduced at some point; for simplicity, we chose to perturb the initial vertex positions.

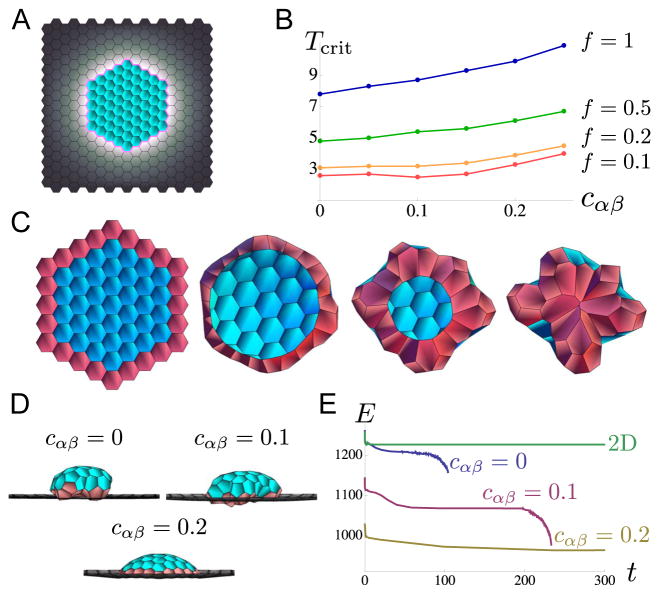
Figure 6. An example of an intrinsically 3d event, budding, simulated using our version of the vertex model.

A. Initial configuration of cells in simulation; a small perturbation in the z direction is given to allow out-of-plane motion; the domain of cells is fixed at its equilibrium size at the boundaries. Color-coding denotes vertex model parameter patterning: blue cells have dimensionless parameter values a_α = a = 1, b_α = b = 0.1, and σ_ij = σ = 1; gray cells have a_α = fa = f, b_α = fb = f0.1, and σ_ij = fσ = f; pink line indicates edges with σ_ij ≈ T ≥ 1 with some noise (see discussion in the main text). The ring of high tension at the boundary between patch and non-patch cells eventually causes the patch to “pinch off”. B. Plotted are the critical tension T_crit as a function of the bending parameter c_αβ required to cause the patch of cells to pinch off. The value T_crit is explored for f = 1 (blue), f = 0.5 (green), f = 0.2 (orange), and f = 0.1 (red). It is clear that T_crit is lower for smaller values of f, and T_crit is larger for larger values of c_αβ since tissues averse to bending will require larger tensions to pinch off. C. Frames from the simulation with parameters in part A, setting f = 0.5, T = 5.5 and c_αβ = 0.1, viewed from beneath the dome of cells (Movie S10); the row of patch cells initially contacting the non-patch cells are colored pink for easy identification. It is clear that several intercalations occur between initial and final configurations at the patch edge due to the presence high tension there. D. Final steady states of the system viewed from the side with parameters in part C except for c_αβ which is varied as c_αβ = 0, 0.1 and 0.2. While for c_αβ = 0, 0.1, the patch of cells pinches off (Movies S9–S10), for c_αβ = 0.2, this does not occur (Movies S11–S12). E. Total energy E plotted as a function of time for cells time-evolved from an initial configuration, for c_αβ = 0, 0.1, 0.2 and for a system confined to 2d (z component is 0). While for c_αβ = 0, 0.1 the energy drops sharply when the patch of cells pinch off, for c_αβ = 0.2 and for the cells confined to 2d, the energy equilibrates to a stable value. Note that the final stable energy E is lower for the cases where cells are allowed to move in 3d than for the case where the cells are confined to 2d. Note also that the final pinched-off configuration for the c_αβ = 0 and c_αβ = 0.1 cases are not equilibrium states.

From such simulations, we find that for relatively small values of T, the patch of cells buckles out of plane and eventually reaches an equilibrium, with few to no cell intercalation events. However, above a large enough value of T (which we call T_crit), given a particular f, first, the patch of cells buckles out-of-plane, then intercalations appear at the edge of the patch along the cable (Figure 6C), and finally, the ring of tension shrinks down to a point due to subsequent intercalation events, and the patch of cells pinches off the sheet. Our formulation of the vertex model does not provide for cells pinching off to form a disconnected tissue, therefore, the simulation ends at this point without reaching equilibrium (Figure 6E). We explored the critical cable tension T_crit as a function of the bending parameter c_αβ for various values of f, indicated in Figure 6B, D and simulations in Movies S9–S12. We found that the required T_crit is larger for larger values of c_αβ as well as for larger values of f. This makes intuitive sense since for tissue more averse to bending and for non-patch cells that are less compliant, there should be more cable tension required to pull a patch of cells inward and pinch it off.

Both the appendage formation and budding examples discussed above demonstrate that combining 3d freedom of motion and cell intercalations in the same model can result in morphogenetic changes not easily predicted when considering these effects separately. This is due to an iterative process in which buckling in 3D allows for the initiation of cell intercalation events that would be energetically unfavorable if the cells were confined to 2d, and the cell intercalation events allow the tissue to deform further into previously inaccessible morphologies.

Discussion

We have described a model for packed epithelial cells that is capable of representing a variety of morphogenetic events. Many elements of this model borrow from previously established vertex models, but the introduction of three-dimensional freedom of movement and 3d elements such as bending energy increase the scope of biological problems that can be addressed.

In this manuscript, we showed how our model may be used to explore buckling of a sheet in 3d due to simple patterns of 2d surface anisotropies. Supplementing other research [43, 44], we gave a careful energetic analysis of a single intercalation in the setting of a 2d vertex model. Finally we combined these approaches to examine how cell rearrangements and 3d tissue deformations can interact to produce complex 3d shapes from mechanically patterned 2d sheets.

Although vertex and other models have previously been used to examine three-dimensional epithelial morphogenesis, the approach we described here is novel in representing an epithelial sheet as a two-dimensional object that moves in three dimensions. In recent years, a number of fully 3d models of morphogenesis have been introduced [45–49], with some models taking into account subcellular elements such as gene regulation [50]. However, at this point, it is not entirely clear which of these formulations best captures the subcellular forces most important to shaping epithelial morphology. Furthermore, the relative magnitudes of these forces are so far relatively unexplored experimentally, resulting in poorly constrained model parameters. Additionally, the implementation of these models may be computationally demanding and mathematically complex. Our model captures at least some phenomena of 3d epithelial deformations using the computational complexity of 2d models.

As an alternative to fully 3d models, several published models, including ones for Drosophila ventral furrow formation and ascidian endoderm invagination, describe only a cross-section of the tissue, reducing the problem to two dimensions [14–16, 51–54]. Those approaches are useful, but are limited to geometrically simple cases. The model we present, in contrast, can be used to simulate morphogenetic changes that are intrinsically three-dimensional. Additionally, the approach we describe here implies a different underlying mechanism for epithelial bending. In cross-sectional models, bending is driven by differences in properties on the apical and basal sides of cells [27]. In our model, bending arises from a buckling instability due to nonuniform in-plane tensions within a surface. In many epithelial morphogenesis events that have been studied, from tracheal formation in Drosophila to primary neurulation in vertebrates, myosin localization is patterned in 2d within the apical surface [33,55]. This suggests that, although fully three-dimensional models may be required to describe some developmental events, important insight into a variety of developmental processes may be obtained by our simpler, “deformable-sheet” model.

There are potentially useful changes and extensions to our model that are simple in implementation and do not alter the model’s general approach. For example, the choice of energy function may be varied. Although the particular 2d vertex model on which we based our work has been demonstrated to fit experimental data [23], other energy formulations have been used, and future work is required to determine what functions may be appropriate for other cell types or tissue geometries. Additional extensions to our model could include cell proliferation and death, which are already incorporated in many 2d vertex models. This could be an important extension for a 3d model since buckling may arise from the over-proliferation of cells.

Another, more complex extension may include taking chemical signaling and mechanical feedback into account. For example, as a tissue changes shape, an individual cell may encounter varying levels of chemical signals that influence its properties. Mechanical feedback is also likely to be important during epithelial morphogenesis [56], and in several systems, myosin appears to be recruited to cellular regions under tension [57]. Work has already been done to incorporate diffusible chemical signals, juxtacrine signaling, and/or mechanical feedback into 2d vertex models [37, 58–60]. Extending our 3d-embedded vertex model by incorporating these or similar approaches may greatly increase the scope of morphogenetic processes that can be usefully modeled.

Models

Model formulation

In modeling epithelial cells as a system of packed polygons, an energy function for a system consisting of any number of cells may be defined as a function of the coordinates and the connectivities of the vertices of the polygons [23]:

$$E=\sum _{\alpha }\left(a_{\alpha }{\left(A_{\alpha }-A_{\alpha }^0\right)}^2+b_{\alpha }{L}_{\alpha }^2\right)+\sum _{\langle ij\rangle }{\sigma }_{ij}{l}_{ij}+\sum _{\langle \alpha ,\beta \rangle }{c}_{\alpha \beta }\left(-{\widehat{\mathbf{A}}}_{\alpha }·{\widehat{\mathbf{A}}}_{\beta }+1\right).$$ (2)

The first term in this expression corresponds to an area elasticity, where A_α is the area of cell α, the parameter $A_{\alpha }^0$ indicates the preferred area of cell α, and a_α is its elasticity coefficient; this term, corresponding to a restoring force toward a resting area $A_{\alpha }^0$, may represent such biological constraints for volume or apical membrane area. Similarly, the second term corresponds to perimeter elasticity, where L_α is the perimeter and b_α is the elasticity coefficient for the perimeter of cell α; this term also corresponds to a restoring force, with the resting perimeter set to 0, and might represent, for example, the elastic effect of the cortical actin ring around the apical surface of epithelial cells [23]. The sum over α indicates a sum over all cells. The third term describes line tension, where l_ij is the length of the edge connecting vertices indexed by i and j, and σ_ij is the line tension coefficient for the bond connecting vertices i and j; this term corresponds to a constant surface tension force between vertices and comes from the empirical characterization of many types of interfaces including lipid membranes. The sum over 〈ij〉 indicates a sum over all bonds. The last term corresponds to a force that resists bending of the epithelial sheet in three dimensions with bending coefficient c_αβ. The indices α and β indicate cells sharing an edge. The values Â_α and Â_β represent unit normal vectors to the apical surfaces of the cells, defined in 3d in the sections below. This term has purely 3d effects. Note that in 2d, the value of Â_α · Â_β would always be 1, causing the last term of the energy expression to vanish. A dimensionless version of the energy function in equation 2 is presented in the Supplementary Materials.

Given a particular connectivity of vertices, the force on each vertex is determined by the negative gradient of the energy with respect to the coordinates of that vertex:

$${\mathbf{f}}_{\mathbf{x}}=-\frac{\partial E}{\partial \mathbf{x}},$$ (3)

where f_x denotes the force applied to a vertex whose position is x. Assuming that the vertex is a material element embedded in viscous medium that applies a drag force on it with mobility η, and using the limit of over-damped dynamics, we obtain the equations of motion for each vertex:

$$-\frac{1}{\eta }\frac{d\mathbf{x}}{dt}+{\mathbf{f}}_{\mathbf{x}}=0$$ (4)

or

$$\frac{d\mathbf{x}}{dt}=-\eta \frac{\partial E}{\partial \mathbf{x}}.$$ (5)

The mobility η simply determines the scale of time and does not alter steady states. A stable steady state configuration of vertex positions (dx/dt = 0, ∀x), that is, a mechanical equilibrium, corresponds to a stable local minimum of the energy E. If equations of motion are satisfied [22], we have

$$\frac{dE}{dt}=\sum _i\frac{d{\mathbf{x}}_i}{dt}·{\nabla }_{{\mathbf{x}}_i}E+\frac{\partial E}{\partial t}=\sum _i-\eta {\left(\frac{d{\mathbf{x}}_i}{dt}\right)}^2+\frac{\partial E}{\partial t},$$ (6)

where the sum is over all vertices i. If no active forces are supplied to the system externally, that is, if ∂E/∂t = 0, then the total energy decreases: dE/dt ≤ 0. The total energy can, of course, increase, if energy is added to the system, that is, if ∂E/∂t > 0. The mechanical equilibria of Equation 5 depend on the positions and connectivities of the vertices. Our vertex model employs both time-evolution using Equation 5 for a particular connectivity as well as changing connectivities according to discrete transformations as described in previous sections.

Evaluation of forces

The force on a vertex is obtained as the negative gradient of the energy expression in Equation 2 with respect to the coordinates of that vertex. If a vertex at x is connected to vertices at {r_i} and cells {α_i}, then the force on this vertex depends only on the geometries of these bonds and cells. Let α ∈ {α_i}, r ∈ {r_i}, and 〈αβ〉 be adjacent cells with α, β ∈ {α_i}. Letting f_x denote the force on a vertex at x, we have:

$${\mathbf{f}}_{\mathbf{x}}=\sum _{\alpha }({\mathbf{f}}_{\mathbf{x}\alpha }^a+{\mathbf{f}}_{\mathbf{x}\alpha }^p)+\sum _{\mathbf{r}}{\mathbf{f}}_{\mathbf{xr}}+\sum _{\langle \alpha \beta \rangle }{\mathbf{f}}_{\mathbf{x}\langle \alpha ,\beta \rangle }^c+{\mathbf{f}}_{\mathbf{x}}^{\text{ext}},$$ (7)

where f_xα denotes the force on a vertex at x due to this vertex being part of cell α, with superscripts “a” and “p” indicating forces due to area and perimeter terms of Equation 2; here, f_xr denotes force on a vertex at x due to a connected vertex at r, and $f_{\mathbf{x}\langle \alpha \beta \rangle }^c$ denotes the force on a vertex at x due to the bending energy of any two adjacent cells around x. The quantity ${\mathbf{f}}_{\mathbf{x}}^{\text{ext}}$ denotes any other external forces that are applied to the vertex at x, for example normal forces to simulate contact with an external surface or external pulling forces to simulate stretching experiments.

Expressions for forces

Below, we calculate each of the terms in equation 7. The force on a vertex at x due to a connected vertex at r is

$${\mathbf{f}}_{\mathbf{xr}}={\sigma }_{\mathbf{xr}}\left(-\frac{\partial \mid \mathbf{r}-\mathbf{x}\mid }{\partial \mathbf{x}}\right)={\sigma }_{\mathbf{xr}}{\widehat{\mathbf{u}}}_{\mathbf{rx}}.$$ (8)

where σ_xr denotes the line tension between vertices at x and r and û_rx = (r − x)/|r − x| is the unit vector from x to r.

The perimeter of an n-sided cell α is evaluated as:

$$L_{\alpha }=\sum _{i=0}^{n-1}\mid {\mathbf{x}}_{i+1}-{\mathbf{x}}_i\mid ,$$ (9)

where {x_{0, …, n−1}} denote the vertices numbered in either a clockwise or counter clockwise order, and where x_n is identified to x₀. For notational simplicity, from now on, let x_n be identified to x₀, and let the sum ${\sum }_{i=0}^{n-1}$ be denoted Σ_i. The force from the perimeter term contributed by cell α on a vertex at x_i belonging to α is then:

$$f_{{\mathbf{x}}_i\alpha }^p=2b_{\alpha }{L}_{\alpha }\left(-\frac{\partial L_{\alpha }}{\partial {\mathbf{x}}_i}\right)=2b_{\alpha }{L}_{\alpha }\left({\widehat{\mathbf{u}}}_{{\mathbf{x}}_{i+1}{\mathbf{x}}_i}+{\widehat{\mathbf{u}}}_{{\mathbf{x}}_{i-1}{\mathbf{x}}_i}\right).$$ (10)

The above expressions are defined the same way for vertex models in either two or three dimensions. However, the area of a cell in three dimensions is not obviously-defined given only the positions of the vertices, since vertices in 3d are not in general coplanar. Although the minimum surface area bounded by a polygon can be determined with high precision [61–63], the minimal area in the nearly flat hexagons of this model can be closely approximated by simple triangulation. In this case, a choice for triangulation for the vertices of a cell should be made in order to unambiguously define the area. As a choice, we may compute the average position (or centroid) of the vertices belonging to each cell as x_c = Σ_i x_i/n and use this position to define a triangulation among the vertices in order to calculate an effective area. That is, in 3d, we might compute the cell area as the sum of the areas of small triangles emanating from the centroid:

$$A_{\alpha }^{3\text{dapprox}}=\sum _i\frac{1}{2}\mid ({\mathbf{x}}_{i+1}-{\mathbf{x}}_c)\times ({\mathbf{x}}_i-{\mathbf{x}}_c)\mid .$$ (11)

Note that in two dimensions, this expression simplifies to:

$$A_{\alpha }^{2\mathrm{d}}=\left|\sum _i\frac{1}{2}({\mathbf{x}}_{i+1}\times {\mathbf{x}}_i)\right|,$$ (12)

assuming clockwise numbering of {x_i} [64]. We now introduce a simplification. In 3d, assuming that the vertices defining a cell are approximately coplanar, we can approximate the right hand side of Equation 11 as:

$$\sum _i\frac{1}{2}\mid ({\mathbf{x}}_{i+1}-{\mathbf{x}}_c)\times ({\mathbf{x}}_i-{\mathbf{x}}_c)\mid \approx \left|\sum _i\frac{1}{2}({\mathbf{x}}_{i+1}-{\mathbf{x}}_c)\times ({\mathbf{x}}_i-{\mathbf{x}}_c)\right|.$$ (13)

This approximation is useful because now, the right hand side of Equation 13 does not depend on x_c; that is, it does not depend on triangulation, so x_c can be replaced with the origin of the coordinate system. The independence of the RHS of Equation 13 from triangulation is based on Stokes Theorem and is shown in the Supplementary Materials. The vectorial area expression with which we will proceed in our model is now modified to the vectorial expression within the RHS of Equation 13, with x_c set to 0:

$${\mathbf{A}}_{\alpha }=\sum _i\frac{1}{2}({\mathbf{x}}_{i+1}\times {\mathbf{x}}_i).$$ (14)

The scalar area will be notated A_α ≡ |A_α|. Note that we have dropped the label “3d” because the 2d and 3d area expressions are now the same. This approximation makes analytical expressions for force more tractable.

The force due to the area term in the energy expression, contributed by cell α on a vertex belonging to it with position x_i is:

$$f_{{\mathbf{x}}_i\alpha }^a=2a_{\alpha }(A_{\alpha }-A_{\alpha }^0)\left(-\frac{\partial A_{\alpha }}{\partial {\mathbf{x}}_i}\right).$$ (15)

Explicitly,

$$\frac{\partial A_{\alpha }}{\partial {\mathbf{x}}_i}=\frac{1}{A_{\alpha }}\sum _{k=1}^3{A}_{\alpha }^k\frac{\partial A_{\alpha }^k}{\partial {\mathbf{x}}_i},$$ (16)

where $A_{\alpha }^k$ is the kth component of A_α. It can be shown that

$$\frac{\partial A_{\alpha }^k}{\partial {\mathbf{x}}_i}=\frac{1}{2}({\mathbf{x}}_{i-1}-{\mathbf{x}}_{i+1})\times {\mathbf{e}}^k,$$ (17)

where e^k is a unit vector in the kth direction.

For the force due to bending, assume that the vertex at x participates in adjacent cells α and β. For the force, we have:

$${\mathbf{f}}_{\mathbf{x}\langle \alpha \beta \rangle }^c=-\frac{\partial }{\partial \mathbf{x}}\left(-{\widehat{\mathbf{A}}}_{\alpha }·{\widehat{\mathbf{A}}}_{\beta }\right)=\frac{\partial }{\partial \mathbf{x}}\left(\frac{1}{A_{\alpha }{A}_{\beta }}\sum _{k=1}^3{A}_{\alpha }^k{A}_{\beta }^k\right).$$ (18)

This derivative is easily evaluated using the usual product rule and the identities in Equations 16 and 17.

Equations 8, 10, 15, and 18 are substituted into Equation 7, with the specification of ${\mathbf{f}}_{\mathbf{x}}^{\text{ext}}$, and multiplied by the mobility constant η give the full expression on the right hand side of Equation 5. These forces completely determine the trajectories of all vertices given a particular connectivity. If an edge shrinks to length zero, then the equations become ill-defined, the connectivity must be modified through a discrete transformation as described earlier, and the equations of motion effectively rewritten before equilibrium positions of the vertices can be found. We stress that the above presentation of the energy and force expressions apply for vertices existing in either two or three dimensions, while the object defined by the model is essentially 2d. That is, our vertex model represents an epithelium as a 2d sheet-like object that moves in a 3d world.

Providing for patterning in the model

A central aspect to the formulation of the mathematical model is the choice of parameters a_α, b_α, $A_{\alpha }^0$, σ_ij, and c_αβ for each cell and bond in Equation 2. The authors in [23] determined realistic values for the parameters a_α, b_α, $A_{\alpha }^0$, and σ_ij for the Drosophila wing disc in 2d through comparison of numerical experiments with real experiments. Their method can be generalized and applied to a variety of biological systems.

To usefully employ the generic vertex model for specific biological systems, we need to distinguish cells of different types according to their properties. Applying patterning to the model, cells of different types are assigned parameter values that represent hypothesized differences in mechanical properties. This approach is taken in [65], where a pattern of high line tension is prescribed along edges of particular cells, representing a compartment boundary in the wing disc. We take a similar approach to describe a way for the the 2d patterning of epithelia to give rise to three-dimensional deformations.

Applying boundary conditions

Boundary conditions can be set at the edge of the simulation domain to suit the biological system under investigation. In some cases, an entire tissue may be simulated [37]; however, if only some part of the physical system is considered in a numerical simulation, boundary conditions need to be applied to vertices at the boundary of the simulation in order to approximate reality. In many applications, we would like to simulate a local tissue inhomogeneity within a large or effectively infinite system of many cells. It is useful, in this case, to calculate the equilibrium size of cells within an infinite uniform system if we wish to used fixed boundary conditions on a smaller simulation domain. Here, we will assume that the fixed boundary will be in 2d, so that the equilibrium configuration is known to be flat with c_αβ = 0. To do this, consider the following.

In an infinite system of identical hexagonal cells with given parameter values a, b, and A₀ for each cell, and σ for each of a cell’s six edges, the effective energy per cell as a function of ℓ, the length of a single cell edge, is:

$$E_c(\ell )=a{\left(\frac{3\sqrt{3}}{2}{\ell }^2-A_0\right)}^2+b{(6\ell )}^2+\frac{1}{2}6\sigma \ell ,$$ (19)

where the factor of 1/2 in front of the last term comes from the fact that each edge is shared between two cells. The equilibrium side ℓ₀ of a cell is computed by minimizing this per-cell energy expression. Computing a derivative of E_c with respect to ℓ, we get that the force on a cell of side ℓ₀ vanishes if and only if:

$$0={\frac{d{E}_c}{d\ell }|}_{{\ell }_0}=3\left(9a{\ell }_0^3+(24b-2\sqrt{3}a{A}_0){\ell }_0+\sigma \right)$$ (20)

Solving this cubic equation for ℓ₀ and choosing a real and positive solution that gives a stable equilibrium for E_c, we can find the equilibrium side length ℓ₀ for a hexagonal cell in an infinite system as a function of the parameters a, b, σ, and A₀. As an example, using dimensionless values $A_0=3\sqrt{3}/2$ and σ = 1 and scaled values a = 1 and b = 0.1 from [23], we have ℓ₀ ≈ 0.77; note that here and throughout the remainder of this paper all parameter values are dimensionless, with scaling determined in the Supplementary Materials. Note that a stable minimum of the right hand side of Equation 19 at a positive value of ℓ does not exist for all values of a, b, A₀, and σ. For example, it is intuitively clear that if the cells had no spring force associated with either area or perimeter, that is a = b = 0, and cell adhesion was sufficient for surface tension to be negative with σ < 0, the cells would spread to infinite size; mathematically, this can be seen from the fact that there are no real, positive, and stable solutions to equation 20 for this set of parameters. Similarly, if contracting forces on the cell outweigh the restoring force, for example if σ and b were large enough compared to a, then the cell will collapse to size zero.

Fixing the size of the simulation domain to its equilibrium size simulates embedding the system into an infinite system that has free boundary conditions. Extending this idea, fixing the size of the simulation domain to a size larger or smaller than its equilibrium size simulates embedding the system into an infinite system that is under tension or compression, respectively; see Results section and Figure 2 for an example of stretched systems. Other physical constrains and phenomena can also find rough representation in the setup of boundary conditions. For example, vertices at the boundary of a simulation can be restricted to move in only one or two dimensions to simulate constraints imposed by a neighboring tissue, or an external force can be imposed on the vertices on one side of the simulation domain while the other side is held fixed to simulate stretching.

Supplementary Material

PB066007_figureS1.pdf. Figure S1. Example of our implementation of noise to efficiently integrate the equations of motion through the repeated formations of T1 junctions.

Simulation of a uniform array of hexagonal cells, fixed at the boundaries to their equilibrium sizes where all bonds have edge tension σ_ij = 1 with the exception of the intercalating bond, for which σ_ij = 3 if the bond is formed horizontally, and σ_ij = 1.5 if the bond is formed vertically. The final stable configuration has a very short vertical bond. A. The energy E (with the energy of uniformly patterned domain subtracted out) and magnitude of concatenated force |F| are plotted as functions of time t when the simulation is done without implementation of noise for repeated T1 junctions (Movie S7). The T1 junction repeatedly forms 15 times, indicated by the black arrow and the discontinuities in |F|, and it takes 26000 simulation steps to go from t = 0.78 (the time of the first T1 junction formation) to t = 4. The light blue line indicates the energy E₀ of the final stable configuration. B. The quantities E and |F| are plotted as functions of time t when the simulation is done with implementation of noise for repeated T1 junctions (Movie S8). Black arrows indicate the formation of repeated 4-vertices; green arrows indicate times when bond tensions are restored after t_relax = 1 had passed since the last T1 junction formation; the quantity |F| is discontinuous at these points. Note that it is possible to have E < E₀ since the tension of the bond may be temporarily artificially lowered. The T1 junction repeatedly forms 9 times in the simulation, and it takes 11000 simulation steps to of from t = 0.78 to t = 4.

PB066007_movie1.avi. Movie S1.

Related to Figure 2A–C

PB066007_movie10.avi. Movie S10.

Related to Figure 5D

PB066007_movie11.avi. Movie S11.

Related to Figure 5D

PB066007_movie12.avi. Movie S12.

Related to Figure 5D

PB066007_movie13.avi. Movie S13.

Related to Figure 6

PB066007_movie2.avi. Movie S2.

Related to Figure 2D–F

PB066007_movie3.avi. Movie S3.

Related to Figure 4A

PB066007_movie4.avi. Movie S4.

Related to Figure 4B

PB066007_movie5.avi. Movie S5.

Related to Figure 4C

PB066007_movie6.avi. Movie S6.

Related to Figure 4D

PB066007_movie7.avi. Movie S7.

Related to Figure S1A

PB066007_movie8.avi. Movie S8.

Related to Figure S1B

PB066007_movie9.avi. Movie S9.

Related to Figure 5D

PB066007_suppdata.pdf. Supporting Document S1.

Details of methods and implementation.