The Role of an Active Site Mg²⁺ in HDV Ribozyme Self-Cleavage: Insights from QM/MM Calculations

Abstract

The hepatitis delta virus (HDV) ribozyme is a catalytic RNA motif embedded in the human pathogenic HDV RNA. It catalyzes self-cleavage of its sugar-phosphate backbone with direct participation of the active site cytosine C75. Biochemical and structural data support a general acid role of C75. Here, we used hybrid quantum mechanical/molecular mechanical (QM/MM) calculations to probe the reaction mechanism and changes in Gibbs energy along the ribozyme's reaction pathway with an N3-protonated C75H⁺ in the active site, which acts as the general acid, and a partially hydrated Mg²⁺ ion with one deprotonated, inner-shell coordinated water molecule that acts as the general base. We followed eight reaction paths with distinct position and coordination of the catalytically important active site Mg²⁺ ion. For six of them, we observed feasible activation barriers ranging from 14.2 to 21.9 kcal/mol, indicating that the specific position of the Mg²⁺ ion in the active site is predicted to strongly affect the kinetics of self-cleavage. The deprotonation of the U-1(2′-OH) nucleophile and the nucleophilic attack of the resulting U-1(2′-O⁻) on the scissile phosphodiester are found to be separate steps, as deprotonation precedes the nucleophilic attack. This sequential mechanism of the HDV ribozyme differs from the concerted nucleophilic activation and attack suggested for the hairpin ribozyme. We estimated the pK_a of the U-1(2′-OH) group to range from 8.8 to 11.2, suggesting that the pK_a is lowered by several units from that of a free ribose, comparable to and most likely smaller than the pK_a of the solvated active site Mg²⁺ ion. Our results thus support the notion that the structure of the HDV ribozyme, and particularly the positioning of the active site Mg²⁺ ion, facilitates deprotonation and activation of the 2′-OH nucleophile.

Introduction

The hepatitis delta virus (HDV) ribozyme is a unique member of the class of small self-cleaving (nucleolytic) ribozymes as it is the only known ribozyme embedded in the genomic and antigenomic RNAs of a human pathogen.¹ The HDV ribozyme was proposed to use both metal ion and nucleobase catalysis in its reaction mechanism² and was the first ribozyme for which structural and biochemical data suggested direct participation of a specific side-chain nucleobase, cytosine 75 (C75) in the cleavage reaction.^1,3,4 The active site of the HDV ribozyme shifts the pK_a of C75 from 4.2 of the free cytosine⁵ towards neutrality, as Raman measurements estimated a pK_a of C75 equal to ∼6.⁶ As for the other members of the small ribozyme class, the catalytic reaction of the HDV ribozyme (classified as an internal or cis-transesterification) is initiated by the attack of the 2′-hydroxyl group of the uracil immediately upstream of the cleavage site (U-1) on the adjacent scissile phosphate, proceeds through a pentacoordinated phosphorane transition state (TS), and generates products (P) with 2′,3′-cyclic phosphate and 5′-hydroxyl termini.⁷

Two kinetically equivalent reaction mechanisms differing in the role played by C75 during self-cleavage have been proposed. On the basis of crystal structures of the pre-cleavage state inhibited by a C75U mutation or chelation of Mg²⁺, as well as of subsequent molecular dynamics (MD) simulations starting from these structures, the active site C75 was proposed to act as the general base, using its N3 nitrogen to activate (deprotonate) the nucleophilic U-1(2′-OH) group. Complementarily, the hydrated Mg²⁺ ion was contended to act as the general acid to protonate the G1(O5′) leaving group.^8,9 MD simulations together with combined quantum mechanical/molecular mechanical (QM/MM) calculations suggested that this mechanism is both chemically and structurally feasible.^10-12 However, the C75 base mechanism does not explain more recent biochemical¹³ and crystal structure data¹⁴ based on multi-stranded ribozyme constructs incorporating external (trans) substrate analog inhibitor strands. A second reaction mechanism, which was proposed based on the structure of the post-cleavage state¹⁵ and posits that the roles of C75 and the hydrated Mg²⁺-ion are switched (i.e., the protonated N3 nitrogen of C75H⁺ instead acts as the general acid to protonate the leaving group),¹⁶ agrees better with these data.^13,14

The recent high-resolution (1.9 Å) crystal structure of the trans-acting HDV ribozyme in the pre-cleavage state, with a series of three 2′-deoxy modifications in place at the active site U-1 and neighboring nucleotides to inhibit cleavage, was solved by molecular replacement from the previous post-cleavage structure while modeling the crystallographically disordered active site.¹⁴ The resulting structural model resembles the post-cleavage structure and differs significantly in important aspects from the prior pre-cleavage structure.⁸ In particular, C75 is bound more tightly to the G1 scissile phosphate, suggesting that it may be protonated prior to cleavage and thus can act as the general acid.^14,17 Taking together all the available biochemical and structural data, the Mg²⁺ ion may be able to activate the U-1(2′-OH) group through one of its coordinated water molecules (which has to be previously deprotonated) and thus serve as the general base in the reaction.¹⁷ Subsequent MD simulations supported the role of C75 as general acid since the protonated C75H⁺ seemed to assist in the local organization of the active site.¹⁸ Successive QM/MM calculations starting from the state with already activated U-1(O2′) nucleophile predicted a concerted reaction mechanism of nucleophilic attack and proton transfer from C75H⁺ to the G1(O5′) leaving group with a phosphorane-like TS in the presence of an active site Mg²⁺ ion. An altered, sequential mechanism was suggested to occur in the absence of divalents, when the catalytic Mg²⁺ was replaced by a monovalent metal ion. However, the observed reaction barriers in both suggested mechanisms are significantly above the experimentally observed value.¹⁹ Both mechanisms were further supported by very recent QM/MM free energy calculations that also started from the activated precursor with the U-1(2′-O⁻) group already deprotonated.²⁰ The latter QM/MM free energy calculations reported a significantly smaller activation barrier than the original estimate, which, after adding the correction corresponding to the thermodynamic penalty for the rare ionization states of the catalytic species, was in excellent agreement with experiment. The supported mechanism assumed a triple-inner-shell coordination of the Mg²⁺ to U-1(O2′) and the nonbridging oxygens of the G1 and U23 phosphates. The direct inner-shell coordination of the Mg²⁺ to the U-1(O2′) was proposed to serve to activate this functional group as a nucleophile by increasing its acidity, leading to an estimated pK_a shift by ∼1.3-2.7 units.²⁰ In addition, the inner-shell coordination to the nonbridging oxygen of G1 phosphate (the scissile phosphate) may stabilize the developing negative charge in the TS. However, the position of the Mg²⁺ ion and its coordination within the active site were deduced from a disordered part of the crystal structure, with a modeled U-1, which may significantly compromise the structure. Moreover, the Mg²⁺ was suggested to be coordinated to the U-1(O2′), which is missing in the crystal structure due to 2′-deoxy modification (a water molecule was resolved in that position instead). This uncertainty regarding both the position and ligand coordination of the active site Mg²⁺ ion warrant further evaluation.

In the current study, we present results from extensive hybrid QM/MM calculations of the self-cleavage reaction of the HDV ribozyme with the protonated C75H⁺ acting as the general acid in conjunction with a hydroxide ion coordinated to the active site Mg²⁺ acting as a general base. We focused on an energetic description of this mechanism and particularly of the initial step of the reaction, i.e., the so far unexplored deprotonation and activation of the U-1(2′-OH) nucleophile by the hydroxide ion. We explicitly compared multiple plausible positions of the Mg²⁺ ion and analyzed the impact of Mg²⁺-ligand coordination on the reaction mechanism. Our results strongly support a sequential activation and attack of the U-1(2′-OH) nucleophile for the HDV ribozyme, distinct from the concerted mechanism suggested for other ribozymes.^21,22

Methods

Molecular dynamics simulations

We used explicit solvent MD simulations of the HDV ribozyme to prepare starting structures for subsequent QM/MM calculations. These simulations were carried out using the AMBER package²³ with the all-atom ff99bsc0χ_OL3 force field The ff99bsc0χ_OL3 force field is derived from the AMBER ff99 force field^24,25 by adding the Barcelona α/γ²⁶ and Olomouc χ_OL3^27,28 torsional potential reparameterizations. The ff99bsc0χ_OL3 variant is the standard AMBER RNA force field since 2011 and has been tested extensively.^27,29-33 To avoid confusion we note that the ff99bsc0χ_OL3 version is internally marked as ff10, ff12 or ff14 RNA force field in the recent AMBER code versions.

The starting structure for our MD simulations was based on the most recent crystal structure of the trans-acting genomic HDV ribozyme (PDB ID 3NKB; resolution 1.9 Å).¹⁴ All 2′-deoxy modifications were replaced with 2′-OH and the missing U-1 nucleotide was modeled in using the hammerhead ribozyme structure (PDB ID 2OEU) as suggested by Golden and coworkers.¹⁴

The MD simulations were carried out with the TIP3P explicit solvent model under net-neutral conditions. We performed three 80 ns long simulations, one with monovalent counter ions only, one with the catalytic Mg²⁺ ion and monovalent ions, and the last one with the catalytic Mg²⁺, several structural Mg²⁺ ions, and monovalent ions. The catalytic Mg²⁺ ion was placed based on the crystal structure;¹⁴ see ESI^† for details. Note that in the case of simulations with monovalent ions only, the active site was also occupied by ions as the monovalent ions readily entered the active site in absence of the divalents.¹¹ The monovalent ions efficiently sampled different positions within the active site and allowed us to identify a diverse set of ion-binding patterns. In contrast, the Mg²⁺ ions were, due to the limited timescale, typically kinetically trapped in their selected starting positions. In total, we evaluated 22 different coordination arrangements for the active site monovalent and divalent ions over all our MD simulations. We then considered a total of 16 snapshots from these simulations as starting geometries for our QM/MM calculations (if necessary with the Na⁺ ion at the catalytic center replaced by Mg²⁺, for details see Table S1 in ESI^†).

QM/MM calculation setup

A two-layer ONIOM method³⁴ with the electronic embedding implemented in Gaussian09³⁵ was used for the QM/MM calculations. The MM region was treated by the ff99bsc0χ_OL3 force field. The QM region was described by density functional theory (DFT) methods. The faster BLYP/6-31+G(d,p) method was used for the initial geometry optimizations and preliminary localizations of the reaction coordinate in one particular active site arrangement, for which the potential energy surface of the reaction was explored in details (see below). The more accurate hybrid MPW1K functional (optimized for kinetics^36,37) with the 6-31+G(d,p) basis set was used for subsequent reoptimizations of all the reaction paths and for calculating the final energy profiles. Detailed information on the performance of these methods can be found in our recent review.³⁸ As noted above, we followed the self-cleavage reaction based on 16 distinct active site arrangements, differing mostly in the position and coordination of the active site Mg²⁺ ion. We first explored the potential energy landscape in details and localized the reaction path based on one particular active site arrangement. We then used the active site conformations obtained along this particular reaction path as initial guesses for subsequent reoptimization of the reaction paths for the remaining active site arrangements. Based on these calculations, we finally found 8 different reaction paths that differed in the position and coordination of the active site Mg²⁺ ion (see ESI^† for more details).

We used three different QM regions (Fig. 1) depending on the specific coordination of the active site Mg²⁺ ion. The first QM region was abbreviated as QM_AS (84 atoms in total, including hydrogen link atoms) and comprised nucleobases G25 and C75H⁺ with hydrogen-capped C1′ methyl groups (see below for details regarding the capping of dangling bonds at the QM-MM interface), the U-1 nucleotide, the G1 phosphate (i.e., the scissile phosphate), and the active site Mg²⁺ ion with its four inner-shell coordinated water molecules (three water molecules and a hydroxide ion in case of the pre-cleavage state). The second QM_PHOS model (94 or 97 atoms in total) comprised, in addition to the QM_AS region, the U23 phosphate with hydrogen-capped methyl groups at the C3′ and C5′ ends. In contrast to QM_AS model, the Mg²⁺ ion was coordinated by a hydroxide ion and two or three inner-shell water ligands (two in the case of triple-inner-shell and three in the case of double-inner-shell coordination). Finally, the QM_U20 model (96 atoms in total) comprised, in addition to the QM_AS region, the U20 nucleobase with a hydrogen-capped C1′ methyl group (see ESI^† for more details).

Fig. 1.

(A) Scheme of the three QM regions: (i) the QM_AS region containing part of the sugar-phosphate backbone around the scissile phosphate, a deprotonated hydroxide anion coordinated to a partially hydrated [Mg(H₂O)₃.OH]⁺ ion, and a protonated C75H⁺ species (black), (ii) QM_PHOS with additional U23 phosphate (black and blue), and (iii) QM_U20 with additional U20 nucleobase (black and green). The coordination of Mg²⁺ is not shown as it varies in the staring structures, see Methods and ESI^†. (B) An initial snapshot (taken from MD simulations) of one particular QM/MM reaction pathway with double-inner-shell coordination of Mg²⁺ to [U-1(O2), U-1(O2′)]. The MM region and the QM core (corresponding to the QM_AS model from panel A) are rendered as wires and thicker sticks, respectively. Water molecules and sodium counter ions of the MM part are not shown for simplicity.

Hydrogen atoms were added to saturate the dangling bonds at the interface between the QM and MM regions. We adopted the same QM/MM scheme that was successfully applied in our recent studies on halogenalkane dehalogenase, as well as the HDV and hairpin ribozymes.^12,21,22,39 The Mg²⁺ positions were derived using the Mg²⁺ and Na⁺ ion positions sampled in the simulations (see above) that provided broad sampling of plausible positions and coordinations of the active site ion. In all QM/MM calculations, the ribozyme was immersed in a water droplet with an ∼10 Å thick layer of water molecules surrounding the entire RNA molecule. A ∼5 Å thick layer of waters on the surface of the droplet and counter ions outside the droplet were fixed in space during all QM/MM calculations to prevent any changes in energy caused by hydrogen bond network reorganization at the water-vacuum interface.

The reaction profile was first explored in detail for one particular active site arrangement (specifically for the structure featuring a double-inner-shell coordination to [U-1(O2), U-1(O2′)]) by a set of flexible forward and reverse scans (lengthening and shortening of the U-1(O2′)…G1(P) and G1(P)…G1(O5′) distances, respectively). The scans were performed in 0.1 Å steps and all remaining degrees of freedom were fully relaxed at each point (except for the fixed water molecules at the surface of the water droplet). In addition, two-dimensional scans on the potential energy surface were performed for accurate localization of the TS: i) a scan in the direction of the nucleophilic attack of U-1(O2′) on the scissile phosphate and the proton transfer from the U-1(2′-OH) hydroxyl to the hydroxide anion coordinated to the active site Mg²⁺ ion, and ii) a scan in the direction of the nucleophilic attack and the proton transfer from C75H⁺ to the G1(O5′) leaving group. Subsequently, we utilized this reaction path to model the initial guess paths in the remaining active site arrangements (with distinct coordinations of Mg²⁺ ion) and explore their reaction profiles by reoptimization of the geometries along these reaction paths with constrained distances equivalent to those in the initial scans. The R, R′ precursors and P states were fully minimized as well. As the TS state was originally explored by a 2D scan, that is, by scanning the G1(P)…G1(O5′) and G1(O5′)…H distances (see Fig. 3A), the TS states of the remaining paths were reoptimized using constrains of these two distances at values corresponding to the minimum energy path (MEP) in structure with double-inner-shell coordination to [U-1(O2), U-1(O2′)]. We note that, although the MEPs in the G1(P)…G1(O5′) and G1(O5′)…H directions of the entire system are likely similar to the MEP of the structure used for an initial guess, their TS states may be slightly shifted within this 2D space. The usage of the MEP derived for one particular structure as an initial guess for the others therefore may slightly overestimate the energies of the TS, yet most likely by less than 1 kcal/mol (see Fig. 3A).

Fig. 3.

The reaction pathways describing the sequential mechanism, where the first proton transfer step is separated from the subsequent nucleophilic attack. (A) Scatter chart showing optimized points along the initial reaction coordinate with double-inner-shell coordination to [U-1(O2), U-1(O2′)] as a function of the U-1(O2′)…G1(P) and G1(P)…G1(O5′) distances. Both proton transfers (black insets) were investigated further by 2D scans. The diagram on the left displays the initial proton transfer from the U-1(2′-OH) group to the deprotonated water molecule of the partially hydrated [Mg(H₂O)_3·OH]⁺ ion, where a pre-cleavage state R and an intermediate R′ were found. The second 2D diagram on the right represents the subsequent proton transfer from the protonated C75H⁺ to G1(O5′), where the TS state was localized. QM/MM Gibbs energies (in kcal/mol, shown as contours and colors) were calculated at the MPW1K/6-31+G(d,p):AMBER(ff99bsc0χ_OL3) level and are depicted without any additional correction (see the Methods and the Table 1). (B) The active site of the R state with double-inner-shell coordination to [U-1(O2), U-1(O2′)] highlights the key atoms and bonds involved in the cleavage reaction. (C) Calculated QM/MM (MPW1K/6-31+G(d,p):AMBER(ff99bsc0χ_OL3)) energies for the eight complete reaction pathways with different coordination of the Mg²⁺ ion plotted against the reaction coordinate, i.e. the sum of coordinates corresponding to nucleophilic attack, first and second proton transfer defined as differences (U-1(O2′)…G1(P))-(G1(P)…G1(O5′)), (OH⁻(O)…H)-(U-1(O2′)…H), and (C75H⁺(N3)…H)-(G1(O5′)…H), respectively.

To estimate the necessary Gibbs energy corrections, we used a model of the uncatalyzed reaction (see ESI^† for details) for which the Gibbs energy corrections (involving zero-point vibration energy, enthalpy correction to finite temperature, and entropy contribution derived by the standard harmonic oscillator approximation in the canonical ensemble) corresponding to the R, TS and P states were calculated and extrapolated to the ribozyme-catalyzed reaction. Note that only the entropic contribution of the solute was taken into account, whereas the solvent entropic changes typically involved in cavitation energy (the least accurate term in implicit solvent calculations) were omitted. However, the cavitation energy does not significantly contribute to the Gibbs energy differences between R, TS, and P of this particular reaction, as their cavities are rather similar (data not shown). A similar extrapolation of the Gibbs energy corrections from the uncatalyzed to the catalyzed reaction was used in our previous QM/MM studies of the HDV and hairpin ribozymes.^12,21,22 Similarly to our recent studies, we used a model of the uncatalyzed reaction that shares the mechanism with the ribozyme reaction, i.e., a model involving a hydroxide ion coordinated to Mg²⁺ acting as the general base and a protonated C75H⁺ acting as the general acid. Note that the Gibbs energy corrections calculated in the current study are similar to those obtained in our recent studies, calculated for a mechanism of self-cleavage with swapped general acid/base.^12,21

The active site contains two titratable residues, C75 and a specific water molecule coordinating the Mg²⁺ ion, with estimated pK_as of 6.15⁶ and 11.4⁴⁰, respectively. The major ionization forms under physiological conditions (pH ∼7) are expected to be the canonical (neutral) form of C75 and the doubly positively charged, partially water-coordinated Mg²⁺ ion ([Mg(H₂O)₃]²⁺ or [Mg(H₂O)₄]²⁺. Note that alongside the three or four water molecules, the Mg²⁺ ion is coordinated to one [single-inner-shell], two [double-inner-shell] or three [triple-inner-shell] groups in the active site, yielding a canonical hexa-coordination of this Mg²⁺ ion in six paths and penta-coordination in the other two paths (single-inner-shell coordination to [U-1(O2)] and double-inner-shell coordination to [G1(pro-R_P), U20(O2)]). While QM/MM calculations reveal the Gibbs energy barrier between the rare ionization form of the pre-cleavage state and the TS, the overall kinetic barrier also has to include the Gibbs energy difference between the dominant and minor ionization forms of the pre-cleavage state. Consequently, the calculated Gibbs energy of the pre-cleavage ribozyme (and of all intermediates and TS states along the QM/MM pathway) with non-canonical but catalytically competent ionization forms of these residues (i.e., the protonated C75H⁺ and the deprotonated water molecule in the inner shell of the Mg²⁺ ion) must be corrected for the thermodynamic penalty to adopt a minor equilibrium population. The corrections for the protonated C75H⁺ and hydrated [Mg(H₂O)₃.OH]⁺ (or [Mg(H₂O)₂.OH]⁺) ions are:

$$\begin{array}{l}\mathrm{\Delta }{G}_{C75H^{+}}^{\mathit{\text{corr}}}=RTln10(\mathrm{p}\mathrm{H}-\mathrm{p}{K}_a^{C75})\\ \mathrm{\Delta }{G}_{{\left[Mg{(H_{2}O)}_5\cdot OH\right]}^{+}}^{\mathit{\text{corr}}}=RTln10\left(\mathrm{p}{K}_a^{{\left[Mg{(H_{2}O)}_6\right]}^{2+}}-\mathrm{p}\mathrm{H}\right)+RTln(6)\end{array}$$

yielding 1.2 and 7.1 kcal/mol (at 298 K and pH 7), respectively, and thus a total energetic penalty of 8.3 kcal/mol. Note that the total correction is independent of pH as the terms involving pH cancel each other. The second term of the correction for deprotonation of the hydrated Mg²⁺ ion, i.e., RTln(6), reflects the fact that only the deprotonation of a specific of the six inner-shell water molecules results in the proper reactive state.

Results and Discussion

Generating a broad set of starting structures

Results of QM/MM computations are very sensitive to the selected starting conformation(s). In general, QM/MM schemes are limited by conformational sampling, which is efficiently accomplished by, for example, selection of specific snapshots from classical MD simulations (as QM or QM/MM MD simulations are restricted to only a few picoseconds of sampling). Accordingly, we here used classical MD simulations to obtain a diverse set of starting structures for our QM/MM calculations. However, even MD simulations are (to a lesser extent) dependent on the accuracy of the starting crystal structures as they typically cannot overcome, on a reasonably accessible timescale, possible bias in the structures caused by, for example, inactivating chemical modifications.⁴¹ For example, in our previous QM/MM study¹² we used snapshots from MD simulations based on the cis-acting, C75U mutant crystal structure.⁸ The architecture of its pre-cleavage active site significantly differed from that observed in the most recent, more product-like trans-acting ribozyme crystal structure trapped at low pH by a 2′-deoxy U-1 modification.¹⁴ Even extensive MD simulations based on the C75U mutant structure did not detectably sample the product-like architecture.^10-12

Here, we investigated multiple reaction pathways of the HDV ribozyme for C75H⁺ and a Mg²⁺ coordinated hydroxide ion as the general acid and base, respectively. In particular, we explored the reaction for a diverse set of Mg²⁺ ion positions and ligand coordinations. To obtain suitable starting structures for our QM/MM calculations, we carried out three 80-ns explicit-solvent MD simulations based on the recent trans-acting ribozyme structure.¹⁴ The simulations with Mg²⁺ in the active site revealed a high tendency for the ion to be trapped in its starting position, as it developed a triple-inner-shell coordination to [U-1(O2′), G1(pro-R_P), U23(pro-S_P)], representing 99.3% and 30.1% of the simulated trajectory time in our two Mg²⁺-containing simulations (see Table S1 in ESI^†). This Mg²⁺ coordination agrees with that proposed based on the starting crystal structure of the deoxy U-1 modified ribozyme with the disordered U-1 modeled in.¹⁴ We used this coordination as a starting conformation in our work, as was also done in other recent QM/MM free-energy calculations.^19,20 In the second of our two Mg²⁺ simulation (the one with additional Mg²⁺ ions, see Methods), we also observed a shift to a double-inner-shell coordination of the active site Mg²⁺ to the G1(pro-R_P) and U23(pro-S_P) nonbridging oxygens, representing the remaining 69.9% of the simulation. Thus, simulations directly using Mg²⁺ revealed only two Mg²⁺ binding geometries. However, it is well known that divalent ions have very limited sampling in MD simulations and are poorly described by the approximate non-polarizable force field. The inner-shell ligands of a Mg²⁺ ion have residence lifetimes on the order of microseconds so that a spontaneous reorganization of the Mg²⁺ inner coordination shell is unlikely to be observed on the accessible simulation timescale. Thus, simulations with divalent ions can be susceptible to an accumulation of simulation artifacts,⁴² and generally are not able to sample the Mg²⁺ position within the active site sufficiently, in contrast to simulations with monovalent ions.^38,43 We therefore cannot exclude the possibility that the behavior of the active-site Mg²⁺ ion in our corresponding simulations may be dominantly determined by the starting structure, which in turn resulted from a modeling of the crystallographically disordered U-1 into the active site. To enhance our sampling we therefore carried out a third simulation lacking Mg²⁺, where the active site was sampled instead by Na⁺ ions, which revealed a significantly different and more dynamic behavior of the active site ion. The most populated configuration (36.4%) was the Na⁺ inner-shell coordination with six water molecules (i.e., canonical hexa-coordination), relegating the RNA to the outer coordination shell. However, we observed also four different triple-inner-shell coordinations, ten distinct double-inner-shell coordinations, and six single-inner-shell coordinations representing at least a 0.1% population over the entire MD trajectory (Table S1 in ESI^†). To prepare more structures for the QM/MM computations, we selected many snapshots from this simulation and replaced the active site Na⁺ ion with a Mg²⁺ ion. Note that Na⁺ and Mg²⁺ ions share a sufficiently similar structure of their first, hexa-coordinated ligand shells to support such a replacement.

In total, sixteen snapshots were selected as representative starting structures on the basis of our population analysis and the following structural criteria for a reactive conformation: a high value for the in-line attack angle of U-1(O2′)…G1(P)-G1(O5′), typically above 160°; and the presence of two strong (< 2.8 Å) hydrogen bonds, C75H⁺(N3H)…G1(O5′) and between U-1(O2′) and one of the water molecules from the inner solvation shell of the active site ion (see Methods and ESI^† for details).

Prior to the QM/MM calculations, snapshots with the Na⁺ ion in the active site required its replacement with a partially hydrated Mg²⁺ ion. In addition, the water molecule from the Mg²⁺ ion's first solvation shell that donated the hydrogen bond to U-1(O2′) was deprotonated to form a hydroxide ion. Subsequently, each system was minimized on the MM level, which further reduced the number of suitable starting structures to thirteen (see ESI^† for details) that were then prepared for QM/MM calculations (Methods).

QM/MM calculations predict a sequential reaction mechanism

In our QM/MM calculations, we aimed to localize self-cleavage reaction paths of the HDV ribozyme with C75H⁺ acting as the general acid and a Mg²⁺-coordinated hydroxide ion acting as the base, and to calculate the Gibbs energies along these paths. We investigated thirteen positions of the active site Mg²⁺ ion with different functional groups participating in its coordination (Table S1 in ESI^†). We obtained eight complete reaction paths with distinct coordination of the Mg²⁺ ion (Table 1). In the other five paths, the Mg²⁺ ion changed its coordination so that it resulted in one of the eight already explored paths. In the initial part of the reaction, the pre-cleavage (or reactant) configuration R (Fig. 2), containing a hydroxide ion coordinated to the Mg²⁺ ion, abstracted the proton from the U-1(2′-OH) group. Deprotonation of the U-1(2′-OH) group was achieved at U-1(O2′)…G1(P) distances ranging from 2.8 to 3.5 Å, i.e., prior to the nucleophilic attack, indicating that the activation of the U-1(2′-OH) nucleophile and its nucleophilic attack on the G1(P) are separate and consecutive events. A similar QM/MM study of the mechanism of the hairpin ribozyme suggested that the initial activation of the 2′-OH nucleophile via deprotonation by the general base (in that case a deprotonated active site guanine G8⁻) and the nucleophilic attack are simultaneous events, both occurring in a single rate-limiting TS, representing the highest barrier along the reaction path.²¹ By contrast, in the case of the HDV ribozyme the state with the deprotonated and thus activated 2′-O⁻ nucleophile (before its nucleophilic attack, R′, Fig. 2) almost exclusively corresponds to a meta-stable intermediate state that precedes the rate-determining TS (Fig. 3). This may be a consequence of the higher basicity of a Mg²⁺ coordinated hydroxide ion compared to the deprotonated guanine in the hairpin ribozyme.

Table 1.

Gibbs energy barriers (in kcal/mol) of the reaction pathways with distinct coordination of the Mg²⁺ ion in the HDV ribozyme.^a

Coordination of Mg2+ b	QM region c	R	R′ d	TS	P
[U-1(O2), G25(N7)]	QM_AS	8.3	6.1	28.8	11.1
[G1(pro-RP), U20(O2), G25(O6)]	QM_U20	8.3	11.5	28.0	-1.1
[U-1(O2)]	QM_AS	8.3	8.7	21.9	4.4
[G25(O6), G25N7)]	QM_AS	8.3	4.1	18.2	2.2
[G1(pro-RP), U20(O2)]	QM_U20	8.3	4.4	17.6	-9.4
[U-1(O2′), G1(pro-RP), U23(pro-SP)]	QM_PHOS	8.3	3.7	15.7	-4.8
[G1(pro-RP), U23(pro-SP)]	QM_PHOS	8.3	5.0	15.6	-21.2
[U-1(O2), U-1(O2′)]	QM_AS	8.3	7.0	14.2	1.1

^aThe energies are calculated at the MPW1K/6-31+G(d,p) level and include all necessary corrections, i.e., the pK_a correction for the rare ionization forms of the active site (8.3 kcal/mol, see Methods) with the Gibbs energy estimated using the model reaction (-0.7 and -5.0 kcal/mol for TS and P state, respectively, see ESI^†).

^bThe active site groups participating in the coordination.

^cQM region used in the particular calculation (see Methods, Fig. 1A).

^dThe R′ state contains already deprotonated U-1(2′-O⁻) group.

Fig. 2.

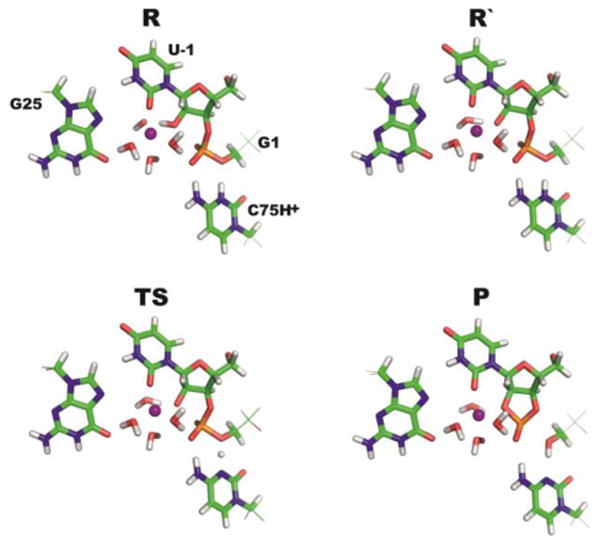
Detailed QM core geometries obtained by calculations of the QM/MM reaction pathway with double-inner-shell coordination to [U-1(O2), U-1(O2′)]: (i) The initial R containing a deprotonated [Mg(H₂O)₃.OH]⁺ ion, (ii) the subsequent state (R′) with the [Mg(H₂O)₄]²⁺ ion and deprotonated/activated U-1(2′-O⁻) group, (iii) TS, and (iv) the cleavage P state. Fig. S2 in ESI^† displays comparable states obtained along the remaining reaction pathways.

The calculations further show that the activated intermediate R′ is 1.3 to 4.6 kcal/mol lower in energy than the initial R state in six paths (Table 1). By contrast, in the remaining two cases, with either a Mg²⁺ triple-inner-shell coordination to [G1(pro-R_P), U20(O2), G25(O6)] or a single-inner-shell coordination to [U-1(O2)], the activated intermediate R′ is higher in energy by 3.2 and 0.4 kcal/mol than the initial R state, respectively. The mechanism of the part of the reaction past the R′ state (i.e., after the activation of the 2′-OH nucleophile) derived from our QM/MM calculations in all eight paths agrees with the mechanism proposed by Hammes-Schiffer and coworkers.^19,20 That is, the cleavage reaction proceeds through a phosphorane TS (Fig. 2) and the nucleophilic attack of U-1(2′-O⁻) on the scissile phosphate is concurrent with the proton transfer from the protonated C75H⁺ cytosine to the G1(O5′) leaving group (Figs. 2 and 3).

Energetics of the self-cleavage reaction

To calculate the overall Gibbs energy barriers, all states along the reaction path were elevated in Gibbs energy by the correction originating from the rare protonated form of the active site at physiological pH (see Methods), so that the reference state with zero Gibbs energy effectively corresponded to the pre-cleavage state with dominant protonated form of the active site. In addition, the raw energy profiles (Fig. 3C) were adjusted with the necessary Gibbs energy corrections (entropic contributions, zero-point vibration energies, and enthalpy contribution for the finite temperature 298 K) estimated within the harmonic approximation for a small model system containing all relevant chemical contributors of the reaction (i.e., the sugar-phosphate backbone segment around the scissile phosphate, the protonated C75H⁺ and the partially hydrated and deprotonated Mg²⁺ ion; see ESI^† for more details) to make the values directly comparable with those experimentally observed.

Finally, we need to make one cautionary comment. As we use several starting structures differing in position and coordination of the active site Mg²⁺ ion, the relative (free) energies of the reactants should in principle be taken into account. The reference state should correspond to the dominantly populated position of the Mg²⁺ ion. However, the theoretical estimation of such relative free energies and/or corresponding populations is inaccessible for theoretical calculations (or at least seriously inaccurate) for a number of reasons, e.g., the QM/MM energies of different starting structures are not directly comparable due to different arrangement of the water molecules and ions in the MM region. We here thus present results from reaction profiles with aligned energies of the reactants, i.e., all R states are supposed to be isoenergetic. We assume that this approximation is plausible, as all the structures were accessible spontaneously in our MD simulations, albeit with a monovalent rather than divalent ion. Note that this issue concerns not only the present paper, but all QM/MM studies on RNA enzymes available in contemporary literature, although it may be at first sight not so explicitly apparent in studies considering only one reactant structure.

The resulting overall Gibbs energy barriers ranged from 14.2 to 28.8 kcal/mol depending on the specific coordination of the active site Mg²⁺ ion during the reaction (Table 1). The path with double-inner-shell coordination to [U-1(O2), U-1(O2′)], used for our first detailed exploration of the potential energy surface by 2D scans (Figs. 3A, 3B), displayed the lowest activation barrier of 14.2 kcal/mol. However, five other coordinations, i.e., the single-inner-shell coordination to [U-1(O2)], the double-inner-shell coordinations to [G1(pro-R_P), U23(pro-S_P)], [G1(pro-R_P), U20(O2)], and [G25(O6), G25N7)], and the triple-inner-shell coordination to [U-1(O2′), G1(pro-R_P), U23(pro-S_P)], revealed comparable or only slightly higher activation barriers of 21.9, 15.6, 17.6, 18.2, and 15.7, kcal/mol, respectively. In these paths, the localization of the TS states was slightly less accurate compared to the path explored by 2D scans, so that the associated barrier heights may be slightly overestimated, by less than 1 kcal/mol (see Methods). Therefore, we suggest that these six pathways, roughly equivalent within the accuracy of QM/MM calculations, are all plausible contributors to the chemical reaction. The remaining two reaction pathways, where the Mg²⁺ ion had a triple-inner-shell coordination to [G1(pro-R_P), U20(O2), G25(O6)] and a double-inner-shell coordination to [U-1(O2), G25(N7)], showed significantly higher Gibbs energy barriers of 28.0 and 28.8 kcal/mol, respectively. It is worth noting that half of all paths indicated endergonic reactions, where the P state is located higher in Gibbs energy than the initial pre-cleavage R state, whereas the others revealed an exergonic profile (Table 1). That is, the estimation of the net reaction Gibbs energy appears to be rather sensitive to the position of the Mg²⁺ ion and/or is less accurate than the estimation of the Gibbs energy barrier presented by the TS.

Although the high-resolution trans-acting ribozyme crystal structure revealed a specific position for the Mg²⁺ ion,¹⁴ the modeled U-1(2′-OH) hydroxyl group overlapped with a resolved water molecule coordinated to the ion. The lack of the 2′-O atom in the crystallized RNA is thus likely affecting the precise position and coordination of the active site Mg²⁺. We note that, while we calculated eight distinct reaction profiles with different Mg²⁺ positions and coordinations, we obtained a relatively narrow range of calculated activation barriers with no clear relation to a specific position and/or coordination environment of the catalytic Mg²⁺.

The experimentally measured rate constants indicate an activation barrier of 19-20 kcal/mol^44,45 for the trans-acting HDV ribozyme under physiological conditions (298 K, pH 7). The Gibbs energy barriers of the paths we identified range from 14 to 29 kcal/mol, i.e., cover the typical range (10-20 kcal/mol) of many enzymatic reactions⁴⁶ and the experimental measurements for several small self-cleaving ribozymes (19-21 kcal/mol).^47-50 Clearly, our results reveal sensitivity of the reaction to the specific arrangement of the active site, particularly the position and the coordination of the active site Mg²⁺ ion. We found at least six different micro-pathways that appear to be plausible for the reaction. We also note that the results to some extent may be affected by: (i) the limited accuracy of the QM/MM approach, (ii) the indirect estimation of the Gibbs energy corrections extrapolated from the uncatalyzed reaction of a small model system, (iii) the finite set of starting structures, (iv) the assumption of isoenergetic pre-cleavage states with different position and coordination of Mg²⁺ ion within the active site, and/or (v) the uncertainty in the additional corrections for the deprotonation of the partially hydrated [Mg(H₂O)₄]²⁺ ion arising from the assumption that its pK_a within the structural context of the HDV ribozyme active site is not significantly shifted from the pK_a of free [Mg(H₂O)₆]²⁺ ion (see more details next section).

pK_a shift of the U-1(2′-OH) nucleophile

Our full reaction path proceeds from the dominant (highly populated) protonated form of the pre-cleavage state through the rare protonated form of the pre-cleavage state to the TS and finally P states. The overall Gibbs energy barrier, which is related directly to the observable kinetic constant, thus corresponds to the difference between the Gibbs energies of the TS and the dominant protonated form of the pre-cleavage state. This first step of the reaction, i.e., the (de)protonation of the pre-cleavage state, cannot easily be included in QM/MM calculations. However, the population of specific ionization forms in the active site at a given pH and the corresponding Gibbs energy corrections are related to the pK_a constants of the titrable groups. Therefore, the overall accuracy of the Gibbs energy barrier estimation depends on the accuracy of the pK_a constant within the environment of the ribozyme active site, in addition to the accuracy of the QM/MM method.

In the reaction mechanism studied here, we assumed two titrable groups to be in rare ionization forms. The first group is the protonated cytosine C75H⁺, for which the pK_a constant (within the environment of the HDV ribozyme active site) was measured by Raman crystallography.⁶ The second group is either a hydroxide anion coordinated to the catalytic Mg²⁺ ion (found in the R state) or the already deprotonated U-1(2′-O⁻) nucleophile (corresponding to the R′ state). The experimental values of the pK_a constant of the ribose 2′-hydroxyl are ambiguous, ranging from 12 up to 15,^51-57 while probably the most relevant value of 12.8 was measured by NMR in a UpG dinucleotide.⁵⁷ The direct, inner-shell coordination of the 2′-OH group to the active site Mg²⁺ ion most likely shifts the pK_a of this hydroxyl within the HDV ribozyme active site to lower values, as suggested by proton inventory experiments⁵⁸ and NMR spectroscopic measurements.²⁰ By contrast, the pK_a value of a hydrated Mg²⁺ ion was unambiguously measured (pK_a of 11.4⁴⁰) and is expected to be less affected by the active site environment. Therefore, the correction terms for the rare ionization forms used in this study were estimated from the pK_a of C75 (already shifted in the HDV ribozyme active site environment) and the pK_a of a hydrated Mg²⁺ ion.

Our data suggest that both the pre-cleavage state R (i.e., the state with the native U-1(2′-OH) and a hydroxide coordinated to the Mg²⁺ ion) and the intermediate state R′ (i.e., the state with already deprotonated U-1(2′-O⁻) and a water molecule coordinated to Mg²⁺) are close in Gibbs energy (Table 1). Based on this Gibbs energy difference and the assumption that the pK_a of the active site Mg²⁺ ion is not significantly affected by the active site environment, we estimate the pK_a of the U-1(2′-OH) group to be between 8.8 and 14.5 (see Table 1). If we discount the Mg²⁺ coordinations resulting in the highest activation barriers (28.0 and 28.8 kcal/mol) that represent the least feasible reaction paths, as well as the [U-1(O2)] single-inner-shell path where the R′ state is not well defined (see Fig. 3), the range for the estimated pK_a is reduced to 8.8-11.2. Comparing with the experimentally measured pK_as for the 2′-hydroxyl, we conclude that the pK_a of the U-1(2′-OH) group in the environment of the HDV ribozyme active site is likely lowered by ∼1.6–4.0 units, rendering it close to or even below the pK_a of ∼11.4 for the solvated Mg²⁺ ion. Our observations are thus in agreement with the latest kinetic and NMR measurements, where the pK_a of the U-1(2′-OH) group in the presence of Ca²⁺ ions (11.4–11.9) was lowered by ∼1.3–2.7 units in comparison with comparable experiments using monovalent (K⁺ and Na⁺) ions.²⁰

Conclusions

We performed QM/MM calculations of the self-cleavage reaction of the HDV ribozyme based on a mechanism wherein the U-1(2′-OH) nucleophile is deprotonated/activated by a hydroxide ion coordinated to the active site Mg²⁺ ion, i.e., with the partially hydrated active site Mg²⁺ ion acting as a Brønstead base. We followed the reaction path starting from various active site arrangements differing in the position and coordination of the active site Mg²⁺ ion, localizing eight distinct reaction micro-pathways.

We found that the deprotonation of the U-1(2′-OH) nucleophile and nucleophile attack are sequential steps so that the deprotonation of the U-1(2′-OH) precedes the nucleophilic attack. The nucleophilic attack then occurs concurrently with the second proton transfer from the protonated C75H⁺, which acts as the general acid, to the leaving G1(O5′) group.

We estimated the activation barriers along the eight reaction pathways to range from 14.2 to 28.8 kcal/mol. The wide range of activation energies indicates that the specific position and coordination of Mg²⁺ ion in the active site have a significant direct impact on the self-cleavage reaction. Importantly, for six of these paths we obtained a feasible reaction barrier ranging from 14.2 to 21.9 kcal/mol, indicating that these paths can be considered plausible for the reaction. However, no clear correlation between the specific Mg²⁺ coordination in the active site and the activation barrier was found. The fact that we identified (within the inherent uncertainty of QM/MM computations) six distinct micro-pathways that have the potential to independently contribute to the reaction may be functionally relevant since recent studies of the trans-acting HDV ribozyme have found evidence for several conformations that are catalytically active with distinct rate constants.⁵⁹

Our data (relative QM/MM energies of the R and R′ states), together with the assumption that the pK_a of the hydrated Mg²⁺ ion is less affected by the HDV ribozyme active site than the pK_a of the U-1(2′-OH) group, suggest that the pK_a of U-1(2′-OH) is shifted by ∼1.6–4.0 units, rendering it comparable to or even lower than the pK_a of the solvated active site Mg²⁺ ion. This prediction is in agreement with recent kinetic and NMR measurements on the HDV ribozyme.²⁰ The lowering of the U-1(2′-OH) pK_a may strongly facilitate activation of the 2′-OH nucleophile and thus contribute to catalysis.