A Hypothesis-Driven Parametric Study of Effects of Polymeric Scaffold Properties on Tissue Engineered Neovessel Formation

Abstract

Continued advances in the tissue engineering of vascular grafts have enabled a paradigm shift from the desire to design for adequate suture retention, burst pressure, and thrombo-resistance to the goal of achieving grafts having near native properties, including growth potential. Achieving this far more ambitious outcome will require the identification of optimal, not just adequate, scaffold structure and material properties. Given the myriad possible combinations of scaffold parameters, there is a need for a new strategy for reducing the experimental search space. Toward this end, we present a new modeling framework for in vivo neovessel development that allows one to begin to assess in silico the potential consequences of different combinations of scaffold structure and material properties. To restrict the number of parameters considered, we also utilize a non-dimensionalization to identify key properties of interest. Using illustrative constitutive relations for both the evolving fibrous scaffold and the neotissue that develops in response to inflammatory and mechanobiological cues, we show that this combined nondimensionalization – computational approach predicts salient aspects of neotissue development that depend directly on two key scaffold parameters, porosity and fiber diameter. We suggest, therefore, that hypothesis-driven computational models should continue to be pursued given their potential to identify preferred combinations of scaffold parameters that have the promise of improving neovessel outcome. In this way, we can begin to move beyond a purely empirical trial-and-error search for optimal combinations of parameters and instead focus our experimental resources on those combinations that are predicted to have the most promise.

1. Introduction

Diverse approaches have shown promise in the tissue engineering of vascular grafts [1–3]. Amongst these approaches, implantation of a biodegradable polymeric scaffold has been shown both in animal studies [4,5] and clinical trials [6–8] to enable neovessel development in low pressure regions of the vasculature without the development of intraluminal thrombus or aneurysmal dilatation. Given these successes, there is now an opportunity to turn our attention towards the potential optimization of these scaffolds. There are, however, many parameters that define each scaffold, including the type of polymer(s), pore size, fiber alignment, and so forth. Although trial and error approaches have led us to the current level of successes, identification of an optimal combination of so many scaffold parameters demands a new approach.

In this paper, we meld ideas of non-dimensionalization for experimental design with theoretical analyses of polymer properties and novel computational modeling to explore parametrically the in vivo development of a tissue engineered vascular graft (TEVG) as a function of six key parameters for a fibrous poly(glycolic acid) – poly(ε-caprolactone – L-lactide), or PGA-P(CL/LA), construct: pore size, porosity, polymer stiffness, degradation rate, fiber diameter, and fiber alignment. We selected these parameters because of their demonstrated importance in experimental studies and structure-function relationships [9–12], particularly as related to the host inflammatory response, and because of their influence on other parameters of importance, including bulk properties of the scaffold. In addition, we evaluated computationally four competing hypotheses regarding the prestress and rate of degradation of the polymer as well as the stiffness and extent of degradation of the deposited collagen. Noting that “compliance mismatch” has long been considered a determinant of graft failure, we computed the evolving stiffness of the TEVGs as the polymer degrades and is replaced by native matrix. Although different combinations of initial polymer properties affect this evolution, four basic phases persist and thereby reveal the challenge of fine tuning the structure and material properties of the polymeric scaffold as well as the associated biochemomechanical responses of the cells responsible for building the neovessel. In summary, notwithstanding several simplifications, this first generation model predicts salient aspects of TEVG evolution and suggests values of physical parameters that may yield an improved scaffold design and thus an overall improvement in neovessel development. We submit, therefore, that a combination of non-dimensional analysis and growth and remodeling (G&R) models could advance the field of vascular, as well as related areas of, tissue engineering.

2. Background

Computational models can enable cost- and time-efficient evaluations of fundamental hypotheses [13] and studies of parameter sensitivity [14]. Another advantage of such models is that they can thereby help to reduce the experimental search space, which we suggest is sorely needed to optimize scaffold design in vascular tissue engineering. Computational models are most revealing, however, given a modest number of parameters.

The current literature on tissue engineering and biomaterials reveals a multitude of structural and material parameters of a polymeric scaffold that can influence both the mechanical and the biological function of an implanted graft, including the host inflammatory response to the scaffold and thus the overall development of a neovessel in vivo (cf. [11,15]). For the purposes herein, we first reduced this extensive list of parameters to a focused list consisting of those scaffold parameters that have been most frequently investigated experimentally (Table 1). Next, we reduced this list further to a tractable set of six parameters for non-dimensionalization; these parameters represent fundamental physical properties of a fibrous scaffold (e.g., Fig. 1) that are easily measured and known to affect the foreign body response (Table 1). We then used the Buckingham Pi approach to accomplish the non-dimensionalization [16], which required that we postulate characteristic “scales” for the primary dimensions of interest. The scales needed herein were those for length, time, and mass. Perhaps the best known similar non-dimensionalization is the identification of the Reynolds number in fluid mechanics, which reduces effects of fluid density, mean velocity, tube diameter, and viscosity to a single parameter.

Table 1.

Of the many parameters that can modulate the host inflammatory response to a fibrous scaffold, we first reduced an initial set of 20 (listed in the left column) to a focused set of 10 (highlighted in grey), which in turn was reduced to a final set of 6 (in bold) parameters that were used for non-dimensionalization (cf. Table 2) and the subsequent computational study. References for each parameter are classified as (i) from the general biomaterials literature or specific to vascular applications, and (ii) by the experiments performed in vitro versus in vivo, which in turn were either sub-cutaneous (SQ) or tissue specific (TS). Note that review articles are only classified by (i).

Parameters	General Biomaterials	Vascular Specific	In vitro	In vivo (SQ)	In vivo (TS)
Chemical side groups	53,56	12,15	53	53
Composition	11	15,54	11,54	11	54
Contact duration	18,53,55,56	15	18,53	53,55
Filament structure	63		63	63
Host-dependencies	53	12	53	53
Material weight		64			64
Morphology	9,28	15	28	9,28
pH end products	63	64	63	63	64
Sterility		15
Topography	11,26,28,62	15,54	11,26,28,54	11,28	54
Roughness	11,26,62	15	11,26	11
Shape	9,26,53	15	26,53	9,53
Surface chemistry	11,43,55,62,63	12,15,54,61,65	11,43,54,61,63,65	11,55,61,63	54
Wettability	9,11	12,15,61	11,61	9,11,61
Degradation rate	9,53	12,15,57	53	9,53	57
Porosity	9,20,53,55,58–60	15,54,61	20,53,54,58,60,61	9,53,55,59,61	54
Stiffness	53,66	12,15,54,67,68	53,66,67	53	54,6 8
Fiber diameter	10,18,24,25,26,28,43,60,63,69	12,17,46,65,67	17,18,25,26,28,43,46,60,63,65,67	10,24,28,63,69	46
Pore size	10,18,20,24,45,53,58–60	12,46,61,67	18,20,46,53,58,60,61,67	1,450,24,53,59,61
Alignment	11,26,28	12	11,26,28	11,28

Figure 1.

Scanning electron microscopy image of a PGA-P(CL/LA) scaffold showing the primary parameters considered computationally: normalized fiber diameter ω* and normalized pore size r*. Note that scaffold alignment should also be considered in the future, where ϕ^p,k = 0 indicates a highly aligned scaffold and ϕ^p,k = 1 a scaffold with randomly organized fibers. SEM image courtesy of Kevin Rocco.

Given that the selection of the requisite length, time, and mass scales was not unique, we explored multiple possibilities (Appendix A). Motivated in part by experimental findings that reveal the particular importance of scaffold pore size and degradation rate [cf. 12,15], we selected the following scales: L_s = r_min, $T_s={(k_q^p)}^{-1}$, and $M_s=c^p{r}_{\mathit{\text{min}}}/{(k_q^p)}^2$, where r_min is the minimum pore size that admits cellular infiltration (having units of microns), $k_q^p$ is the rate of degradation (having units of days⁻¹), and c^p is the shear modulus of the scaffold (having units of Pa). Using this set of scales, the Buckingham Pi analysis suggested a reduction in parameters from 6 to 4 (Table 2), namely

$$f(k_q^p,\epsilon ,c^p,\omega ,r,{\varphi }^k)\to \mathrm{f̌}(\epsilon ,\frac{\omega }{r_{\mathit{\text{min}}}},\frac{r}{r_{\mathit{\text{min}}}},{\varphi }^k)$$ (1)

where ε represents scaffold porosity, ω is the diameter of the polymeric fibers composing the scaffold, r is the mean pore size, and ϕ^k describes the alignment of the fibrous scaffold (cf. Fig. 1).

Table 2.

A) Sample Buckingham Pi non-dimensional analysis demonstrating a reduction of tractable physical parameters for a fibrous scaffold from 6 (cf. bold in Table 1) to 4. Note that L, T, and M denote length, time, and mass. B) Selection of scales for the 3 primary dimensions, or units, for quantifying effects of the polymeric scaffold on the mechanobiology, plus a reduced list of non-dimensionalized parameters.

	Inflammatory Response, $y=f(k_q^p,\epsilon ,c^p,\omega ,r,{\varphi }^k)$
A.	Scaffold Parameter	Symbol	SI Units	General Units	π Group
	Degradation rate	$k_q^p$	days−1	L0T−1M0	1
	Porosity	ε	$\frac{\mathrm{g}/{\text{cm}}^3}{\mathrm{g}/{\text{cm}}^3}$	L0T0M0	ε
	Modulus	cp	MPa	L−1T−2M1	1
	Fiber diameter	ω	cm	L1T0M0	ω/rmin
	Pore size	r	cm	L1T0M0	r/rmin
	Alignment	ϕk	--	L0T0M0	ϕk

B.	Scales for L (length), T (time), and M (mass)			Inflammatory Response
	Ls = rmin, $T_s=1/k_q^p,M_s=c^p{r}_{\mathit{\text{min}}}/{(k_q^p)}^2$			y = f̌ (ε, ω/rmin,r/rmin,ϕk)

Previous experiments indicate that these physical parameters strongly influence the initial mechanical properties of the scaffold and the biological responses following implantation (cf. Table 1). In particular, several studies suggest that pore size may be a primary determinant of the overall success of implanted polymeric constructs, as adequate pore size is necessary for cell infiltration [17–20]. If cells cannot enter the scaffold, a scar plate of collagen may form on the outside of the scaffold, thus encapsulating the construct and increasing the probability of fibrosis or graft failure [21]. It has been suggested that 10 µm is the minimum pore size for cells to infiltrate a scaffold without detrimental shearing [22,23] though the optimal value remains unclear.

Scaffold fiber diameter (in combination with spacing between adjacent fibers, i.e., pore size) determines the surface area on which cells can attach and spread, hence it can influence cell phenotype and differentiation [10,24]. Experiments show that increasing fiber diameter increases the magnitude of the inflammatory response and subsequent matrix accumulation [10,25]. For example, increasing fiber diameter increases macrophage activation and their secretion of proinflammatory molecules [26]. Although the optimum fiber diameter remains unknown, a threshold may modulate cellular responses: fiber diameters below 6 µm (if separated adequately) reduce the number of activated macrophages (cells remain quiescent) and fibrous capsule thickness [10,24]. Fiber diameter may also influence scaffold stiffness, but this effect depends on the fabrication technique.

Correspondingly, porosity also influences the surface area available for cell attachment and foreign body detection. Increased porosity appears to increase the immune response to polymeric scaffolds that have a wettability attractive to cell infiltration [9]. Increased porosity also increases the surface area available to cells as the polymer degrades, thus increasing the magnitude of the foreign body response. Furthermore, porosity is a major determinant of polymer relative density and scaffold mechanical properties [27].

Scaffold alignment can also influence the mechanical and biological properties of evolving TEVGs. Aligned scaffolds tend to increase cellular infiltration, which decreases the thickness of the fibrous capsule around the construct relative to that for randomly aligned scaffolds [28]. Furthermore, cells may preferentially align with the direction of fibers [29,30], although it is not clear if cell alignment necessarily dictates the alignment of deposited matrix. Alignment also influences the mechanical properties of the scaffold, including the magnitude of its biaxial stiffness, that is, anisotropy [29].

Bulk properties of the polymeric scaffold are likely important as well (e.g., bulk modulus, wettability, degradation characteristics). Bulk polymer stiffness and microstructure (e.g., porosity and alignment) can be used to calculate scaffold modulus: c^p,dry(0)/E^s,dry = 0.03(1 − ε(0))² where ε(0) is the initial porosity of the scaffold, E^s,dry is Young’s modulus for the bulk polymer, and c^p,dry(0) is the effective shear modulus of the fabricated scaffold under dry conditions at room temperature [27,31,32]. The bulk polymer considered herein, poly(glycolic acid), has a wettability favorable for cell infiltration [33]; relationships between bulk physiochemical and physical properties would need to be determined for other polymers, however, to extend the following proposed constitutive relations to other constructs of interest.

Noting that porosity and fiber alignment are non-dimensional, they will be present regardless of the choice of scales. Albeit not motivated by a Buckingham Pi analysis, theoretical studies suggest further relationships among three of the key parameters considered here [22,27,29,30,34]. For example, in a 2D case, the mean pore diameter depends on fiber diameter and porosity, whereby a normalized mean pore diameter can be estimated $\frac{r}{r_{\mathit{\text{min}}}}=-\frac{\sqrt{\pi }}{2}(1+\frac{\pi }{2\text{log}(\epsilon )})\frac{\omega }{r_{\mathit{\text{min}}}}$ for 0.2 ≤ ε < 1 [22,34]; our division by the length scale, L_s = r_min, non-dimensionalized the prior result. Thus, considering both a Buckingham Pi analysis and this phenomenological theory, we can consider a functional response as $\mathrm{f̃}=(\frac{r}{r_{\mathit{\text{min}}}},{\varphi }^k)$ with $\frac{r}{r_{\mathit{\text{min}}}}=g(\epsilon ,\frac{\omega }{r_{\mathit{\text{min}}}})$ or alternatively, as assumed below,

$$\mathrm{f̌}(\epsilon ,\frac{\omega }{r_{\mathit{\text{min}}}},{\varphi }^k)$$ (2)

in terms of three primary non-dimensional parameters of interest. Hence, of the initial six parameters, only three remained that are influenced by all of the non-dimensional parameters of interest: r is a function of ε and ω; modulus, c^p, is a function of alignment and porosity [27,29], where it has been suggested that scaffold fiber diameter may affect c^p for certain fabrication techniques; finally, for a given polymer, degradation rate, $k_q^p$, is strongly influenced by porosity and fiber diameter, which determine the available surface area for polymer-cell interaction [22].

Utilizing these results, we next identified illustrative constitutive relations in terms of these three non-dimensional scaffold parameters consistent with a general modeling approach introduced previously [35]. In each case, results from the literature on observed structure-function relationships motivated the selected constitutive relations (cf. Table 1), including postulated mechanical and biological consequences for each parameter. Rather than nondimensionalizing the governing equation and plotting final results in terms of non-dimensional time, we present results in terms of the more intuitive actual time in days.

3. Computational Model

3.1 G&R Framework

Details on the original motivation and theoretical framework for our general G&R approach can be found elsewhere [36,37]. Briefly, α = p (polymer), 1, …, n (matrix) structurally significant constituents are allowed to possess different material properties, different rates of production and removal, and different natural (stress-free) configurations, yet they are all constrained to deform with the bulk material. The deformations experienced by individual constituents can thus be quantified given both the gross deformations of the composite TEVG, which are measurable in vivo, and deformations associated with the incorporation of individual matrix constituents within the extant material. Together, these two deformations yield the constituent-specific deformation gradients, ${\mathbf{F}}_{n(\tau )}^{\alpha }(s)$, where n(τ) denotes the constituent-specific natural configuration and τ ∈ [0, s] the time of deposition during the G&R simulation. The net elastic energy stored in the TEVG at G&R time s, namely W(s), is estimated as the sum of the energies W^α stored in all constituents, which in turn depend upon the individual ${\mathbf{F}}_{n(\tau )}^{\alpha }(s)$. That is, W(s) = ΣW^α(s), where

$$W^{\alpha }(s)=\frac{{\rho }^p(0)Q^p(s)}{{\rho }^p(s)}{W}^p({\mathbf{F}}_{n(0)}^p(s))+{\int }_0^s\frac{m^{\alpha }(\tau )}{\rho (s)}{q}^{\alpha }(s-\tau )W^{\alpha }({\mathbf{F}}_{n(\tau )}^{\alpha }(s))d\tau$$ (3)

describes the constituent-specific stored energies. Here, ρ^p(0) is the initial apparent mass density of the polymeric scaffold, Q^p(s) ∈ [0, 1] is the fraction of the scaffold that was present at time 0 that remains at the current time s, m^α(τ) is the extracellular matrix constituent-specific rate of new mass density production, and q^α (s − τ) ∈ [0, 1] is the fraction of the constituent produced at time τ ∈ [0, s] that remains at s.

Note that polymer porosity is a determinant of the initial density of the scaffold [27], and it increases as the polymer degrades. It was assumed that a porous scaffold essentially fills with interstitial water at time 0, the volume fraction of which increases further as the polymer degrades following implantation. Hence, the apparent mass density of the scaffold can be calculated at any time s as, ρ^p(s) = ρ^pga(1 − ε(s)) + ρ^wε(s), where ρ^pga is the apparent mass density of the bulk polymer, ε(s) is the porosity of the scaffold at time s, and ρ^w is the apparent mass density of the interstitial water (note: if ε = 0, ρ^p = ρ^pga; if ε = 1, ρ^p = ρ^w). Of course, the polymeric construct is the only constituent present at time 0, hence α = p initially, with only matrix produced thereafter.

This simple “rule-of-mixtures” framework enables a classical formulation of the wall mechanics, including equilibrium and stress constitutive relations [38], namely

$$\mathit{\text{div}}\mathbf{t}=\mathbf{0}\text{with the Cauchy stress}\mathbf{t}=\frac{2}{\mathit{\text{det}}\mathbf{F}}\mathbf{F}\frac{\partial W}{\partial \mathbf{C}}{\mathbf{F}}^T,$$ (4)

where F is the overall deformation gradient and C = F^TF the overall right Cauchy-Green tensor. Implementation of this framework thus requires three constituent-specific constitutive relations: the rate of mass density production m^α( τ), the rate of removal (i.e., the survival fraction) q^α(s − τ) ∈ [0, 1], and the stored energy function $W^{\alpha }({\mathbf{F}}_{n(\tau )}^{\alpha }(s))$. This framework has predicted salient features of both arterial adaptations and disease processes in response to diverse chemomechanical perturbations by assuming that mass density production depends on deviations in intramural and wall shear stresses from preferred (“homeostatic”) target values, that removal follows a first order kinetic decay that may depend on stress, and that the constituent mechanical behaviors can be described with classical neo-Hookean or Fung exponential models [37].

Recently, this framework was extended to model evolving TEVGs in vitro [39] and in vivo in the murine venous circulation [35]. Prior constitutive relations were augmented to incorporate (i) the monotonic loss of a load-bearing polymeric scaffold over time and, in the latter case, (ii) an additional inflammatory-mediated production of matrix that precedes the typical mechanomediated production. Of particular importance herein, the model of Miller et al. [35] described well the experimentally observed evolving mechanical behaviors of TEVGs implanted in the murine inferior vena cava [5]. Here, we extended this model of in vivo neovessel development to consider parametrically the roles of scaffold physical parameters on TEVG evolution via their effects on the kinetics of matrix production and removal during both the early inflammatory phase and the subsequent mechano-mediated phase. Selected constitutive relations and model parameters were informed by longitudinal data on cell biological, histological, and mechanical changes in a murine inferior vena cava (IVC) interposition TEVG studied for 24 weeks as well as related data from the native murine IVC [4,5,32,40,41]. Given a lack of detailed information on initial and evolving changes in polymer fiber alignment within the TEVG (as well as insufficient data to formulate illustrative constitutive functions relating alignment with the host inflammatory response and TEVG mechanical properties), however, we focused on effects due to porosity and fiber diameter, namely $\mathrm{f̌}(\epsilon ,\frac{\omega }{r_{\mathit{\text{min}}}})$ for the non-woven scaffold used. Additional experimental data are needed to extend the proposed constitutive framework to evaluate the role of scaffold alignment in TEVG evolution.

3.2 Illustrative Constitutive Relations

First consider the polymeric scaffold (i.e., α = p). Given that polymer is not produced in vivo, we need only consider its loss (and associated time-dependent increase in porosity). In lieu of experimental data on changes in porosity as the scaffold degrades, we let porosity increase proportional to decreasing scaffold mass [5,35]. Adopting a prior neo-Hookean descriptor for the mechanical behavior of the polymer,

$$W^p({\mathbf{F}}_0^p(s))=c^p({({\lambda }_{\theta }^p)}^2+{({\lambda }_z^p)}^2+\frac{1}{{({\lambda }_{\theta }^p{\lambda }_z^p)}^2}-3),$$ (5)

where theoretical and experimental observations enable c^p to be estimated as a function of initial porosity [27,31,32]. Following [35], the structural integrity of the scaffold was assumed to be lost prior to its complete loss of mass, hence c^p(s) = c^p(0) − 0.1c^p < s − 7 >, where the 7 day delay was motivated by experimental observations [5] and held fixed across the initial parametric studies.

Next, consider the extracellular matrix constituents. We previously introduced an approach to account for both inflammatory (infl) and mechanical stress (strs) mediated phases of remodeling [35]. Motivated by data on monocyte / macrophage activity [42], the inflammation-mediated mechanism of production was modeled phenomenologically using a gamma distribution function to capture the production of collagen due to the foreign body response, hence $m_{\mathit{\text{infl}}}^k(\tau )\equiv K_{\mathit{\text{infl}}}(\alpha \tau e^{1-\alpha \tau })$ where K_infl is a rate parameter representing an increased synthetic capability and 1/α represents the peak time of macrophage infiltration. The value of K_infl was identified previously via a brute force parametric study to best-fit experimental data [5,35], but here we introduced a linear dependence on the normalized pore size, r*, which is a function of current values of ε and ω*. That is, K_infl = K_αr* +, K_wound where K_α = 2 is a constant and K_wound = 5 models the inflammatory response due to the implantation surgery alone [33]. This functional form was motivated by qualitative information that increased fiber diameter and increased porosity (which coincides with increased pore size) stimulate greater inflammatory responses and subsequent accumulation of matrix [9,18,25,43].

Because intramural cells should sense increasing loads as the stiff polymer loses load-bearing integrity, following [37] we let the mechanical stress-mediated production of collagen be modeled by $m_{\mathit{\text{strs}}}^k(\tau )\equiv (1-\frac{c^p(\tau )}{c^p(0)}{K}_{\mathit{\text{strs}}}^k\mathrm{\Delta }{\sigma }^k(\tau )$ where $(1-\frac{c^p(\tau )}{c^p(0)})\in [0,1]$ captures the initial stress-shielding effect of the stiff polymer, Δσ^k(τ) denotes the normalized difference in intramural stress from a target value, and $K_{\mathit{\text{strs}}}^k$ is a rate-type parameter. Because the inflammatory response increases cytokines, chemokines, and growth factors in the extracellular mileu, it may increase the ability of the intramural synthetic cells to respond to deviations from the preferred state of stress [12,33]. Given that multiple cell types (e.g., fibrocytes, smooth muscle cells, and fibroblasts) may contribute to matrix production during the inflammatory period, we let $K_{\mathit{\text{strs}}}^k(\tau )\equiv K_{\mathit{\text{strs}}}^b(r^{*}+1)$, where $K_{\mathit{\text{strs}}}^b=0.1$ represents the rate parameter for the healthy, normal murine IVC and r* allows the proliferative capability to increase as a function of the inflammatory response (thus assuming that increased monocyte/macrophage presence will increase the presence of additional matrix-producing cells). In this way, potentially coupled inflammatory and mechano-mechanisms could be captured phenomenologically.

It is not known whether collagen produced in response to inflammation or mechanical stress has different degradation kinetics, hence we let $q^k(s,\tau )=\text{exp}({\int }_{\tau }^s-k^q(t)dt)$ where k^q(t) is a general rate-type parameter for matrix removal having units of days⁻¹. Nevertheless, it is reasonable to assume that increased inflammation involves increased macrophages and neutrophils, and thus matrix metalloproteinases (MMPs), that may decrease the constituent half-life [18,21]. Therefore, to increase degradation as a function of the inflammatory response, we let $k^q(t)=k_{\mathrm{h}}^{\mathrm{q}}(1+K_{\mathit{\text{infl}}}/K_{\mathit{\text{infl}}}^{\mathit{\text{max}}})$ with $k_{\mathrm{h}}^{\mathrm{q}}$ a basal rate parameter, $K_{\mathit{\text{infl}}}^{\mathit{\text{max}}}=100$ and $K_{\mathit{\text{infl}}}/K_{\mathit{\text{infl}}}^{\mathit{\text{max}}}\in [0,1]$ for constituents produced via the inflammatory response.

For completeness, note that the mechanical behavior of collagen and passive smooth muscle were again described using a Fung-type exponential equation [13,35,39]. Additionally up to 5% of total mass following polymer degradation was considered as noncollagenous matrix (e.g., proteoglycans and glycosaminoglycans) and its mechanical behavior was described with a classical neo-Hookean response.

3.3 Model Parameters

The requisite parameters can be categorized as measured or calculated (see Table 2 in [35] and also [14]) as well as unknown but bounded. The latter were identified previously (Table 4 in [35]), with the exception of the two new parameters introduced to determine K_infl. All bounded parameters were maintained fixed throughout the parametric studies. That is, they were assumed to be applicable for all interposition PGA-P(CL/LA) TEVGs in SCID/bg mice regardless of scaffold porosity or fiber diameter (cf. [5,35]).

3.4 Parametric studies

To assess consequences of altering the structure and properties of the scaffold on TEVG evolution, parametric studies were performed for multiple pairs of scaffold porosity, ε ∈[0.6,0.95], and normalized fiber diameter, ω*∈[0.01,1.4]. For each pair, the following evolving properties were examined over two year simulations (note: two years is the normal murine lifespan): TEVG thickness, fold-changes in mass density production for inflammatory-and mechano-mediated mechanisms (normalized to the basal rate of production for healthy, normal murine IVC), structurally significant-constituent mass fractions, estimated circumferential and axial in vivo stretches, and biaxial mechanical properties. As indicators of evolving TEVG mechanical behavior, pressure – diameter and circumferential tension – stretch experiments were simulated throughout the evolution of the TEVG; consistent with the G&R model, these simulated tests were assumed to consist of quasi-static loading and to yield nonlinear, anisotropic, hyperelastic responses. Finally, the theory of “small deformations superimposed on large” was used to compute material stiffness linearized appropriately at a prescribed in vivo state defined by venous pressure (~2 mmHg) and axial stretch throughout TEVG evolution [44].

Following an initial parametric study, a small series of hypothesis-driven parametric studies were performed to guide future TEVG experiments that seek to improve neovessel development and final outcome. These studies focused primarily on elucidating parameter contributions to the evolving construct stiffness. Motivated by the initial parametric studies, we fixed porosity ε = 0.80 and normalized fiber diameter ω* = 1.4 and studied the hypotheses that: (i) decreasing the rate at which the polymer loses load-bearing integrity (ξ^p∈[0.01, 0.3]c^p(0)) will decrease changes in linearized stiffness at early time points; (ii) pre-stressing the polymer construct at the time of implantation (G^p∈[1.0,1.14]) will decrease changes in the unloaded configuration of the TEVG as the polymer degrades, thus decreasing the peak in linearized stiffness following loss of polymer integrity; (iii) increasing the rate of degradation of collagen produced during the inflammatory response $K_{\mathit{\text{infl}}}^{\mathit{\text{max}}}=50$ will decrease the peak in evolving linearized stiffness at the transition between the two production mechanisms; and (iv) decreasing the stiffness of the matrix constituents, particularly via collagen cross-linking and type I collagen ($c_1^k$ and $c_2^k$) parameters set to calculated values for normal, healthy SCID/bg IVC [41], will decrease the linearized stiffness values.

4. Results

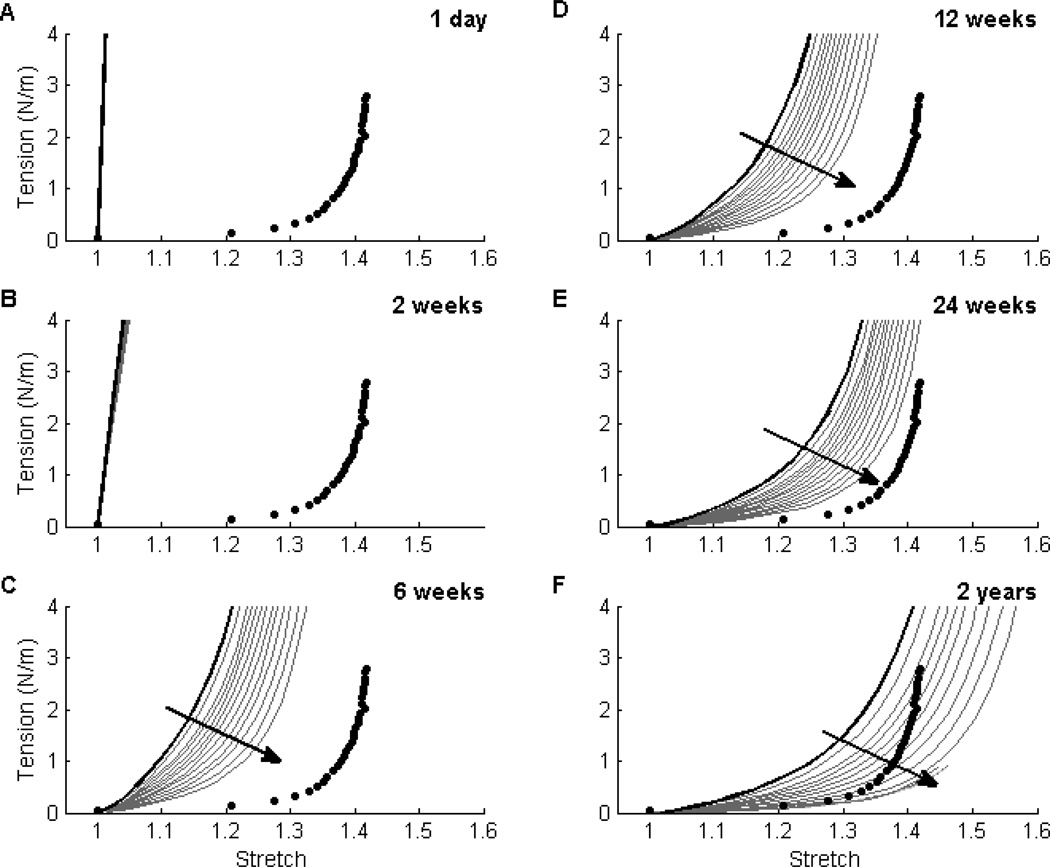
Theory suggests that increasing the normalized fiber diameter, ω*, and/or porosity, ε, increases the normalized pore size, r*, which in turn increases the inflammatory response to the implanted foreign body. Our simulated results captured this effect: for a fixed porosity, decreasing ω* decreased the inflammatory response, which in turn decreased matrix production and indirectly increased the compliance of the TEVG at later times (Fig. 2). Note that the polymer construct dominated the mechanical behavior at early times regardless of the value of ω* (Fig. 2, panels A and B). Following polymer degradation (which occurred between panels B and C), however, the mechanical behavior was driven by the matrix and thus depended strongly on the initial value of ω* and its effect on cellular responses. The intensity of the stress-mediated deposition decreased throughout the simulation as matrix accumulated, thus resulting in a more compliant TEVG at later times. Qualitatively, this trend was preserved across all values of ε of interest though the net effect of ω* was greater for higher values of ε. Note that ε = 0.80 and ω* = 1.4 corresponded best with prior experiments [5]; the associated simulations are shown by the solid black line. Hence, while these prior experiments resulted in patent, evolving TEVGs up to 24 weeks [5], the simulations suggested that smaller values of ω* could have increased overall compliance and thereby resulted in a TEVG that was more similar to the native IVC (filled circles) at 2 years (Fig. 2).

Figure 2. Effect of Fiber Diameter ω* on Material Behavior.

Evolving circumferential tension-stretch behaviors for simulated TEVGs (solid lines) at 1 day (Panel A), 2 weeks (Panel B), 6 weeks (Panel C), 12 weeks (Panel D), 24 weeks (Panel E), and 2 years (Panel F) post-implantation are contrasted against mean experimental results for the native murine inferior vena cava (solid symbols; [41]). The solid black curve shows predicted results (cf. [35]) that correlated well with an actual experimental case (cf. [4,5]) for an initial normalized fiber diameter ω* = 1.4 and scaffold porosity ε = 80%; the solid grey curves show predicted results for ω* ∈ [0.01,1.4] at a porosity of 80%. Reducing ω* (indicated by the direction of the dark arrow) decreased the magnitude of the inflammatory response and subsequently resulted in more distensible TEVGs. This trend was preserved across porosities of interest (60 to 95%), but the effect of ω* increased with increasing porosity. Finally, note that an intermediate range of ω* ∈ [0.5,1.0] resulted in simulated TEVGs having a compliance at 2 years that best approached that of the native vein (Panel F).

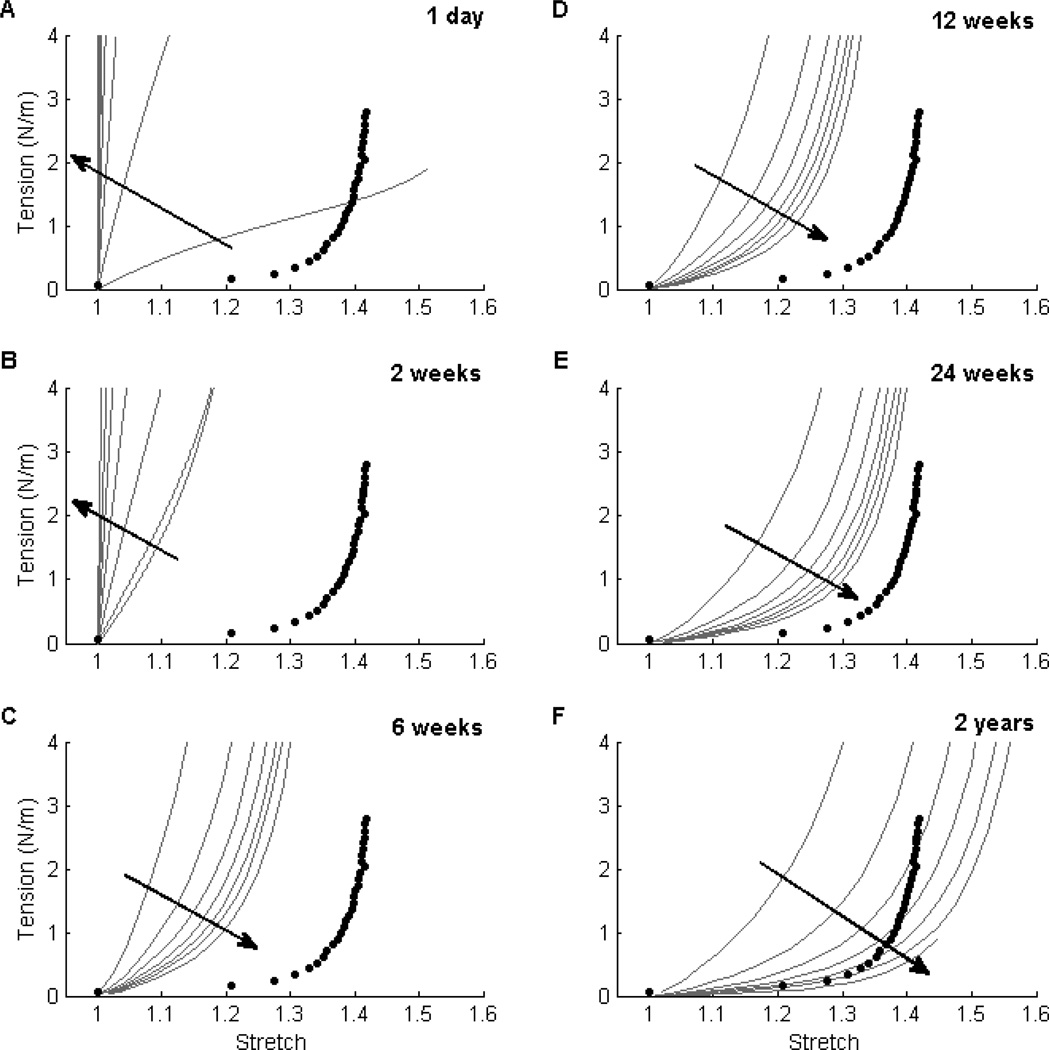
Simulated tension-stretch relationships demonstrated that, for fixed ω*, decreasing the porosity ε increased the initial mechanical contribution of the polymer (Fig. 3, panels A and B). Note the dramatic changes between 2 and 6 weeks, however: the former (Fig. 3, panel B) shows the direct effect of ε on the initial polymer contribution whereas the latter (Fig. 3, panel C) shows an indirect effect via matrix production. Following polymer degradation, smaller values of ε yielded less of an inflammatory response, hence less matrix production and a more compliant TEVG at later times (Fig. 3, panel F). Although the evolution of the simulated TEVG was preserved qualitatively across the parametric studies considered, preferred combinations of porosity and normalized fiber diameter could be identified by comparing the mechanical behavior of each simulation (grey lines) with the native IVC (filled circles) at 2 years (Table 3).

Figure 3. Effect of Porosity ε on Material Behavior.

Similar to Figure 1, evolving circumferential tension-stretch behaviors for simulated TEVGs (solid lines) at 1 day (Panel A), 2 weeks (Panel B), 6 weeks (Panel C), 12 weeks (Panel D), 24 weeks (Panel E), and 2 years (Panel F) post-implantation are contrasted against mean experimental results for the native murine inferior vena cava (solid symbols). The grey curves show results for initial scaffold porosity ε ∈ [60%, 95%] for a fixed initial normalized fiber diameter ω* = 0.6. Noting that the polymer degraded fully by 4 weeks, there were dramatic changes between 2 and 6 weeks: the earlier times revealed strong effects of porosity on polymer stiffness (e.g., Panel B) while the later times showed subsequent effects on matrix production (e.g., panel C). Note, too, that smaller values of ε (indicated by the direction of the dark arrow) resulted in more distensible TEVGs at later times (e.g. Panel F). This trend was preserved across a range of normalized fiber diameters of interest. For the representative ω* = 0.6, the results suggested that a range of porosities ε ∈ [75%, 85%] resulted in a 2-year compliance of the simulated TEVG that approached that of the native vein (Panel F).

Table 3.

Parametric studies suggested that particular combinations of ω* and ε could reduce the peaks in linearized stiffness throughout TEVG evolution and thus better approach the compliance of the native IVC by 2 years. Note that the range of preferred combinations yielded a normalized pore size r* from 2.30 to 3.95, with optimal suggested values between 3.07 and 3.56 for ε = 75, 80, 85% (shaded in light grey). ε = 60 and 95% (not shown) resulted in large peaks in linearized stiffness regardless of the value of ω* given the large discrepancies between polymer modulus and ECM material properties.

Normalized Fiber Diameter, ω*	Porosity, ε	Normalized Pore Size, r*
0.3	0.85	2.30
0.6	0.75	2.37
0.2	0.90	2.47
0.5	0.80	2.68
0.7	0.75	2.77
0.4	0.85	3.07
0.8	0.75	3.16
0.6	0.80	3.21
0.9	0.75	3.56
0.3	0.90	3.70
0.7	0.80	3.75
0.5	0.85	3.84
1.0	0.75	3.95

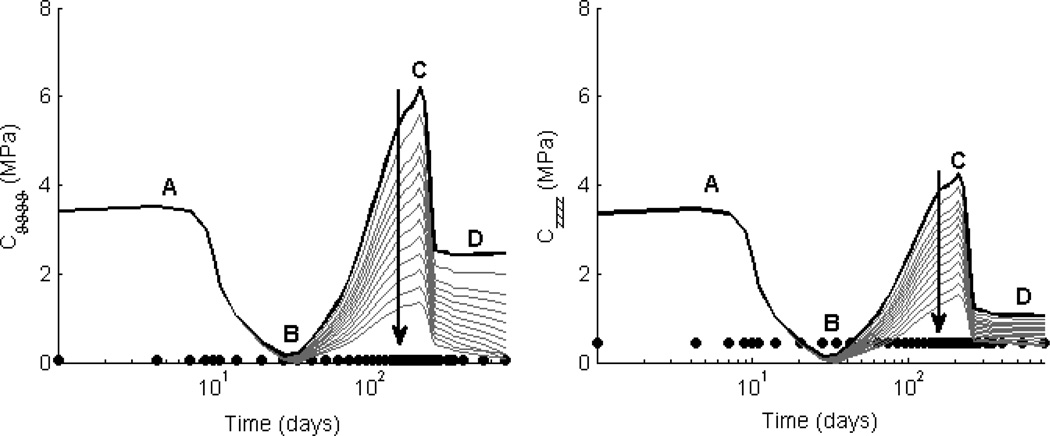
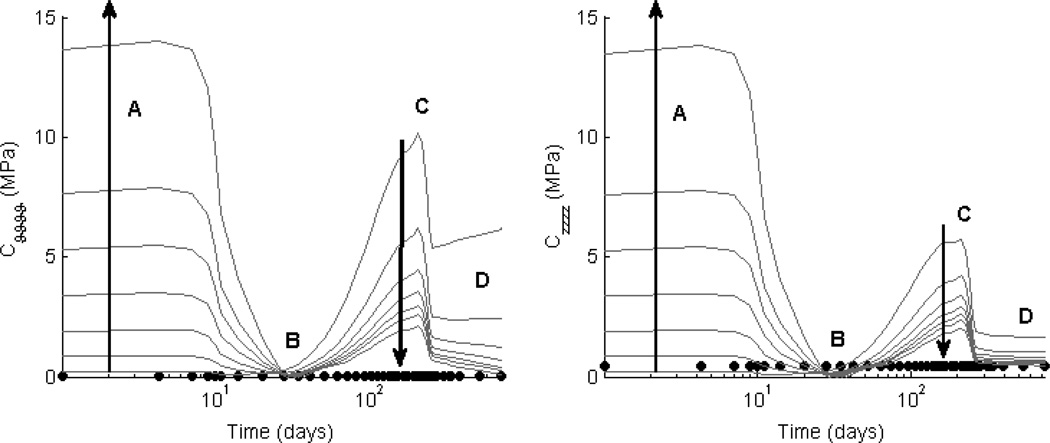
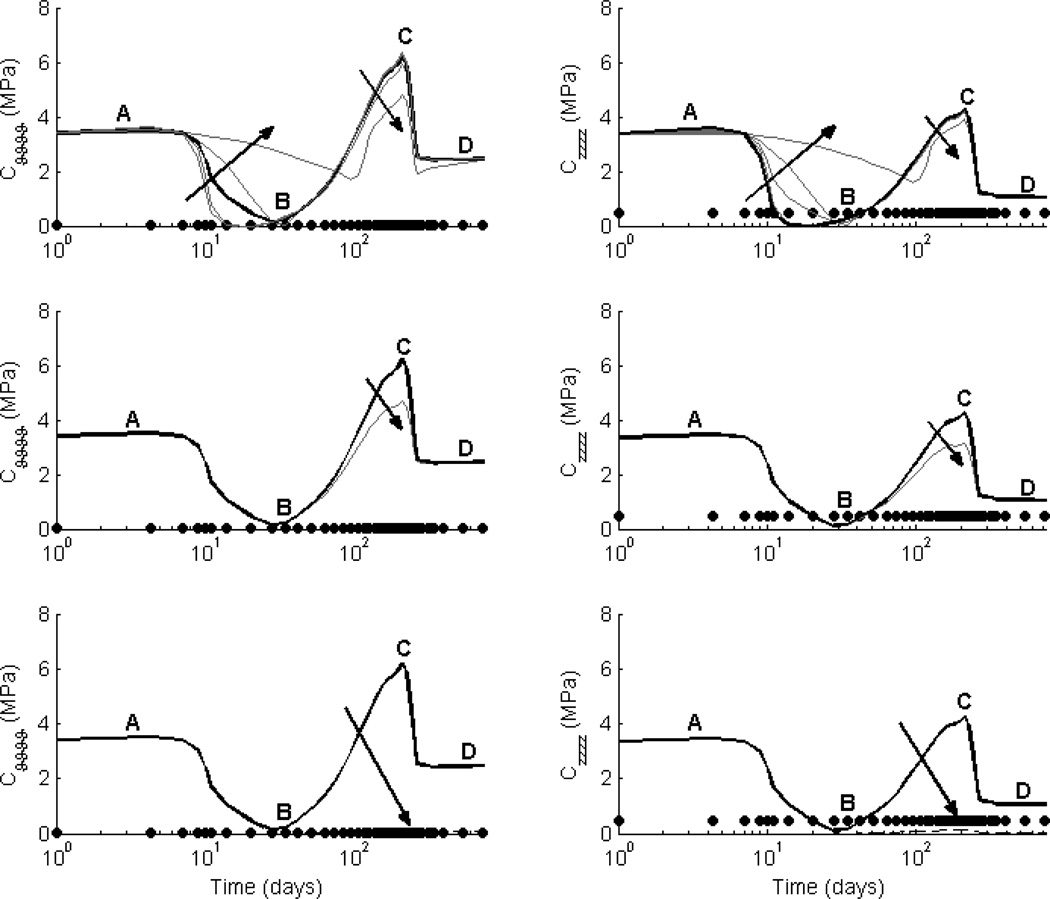
Simulations resulted in an evolving linearized stiffness that was qualitatively similar across all parametric studies (Figs. 4 and 5). Note the four stages. First, linearized stiffness was initially dictated by polymer properties. For a given polymer, porosity ε was the largest determinant of early linearized stiffness; decreasing ε increased the role of polymer properties, drastically changing the initial conditions (cf. Figs. 4 and 5, phase A). Second, the linearized stiffness declined as the polymer began to lose load-bearing integrity (Figs. 4 and 5, leading to phase B). Recall that following day 7, the polymeric scaffolds were assumed to lose mechanical integrity at a constant rate of 10% original modulus/day regardless of the initial value. Third, there was a marked increase in linearized stiffness (Figs. 4 and 5, phase C) driven by the burst of stiff fibrillar collagen produced due to the inflammatory response (modeled by the gamma distribution function representing the foreign body response to the polymer). Indeed, as the polymer lost load-bearing integrity, there was also a ramp increase in stress-mediated matrix production. The peak in linearized stiffness occurred at the peak of matrix accumulation due to the combined effects of both mechanisms of production. Note that decreasing ω* decreased matrix production, subsequently decreasing the peak in linearized stiffness (Fig. 4, phase C). Decreasing ε also decreased matrix production, resulting in a similar decrease in the peak linearized stiffness (Fig. 5, phase C), with dramatic differences in linearized stiffness throughout TEVG evolution from the time of implantation to 2 years for the upper and lower bounds of ε. Fourth, there was a decline and subsequent plateau of the linearized stiffness following the degradation of matrix produced via the inflammatory response as the TEVG reached a steady state remodeled configuration (Figs. 4 and 5, phase D). Decreasing both ε and ω* decreased the value of this plateau by indirectly decreasing matrix production during the mechano-mediated phase of remodeling. While the linearized stiffness across TEVG evolution was preserved qualitatively in these parametric studies, preferred combinations of porosity and normalized fiber diameter could be identified by attempting to minimize the dramatic swings in linearized stiffness and comparing plateau values of linearized stiffness to that of the native IVC in the filled circles (cf. Table 3).

Figure 4. Effect of fiber diameter ω* on Stiffness.

Values of circumferential (left) and axial (right) linearized stiffness, computed at in vivo values of circumferential and axial stretch, are contrasted between the simulated TEVGs (solid lines) and native inferior vena cava (solid symbols). The solid black line shows results for the experimental case of an initial normalized fiber diameter ω* = 1.4 and porosity ε = 80%; the solid grey lines show results for ω* ∈ [0.01,1.4], also for ε = 80%. The time course of changes in linearized stiffness was preserved across all parametric simulations, with early elevated values dominated by the mechanical properties of the polymeric scaffold (phase A), the subsequent decrease due to the polymer losing its load-bearing integrity (B), a late peak in stiffness due to a marked accumulation of ECM due to overlapping inflammatory- and mechano-medicated deposition (C), and final plateau due to mechano-mediated turnover in an unchanging state (D). Decreasing ω* (indicated by the direction of the dark arrow) indirectly decreased matrix production and subsequently resulted in a lower peak (C) and plateau (D) linearized stiffness. Note the possible vulnerable period (B) when the axial stiffness of the TEVG dropped below the native value.

Figure 5. Effect of porosity ε on Stiffness.

Values of circumferential (left) and axial (right) linearized stiffness, computed at in vivo values of circumferential and axial stretch, are contrasted between the simulated TEVGs (solid lines) and native inferior vena cava (solid symbols). The grey lines show results for initial scaffold porosity ε ∈ [60%, 95%] and a representative normalized fiber diameter ω* = 0.6. Decreasing the porosity (indicated by the direction of the dark arrow) increased the initial contribution of the scaffold (phase A) and indirectly decreased matrix production, thus resulting in a decreased peak (C) and plateau values (D) of linearized stiffness. Note, in particular, that ε ∈ [75%, 85%] decreased the overall variation in stiffness as the TEVG evolved, thus suggesting that a reduced range of scaffold properties should be explored experimentally.

The hypothesis-driven parametric studies investigated four potential means to minimize the excursions in linearized stiffness throughout TEVG evolution. First, decreasing the rate at which the polymer lost load-bearing integrity decreased the peak in linearized stiffness at early times (thus reducing the slope of the transition between the polymer-dominated and matrix-dominated mechanical properties) and it decreased the peak stiffness at the time of maximum accumulation of matrix (cf. Fig. 6, top row, phases B and C). Second, pre-stressing the polymer upon implantation increased the linearized stiffness (larger initial deformations for all constituents) at all times, thus negating any advantages of preserving a more consistent unloaded geometry throughout the simulation (data not shown). Third, increasing the degradation of collagen produced during the inflammatory response decreased the peak in linearized stiffness at the transition between the two production mechanisms (Fig. 6, middle row, phase C). This result suggested a possible advantage of encouraging degradation of the stiff, fibrillar collagen produced during the inflammatory period following substantial production of matrix from the mechano-mediated phase. Fourth, decreasing the stiffness of the collagen (representing a decrease in collagen cross-linking and type I collagen) drastically decreased the linearized stiffness values following polymer degradation (Fig. 6, bottom row, phases C and D).

Figure 6. Hypothesis-Driven Studies to Improve Evolving Linearized Stiffness.

Values of circumferential (left) and axial (right) linearized stiffness, computed at in vivo values of circumferential and axial stretch, are contrasted between the simulated TEVGs (lines) and native inferior vena cava (solid symbols). All simulations are for experimental scaffold parameters ε = 80% and ω* = 1.4, with the baseline case from Figures 2 and 3 indicated by the solid black curve for comparison. The top row shows potential effects of reducing the rate at which the polymer loses load-bearing integrity via ξ^p ∈ [0.01c^p, 0.3c^p], the middle row shows potential effects of decreasing the survival fraction of ECM constituents produced during the inflammatory period, and the bottom row shows a single case wherein all deposited matrix has the same mechanical properties of the native vein. Of particular note (top row), tuning the polymer degradation rate could result in a linearized stiffness that is more consistent throughout the evolution of the graft (i.e., less of a valley at B and less of a peak at C), albeit still at overall higher biaxial values than native. Indeed, only if all newly deposited matrix has properties identical to native can the graft evolve to become truly normal after the polymer degrades, though in all cases the polymer creates a “compliance mismatch” with the native host vessels early on.

5. Discussion

Given recent advances in techniques for fabricating scaffolds in vascular tissue engineering (e.g., electrospinning), there is a pressing need to understand better how the structure and material properties of the polymeric construct influence the biochemomechanical mechanisms that govern the development, maintenance, and remodeling of a neovessel. Towards this end, we proposed a new modeling approach to examine effects of six key scaffold parameters on the possible in vivo development of an interposition TEVG in the murine venous circulation. This model considered, for the first time, the influence of scaffold physical parameters on the foreign body response during the inflammatory period of neotissue development and subsequent matrix turnover (production and removal). The model was motivated by prior experimental data that revealed an important role of particular physical parameters in modulating the inflammatory response as well as a Buckingham Pi non-dimensional analysis and related theoretical results (cf. [22]). We conjectured that neotissue development (i.e., matrix production and removal) is driven largely by pore size, noting that pore size relates directly to porosity and polymer fiber diameter. We thus introduced new data-driven constitutive relations to predict matrix kinetics as a function of porosity and polymer fiber diameter as well as deviations in mechanical stress from a preferred state for each matrix constituent.

We previously used experimental data on monocyte/macrophage infiltration to motivate a phenomenological representation of the inflammatory response via a gamma distribution function [35]. We also estimated the value of an associated rate parameter that augmented mechano-mediated matrix production (in response to deviations from a preferred state of stress) via a brute force parametric study (i.e., a value of K_strs = 1, where the basal value for a healthy IVC was assumed to be $K_{\mathit{\text{strs}}}^{\mathit{\text{basal}}}=0.1$). This elevated rate parameter phenomenologically represented the potential paracrine influence of monocytes/macrophages (i.e., their production of cytokines, chemokines, and growth factors) on matrix-producing cells, which may augment production beyond the time of polymer degradation (note that elevation of this parameter, K_strs = 1, was essential to fit the 24 week experimental data in [35]). Building on this prior work, we conjectured that interactions between monocytes / macrophages and other cells types can be modeled phenomenologically as a function of r*, the normalized mean pore size, which yielded simulations that matched well the available macroscopic data. Additional experimental quantification will be needed, however, before more robust, cell-specific constitutive relations can be developed. This issue is of particular importance as recent studies indicate that physical properties of the scaffold may dictate macrophage phenotype [45,46], thus supporting our hypothesis that these properties influence the matrix kinetics and guide TEVG evolution.

We investigated a single criterion for success or failure. Simply put, failure can be defined as an inability to fulfill an intended purpose. Failure of TEVGs is thus often defined as (i) a high or low TEVG stiffness that leads to compliance mismatch and thus altered hemodynamics that induce unfavorable mechanobiological consequences (e.g., fibrosis), (ii) development of a stenosis via excessive local matrix accumulation, (iii) aneurysmal dilation, or (iv) frank rupture. Ultimately, one would like to solve each of these concerns and focus primarily on the following failure: (v) an inability to adapt to somatic growth or altered hemodynamics, particularly in TEVGs used in the pediatric population. Whereas prior attention has focused on more obvious or dramatic types of failure (e.g., the burst pressure, that is, the pressure at rupture, or suture retention strength), our focus was on compliance mismatch between the TEVG and adjacent native IVC. While all methods of failure must eventually be considered, given the lack of quantifiable data on failure criteria for the native murine IVC, we were unable to evaluate frank rupture. Clearly, there is a need for such data.

Simulated linearized stiffness was compared with the target value of linearized stiffness for healthy, normal murine IVCs (Figs. 4, 5, 6; native in filled circles). The predicted evolution of TEVG stiffness suggested that certain combinations of physical parameters may result in excessive stiffness and large compliance mismatches between the TEVG and adjacent vein. High values of stiffness may result in altered cell phenotype, which may increase the risk of chronic inflammation and fibrosis [47–50]. Large fluctuations in stiffness throughout TEVG evolution may also result in unstable or unpredictable cell phenotypes, which may impede one’s ability to evaluate or predict patient progress clinically. Hence, such combinations should be avoided to prevent potential unfavorable or unpredictable mechanobiological consequences. Results from our parametric study suggested several sets of physical parameters that may reduce deviations in linearized stiffness (Figs. 4 and 5), with overall compliance approaching that of the native IVC at 2 years. These parameter values should be considered in future experiments (cf. Table 3).

To further guide future experiments, we performed a series of hypothesis-driven parametric studies in an attempt to reduce the excursions in linearized stiffness throughout TEVG evolution. These studies suggested that it may be advantageous to alter the rate at which the polymer loses load-bearing integrity and/or to decrease the half-life of the matrix that is deposited during the inflammatory phase. Following the loss of load-bearing integrity by the polymeric construct, the unloaded configuration will be dictated solely by the deposited matrix constituents (and configurations at which these constituents were deposited at time τ). Both our simulations and prior experimental data (cf. Figure 6A in [5]) suggest an abrupt change in in vivo stretches (driven by a change in the unloaded geometry following loss of polymer integrity) between 2 and 6 weeks, which would contribute to the fluctuations in linearized stiffness during phases B and C in Fig. 6 (top row). Hence, increasing the degradation of residual matrix produced during the inflammatory period could lower the peak linearized stiffness at phase C in Fig. 6 (middle row).

Decreasing the stiffness of the collagen produced via both mechanisms also reduced the linearized stiffness throughout TEVG evolution, particularly following the loss of load-bearing integrity by the scaffold (Fig. 6, bottom row). While the stiffness values from this simulation were the closest to that of the native IVC (filled circles), tension-stretch and pressure-diameter relationships (not shown) suggested that collagen and passive smooth muscle alone (at native IVC material parameter values) were much more distensible and extensible than native IVC. Hence, until we as a community discover how to promote in TEVGs elastic fibers and contractile smooth muscle cells comparable to native IVC, we must remember that producing near native collagen (and passive smooth muscle) in the absence of other constituents need not result in a native neovessel. It may thus be necessary at present to appropriately compensate for the lack of functional elastin and contractile smooth muscle cells. Of course, there is also considerable motivation to determine if collagen type, crosslink density, prestretch, alignment, and so forth are influenced by cell phenotype and if this could be controlled.

Despite the encouraging results presented herein, there remains a pressing need for significantly more longitudinal data to inform, validate, and extend the model. For example, we focused on but six of the many parameters that affect neovessel formation (cf. Table 1); more data will allow the effects of more parameters to be studied computationally, as, for example, those due to transmural differences in polymer fiber alignment. Indeed, more data will be needed to increase the basic sophistication of the model. Albeit structurally motivated, the present model is yet phenomenological, with many parameter values determined by fitting macroscopic data. Such phenomenology allows one to compensate for a lack of information (e.g., on actual evolving hydration or cross-links), but more information would clearly enable more robust predictions. Given that continuing advances in fabrication techniques, such as electrospinning, will allow more and more control of the scaffold design, including functionality grading, the computational models must keep pace with manufacturing advances. We also note that we considered a simple case characterized by material homogeneity. There is also a need to model heterogeneously distributed properties and responses (cf. [51]), but fortunately this is simply an issue of numerics in solving more complex initial – boundary value problems because the constitutive framework is defined point-wise and can easily address spatial and temporal heterogeneity. Failure, whether by stenosis, aneurysmal dilatation, or frank rupture, is often local, hence this aspect must be considered carefully in design and quality control. Finally, even with considerably more data, there will be a need to incorporate uncertainty analysis within any predictions that seek to define specific design parameters for new scaffolds for there is uncertainty in all experimental measurements and clear biological variations, even within mouse colonies. It is fortunate that such analyses can be included within our models non-intrusively (cf. [52]).

In summary, we introduced a melding of non-dimensional analysis and computational modeling to evaluate fibrous scaffold parameters for experimental consideration in interposition TEVGs implanted within the murine venous circulation. We showed that this framework suggests sets of key scaffold parameters that may reduce compliance mismatch with the adjacent IVC. This study also illuminated gaps in our current understanding of TEVG evolution, hence it is hoped that computational modeling will continue to mature and guide the experimentation that is needed to generate the data that can be used to take us ever closer to the rational design of TEVGs via scaffold optimization, whether having a fibrous or foam-type microstructure.

Appendix A. Different scales for Buckingham Pi analysis

Table A1.

	Choice of scales:Ls = ω$T_s=1/k_q^p,M_s=\rho {\omega }^3$
Parameter	Symbol	SI Units	General Units (MLT)	π Gropus
Degradation rate	$k_q^p$	days−1	M0L0T−1	1
Porosity	ε	$\frac{\mathrm{g}/{\text{cm}}^3}{\mathrm{g}/{\text{cm}}^3}$	M0L0T0	ε
Modulus	cp	MPa	M1L−1T−2	$c^p/(\rho {\omega }^2{(k_q^p)}^2)$
Size fiber diameter	ω	cm	M0L1T0	1
Pore size	r	cm	M0L1T0	r/ω
Alignment	ϕk		M0L0T0	ϕk
	Inflammatory Response, $y=\mathrm{y̌}(\epsilon ,c^p/(\rho {\omega }^2{(k_q^p)}^2),r/\omega ,{\varphi }^k)$

Table A2.

	Choice of scales: Ls = r, $T_s=1/k_q^p,M_s=c^{p}r/k_q^{p2}$
Parameter	Symbol	SI Units	General Units (MLT)	π Gropus
Degradation rate	$k_q^p$	days−1	M0L0T−1	1
Porosity	ε	$\frac{\mathrm{g}/{\text{cm}}^3}{\mathrm{g}/{\text{cm}}^3}$	M0L0T0	ε
Modulus	cp	MPa	M1L−1T−2	1
Size fiber diameter	ω	cm	M0L1T0	ω/r
Pore size	r	cm	M0L1T0	1
Alignment	ϕk		M0L0T0	ϕk
	Inflammatory Response, y = y̌(ε, ω/r, ϕk)