Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Dec 5;4:7328. doi: 10.1038/srep07328

Anisotropic giant magnetoresistance in NbSb2

Kefeng Wang 1,a,*, D Graf 2, Lijun Li 1,†, Limin Wang 1, C Petrovic 1,b
PMCID: PMC4256591  PMID: 25476239

Abstract

The magnetic field response of the transport properties of novel materials and then the large magnetoresistance effects are of broad importance in both science and application. We report large transverse magnetoreistance (the magnetoresistant ratio ~ 1.3 × 105% in 2 K and 9 T field, and 4.3 × 106% in 0.4 K and 32 T field, without saturation) and field-induced metal-semiconductor-like transition, in NbSb2 single crystal. Magnetoresistance is significantly suppressed but the metal-semiconductor-like transition persists when the current is along the ac-plane. The sign reversal of the Hall resistivity and Seebeck coefficient in the field, plus the electronic structure reveal the coexistence of a small number of holes with very high mobility and a large number of electrons with low mobility. The large MR is attributed to the change of the Fermi surface induced by the magnetic field which is related to the Dirac-like point, in addition to orbital MR expected for high mobility metals.

The magnetic field response of the transport properties of condensed matter, especially the magnetoresistance (MR) (such as the giant magnetoresistance in magnetic multilayers and colossal magnetoresistance in manganites)1,2, gives information about the characteristics of the Fermi surface3 and provides promising candidates for magnetic memory or other spin-tronic devices4. Correspondingly the exploratory search for the new materials exhibiting extraordinary response to the magnetic field (such as the large MR) keeps being a central topic of the condensed matter physics and material science. Unlike the magnetic mechanism of the MR in manganites and mangetic multilayers, the large positive magnetoresistance was discovered in some nomagnetic metals (such as Ag2−δTe/Se5,6, topological insulator Bi2Te37,8,9, semimetal Bi10, graphite11,12,13 and Cd3As214,15,16, as well as (Sr/Ca)MnBi217,18). These large MR effects are in contrast to the normal MR in simple metals which is usually very small because semiclassical transport gives quadratic field-dependent MR in the low field range which would saturate in the high field3. Some MR (Ag2−δTe/Se and topological insulator Bi2Te3) were related to the Dirac fermions with linear energy dispersion in the quantum limit19, while some (such as Bi) were related to the Fermi surface (FS) compensation of the semimetals.

Besides the change in the value of resistivity, the magnetic field could also induce the change in the temperature-dependent behavior of the resistivity, and then induce the nometallic behavior. The transition or crossover usually is accompanied by the extremely large MR. A typical example is the magnetic field induced melting of the charge-ordered state and correspondingly colossal magnetoresistance in manganite2,20. Recently, the metal-semiconductor crossover induced by magnetic field was observed in several nomagnetic metals/oxides such as PtSn421, PdCoO222, WTe223 and semimetal graphite11,12,13 and Bi10. This was accompanied by the extremely large magnetoresistant effect where the magnetoresistant ratio MR = (ρ(H) − ρ(0))/ρ(0) approaches ~105% at low temperature. These extraordinary metal-semiconductor crossover and extremely large MR effects induces the revival of the study on the magnetic field response of the transport behavior and the detailed mechanism remains unclear. Since PdCoO2 and WTe2 has layered structure and the large MR is related to the quasi-two-dimensional (quasi-2D)FS22,23, it is important to explore new materials that crystallize in different crystal structure but host similar phenomena. New materials and mechanisms of large MR are of high interest.

Here we report the extremely large MR and the possible magnetic field induced semiconducting gap in NbSb2 single crystal. Transverse MR approaches 1.3 × 105% in 2 K and 9 T, and 4.3 × 106% in 0.4 K and 32 T field without saturation, with electric current parallel to the b-axis. The large MR is significantly suppressed but the metal-semiconductor-like transition persists when the current is along the ac-plane. The first-principle electronic structure calculation and quantum oscillations reveal two types of carrier pockets. Their distinct density and mobility induces the sign reversal of the Hall resistivity. The large MR effects are attributed to the change of the Fermi pocket with high mobility induced by magnetic field, in addition to orbital MR expected for high mobility metals.

Results

Crystal structure and giant magnetoresistance

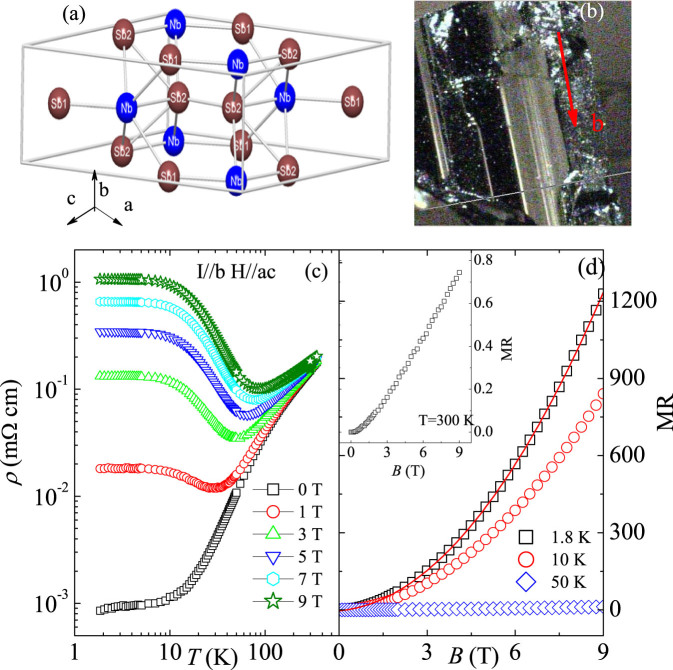
NbSb2 single crystals grew from high-temperature self flux method and crystallize in a complex monoclinic structure (Fig. 1(a)) with C12/m1 space group with the refined lattice parameters are a = 10.233(1)Å, b = 3.630(1)Å, c = 8.3285(2)Å, β = 120.04(2)° (see Supplementary Figure 1). The b-axis is perpendicular to the ac-plane (Fig. 1(a)). The image of a typical single crystal of NbSb2 is shown in Fig. 1(b). It was found that the crystal grows along the b-axis more quickly and the red arrow in Fig. 1(b) shows the b-axis. The temperature dependent resistivity in different magnetic field of NbSb2 with the current parallel to the b-axis and the magnetic field perpendicular to the current (parallel to the ac-plane) is shown in Fig. 1(c). The crystal shows metallic behavior and the residual resistivity ratio (ρ300K/ρ2K) in zero field is about 450 (with current along the b-axis) which suggests high sample quality since the defects (such as grain boundaries and impurities) contribute to the residual resistivity ρ0 in the metal.

Figure 1. Crystal structure and giant magnetoresistance of NbSb2.

Figure 1

Open in a new tab

(a) Crystal structure of NbSb2. The angle β is between the a and c axis. (b) A typical crystal of NbSb2. The long axis of the crystal is b-axis. (c) The temperature dependence of the resistivity in magnetic fields with the current parallel to b-axis and the magnetic field perpendicular to the current (parallel to the ac-plane). (d) The magnetic field dependence of the magnetoresistant ratio defined as MR = (R(H) − R(0))/R(0), with same configuration as in (a). The red line is the fitting result using quadratic field dependence.

The external magnetic field significantly enhances the low-temperature resistivity and also changes its temperature-dependence. The ρ(T) is metallic in 1 T [Fig. 1(c)] but the slope increases with temperature decrease from 300 K. At about 300 K the ρ(T) shows a minimum and then increases with further decrease in temperature, which is similar to the metal-semiconductor crossover induced by external field observed in PtSn4, PdCoO2 and WTe222,23. The resistivity nearly saturates below 10 K and its value increases from 0.009 mΩ cm in zero field to 0.02 mΩ cm in 1 T field. Higher field induces higher metal-semiconductor crossover temperature and larger MR. In 9 T field, the MR ratio approaches ~1.3 × 105% in 2 K (as shown in Fig. 1(d)) and the metal-semiconductor crossover temperature is about 70 K. The magnetic field dependence of the MR (as shown in Fig. 1(d)) can be described very well by the parabolic behavior (the red line is the fitting result using MR = aB2). With increasing temperature, MR is suppressed significantly but the ratio is still around 80% at 300 K [Fig. 1(d) inset]. Magnetotransport in semiclassical single-band metals scales as MR = f(Hτ) = F(H/ρ0) with the assumption of the single scattering time τ, i.e. 1/τ(T) ∝ ρ0(T)24. MR of NbSb2 in high field shows 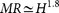Inline graphic but deviates somewhat from Kohler scaling at low temperatures (Fig. 2(a)). The low field MR (inset of Fig. 2(a)) does not follow H1.8 dependence but overall satisfies the scaling. The MR and metal-semiconductor-like transition is observed in several crystals from different batches, showing very good repeatability (See Supplementary Figure 2).

Figure 2. The anisotropic giant magnetoresistance of NbSb2.

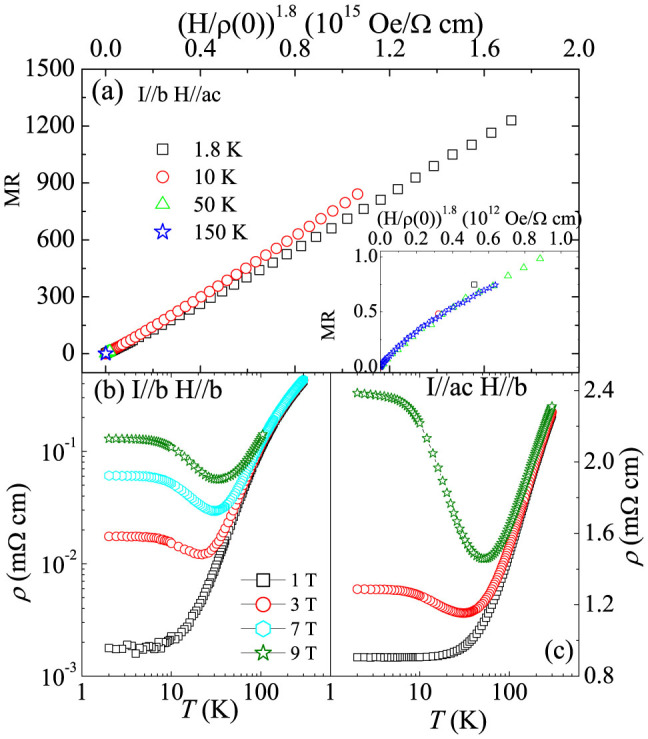
Figure 2

Open in a new tab

(a) A Kohler plot using 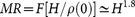Inline graphic for NbSb2 with the current parallel to the b-axis and the magnetic field perpendicular to the current. Inset shows low field part enlarged for clarity. (b) The ρ(T) with the current parallel to b-axis and the magnetic field parallel to the current (parallel to the b-axis. (c) The ρ(T) with the current parallel to ac-plane and the magnetic field perpendicular to the current (parallel to the b-axis.

The ρ(T) and MR of NbSb2 is significantly dependent on the electric current and magnetic field direction. When the electric current is still along the b-axis but the magnetic field is parallel to the current, the MR ratio is suppressed and is around 104% in 9 T field and 2 K, as shown in Fig. 2(b). The anisotropic ratio (δ = ρ(B//b)/ρ(B//ac)) is around 20 in 2 K and 9 T field, which is significantly larger than the value of both ordinary nomagnetic and magnetic metals (the ratio is around 1% for alkali metals and 3% for magnetic metals)3,25. The resistivity along ac-plane (Fig. 2(c)) is three orders of magnitude higher than the resistivity along b-axis. With the electric current along ac-plane and the field perpendicular to the current (parallel to b-axis) the MR ratio is suppressed and is only 300% in the same temperature and field (Fig. 2(c)). However, the metal-semiconductor crossover is preserved and the crossover temperature is nearly the same in same magnetic field, in all configurations.

Electronic structure from quantum oscillation and first-principles calculation

In monoclinic phase of NbSb2, the bond length of Nb-Nb is about 3.6Å along the b-axis and is about 5.4Å and 4.9Å along the a and c axis respectively. This indicates that NbSb2 is formed by quasi-one-dimensional Nb chains along the b direction (Fig. 1(a) and Ref. 41). Fig. 3(a) and (b) shows the results of the Shubnikov-de Haas (SdH) oscillation for NbSb2 crystals where the current is along b-axis but the field direction changes between parallel to the ac-plane (perpendicular to b-axis, θ = 0°) and perpendicular to ac-plane (θ = 90°). The MR of NbSb2 shows clear oscillations above 8 T field (inset in Fig. 3(a)), and the oscillation is very clear in the whole angle range implying dominant 3D FS. The MR does not saturate even in 35 T field. Instead it shows the quantum oscillations where MR approaches 4.3 × 106% in 0.4 K and 32 T field [Fig. 3(a) inset]. The fast Fourier transformation (FFT) spectrum of oscillation (Fig. 3(a)) shows two major peaks at 227 T and 483 T oscillation frequency. In metal or semiconductor, the SdH oscillations correspond to successive emptying of Landau levels and the corresponding periodic singularity in the density of states as the magnetic field is increased. In quantum oscillation, the period or the frequency, when plotted against 1/B (B is the magnetic field), is inversely proportional to the area S of the extremal orbit of the Fermi surface, in the direction of the applied field. For a general system, the oscillatory part of the magnetoresistance (described as magnetoconductivity Δσ) is given by

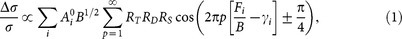graphic file with name srep07328-m1.jpg

where the frequency Fi of the quantum oscillation is proportional to the extremal area Ai of the i-th Fermi pocket in the direction of the magnetic field and can be described as 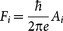Inline graphic. The two oscillation frequencies (two peaks in the FFT spectrum, Fig. 3(a)) observed in NbSb2 clearly indicate the existence of two Fermi pockets which are of different size. Besides, the temperature dependence of the oscillation amplitude is given by the thermal factor RT in the above equation and is described by the Lifshitz-Kosevitch formula

graphic file with name srep07328-m2.jpg

The temperature dependence of the oscillation amplitude (Fig. 3(b)) can be fitted well by the Lifshitz-Kosevitch formula26, which gives the effective cyclotron resonant mass m* = 0.68me and 1.69me (me is the mass of bare electron) for 227 T and 483 T Fermi pockets respectively.

Figure 3. Quantum Oscillation and Hall resistivity of NbSb2.

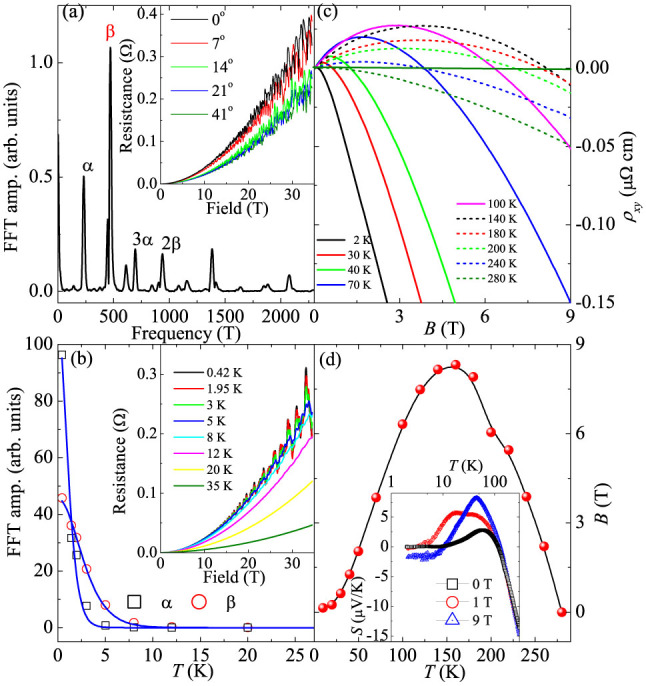
Figure 3

Open in a new tab

(a) The FFT spectrum of the quantum oscillation of NbSb2 crystal. The inset shows the typical SdH oscillation of NbSb2 in 0.42 K with magnetic field up to 32 T. The current is parallel to b-axis and the magnetic field direction changes between perpendicular to the current (parallel to the ac-plane 0 degree) and perpendicular to ac-plane (90 degree). (b) The temperature dependence of the quantum oscillation amplitude for two oscillation frequencies. The blue lines are the fit results which give the effective mass. The inset shows the magnetic field dependence of the oscillation at different temperatures. (c) The magnetic field dependence of the Hall resistivity ρxy at different temperatures. (d) Sign change of Hall coefficient at different temperatures and magnetic fields. The inset shows the temperature dependence of the Seebeck coefficient S with different magnetic field.

The Hall resistivity confirms the multiband characteristic of NbSb2. Fig. 3(c) shows the ρxy(B) in different temperatures with the current parallel to b-axis and the magnetic field perpendicular to the current. At 2 K, ρxy is initially positive below 1 T but changes to negative in higher fields. With increasing temperature, the field where ρxy changes the sign increases but achieves the maximum (8.5 T) in ~150 K. Further increase in the temperature above 150 K induces the decrease of the sign reversal field (Fig. 3(d)). The curvature and sign reversal of the Hall resistivity clearly indicates the coexistence of two types of carriers in NbSb2. This is in agreement with the sign change in Seebeck coefficient in (T,B) (inset in Fig. 3(d)) and with the electronic structure from the first-principles calculation (Fig. 4) which also shows hole and electron pockets. The density of states (DOS) (Fig. 4(a)) reveals that the Fermi level of NbSb2 locates at the valley of the DOS. This is confirmed by the band structure (Fig. 4(b)). In the band structure (Fig. 4(b)), there are two Dirac-like points across the Fermi level, along the M − H and Γ − Z line respectively. The Fermi level (EF) is located in the valley of these two bands, so both contribute somewhat to the density of state at the Fermi level. This is consistent with the nearly vanishing density of states near EF and the states at the Fermi level are dominated by Nb contribution. The FS of NbSb2 consists of electron pocket and hole pocket with different size (Fig. 4(c)), which is consistent with the two oscillation frequencies (two peaks in Fig. 3(a)). Even though most of the pockets are three-dimensional, there is an electron pocket which is anisotropic at the center of the Brillouin zone and it should dominate the anisotropic magnetoresistance in NbSb2.

Figure 4. First-principle electronic structure of NbSb2.

Figure 4

Open in a new tab

(a) The total density of states (DOS), as well as the contribution to DOS from different atoms (Nb, Sb1 and Sb2), (b) the band structure and (c) the Fermi surfaces of NbSb2 crystals from first-principle calculation. The spin-orbit coupling was taking into account in process. For clarity the orientation of the hole pockets (the upper panel in (c)) is rotated in comparison to the electron pockets (the lower panel in (c)). The red rectangle in (b) indicates the area where the conduction band touches the valence band at the Fermi level. The binding energy for FS is 0.6482 eV.

Discussion

Presently there are several possible mechanisms for large unsaturated MR in nomagnetic metals. One is related to the Dirac fermions with linear energy dispersion and possibly originates from the quantum limit7,8,9,19. The quantum limit of Dirac fermions gives linear MR19 which is distinct from the quadratic MR in semiclassical MR3. However, MR of NbSb2 shows parabolic field-dependence. This implies the quantum limit should not dominate the transport. The low-field-induced increase in ρ(T) in graphite may be caused by excitonic insulator transition of the Dirac fermions13 or by the FS compensation (equal numbers of electrons and holes) similar to Bi and PtSn410,12,21.

The diamagnetic behavior of NbSb2 crystal (see Supplementary Figure 3) excludes that the curvature in Hall resistivity is induced by the anomalous Hall effect. The semiclassical expression for the Hall coefficient including both electron and hole type carriers gives Inline graphic, when μ0H → 0, and Inline graphic when μ0H → ∞, where e is the electron charge, ne(h) and μe(h) represent the carrier concentrations and mobilities of the electrons (holes)3. Once there are two carrier types present, the field dependence of ρxy(H) will become nonlinear. However, the sign change of the Hall resistivity in field only occurs when the two kinds of carriers have distinct mobility and density, as observed in Rh27. The holes with higher mobility and small effective mass dominate and induce the positive Hall resistivity in low field. In order to achieve the sign reversal of Hall resistivity in high field, the number of high mobility carriers (holes) should be much smaller than the number of low-mobility carriers (electrons).

The electronic structure results in Fig. 4(c) reveals distinct volumes of the electron and hole pockets. This is also confirmed by two distinct oscillation frequencies in SdH oscillation (Fig. 3(a)). These observations, taken together with Hall resistivity, imply the inadequacy of FS compensation picture in NbSb2. Furthermore, graphite shows a convex MR behavior in low fields and reentrant metallic behavior in high field, also distinct from our results. The crystalline and electronic structure of NbSb2 also discriminates it from quasi-2D PdCoO222 and WTe223.

It was proposed that the magnetic field will induce the breaking of the time reversal invariance and will rearrange the Dirac FS in a Dirac semimetal28,29,30,31. This plus the high mobility of the Dirac carriers could induce very large MR, and is believed to be responsible for the effect observed in Cd3As214,32,33,34. The electronic structure of NbSb2 indeed hosts features similar to a Dirac semimetal. The hole pocket in NbSb2 has very high mobility in comparison to the electron pockets and the effective mass of carriers is very small, as revealed by the quantum oscillation and Hall resistivity. The DOS at the Fermi level is very small (Fig. 4(a)), and the conduction band nearly touches the valence band at both two points at the Fermi level in the band structure whereas the spin-orbit coupling opens a very small gap (Fig. 4(b)). The magnetic field could rearrange the FS so that FS either splits into two disjoint Weyl pockets or two concentric spheres14,29. If the Fermi level locates between the two disjoint Weyl pockets, the system will change to a semiconductor, contributing to MR.

In a multiband metal with diffusion mechanism and electron/hole-type carriers, Seebeck coefficient is given by

graphic file with name srep07328-m3.jpg

Where σe(h) and Se(h) are the contributions of electrons (holes) to the electric conductivity and Seebeck coefficient, respectively. The Seebeck coefficient from electrons and hole in magnetic field follows same diffusion equation and is given by the Mott relationship,

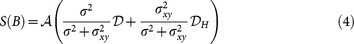graphic file with name srep07328-m4.jpg
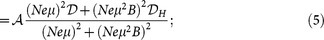graphic file with name srep07328-m5.jpg

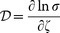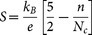where Inline graphic, Inline graphic and Inline graphic (ζ is the chemical potential)35,36,37. The Seebeck coefficient is very sensitive to the change of the Fermi surface and was used to probe the Fermi surface reconstruction in cuprate and other superconductors38,39. In a metal S → 0 as T → 0. This is indeed observed for Seebeck coefficient of NbSb2 in zero field (Fig. 3(d) inset). In contrast, the Seebeck coefficient in 9 T field shows a nearly constant value ~ 2 μV/K below 10 K. The nonzero Seebeck coefficient as T → 0 can be observed in a semi-conductor, where Seebeck coefficient Inline graphic with the conduction band carrier density n from impurity/doping and the intrinsic carrier density Nc35,36. So although the multiband carriers will influence the temperature-dependent behavior of the Seebeck coefficient of the metal, when temperature approaches zero, the total Seebeck coefficient of multiband metal should still tend to be zero since both Se and Sh are proportional to temperature. This suggests that the gap may open in NbSb2 in the magnetic field for both two Dirac-like points. Whereas our observations are fully consistent with this picture, the response of the FS of NbSb2 to magnetic field deserves further study.

In summary, large magnetoresistance and the magnetic field induced semiconducting gap are observed in NbSb2 single crystal. Transverse MR approaches 1.3 × 105% in 2 K and 9 T, and 4.3 × 106% in 0.4 K and 32 T field without saturation, with electric current parallel to the b-axis. The large MR is significantly suppressed when the current is along the ac-plane. The Hall resistivity and the first-principle electronic structure calculation indicate the coexistence of a small number of holes with very high mobility and a large number of electrons with small mobility. The observed effects are consistent with the rearrangement of the Fermi pocket with high mobility induced by magnetic field.

Methods

Single crystals of NbSb2 used in this study were grown using a high-temperature self-flux method40,41. Nb (99.99%) and excess Sb (99.99%) with ratio Nb:Sb = 1:19 were sealed in a quartz tube, heated to 1100°C and slowly cooled to 650°C where the crystals were decanted. X-ray diffraction (XRD) data were taken with Cu Kα (λ = 0.15418 nm) radiation of Rigaku Miniflex powder diffractometer at the room temperature. Electrical transport measurements up to 9 T were conducted on polished samples in Quantum Design PPMS-9 with conventional four-wire method. High field MR and SdH oscillation up to 35 T were measured at National High Magnetic Field Laboratory in Tallahassee. Thermal transport properties were measured in Quantum Design PPMS-9 from 2 K to 350 K using one-heater-two-thermometer method. The direction of heat and electric current transport was along the ab-plane of single grain crystals with magnetic field along the c-axis and perpendicular to the heat/electrical current. The relative error in our measurement was Inline graphic and Inline graphic based on Ni standard measured under identical conditions. Fist principle electronic structure calculation were performed using experimental lattice parameters within the full-potential linearized augmented plane wave (LAPW) method42 implemented in WIEN2k package43. The general gradient approximation (GGA) of Perdew et al.44, was used for exchange-correlation potential. The LAPW sphere radius were set to 2.5 Bohr for all atoms. The converged basis corresponding to Rminkmax = 7 with additional local orbital were used where Rmin is the minimum LAPW sphere radius and kmax is the plane wave cutoff.

Author Contributions

K.W. and C.P. grew the single crystal and planned the experiment. D.G. and L.L. performed the experiment in National High Magnetic Field Laboratory. K.W. and L.W. performed the electronic structure calculation. K.W., D.G. and C.P. analysed the data and wrote the manuscript. All authors contributed to editing the manuscript.

Supplementary Material

Supplementary Information

Supplementary Materials

srep07328-s1.pdf (206.6KB, pdf)

Acknowledgments

We thank John Warren for help with SEM measurements. Work at Brookhaven is supported by the U.S. DOE under contract No. DE-AC02-98CH10886 (K.W., L.L., L.W. and C.P.). Work at the National High Magnetic Field Laboratory is supported by the DOE NNSA DE-FG52-10NA29659 (D. G.), by the NSF Cooperative Agreement No. DMR-0654118 and by the state of Florida.

References

  1. Baibichet M. et al. Giant Magnetoresistance of (001)Fe/(001)Cr Magnetic Superlattices. Phys. Rev. Lett. 61, 2472 (1988). [DOI] [PubMed] [Google Scholar]
  2. Salamon M. B. & Jaime M. The physics of manganites: Structure and transport. Rev. Mod. Phys. 73, 583 (2001). [Google Scholar]
  3. Pippard A. B. Magnetoresistance in Metals (Cambridge University, Cambridge, 1989). [Google Scholar]
  4. Wolf S. A. et al. Spintronics: A Spin-Based Electronics Vision for the Future. Science 294, 1488 (2001). [DOI] [PubMed] [Google Scholar]
  5. Xu R. et al. Large magnetoresistance in non-magnetic silver chalcogenides. Nature 390, 57 (1997). [Google Scholar]
  6. Lee M., Rosenbaum T. F., Saboungi M. L. & Schnyders H. S. Band-Gap Tuning and Linear Magnetoresistance in the Silver Chalcogenides. Phys. Rev. Lett. 88, 066602 (2002). [DOI] [PubMed] [Google Scholar]
  7. Qu D. X. et al. Quantum Oscillations and Hall Anomaly of Surface States in the Topological Insulator Bi2Te3. Science 329, 821 (2010). [DOI] [PubMed] [Google Scholar]
  8. Analytis J. G. et al. Two-dimensional surface state in the quantum limit of a topological insulator. Nature Phys. 6, 960 (2010). [Google Scholar]
  9. Wang X., Du Y., Dou S. & Zhang C. Room Temperature Giant and Linear Magnetoresistance in Topological Insulator Bi2Te3 Nanosheets. Phys. Rev. Lett. 108, 266806 (2012). [DOI] [PubMed] [Google Scholar]
  10. Yang F. Y. et al. Large Magnetoresistance of Electrodeposited Single-Crystal Bismuth Thin Films. Science 284, 1335 (1999). [DOI] [PubMed] [Google Scholar]
  11. Kopelevich Y., Lemanov V. V., Moehlecke S. & Torres J. Landau Level Quantization and Possible Superconducting Instabilities in Highly Oriented Pyrolitic Graphite. Phys. Solid State 41, 1959 (1999). [Google Scholar]
  12. Du X., Tsaim S. W., Maslov D. L. & Hebard A. F. Metal-Insulator-Like Behavior in Semimetallic Bismuth and Graphite. Phys. Rev. Lett. 94, 166601 (2005). [DOI] [PubMed] [Google Scholar]
  13. Kopelevich Y. et al. Reentrant Metallic Behavior of Graphite in the Quantum Limit. Phys. Rev. Lett. 90, 156402 (2001). [DOI] [PubMed] [Google Scholar]
  14. Liang T. et al. Ultrahigh mobility and giant magnetoresistance in Cd3As2: protection from backscattering in a Dirac semimetal. arXiv:1404.7794v1.
  15. Feng J. et al. Large linear magnetoresistance in Dirac semi-metal Cd3As2 with Fermi surfaces close to the Dirac points. arXiv:1405.6611.
  16. He L. P. et al. Quantum transport evidence for a three-dimensional Dirac semimetal phase in Cd3As2. arXiv:1404.2557. [DOI] [PubMed]
  17. Park J. et al. Anisotropic Dirac Fermions in a Bi Square Net of SrMnBi2. Phys. Rev. Lett. 107, 126402 (2011). [DOI] [PubMed] [Google Scholar]
  18. Wang K. et al. Quantum transport of two-dimensional Dirac fermions in SrMnBi2. Phys. Rev. B 84, 220401(R) (2011). [Google Scholar]
  19. Abrikosov A. A. Quantum magnetoresistance. Phys. Rev. B 58, 2788 (1998). [Google Scholar]
  20. Imada M., Fujimori A. & Tokura Y. Metal-insulator transition. Rev. Mod. Phys. 70, 1039 (1998). [Google Scholar]
  21. Mun E. et al. Magnetic field effects on transport properties of PtSn4. Phys. Rev. B 85, 035135 (2012). [Google Scholar]
  22. Takatsu H. et al. Extremely Large Magnetoresistance in the Nonmagnetic Metal PdCoO2. Phys. Rev. Lett. 111, 056601 (2013). [DOI] [PubMed] [Google Scholar]
  23. Ali M. N. et al. Titanic Magnetoresistance in WTe2. Nature 514, 205 (2014). [DOI] [PubMed] [Google Scholar]
  24. Olsen J. L. Electron Transport in Metals (Interscience, New York, 1962). [Google Scholar]
  25. Campbell I. A. & Fert A. in Ferromagnetic Materials, edited by Wohlfarth, E. P. (North-Holland, Amsterdam, 1982). [Google Scholar]
  26. Shoeneberg D. Magnetic oscillation in metals (Cambridge University Press, Cambridge, 1984). [Google Scholar]
  27. Coles B. P. & Taylor J. C. Sign reversal of the hall effect in rhodium. J. Phys. Chem. Solids 1, 270 (1957). [Google Scholar]
  28. Young S. M. et al. Dirac Semimetal in Three Dimensions. Phys. Rev. Lett. 108, 140405 (2012). [DOI] [PubMed] [Google Scholar]
  29. Wang Z. J. et al. Dirac semimetal and topological phase transitions in A3Bi (A = Na, K, Rb). Phys. Rev. B 85, 195320 (2012). [Google Scholar]
  30. Burkov A. A., Hook M. D. & Balents L. Topological nodal semimetals. Phys. Rev. B 84, 235126 (2011). [Google Scholar]
  31. Liu Z. K. et al. Discovery of a Three-Dimensional Topological Dirac Semimetal, Na3Bi. Science 343, 864 (2014). [DOI] [PubMed] [Google Scholar]
  32. Borisenko S. et al. Experimental Realization of a Three-Dimensional Dirac Semimetal. arXiv:1309.7978 (2013). [DOI] [PubMed]
  33. Xu S. Y. et al. Observation of a bulk 3D Dirac multiplet, Lifshitz transition, and nestled spin states in Na3Bi. arXiv:1312.7624 (2013).
  34. Wang Z. J. et al. Three-dimensional Dirac semimetal and quantum transport in Cd3As2. Phys. Rev. B 88, 125427 (2013). [Google Scholar]
  35. Barnard R. D. Thermoelectricity in Metas and Alloys (Taylor & Francis, London, 1972). [Google Scholar]
  36. Ziman J. M. Electrons and Phonons page 500 (Oxford Clarendon Press, Oxford, 1960). [Google Scholar]
  37. Liang T. et al. Evidence for massive bulk Dirac fermions in Pb1?xSnxSe from Nernst and thermopower experiments. Nat. Commun. 4, 2696 (2013). [DOI] [PubMed] [Google Scholar]
  38. Laliberte F. et al. Fermi-surface reconstruction by stripe order in cuprate superconductors. Nat. Commun. 2, 432 (2011) [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Doiron-Leyraud N. Hall, Seebeck, and Nernst Coefficients of Underdoped HgBa2CuO4+δ: Fermi-Surface Reconstruction in an Archetypal Cuprate Superconductor. Phys. Rev. X 3, 021019 (2013). [Google Scholar]
  40. Canfield P. C. & Fisk Z. Growth of single crystals from metallic fluxes. Phil. Mag. B 65, 1117 (1992). [Google Scholar]
  41. Lomnytska Y. F. & Kuzma Y. B. The NbCSb system. J. Alloys Compd. 413, 114 (2006). [Google Scholar]
  42. Weinert M., Wimmer E. & Freeman A. J. Total-energy all-electron density functional method for bulk solids and surfaces. Phys. Rev. B 26, 4571 (1982). [Google Scholar]
  43. Blaha P., Schwarz K., Madsen G. K. H., Kvasnicka D. & Luitz J. WIEN2k, An Augmented Plane Wave + Local Orbitals Program for Calculating Crystal Properties. (Karlheinz Schwarz, Techn. Universitat Wien, Austria), 2001. ISBN 3-9501031-1-2.
  44. Perdew J. P., Burke K. & Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 77, 3865 (1996). [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Materials

srep07328-s1.pdf (206.6KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES