Biased Estimates of Diminishing-Returns Epistasis? Empirical Evidence Revisited

Abstract

Empirical evidence for diminishing fitness returns of beneficial mutations supports Fisher’s geometric model. We show that a similar pattern emerges through the phenomenon of regression to the mean and that few studies correct for it. Although biases are often small, regression to the mean has overemphasized diminishing returns and will hamper cross-study comparisons unless corrected for.

The Problem

EPISTASIS, i.e., the interactive (nonadditive) effect of coexpressed mutations, is widespread (e.g., Weinreich et al. 2006; Flint and Mackay 2009; Huang et al. 2012; Corbett-Detig et al. 2013) and plays a fundamental role in genetic theories of sex and recombination, mutation load, genetic robustness, response to selection, and speciation (Whitlock et al. 1995; Phillips et al. 2000; De Visser et al. 2011; Olson-Manning et al. 2012; Hansen 2013).

A number of recent studies have attempted to demonstrate that as mutations become increasingly beneficial, they are more likely to show negative epistasis for fitness when combined (supporting information, Table S1). The demonstration of such diminishing fitness returns has bearing on evolutionary theory by providing a mechanistic basis for decelerating rates of adaptation, as predicted from Fisher’s geometric model (FGM) (Martin et al. 2007; Chou et al. 2011; Khan et al. 2011; Draghi and Plotkin 2013; Szendro et al. 2013).

Diminishing-returns epistasis has commonly been inferred from a negative correlation between the additive fitness effects of a pair (or set) of mutations and their epistatic effect in interaction with each other (Table S1). To this end, the relative fitness of mutation i (w_i) is typically measured as

$$w_i=\log \left(\frac{{\mathit{w}}_{\text{abs,}i}}{{\mathit{w}}_{\text{abs,ref}}}\right),$$

where w_abs,i is the absolute fitness of a genotype carrying mutation i and w_abs,ref is the fitness of the wild type used as a reference. The relative fitness of a second mutation j (w_j) and that of mutations i and j combined (w_ij) are obtained in the same manner. Subsequently, the epistatic interaction between mutations i and j (E_ij) is obtained as

$$E_{ij}= w_{ij}-\left[w_i+w_j\right]$$ (1)

or, in words, by the difference between the observed fitness of a genotype carrying both mutations i and j (w_ij) and the expected fitness of this double mutant if gene action is completely additive ([w_i + w_j]) (e.g., da Silva et al. 2010). Repeating this for a large number of combinations of mutations, the correlation between E_ij and [w_i + w_j] equals

$$r_{E_{ij},\left[w_i+w_j\right]}=\frac{\sigma \left(E_{ij}, \left[w_i+w_j\right]\right) }{\sqrt{{\sigma }^2\left(E_{ij}\right){\sigma }^2\left(w_i+w_j\right)}}.$$ (2)

In the presence of diminishing-returns epistasis, mutations with large beneficial effects on fitness show more negative epistasis, resulting in this correlation being negative.

However, by calculating epistasis from expected fitness (Equation 1), the two terms to be correlated will share measurement errors, and a statistical dependence is created artificially. In any empirical study w_i, w_j, and w_ij are measured with error. So if w_i = a_i + e_i and w_j = a_j + e_j, where a and e are the additive genetic and residual components of w_i and w_j, respectively, and w_ij = a_i + a_j + i_ij + e_ij, where i_ij is the epistatic effect of mutations i and j, then

$$E_{ij}=i_{ij}+e_{ij}-\left[e_i+e_j\right].$$ (3)

Assuming uncorrelated measurement errors,

$$\begin{array}{l}{r}_{E_{ij},\left[w_i+w_j\right]}\\ =\frac{\sigma \left(i_{ij},\left[a_i+a_j\right]\right)-\left[{\sigma }^2\left(e_i\right)+{\sigma }^2\left(e_j\right)\right]}{\sqrt{\left[{\sigma }^2\left(i_{ij}\right)+{\sigma }^2\left(e_{ij}\right)+{\sigma }^2\left(e_i\right)+{\sigma }^2\left(e_j\right)\right]\left[{\sigma }^2\left(a_i\right)+{\sigma }^2\left(a_j\right)+{\sigma }^2\left(e_i\right)+{\sigma }^2\left(e_j\right)\right]}}.\end{array}$$ (4)

It follows that measurement error in w_i, w_j, and w_ij [i.e., σ²(e_i) = σ²(e_j) = σ²(e_ij) > 0], appearing in the denominator of Equation 4, weakens the correlation. However, [σ²(e_i) + σ²(e_j)] also appears in the numerator, making negative correlations more negative and positive correlations less positive. The latter is the result of correlating [w_i + w_j] with w_ij – [w_i + w_j] and thereby the measurement error in [w_i + w_j] (i.e., e_i + e_j) with itself. On the whole, measurement error can thus result in a negative correlation between expected fitness and epistasis, which could erroneously be interpreted as evidence for diminishing-returns epistasis (Figure 1A).

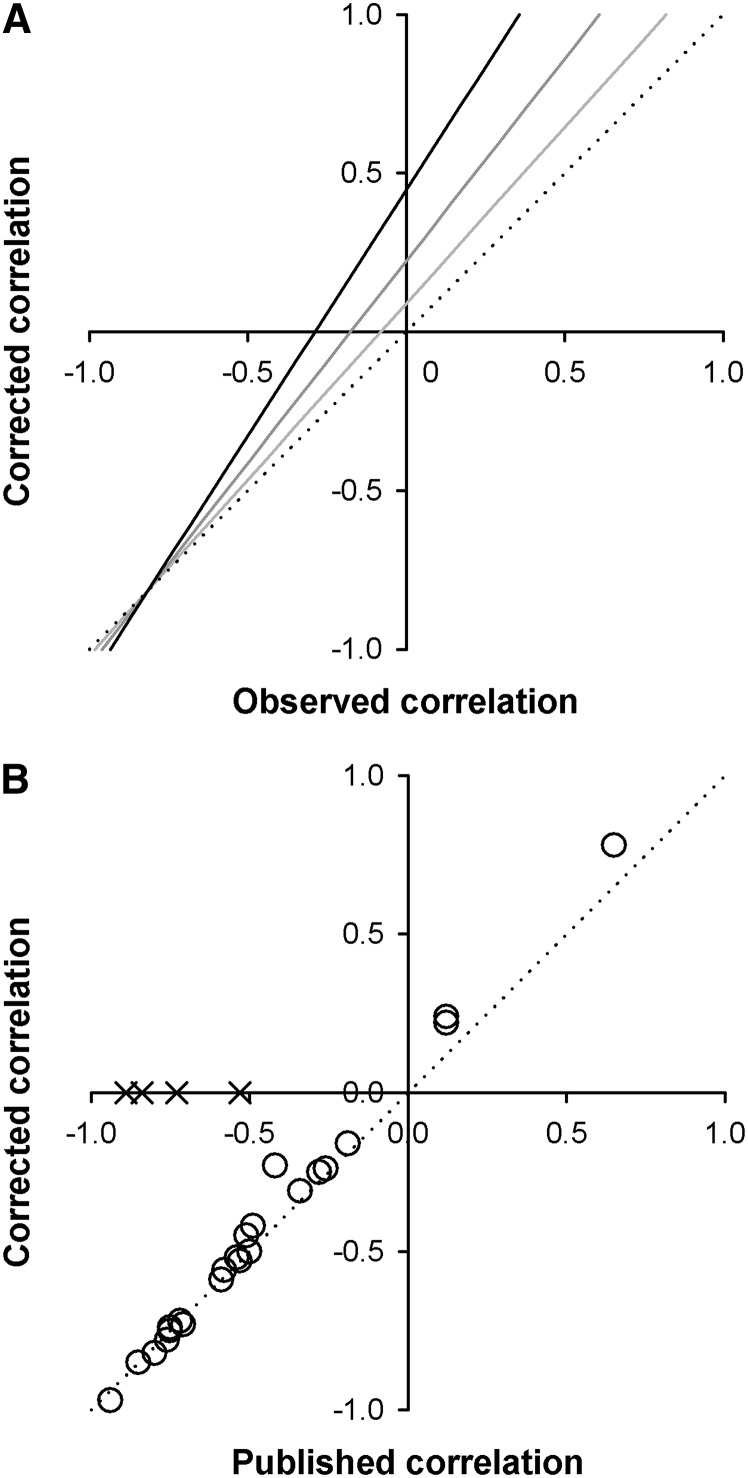
Figure 1.

The relationship between observed and corrected estimates of diminishing-returns epistasis. (A) Predicted relationship between $r_{E_{ij},\left[w_i+w_j\right]}$ (i.e., the observed correlation; Equation 2) and $r_{i_{ij},\left[a_i+a_j\right]}$ (the corrected correlation; Equation 5), showing that for moderately negative and positive correlations, the observed correlation is biased downward, whereas for very strongly negative correlations it is biased upward. For illustrative purposes, σ²(a_i) = σ²(a_j) = 1 and σ²(i_ij) = 0.5. Lines with light shading, lines with dark shading, and solid lines represent σ²(e_i) = σ²(e_j) = σ²(e_ij) = 0.1, 0.2, and 0.5, respectively. The dotted line designates the 1:1 relationship between observed and corrected estimates. (B) Published and corrected estimates of 25 correlations from 15 studies for which variance components were available (see Table S1 and Table S2). The line designates a 1:1 relationship between the published and corrected correlations. An additional four correlations (crosses) could not be corrected due to nonsignificant epistatic variance. Their placement on the x-axis shows their published values. Although there is overall evidence for diminishing-returns epistasis from this body of literature (correlations are still strongly negative on average, following correction), regression to the mean has led to downwardly biased estimates and four cases of published negative correlations based on nonsignificant epistatic variance.

Having knowledge of σ²(e_i), σ²(e_j), and σ²(e_ij), we are able to obtain the corrected correlation between i_ij and [a_i + a_j] that is not biased by measurement error variance, using

$$\begin{array}{l}{r}_{i_{ij},\left[a_i+a_j\right]}\\ =\frac{\sigma \left(E_{ij},\left[w_i+w_j\right]\right)+{\sigma }^2\left(e_i\right)+{\sigma }^2\left(e_j\right)}{\sqrt{\left[{\sigma }^2\left(E_{ij}\right)-{\sigma }^2\left(e_{ij}\right)-{\sigma }^2\left(e_i\right)-{\sigma }^2\left(e_j\right)\right]\left[{\sigma }^2\left(w_i\right)+{\sigma }^2\left(w_j\right)-{\sigma }^2\left(e_i\right)-{\sigma }^2\left(e_j\right)\right]}}.\end{array}$$ (5)

From this it becomes apparent that correcting the variance components in the denominator of Equation 5 for measurement error can lead to both approaching zero whenever error is high relative to additive genetic variance. The latter will be the case whenever correlations are based on statistically nonsignificant variance for epistasis and expected fitness. In such cases, observed correlations run the greatest risk of being inflated. For example, in the extreme scenario when additive genetic variance = 0, it follows from Equation 4 that the uncorrected correlation between epistasis and expected fitness, assuming equal error variances in single and double mutants, = −2/$\sqrt{3\ast 2}$ = −0.82 purely due to measurement error. Generally, statistical significance of the correlation therefore needs to be evaluated using data-resampling techniques.

Although we here focus on negative epistasis of beneficial mutations, the described effect would also generate a pattern where combinations of mutations with increasingly deleterious effects show more positive epistasis. Thereby it may partially explain the lack of empirical support for stronger negative epistasis of increasingly deleterious mutations (i.e., the opposite pattern) as a selective agent maintaining sexual reproduction and recombination (Elena and Lenski 1997; Bonhoeffer et al. 2004). Furthermore, because the correlation between E_ij and [w_i + w_j] is a direct function of the amount of measurement error, variation in the latter can introduce differences in the strength of the correlation among experiments. For example, because the ratio of environmental to genetic variance for fitness often differs between benign and stressful environments (Hoffmann and Merilä 1999; Agrawal and Whitlock 2010), it might erroneously be concluded that epistasic effects are shaped by environmental quality. Similarly, diminishing-returns epistasis might be found to be more pronounced in complex organisms, in which fitness is often estimated with less precision.

The effect outlined here is referred to as “regression to the mean” (Galton 1886) and is a common cause of misinterpretation in biology (Kelly and Price 2005; Postma 2006, 2011; Roff 2011; Verhulst et al. 2013) and other sciences (e.g., Hotelling 1933; Kahneman and Tversky 1973). Although we have focused on one way the phenomenon can introduce biases, it may raise its head in other ways. First, we note that although Equations 4 and 5 need to be modified if epistasis instead is defined in relative terms or by a multiplicative model and/or if epistasis is regressed on the fitness of the genetic background into which new mutations were introduced, bias remains (Table S1). Second, whenever only mutations with relatively strong effects are selected from a larger sample (as is often the case; Table S1) and if fitness is measured with error, these mutations will on average have lower fitness when measured again and therefore show apparent negative epistasis. Third, even when mutant fitness is estimated without error, estimates may be biased when combinations of beneficial mutations are selected for further investigation from experimental evolution studies (which is common too; Table S1). This is because mutations with large positive epistasis for fitness on the particular genetic background of the experimental population are more likely to fix during experimental evolution and thereby to be selected for introduction into other genetic backgrounds, where they will on average have lower fitness (Draghi and Plotkin 2013; Chou et al. 2014; Greene and Crona 2014).

A Brief Literature Survey

Although some authors seem aware of the issue, few have attempted to account for it (Table S1), and the severity of the bias hence remains unknown. We reviewed 30 recent articles that reported results on diminishing-returns epistasis for fitness in microorganisms. In 22 studies, epistasis was directly related to expected fitness, and 18 of these did so without correcting for regression to the mean (Table S1). We note that only one study (Szafraniec et al. 2003) looked for diminishing-returns epistasis by regressing observed on predicted fitness, using reduced major axis regression and testing for a slope significantly <1. This method, although not free of problematic assumptions regarding the nature of error variances (see Warton et al. 2006; Smith 2009), is more robust to the issue raised here. From 15 studies estimating $r_{E_{ij},\left[w_i+w_j\right]}$ we were able to extract estimates of variance components (for details see Table S1, and for a numerical example see Table S2), which allowed us to obtain unbiased estimates of 25 published correlations, using Equation 5. In four additional cases, correlations could not be corrected because of nonsignificant epistatic variance. In these cases, (almost) all variation in E_ij is the result of measurement error variance, resulting in corrected correlations taking on values outside the theoretical boundary (see Table S1). The fact that these correlations were strongly negative before correction, together with the fact that most corrected correlations are less negative than the published estimates, shows that regression to the mean introduces directional bias into empirical estimates of diminishing-returns epistasis (Figure 1B, Table S1). In most cases however, corrections did not affect results qualitatively, which can be attributed to mutant fitness typically being estimated with small error.

Conclusion

Here we have shown how biases due to regression to the mean inflate estimates of diminishing-returns epistasis. Although the majority of studies have not corrected for this, biases are in most cases small. Nevertheless, we do observe bias, most notably with four cases of published negative correlations based on nonsignificant epistatic variances, underlining the importance of performing corrections to allow accurate comparative analyses and prevent publication bias. We also note that we may have underestimated the amount of bias by assuming uncorrelated measurement errors, an assumption that is often violated in experiments by uncontrolled temporal or spatial block effects. Crucially, such effects would lead to undetected measurement errors that would overestimate diminishing-returns epistasis further. Application of appropriate statistical corrections in future studies will further increase our understanding of the manifestation and role of diminishing-returns epistasis in evolution.