Structured Correspondence Topic Models for Mining Captioned Figures in Biological Literature

Abstract

A major source of information (often the most crucial and informative part) in scholarly articles from scientific journals, proceedings and books are the figures that directly provide images and other graphical illustrations of key experimental results and other scientific contents. In biological articles, a typical figure often comprises multiple panels, accompanied by either scoped or global captioned text. Moreover, the text in the caption contains important semantic entities such as protein names, gene ontology, tissues labels, etc., relevant to the images in the figure. Due to the avalanche of biological literature in recent years, and increasing popularity of various bio-imaging techniques, automatic retrieval and summarization of biological information from literature figures has emerged as a major unsolved challenge in computational knowledge extraction and management in the life science. We present a new structured probabilistic topic model built on a realistic figure generation scheme to model the structurally annotated biological figures, and we derive an efficient inference algorithm based on collapsed Gibbs sampling for information retrieval and visualization. The resulting program constitutes one of the key IR engines in our SLIF system that has recently entered the final round (4 out 70 competing systems) of the Elsevier Grand Challenge on Knowledge Enhancement in the Life Science. Here we present various evaluations on a number of data mining tasks to illustrate our method.

1. INTRODUCTION

The rapid accumulation of literatures on a wide array of biological phenomena in diverse model systems and with rich experimental approaches has generated a vast body of online information that must be properly managed, circulated, processed and curated in a systematic and easily browsable and summarizable way. Among such information, of particular interest due to its rich and concentrated information content, but presenting unsolved technical challenges for information processing and retrieval due to its complex structures and heterogeneous semantics, are the diverse types of figures present in almost all scholarly articles. Although there exist a number of successful text-based data mining systems for processing on-line biological literatures, the unavailability of a reliable, scalable, and accurate figure processing systems still prevents information from biological figures, which often comprise the most crucial and informative part of the message conveyed by an scholarly article, from being fully explored in an automatic, systematic, and high-throughout way.

Compared to figures in other scientific disciplines, biological figures are quite a stand-alone source of information that summarizes the findings of the research being reported in the articles. A random sampling of such figures in the publicly available PubMed Central database would reveal that in some, if not most of the cases, a biological figure can provide as much information as a normal abstract. This high-throughput, information-rich, but highly complicated knowledge source calls for automated systems that would help biologists to find their information needs quickly and satisfactorily. These systems should provide biologists with a structured way of browsing the otherwise unstructured knowledge source in a way that would inspire them to ask questions that they never thought of before, or reach a piece of information that they would have never considered pertinent to start with.

The problem of automated knowledge extraction from biological literature figures is reminiscent of the actively studied field of multimedia information management and retrieval. Several approaches have been proposed to model associated text and images for various tasks like annotation [16], retrieval [10, 18] and visualization [3]. However, the structurally-annotated biological figures pose a set of new challenges to mainstream multimedia information management systems that can be summarized as follows:

• Structured Annotation: as shown in Fig. 1, biological figures are divided into a set of sub-figures called panels. This hierarchical organization results in a local and global annotation scheme in which portions of the caption are associated with a given panel via the panel pointer (like “(a)” in Fig. 1), while other portions of the caption are shared across all the panels and provide contextual information. We call the former scoped caption, while we call the later global caption. How can this annotation scheme be modeled effectively?

• Free-Form Text: unlike most associated text-image datasets, the text annotation associated with each figure is a free-form text as opposed to high-quality, specific terms that are highly pertinent to the information content of the figure. How can the relevant words in the caption be discovered automatically?

• Multimodal Annotation: although text is the main source of modality associated with biological figures, the figure’s caption contains other entities like protein names, GO-term locations and other gene products. How can these entities be extracted and modeled effectively?

Figure 1.

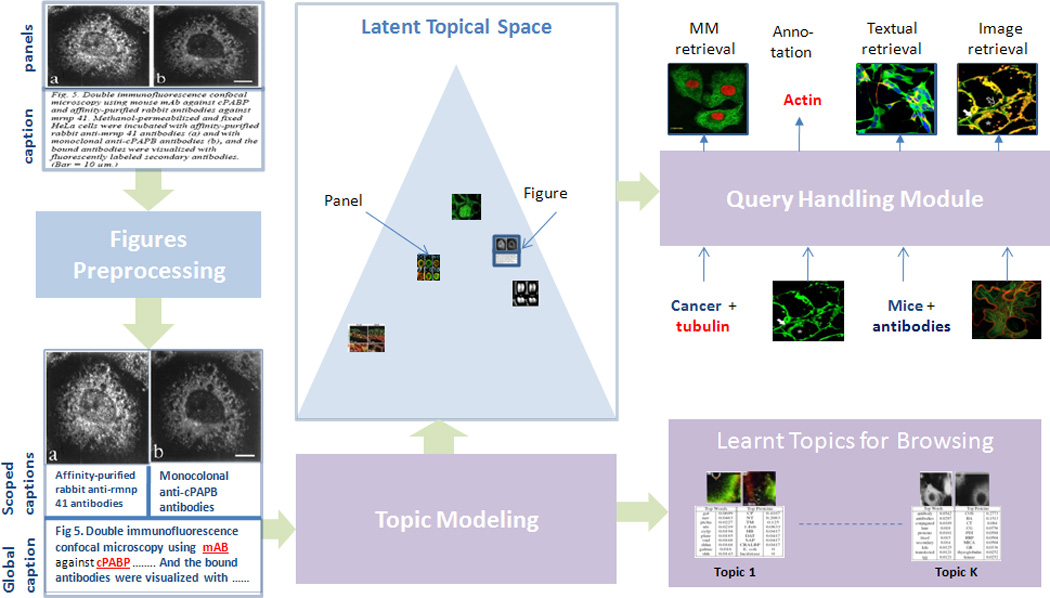
Overview of our approach, please refer to Section 2 for more details. (Best viewed in color)

We address the problem of modeling structurally-annotated biological figures by extending a successful probabilistic graphical model known as the correspondence latent Dirichlet allocation [3] (cLDA) model, which was successfully employed for modeling annotated images. We present the struct-cLDA (structured, correspondence LDA) model that addresses the aforementioned challenges in biological literature figures. The rest of this paper is organized as follows. In Section 2, we give an overview of our approach and basic preprocessing of the data. Then in Section 3, we detail our model in a series of simples steps. Section 4 outlines a collapsed Gibbs sampling algorithm for inference and learning. In Section 5 we provide a comprehensive evaluation of our approach using qualitative and quantitative measures. Finally in Section 6, we provide a simple transfer learning mechanism from non-visual data and illustrate its utility. The model presented in this paper has been integrated into the publicly available Structured Literature Image Finder (SLIF) system , first described in [14]. Our system has recently participated in the Elsevier Grand Challenge on Knowledge Enhancement in the Life Science, which is an international contest created to improve the way scientific information is communicated and used, and was selected as one of the 4 finalists among the 70 participating teams¹.

2. FIGURE PRE-PRECESSING

In this section we briefly give an overall picture of the SLIF system (Structured Literature Image Finder). SLIF consists of a pipeline for extracting structured information from papers and a web application for accessing that information. The SLIF pipeline is broken into three main sections: caption processing, image processing (which are refereed to as figure preprocessing in Fig. 1) and topic modeling, as illustrated as Fig. 1.

The pipeline begins by finding all figure-captions pairs. Each caption is then processed to identify biological entities (e.g., names of proteins)[11]. The The second step in caption processing is to identify pointers from the caption that refer to a specific panel in the figure , and the caption is broken into “scopes” so that terms can be linked to specific parts of the figure [5]. The image processing section begins by splitting each figure into its constituent panels, followed by describing each panel using a set of biologically relevant image features. In our implementation, we used a set of high-quality 26 image features that span morphological and texture features [13].

The first two steps result in panel-segmented, structurally and multi-modally annotated figures as shown in the bottom-left of Fig. 1 (Discovered protein entities are underlined and highlighted in red). The last step in the pipeline, which is the main focus in this paper, is to discover a set of latent themes that are present in the collection of papers. These themes are called topics and serve as the basis for visualization and semantic representation. Each topic consists of a triplet of distributions over words, image features and proteins. Each figure in turn is represented as a distribution over these topics, and this distribution reflects the themes addressed in the figure. Moreover, each panel in the figure is also represented as a distribution over these topics as shown in Fig. 1; this feature is useful in capturing the variability of the topics addressed in figures with a wide coverage and allows retrieval at either the panel or figure level. This representation serves as the basis for various tasks like image-based retrieval, text-based retrieval and multimodal-based retrieval. Moreover, these discovered topics provide an overview of the information content of the collection, and structurally guide its exploration.

3. STRUCTURED CORRESPONDENCE TOPIC MODELS

In this section we introduce the struct-cLDA model (structured correspondence LDA model) that addresses all the challenges in- troduced by structurally-annotated biological figures. As the name implies, struct-cLDA builds on top of and extends cLDA which was designed for modeling associated text and image data. We begin by introducing the cLDA; then in a series of steps we show how we extended the cLDA to address the new challenges introduced by the structurally-annotated biological figures. In Figure 2, we depict side-by-size the graphical representations of the original cLDA model and our struct-cLDA model, to make explicit the new innovations. Following conventions in the machine learning literature, we use bold face letters to denote vectors and normal face letters for scalars. For example, w^p is the vector containing all words that appear in panel p. That is, ${\mathbf{w}}^p=(w_1^p,\dots ,w_{N_p}^p)$, where N_p is the number of words in panel p.

Figure 2.

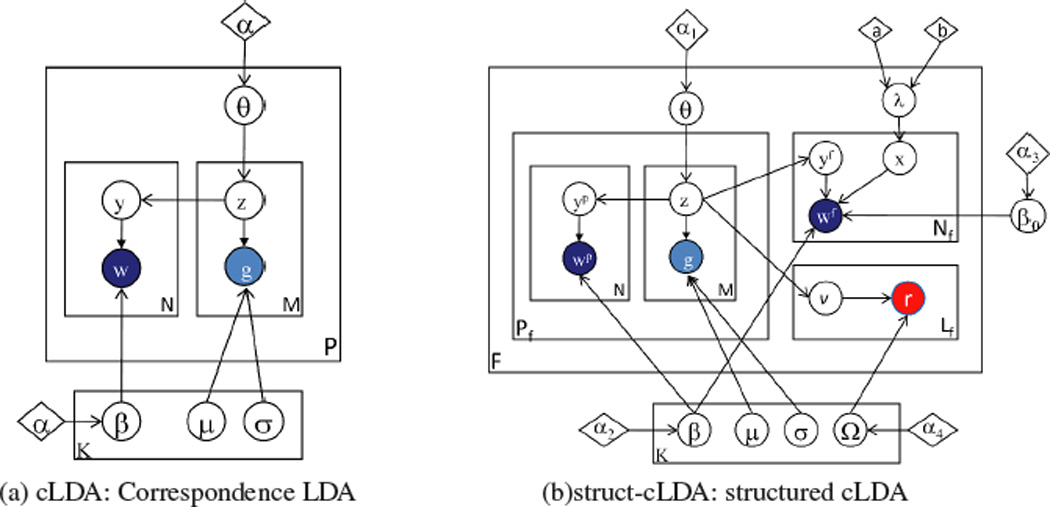
The cLDA and struct-cLDA Models. Shaded circles represent observed variables and their colors denote modality (blue for words, red for protein entities, and cyan for image features), unshaded circles represent hidden variables, diamonds represent model parameters, and plates represent replications. Some super/subscripts are removed for clarity—see text for explanation.

3.1 The Correspondence LDA

The cLDA model is a generative model for annotated data – data with multiple types where the instance of one type (such as a caption) serves as a description of the other type (such as an image). cLDA employs a semantic entity known as the topic to drive the generation of the annotated data in question. Each topic is represented by two content-specific distributions: a topic-specific word distribution, and a topic-specific distribution over image features. The topic-specific word distribution is modeled as a multinomial distribution over words, denoted by Multi(β); and image features are real-valued and thus follow a Gaussian distribution, denoted by N(µ, σ). As mentioned in Section 2, in our study, each panel is described using M = 26 image features, thus each topic has 26 Gaussian distributions: one for each image feature.

The generative process of a figure f under cLDA is given as follows:

1. 1. Draw θ_f ~ Dir (α)

2. 2. For every image feature g_m

   1. Draw topic z_m ~ Multi(θ_f)
   2. Draw $g_m|z_m=k~\mathrm{N}({\mu }_k,m,{\sigma }_{k,m}^2)$
3. For every word ω_n in caption

   1. Draw topic y_n ~ Unif (z₁,…, z_m)
   2. Draw ω_n|y_n = k ~ Multi(β_k)

In step 1 each figure f samples a topic-mixing vector, θ_f from a Dirichlet prior. The component θ_f,k of this vector defines how likely topic k will appear in figure f. For each image features in the figure, g_m, a topic indicator,z_m, is sampled from θ_f , and then the image feature itself is sampled from a topic-specific image-feature distribution specified by this indicator. The correspondence property of cLDA is manifested in the way the words in the caption of the figure are generated in step 3. Since each word should, in principle, describes a portion of the image, the topic indicator of each word, y, should correspond to one of those topic indicators used in generating the image features. Specifically, the topic indicator of the n-th word, y_n, is sampled uniformly from those indicators associated with the image features of the figure as in step 3.(a). Finally, the word, w_n, is sampled from the selected topic’s distribution over words. Since the image feature and word distributions of each topic are highly correlated, the correspondence between image features and words in the caption is enforced.

3.2 Structured Correspondence LDA

In this section we detail the struct-cLDA model that addressed the new challenges introduced by biological figures. Fig. 2 depicts a graphical representation of the model. In a struct-cLDA, each topic, k, now has a triplet representation: a multinomial distribution of words β_k (drawn from Dir(α₂)), a multinomial distribution over protein entities Ω_k (drawn from Dir(α₄)), and a set ofM normal distributions, one for each image feature (whose prior will be detailed in section 3.2.4). The full generative scheme of a multi-panel biological figure, f under this model is outlined below:

1. Draw θ_f ~ Dir(α₁)

2. Draw λ_f ~ Beta(a, b)

3. For every panel p in P_f:

   1. For every image feature $g_m^p$ in panel p:

      1. Draw topic $z_m^p~\text{Multi}({\theta }_f)$
      2. Draw $g_m^p|z_m^p=k~\mathrm{N}({\mu }_k,m,{\sigma }_k^2,m)$
   2. For every word $w_n^p$ in scoped caption of panel p

      1. Draw topic $y_n^p~\text{Unif}(z_1^p,\dots ,z_m^p)$
      2. Draw $w_n^p|y_n^p=k~\text{Multi}({\beta }_k)$
4. For every word $w_n^f$ in global caption:

   1. Draw coin x_n ~ Bernoulli(λ_f)
   2. If(x_n = = 1)

      1. Draw topic $y_n^f~\text{Unif}({\mathbf{z}}^1,\dots ,{\mathbf{z}}^{{\mathrm{P}}_{\mathrm{f}}})$
      2. Draw $w_n^f|y_n^f=k~\text{Multi}({\beta }_k)$
   3. If(x_n = = 0)

      1. Draw $w_n^f~\text{Multi}({\beta }_0)$
5. For every protein entity r_l in global caption:

   1. Draw topic υ_l ~ Unif(z¹, …, z^P_f)
   2. Draw r_l|υ_l = k ~ Multi(Ω_k)

In the following subsections we break the above generative steps into parts each of which addresses a specific challenge introduced by biological figures.

3.2.1 Modeling Scoped Caption

In this subsection, we describe how we approached the problem of modeling scoped and global captions. As shown in Fig. 1, the input to the topic modeling module is a partially-segmented figure where some of the words in the caption are associated directly with a given panel, say p, and the remaining words serve as a global caption which is shared across all the P_f panels in figure f, and provides contextual information. There are two obvious approaches to deal with this problem that would enable the use of the flat cLDA model described in Section 3.1:

• Scoped-only annotation: in this scheme the input to the cLDA model is the panels with their associated scoped captions. Clearly this results in an under-representation problem as contextual information at the figure level is not included.

• Caption replication: in this scheme the whole figure caption is replicated with each panel, and this constitutes the input to the cLDA model. Clearly this results in an overrepresentation problem and a bias in the discovered topics towards over-modeling figures with large number of panels due to the replication effect.

In addition to the above problems, resorting to a panel-level abstraction is rather suboptimal because of the lack of modeling the interaction between panels at the figure level which precludes processing retrieval queries at the whole figure level.

We introduce scoping to model this phenomenon. As shown in Fig. 2.(b), the topic-mixing vector θf of the figure is shared across all the panels (step 1). However, each panel’s set of words, ${\mathbf{w}}^p=(w_1^p,w_2^p\dots ,w_{N_p}^p)$, correspond only to this panel’s image features. Moreover, words in the figure’s global caption, w^f, correspond to all the image features in all the panels of this figure. This suggests a two-layer cLDA generative process:the scoped caption is generated in 3.(b) which with 3.(a) represents exactly the same generative process of cLDA over image features of a panel and words in the scoped caption of this panel. In the next subsection we will detail the generation of words in the global caption.

3.2.2 Modeling Global Caption

As we noted earlier, the global caption is shared across all panels, and represents contextual information or a description that is shared across all panels. This suggests that words in the global caption of figure f can be generated by corresponding them to the collective set of topic indicators used in generating the image features in all the panels – this is in fact equivalent to a flat cLDA model between words in the global caption and the image features in all the panels. If we took this approach, we found that corpus-level stop-words in the form of non content-bearing words(like: bar, cell, red and green) appear at the top of most of the discovered topics due to their high frequencies. In fact, inherent in the modeling assumption of cLDA is the fact that annotations are specific to the figure and of high quality: that is, every word in the caption describes a part in the image. However, captions in biological figures are free-form text and therefore this assumption is violated. To solve this problem, we use factoring which is similar to background subtraction in [4]. Specifically, we introduce a background topic, β₀ (which is sampled from Dir(α₃) once for the whole corpus) that is used to generate the corpus-level stopwords. This process is equivalent to factoring these stopwords from content-bearing topics — we call this process factoring.

The generative process for the global caption now proceeds as follows. With each figure, f, we associate a coin whose bias is given by λ_f (step 2). This bias models the ratio of content-bearing to background words in the figure, and is sampled individually for each figure from a beta distribution. As shown in step 4, to generate a word in the global caption, $w_n^f$, we first flip the coin and name the outcome, x_n. If x_n is head, we pick a topic indicator for this word, $y_n^f$, uniformly from the topic indicators used to generate the image features of the panels in this Figure (step 4.(b)). Then, we generate the word from this topic’s distribution over words, ${\beta }_{y_n^f}$. On the other hand, if x_n is tail, we sample this word from the background topic β₀ (step 4.(c)).

3.2.3 Modeling Multimodal Annotation

The final step is to model multimodal annotations. For simplicity, we restrict our attention here to protein annotations, although other forms of gene products like GO-terms could be added similarly. For simplicity, we place all protein annotations at the level of the global caption (even if they appear in the scoped caption), although it is very straightforward to model scoped multimodal annotation in the same way we modeled scoped word captions. Generating a protein entity is very similar to generating a word in the global caption. To generate a protein entity, r_l, in step 5.(a) we pick a topic indicator for this protein entity, υ_l, uniformly from the topic indicators used to generate the image features of the panels in this Figure (note that the notation Unif(_z¹, …, z^P_f) denotes a concatenation of all the z vectors). Then, we generate the protein entity from this topic’s distribution over protein entities Ω_υl

It should be noted that while protein entities are words, modeling them separately from other caption words has several advantages. First, protein mentions have high variance, i.e.the same protein entity can be referred to in the caption using many textual forms. Mapping these forms, also known as protein mentionsto protein entities is a standard process known as normalization [12]; our implementation followed our earlier work in [11]. Second, protein entities are rare words and have different frequency spectrums than normal caption words, thus modeling them separately has the advantage of discovering the relationship between words and protein entities despite this frequency mismatch. Moreover, endowing each topic with two distributions over words and protein entities results in more interpretable topics (see Section 5.1) and enables more advanced query types (see Section 5.3 and 5.4).

3.2.4 A Note about Hyperparameters

All multinomial distributions in the models in Figure 2 are endowed with a dirichlet prior to avoid overfitting as discussed in [3]. Perhaps the only part that warrants a description is our choice for the prior over the mean and variance of each image feature’s distribution. Each image feature is modeled as a normal distribution whose mean and variance are topic-specific. The standard practice is to embellish the parameters of a normal distribution with an inverse Wishart prior, however, here we took a simpler approach. We placed a non-informative prior over the values of the mean parameters of these image features, that is µk, m ~ Unif. Our intuition stems from the fact that different features have different ranges. However, we placed an inverse prior over the variance to penalize large variances: ${\sigma }_{k,m}^2\propto 1/{\sigma }_{k,m}^2$ (see [7] chapter 3.2). The reason for this choice stems from the noise introduced during calculation of the image features. Without this prior, a maximum likelihood (ML) estimation of σ² in a given topic is not robust to outliers (see [1] for more details).

4. A COLLAPSED GIBBS SAMPLING ALGORITHM

Under the generative process, and hyperparmaters choices, outlined in section 3.2, we seek to compute:

$$P({\mathbf{f}}_{1:F},{\beta }_{1:K},{\mu }_{1:K},{\sigma }_{1:K}^2,{\mathbf{\Omega }}_{1:K},{\beta }_0/{\alpha }_{1:4},a,b,\mathbf{w},\mathbf{g},\mathbf{r}),$$

where f is shorthand for the hidden variables (θ_f, λ_f, y, z, x, v) in figure f. The above posterior probability can be easily written down from the generative model in section 3.2, however, we omit it for the lack for space. The above posterior is intractable, and we approximate it via a collapsed Gibbs sampling procedure [8] by integrating out, i.e. collapsing, the following hidden variables: the topic-mixing vectors of each figure, θ_f, the coin bias λ_f for each figure, as well as the topic distributions over all modalities $({\beta }_k,{\mathrm{\Omega }}_k,{\mu }_{k,m},{\sigma }_{k,m}^2,\text{and}{\beta }_{\text{0}})$. Therefore, the state of the sampler at each iteration contains only the topic indicators for all figures. We alternate sampling each of these variables conditioned on its Markov blanket until convergence. At convergence, we can calculate expected values for all the parameters that were integrated out, especially for the topic distributions over all modalities, and for each figure’s latent representation (mixing-vector). To ease the calculation of the Gibbs sampling update equations we keep a set of sufficient statistics (SS) in the form of co-occurrence counts and sum matrices of the form $C_{eq}^{EQ}$ to denote the number of times instance e appeared with instance q. For example, $C_{wk}^{WK}$ gives the number of times word ω was sampled from topic k. Moreover, we use the subscript −i to denote the same quantity it is added to without the contribution of item i. For example, $C_{wk,-i}^{WK}$ is the same as $C_{wk}^{WK}$ without the contribution of word ω_i. For simplicity, we might drop dependencies on the panel or figure whenever the meaning is implicit form the context.

Sampling a topic ($y_n^p$) for a given panel word ($w_n^p$)

$$P(y_n^p=k|w_n^p=w,{\mathbf{y}}_{-n}^P,{\mathbf{w}}_{-n}^P,{\mathbf{z}}^P)\propto \frac{C_{kp}^{KP}}{{\sum }_{k\prime }{C}_{k\prime p}^{KP}}\frac{C_{wk,-n}^{WK}+{\alpha }_2}{{\sum }_{w\prime }{C}_{w\prime k,-n}^{WK}+W{\alpha }_2}$$ (1)

Sampling a topic (υ_l) for a given protein entity (r_l)

$$P({\upsilon }_l=k|r_l=r,{\mathbf{v}}_{-l},{\mathbf{r}}_{-l},\mathbf{z})\propto \frac{C_{kf}^{KF}}{{\sum }_{k\prime }{C}_{k\prime f}^{KF}}\frac{C_{rk,-l}^{RK}+{\alpha }_4}{{\sum }_{r\prime }{C}_{r\prime k,-l}^{RK}+R{\alpha }_4}$$ (2)

The above two local distributions have the same form which consists of two terms. The first term measures how likely it is to assign topic k to this word (protein entity) based on the topic indicators of the corresponding image features (at the panel level in Eq. (1), and at the figure level in Eq. (2) — i.e. the set of all image features’ indicators in all panels). The second term measures the probability of generating this word (protein entity) from topic k’s distribution over words (protein entities).

Sampling a coin and a topic $(x_n,y_n^f)$ for a given global caption word ($w_n^f$)

For a given word in the shared global caption, it is easier to sample (xn, yfn) as a block— a similar approach was used in [4].

$$P(x_n=0|x_{-n},w_n^f=w,{\mathbf{w}}_{-n})\propto \frac{C_{0f{,}_{-n}}^{XF}+b}{{\sum }_{x\prime }{C}_{x\prime f,-n}^{XF}+a+b}\frac{C_{w,-n}^{W0}+{\alpha }_3}{{\sum }_{w\prime }{C}_{w\prime ,-n}^{W0}+W{\alpha }_3}$$ (3)

where $C_w^{W0}$ is the word count matrix for the background topic, and $C_{xf}^{XF}$ counts, in figure f, how many words were assigned to the background topic (x = 0) and how many words were assigned to a panel’s image feature and were thus sampled from a latent topic (x = 1). Similarly,

$$P(x_n=1,z_n^f=k|x_{-n},w_n^f=w,{\mathbf{w}}_{-n},\mathbf{z})\propto \frac{C_{kf}^{KF}}{{\sum }_{k\prime }{C}_{k\prime f}^{KF}}\frac{C_{1f,-n}^{XF}+a}{{\sum }_{x\prime }{C}_{x\prime f,-n}^{XF}+a+b}\frac{C_{wk,-n}^{WK}+{\alpha }_2}{C_{w\prime k,-n}^{WK}+W{\alpha }_2}$$ (4)

The above two equations can be normalized to form a K + 1 multinomial distribution — K information-bearing topics when x_n = 1, in addition to the background topic when x = 0.

Sampling a topic $(z_m^p)$ for the m^th image feature $(g_m^p)$ in panel p

Perhaps this is the most involved equation as all other topic indicators in the figure/panels are influenced by the topic indicators of the image features. For simplicity, the (| …) in the equation below is a shorthand for all these topic indicators which are: topic indicators of words in the global caption (y^f), topic indicators of words in the scoped caption of panel p (y^p), topic indicators of all other image features in all panels (z¹, …, z^P_f), and topic indicators for protein entities in the global caption (v).

$$P(z_m^p=k|g_m^p=g,\dots )\propto \frac{C_{kf,-m}^{KF}+{\alpha }_1}{{\sum }_{k\prime }{C}_{k\prime f,-m}^{KF}+K{\alpha }_1}t(g;{\widehat{\mu }}_{k,m},{\widehat{\sigma }}_{k,m}^2,C_{mk,-m}^{MK}-1)\times \text{Unif}({\mathbf{y}}^{\mathbf{f}}|z_m^p=k)\times \text{Unif}(\mathbf{v}|z_m^p=k)\times \text{Unif}({\mathbf{y}}^p|z_m^p=k)$$ (5)

where t(g; µ, σ², n) is a student t-distribution with mean µ, variance σ², and n degree of freedom (see [7] chapter 3.2). µ̂_k,m is the sample mean of the values of image feature m that are assigned to topic kand ${\widehat{\sigma }}_{k,m}^2$ is defined similarly. $C_{mk}^{MK}$ is the number of times image feature m was sampled from topic k. The first two parts in Eq. (5) are similar to the previous sampling equations: they measure the comparability of joining a topic given the observed feature and the topics assigned to neighboring image features. However, since every other annotation in the figure is generated based on the topic indicator of the image feature, three extra terms are needed. These terms measure how likely is the current assignment of the topic indicators of other annotations — panel words, figure words, and protein entities—given the new assignment to this image feature’s topic indicator. Notice that this uniform probabilities are exactly the same probabilities that appeared in the generative process, and also the same factors that appeared as the first fraction in Eqs. (4, 2, 1) respectively—however after updating the corresponding C matrix with the new value of $z_m^p$ under consideration (see [1] for more details).

Eqs. (1–5) are iterated until convergence, then expected values for the collapsed variables can be obtained via simple normalization operations over their respective count matrices using posterior samples. Moreover, the expected topics’ distributions over each modality can be calculated similarly.

At test time, to obtain the latent representation of a test figure, we hold the topic count matrices fixed, iterate Eqs. (1–5) until convergence, and then calculate the expected latent representation of each figure from posterior samples after convergence.

5. EXPERIMENTAL RESULTS

We evaluated our models on a set of articles that were downloaded from the publicly available Pubmed Central database². Aftre applying the preprocessing steps described in section 2, the resulting dataset consists of 5556 panels divided into 750 figures. Each figure has on average 8 panels, however some figures have up to 25 panels. After removing words and protein entities that appear less than 3 and 2 times respectively, the resulting number of word types and protein types are 2698 and 227 respectively. Moreover, the average number of words per caption is 150 words. We divided this dataset into 85% for training and 15% for testing. For all the experiments reported below, we set all the α hyperparmaters to .01 (except α₁ = .1), and (a, b) to 3 and 1 respectively. We found that the final results are not largely sensitive to these assignments. We ran Gibbs sampling to learn the topics until the in-sample likelihood converges which took a few hundred iterations for all models.

For comparison, we used cLDA and LSI as baselines. To apply cLDA to this dataset, we duplicated the whole figure caption and its associated protein entities with each panel to obtain a flat representation of the structured figures. Therefore, we will refer to this model as cLDA-d. For LSI, we followed the same strategy and then concatenated the word vector, image features and protein entities to form a single vector. Moreover, to understand the contribution of each feature in our model (scoping vs factoring), we removed factoring from the struct-cLDA model to obtain a model that only employs scoping, and we call the resulting model struct-cLDA^−f. In the following subsections we provide a quantitative as well as a qualitative evaluation of our model and compare it against the LSI and cLDA baselines over various visualization and retrieval tasks. Clearly, our goal from these comparisons is just to show that a straightforward application of simpler flat models can not address our problem adequately. In this paper, we extended cLDA to cope with the structure of the figures under consideration, however, adapting LSI, and other related techniques, to cope with this structure is left as an open problem. Moreover, our choice of comparing against LSI for annotation and retrievals tasks stems from the fact that in these tasks our own proposed model serves merely as a dimensionality reduction technique.

5.1 Visualization and Structured Browsing

In this section, we examine a few topics discovered by the struct-cLDA model when applied to the aforementioned dataset. In Fig. 3, we depict three topics from a run of the struct-cLDA with K = 20. For each topic we display its top words, protein entities, and the top 9 panels under this topic (i.e. the panels with the highest component for this topic in their latent representation θ^f). It is interesting to note that all these topics are biologically meaningful. For instance, the first topic represents the theme related to the EBA (The enucleation before activation) method which is a conventional method of producing an embryo and comprises enucleating “oocytes”, transferring donor cells into “oocytes”, fusing the oocytes and the donor cells, and activating the fused reconstruction cells. Moreover, protein “VP26” has been shown in various studies to interact with protein “actin” during these procedures. The second topics is about various cell structure types. The third topic is about tumor-related experiments. Examining its top words and proteins we found “cbp” and “hbl” which are known tumor suppressors. Moreover “actin” has been shown to be an important protein for tumor developments due to its rule in cell division. Also “Cx43” is a genetic sequence that codes for a protein that has tumor suppressing effect, moreover, protein “Caspases-3” is a member of the Caspases family which plays essential roles in apoptosis (programmed cell death). Interestingly “UNC” appears in this topic due to the wide usage of the University of North Carolina tumor dataset.

Figure 3.

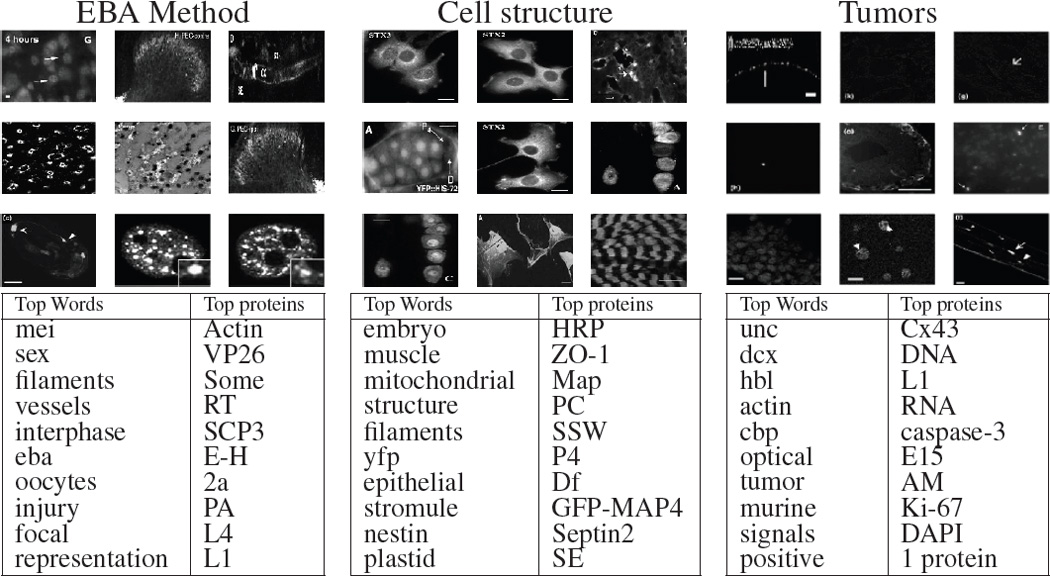
Illustrative three topics from a 20-topics run of the struct-cLDA model. See Section 5.1 for more details.

Moreover, given a figure f, as shown in Fig. 4, the system can visualize its topic decomposition, i.e. what are the topics represented in this figure along with its weights, either at the whole figure level, θ^f, or at the panel level. As shwon in in Fig. 4, the biological figure is composed of 6 panels, and thus our model gives a topic decomposition of each panel, a topic decomposition of the whole figure (bottom-left), and a topic assignment for each word in the caption. This, in fact, is a key feature of our model as it breaks the figure into its themes and allows biologist to explore each of these themes separately. For instance, this figure addresses several phases of cell division, under a controlled condition, that starts from the Anaphase stage (panels (a-c)) and progresses towards post mitosis stages (panels (d-f)). Indeed, our model was able to discern these stages correctly via the latent representation it assigns to each panel. Please note that this figure represents a case in which the scoped-caption module was not able to segment the caption due to the unorthodox referencing style used in this figure, however, the model was able to produce a reasonable latent representation. In the bottom-right of Fig. 4, we show three important topics addressed in this figures. It is quite interesting that Topic 13, which corresponds to various biological processes important to cell division, was associated with this figure mainly due to its image content, not its word content. Moreover, while the figure does not mention any protein entities, the associated protein entities with each topic play key roles during all stages of cell division addressed in the figure: for instance, dna ligase is an important protein for DNA replication. Therefore, the biologist might decide to retrieve similar figures (based on the latent representation of the whole figure) that address cell division under the same conditions, retrieve figures that address a given stage per see (based on the latent representation of some panels), or further explore a given topic by retrieving its representative figures.

Figure 4.

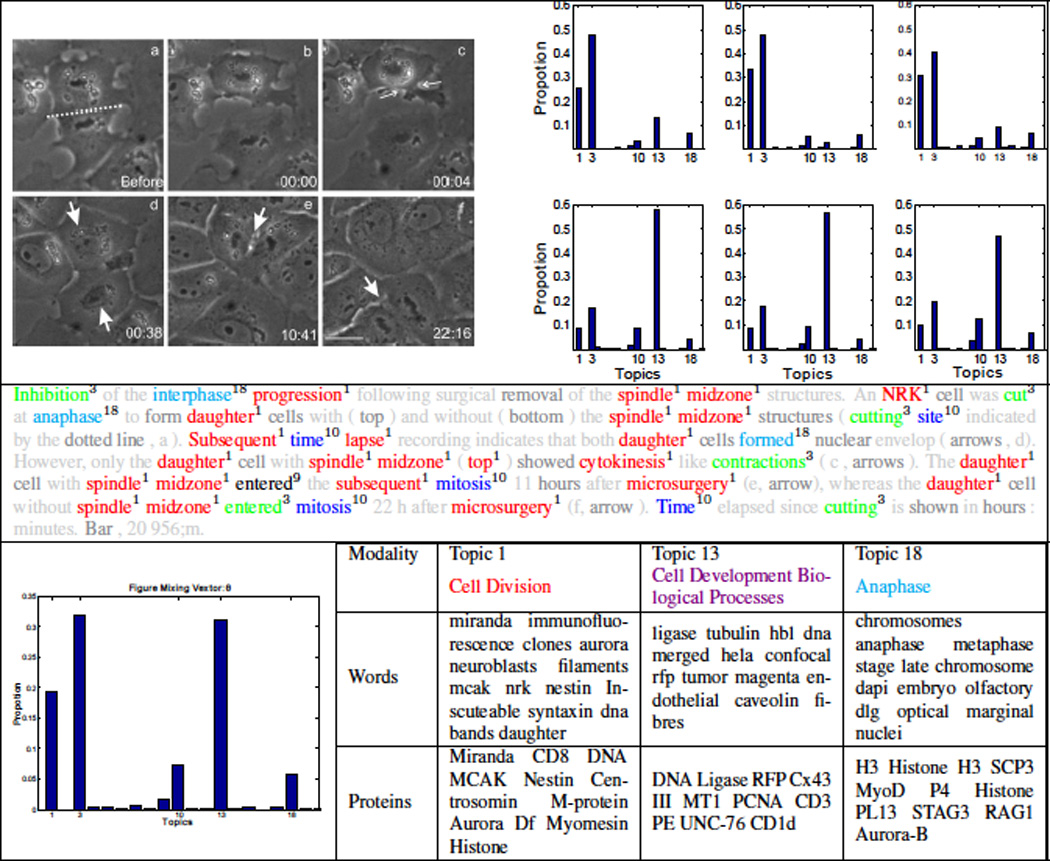
Illustrating topic decomposition and structured browsing. A biological figure tagged with its topic decomposition at different granularities: each panel (top-right), caption words (second row), and the whole figure (bottom-left). In tagging the caption, light grey colors are used for words that were removed during pre-processing stages, and dark grey colors are used for background words. Some topics are illustrated at the bottom row. (best viewed in color)

These features glue the figures in the whole collection via a web of interactions enabled by the similarity between the latent representation of each figure at multiple granularities. Moreover, this unified latent representation enables comparing figures with largely different number of panels.

Finally, in Table 1 we examine the effect of introducing the factored background topic on the quality of the discovered topics. Table 1 shows the background topic from the struct-cLDA model which clearly consists of corpus-level stopwords that carry no information. Examining a few topics discovered using a non-factored model (i.e. by removing the factoring component from struct-cLDA), it is clear that many of these stopwords (underlined in Table 1) found its way to the top list in seemingly information-bearing topics, and thus obscure their clarity and clutter the representation.

Table 1.

The effect of the background topic

Factored Model		Non-factored Model: struct-cLDA−f
Background Topic		Normal Topic 1		Normal Topic 2
cells	0.0559	red	0.0458	cells	0.09
cell	0.0289	green	0.0385	bar	0.0435
bar	0.0265	cells	0.0351	cell	0.0386
gfp	0.0243	infected	0.0346	antibody	0.0318
scale	0.024	actin	0.0244	protein	0.0282
red	0.0197	transfected	0.0222	staining	0.0202
green	0.0188	images	0.0218	visualized	0.0171
images	0.0188	membrane	0.0167	expressed	0.0141
arrows	0.0157	fluorescent	0.0167	section	0.0129
shown	0.0151	fixed	0.0163	tissue	0.0129

5.2 Timing Analysis and Convergence

Fig. 5.b compares the time, in seconds, consumed by each model in performing a full Gibbs iteration. All the models were coded in Matlab. It is clear from this figure that replicating the caption with each panel to anable the use of a standard cLDA model increases the running time considerably. In addition, cLDA and struct-cLDA converges after roughly the same number of iteration (a few hundred for this dataset as depicted for the struct-cLDA model in Fig. 5.a). This result shows that while struct-LDA is seemingly more sophisticated than its ancestor cLDA, this sophistication does not incur an added penalty on the running time, on the contrary it runs even faster, and also enhances the performance qualitatively as shown in Table 1, quantitatively using perplexity analysis in Fig. 5.c (see Sec. 5.3.1), and enables sophisticated retrieval tasks (as will be shown in Sections 5.3 and 5.4).

Figure 5.

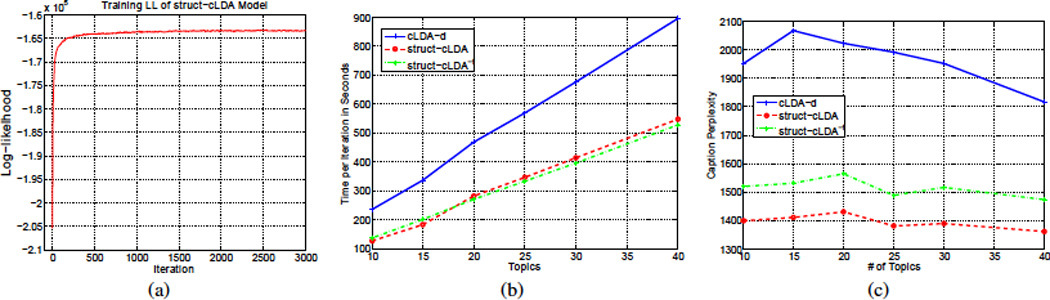
Understating model’s features contributions: (a) Convergence (b) Time per iteration and (c) Perplexity

5.3 Annotation Task

Since the main goal of the models presented in this paper is discovering the correspondence between mixed modalities, in this section, we examine the ability of the struct-cLDA model to predict the textual caption of a figure based on observing its image features, and the protein entity annotations of a given figure based on observing its image features and textual caption.

5.3.1 Caption Perplexity

For the first task, we used the perplexity of the figures’s caption based on observing its image features. Perplexity, which is used in the language modeling community, is equivalent algebraically to the inverse of the geometric mean per-word likelihood, that is:

$$\mathit{\text{Perplexity}}=\text{exp}\left[\frac{-{\mathrm{\Sigma }}_f\text{log}p({\mathbf{w}}^{\mathbf{f}},\{{\mathbf{w}}^{\mathbf{P}}\}|\{{\mathbf{g}}^{\mathbf{P}}\})}{{\mathrm{\Sigma }}_f(N_f+{\sum }_{p=1}^{P_f}{N}_p)}\right]$$

The above conditional probability can be computed by running the Gibbs sampling algorithm of Sec. 4 by iterating Eq. (5) only until convergence (with no words or protein entities used). A number of posterior samples can then be generated from this posterior by resuming the Gibbs Sampling on Eqs. (1, 3 and 4) while holding the image features topic indicators fixed. These samples are then used to compute the average likelihood of the caption conditioned on the image features. Fig. 5.(c) compares caption perplexity using cLDA-d, struct-cLDA, and struct-cLDA^−f. This experiment shows that modeling the figure as a whole via the struct-cLDA^−f model is better than duplicating the caption across panels, as this duplicating results in over representation and less accurate predictions. Moreover, factoring out background words, as in the struct-cLDA model, further improves the performance because, as was shown in Table 1, it excludes non content-bearing words from being associated with image features and thus misleading the predictions.

5.3.2 Protein Annotation

To annotate a test figure based on its image features and caption words, we first project the figure to the latent topic space using the observed parts of the figure by first iterating Eqs. (1,3,4,5 until convergence, and then collecting posterior samples for θ_f. Moreover, from the training phase, we can compute each topic’s distribution over the protein vocabulary (Ω_k). Finally, the probability that figure f is annotated with protein r, can be computed as follows:

$$P(r|f)=\sum _{k}P(k|f)P(r|k)=\sum _k{\theta }_{kf}{\mathrm{\Omega }}_{rk}$$ (6)

It is interesting to note that the above measure is equivalent to a dot product in the latent topic space between the figure representation θ_f and the latent representation of the protein entity r — as we can consider Ω_rk as the projection of the protein entity over the k^th topical dimension. Protein entities can then be ranked based on this measure. We compare the ranking produced by the struct-cLDA with that produced by LSI. Applying LSI to the training dataset results in a representation of each term (image feature, protein entity, and text word) over the LSI semantic space. These terms are then used to project a new figure in the testset onto this space using “folding” as discussed in [6]. Afterwards cosine similarity is used as the distance measure for ranking. We evaluated each ranking using three measures: the highest (low in value) rank, average rank and lowest rank (Rank at 100% recall) of the actual annotations as it appear in the recovered rankings. Fig. 6 shows the result across various number of topics (factors for LSI).

Figure 6.

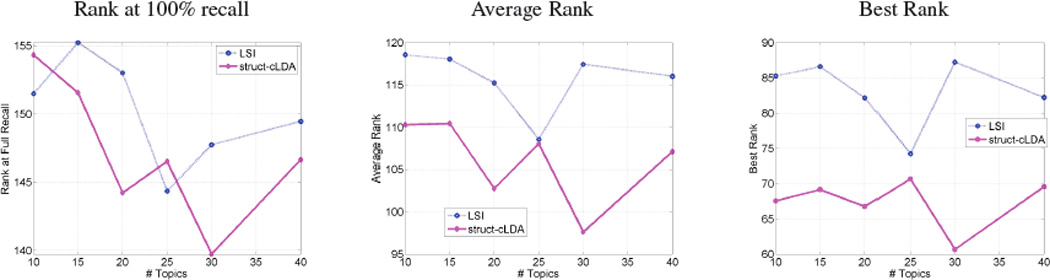
Evaluating protein annotation quality based on observing text and image features (Lower better)

5.4 Multi-Modal Figure Retrieval

Perhaps the most challenging task in multimedia retrieval is retrieving images based on a multimodal query. Given a query q = (ω₁, …, ω_n, r₁, …, r_m) composed of a set of text words and protein entities, we use the query langauge model [17] to evaluate the likelihood of the query given a test figure as follows:

$$P(q|f)=\prod _{w\in q}P(w|f)\prod _{r\in q}P(r|f)=\prod _{w\in q}[\sum _k{\theta }_{kf}{\beta }_{wk}]\prod _{r\in q}[\sum _k{\theta }_{kf}{\mathrm{\Omega }}_{rk}]$$ (7)

As we noted in Eq. (6), p(ω|f) is a simple dot product operation between the latent representations of word ω and the latent representation of figure f in the induced topical space. The above measure can then be used to rank figures in the testset for evaluation. We compared the performance of struct-cLDA to LSI. Each of the two models has access to only the image features of the figures in the testset. Query computations in LSI are handled using cosine similarity after folding both the test figures and the query onto the LSI space [6]. Fig. 7 shows the precision-recall curves over 4 queries. For a given query, an image is considered relevant if the query words appear in its caption (which is hidden from both models, and is only used for evaluation). As shown in Fig. 7, struct-cLDA compares favorably to LSI across a range of factors (we only show the result for K = 15 for space limitations but we observed the same behavior as we vary the number of factors).

Figure 7.

Illustrating figure retrieval performance. Each column depicts the result for a give query written on its top with the number of true positives written in parenthesis (the size of the test set is 131 figures). The figure shows comparisons between struct-cLDA and LSI. The horizontal lines are the average precision for each model. (Better viewed in color)

6. TRANSFER LEARNING FROM PARTIAL FIGURES

In this section we explore the utility of using non-visual data in the form of textual date accompanied with protein entities. Examples of such data include biological abstracts tagged with protein entities, and biological figures that lack visual data which we refer to as partial figures (i.e. figures with no panel images).Partial figures occur frequently in our pipeline due to the absence of the figure’s resolution which is necessary for normalization of the image features. We focus here on partial figures, although the former case can be handled accordingly. A partial figure f that comprises a set of global words and protein entities can be generated as follows:

1. Draw θ_f ~ Dir(α₁)

2. Draw λ_f ~ Beta (a, b)

3. For every word $w_n^f$ in global caption:

   1. Draw coin x_n ~ Bernoulli(λ_f)
   2. If(x_n = = 1)

      1. Draw topic $y_n^f~\text{Mult}({\theta }_f)$
      2. Draw $w_n^f|y_n^f=k~\text{Multi}({\beta }_k)$
   3. If(x_n = = 0)

      1. Draw $w_n^f~\text{multi}({\beta }_0)$
4. For every protein entity r_l in global caption:

   1. Draw topic ${\upsilon }_l~\text{Unif}(y_1^f,\dots ,y_{N_f}^f)$ display math
   2. Draw r_l|υ_l = k ~ Multi(Ω_k)

In essence, captions words are moved to the highest level in the correspondence hierarchy, and a factored, flat cLDA model is used to generate protein entities from the topic indicators used in generating the figure’s words. As we made explicit in the above generative process, the partial figures share the same set of topic’s parameters (β_1:K, Ω_1:K) with those parameters used to generate the full figures. Extending the collapsed Gibbs sampling algorithm from Sec. 4 is straightforward and omitted for space limitations.

To balance the contribution of partial and full figures to the learnt topics, we first extract the word and protein vocabularies using only the full figures. We then project the partial figures over this vocabulary (i.e we remove words and protein mentions that do not occure in the vocabulay extracted from the full figures). Finally, we keep partial figures that retain at least one protein annotation, and train the topic model using both full and partial figures. To evaluate the utility of partial figures, we used the protein annotation task of Sec. 5.3 (note that the test figures in this task are full figures, but the training set contains both full and partial figures). In this task, a test figure is annotated based on its text and image features. As shown in Fig. 8.(a), the performance increases as the ratio of partial figures in the training set increases . This behavior should be expected because the annotation is based on both the text and image features of the test figure. However, interestingly, we found that the annotation quality also increases if we annotate the test figures after observing only its image features as shown in Fig. 8.(b). This shows that, during training, the model was able to transfer text-protein correlations form the partial figures to image-protein correlations via the triplet topic representations.

Figure 8.

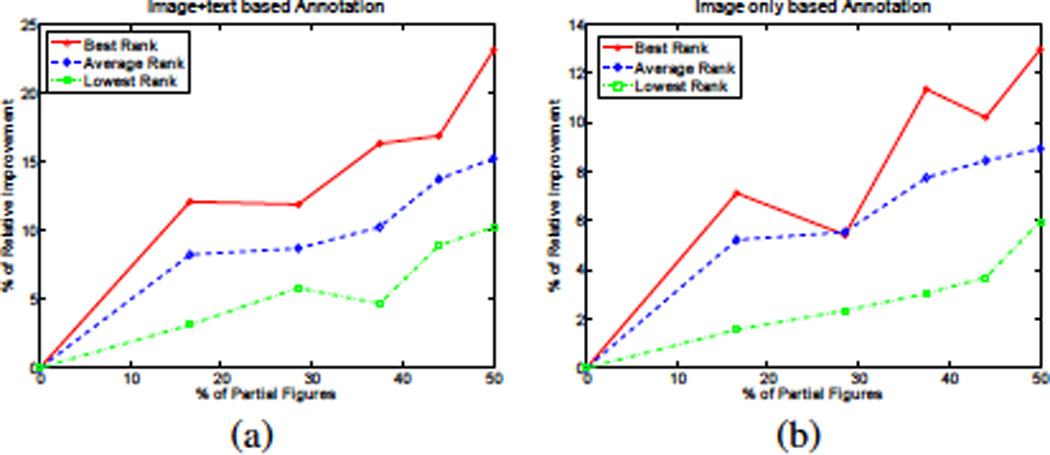
Illustrating the utility of using partial figures as a function of its ratio in the training set. The task is protein annotation based on (a) Figure’s image and text and (b) Image content of the figure only

7. CONCLUSIONS AND DISCUSSION

In this paper we addressed the problem of modeling structurally and multimodally annotated biological figures for visualization and retrieval tasks. We presented the structured correspondence LDA model that addresses all the challenges posed by these figures. We illustrated the usefulness of our models using various visualization and retrieval tasks. Recent extensions to LDA and cLDA bear resemblances to some features in the models presented in this paper, such as [15] in its ability to model entities, and [2, 9] in their abilities to model many-many annotations. However, our goal in this paper was mainly focused on modeling biological figures with an eye towards building a model that can be useful in various domains were modeling uncertain hierarchical, scoped associations is required. In the future, we plan to extend our model to incorporate other sources of hierarchal correspondences like modeling the association between figures and the text of their containing papers.