Expanding the potential of standard flow cytometry by extracting fluorescence lifetimes from cytometric pulse shifts

Abstract

Fluorescence lifetime measurements provide information about the fluorescence relaxation, or intensity decay, of organic fluorophores, fluorescent proteins, and other inorganic molecules that fluoresce. The fluorescence lifetime is emerging in flow cytometry and is helpful in a variety of multiparametric, single cell measurements because it is not impacted by nonlinearity that can occur with fluorescence intensity measurements. Yet time-resolved cytometry systems rely on major hardware modifications making the methodology difficult to reproduce. The motivation of this work is, by taking advantage of the dynamic nature of flow cytometry sample detection and applying digital signal processing methods, to measure fluorescence lifetimes using an unmodified flow cytometer. We collect a new lifetime-dependent parameter, referred to herein as the fluorescence-pulse-delay (FPD), and prove it is a valid representation of the average fluorescence lifetime. To verify we generated cytometric pulses in simulation, with light emitting diode (LED) pulsation, and with true fluorescence measurements of cells and microspheres. Each pulse is digitized and used in algorithms to extract an average fluorescence lifetime inherent in the signal. A range of fluorescence lifetimes is measurable with this approach including standard organic fluorophore lifetimes (∼1 to 22 ns) as well as small, simulated shifts (0.1 ns) under standard conditions (reported herein). This contribution demonstrates how digital data acquisition and signal processing can reveal time-dependent information foreshadowing the exploitation of full waveform analysis for quantification of similar photo-physical events within single cells. © 2014 The Authors. Published by Wiley Periodicals, Inc.

Fluorescence lifetime detection continues to emerge as a quantitative methodology for reporting the state and behavior of various organic fluorophores, particularly when expressed within intracellular environments. The fluorescence lifetime, or average time a fluorophore resides in its excited state, is known to fluctuate with molecular composition and changing microenvironments in which any given fluorophore resides ¹. The excited state lifetime of a molecule can be considered as a state function because it does not depend on initial perturbation conditions. For example, it is not affected by the magnitude and exposure time of the excitation source on the fluorescent species nor the inherent and periodic photo bleaching of the fluorophore itself ^2,3. In addition, the fluorescence lifetime is independent of the total emission output for a range of fluorophore concentrations when intermolecular chemical and photonic interactions are absent ^4,5. These properties of fluorescence decay kinetics (i.e. environmental sensitivity and parametric independence) render the fluorescence lifetime a complementary quantitative method to traditional fluorescence intensity measurements.

The fluorescence lifetime has been used in single cell analysis quite extensively, and in more recent studies, it is used to confirm FRET efficiency and intermolecular distances between FRET partners. The fluorescence lifetime is a powerful metric of FRET, which enables the validation of protein function and signaling events that occur inside mammalian cells. Some examples of these include understanding the dynamics of conformational changes of epidermal growth factor receptor ⁴, the occurrence of protein-protein interactions ⁵, the visualization of intracellular signaling dynamics ⁶, and the presence of matrix metalloproteinase-2 in tumor cells ⁷. These examples of recent studies exploit the fluorescence lifetime to confirm if and when FRET occurs. In addition to FRET applications, the fluorescence lifetime of fluorescent proteins, intrinsic, and extrinsic fluorophores has recently been measured in order to track intracellular movement of proteins during autophagy ⁸, to localize groups of nanoparticles inside the cells ⁹, to visualize intracellular delivery of doxorubicin ¹⁰ and to track metabolic changes in viable cells that are label-free ¹¹. Measuring the fluorescence lifetime of organic and inorganic molecules in these contexts is important to alleviate spectral overlap issues and leverage the autofluorescence background in cells and tissue for optical-based diagnostics and theranostics. In addition to recent applications, historic uses of the fluorescence lifetime in single cells include characterizing cellular microenvironments indirectly by measuring how the de-excitation times of molecular probes are altered when the biochemistry surrounding the chromophore changes. These changes might include pH, temperature, recruitment of quenchers, levels of oxygen or atoms with net charges, organelle alteration, and nearby proteins associating and de-associating from each other ^2,9–13. Therefore singular changes in these factors (e.g. rise vs. fall, presence vs. absence, increase vs. decrease) are “reported” by fluorescence lifetime differences.

Fluorescence lifetime measurements can be quite powerful when combined with flow cytometry where cell-by-cell tracking of conserved intracellular events and high-throughput cell-surface phenotype discrimination with multiple fluorescent tags are necessary. Time-resolved cytometry studies began to rise in the late 1990s whereby experimentation with lifetime-dependent cytometry began to demonstrate utility in situations where the estimation of receptor site saturation on cell surfaces was important yet difficult with intensity-based measurements that suffer from nonlinearity owing to fluorophore self-quenching ⁶. It was also noted as useful for microsphere-based multiplexing and cell cycle studies ¹². A number of applications with DNA intercalating dyes were particularly popular because of the natural change in the fluorescence lifetime of ethidium bromide and propidium iodide when bound to nucleic acids. For example, fluorescence lifetime analysis enabled extraction of total DNA content in the presence of RNA ¹³, and reported apoptotic from nonapoptotic cell populations using deuterium oxide treatments, which enhanced lifetime shifts for fluorophores bound to fragmented DNA ².

Average fluorescence lifetimes of organic molecules range from about 100 ps to 20 ns and are measured with a flow cytometer by changing how the cells are excited by laser light. The two main approaches that have been implemented in cytometry are “frequency-domain” and “time-domain” methods. With frequency-domain systems, the excitation laser is sinusoidally modulated at high frequencies, which results in oscillatory fluorescence at the same frequency as the incident light, yet the modulated fluorescence light is phase shifted and amplitude attenuated relative to the excitation source. The phase shift ^14–16 ϕ, and demodulation,¹⁷ m, are proportional to fluorescence lifetime, τ, as shown by Eq. ¹ when assuming single exponential decay kinetics.

(1)

With time-domain methods, the excitation source is typically pulsed at a femtosecond rate and directed onto the sample or cell. Assuming single exponential decay kinetics the intensity function after pulse excitation can be expressed as:

(2)

where I₀ is the intensity at time, t = 0. The fluorescence lifetime is then resolved by observing the fluorescence decay over time (picoseconds to nanoseconds) with a gated photodetector and fitting the data to an appropriate exponential decay model such as that shown by Eq. ^{2 18}.

Both time- and frequency-domain approaches significantly increase the cost and complexity of a traditional flow cytometer. The limited numbers of time-domain flow cytometry systems that have been tested require precise timing of the detectors, yet can be useful for rare event detection ^6,8, characterization of long-lived lanthanide species ¹⁹, biological process monitoring ²⁰, and environment sensing ²¹. Alternatively frequency-domain theory has made phase sensitive flow cytometry (PSFC) a more practical approach, most importantly for cell sorting ²². However, several high-frequency hardware components must be added to a simple flow system to perform PSFC ^15,23. These modifications include high frequency mixing and filtering steps when the data acquisition system employed is unable to sample the high-frequency signals. Additionally, digital phase sensitive flow cytometry (dPSFC) approaches have been demonstrated ^24,25 owing to the dramatic increase in processing speeds of computers and data acquisition electronics. dPSFC replaces the complex analog hardware with a high speed analog-to-digital converter ²⁶ (ADC) and flexible digital signal processing ²⁷ (DSP) algorithms. A dPSFC system simplifies the hardware required yet still relies on modulated lasers and high-speed detection electronics to preserve the modulated optical signals.

In this contribution, we present a paradigm shift from laser pulsed time-domain and laser modulated frequency-domain flow cytometry. We introduce a new method to detect fluorescence decay using information that can be extracted directly from traditional flow cytometry waveforms. This approach avoids modulating the laser at different frequencies (pulsed or modulation) and effectively presents a platform for lifetime detection that could more practically be implemented on any standard flow cytometer. The new “non-modulated” lifetime parameter is taken directly from amplified cytometry waveforms after digitization on an event-by-event basis. In the following sections we describe the process of non-modulated fluorescence lifetime cytometry (nFLIC), evaluate by simulations and experimentation, and suggest three possible signal-processing algorithms that can be used to extract the average fluorescence lifetime.

Materials and Methods

Theory

The methodology of nFLIC involves approximating the average fluorescence lifetime by performing signal processing on standard photodetector-based, correlated, and digitized fluorescence and scattering signals. These signals are often referred to as “cytometric pulses” or “waveforms” because they are the result of a fluorescently labeled cell's rapid transit through a tightly focused laser beam with a Gaussian profile ²⁸. The Gaussian profile is mathematically expressed as:

(3)

where the values a, b, and c in Eq. ³ are constants representing the height of the curve's peak, the center position of the peak, and the width of the curve, respectively. During this transit, fluorescence emission light and Rayleigh scattered light increase, reach a peak, and then decrease when the cell leaves the excitation spot thus forming the prototypical Gaussian-like shape (Fig. 1A). When compared closely, the correlated fluorescence and Rayleigh scattered Gaussian waveforms are delayed in time relative to each other owing to the inherent fluorescence decay kinetics of fluorophores in or on a given cell. Thus the nFLIC approach observes pairs of nonmodulated waveforms (i.e. correlated light scatter and fluorescence) and extracts through signal processing the differences in delay times between each pair. Conceptually this is similar to PSFC because the increase and decrease in fluorescence and Rayleigh scattered light intensity is similar in shape to one cycle of a sinusoidally modulated signal (Fig. 1B). Applying nFLIC theory also relies on the notion that scattered light waveforms adequately represent the behavior, timing, and profile of the excitation source. In order to compare the time-shift between pairs of waveforms a singular “time value,” that is characteristic of each correlated waveforms is required; this value can be thought of as the “pulse-time” of any given waveform. After validating and determining pulse-times for each pair of fluorescence and scattering waveform a simple subtraction is made to identify the average time-delay. The subtracted value is referred to throughout our analyses as the fluorescence pulse delay (FPD).

Figure 1.

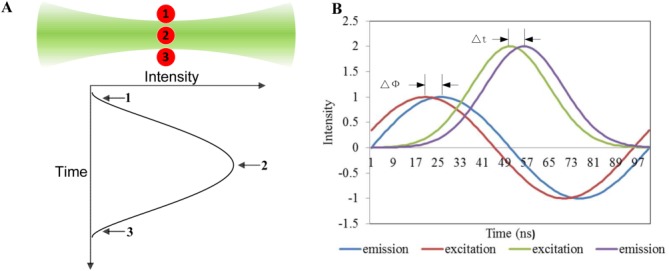
Illustration showing the theory behind the nFLIC approach. A: Image depicting the transit of a fluorescently labeled microsphere (red circles) through a focused laser, and a Gaussian-like trace reflecting the resulting signal. The fluorescence emission begins to increase at position 1, peaks at position 2, and decreases as the microsphere moves from position 2 to position 3. B: Traces of sinusoidal waveforms demonstrating how the fluorescence lifetime can be measured using frequency-domain analysis as well as the nFLIC approach. The lag Δϕ in the emission signal (blue line) relative to the excitation signal (red line) is revealed in a phase shift that is proportional to the fluorescence lifetime [see Eq. ¹]. Compared with the frequency-domain approach, only one “modulation cycle” is present using nFLIC. The purple trace indicates a time-delayed fluorescence signal, Δt, relative to the green line, a side or forward scatter signal. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Based on the Taylor expansion series, a standard tangential function tanϕ in Eq. ¹ is approximated by:

(4)

With traditional frequency-domain theory [see Eq. ¹], as the modulation frequency, ω, becomes lower, the tanϕ and ϕ also reduce given a constant lifetime τ, [see Eq. ⁴]. Thus, the value of tanϕ and ϕ begin to converge to the same value. When the ϕ is small enough (<5 angular degrees) at low modulation frequencies, the small-angle approximation (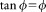) is applied and Eq. ¹ can be rewritten as:

(5)

Rearranging results in:

(6)

where f is the modulation frequency in Hz, T is the period of the sinusoid modulation function, and ϕ is the phase shift in radians. The ratio,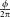, represents the percentage of the phase shift compared with one cycle, while 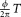represents the time delay between a fluorescence signal and excitation signal in seconds. By following this rationale [Eqs. ^4–6], we establish a valid representation of the fluorescence lifetime's proportionality to the time delay between the fluorescence and side scattering signals (i.e. FPD values).

Signal Processing

Three signal processing algorithms were developed to extract a pulse-time and FPD parameter from pairs of correlated side scatter and fluorescence waveforms. For all approaches, MATLAB (MathWorks®, Natick, MA) was used to process the digitized waveforms in order to extract the pulse-time for each waveform. The pulse-times for correlated waveform pairs (from scatter and fluorescence detectors) were then subtracted from each other to calculate the FPD values for each event. The approaches include a ‘direct' method, a Gaussian-fitting method, and a half-area method.

Direct method

Calculation of pulse-times “directly” involves selecting the time-location for the maximum value of each waveform. This simple approach will be limited by the time between samples, since it simply selects the maximum sample value and determines at what time that sample was captured.

Gaussian-fitting method

A regression technique was also implemented which involves fitting the digitized waveforms to a standard Gaussian function. Equation ³ represents this function where the values a, b, and c represent the height of the curve's peak, the center position of the peak, and the width of the curve, respectively. Standard nonlinear regression provides the parameters a, b, and c after initial guesses are provided. The advantage of this approach is the ability to determine a pulse-time with high temporal accuracy. The fitting method is then evaluated using the sum of squared errors.

Half-area method

The half area method is an approach that calculates the centroid of each pulse and uses that as the pulse-time. This is implemented by sequentially summing the digitized values starting at the beginning of the waveform, and extrapolating when the sum reaches exactly half of the total area (the sum of all of the samples).

The calculated FPD parameters were converted to list-mode form to ultimately display and analyze using standard cytometric histograms. All data were imported into FCS Express (DeNovo™ Software, Los Angeles, CA) for plot generation and statistical analyses.

Modeling, Simulations, and Experimentation

The nFLIC method is evaluated in four ways: ¹ by modeling of cytometric waveforms in MATLAB; ² by generating simulated flow cytometry signals using an arbitrary function generator and delay lines; ³ by generating noise-free optical signals through a light-emitting diode (LED); and ⁴ by measuring real fluorescence lifetime values from true fluorescence and side-scatter waveforms with a standard flow cytometer. The signals for each step were collected with a high-speed data acquisition system and analyzed by the three aforementioned mathematic methods. Below is a description of the modeling approach, simulation, and experimental set up.

Modeling

Fluorescence signals are modeled with MATLAB by Eq. ⁷, which is a convolution of the fluorescence impulse response function [Eq. ²] and a Gaussian function [Eq. ³]. The side scatter signals can be modeled by Eq. ³, which is the Gaussian function that directly represents the excitation profile.

(7)

The analog convolution [Eq. ⁷] of the fluorescence pulse response function and the Gaussian functions generated from the laser profile is an error function. We purposely modeled the convolution digitally with computational methods to circumvent this issue for the first phase of our evaluation of nFLIC. The fluorescence signals modeled with MATLAB had pulse widths of 5 to 20 µs, delays from 0 to 30 ns, and discrete step sizes of 0.01 ns.

Delay-line system

The next evaluation was accomplished with simulated signals using standard function generators and delay lines. We collected Gaussian waveforms generated by a dual channel arbitrary function generator (Tektronix Inc., Beaverton, model AFG3120). Thus, true Gaussian-shaped pulses were artificially created having an average peak voltage of 5-V and average pulse full width at half maximum (FWHM) ranging from 1 to 3 µs. The peak voltage was controlled to optimize signals into the digital data system. For the nFLIC study, we synchronously generated two Gaussian pulses and delayed them in time (i.e. imparting a simulated FPD) by adding delay lines. Then the signals were routed to the two inputs of a high-speed data acquisition system (DAQ). The digitization rate of the DAQ system was 50 mega samples per second (MSPS), which is equivalent to a 20 ns interval between any two adjacent points. Figure 2A, is an illustration of the delay line instrumentation. In order to simulate actual cytometric transit times we tested different pulse widths and verified with an oscilloscope (Tektronix, Fort Worth, Texas, TDS 2004B) according to visible tail-to-tail widths. The FWHM observed was 1, 2, and 3 µs. Additionally, a range of fluorescence pulse delays between the “scattering” and “fluorescence” waveforms was tested by artificially dialing in seven delay times with delay lines to range from 0, 0.7, 3, 5.5, 10.5, 21 to 44.5 ns. The time delays between two Gaussian waveforms were also verified by oscilloscope (Tektronix, Fort Worth, Texas, TDS 2004B). Results presented herein are for 2 µs transit times. For each single delay time, 1000 events were collected and processed.

Figure 2.

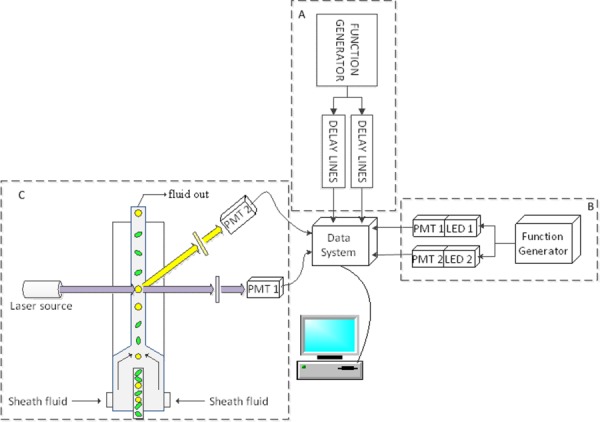
A simple diagram of the nFLIC instrumentation. A: Gaussian-like waveforms are generated digitally using a function generator (Tektronix Inc., Beaverton, model AFG3120). Two waveforms are passed through separate delay lines (Allen Avionics Inc., Mineola) to introduce FPDs between the artificial signals. The waveforms are digitized at a sampling rate of 50 MSPS and input into two separate channels on the data system. A fire-wire connected computer is used for offline analysis using MATLAB (The MathWorks®). B: Identical LEDs are pulsed using a function generator (Tektronix Inc., Beaverton, model AFG3120). Each LED is pulsed at exact repetition rates; a delay between both is introduced. LED light output from each source is focused (diffusely) onto two separate but identical PMT (Hamamatsu, San Diego, Model R636-10) windows. No light attenuation was performed. C: A 488-nm OBIS™ laser (Coherent Inc.) at 150 mW excites microspheres driven by a pressurized fluidic system. The yellow and green colored circles and ovals represent injected microspheres, although for a given experiment only one type of microspheres was measured at a time. The laser was focused with two crossed cylindrical lenses onto the core of the flow stream. At 90-degrees fluorescence (PMT 1) and side scattering signals (PMT 2) are focused onto the side of two similar PMTs (Hamamatsu, San Diego, Model R928). Both signals are digitized and collected with the same 250 MSPS high-speed data acquisition system. After collection of the full waveforms by a fire-wire connected PC, MATLAB was used for offline analyses. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

LED hybrid system

A cross between simulated waveforms and real cytometry waveforms were established with a hybrid system. This compact system was constructed so that standard photomultiplier tubes (PMTs) could be used and allow us to evaluate real pulses from real photodetectors, while still permitting very clean Gaussian-like signals. Therefore, two PMTs were configured to collect light signals from light emitting diodes (LEDs) that were repetitively pulsed yet delayed in time by amounts typical of real fluorescence decays (i.e. nanoseconds). The LED-based hybrid system is shown in Figure 2B. Two LEDs (Optek, Carrollton, TX, OVLGY0C9B9) were pulsed with a dual channel arbitrary function generator (Tektronix Inc., Beaverton, model AFG3120) and each focused onto a separate PMT (Hamamatsu, Bridgewater, NJ, H6780-20). The signals from the two PMTs were preamplified by custom-built transimpedance amplifiers with 80 k gain. The signals were routed to the two inputs of the same high-speed data system. The waveforms collected from two PMTs were inspected with an oscilloscope and were found to have an approximate “transit time” of 10 µs. In order to verify the three processing methods, a series of five artificial fluorescence delays were introduced by setting the FPD values between the LED pulses to be 0, 5, 10, 50, and 100 ns. For each group of delays, 1,000 events were collected and processed.

Real flow cytometry samples

All three processing methods were finally evaluated with true cytometric waveforms using a modified FACSVantage™ SE flow cytometer (Becton Dickinson, CA) with an updated DAQ, with a sampling rate of 250 MSPS. A 488-nm, 150 mW solid state OBIS™ laser (Coherent, Inc., Santa Clara, CA, 1220123) was focused to a ∼30 µm spot size onto the sample stream. Sheath was pressurized at 6 psi for standard laminar velocities and hydrodynamic focusing. The transit times for each event were found to be approximately 8 µs. Fluorescence and side scatter detection were collected with a 496-nm long pass filter and 488-nm band pass filter in microsphere experiments, and forward scatter signals were collected as opposed to side scatter signals for the fluorescently labeled cell experiments. All cytometry components (i.e. fluidics, PMTs, CellQuest™ Pro analysis software) were standard to the FACSVantage (Becton Dickinson, CA). On this instrument are also high frequency preamplifiers (60 dB, DC-100, Advanced Research Instruments, CO). During sample measurement both the side scattering (or forward scatter) and correlated fluorescence signals from each PMT were preamplified then directed into respective input channels of the high speed DAQ system. The PMT voltages were kept constant between experiments. As with the simulation and hybrid instrument studies, a total of 1,000 events were digitized, saved, and collected for off line signal processing. Figure 2C is an abbreviated illustration of the cytometry system.

Calibration

Calibration is necessary for each mathematical method for two reasons: ¹ to correct for inherent time delays introduced by hardware variables such as differences in cable length, and ² to determine unknown FPD values based on known fluorescence lifetime reference values. The calibration steps for the simulation and LED experiments involved calculating with all models an FPD value between two waveforms for scenarios when no actual delay was introduced into the measurement (i.e. 0 ns). One might expect to obtain a zero FPD-value under these conditions, however, a non-zero delay times do occur owing to the reasons listed above. Therefore, the FPD values we calculated using all three mathematic methods, during the 0 ns experiments, were used for calibration. The inherent delays were subtracted from all other experimental FPD results using the respective mathematical method from which they originated. For measurements using fluorescent microspheres and fluorescently labeled cells, fluorescein, which has a well-characterized fluorescence lifetime, was chosen as a reference fluorophore standard. The mean of the FPD values measured using any given fluorescence microsphere was recorded and calibrated to the a priori fluorescence lifetime of fluorescein. In other words, the difference between the mean FPD value and known lifetime was found.

Fluorescence microspheres

Three fluorescently tagged microsphere samples (Bangs Laboratories Inc., Fishers, IN) were selected for the fluorescence lifetime measurements. The microspheres included fluorescein-tagged (Catalog Code: 891), phycoerythrin-tagged (PE, Catalog Code: 899), and propidium iodide-tagged (PI, Catalog Code: 892). Each of these fluorophores has high quantum efficiency at the excitation wavelength (488 nm). All fluorescence microsphere populations selected had the same diameter range of 7 to 9 µm. Additionally the fluorophores were chosen for their known fluorescence lifetime values; fluorescein ²⁹, phycoerythrin ³⁰, and propidium iodide ⁸ have approximate lifetimes of 4 ± 0.2 ns, 2.5 ± 0.6 ns, and 16 ± 0.5 ns, respectively. A small volume of the microspheres were diluted in DI water to a concentration of 1 × 10⁶/mL before use.

Cell Staining

Supporting Information data include measurements using Chinese Hamster Ovary (CHO) cultures. For this work, we demonstrate nFLIC in cells labeled with DNA intercalating fluorophores. CHO cells were grown attached to the wall of T-25 flasks (Santa Cruz Biotechnology, Santa Cruz, CA) in DMEM/F12 media (Life technologies, Grand Island, NY) supplemented with 10% Fetal Bovine Serum. Standard mammalian cell culture incubation was followed (i.e. 80% relative humidity, with 5% CO₂ at 37°C). At slightly under full confluence the cells were detached, (1 mL of 0.25% Trypsin-EDTA, Life technologies, Grand Island, NY), centrifuged, and resuspended in phosphate buffered saline to obtain three volumes at a concentration of 10⁶ cells/mL. After fixation with 95% ethanol solution the cells were treated with RNase at 30 µL of 1 µg/mL and fluorescently stained with ethidium bromide (EB, AnaSpec, Inc., Fremont, CA) or propidium iodide (PI, AnaSpec, Inc., Fremont, CA). EB and PI are DNA intercalating agents often used for cell viability and cell cycle analyses (31–34). When excited with 488 nm, both of the dyes fluoresce red. The fluorescence lifetime of EB increases dramatically from 1.67 ns to 19 ns when bound to DNA content ³⁵, and the fluorescence lifetime of PI has been reported as 16 ns ^25,36.

Results

Simulation

Figure 3 is a plot of fluorescence lifetime versus FPD using computational MATLAB models on delays that range between 0 and 30 ns with a 10 µs transit time. The solid line in Figure 3 represents the correlation between FPD values calculated and the fluorescence lifetimes simulated. The dashed line in Figure 3 is a diagonal reference line, which passes through the origin with a slope of unity. If the FPD values perfectly predict the fluorescence lifetime, the solid line should coincide with the dashed line. As shown in the plot, FPD values closely match the fluorescence lifetimes. However, as the fluorescence lifetime increases the FPD (solid line) values deviate (dashed line). This is expected; when the fluorescence lifetime is longer, the delay is also longer, and the corresponding phase shift ϕ increases so that the small-angle approximation becomes less accurate. As is shown in Figure 3, we noticed for common transit times, the fluorescence lifetime when under 20 ns (absolute error <0.7 ns) can be very well represented by FPD values, but becomes inaccurate when the fluorescence lifetime is longer.

Figure 3.

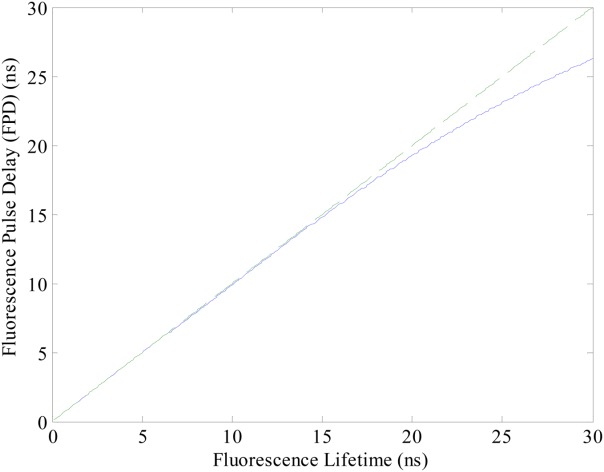
Relationship between fluorescence lifetime and FPD values for a 10 µs transit time. The solid line represents the FPD values calculated for a simulated range of fluorescence lifetimes. The dashed line represents a diagonal reference line passing through the origin with the slope of 1. The solid line will coincide with the dashed line if the FPD values perfectly predict the fluorescence lifetime. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Delay Line Experiments

Figure 4 presents histograms obtained with the nFLIC approach when the waveforms were simulated with a function generator and delay lines. The figure displays results from all three processing methods. The results are from correlated waveforms with 2 µs transit times, delayed in time from each other by 3 ns. Figure 4A presents a histogram generated by the direct method. Three markers drawn on this histogram (M1, M2, and M3, colored red) indicate that 26.3% of all artificially generated events were 20 ns and 73.3% events were 0 ns when resolved with the direct method approach. The remaining FPD events were 40 ns. The standard deviation of all populations was 0 ns, illustrating the discrete distribution properties of the direct method. That is, of all one thousand events with an artificially introduced lifetime of 3 ns only FPD values of 0, 20, and 40 ns resulted. These are far from 3 ns because the sampling interval rate of the DAQ system was 20 ns. When all populations are grouped and averaged the mean is 5.42 ns (−0.11 ns after calibration), with a standard deviation of 9.07 ns. Figure 4B is a histogram of the FPD values for all events calculated using a Gaussian function regression. Of all events measured, 98% produced similar FPDs (see statistics within the lower and upper bound of Marker 4) with a mean of 6.057 ns (2.9 ns after calibration) and standard deviation of 0.35 ns. The histogram in Figure 4C provides the half area processing method results where 98.2% of all events within Marker 5 have a mean FPD value of 5.697 ns and 2.87 ns after calibration with standard deviation of 0.36 ns. All statistics for these data are provided in Table1.

Figure 4.

Example results from the delay line experiments. In the three panels, A–C: different FPD values are compared for each signal processing approach implemented. The statistical values for each of these panels are shown in the Table1. For this example, the simulation results chosen were for a “transit time” of 2 µs and a simulated FPD of 3 ns, as measured by an oscilloscope (Tektronix, Fort Worth, TX, TDS 2004B). A: Histogram of the FPD values calculated using the direct method with red markers labeled M1, M2, and M3 placed on the histogram to indicate the statistical outcomes in the population after the FPD calculation. B: Histogram of FPD values calculated from the Gaussian regression method with a red marker labeled M4. C: Histogram of FPD values calculated from the half-area interpolation method with a red marker labeled M5. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Table 1.

Comparison of FPD values determined by the direct, Gaussian-fitting and the half-area methods

Method	Marker	No. events	No. gated events	Arithmetic mean (ns)	Standard deviation (ns)
Direct	M1	263	26.3	0	0
	M2	733	73.3	20	0
	M3	1000	100	5.42	9.07
GaussFit	M4	980	98	6.057	0.35
Half-area	M5	982	98.2	5.697	0.36

The example data are when delay lines are used with a 3.0 ns delay imposed.

Figure 5 provides three x–y plots of the seven calculated mean FPD values versus seven generated delay values obtained by the three FPD processing methods. Again, these results pertain only to data collected with function generator-generated waveforms. A linear fit is also applied to evaluate the accuracy of each method. As these delays are not actual fluorescence lifetimes, the regression should yield near-perfect fits. The direct method (panel A) deviations are greater than the other two methods (panel B and C), with adjusted r² values of 0.84232, 0.99991, and 0.99988, respectively.

Figure 5.

x–y scatter plot of FPD estimates versus artificial delays (red lines are linear regression, black bars represent standard deviations). A–C present FPD values calculated from the direct, Gaussian-fitting, and half-area methods, respectively. Inset tables provide parameter results for each of the mathematic methods. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

LED Experiments

The different “fluorescence lifetimes” that were collected after artificially introducing delays using the LED-dependent hybrid cytometer are provided in Figure 6. The results in Figure 6 are for a 100 ns lifetime yet the variability in the data are representative of the several other delays generated between the hypothetical “scatter” and “fluorescence” waveforms. The direct approach (Fig. 6A) yielded a mean of 184.48 ns (102.48 ns after calibration) for 100% of all events (shown with the red M3 marker) and a standard deviation of 8.49 ns. The mean values under Markers 1 and 2 are 180 and 200 ns, respectively—again showing the discrete distribution properties of the direct method with a DAQ resolution of 20 ns. Figures 6B and 6C provide the Gaussian-fitting and half-area method results. The Gaussian fitting resulted in a mean FPD of 183.67 ns (100.05 ns after calibration) with a standard deviation of 0.62 ns, and the half-area method resulted in a mean FPD of 179.02 ns (97.33 ns after calibration) with a standard deviation of 1.16 ns. All statistics are provided in Table2.

Figure 6.

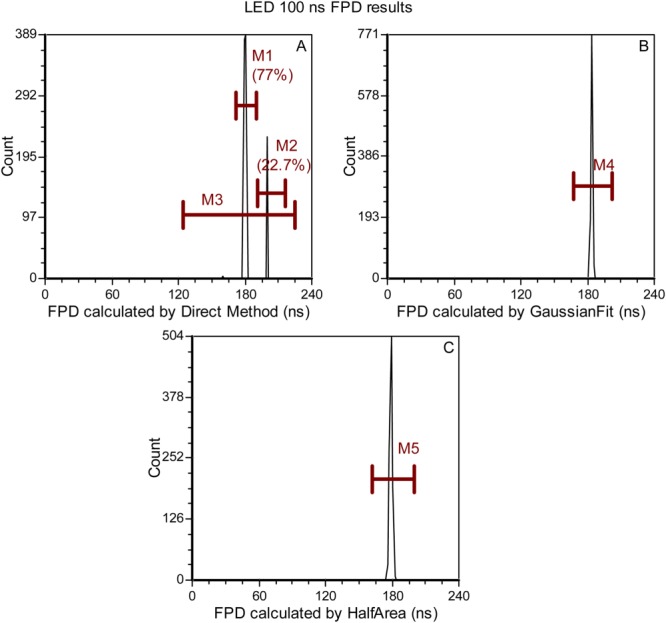
Example results from the hybrid-LED cytometry nFLIC experiments. In the four panels, A, B, and C different FPD values are compared for each signal processing approach implemented. Also, the statistical values for each of these panels are shown in the Table2. For this example, the simulation results chosen were for a transit time of 10 µs and a simulated FPD of 100 ns, as measured by an oscilloscope (Tektronix, Fort Worth, TX, TDS 2004B). A: Histogram of the FPD values calculated using the direct method with red markers labeled M1, M2, and M3 placed on the histogram to indicate the statistical outcomes in the population after the FPD calculation. B: Histogram of FPD values calculated from the Gaussian regression method with a red marker labeled M4. C: Histogram of FPD values calculated from the half-area interpolation method with a red marker labeled M5. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Table 2.

Comparison of FPD data determined by the direct, Gaussian fitting, and half-area methods

Method	Marker	No. events	% of Gated events	Arithmetic mean (ns)	Standard deviation (ns)
Direct	M1	159	77	180	0
		M2	266	22.7	200	0
		M3	1,000	100	184.48	8.49
GaussFit	M4	1,000	100	183.67	0.62
Half-area	M5	1,000	100	179.02	1.16

The example data are taken from LED experiments using 100 ns imposed delay.

The LED experiments were also evaluated by creating x-y plots of the estimated mean FPD calculated versus the true input delay (Fig. 7). As with the function-generator study, these delays are not actual fluorescence lifetimes therefore linear regression should yield near-perfect fits. Five different delays were introduced and the mean FPDs with their respective standard deviations are plotted. A linear regression is shown to evaluate the accuracy of each method. The direct method (panel A) has larger standard deviations compared with the other two methods (panels B, C). In addition, the linear fit for the direct method deviates greatly from a linear function (r² = −0.11073 intercept = 8.088, slope = 0.345). Compared with the direct method, the Gaussian-fitting and half-area results (panels B, C) predict the true FPD values quite accurately (Gaussian-fitting: r²= 0.99968, intercept = 1.012, slope = 0.993. Half-area: r² = 0.99969, intercept = 0.994, slope = 0.966).

Figure 7.

Evaluation of FPD value measurements by direct, Gaussian-fitting and half-area methods for LED experiments. A–C present FPD values calculated from the direct, Gaussian-fitting, and half-area methods, respectively. The red lines are the linear function best fit to the mean of PFD values for different calculated FPD values. Black bars represent the standard deviation for each of the delay experiments. Tables in each panel provide fitting parameters for each method. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

FACSVantage™ SE Cytometry Experiments Using Fluorescence Microspheres

The FPD results computed after collection of waveforms from the FACSVantage SE system using the fluorescein-, PE-, and PI-labeled microspheres are provided in Figure 8. The histograms provide results from the Gaussian-fitting and half-area methods. Three markers, M1, M2, and M3, provide a reference framework for all reported statistics. Figure 8A shows the FPD histogram extracted from the Gaussian-fitting method. The mean FPD values of fluorescein, PE and PI were 7.51, 5.67, and 21.86 ns, respectively. After calibration based on the known fluorescence lifetime of fluorescein (4 ns), the mean FPD values of fluorescein, PE and PI were 4.0, 2.16, and 18.35 ns with standard deviations of 1.82, 1.91, and 1.78 ns, respectively. Figure 8B is a FPD histogram of the half-area algorithm results. The mean FPD values of fluorescein, PE, and PI calculated from half-area method were 8.11, 5.82, and 21.10 ns, respectively. After calibration based on the known fluorescence lifetime of fluorescein (4 ns), the mean FPD values of fluorescein, PE and PI were shifted to 4.0, 1.71, and 16.99 ns with standard deviations of 1.83, 2.02, and 1.81 ns, respectively. Table3 provides a summary.

Figure 8.

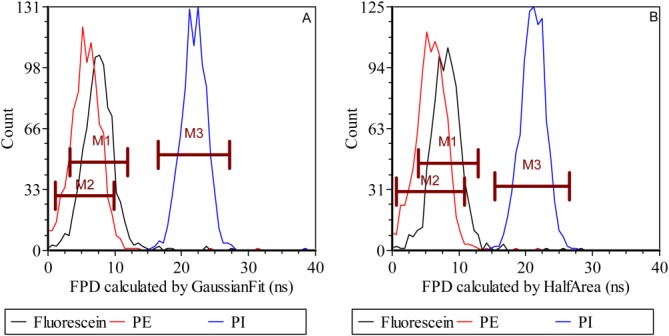
Histograms of FPD values for fluorescein, PE and PI microsphere data using the Gaussian-fitting (A) and half-area (B) methods. Three markers (M1, M2, and M3) were used to calculate the mean FPD values and other statistical parameters. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Table 3.

Comparison of FPD data determined with the Gaussian-fitting and half-area methods

Microspheres	Methods	Mean (ns)	Calibrated mean (ns)	Standard deviation (ns)
Fluorescein	GaussFit	7.51	4.0	1.82
	Half-area	8.11	4.0	1.83
Phycoerythrin	GaussFit	5.67	2.16	1.91
	Half-area	5.82	1.71	2.02
Propidium iodide	GaussFit	21.86	18.35	1.78
	Half-area	21.10	16.99	1.81

Data are from measurements of fluorescence microspheres.

FACSVantage™ SE Cytometry Experiments Using Labeled Cells

FPD results computed after collection of waveforms of the EB and PI labeled cells are provided in Supporting Information Figure S1. The histograms are of the Gaussian-fitting and half-area methods. Two markers, M1 and M2, provide a reference framework for all reported statistics. After calibration based on the known fluorescence lifetime of fluorescein (4 ns) microspheres, the mean FPD values of EB and PI determined using Gaussian fitting were found to be 18.51 ns and 15.93 ns with standard deviations of 1.74 ns and 1.37 ns, respectively. The calibrated mean FPD values using the half-area method were 23.69 ns and 15.45 ns with standard deviation of 1.79 ns and 1.44 ns, respectively. Table S1 provides a Supporting Information data summary.

Discussion

This application expands the use of standard flow cytometry so that a new time-resolved parameter can be measurable and used for histogram formation, cytometric analysis, and in the future, cell sorting. The time parameter we introduce, FPD, can be rapidly calculated from fluorescence and scattering waveforms from any past or presently marketed bench-top instrument. We show that the FPD, which represents the average fluorescence lifetime of fluorophores at any given detection bandwidth, is inherent to all cytometry systems and proved this by simulation and evaluation with different algorithms. As the FPD only represents the average fluorescence lifetime, it is limited to the approximation of single-exponential fluorescence decay theory. Despite this fact, if developed as a list-mode parameter, as we demonstrate herein, it can be used for gating, multiplexing, and cytometric analyses that include multiparametric data. The FPD can be determined quite rapidly and therefore the possibly of sorting based on this value is an important future direction.

We demonstrate FPD parameter extraction using three methods: a direct, Gaussian fitting, and half-area approach. When the computed FPDs are compared with previously reported fluorescence lifetimes of fluorescein (4 ns), PE (2–3 ns), and PI (16 ns) ^8,29,30, the values are found to be quite consistent (Table3). Additionally we found that with the pulse widths of our standard FACSVantage™ SE, fluorescence lifetimes that are under ∼30 ns can be measured. The digitization, or sampling, rate of 50 MHz permitted this resolution; the waveforms collected had an interval step size between each discrete sample equivalent to 4 ns. A typical cytometry waveform can be as long or longer than 10 µs; therefore if a 20-µs detection window is achieved then 5,000 samples or “time bins” are collected for one full waveform.

Our error analysis revealed a reasonable variability in each FPD value with regard to the length of the delay imposed and the algorithm employed. The fluorescence lifetimes measured from fluorescently labeled cells (Supporting Information data) were found to align well with previously measured lifetimes of EB and PI, when intercalated into DNA ^2,37 and when measured with traditional frequency-domain flow cytometry.

It is important to note that the nFLIC method has challenges as well as benefits that are both directly related to the fundamental aspects a flow cytometer's architecture. For example, all three algorithms are impacted by waveforms that are not perfectly Gaussian-shaped. Doublets, coincidences, aggregates, gradient changes in the fluorescent labels across a given cell or microsphere, rapid photo bleaching and photo saturation ^38,39 for any given fluorophore, imbalanced ratios of the sample diameter relative to the beam height, and the alignment of the flow cytometer can each alter the waveform shape making it skewed in height. Additionally, the side scattering signals can become quite complex owing to subcellular morphology/granularity. We have demonstrated that this can be mitigated by using the forward scattering signal to calculate the FPD values, as is shown by our Supporting Information cell data.

A variety of electrical and instrumental components may also impact noise distributed through each waveform. Examples of these components include photodetector dark noise and rise times, imperfect amplification, trigger levels, waveform rise times, baseline levels, and imperfections in the laser output and the spot size relative to the interrogation zone. The spot size of the laser is of particular importance because if the sample diameter is larger than the laser height, slit-scanning (only illuminating a small piece of the sample at a time) scenarios ensue and the comparison of correlated scatter and fluorescence signals results in localized changes across the particle. When manifested in measurement noise, each of the abovementioned factors decreases the accuracy of the FPD values. When the raw digitized data deviates from Gaussian shapes then it limits the use of Gaussian-fitting. Likewise when the waveforms are distorted or asymmetric the location of the centroid of the waveform is difficult to accurately predict using the half-area method. However, the advantage of digital signal processing is that most of these issues can be corrected either with digital filters or pre-antialiasing filters before digitization. Similarly some of the algorithms have advantages such as the half-area approach; it is based on the area under the waveform, thus, the integration of the noise is low-to-zero rendering this method very useful in high noise scenarios.

Conclusion

In this study, a new parameter, the fluorescence-pulse-delay (FPD), is introduced for fluorescence lifetime extraction and to simplify the ways in which fluorescence lifetime detection in flow cytometry are accomplished. Observing an overall shift in time between scatter and fluorescence is a basic concept; it does not require modulation of a laser source or other complex mixing and detection steps ⁴⁰. Therefore, it maximizes the potential of any bench-top flow cytometer by simply processing the same waveform data that are obtained from simple analyzers and sorters (i.e., two-color, PMT based). In an intuitive way, this idea introduces a combination of time and frequency-domain analyses, yet without the complex laser pulsation. We demonstrate processing algorithms, introduce a time-resolved parameter, and implement this approach using fluorescently labeled cells. Future work will involve measuring the fluorescence dynamics with multiple fluorophores, expanding to cell sorting systems, and using the approach to alleviate intensity-related problems such as spectral overlap, autofluorescence noise, and quantification of FRET events. We project that the FPD parameter we introduce is the first of many dynamic, informative, and correction-based parameters that might be extracted from entire waveforms signals from any given flow cytometer; the premise here is that each waveform contains and can reveal more information than the traditional data obtained by peak-area-width list mode data.

Supporting Information

Additional Supporting Information may be found in the online version of this article.