ACHESYM: an algorithm and server for standardized placement of macromolecular models in the unit cell

An algorithm is proposed for selecting a unique description of macromolecular crystal structures. It is recommended that authors use the procedure before deposition and publication, so that crystal structures are easier to interpret and compare by noncrystallographers.

Abstract

Despite the existence of numerous useful conventions in structural crystallography, for example for the choice of the asymmetric part of the unit cell or of reciprocal space, surprisingly no standards are in use for the placement of the molecular model in the unit cell, often leading to inconsistencies or confusion. A conceptual solution for this problem has been proposed for macromolecular crystal structures based on the idea of the anti-Cheshire unit cell. Here, a program and server (called ACHESYM; http://achesym.ibch.poznan.pl) are presented for the practical implementation of this concept. In addition, the first task of ACHESYM is to find an optimal (compact) macromolecular assembly if more than one polymer chain exists. ACHESYM processes PDB (atomic parameters and TLS matrices) and mmCIF (diffraction data) input files to produce a new coordinate set and to reindex the reflections and modify their phases, if necessary.

1. Introduction  

A crystal structure is described by the unit cell, symmetry and the atoms located within the asymmetric part of the unit cell. Theoretically, there is an infinite number of equivalent ways of describing the same crystal structure, and even if limited by common sense, for example using smaller numbers rather than larger, the choice may still be plentiful. It is easier to interpret a crystal structure when connected atoms are placed close together and when molecules are placed within one unit cell, preferably not far from the origin. Unlike the case of selecting the limits of the asymmetric unit, which is well standardized and defined in International Tables for Crystallography volume A (Koch et al., 2005 ▶), there is no analogous convention for selecting a standardized location of a unique molecule in the unit cell and, even worse, macromolecular crystallo­graphers often show a surprising lack of sensibility in the selection of the unique cell contents (Dauter et al., 2014 ▶). In consequence, it is sometimes difficult to compare independent representations of the same or related crystal structures. This may create complications at the stage of macromolecular structure interpretation and may be perceived as an insurmountable difficulty by noncrystallographers, not infrequently leading to misunderstanding and error.

Recently, a solution was proposed for the problem of uniform description of molecule placement within the crystal structure (Dauter, 2013a ▶,b ▶). In that proposition for all space groups compatible with the macromolecular crystals, the unique regions within the unit cell where the mean atomic coordinate should be located were tabulated. These regions are related to the asymmetric unit of the anti-Cheshire unit cell (Dauter, 2013b ▶). The anti-Cheshire symmetry, or chirality-preserving Euclidean normalizer (Aroyo et al., 2006 ▶), corresponds to the group that contains all symmetry operations of the first kind (e.g. without rotoinversions) that map all symmetry elements of the original space group onto themselves.

The anti-Cheshire asymmetric unit is a concept inspired by the Cheshire symmetry and unit cell of Hirshfeld (1968 ▶). The structural motifs of macromolecular crystals can always be positioned within the anti-Cheshire asymmetric unit by symmetry transformations of the space group, permissible shifts of the unit-cell origin or permutation of the cell axes, as summarized in Table 1 ▶.

Table 1. List of space groups having only rotational symmetry elements (Sohncke groups) and the corresponding anti-Cheshire symmetry and limits for the optimal positioning of a molecule in the appropriate orientation.

The limits of the positioning region correspond to the asymmetric unit of the anti-Cheshire cell. x, y, z are fractional coordinates of the original cell. The symbol ‘Z’ relates to an infinitesimally small cell dimension in a particular direction. The location limits are somewhat modified from the version in Dauter (2013b ▶).

Space group No.	Symbol	Anti-Cheshire symmetry	Molecule location limits
1	P1	Z 31	x, y, z = 1/2
3	P2	Z 12	0 x 1/4; 0 z 1/2; y = 1/2
4	P21	Z 12	0 x 1/4; 0 z 1/2; y = 1/2
5	C2	Z 12	0 x 1/4; 0 z 1/2; y = 1/2
16	P222	P222	0 x, y 1/4; 0 z 1/2
17	P2221	P222	0 x, y 1/4; 0 z 1/2
18	P21212	P222	0 x, y 1/4; 0 z 1/2
19	P212121	P222	0 x, y 1/4; 0 z 1/2
20	C2221	P222	0 x, y 1/4; 0 z 1/2
21	C222	P222	0 x, y 1/4; 0 z 1/2
22	F222	I222	0 x, y, z 1/4
23	I222	P222	0 x, y 1/4; 0 z 1/2
24	I212121	P222	0 x, y 1/4; 0 z 1/2
75	P4	Z 1422	0 x 1/4; x y 1/2 x; z = 1/2
76	P41	Z 1422	0 x 1/4; x y 1/2 x; z = 1/2
77	P42	Z 1422	0 x 1/4; x y 1/2 x; z = 1/2
78	P43	Z 1422	0 x 1/4; x y 1/2 x; z = 1/2
79	I4	Z 1422	0 x 1/4; x y 1/2 x; z = 1/2
80	I41	Z 1422	0 x 1/4; x y 1/2 x; z = 1/2
89	P422	P422	0 x 1/4; x y 1/2 x; 0 z 1/2
90	P4212	P422	0 x 1/4; x y 1/2 x; 0 z 1/2
91	P4122	P4222	0 x 1/4; x y 1/2 x; 0 z 1/2
92	P41212	P4222	0 x 1/4; x y 1/2 x; 0 z 1/2
93	P4222	P422	0 x 1/4; x y 1/2 x; 0 z 1/2
94	P42212	P422	0 x 1/4; x y 1/2 x; 0 z 1/2
95	P4322	P4222	0 x 1/4; x y 1/2 x; 0 z 1/2
96	P43212	P4222	0 x 1/4; x y 1/2 x; 0 z 1/2
97	I422	P422	0 x 1/4; 1/2 x y 1/2 + x; 0 z 1/2
98	I4122	P4222	0 x 1/4; 1/2 x y 1/2 + x; 0 z 1/2
143	P3	Z 1622	0 x 1/3; 0 y x/2; z = 1/2
144	P31	Z 1622	0 x 1/3; 0 y x/2; z = 1/2
145	P32	Z 1622	0 x 1/3; 0 y x/2; z = 1/2
146	R3	Z 1312	0 x 1/3; 0 y x; z = 1/2
149	P312	P622	0 x 1/3; 0 y x/2; 0 z 1/2
150	P321	P622	0 x 2/3; 0 y x/2; y 2x 1; 0 z 1/2
151	P3112	P6222	0 x 1/3; 0 y x/2; 0 z 1/2
152	P3121	P6222	0 x 2/3; 0 y x/2; y 2x 1; 0 z 1/2
153	P3212	P6422	0 x 1/3; 0 y x/2; 0 z 1/2
154	P3221	P6422	0 x 2/3; 0 y x/2; y 2x 1; 0 z 1/2
155	R32	R32	0 x 1/3; 0 y x/3; 0 z 1/2
168	P6	Z1622	0 x 2/3; 0 y x/2; y 2x 1; z = 1/2
169	P61	Z 1622	0 x 2/3; 0 y x/2; y 2x 1; z = 1/2
170	P65	Z 1622	0 x 2/3; 0 y x/2; y 2x 1; z = 1/2
171	P62	Z 1622	0 x 2/3; 0 y x/2; y 2x 1; z = 1/2
172	P64	Z 1622	0 x 2/3; 0 y x/2; y 2x 1; z = 1/2
173	P63	Z 1622	0 x 2/3; 0 y x/2; y 2x 1; z = 1/2
177	P622	P622	0 x 2/3; 0 y x/2; y 2x 1; 0 z 1/2
178	P6122	P6222	0 x 2/3; 0 y x/2; y 2x 1; 0 z 1/2
179	P6522	P6422	0 x 2/3; 0 y x/2; y 2x 1; 0 z 1/2
180	P6222	P6422	0 x 2/3; 0 y x/2; y 2x 1; 0 z 1/2
181	P6422	P6222	0 x 2/3; 0 y x/2; y 2x 1; 0 z 1/2
182	P6322	P622	0 x 2/3; 0 y x/2; y 2x 1; 0 z 1/2
195	P23	I432	0 x 1/4; x y, z 1/2 x
196	F23	I432	0 x 1/8; x y, z 1/4 x
197	I23	I432	0 x 1/4; x y, z 1/2 x
198	P213	I4132	3/8 x 1/8; 1/8 y 1/8; max(x, y, y x 1/8) z y + 1/4
199	I213	I4132	3/8 x 1/8; 1/8 y 1/8; max(x, y, y x 1/8) z y + 1/4
207	P432	I432	0 x 1/4; x y, z 1/2 x
208	P4232	I432	0 x 1/4; x y, z 1/2 x
209	F432	I432	0 x 1/8; x y, z 1/4 x
210	F4132	I432	0 x 1/8; x y, z 1/4 x
211	I432	I432	0 x 1/4; x y, z 1/2 x
212	P4332	I4132	3/8 x 1/8; 1/8 y 1/8; max(x, y, y x 1/8) z y + 1/4
213	P4132	I4132	3/8 x 1/8; 1/8 y 1/8; max(x, y, y x 1/8) z y + 1/4
214	I4132	I4132	3/8 x 1/8; 1/8 y 1/8; max(x, y, y x 1/8) z y + 1/4

In this paper, we present an algorithm and a computer program called ACHESYM that can be used to transform alternative crystal structure descriptions to the unique setting satisfying the definition of the standard anti-Cheshire region. The ACHESYM program transforms the unit-cell description and atomic parameters (coordinates and anisotropic ADPs), and if necessary reindexes the diffraction data, to yield a standardized model of the macromolecule (or macromolecules) within the anti-Cheshire unit cell. The program reads a standard PDB file and outputs the results as a new PDB file that follows the standards as closely as possible. It can also appropriately modify the reflection indices and phases. In special cases, however, final hand-editing of textual information may also be necessary.

2. The algorithm  

The coordinate transformation problem can be split into two separate, consecutive problems.

• Problem A. If there are two or more macromolecules (chains) within the structure, they should be moved to form the most compact assembly, unless the user explicitly selects a different assembly, for example because of known biological functionality.

• Problem B. Finding such a description of the unit cell, symmetry and transformation of atomic coordinates that will bring the mean coordinate of the whole assembly to within the desired asymmetric unit of the anti-Cheshire cell.

2.1. Finding the optimal assembly of macromolecular chains (problem A)  

Problem A is difficult because the term ‘compact’ is nebulous and may have different interpretations. For example, one might want to bring all of the molecules together as close as possible or require that they occupy the smallest volume, or else that the shape of the assembly is as close as possible to a sphere etc. In yet another approach, one might want to minimize the variance of all atomic coordinates. In some cases it might be logical to find the strongest chemical interactions between the molecules or to create an oligomer compatible with solution studies or with its known biological function. Whatever approach is used, before proceeding to step B the user should make sure that the molecules in the asymmetric unit create an optimal assembly. Users may, for example, apply well established oligomer-detection methods, such as PISA (Krissinel & Henrick, 2007 ▶), or distance-oriented programs, such as CONTACT or DISTANG from the CCP4 package (Winn et al., 2011 ▶), before submitting a PDB file to the ACHESYM server.

Alternatively, ACHESYM has a built-in procedure for automatic solution of problem A based on a novel algorithm called ‘Volume Intersection of Proteins’ (VIP; to be described in detail elsewhere). Briefly, in the VIP method the optimal set of chains is assembled in such a way that the common volume shared by the chains is maximized. A point belongs to the volume of molecule X if it is closer than r (default 2.3 Å) to at least one non-H atom of chain X, and it may therefore belong to more than one chain. Atoms in HETATM records are ignored in these calculations. The radius r can be adjusted using advanced options. Several molecules are considered to be in contact if the intersection of their volumes is nonzero.

For all structures in our test set, the VIP procedure finds the assembly preferred by a human referee. If the automatic selection of the most compact VIP assembly is not satisfactory, the program allows the user to group the molecules manually. A user-defined group of chains is treated by the program as one unit. By running the VIP procedure several times in the manual mode and joining together successively more and more chains, it is possible to obtain the desired assembly. The user specifies chain grouping using the ‘group’ option of the ACHESYM program. The argument of this option is a text string in which all chain identifiers from the input PDB file should be used. The groups are separated by semicolons and the chains in a group are separated by commas. For example, if there are six chains labeled A, B, C, D, E, F and they should be paired into AB, CD and EF dimers, the grouping argument should be ‘A,B;C,D;E,F’.

The server version of the program will create a snapshot image of the input and output structures in the PDB files to visualize the changes. Views down the crystallographic directions a, b and c are generated with PyMOL v.1.5.0.4 (Schrödinger).

2.2. Transformation to the anti-Cheshire asymmetric unit (problem B)  

When the desired optimal assembly of multiple unique molecules has been found (for example by using the built-in VIP procedure), or there is only one molecule (chain) in the asymmetric unit, the ACHESYM program starts the main procedure to search for operations that transform that assembly to the desired anti-Cheshire cell. The search is performed using only atoms of the macromolecules in the PDB file, i.e. in ATOM records. However, when a given transformation is applied, it affects all atoms with a given chain ID, including HETATM records.

In order to transform the center of coordinates of the molecular assembly to the standard region of the unit cell (as specified for each relevant space group in Table 1 ▶), the possible origin shifts and symmetry operations of the anti-Cheshire cell are checked and the selected transformation is then applied to all atoms in the assembly and the atomic coordinates are saved to a file. The appropriate anti-Cheshire symmetry operations (normal and screw rotations and origin translations) are tabulated in the list of the chirality-preserving Euclidean normalizers at the Bilbao Crystallo­graphic Server (Aroyo et al., 2006 ▶). A list of alternate cell origins for the 65 ‘macromolecular’ (Sohncke) space groups can be found in the CCP4 web documentation at http://www.ccp4.ac.uk/dist/html/alternate_origins.html.

The anti-Cheshire unit cells listed in Dauter (2013b ▶) have been somewhat modified and standard positions along directions corresponding to infinitesimally small anti-Cheshire unit-cell parameters have been changed from 0 to 1/2. In the special cases of space groups P2₁3, I2₁3, P4₁32, P4₃32 and I4₁32, the desired anti-Cheshire region extends outside the reference 0 ≤ x, y, z < 1 unit cell. In all other space groups the model lies within the unit cell, close to its origin.

The ACHESYM program also appropriately transforms by symmetry the anisotropic atomic displacement parameters (ADPs) in the ANISOU records of the affected atoms, and correctly transforms the TLS tensors, if present.

All of the operations that are applied to atomic coordinates can be described using rotation–translation matrices (see Appendix A ). Since only the anti-Cheshire symmetry operations and axial translations are used, the operations are reversible. By default, the program saves all matrices used and documents the changes applied to each of the original chains using a dedicated ACHESYM remark section of the PDB file. The rotation–translation matrices are described by nine rotational parameters and three translation parameters in Cartesian coordinates, and are included in the output PDB file in the appropriate REMARK records. Three such records, containing the keyword ‘ACHESYM’, the chain identifier and the transformation matrix, are included for each, separately transformed, element (chain) of the assembly, as shown in Fig. 1 ▶.

Figure 1.

Example of the ACHESYM records in the output PDB file, specifying the transformation matrices applied to each, separately moved chain of PDB entry 1woc.

As mentioned above, the HETATM records with chain identifier ID are transformed using the operation generated for that chain ID. If a given HETATM chain ID is not found among the ATOM records, the corresponding HETATM records are not changed. Water and ligand molecules that belong to this category can be subsequently segregated using the standard procedures applied by the Protein Data Bank (Berman et al., 2000 ▶).

The input PDB file may contain coordinate-related and/or symmetry-related information in textual REMARK records. Unfortunately, it is not possible to foresee all possible changes that might need to be introduced in the textual section. The program will copy the original REMARK sections with a warning that they might be invalid. Therefore, the user should carefully check and appropriately modify the affected REMARKs in the output PDB file.

2.3. Treatment of the diffraction data  

Some normalizer operations in real space may also require re­indexing of the reflection data, if the crystal symmetry contains polar rotation axes in point groups 4, 3, 32, 6 and 23. If this is the case, the corresponding symmetry operation is applied by ACHESYM to the structure-factor file. The re­indexing matrix is calculated from one of the anti-Cheshire symmetry operations that is not part of the original space group. The inverse of the rotational component of such a matrix is the required hkl re­indexing matrix. F _obs, σ(F _obs) and the status flag associated with each index are not changed. It should be noted, however, that when the Euclidean normalizer changes the relative origin position, the structure-factor phases should be changed accordingly. By default, ACHESYM corrects phases in the _refln_phase_calc mmCIF tag only. The program reads and processes structure-factor data in mmCIF format only.

Let us consider as an example a symmetry operation 1/4 − y, 1/4 − x, 1/4 − z from the Euclidean normalizer of space group I2₁3, which according to Table 1 ▶ is I4₁32. This is a twofold rotation around the [1, 1, 0] direction and it does not belong to the original space group I2₁3, but exists in the full symmetry of the cubic lattice. The h, k, l index is changed upon this operation to h′, k′, l′ = −k, −h, −l and the new phase will be ϕ′(h′k′l′) = ϕ(hkl) + 2π(1/4h′ + 1/4k′ + 1/4l′). It should be noted that the new reflection indices h′, k′, l′ after reindexing may lie outside the standard CCP4 asymmetric unit (Winn et al., 2011 ▶) in the reciprocal lattice. It is ensured, however, that the anomalous signal/chirality is not changed, i.e. that the anomalous signal remains correctly assigned to the reflection indices. Any additional transformation of the reflection indices, required for example to standardize the index ranges, can be performed using the CCP4 suite or other utilities.

3. The ACHESYM server  

An implementation of the algorithm has been programmed in Python (Python Software Foundation, 2014 ▶) with the use of the cctbx library (Grosse-Kunstleve et al., 2002 ▶). Several time-consuming calculations have been implemented in the C++ language for efficiency. The program is capable of processing coordinate PDB files and structure-factor files in mmCIF format.

To run the program using the ACHESYM server, the user should upload a PDB file using the upload form. A structure-factor mmCIF file may be uploaded as well. If a VIP search for compact packing of the molecules is required, the user should tick the appropriate checkbox. The grouping argument may be specified as well if the packing-search option has been selected. The server will queue the submitted request and after its execution will print out a summary with the applied symmetry operations. Three snapshot images of the crystal structure are also displayed before and after the transformation. From the summary web page, it is possible to download the output PDB and structure-factor mmCIF files. The calculations may take several minutes, but a progress bar is displayed for convenience. In the case of failure, an error message will help to diagnose the problem. The downloaded output PDB file should be inspected using a molecular-graphics program. Also, the REMARK sections of the output PDB file should be inspected and corrected if necessary, according to the instructions printed by the program. The ACHESYM server is available at http://achesym.ibch.poznan.pl. The program is also available from the corresponding author for noncommercial offline use.

4. Examples  

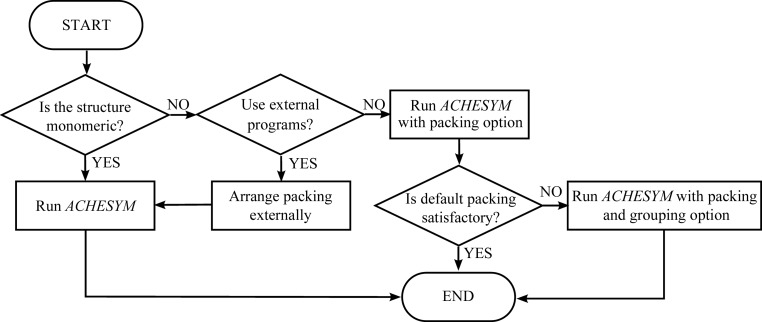
In this section, we illustrate by practical examples how to work with the ACHESYM program. Before structure submission, it is recommended that two main questions should be addressed. If the answer to the first question, ‘is there only one macromolecular chain in the PDB file?’, is ‘yes’ then the user can start the calculations right away. Otherwise, the user should check the ‘packing’ before calculations. After visual inspection of the molecular packing, the user should answer the second question: ‘do the molecules form a satisfactory packing assembly?’. Assembling the chains into a compact complex can be carried out in external software (e.g. PISA); the user would then return to ACHESYM with a satisfactory quaternary model. Alternatively, the built-in VIP procedure may be selected for this task. If the output from the default VIP packing algorithm is not satisfactory, the user should submit the structure again and use the ‘grouping’ option with an appropriate argument. The decision scheme is shown in Fig. 2 ▶. Below, ACHESYM is illustrated using examples from the PDB, which are identified by their accession codes.

Figure 2.

Option choice in ACHESYM.

4.1. 1qlq (space group P4₃2₁2)  

If there is only one chain in the structure, the calculations are straightforward, as there is no need to select additional options. After uploading the PDB coordinate file and, if desired, the structure-factor mmCIF file, the user is redirected to the results webpage, where the progress bar is displayed. When the calculations have been completed, the applied transformation is visualized using snapshot images of the unit cell projected down the crystallographic a, b and c directions. The first row shows the original crystal structure and the second row shows the structure after the transformations. A text log is also printed. Below the message ‘Success’, all transformation matrices are listed.

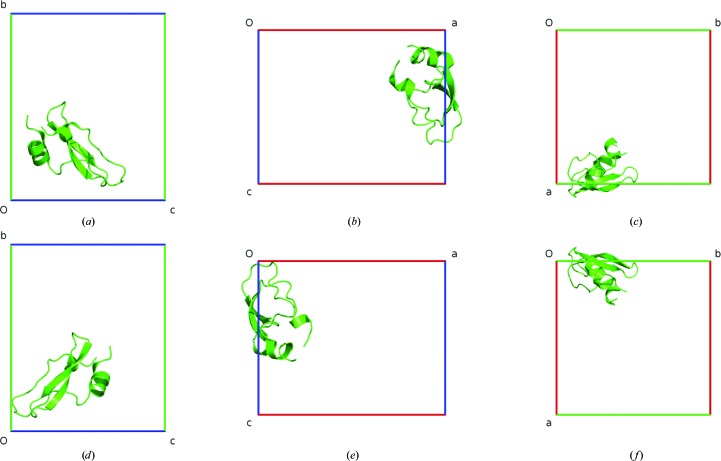
Such a simple case is illustrated by PDB entry 1qlq (Czapinska et al., 1999 ▶; Addlagatta et al., 2001 ▶). There is only one monomeric protein chain in space group P4₃2₁2 (Fig. 3 ▶). It requires the following transformation described in fractional coordinates: 1 − x, y, 3/4 − z.

Figure 3.

The PDB crystal structure 1qlq before (a–c) and after (d–f) ACHESYM transformation. Views are along a (a, d), along b (b, e) and along c (c, f).

The operations applied to the mean of coordinates transform it from (in fractional coordinates) 0.926, 0.262, 0.401 to 0.074, 0.262, 0.349 within the anti-Cheshire asymmetric unit-cell region 0 ≤ x ≤ 1/4, x ≤ y < 1/2 − x, 0 ≤ z < 1/2.

4.2. 1g96 (space group I432)  

PDB entry 1g96 (Janowski et al., 2001 ▶) also does not require user intervention. However, in this case the single protein chain in space group I432 forms a three-dimensional domain-swapped crystallographic dimer generated by the twofold rotation of the 4₂ screw axis. After the application of ACHESYM, the mean atomic position 0.516, −0.017, 0.124 is transformed to 0.016, 0.376, 0.483 (Fig. 4 ▶) using the following combined operation in fractional coordinates: x − 1/2, −z + 1/2, y + 1/2.

Figure 4.

The PDB crystal structure 1g96 before (a–c) and after (d–f) ACHESYM transformation. Views are along a (a, d), along b (b, e) and along c (c, f).

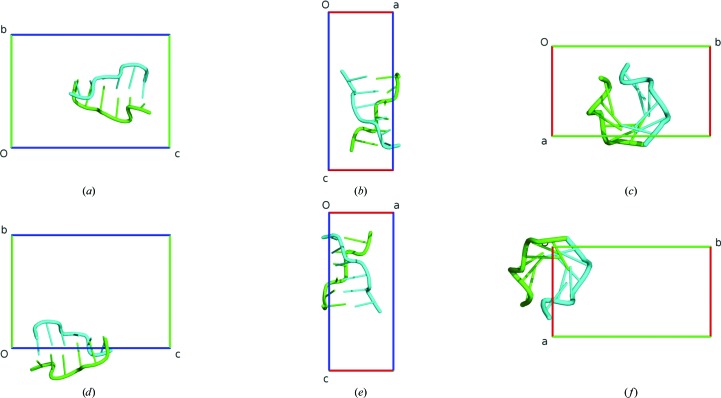
4.3. 3p4j (space group P2₁2₁2₁)  

A case of a nucleic acid structure is illustrated by PDB entry 3p4j, which contains a Z-DNA hexamer duplex in the asymmetric unit (Brzezinski et al., 2011 ▶). The dimeric duplex molecule is recognized by the VIP packing algorithm correctly and no changes are necessary. The anti-Cheshire standardization is achieved with the following operation described in fractional coordinates: 1 − x, y − 1/2, 1 − z. The mean point is transformed from 0.772, 0.503, 0.626 to 0.228, 0.003, 0.374 in fractional coordinates. The crystal structure before and after the transformation is shown in Fig. 5 ▶.

Figure 5.

The PDB crystal structure 3p4j before (a–c) and after (d–f) ACHESYM transformation. Views are along a (a, d), along b (b, e) and along c (c, f).

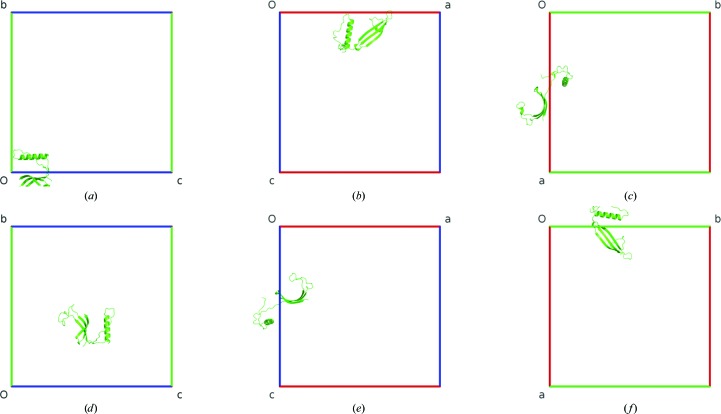
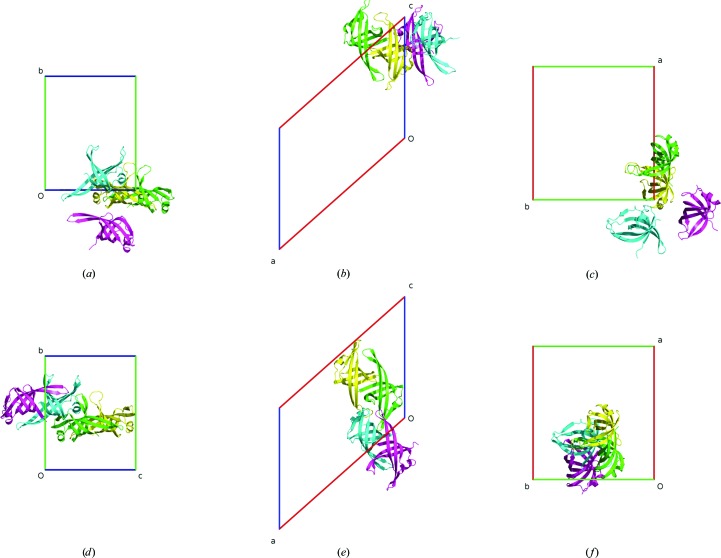
4.4. 1woc (space group C2)  

Visual inspection of PDB entry 1woc (Shioi et al., 2005 ▶) reveals that chains A and D create a dimer but chain B is not associated with chain C. Since there is more than one chain in the structure and the placement of the chains within the unit cell is evidently not compact, the ACHESYM program is run with the VIP packing option. The optimal assemblies are selected by analyzing the molecular contacts. ACHESYM with the VIP packing procedure finds the following operations to put the chains into a compact assembly, as shown in Fig. 6 ▶: chains A and D, 1/2 − x, 0.44804 + y, 3/2 − z; chain B, 1/2 + x, 0.44804 + y, −1/2 + z; chain C, −x, 0.94804 + y, 1/2 − z. The fractional shift along the monoclinic b axis locates the assembly at y = 1/2.

Figure 6.

The PDB crystal structure 1woc before (a–c) and after (d–f) ACHESYM transformation. Views are along a (a, d), along b (b, e) and along c (c, f).

Chains B and C, after appropriate transformations, have the largest common volume (∼360 ų). Chains A and D create the next ‘best’ dimer (common volume ∼320 ų). Finally, the BC and AD dimers are connected by contact A–B (∼170 ų). After the VIP packing procedure, the dimers AD and BC are correctly recognized and occupy close positions (Fig. 6 ▶).

5. Conclusions  

In this work, we have demonstrated in practice how macromolecular structures can be standardized to occupy the uniquely defined position in the unit cell, even though (or actually because) they were solved, refined and presented in an arbitrary, often illogical, location in the crystal frame. The standardization problem becomes more complicated when there are many macromolecules in the asymmetric unit. To overcome this difficulty, we have developed and implemented a novel procedure, called VIP, for finding the most compact assembly (or assemblies) among the polymer chains. The algorithm works successfully even with complicated cases and is able to recognize assemblies that might be of biological relevance. Although the main goal of ACHESYM is the standardized placement of molecules in the unit cell, we note that the newly developed algorithm for quaternary-structure recognition may be an interesting alternative to existing procedures such as PISA (Krissinel & Henrick, 2007 ▶). The PISA software calculates contact surface areas between molecules and is able to detect oligomers with high prediction accuracy (80–90%), but does not always create the most compact assembly of the individual chains. Recently, Krissinel (2010 ▶) compared the PISA algorithm with protein–protein docking calculations and showed that both methods have limits in predicting protein quaternary structure. Since our VIP approach uses a common volume concept for the detection of protein or/and nucleic acid assemblies, it can complement the existing algorithms. A detailed comparison of the assembling algorithms will be published elsewhere.

Eventually, the optimal assembly is transformed by ACHESYM to the uniquely defined anti-Cheshire unit cell. The program applies the required symmetry transformations to the PDB (input or passed from VIP) and (if necessary) mmCIF files. It is recommended that all crystal structures shoule be standardized before their submission to the Protein Data Bank. It might be useful to standardize the existing PDB database as well.

Appendix A. Transformations used in ACHESYM

Procedure A (VIP) for each chain with identifier ID generates a space-group symmetry operation R _ID and translation vector T _ID. After procedure B, as the final result of ACHESYM, we obtain four operations: the initial translation vector T ₁, the normalizer matrix N, the space-group symmetry operation matrix R and the final translation vector T ₂. All of the matrices and vectors are described in Cartesian coordinates. Whenever the atomic positions are transformed, the corresponding anisotropic atomic displacement parameters (in ANISOU records) and group TLS tensors (if present) are transformed accordingly.

In the ATOM and HETATM records, only the P = (X, Y, Z) orthogonal coordinates are affected. The transformed coordinates P′ = (X′, Y′, Z′) are calculated with the formula

The ANISOU U _ij tensor is updated using the rotational parts of matrices R _ID, N and R as follows,

The TLS origin O is transformed analogously to the atomic coordinates,

Since the origin and the atomic coordinates are changed simultaneously, the T, L and S tensors are updated analogously to the U _ij tensor,

It must be pointed out that the TLS transformation is only correct when the rotational parts of the R, N, R _ID matrices are orthogonal in Cartesian coordinates.

For each matrix, we can find its representation in fractional coordinates (marked by a superscript f) by multiplying the matrix by the orthogonalization matrix G (equivalent to the PDB SCALE matrix). For example, for matrix R and translation T ₁ we have

All of the operations applied by ACHESYM are reversible by the application of inverse symmetry operations and translations in the opposite direction, performed in the reverse order to that used by the program.