Abstract
Background and purpose
A behavioral intervention is a program aimed at modifying behavior for the purpose of treating or preventing disease, promoting health, and/or enhancing well-being. Many behavioral interventions are dynamic treatment regimens, that is, sequential, individualized multicomponent interventions in which the intensity and/or type of treatment is varied in response to the needs and progress of the individual participant. The multiphase optimization strategy (MOST) is a comprehensive framework for development, optimization, and evaluation of behavioral interventions, including dynamic treatment regimens. The objective of optimization is to make dynamic treatment regimens more effective, efficient, scalable, and sustainable. An important tool for optimization of dynamic treatment regimens is the sequential, multiple assignment, randomized trial (SMART). The purpose of this article is to discuss how to develop optimized dynamic treatment regimens within the MOST framework.
Methods and results
The article discusses the preparation, optimization, and evaluation phases of MOST. It is shown how MOST can be used to develop a dynamic treatment regimen to meet a prespecified optimization criterion. The SMART is an efficient experimental design for gathering the information needed to optimize a dynamic treatment regimen within MOST. One signature feature of the SMART is that randomization takes place at more than one point in time.
Conclusions
MOST and SMART can be used to develop optimized dynamic treatment regimens that will have a greater public health impact.
Keywords: Multiphase optimization strategy, MOST, sequential, multiple assignment, randomized trial, SMART
Background and purpose
A behavioral intervention is a program aimed at modifying behavior for the purpose of treating or preventing disease, promoting health, and/or enhancing well-being. More than 800,000 deaths each year in the US alone are directly attributable to behavioral factors such as smoking, excessive alcohol use, drug use, risky sex, poor eating habits, and physical inactivity. Interventions that effectively modify these behaviors have the potential to save many lives.
One type of behavioral intervention, the dynamic treatment regimen (dynamic treatment regimen), may be particularly useful in the treatment of chronic and relapsing disorders, disorders for which there is wide treatment effect heterogeneity, or disorders for which there is an array of effective treatments, some of which may be costly or burdensome. A dynamic treatment regimen is a sequential, individualized, multicomponent intervention in which the intensity or type of treatment is varied in response to the evolving needs and progress of the individual participant. Dynamic treatment regimens are a special case of adaptive interventions [1] in which there are multiple decision points over time. Dynamic treatment regimens are also called adaptive treatment strategies [2,3], stepped care [4], multistage treatment strategies [5], and treatment policies [6].
As a concrete example of a dynamic treatment regimen, consider the treatment of young adults (ages 18-25) who are at-risk drinkers in a college or workplace setting. At-risk drinkers exhibit a pattern of alcohol consumption (i.e., 4 or 5 drinks in one occasion for females or males, respectively) that places them at risk for adverse health events and consequences, such as alcohol use disorders, unintentional injuries, and motor vehicle accidents [7,8]. Brief treatments to correct misperceived norms about drinking using approaches such as personalized normative feedback [9,10] have been shown to reduce alcohol consumption [9,11]. However, some young adults might require more intensive intervention. The following example dynamic treatment regimen aimed at young adult at-risk drinkers seeks to address this type of heterogeneity: Offer a brief online personalized normative feedback intervention, and after 3 months, assess at-risk drinking. If the young adult is again identified as an at-risk drinker (i.e., a non-responder), then offer more intensive online personalized normative feedback. Otherwise, if the young adult is no longer at-risk (i.e., a responder), then discontinue brief intervention and continue to monitor drinking.
A dynamic treatment regimen is composed of four main components: (1) decision points, time points when treatment decisions must be made; (2) tailoring variables, person information used to make decisions; (3) intervention options, the type or dose/intensity/duration of the treatment; and (4) decision rules linking the tailoring variables to intervention options at decision points. In the example dynamic treatment regimen above, there was a decision point immediately after identifying the young adult as an at-risk drinker, and another three months later. The tailoring variable in this example was whether or not the young adult continued to be identified as an at-risk drinker at 3 months. The intervention option at the first decision point was personalized normative feedback. At month 3 there were two intervention options: discontinue treatment or provide more intensive personalized normative feedback. The decision rules were (1) initially offer personalized normative feedback for all young adults who are at-risk drinkers, and (2) for continued at-risk drinkers, intensify personalized normative feedback; for all others, discontinue intervention. Dynamic treatment regimens are considered multicomponent interventions because the decision point, the decision rule, the treatment option, and the tailoring variable are separable components.
A treatment package method has been the standard for developing multicomponent behavioral interventions, including dynamic treatment regimens. In this method the intervention components are assembled into a treatment package, which is compared to a suitable control group in a randomized controlled trial (RCT). For instance, an investigator might first assemble a dynamic treatment regimen such as the example given above, based on the investigator’s expertise, study staff consensus, and a careful consultation of the available literature and conceptual/theoretical models. An RCT would then be used to compare this dynamic treatment regimen against a suitable control group.
The RCT is unarguably the best tool available for evaluating a previously constructed intervention vs. a suitable control group. In our view, however, it should be recognized that the RCT’s intended purpose is to evaluate the performance of a treatment package as a whole, not to provide a window through which the performance of the components making up a treatment package can be investigated or understood. For this reason, sole reliance on the treatment package method and the RCT is insufficient to move behavioral intervention science forward quickly and in a way that manages study/research resources most effectively.
Many questions arise in development of a dynamic treatment regimen, such as the following: Which of the components are having the desired effect, and which can be discarded? Which first- or second-stage treatment components are best? Which work well together at each stage or in sequence? How might treatments best be timed or sequenced? What baseline and time-varying variables can be used as tailoring variables? How might treatment dosage or approach best be changed over time to meet the changing needs of participants and produce the best outcome? The answers to questions such as these hold the key not only to developing optimized dynamic treatment regimens that achieve a high degree of effectiveness without wasting time, money, and other resources, but also to developing a coherent and integrated basis of scientific knowledge about what does and does not work, when, and for whom.
As an alternative to sole reliance on the treatment package method, we suggest an engineering-inspired framework called the multiphase optimization strategy (MOST). In this framework, behavioral interventions are optimized before they are brought to an RCT for evaluation. The objective of optimization is to make a behavioral intervention more effective, efficient, scalable, and/or sustainable. Optimization is based on empirical data, typically gathered by randomized experimentation. Previous articles discussing optimization of fixed (i.e., not dynamic) treatments using MOST [12-14], have shown that a factorial experiment is often the most efficient experimental design for obtaining the information necessary for optimization. Optimization of a dynamic treatment regimen requires identifying the best set of decision points, decision rules, treatment options, and tailoring variables. Here a special case of the factorial experiment, the sequential, multiple assignment, randomized trial (SMART), is usually most appropriate and efficient.
The purpose of this article is to discuss how to develop optimized dynamic treatment regimens using the MOST framework. In the next section we provide a brief overview of MOST. This is followed by a hypothetical case study of intervention optimization using a SMART and a brief discussion of how the use of MOST and SMARTs can help move intervention science forward.
Methods and results
Brief introduction to the MOST framework
MOST is a comprehensive framework for optimizing and evaluating multicomponent behavioral interventions. Here the definition of optimization is “the process of finding the best possible… subject to given constraints.” [15] Intervention optimization involves selecting intervention components and component levels so as to assemble the most effective intervention, subject to realistic and clearly articulated constraints on resources required to implement the intervention.
As Table 1 shows, MOST consists of three phases. (The phases have been reorganized and relabeled since previous literature.) In the first phase, preparation, the groundwork is laid for intervention optimization. Here information drawn from prior theoretical and empirical literature, clinical experience, data analyses, and any other sources are integrated into a theoretical model. This model guides the selection of intervention components to examine and the key scientific questions to be addressed in the next phase. Any necessary pilot testing of these intervention components is done in the preparation phase.
Table 1.
Phases of the Multiphase Optimization Strategy (MOST)
| Phase | Objective | Examples of Activities |
|---|---|---|
| Preparation | Lay groundwork for optimization | Gather information to inform theoretical model |
| Review prior research literature | ||
| Review clinical experience | ||
| Analyze data | ||
| Gather information from other sources | ||
| Derive theoretical model | ||
| Select intervention components to examine based on theoretical model | ||
| Conduct pilot/feasibility research | ||
| Identify and operationalize intervention optimization criterion | ||
|
| ||
| Optimization | Form a treatment package meeting the intervention optimization criterion | Randomized experimentation (e.g., SMART) to investigate effects of intervention components |
| Data analysis, including selected secondary analyses of experimental data | ||
| Select set of components/component levels to meet optimization criterion | ||
|
| ||
| Evaluation | Evaluate whether optimized treatment package has a statistically significant effect | Experimentation to compare treatment packages directly |
A critical part of the preparation phase is identifying and operationalizing the intervention optimization criterion. This is a definition of the end product to be achieved by optimization. The intervention optimization criterion includes both the ideal and the constraints. One straightforward intervention optimization criterion is simply the “most effective intervention that can be achieved.” Like all intervention optimization criteria, this includes the implicit constraint “given the components currently under examination.” Other constraints on cost, time, cognitive burden, and so on must be explicitly identified if they are to be considered. For example, one project funded by the National Institute of Diabetes and Digestive and Kidney Diseases (B. Spring and L. Collins, co-PIs) is using MOST to develop the most effective weight reduction intervention that can be implemented for $500 per person or less.
In the next phase, optimization, the investigator gathers the information necessary to decide which set of components meets the optimization criterion, typically by means of a randomized experiment designed both to be highly efficient and to provide information about individual and combined component effects. The results from this experiment, possibly augmented by secondary data analyses, form the basis for making decisions about component selection and formation of the optimized intervention.
Next is the evaluation phase, in which a standard RCT is used to determine whether the optimized intervention has a clinically and statistically significant effect. Of course, if the results of the optimization phase indicate that no combination of the components under consideration is likely to achieve a statistically or clinically significant effect, it would not make sense to move to the evaluation phase. In this case the intervention scientist would return to the preparation phase, integrate the information obtained in the optimization phase about which components were effective and which were not, possibly revise the theoretical model, and select a new set of intervention components for examination.
MOST rests on two basic principles. The resource management principle states that the experimentation conducted in MOST must make the most efficient use of available resources to obtain the greatest scientific yield. The continuous optimization principle states that optimization is a process rather than an end point. Thus optimization is never finished as long as further improvement is possible.
SMART in the context of MOST: Building an optimized dynamic treatment regimen
Suppose an intervention scientist is interested in developing an optimized, two-stage, web-based dynamic treatment regimen to reduce risky drinking among young adults, and to address three questions that are critical for the development of this optimized intervention. The first question is whether the best first-stage treatment for young adults who engage in risky drinking is personalized normative feedback or stress management training stress management training. The second question is whether participants who respond to the first treatment should be offered a web-based booster session. The third question is whether non-responders to the first treatment should be offered a more intensive version of the initial treatment, or the alternative intervention (stress management training or personalized normative feedback, whichever was not provided as the first-stage treatment).
A SMART is an experimental design that was specifically developed to help investigators address scientific questions such as these, and thereby obtain data that can inform the construction of optimized dynamic treatment regimens. A SMART is a special case of the factorial experiment [16]. A complete factorial experiment is a randomized trial that involves more than one factor, in which the levels of the factors are systematically varied, or “crossed,” such that all possible combinations of levels of the factors are implemented [14,17-19]. As demonstrated below, in a SMART not all factors need to be crossed. SMARTs involve multiple randomizations that are sequenced over time. Each randomization corresponds to a critical decision point and aims to address a scientific question concerning two or more treatment options at that decision point.
In the hypothetical example above, the investigator needs to gather information to support decisions about three intervention components: the first-stage treatment, the second-stage treatment for responders, and the second-stage treatment for non-responders. A SMART that can be used to investigate these three components in an efficient manner is depicted in Figure 1. This design involves three independent variables, or factors, each corresponding to an intervention component. Each factor has two levels (in a SMART, as in a standard factorial experiment, factors may have more than two levels and different factors may have different numbers of levels). The randomization in this experimental design is sequenced in a way that corresponds to the two stages of treatments comprising the dynamic treatment regimens under investigation. Randomization to Factor 1 is conducted first, and randomizations to Factors 2 and 3 are conducted subsequently, 3 months after the initial randomization.
Figure 1.
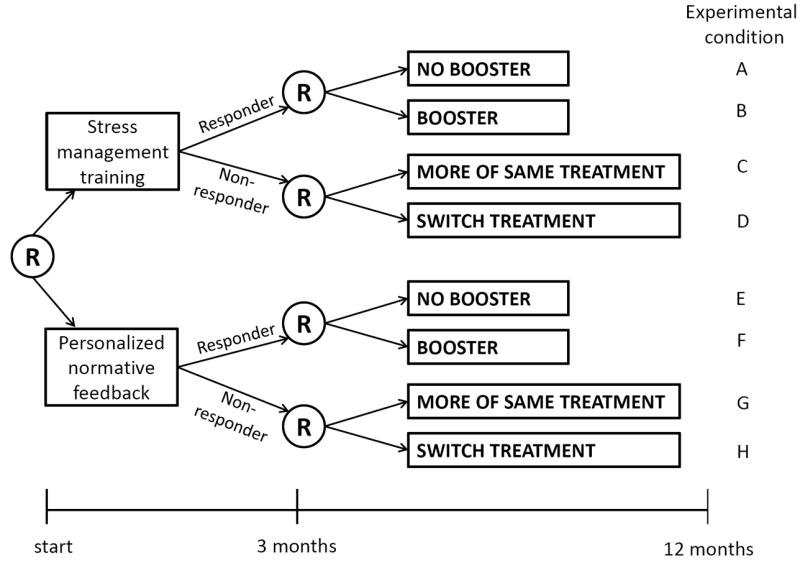
Schematic of hypothetical sequential, multiple assignment, randomized trial showing randomization at different time points.
At the outset of this hypothetical SMART, young adult at-risk drinkers are randomized to one of two levels of Factor 1, that is, to either stress management training or personalized normative feedback as the initial treatment. At month 3, all participants are assessed to determine whether they responded satisfactorily to the initial treatment (transitioned to non-risky drinking patterns) or did not (maintained risky drinking patterns). Treatment responders were re-randomized to one of two levels of Factor 2, that is, to receive either a web-based booster session or no booster session. Non-responders were re-randomized to one of two levels of Factor 3, that is, either to receive more of the initial intervention modality or switch to the alternative. The outcome of primary interest is a 12 month follow-up assessment of the number of heavy drinking days in the past 30 days.
Figure 1 illustrates a SMART in which Factor 1 and Factor 2 are fully crossed, and Factor 1 and Factor 3 are fully crossed, but Factor 2 and Factor 3 are not crossed. This means that, for example, every combination of the levels of Factors 1 and 2 appear in the design, but there is no experimental condition in which participants are assigned to both Booster and Switch Treatment. This is because only responders could be re-randomized to the two second-stage treatments aimed at responders (i.e., to the two levels of Factor 2), and only non-responders could be re-randomized to the two second-stage treatments aimed at non-responders (i.e., to the two levels of Factor 3). This restriction occurs by design, because, for scientific or practical reasons, different subsequent treatments are under consideration for responders vs. non-responders. In other words, this restriction occurs because response/non-response is a tailoring variable that is integrated into this SMART design—it is used to determine whether the participant will be re-randomized to the two levels of Factor 2 (if a responder), or to the two levels of Factor 3 (if a non-responder). A SMART design can be equivalent to a typical complete factorial experiment if there are no tailoring variables that are integrated in the design. For example, this might be the case if all participants were re-randomized to either more of the same treatment or switch treatments whether they responded or not (for more information see Nahum-Shani el al. [20]).
A signature feature of SMARTs is that the intervention components under investigation, and therefore the randomization to different levels of intervention components, are provided at different time points. This is consistent with the overarching aim to develop a dynamic treatment regimen, which, as described above, consists of a sequence of treatments provided at different time points.
The efficiency of SMART designs
Any experimental design may be used in the optimization phase of MOST, as long as it makes the best and most efficient use of available resources to address the research questions at hand. One resource of primary concern to intervention scientists is research subjects. Let us compare the sample size requirements of a SMART to an alternative approach: conducting two separate experiments, with different subjects, corresponding to each of the two intervention stages. Suppose an investigator has resources to obtain 400 participants (for simplicity we assume no attrition). In a SMART, one determinant of power for addressing scientific questions concerning the second-stage treatment is the proportion of responders to each first-stage treatment j, Pj. To keep the comparison of the two approaches straightforward we assume Pj=0.5; we return to this issue below.
Consider first the SMART design in Figure 1. Here 400 participants enter the study and 400 × 0.5 = 200 respond to the initial treatment. These 200 responders are then randomly assigned to receive or not receive the booster (A, B, E, or F in Figure 1), and the 200 non-responders are randomly assigned to more of the same treatment or switch treatments (C, D, G, or H). The first question concerning the effect of the initial intervention will be addressed based on all N=400 study participants by comparing the mean outcome for the participants who were offered stress management training (A+B+C+D) to the mean outcome for those who were offered personalized normative feedback (E+F+G+H). The second scientific question, concerning the effect of the booster session, will be addressed based on the 200 responders by comparing the mean outcomes for the responders who were assigned a booster session (B+F) and those who were assigned no booster session (A+E). Similarly, the third scientific question, concerning the second-stage treatment for non-responders, will be addressed based on the 200 non-responders, by comparing the mean outcomes for the non-responders who were assigned to the more of the same treatment option (C+G) and those who were assigned to the switch treatments option (D+H).
Now consider the alternative approach, in which instead of a SMART, an investigator who has access to N=400 will conduct two separate experiments. (This approach has some conceptual disadvantages as compared to a SMART; for a discussion of this, see Lei et al. [21], Murphy et al. [22].) Half of the subjects (i.e., 200) will be allocated to Experiment 1 to investigate which of the two initial interventions is best overall, and the remaining subjects will be reserved for Experiment 2 to determine which subsequent treatment is best for responders and non-responders. Suppose based on Experiment 1 it is determined that stress management training is best. In Experiment 2, the 200 subjects who did not participate in Experiment 1 are provided with stress management training to determine their response status. Then, the responders in Experiment 2 are randomly assigned to receive or not to receive a booster, and the non-responders are randomly assigned to either the more of the same treatment or the switch treatments option.
The SMART and the separate-experiments approaches differ in the amount of power they provide. Assuming α = 0.05, small to moderate (d=0.4) effect sizes for all comparisons, a normal model, and Pj=0.5, the SMART will yield 98% power for detecting a difference between starting with personalized normative feedback vs. with stress management training; 80% power for detecting a difference between the two second-stage treatments for non-responders; and 80% power for detecting a difference between the two second-stage treatments for responders. Power for the second and third comparisons is less than power for the initial comparison because the sample size available for these comparisons is smaller. By contrast, the separate-experiments approach will yield 80% power for detecting a difference between personalized normative feedback and stress management training; 50% power for detecting a difference between the second-stage treatments for responders; and 50% power for detecting a difference between the two second-stage treatments for non-responders. In the separate-experiments approach subjects are used for a single effect estimate and then discarded; as a result many fewer subjects are available for each one of the effect estimates, with a corresponding reduction in statistical power. The SMART provides more power because all N=400 participants are used to estimate the difference between personalized normative feedback and stress management training, and subsets of these same subjects are used again for each of the other two comparisons. This is an example of how factorial experiments make very economical use of research subjects by using data from the same subjects to estimate several effects, a property that has been referred to as “recycling” of subjects by Collins et al. [17].
As mentioned above, power may be affected by Pj. Suppose in the above example Pj=0.7 instead of Pj=0.5. In both the SMART and separate-experiments approach this results in increased power for the booster vs no booster comparison (because there are more responders) and decreased power for the more of the same treatment vs. switch treatments comparison, but no change in the personalized normative feedback vs stress management training comparison.
In any factorial experiment, main effects, by definition, compare outcomes by averaging over other factors in the experiment. Investigators may also be interested in how factors in the first and second stages interact with each other, which is a separate, and often important, question. In this case, investigators may want to compare individual dynamic treatment regimens. This possibility is discussed in the next section.
Using SMARTs to compare embedded dynamic treatment regimens
SMARTs may have numerous dynamic treatment regimens embedded within them. One example is the dynamic treatment regimen described in the Background and purpose section above, which corresponds to experimental conditions E+G in Figure 1. Another is Offer a brief, online stress management training intervention. After 3 months, assess risky drinking. If the young adult does not respond to treatment, then provide more stress management training. Otherwise, provide booster sessions. This corresponds to experimental conditions B+C. Table 2 lists the eight dynamic treatment regimens embedded in the example.
Table 2.
The Eight dynamic treatment regimens Embedded in the Example SMART Given in Figure 1.
| Embedded dynamic treatment regimen | First-stage Treatment | 3 Month Status | Second-Stage Treatment | Experimental Conditions in Figure 1 |
|---|---|---|---|---|
| 1 | SMT | Responder | No Booster | A+C |
| Non-responder | More of same | |||
| 2 | SMT | Responder | No Booster | A+D |
| Non-responder | Switch treatment | |||
| 3 | SMT | Responder | Booster | B+C |
| Non-responder | More of same | |||
| 4 | SMT | Responder | Booster | B+D |
| Non-responder | Switch treatment | |||
| 5 | PNF | Responder | No Booster | E+G |
| Non-responder | More of same | |||
| 6 | PNF | Responder | No Booster | E+H |
| Non-responder | Switch treatment | |||
| 7 | PNF | Responder | Booster | F+G |
| Non-responder | More of same | |||
| 8 | PNF | Responder | Booster | F+H |
| Non-responder | Switch treatment |
Note. SMT=stress management training; PNF=personalized normative feedback
An advantage of SMARTs is that they provide data that may be used to compare mean outcomes between any two (or more) of the embedded dynamic treatment regimens. Like the analyses addressing the component-screening aims above, the analyses comparing embedded dynamic treatment regimens pool information across multiple experimental conditions. For example, a comparison of the two example dynamic treatment regimens discussed in the previous paragraph involves comparing the mean outcome for the dynamic treatment regimen described in the Background and purpose section (mean across experimental conditions E+G in Figure 1) to the mean outcome for the second dynamic treatment regimen (mean across B+C). Straightforward regression-based data analysis methods have been developed [23-25] for improved statistical power in the comparison of embedded dynamic treatment regimens.
Using SMARTs to investigate additional tailoring variables
Data arising from a SMART can be used to optimize a dynamic treatment regimen by investigating candidate tailoring variables that were not embedded in the SMART by design. Consider again the SMART in Figure 1, which involves only one tailoring variable: whether or not the individual transitioned to non-risky drinking patterns by month 3. In a SMART, investigators may also collect additional information concerning baseline variables (e.g., psychological distress at baseline) and post-baseline measures (e.g., adherence to the initial treatment, or social and coping drinking motives at month 3) that may also be useful in developing a more deeply tailored (more individualized) and more effective dynamic treatment regimen. The SMART is ideal for exploring whether these baseline and post-baseline variables are useful as additional tailoring variables. Q-learning, a data analytic method drawn from computer science, is suitable for addressing this aim [24, 26].
Discussion
In addition to enabling efficient use of available resources to optimize behavioral interventions, thereby producing more effective and efficient dynamic treatment regimens, the use of SMART designs in the context of MOST can help intervention science develop a coherent base of knowledge about dynamic treatment regimens. Development of future dynamic treatment regimens can be informed by empirical evidence gained about which decision points, tailoring variables, intervention options, and decision rules are most effective individually and in combination. In addition, secondary data analyses based on Q-learning can be applied to data from SMARTs to identify more deeply tailored sequences of decision rules [24, 26].
It should be noted that the optimization and evaluation phases of MOST have different objectives. These objectives require different decisions. To evaluate a dynamic treatment regimen, that is, to establish whether or not a dynamic treatment regimen has a statistically significant effect to the satisfaction of the intervention science community, it is necessary to conform to generally accepted scientific conventions by conducting an RCT that is adequately powered using α ≤ .05. By contrast, to optimize a dynamic treatment regimen, it is necessary to make decisions about which decision points, tailoring variables, treatment options, and decision rules will be included in the dynamic treatment regimen, keeping in mind that in a subsequent evaluation phase the resulting dynamic treatment regimen will be evaluated to determine whether it has a statistically significant effect. According to the resource management principle, the investigator needs to consider how best to use the available resources to inform the decision making. In a particular situation the cost of a Type II error (i.e., failing to detect a true difference between two levels of a factor) may be more costly than a Type I error (i.e., mistakenly concluding that there is a difference). In this case, the best allocation of resources may be to reduce the Type II error rate by increasing the Type I error rate. Alternatively, decision making may be based on detecting clinically meaningful effects, rather than hypothesis testing.
Conclusions
MOST with SMARTs can be used to make dynamic treatment regimens more effective, efficient, scalable, and sustainable. This has the potential to improve the public health impact of dynamic treatment regimens, and ultimately reduce morbidity and mortality.
Acknowledgments
Funding
This work was supported by Award Number P50 DA010075 from the National Institute on Drug Abuse, R03 MH097954 from the National Institute of Mental Health (Almirall), RC4 MH092722 from the National Institute of Mental Health, R01 HD073975 from the Eunice Kennedy Shriver National Institute of Child Health and Human Development, P50 CA143188 from the National Cancer Institute, and R01 DK097364 from the National Institute of Diabetes and Digestive and Kidney Diseases. Funding for this conference was made possible (in part) by R13 CA132565 from the National Cancer Institute. The views expressed in written conference materials or publications and by speakers and moderators do not necessarily reflect the official policies of the Department of Health and Human Services; nor does mention by trade names, commercial practices, or organizations imply endorsement by the U.S. Government. This manuscript benefitted from discussions with Peter Bamberger, Samuel Bacharach, Mary Larimer, Irene Markman Geisner, and numerous colleagues at The Methodology Center. We gratefully acknowledge the editorial assistance of Amanda Applegate.
Footnotes
The material in this article was originally presented at the 6th Annual University of Pennsylvania Conference on Statistical Issues in Clinical Trials.
Conflict of Interest
None declared.
Contributor Information
Linda M Collins, The Pennsylvania State University, University Park, PA, USA.
Inbal Nahum-Shani, The University of Michigan, Ann Arbor, MI, USA.
Daniel Almirall, The University of Michigan, Ann Arbor, MI, USA.
References
- 1.Collins LM, Murphy SA, Bierman KL. A conceptual framework for adaptive preventive interventions. Prev Sci. 2004;5:185–96. doi: 10.1023/b:prev.0000037641.26017.00. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Lavori, Dawson DA. A design for testing clinical strategies: biased individually tailored within-subject randomization. J Royal Stat Soc. 2008;163:29–38. [Google Scholar]
- 3.Murphy SA. An experimental design for the development of adaptive treatment strategies. Stat Med. 2005;24:1455–81. doi: 10.1002/sim.2022. [DOI] [PubMed] [Google Scholar]
- 4.Sobell MB, Sobell LC. Stepped care as a heuristic approach to the treatment of alcohol problems. J Consult Clin Psychol. 2000;68:573–9. [PubMed] [Google Scholar]
- 5.Thall PF, Sung HG, Estey EH. Selecting therapeutic strategies based on efficacy and death in multicourse clinical trials. J Am Stat Assoc. 2002;97:29–39. [Google Scholar]
- 6.Wahed AS, Tsiatis AA. Semiparametric efficient estimation of survival distributions in two-stage randomisation designs in clinical trials with censored data. Biometrika. 2006;93:163–77. [Google Scholar]
- 7.Reid MC, Fiellin DA, O’Connor PG. Hazardous and harmful alcohol consumption in primary care. Arch Int Med. 1999;159:1681. doi: 10.1001/archinte.159.15.1681. [DOI] [PubMed] [Google Scholar]
- 8.Naimi TS, Brewer RD, Mokdad A, et al. Binge drinking among US adults. J Am Med Assoc. 2003;289:70–5. doi: 10.1001/jama.289.1.70. [DOI] [PubMed] [Google Scholar]
- 9.Osilla KC, Zellmer SP, Larimer ME, et al. A brief intervention for at-risk drinking in an employee assistance program. J Stud Alcohol Drugs. 2008;69:14–20. doi: 10.15288/jsad.2008.69.14. [DOI] [PubMed] [Google Scholar]
- 10.Perkins HW. College student misperceptions of alcohol and other drug norms: Exploring causes, consequences, and implication for prevention programs. In: Perkins HW, Berkowitz A, editors. Designing alcohol and other drug prevention programs in higher education. Newton, MA: Higher Education Center for Alcohol and Other Drug Prevention; 1997. pp. 177–206. [Google Scholar]
- 11.Neighbors C, Larimer ME, Lewis MA. Targeting misperceptions of descriptive drinking norms: efficacy of a computer-delivered personalized normative feedback intervention. J Consult Clin Psychol. 2004;72:434–47. doi: 10.1037/0022-006X.72.3.434. [DOI] [PubMed] [Google Scholar]
- 12.Collins LM, Murphy SA, Nair VN, et al. A strategy for optimizing and evaluating behavioral interventions. Ann Beh Med. 2005;30:65–73. doi: 10.1207/s15324796abm3001_8. [DOI] [PubMed] [Google Scholar]
- 13.Collins LM, Murphy SA, Strecher VJ. The multiphase optimization strategy (MOST) and the sequential multiple assignment randomized trial (SMART): New methods for more potent eHealth interventions. Am J Prev Med. 2007;32:S112–8. doi: 10.1016/j.amepre.2007.01.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Collins LM, Baker TB, Mermelstein RJ, et al. The multiphase optimization strategy for engineering effective tobacco use interventions. Ann Behav Med. 2011;41:208–26. doi: 10.1007/s12160-010-9253-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Clapham C, Nicholson J. The concise oxford dictionary of mathematics. New York, NY: Oxford University Press; 2009. [Google Scholar]
- 16.Murphy SA, Bingham D. Screening experiments for developing dynamic treatment regimes. J Am Stat Assoc. 2009;104:391–408. doi: 10.1198/jasa.2009.0119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Collins LM, Chakraborty B, Murphy S, et al. Comparison of a phased experimental approach and a single randomized clinical trial for developing multicomponent behavioral interventions. Clin Trials. 2009;6:5–15. doi: 10.1177/1740774508100973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Dziak JJ, Nahum-Shani I, Collins LM. Multilevel factorial experiments for developing behavioral interventions: Power, sample size, and resource considerations. Psychol Methods. 2012;17:153–75. doi: 10.1037/a0026972. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Chakraborty B, Collins LM, Strecher VJ, et al. Developing multicomponent interventions using fractional factorial designs. Stat Med. 2009;28:2687–708. doi: 10.1002/sim.3643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Nahum-Shani I, Qian M, Almirall D, et al. Experimental design and primary data analysis methods for comparing adaptive interventions. Psychol Methods. 2012;17:457–77. doi: 10.1037/a0029372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Lei H, Nahum-Shani I, Lynch K, et al. A “SMART” design for building individualized treatment sequences. Ann Rev Clin Psychol. 2012;8:21–48. doi: 10.1146/annurev-clinpsy-032511-143152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Murphy SA, Lynch KG, Oslin DW, et al. Developing adaptive treatment strategies in substance abuse research. Drug Alcohol Depen. 2007;88:S24–30. doi: 10.1016/j.drugalcdep.2006.09.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Orellana L, Rotnitzky A, Robins JM. Dynamic regime marginal structural mean models for estimating optimal dynamic treatment regimes, Part I: Main content. Int J Biostat. 2010;6 [PubMed] [Google Scholar]
- 24.Nahum-Shani I, Qian M, Almirall D, et al. Q-Learning: A data analysis method for constructing adaptive interventions. Psychol Methods. 2012;17:478–94. doi: 10.1037/a0029373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Oetting AI, Levy JA, Weiss RD, et al. Causality and psychopathology: Finding the determinants of disorders and their cures. Arlington, VA: American Psychiatric Publishing; 2011. Statistical methodology for a SMART Design in the development of adaptive treatment strategies; pp. 179–205. [Google Scholar]
- 26.Chakraborty B, Moodie EE. Statistical methods for dynamic treatment regimes. Springer; 2013. [Google Scholar]


