Cascaded spiral microfluidic device for deterministic and high purity continuous separation of circulating tumor cells

Abstract

Inertial microfluidics is an emerging class of technologies developed to separate circulating tumor cells (CTCs). However, defining design parameters and flow conditions for optimal operation remains nondeterministic due to incomplete understanding of the mechanics, which has led to challenges in designing efficient systems. Here, we perform a parametric study of the inertial focusing effects observed in low aspect ratio curvilinear microchannels and utilize the results to demonstrate the isolation of CTCs with high purity. First, we systematically vary parameters including the channel height, width, and radius of curvature over a wide range of flow velocities to analyze its effect on size dependent differential focusing and migration behaviors of binary (10 μm and 20 μm) particles. Second, we use these results to identify optimal flow regimes to achieve maximum separation in various channel configurations and establish design guidelines to readily provide information for developing spiral channels tailored to potentially arbitrary flow conditions that yield a desired equilibrium position for optimal size based CTC separation. Finally, we describe a fully integrated, sheath-less cascaded spiral microfluidic device to continuously isolate CTCs. Human breast cancer epithelial cells were successfully extracted from leukocytes, achieving 86.76% recovery, 97.91% depletion rate, and sustaining high viability upon collection to demonstrate the versatility of the device. Importantly, this device was designed without the cumbersome trail-and-error optimization process that has hindered the development of designing such inertial microfluidic systems.

I. INTRODUCTION

The most common cause of cancer related deaths is from the ability of cancer to spread to various distant organs through metastatsis.¹ This metastatic progression is driven by circulating tumor cells (CTCs) shed from the primary tumor into the peripheral bloodstream of patients.² Thus, isolation and analysis of CTCs are becoming important for many clinical applications, including but not limited to serving as a surrogate for invasive biopsy as an emerging biomarker for early cancer diagnosis, progression, and evaluation of drug's therapeutic efficacy for personalized treatment.^3–5 However, due to their extremely rare frequency in patient blood samples (∼1–100 CTCs per 10⁹ hematologic cells), separating CTCs with high sensitivity and specificity remains a challenge.

Microfluidic technologies for CTC isolation are promising due to their low cost, rapid operation, and the control they offer over the sample processing environments with improved sensitivity. Existing microfluidic CTC separation methods are mainly based on size-based filtration,⁶ immunoaffinity based capture,^7,8 or external force field mediated cell manipulation (i.e., dielectrophoresis,^9,10 magnetophoresis,^11,12 acoustic wave,¹³ and optical interference^14,15). Among various strategies, affinity based CTC binding methods targeting tumor membrane epitopes with antibodies against the epithelial cellular adhesion molecule (EpCAM) provide enhanced recovery rates at a great level of purity. However, non-efficient retrieval of captured CTCs from the chemically functionalized channel surfaces is a major hurdle for these platforms along with their limited sample processing rate.¹⁶ Most importantly, CTCs continuously change their expression level and morphology through the process of epithelial-to-mesenchymal transition (EMT) during blood circulation,¹⁷ and therefore heterogeneously expressed epithelial markers alone cannot adequately identify every subpopulation of CTCs.^18,19

Recently, inertial focusing of finite sized particles using microfluidic systems has emerged as an effective method for continuous CTC isolation.^20–25 Although fluid inertia has historically been neglected in low Reynolds fluid flows, studies show that precise manipulation of particles can be achieved using geometry dependent hydrodynamic forces, which cause size based lateral migration of particles into distinct equilibrium positions.^20,26–29 Such simple passive devices demonstrate the potential for application in biological filtration or purification, as well as blood cell sorting, and may serve as a promising alternative to traditional separation techniques.³⁰ Since the diameter of epithelial tumor cells is generally larger than that of normal blood cells,³¹ microfluidic devices exploiting this strong size dependent inertial effect (known as inertial microfluidics) are capable of high throughput, continuous CTC separation without pre-labeling, or loss of cell viability. Also, the capability to sort and analyze CTCs without fixation under conditions compatible with downstream molecular and functional characterization steps will allow the utilization of their full clinical potential, beyond simple enumeration.³²

Despite the effectiveness of inertial microfluidic devices, large background contamination associated with normal blood cells in whole blood limits its practical use for CTC specific applications. Since cells are concentrated to a few relatively narrow streamlines during separation, the total volume fraction of suspension is typically required to be below 1% to minimize any cell-to-cell interactions and steric crowding effects that can severely deteriorate the focusing behavior.^27,30 This necessitates a significant dilution of the running sample, which increases the overall processing time or sacrifices the purity of CTCs collected. In addition, various channel configurations, diverse flow parameters defined, and the limited flow ranges tested across previous studies complicate the development of newly designed inertial microfluidic devices due to the lack of continuity between experiments.^27,33–35 This makes them applicable only to particular channel geometries and flow conditions and eventually leads to an unavoidable time-consuming trail-and-error flow optimization process. Currently, due to the lack of controlled information on some structural parameters as well as an incomplete understanding of focusing mechanics, no successful general engineering strategy for design has been proposed and established as of yet. To address these challenges, a systematic channel design strategy for precise control over cell streak equilibriums relative to various flow conditions is necessary. This will allow flexibility and ease of integration with other upstream/downstream lab-on-chip devices to improve critical device performances such as throughput, CTC recovery rate, and purity for clinical cancer research.

In this work, spiral microfluidic devices of varying configurations have been investigated to comprehensively study the effect of channel geometry on size based particle migration and separation. We systematically examine the dependence of channel width (W), height (H), and radius of curvature (R) and separately determine their influence on focused particles streak behaviors. By varying each channel parameter, several ordered focusing positions can be achieved at new flow rates, thus allowing application defined flow conditions to be chosen for optimal separation, instead of settling for a fixed flow rate yielding sub-optimal separation and purity. Based on this renewed understanding, we propose an optimal design approach targeting desired flow conditions in a spiral microfluidic device to provide additional flexibility in design with deterministic equilibrium predictions and to enable better integration with other microfluidic technologies. Finally, we introduce a high throughput cascaded spiral CTC separator using our suggested design principles.

II. THEORETICAL BACKGROUND

After Segré and Silberberg first introduced inertial focusing of particles in cylindrical Poiseuille flow,³⁶ the mechanics of particle train migration across streamlines in finite Reynolds number (Re) fluid flow has been well characterized as the balance of two dominant inertial lift forces acting normal to the flow direction.^37,38 A shear induced lift force (F_S) caused by the parabolic velocity gradient drives particles toward the channel wall, while a wall induced lift force (F_W) pushes back particles toward the channel center due to the interaction with adjacent walls. This yields an annulus equilibrium at ∼0.2D away from wall, where D is the diameter of the pipe. However, in straight microfluidic channels, there is a radial asymmetry present from the normally square or rectangular cross-section geometry. In this case, particle streaks similarly migrate and settle at ∼0.22H (or W) near the channel wall³⁹ but concentrate toward the wall's center from the rotation induced lift force (F_R).⁴⁰ More specifically, for high or low aspect ratio channels (H/W ≫ 1 or ≪ 1), only two equilibriums centered at the longer sidewalls develop from the added asymmetry rather than four. Using a point-particle assumption, the net inertial lift force (F_L) is known to scale uniformly throughout the channel and is given by

$$F_L=\frac{\rho U_m^2{a}_p^4}{D_h^2}{C}_L,$$

where ρ is the density of the fluid medium, U_m is maximum fluid velocity approximated as U_m ≈ 1.5 × U_avg, and C_L is a non-dimensional lift coefficient that is a function of channel Reynolds number (R_c = $\rho U_m{D}_h/\mu$) and is dependent on the particle's position.^38,41

Introducing a curvature to the channel structure develops a secondary lateral flow, known as Dean flow, which is characterized by two counter-rotating vortices located above and below the central plane of symmetry of the channel.^26,33,39 The magnitude of this flow is described by a dimensionless Dean number (D_e) given by

$$D_e=\frac{\rho U_m{D}_h}{\mu }\sqrt{\frac{D_h}{2R}}=R_c\sqrt{\frac{D_h}{2R}}\hspace{0.17em},$$

where μ is the fluid viscosity and R is the radius of curvature of the channel. According to Stokes' law, Dean flow leads to a drag force upon particles (Dean force, F_D) expressed as²⁷

$$F_D\hspace{0.17em}\sim \hspace{0.17em}5.4\times {10}^{-4}\hspace{0.17em}\pi \mu D_e^{1.63}{a}_p.$$

Thus, in curved microfluidic channels, the combination of inertial lift force (F_L) and additional Dean force (F_D) results in a Dean coupled inertial migration of particles, which ultimately determines the final equilibrium.

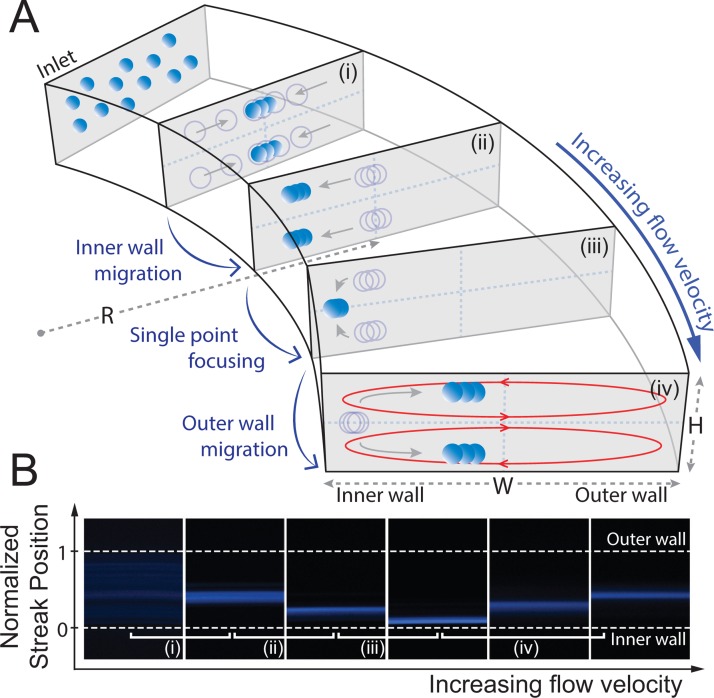
A visual representation of the Dean coupled inertial focusing profiles of particles in a curved low aspect ratio microchannel is shown in Figure 1. Randomly dispersed particles injected from the inlet are first abruptly driven towards the top and bottom wall due to a steep shear gradient along the vertical direction of the channel. These particles constantly settle at 22% and 78% of the channel depth³⁹ from the counterbalancing wall lift, forming two broad bands. Comparatively, the flat shear gradient in the horizontal direction has less effect at this stage. At a low flow velocity, rotation lift forces slowly concentrate these bands into two focusing streaks near the channel center as particles propagate further through the channel (Figure 1(a-i)). Here, particle migration occurs as if in straight channels where Dean flow is mostly negligible from the strong lift as a result of limited fluid flow. However, as the flow velocity is increased, an inner wall migration is induced by the apparent Dean forces oriented toward the inner wall, which become nontrivial at higher channel Reynolds numbers (Figure 1(a–ii). This migration occurs until a particular threshold where single point focusing is achieved along the height of the channel resulting in a tight equilibrium closest to the inner wall (Figure 1(a-iii)).³⁵ Increasing the flow velocity past this threshold results in an outer wall migration where, again, the two particle equilibrium position near the top and bottom of the channel emerges and shifts back towards the outer wall (Figure 1(a-iv)).

FIG. 1.

Inertial focusing and migration behaviors of particles with increasing fluid flow velocity (U_avg) in a curved low aspect ratio microchannel. (a) Particles injected from the inlet of the channel first abruptly equilibrate into two broad bands near the longer channel wall under the influence of shear lift (F_S) and wall lift forces (F_W) acting vertically with respect to the channel height. (i) At a relatively low flow velocity, particles migrate laterally towards the center equilibrium due to a rotation lift force (F_R), forming two focusing streaks. (ii) As the flow velocity increase, the two streaks start to migrate towards the inner channel wall, followed by (iii) a single point focusing at a particular threshold due to the differential interplay between the net lift force (F_L) and the Dean drag force (F_D). (iv) Outer wall migration is induced as the flow velocity is increased above this threshold. (b) Top down view of fluorescent images illustrating the migration pattern of 10 μm diameter particle in a curved microchannel (200 μm $\times$ 50 μm cross-section at 20 000 μm radius of curvature).

III. MATERIALS AND METHODS

A. Sample preparation

Neutrally, buoyant polystyrene microspheres (Polysciences, Inc.) with diameters of 10 μm (10.08, σ = 1.3 μm) and 20 μm (18.68, σ = 0.73 μm) were used to examine the size dependent focusing streak behaviors in the spiral channel geometries. Each particle was fluorescently labeled with either 4′,6-diamidino-2-phenylindole (DAPI) (10 μm particles) or fluorescein isothiocyanate (FITC) (20 μm particles). Particle suspensions were diluted in deionized water to a final concentration of 2 × 10⁵ particles/ml before running through the device. Mixtures of binary particles were also prepared in solution at a 1:1 ratio (same concentration) mixing to demonstrate the separation quality of these spiral devices.

To further validate its clinical applicability, cells from malignant human breast cancer epithelial cell line, MCF-7 (diameter of 16–24 μm), were recovered from a suspension containing leukocytes (diameter of 6–15 μm). The mean size of MCF-7 cells and leukocytes used in this experiment was measured as 17.58 μm (σ = 2.21 μm) and 9.02 μm (σ = 0.99 μm), respectively. Leukocytes were extracted from fresh blood specimens drawn from healthy donors using a dextran sedimentation and fractionation method: one part filtered 6% dextran in 0.9% NaCl (Sigma) was added to an EDTA tube containing 10 parts of whole blood.⁴² Samples were kept at room temperature for 40 min to allow red cells to settle on the bottom of the tube. After collecting the supernatant, the solution was centrifuged at 12 000 rpm for 1 min to remove the remaining blood plasma. Cytofix/Cytoperm (BD Biosciences) was then applied to the processed sample and incubated for 30 min followed by re-suspension in 1× phosphate buffered saline (PBS, GIBCO, Life Technologies) of pH 7.4. The nuclei of the isolated leukocytes were labeled with DAPI, washed, and again re-suspended to the original blood sample volume. The concentration of this leukocyte suspension averaged around 3–4 × 10⁶ cells/ml. Subsequently, approximately 1 × 10⁶ cultured MCF-7 cells labeled with green cell tracker dye (Invitrogen, CellTracker Green CMFDA, C7025) were counted and spiked into the leukocyte suspensions, serving as the input sample for the cell separation experiments (Figure S1 in the supplementary material).⁴⁷ MCF-7 cells were cultured in Dulbecco's modified Eagle's medium (DMEM) containing 10% fetal bovine serum and 1% penicillin-streptomycin solution and harvested when they reached ∼70%–80% confluence. A hemacytometer (Reichert bright line, Hausser Scientific) was used to determine the number of particles and cells in suspension during experiments. Cell culture reagents, unless otherwise specified, were purchased from GIBCO Invitrogen Corporation/Life Technologies Life Sciences. Cell samples were processed through the microfluidic chip within 3 h of preparation.

B. Experimental setup

Following air plasma exposure and glass bonding, the polydimethylsiloxane (PDMS) microchannels were soaked with 0.1% pluronic (F127, Sigma) and incubated for 30 min to block the channel surfaces and prevent adhesion or clogging during sample flow.⁴³ After washing with deionized water, the device was mounted on an inverted epifluorescence microscope (Ti Eclipse, Nikon) equipped with a 12-bit monochromatic CCD camera (Retiga 200R, Qimaging). Particle or cell suspensions were loaded with a syringe and infused through the channel at varying flow rates using a syringe pump (PHD2000, Harvard Apparatus). For a given channel geometry, streak positional data and width measurements were obtained by averaging five consecutive line scan images taken with Nikon NIS-Elements AR 4.0 software at each flow rate. For every initial sample flow and changing flow rates, images were captured after waiting 1 min to ensure a complete flow development and pressure stabilization.

IV. RESULTS AND DISCUSSION

A. Size based differential focusing

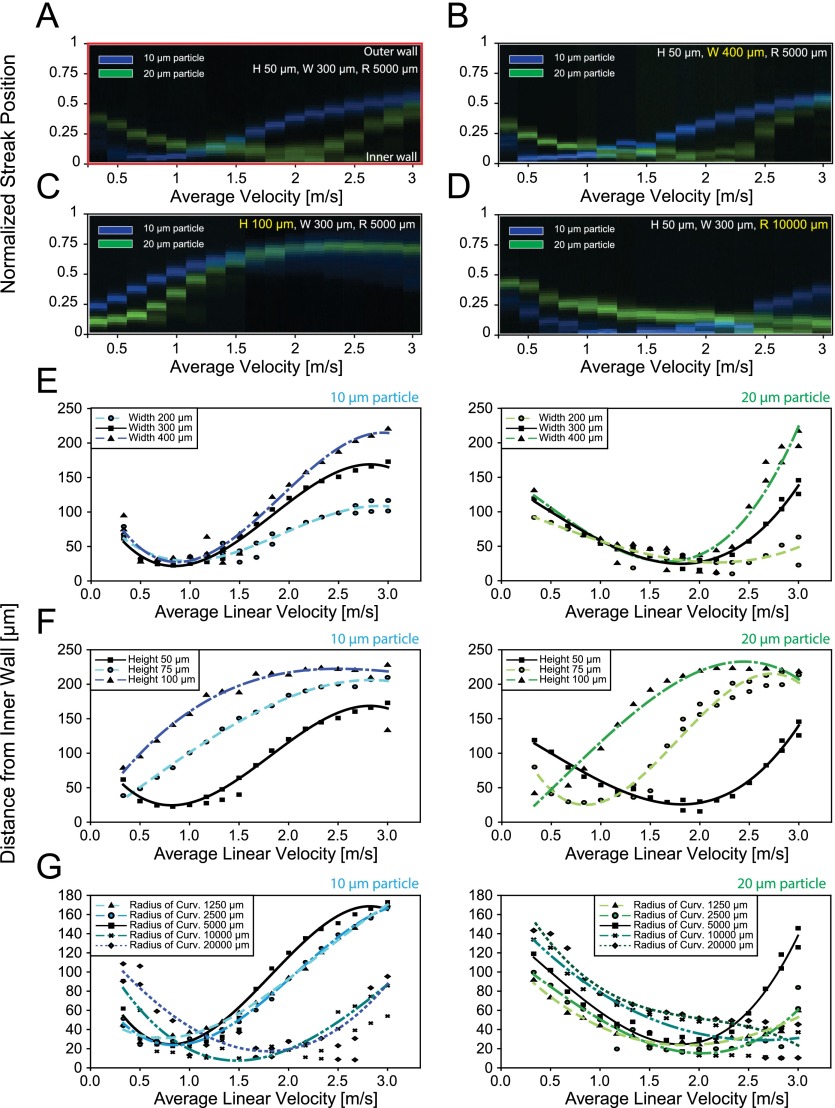
Inertial focusing and migration behavior of particles of different sizes were evaluated by analyzing the fluorescent intensity profiles of the particle streak distributions across the channel width (Figure S2 in the supplementary material).⁴⁷ 10 μm and 20 μm diameter particles, fluorescently labeled with DAPI and FITC, were used to model leukocytes and CTCs. For these experiments, a curved channel of 300 μm width, 50 μm height, and 5000 μm radius of curvature was used. Composite images of 10 μm and 20 μm diameter particle streams were captured and arranged (Figure 2(a)). Focused particle streak patterns were plotted as a function of average flow velocity, a parameter included in both non-dimensional channel Reynolds number (R_c) and Dean number (D_e).

FIG. 2.

Inertial focusing and migration behaviors of different sized particles in varying channel geometries. (a) Composite fluorescent line-scan images of 10 μm (blue) and 20 μm (green) polystyrene particle streaks are plotted as a function of average flow velocity (U_avg) in a curved microchannel with a 300 μm $\times$ 50 μm cross-section at 5000 μm radius of curvature. Y-axis represents the normalized streak distance from the inner channel wall. Migration pattern of 10 μm and 20 μm diameter particles is re-constructed at a modified channel (b) width (W = 400 μm), (c) height (H = 100 μm), and (d) curvature of 10 000 μm. Positional information where peak intensity of 10 μm and 20 μm particle streaks occurred is measured for varying channel (e) width (W = 200–400 μm), (f) height (H = 50–100 μm), and (g) radius of curvature (R = 1250–20 000 μm). Data points represent the raw measurement value and are curve fitted through the averaged peaks.

Similar migration patterns were observed regardless of size as both 10 and 20 μm particles experienced inner wall migration followed by outer wall migration with increasing flow velocity; however, the size difference caused a relative shift in the overall migration pattern which allows for efficient sized based separation of the particles. Specifically, a “left shift” in the migration pattern of the 10 μm particles was observed relative to the 20 μm particles. This was produced by two differential size-dependent factors reliant upon the interplay between Dean and lift forces: the initial focused streak position and particle migration rate.

Initial focused streak positions, defined as the first equilibrium positions that arose once a minimum focusing velocity was reached by both particles, were a function of particle size where the initial focused streak position of 10 μm particles was closer to the inner wall in the given channel geometry. For these small particles, the Dean force appeared to be non-negligible relative to the net lift, which scales with the fourth power of the particle diameter, even at the minimum focusing velocities. In contrast, stronger net lift forces experienced by larger particles dominated the Dean force thereby maintaining the 20 μm particles' initial equilibrium position near the channel center for a greater span of velocities. In effect, there was a delayed response for larger particles, which required higher fluid velocities to begin the inner wall migration phase. Furthermore, migration rate with constant flow increment for both inner and outer wall migration differed with particle size. With increasing fluid velocities, 20 μm particle streaks slowly migrated towards the inner wall, while faster migration was observed during the outer wall migration compared to 10 μm particle streaks. Thus, this distinct response, which is highly dependent on the diameter of particles, enables size based differential streak positioning and hence successful separation of binary particles in curved microchannel geometries.

B. Effect of channel geometry on focused particle streak patterns

To investigate the effect of channel geometry on the lateral migration of particle trajectories, width, height, and radius of curvature were individually varied from the previous spiral design with initial dimensions of 300 μm width, 50 μm height, and 5000 μm radius of curvature prior to the outlet. Channel Reynolds number and Dean number values corresponding to each channel structures are given in Figure S3 in the supplementary material.⁴⁷ Images and experimental data illustrating the channel's geometric dependency of streak motion behaviors are shown in Figure 2. With a large span of average velocity, ranging from 0 up to 3 m/s, focusing particle equilibrium positions were measured by calculating the distance from the inner channel wall to the peak fluorescence position for 10 μm and 20 μm diameter particles.

As shown in Figure 2(b), channels of varying width (W = 200 μm–400 μm) displayed little effect on the normalized streak migration patterns. Regardless of channel width, particle streaks exhibited a similar behavior in inner wall migration patterns, reaching a minimum distance to the inner wall at a specific flow velocity around 0.8 m/s and 1.8 m/s for 10 μm and 20 μm diameter particles, respectively (Figure 2(e)). In contrast, channels of varying height (H = 50 μm–100 μm) induced a major shift in the normalized streak migration patterns (Figure 2(c)). With increasing height, streak patterns of both particle sizes tended to shift left (Figure 2(f)). This can be explained by the growing Dean force paired with decreasing inertial lift forces at a given average flow velocity. Interestingly, for channel heights above 75 μm, the inner wall migration patterns were no longer observable. This provides insight as to why only the outer wall migration was observed in certain previous geometries in the literature.^27,39 These two results confirm that in a curved low aspect ratio microchannel, the shortest channel dimension in the channel cross-section acts as the critical factor in determining streak equilibration positions.⁴⁴ Also, this clearly indicates that a simplistic geometric aspect ratio is insufficient to predict the final focusing positions of particles. Rather than the aspect ratio value itself, each channel parameters that show different effects on migration patterns should be independently considered.

Along with the width and height, the effect of the channel's radius of curvature (R = 1250 μm–20 000 μm) on particle focusing position is shown in Figures 2(d) and 2(g). Differences in channel curvature modify the Dean number ($D_e\propto \hspace{0.17em}\frac{1}{\sqrt{R}}$) and therefore the Dean force, although the linear velocity remains constant. This allowed for further investigation into particle streak behavior by imposing a distinct Dean flow field on a constant net lift force. The Dean and lift forces could then be uncoupled and compared so that the curvature could be manipulated in order to achieve maximum separation for a given system. With increasing curvature, the Dean force decreased resulting in a diminished rate of inner wall migration. As a result, particle focusing positions reached a minimum distance from the inner wall at higher linear flow velocities (Figure 2(d)). Additionally, the inner wall migration occurred in order of ascending curvature, where migration in smaller channel curvatures began at lower flow velocities (Figure 2(g)). Beyond a curvature of 20 000 μm, where Dean numbers approached their asymptotic limit, no obvious change in streak behaviors was observed.

Through the quantification of equilibrium positions, migration rates of each particle streak not only differed by particle size but also had distinct slope constants dependent on each channel configuration. However, these slope constants within the presented experimental data set slightly differed from previous classifications.³⁵ During streak measurements, it was found that at high flow rates, high pressure built up inside the PDMS microchannels and started to distort the cross sectional dimensions, thus altering the equilibrium positions significantly. To examine how the pressure induced geometric deformation affects streak equilibriums, two spiral channels were fabricated with different channel lengths (Figure S4(a) in the supplementary material).⁴⁷ At the overlapping flow ranges tested (900–1000 μl/min) with the two spirals, the device with longer length showed a large channel expansion due to higher pressure (Figure S4(b) in the supplementary material).⁴⁷ Increase in channel cross section tended to decrease the average linear flow velocity while increasing the Dean flow, causing a large shift in streak patterns under identical flow conditions and channel geometric parameters (H, W, R). This was similar to increase the height of the channel, since the deformation mainly occurred in the height direction in low-aspect-ratio microchannels.⁴⁵ Thus, to acquire accurate particle response to inertial force effects, streak positions needed to be measured taking into account of the total channel length not only to ensure complete focusing but also to avoid pressure induced geometric deformation of the PDMS microchannels. In our experiments, each data was acquired before the channel had observable deformation.

C. Optimal flow regimes for efficient particle separation

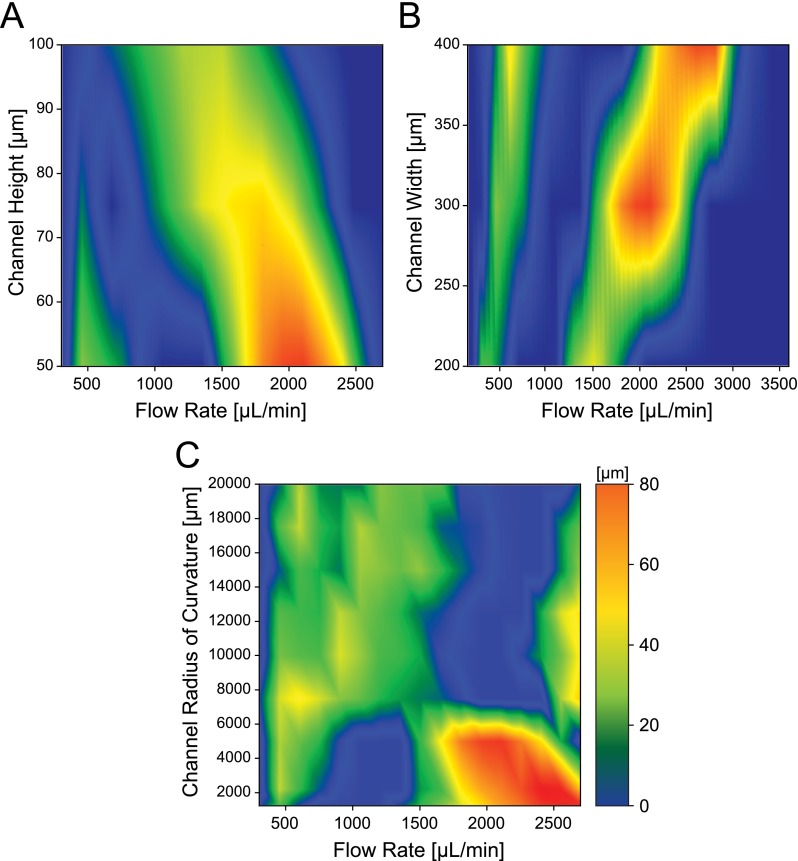
State diagrams for the separation distance between 10 μm and 20 μm particle streaks were acquired by measuring the proximity between the boundaries of the focused streak widths, which was calculated from the full width at half peak maximum of the fluorescent intensity profile from the background noise floor (Figure 3). To better apply these parametric data sets in designing spiral devices for separation and estimating the proper flow conditions, state maps were plotted as a function of volumetric flow rates.

FIG. 3.

State diagrams of separation distances between 10 μm and 20 μm focused particle streaks measured by the half-width-peak intensity as a function of volumetric flow rate in a (a) curved channel with rectangular cross section of 300 μm width and varying height, at a 5000 μm radius of curvature; (b) curved channel with rectangular cross section of 50 μm height and varying width, at 5000 μm radius of curvature; (c) curved channel with rectangular cross section of 50 μm × 300 μm (H $\times$ W) with varying curvature. State maps are generated using linear interpolation from individual data points obtained experimentally in units of micrometer.

From the difference in equilibrium patterns, two distinct separation regimes existed, respectively, at low flow and high flow rate ranges. For these two regimes, the ordering of focused particles occurred in a reversed manner; that is, in the low flow separation regime, the smaller particle streak was closer to the inner channel wall, whereas the opposite occurred in the high flow separation regime (Figure S6(a) in the supplementary material).⁴⁷ Once the focused particles reached the nearest inner channel wall, the finest focusing quality was obtained which was specified by a narrow fluorescent intensity profile with few fluctuations. Better focusing near the inner channel wall indicated that the counterbalance between competing Dean drag and net lift forces was occurring at this point. Additionally, this focusing position for 20 μm particles remained constant for a longer span as the flow velocity increased. In contrast, the 10 μm diameter particle streaks switched their migration direction more abruptly and a slightly higher separation resolution was achieved between the two streaks in the high flow separation regime. However, both regimes offered a high separation rate (>90%) of binary particles, providing an additional flexibility in flow rate defined designing of inertial based spiral devices.

D. Flow rate defined channel design strategies for optimal particle separation

Quantitative characterization of the effect of channel geometry on particle focusing and migration behaviors to better understand their full transient behavior in response to the change in flow rate in curved microchannels offers a systematic design guideline for efficient inertial separation of particles under various conditions. To efficiently adjust the channel design to a desired optimal flow condition, each of the geometric factors can be independently modified based on predictions of its influence on equilibrium patterns. Since focusing positions of particles are most sensitive to the variation in channel height, it is essential to first accurately define the channel height and the corresponding flow velocity that allows greatest separation. In particular, cases that require specific particle positions and the ordering must operate in the low flow separation regime, consequently the height of the channel needs to be designed below 75 μm for 10 and 20 μm particle separation (Figure 3(a)). The optimal flow rate in the high flow separation regime, on the other hand, can be freely tuned by varying the channel height as long as the particle focusing requirement a_p/D_h ≥ 0.07 is satisfied.²⁶

Once the height is determined, the total sample throughput can be subsequently adjusted by modifying channel width. As long as the low aspect ratio condition is preserved, the normalized streak patterns are mostly invariant to the width factor. Increasing the channel width not only offers a simple linear increase in volumetric flow rate but also in separation resolution (Figure 3(b)), since the gap between the two particle streaks as well as the streak dispersion (streak width) scales linearly with the channel width. One tradeoff of this would be an increase in device footprint due to the longer channel length required for complete focusing.

With increasing radius of curvature, both inner wall and outer wall migration phase occurred gradually. This adds tolerance to any flow rate variations during device operation since streak equilibrium position varies less per unit flow increments. Applying precise flow is critical for inertial separation devices, yet this is often difficult to control. However, desensitizing a device to flow rate variation through increased channel curvature can offer improved stability and yield in separation performances. Optimal flow rates for both separation regimes can also be pushed further up to a higher flow rate in a large channel curvature as long as the pressure accumulation does not exceed the device failure condition (Figure 3(c)). Thus, by engineering the channel width, height, and radius of curvature simultaneously, inertial devices tailored to operate at any flow rate conditions within the range of approximately 200–3000 μl/min can be easily designed and controlled for optimal particle separation.

E. Cascaded spiral for CTC isolation

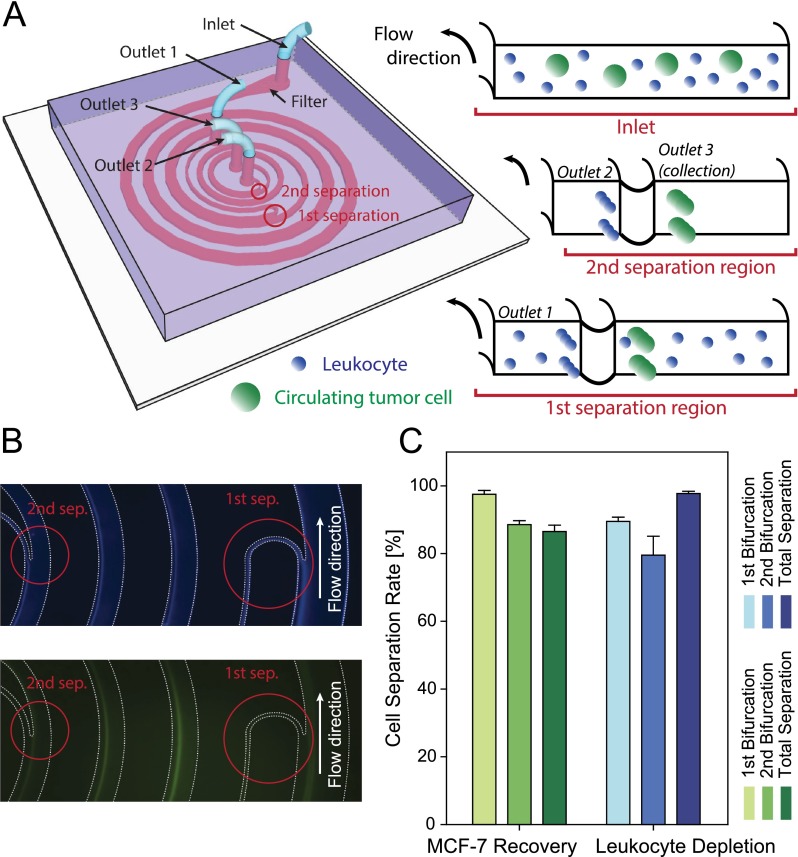
Based on these parametric observations, we designed and fabricated a fully integrated cascaded spiral microfluidic chip for CTC isolation. Through these studies we aimed to establish the clinical applicability of the founding principles to design better device for sensitive and specific separation. For a sheath-less, continuous two-stage separation, two consecutive spiral structures were serially connected with bifurcating channel sections located at the end of each spiral channels to isolate CTCs from leukocytes with high purity (Figure 4(a)). Operating flow rate was determined from the low flow separation regimes to specifically position CTCs, which are generally larger than the rest of the blood cells, closer to the channel center during separation. Without any repetitive optimization processes, this cascaded channel structure including the dimension of both bifurcating outlets was designed in a single attempt by precisely predicting cell equilibrium positions at specific flow conditions.

FIG. 4.

(a) Schematic illustrating the fully integrated cascaded spiral microfluidic device. (b) Top view of the fluorescent streamline image of focusing streaks of leukocytes (top) and MCF-7 cells (bottom) near the two bifurcation region in the cascaded spiral separator. (c) Characterization of cell separation efficiency. Channel dimensions are shown in Figure S9 in the supplementary material.⁴⁷

Sample mixtures of MCF-7 and human leukocytes were used, which were previously represented by the 20 and 10 μm diameter particles, respectively. MCF-7 breast cancer cells were chosen here to model the presence of CTCs in human peripheral blood of metastatic cancer patients. Cells injected at an initial flow rate of 550 μl/min from the inlet started to focus while traveling along the 400 μm width and 50 μm height spiral channel. By the time cells reached the first bifurcating region (R = 5000 μm), the majority of leukocytes were focused near the inner channel wall and filtered out through a 30 μm width sub channel, while MCF-7 cells and the remaining leukocytes continued to flow along the main channel which narrows down to a width of 200 μm. Finally, after an additional focusing and second bifurcation (at R = 2200 μm), MCF-7 cells were recovered at an average separation efficiency of 86.76% with a 97.91% leukocyte depletion rate (Figures 4(b) and 4(c)). These numbers were comparable to complicated current continuous immunoaffinity based depletion techniques.⁴⁶ Interestingly, when the spiking concentration of MCF-7 cell was lowered to ∼200–400 cells/ml, the average separation efficiency increased to 97.18% (Table S1 in the supplementary material),⁴⁷ since they were able to occupy tightly in their equilibrium positions. These results verify that our cascaded spiral device is well suited for CTC isolation. The viability of MCF-7 cells after collection was examined with live/dead cell viability assay (GIBCO, Life Technologies) and remained above >90% with most cells retaining their initial morphology.

Optimal flow conditions for separation predicted from the particle studies matched well with cell experiments but showed subtle differences in streak positions. Since the cells had a wider size distribution compared to the well-defined particles, a slight broadening of both cell streaks was observed. Also, in contrast to rigid leukocytes, MCF-7 cell streaks tended to migrate towards the inner channel wall earlier than the estimated flow rate, causing a slight left-shift in its overall streak pattern. The cell elasticity and deformability of MCF-7 cells subject to high shear resulted in a physical shape change, compared to rigid spherical particles. However, this was not significant enough to deteriorate the quality of the separation and with a slight calibration accounting for the streak shift of cells (adjusted within a few ∼10 s of μl/min), a successful sheath-less, two-step CTC isolation was achieved with high purity using the given geometric design parameters. Although, the total number of blood cell contamination rate over collected MCF-7 cells still remained limited for direct downstream molecular analysis of CTCs, it is on par with the current state-of-art label free separation techniques. Furthermore, by simply adding another bifurcation channel or easily integrating immunoaffinity based separation techniques, we envision that the channel designing guidelines provided herein would facilitate future development of CTC isolation chips to meet the expected purity level along with a high throughput.

V. CONCLUSIONS

In this work, we present and experimentally examine the inertial focusing mechanics and streak behaviors in various curved channel configurations over a large parametric space. The channel height, width, and radius of curvature each independently had distinct effects on particle equilibrium and streak patterns. This complete systematic study of geometric factors would be advantageous in envisioning a base guideline for predicting the equilibrium positions of particles and cells in the device development stage with an improved understanding of the underlying physical mechanisms and their limitations. Channel design strategies for specific flow rates introduced along with the state diagrams would simplify the process and reduce the trials attempted for device optimization as well as permitting additional flexibility that enables integrations with other lab-on-chip systems and microfluidic technologies, which is currently limited. Based on this design principal, we developed a high-throughput, fully integrated cascaded spiral microfluidic device to isolate MCF-7 cells from leukocytes with high purity in a continuous manner. The device was designed in a single attempt to operate at a pre-determined flow condition without any repetitive channel optimization procedures or complicated sheath flow control, to achieve an overall MCF-7 recovery rate of 86.76% and 97.91% leukocyte depletion rate. By applying and demonstrating the robust ability and performance of a spiral design to enrich cancer cells from leukocyte mixtures, we expect that the deterministic models for channel design suggested in this report will be readily applicable to the further development of low cost, high throughput, continuous CTC separation medical devices.