Sound pressure distribution within natural and artificial human ear canals: Forward stimulation

Abstract

This work is part of a study of the interaction of sound pressure in the ear canal (EC) with tympanic membrane (TM) surface displacement. Sound pressures were measured with 0.5–2 mm spacing at three locations within the shortened natural EC or an artificial EC in human temporal bones: near the TM surface, within the tympanic ring plane, and in a plane transverse to the long axis of the EC. Sound pressure was also measured at 2-mm intervals along the long EC axis. The sound field is described well by the size and direction of planar sound pressure gradients, the location and orientation of standing-wave nodal lines, and the location of longitudinal standing waves along the EC axis. Standing-wave nodal lines perpendicular to the long EC axis are present on the TM surface >11–16 kHz in the natural or artificial EC. The range of sound pressures was larger in the tympanic ring plane than at the TM surface or in the transverse EC plane. Longitudinal standing-wave patterns were stretched. The tympanic-ring sound field is a useful approximation of the TM sound field, and the artificial EC approximates the natural EC.

I. INTRODUCTION

The sound pressure distribution near the tympanic membrane (TM) in response to sound entering the lateral end of the ear canal (EC; “forward stimulation”) is a measure of the effective stimulus to the auditory system. The sound pressure distribution at more lateral locations within the EC affects estimation of the sound pressure near the TM. At the same time, significant spatial variations in the displacement of the TM occur across its surface at frequencies as low as 1–2 kHz (Rosowski et al., 2009; Cheng et al., 2010, 2013), and it has been suggested that these motions disturb the sound field near the TM and that these disturbances propagate laterally up the EC.

The human EC is not straight, and its cross-section area varies and is not circular (Stinson, 1985b; Stinson and Daigle, 2005). In many cases, the EC narrows somewhat at its midpoint (“isthmus”) and flares near the TM (e.g., Stinson and Lawton, 1989). The TM is roughly conical and terminates the EC at an ∼45-degree angle to the vertical plane (DiMaio and Tonndorf, 1978; Stinson, 1985b). In addition, the EC approaches the TM from the postero-superior direction, so that the posterior-superior aspect of the TM is closest to the isthmus and the anterior-inferior aspect (EC vertex) is furthest from the isthmus (e.g., Sanna et al., 2002; 3-D Model of the Visible Ear, http://research.meei.harvard.edu/Otopathology/3dmodels/index.html). This geometry can cause transverse spatial variations in the EC sound field (e.g., Stinson, 1985b; Rabbitt and Holmes, 1988). In addition, the EC length is a significant fraction of the wavelength of sound at moderate frequencies and exceeds the wavelength at high frequencies, which leads to longitudinal spatial variations in the EC sound field, including standing waves at high frequencies (Stinson, 1985b; Lawton and Stinson, 1986).

The sound pressure variations within the EC complicate efforts to estimate sound pressure near the TM. If the sound pressure in the EC varies substantially between the measurement location and the TM, the measurement provides a degraded estimate of the TM sound pressure. Similarly, if sound pressure varies across the TM surface, the actual sound stimulus input to the middle ear cannot be defined simply from measurements made at a single point. Such variations also complicate efforts to describe the sound field within the EC.

Previous reports include measurements and models of the longitudinal EC pressure distribution (e.g., Stinson, 1985b; Lawton and Stinson, 1986; Stinson and Daigle, 2005), but few measurements of the distribution of sound pressure transverse to this axis exist, especially at the medial end of the EC near the TM. In this paper, we present measurements of sound pressure in (shortened) natural ECs and in an artificial EC. In all preparations, sound pressure was measured (i) across the roughly conical TM within 0.5–1 mm of the TM surface (P_TM) and (ii) in two planes: the plane of the tympanic ring (TR), 2–4 mm lateral to the umbo (P_TR), and a transverse plane perpendicular to the EC axis that intersects the TR plane at the posterior edge (P_EC).¹ Additionally, sound pressure was measured (iii) longitudinally, approximately along the EC axis. We provide a more comprehensive description of the sound field in the medial EC than provided previously, including transverse variations. We examine the similarity of the sound field in our artificial EC to that in the natural EC.

It is commonly understood that the motion of the TM surface in response to sound can be quite complicated and varies among different frequency ranges (Tonndorf and Khanna, 1972; Rosowski et al., 2009; Cheng et al., 2010, 2013). In the human, TM surface motion changes from a simple to a complex regime ≳4 kHz and to an ordered regime ≳8 kHz (Rosowski et al., 2009). We use our measurements to test whether the complicated TM motions are associated with similar variations in sound pressure near the TM and, if so, how far laterally up the EC these variations propagate.

II. METHODS

A. Preparation

Four human temporal bones (TB7, 12, 13, 14) were extracted at autopsy and prepared as described in Cheng et al. (2010). The bones (all male) ranged in age from 49 to 73 years (mean 66 years). All bones appeared normal on anatomical inspection, and stapes velocity in these bones (normalized by P_TM near the umbo) was generally within or just below the normal criterion range established for use of cadaver ears in evaluating hearing devices (Rosowski et al., 2007).

In two ears (TB12 and TB13), the natural bony EC was shortened (from ∼25 mm to 17 or 13 mm, respectively) to allow better access to the medial EC with the microphone probe tube (described below), and a brass ring was glued around the EC opening with dental cement to define the opening [Fig. 1(A)]. Although the EC was shortened, we will continue to refer to it as a “natural EC.” Later, the EC of TB13 was drilled away to the TR, and an artificial EC (described below) was coupled to the TR [Fig. 1(C)]. In ears TB7 and TB14, the EC was drilled away to the TR at the time of initial preparation, and measurements were made only with the artificial EC.

FIG. 1.

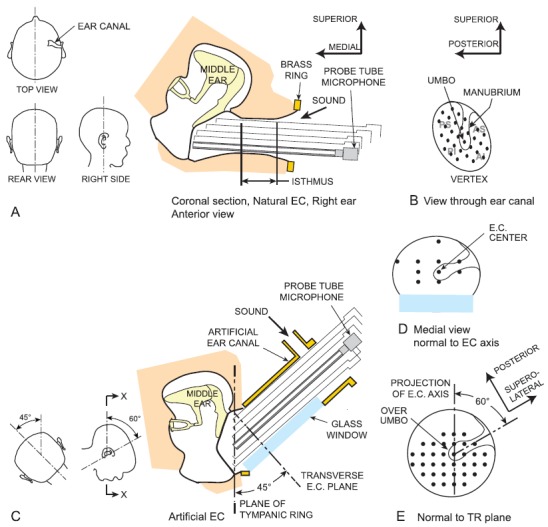
(Color online) (A) Coronal section of a right temporal bone and most of the bony EC, oriented approximately as in a seated subject (see also top view, rear view, and right side view insets at left). Because the EC approaches the inclined TM slightly posteriorly (see top view inset), the EC axis is above the plane of the page at its lateral end. Sound was delivered to the entrance of the remaining EC, and sound pressure was measured with a microphone and long probe tube attached to a 3-axis micromanipulator so it could be positioned repeatedly at locations across the TM surface. The “isthmus” is the narrowest (approximately cylindrical) part of the EC lateral to the flare near the TM. (B) View of the TM (foreshortened) antero-medially through the EC showing the EC vertex, TM clinical quadrants (PS = posterior superior, AI = anterior inferior, etc.), and representative measurement locations (black dots). The isthmus limited access to the TM. (C) Cross-section of the right temporal bone (X-X in inset to left) with the artificial EC in the experimental setup. In this view, the bone is rotated ∼60° forward and 45° upward to the left relative to (A) (see insets at left). The bone around the TR was drilled away, and an artificial EC was coupled to the temporal bone around the TR with an orientation similar to the natural EC: 45° to the TR plane, ∼60° posterior to the manubrium [see insets at left; (E)] and sealed with EC impression material. The artificial EC included a sound port and a glass window for viewing the TM. Sound was delivered to the artificial EC through a tube attached to the sound port. In both natural and artificial ECs, sound pressure was also measured in the plane of the TR [(E), the view through the glass window), in a plane perpendicular to the EC axis (D), and at locations along the EC axis (not shown).

The artificial EC was constructed to mimic the natural EC and had a cross-section area and shape similar to a typical natural EC (though the length was ∼10 mm longer). The artificial EC cross-section was oval (11.1 mm and 8.6 mm diameters) and provided a circular opening at the oblique end. A flat glass window sealed into the underside of the artificial EC provided visibility of the TM from a direction approximately perpendicular to the TR [see Fig. 1(E)]. A nipple [4.5 mm inner diameter (dia.)] attached to a hole in the wall ∼5 mm from the lateral end of the artificial EC provided a means to introduce sound to the TM while keeping the lateral end open.

In ears TB7, TB13, and TB14, the artificial EC was coupled to the TR at an angle of ∼45° to the TR [Fig. 1(C)] to mimic the natural EC. As mentioned in Sec. I, the EC approaches the TM from the postero-superior direction; in our experience, the projection of the EC axis on the TR plane makes an angle of ∼60° with the superior-inferior line defined by the manubrium with the umbo at the origin (see also 3-D Model of the Visible Ear, http://research.meei.harvard.edu/Otopathology/3dmodels/index.html). We therefore oriented the artificial EC so the projection of its axis on the TR plane was ∼60° posterior to the manubrium [Fig. 1(E)] to mimic its orientation in the natural EC. The artificial EC was sealed to the bony annulus around the TR with silicone EC impression material (Westone, Colorado Springs, CO). The seal was checked by evaluating the increase in EC sound pressure when the lateral end of the artificial EC was blocked.

B. Sound stimulus and measurement

Sound was delivered from a midrange speaker (CM-1; Tucker-Davis Technologies, Alachua, FL) through a 10-cm length of gum tubing (4.5 mm inner dia.) to the EC. With the natural EC, the tube was located near the EC opening. With the artificial EC, the tube was attached to the nipple near the open end [see Fig. 1(C)]. The artificial EC was sufficiently long that transverse variations in the EC sound field due to the asymmetric coupling of the sound source to the EC had dissipated before they reached the transverse EC plane (see Sec. IV C). Sound stimuli were broadband chirps 49 Hz–25 kHz at ∼102 dB sound pressure level. Stimuli were synthesized with custom software, attenuated to the desired level (PA5, Tucker-Davis, Alachua, FL), and sent through a power amplifier (D45; Crown Audio, Elkhart, IN) to the speaker.

EC sound pressure was measured with a hearing-aid microphone (EK23027, Knowles Electronics, Elk Grove Village, IL) glued to a rod mounted in a 3-axis micromanipulator (MM33, Märzhäuser, Wetzlar, Germany). A long, thin rigid probe tube (stainless steel hypodermic tubing, 0.8 mm outer dia., 0.5 mm inner dia., 45 mm long) was attached to the microphone with a short flexible link of Tygon tubing, which (i) allowed the probe tube to be removed for cleaning and replaced, (ii) allowed small lateral displacements of the probe tube without damaging it, and (iii) returned the probe tube to its original orientation once the laterally displacing force was removed. Microphone outputs were amplified ×10 with a custom amplifier. Microphone outputs were above the noise floor between 100 Hz and ∼19 kHz. The receptive field of the probe tube microphone was ∼0.5 mm in diameter (Ando, 1968; Beranek, 1986).

Microphone and preparation stability were checked by (a) repeating measurements at several locations at the beginning and the end of the experiment and (b) comparing low-frequency microphone outputs among all measurements. Assuming that the sound field is fairly uniform within the EC at low frequencies, low-frequency variations would indicate that the temporal bone specimen dried out during the 45–60 min measurement period. Below 1 kHz, the sound pressure varied over the TM surface, generally, by <1.5 dB, and repeated measurements at the same location were generally within 0.5 dB, which indicates that the state of the temporal bone remained constant throughout the experiment.

We checked that the microphone responded only to sound traveling up the probe tube from its open tip by measuring the microphone response in the sound field when the probe tube tip was plugged with heavy clay. EC sound pressure measured in this situation was at least 20–30 dB below that measured with the probe tube tip open. This result indicates that sound pressures measured at the microphone were accurate representations of the sound pressure at the probe tube tip and were not affected by the sound field near the microphone body.

C. Measurement technique

Sound pressure was measured by positioning the probe tube tip at 60–100 locations within the EC, spaced at 0.5–2 mm. With the micromanipulator, the microphone and probe tube could be moved repeatedly to locations along the EC axis and transversely across the EC, TR, or TM surface with a precision and accuracy of <200 μm. The location of the probe tube tip was checked by viewing it down the EC with an operating microscope or through the transparent window in the artificial EC. A three-dimensional map of measurement locations was generated from micromanipulator readings and referenced to the TM by touching the TM with the probe tube tip occasionally. P_TM measurement locations were 0.5–1 mm from the TM surface [Fig. 1(A)].

In the artificial EC, P_TR and P_EC measurements were coplanar within their respective measurement planes [Figs. 1(E) and 1(D), respectively] within ±0.1 mm. The TR measurement plane was 1–2 mm lateral to the TM surface at the annulus due to irregularities in the bony sealing surface and the presence of the sealing material. In the natural EC, establishing these planes was more difficult. We made measurements at a surplus of locations and chose P_TR and P_EC measurements that were within ±0.3 mm of the TR or EC plane.

The 3-D map of TM and TR measurement locations (in a micromanipulator-based coordinate system) was transformed into a TR-based coordinate system by a simple rotation. Measurements in the artificial EC were rotated by the 45° angle between the EC axis and the normal to the TR plane. In the two natural ECs, the rotation angle was either 45° or 60°.

Custom experimental control software (Hi-freq meas system, Eaton-Peabody Lab., Boston, MA) written in LabView on a PXI system (National Instruments, Austin, TX) synthesized stimuli, controlled the attenuator, averaged microphone responses synchronously with the stimulus, and saved data files. Data were analyzed using MATLAB (MathWorks, Natick, MA).

III. RESULTS

A. Sound pressure maps

1. Over the TM

Maps of the sound pressure across various planes at 21 representative frequencies were constructed from the sound pressure responses to broadband stimuli at the measurement locations. At each frequency evaluated, the sound pressure at that frequency was extracted from the broadband spectrum recorded at each location. For example, maps of the sound pressure over the TM surface in ear TB13 with a natural EC are shown at four representative frequencies (2.0, 8.5, 11.6, and 15.8 kHz) in Figs. 2(A)–2(D). Each map shows a view in the TR plane as in Fig. 1(E), rotated 45° to the left so the manubrium is at the top. Each colored square represents a measurement location, and the size of the square is approximately equal to the microphone receptive field (0.5 mm dia.). Figure 2 shows that we were able to achieve fairly representative and complete coverage of the TM surface. The location of the umbo is marked with a cross, and the manubrium is outlined in white. To normalize for variations in sound pressure with frequency, we compute P_TM at each location as the measured sound pressure normalized by sound pressure at the umbo. The values of the normalized P_TM magnitude |P_TM| and phase ∠P_TM are coded by color. The top panels show (normalized) P_TM in dB; the bottom panels show (normalized) ∠P_TM in cycles.

FIG. 2.

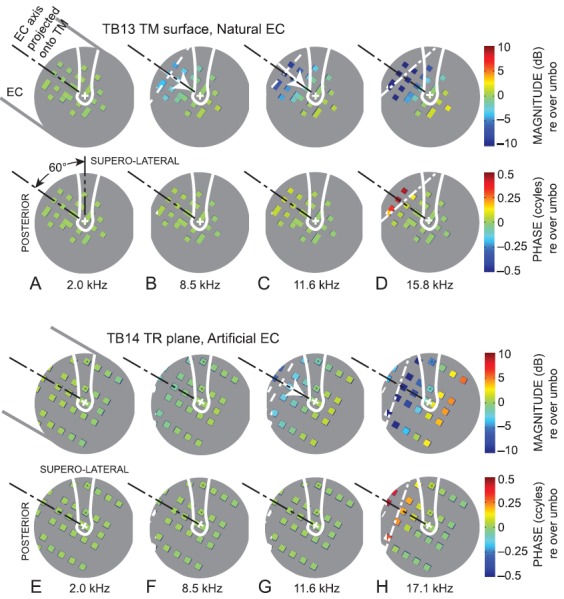
Sound pressure maps at representative frequencies generated from (A)–(D) measurements over the TM in ear TB13 (right ear) with a natural EC and (E)–(H) measurements in the TR plane in ear TB14 (right ear) with an artificial EC, normalized by sound pressure at or near the umbo: (A),(E): 2.0 kHz; (B),(F): 8.5 kHz; (C),(G): 11.6 kHz; (D) 15.8 kHz; (H) 17.1 kHz. The viewpoint is normal and lateral to the TR plane as in Fig. 1(E), but rotated to orient the manubrium toward the top of the page (supero-lateral). The umbo is marked by “+,” and the manubrium is outlined in white. Sound enters from the EC 60° postero-superior to the umbo; see (A). The projection of the EC axis on the TM or TR plane is shown by the black dotted-dashed line. Each colored square denotes a measurement location; its size is approximately equal to the microphone receptive field (∼0.5 mm dia.). The gray background (no measurements) is about 8 mm in diameter and approximates the TM. (Top) magnitude; (bottom) phase; color scales at right. At 8.5 kHz (B) and 11.6 kHz (C),(F), a sound pressure gradient is evident (white arrow from low to high sound pressure), which is perpendicular to a sound pressure isobar (white dashed line). At 15.8 kHz (D) and 17.1 kHz (H), a nodal line (white dotted-dashed lines) can be identified by the line of minimum pressure magnitude (top) and 0.5-cycle phase step at the same location (bottom).

The P_TM maps show that P_TM magnitude and phase are approximately constant over the entire accessible TM surface at frequencies below ∼6 kHz [e.g., 2.0 kHz, Fig. 2(A)]. At 8.5 kHz in this ear [Fig. 2(B)], |P_TM| starts to vary across the TM; |P_TM| is lowest in the postero-superior aspect [where the TM surface is closest to the EC isthmus; see Fig. 1(A)] and highest in the antero-inferior aspect (the region farthest from the isthmus, at bottom). At higher frequencies [e.g., 11.6 kHz, Fig. 2(C)], the variation increases and, at 15.8 kHz [Fig. 2(D)], P_TM shows a magnitude minimum <−10 dB (relative to P_TM at the umbo) that forms a line across the TM approximately perpendicular to the projection of the EC axis and posterior to the manubrium (top panel) and a 0.5-cycle phase step in the same location (bottom panel), indicative of a node in a standing-wave pattern.

2. Over other transverse planes

The sound pressures measured in the TR plane have many similarities to those measured at the TM surface. Figures 2(E)–2(H) show maps of the sound pressure measured in the TR plane in ear TB14 with an artificial EC at similar representative frequencies as shown in Figs. 2(A)–2(D). (It was much easier to locate and measure sound pressure in the TR plane in the more regular artificial EC than in a natural EC.) The sound pressure at each location P_TR (normalized by sound pressure in the TR plane over the umbo) in Figs. 2(E)–2(H) shows many of the same variations as P_TM in Figs. 2(A)–2(D) at these frequencies: P_TR is approximately constant at low and moderate frequencies [Fig. 2(E)], a magnitude gradient increasing from the postero-superior region to the anterio-inferior region is evident at higher frequencies [Figs. 2(F) and 2(G)], and a nodal line appears across the TR plane approximately perpendicular to the EC axis at the highest frequencies, with a |P_TR| notch and corresponding 0.5-cycle ∠P_TR step [Fig. 2(H)]. These basic patterns were observed in all ears with both natural and artificial ECs.

The sound pressure P_EC in an EC transverse plane that intersected the TR plane in the superior-posterior aspect (normalized by sound pressure at the EC center) is fairly uniform at all frequencies and, generally, shows little of the variation with location and frequency observed in the TR plane. Quantitative similarities and differences between the sound pressure variations across the three measurement planes will be discussed in Sec. III B.

The |P_TM| and |P_TR| variations in Fig. 2 are examined more quantitatively in Fig. 3, which plots |P_TM| (in a natural EC, top panels) or |P_TR| variations (in an artificial EC, bottom panels), respectively, along lines parallel or perpendicular to the projected EC axis at two frequencies from Fig. 2. At 8.5 kHz, |P_TM| decreases by ∼5 dB from the vertex to the most lateral measurement points [Fig. 3(A)], while |P_TM| is virtually invariant transversely across the TM [Fig. 3(B)]. |P_TR| variations are similar but smaller in the EC direction [Figs. 3(C) and 3(D)]. At higher frequencies (e.g., 15.8 kHz), the decrease in |P_TM| is much greater, ∼25 dB from the vertex laterally [Fig. 3(E)]. |P_TM| also decreases transversely from the postero-inferior to the antero-superior side of the TM [Fig. 3(F)], and the transverse variation is larger near the lateral edge of the TM (∼8 dB; open triangles) than near the umbo (∼2 dB). |P_TR| has a similar but smaller variation along the EC axis direction [∼15 dB; Fig. 3(G)], but the transverse variation is much smaller and in the opposite direction [Fig. 3(H)]. These patterns, especially the variations along the EC direction, were generally consistent among all ears.

FIG. 3.

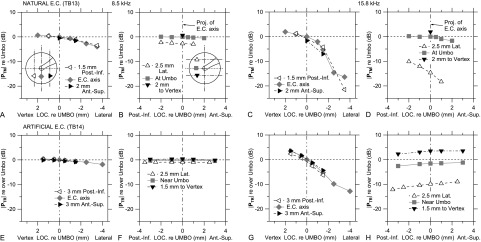
(A),(B) |P_TM| (relative to at the umbo) at 8 kHz in right ear TB13 [natural EC; see Fig. 2(B)]. (A) |P_TM| along the projection of the EC axis (gray diamonds) and parallel lines ∼2 mm postero-inferiorly (Post.-Inf., left triangles) or antero-superiorly (Ant.-Sup., right triangles; see inset); (B) |P_TM| along perpendiculars to the EC axis projection at the umbo (gray squares) and ∼2 mm toward the lateral EC axis projection (Lat., open triangles) or toward the vertex (closed inverted triangles; see inset). (E),(F) |P_TR| (relative to over the umbo) at 8 kHz in right ear TB14 [artificial EC; see Fig. 2(F)], plotted as for (A) and (B). (C),(D) and (G),(H) |P_TM| and |P_TR| as for (A),(B) and (E),(F), respectively, at 16 kHz.

B. Derivative measures from sound pressure maps

To aid comparisons among ears, locations, and frequencies, we developed simple metrics of the sound field at the TM and in the TR and transverse EC planes (where appropriate) that describe nearly all the variation with a few parameters, defined in more detail in Secs. III B 1–III B 3.

• (1)The direction of the sound pressure magnitude gradient relative to the EC direction;
• (2)If nodal lines are present, their orientation relative to the EC axis and their location relative to the umbo;
• (3)Maximum and minimum sound pressure magnitude and phase anywhere over the TM surface or measurement plane. Magnitude and phase gradients imply a maximum and minimum sound pressure. The depth of a standing-wave node is described by the difference between the magnitude maximum and minimum (range), and an ∼0.5-cycle increase in the phase range confirms the presence of a standing-wave node. A simpler plot of magnitude and phase range is useful for comparisons between measurement locations and between ears.

It should be noted that our choice of simple metrics has its limitations; for instance, these simple metrics do not describe the P_TM variations at a few isolated high frequencies that show gradients in more than one direction or that show a |P_TM| minimum without a corresponding ∠P_TM step (or a step in a different location). Nevertheless, they provide a quantitative description of the entire sound field near the TM and in the TR and EC planes at nearly all frequencies.

1. Sound pressure gradients and nodes near the TM

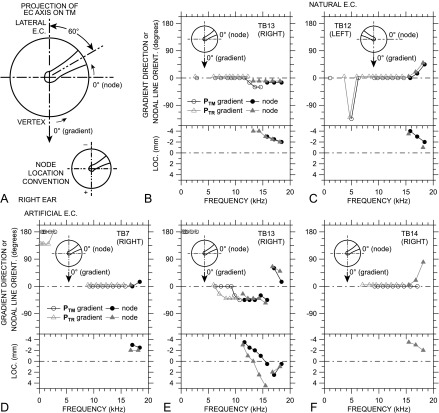
To evaluate sound pressure gradients, we consider only cases with a sound pressure magnitude range of ≥2 dB. We define the 0° direction to be aligned with the projection of the medial EC axis onto the TM or TR plane (from posterior-superior to anterior-inferior; vertically downward in Figs. 2 and 3), with positive and negative direction angles defined in the standard way (clockwise negative, counterclockwise positive); see Fig. 4(A).

FIG. 4.

Description of sound pressure variations over the TM surface and in the TR plane, relative to the projection of the EC axis onto the TM or TR plane [see (A) and insets in other panels]. Note that the view is rotated from Fig. 2 so that the EC approaches the TM from the top [as in Fig. 1(E)]. The manubrium is outlined, and the umbo is at the intersection of the crossed centerlines. |P_TM| and |P_TR| gradient direction is defined as 0° (arrow) when sound pressure increases from the postero-superior TM (lateral EC) to the antero-inferior TM (vertex). Nodal line orientation is defined as 0° when the nodal line is perpendicular to the EC axis projection. Gradient directions and nodal line orientations increase counterclockwise as shown by arrows. (B)–(F) (Top) Directions of |P_TM| (black open circles) and |P_TR| gradients (gray open triangles). Natural ECs: (B) TB13, (C) TB12; artificial ECs: (D) TB7, (E) TB13, (F) TB14. Also shown in the top panels are the orientations of P_TM nodal lines (filled circles) and P_TR nodal lines (filled triangles), where present. In most cases, nodal lines are visible only at the highest frequencies. Symbols denoting P_TR gradient directions and nodal line orientations have been offset −0.3 kHz and 5° for clarity. (Bottom) The location of the intercept of the P_TM (filled circles) and P_TR nodal lines (filled triangles) on the projected EC axis. Negative locations are above the umbo toward the lateral EC, positive locations are below the umbo toward the EC vertex [see panel (A) bottom].

Gradients were determined by inspection of pressure maps such as those shown in Fig. 2. The gradient direction is defined as the direction of the highest rate of increase in sound pressure magnitude with position [white arrow in Figs. 2(B), 2(C), and 2(G)]. In some ears, it was easier to construct sound pressure isobars [lines of constant sound pressure; white dashed line in Figs. 2(B), 2(C), and 2(G)] and define the gradient direction perpendicular to the isobar. The precision of direction estimation of these gradients is ∼15°, based on visual inspections of TM orientation in natural ECs and visual interpolation of the relatively sparse measurement locations.

|P_TM| gradient directions in ears TB12 and TB13 with a natural EC are shown in the top panels of Figs. 4(B) and 4(C) and in ears TB7, TB13, and TB14 with an artificial EC in the top panels of Figs. 4(D), 4(E), and 4(F), respectively (open circles). In nearly all ears, |P_TM| shows a gradient at frequencies between 5 and 15 kHz, with a direction of ∼0° (between 0° and 45° in TB13) along the projection of the EC axis on the TM as defined above (see insets). This gradient direction is seen in left (TB12) and right ears (others).

In artificial ECs in ears TB7 and TB13, gradients were also observed at ≤3 kHz, in a direction roughly opposite to the higher-frequency gradients. Because these low-frequency gradients were not observed in natural ECs, we suspect that they are due to small leaks between the bottom of the artificial EC sealing surface and the bony annulus around the TR [Fig. 1(C)]. Consistent with a small leak, these low-frequency gradients are not apparent above 3 kHz.

The lines of minimum |P_TM| and corresponding half-cycle ∠P_TM step, observed at high frequencies in Fig. 2(D) (and in most other ears), are consistent with nodal lines in a standing-wave pattern. Because nodal lines are perpendicular to the directions of the |P_TM| gradients on either side (like an isobar), we define the 0° nodal line orientation to be normal to the EC axis projection [Fig. 4(A) and insets].

P_TM nodal line orientations are also shown in the top panels of Figs. 4(B)–4(E) (filled circles). A nodal line appears in nearly all ears at higher frequencies: >11 kHz (TB13 artificial)–16 kHz (others). Note that no P_TM nodal line is observable in ear TB14 [Fig. 4(F)] even at the highest frequency (18.4 kHz) (although nodes are apparent in P_TR at frequencies >15 kHz). In all other ears, the orientation angle of the nodal line at the lowest frequency observed is approximately the same as the direction angle of the gradient, implying that the lowest-frequency nodal line is normal to the direction of the gradient. Because we defined the nodal line direction angle to be equivalent to the direction of a gradient isobar, this result indicates a smooth transition from a gradient to a standing-wave node as frequency increases.

The location of the nodal line is described by the intercept of the nodal line with the projection of the EC axis on the TM, defined to be positive antero-inferior to the umbo, negative postero-superior to the umbo [Fig. 4(A)]. The location of the P_TM nodal line in each ear is shown in the bottom panels of Figs. 4(B)–4(F) (filled circles). The P_TM nodal line is evident at postero-superior locations (corresponding to the lateral EC) at lower frequencies and moves antero-inferiorly as frequency increases. In ear TB13 with an artificial EC, a second higher-frequency nodal line appears above 16 kHz at an orientation ∼90° to the first lower-frequency nodal line. This higher-frequency node arises over the anterior TM and moves posteriorly as frequency increases.

The |P_TM| gradient directions between 6 and 12 kHz are generally the same relative to the EC axis in both left and right ears (Fig. 4). This result suggests that P_TM variations in this frequency range are influenced more by the EC than by the properties of the TM. At higher frequencies, nodal line orientations shift more perpendicular to the manubrium in two ears: positive (counterclockwise) in a left ear [TB12, Fig. 4(C)], negative (clockwise) in a right ear (TB13, Figs. 4(B) and 4(E)]. [In right ear TB7, Fig. 4(D), the shift was opposite, but much smaller and only >18 kHz.] This shift implies that the relative influence of the TM on P_TM variations can increase above 12–15 kHz.

A surprising result is that, even in the natural EC, nodal lines appear on the TM surface at frequencies below the upper range of human hearing (∼20 kHz). These nodal lines appear over the manubrium superior to the umbo and may influence the coupling of EC sound to the ossicles at high frequencies. This result is discussed further in Sec. IV B.

2. Sound pressure gradients and nodes in the TR plane

|P_TR| gradient directions are also shown for all ears in Figs. 4(B)–4(F) (open triangles). In general, all features of the |P_TM| gradients are also seen in the |P_TR| gradients. There are a few small differences: |P_TR| gradients have a slightly different direction in ear TB7 at low frequencies and in TB13 at middle frequencies than |P_TM| gradients.

P_TR nodal line orientations and locations (filled triangles) are also shown for all ears in Figs. 4(B)–4(F). As with the gradients, the P_TR nodal line orientations and locations are quite similar to those for the P_TM nodal lines. In general, P_TR nodal lines appear at slightly lower frequencies than P_TM nodal lines and appear 0.5–1 mm closer to the EC vertex at the same frequency, consistent with the more lateral location of the TR plane. The second node in ear TB13 (artificial EC) is quite similar at the TM surface and in the TR plane.

The result that P_TM and P_TR gradients and nodal lines are similar suggests that, at most frequencies, P_TR in the TR plane may be a useful estimate of P_TM over the TM surface.

3. Sound pressure maximum and minima across measurement surfaces and planes

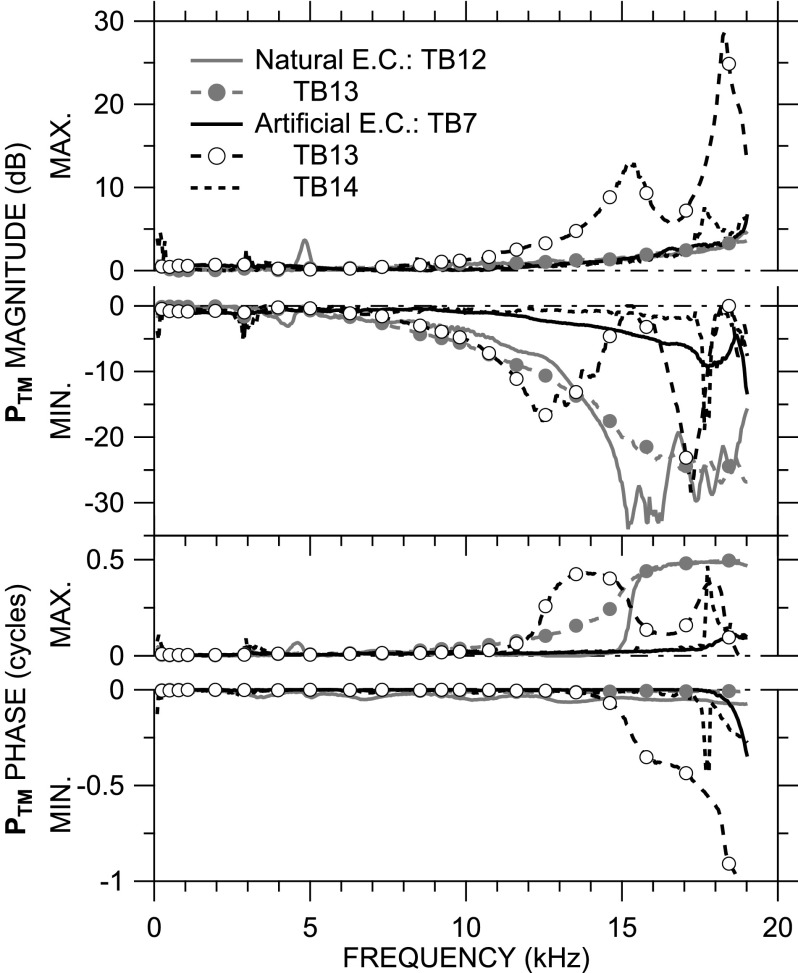
P_TM magnitude and phase maxima and minima (normalized by sound pressure at the umbo as before) are shown in Fig. 5 for all four ears and the two EC types. In all ears with either a natural or artificial EC, |P_TM| and ∠P_TM maxima and minima differ very little from 0 dB below 7 kHz. In all ears, the overall |P_TM| range increases as frequency increases, but this increase in range is due mostly to a decrease in the minimum |P_TM|.

FIG. 5.

P_TM magnitude and phase maxima and minima (normalized by P_TM at the umbo as before) across frequency in the four ears. Maxima above zero line; minima below. (Top) magnitude; (bottom) phase.

In ears with a natural EC (TB12, TB13), the maximal |P_TM| is equal to or only slightly larger than the sound pressure at the umbo at nearly all frequencies, but a deep (>30 dB) |P_TM| minima occurs in TB12 at 15 kHz. In both TB12 and TB13, the maximum ∠P_TM increases to about 0.5 cycles near 15 kHz, the frequency of the |P_TM| minimum in TB12, consistent with the standing-wave node in P_TM >15 kHz [Fig. 4(A)]. The increase in maximum ∠P_TM in TB13 is more gradual, and though the |P_TM| minimum decreases in this ear at high frequencies, no |P_TM| notch is evident.

Similar phenomena are observed in ears TB7 and TB14 (with artificial EC), while TB13 with an artificial EC shows additional features. In ear TB7, only a slight dip in the minimum |P_TM| and increase in maximum ∠P_TM are seen at 19 kHz, whereas TB14 has a sharp local increase in |P_TM| and ∠P_TM maxima and minima just below 18 kHz. In ear TB13, the notch in minimum |P_TM| and 0.5-cycle step in maximum ∠P_TM occur at a lower frequency (12.5 kHz) than in the other ears. The peak in |P_TM| maximum, |P_TM| minimum ∼ 0 dB, and downward 0.5-cycle shift in ∠P_TM maximum and minimum near 15 kHz indicate the presence of a standing-wave node at the umbo [see Fig. 4(D) for confirmation]. A second |P_TM| minimum notch and 0.5-cycle maximum ∠P_TM step near 17 kHz indicate a second nodal line on the TM [see Fig. 4(E)]; a second maximum |P_TM| peak, minimum |P_TM| ∼ 0 dB, and downward 0.5-cycle shift in ∠P_TM maximum and minimum indicate that the second nodal line crosses the umbo near 18.5 kHz, a level of detail not available in the gradient plots.

To summarize, Fig. 5 shows that P_TM is nearly uniform over the TM below 7 kHz, but that |P_TM| can vary by as much as 35–40 dB at higher frequencies. Similarly, at high frequencies, ∠P_TM varies over 0.5 cycle, which indicates that the sound pressure over parts of the TM is out of phase with other parts at these high frequencies.

We use magnitude and phase ranges for comparisons of sound pressure distribution among measurement locations and ears. P_TM, P_TR, and P_EC ranges in ears TB12 and TB13 with a natural EC are shown in Figs. 6(A) and 6(B), respectively. In both ears, the variations in P_TM, P_TR, and P_EC with frequency are very similar: Both show a gradual increase in magnitude range with frequency and a 0.5-cycle increase in phase range at a frequency near the magnitude range peak frequency. In TB13, the frequency of the ∠P_TR range step and |P_TR| range plateau are slightly lower than those observed for P_TM, consistent with the greater distance between the TR measurement locations and the TM.

FIG. 6.

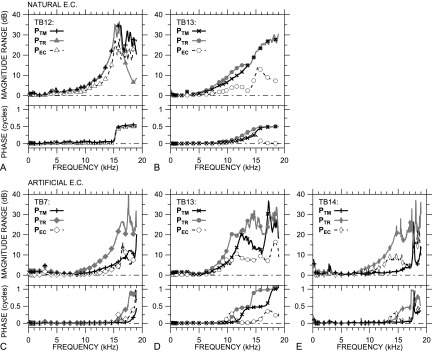
Range of P_TM (+ or ×), P_TR (filled symbols), and P_EC magnitude and phase (open symbols) across frequency. Natural EC: (A) TB12 triangles, (B) TB13 circles; artificial EC: (C) TB7 diamonds, (D) TB13 circles, (E) TB14 thin diamonds. (Top) magnitude; (bottom) phase.

In ears with an artificial EC [Figs. 6(C)–6(E)], the difference in magnitude range peak and phase step frequencies between P_TR and P_TM is larger, which is consistent with the greater distance between the TR plane and the TM surface with the artificial EC (see Sec. II C). In these ears, the maximum |P_TR| range (filled symbols) is generally higher than the maximum |P_TM| range, which indicates that sound pressure variation is higher in the TR plane with the artificial EC than on the TM surface.

Figure 6 also shows that P_EC ranges are generally smaller than P_TM or P_TR ranges. In ear TB12, |P_EC| range is ∼25 dB (compared with 35 dB for |P_TM| and |P_TR|), but |P_EC| range is <18 dB in all other ears, 15–20 dB smaller than the |P_TM| or |P_TR| ranges. Similarly, ∠P_EC range is <0.3 cycles in all ears except TB12, except at the highest frequencies, which suggests that ∠P_EC variations are not due to a standing wave but to some more local phenomenon. Overall, the transverse sound pressure distribution is nearly uniform at a distance of 4–6 mm from the TM across the frequency range, even though longitudinal P_EC variations exist (see Sec. III C below).

C. Sound pressure variations longitudinally along the EC

Just as broadband sound pressure measurements at several locations over the TM and TR plane were used to construct pressure maps at selected frequencies, P_EC measurements at 8–20 locations along the EC axis were used to construct maps of longitudinal P_EC variations at selected frequencies. At each measurement location, a broadband spectrum was recorded, P_EC was computed by normalizing by P_TM at the umbo, and the nodal frequencies at each location were identified as the frequencies of |P_EC| notches (per Ravicz et al., 2007, 2012) or the frequencies at which the unwrapped ∠P_EC is an odd multiple of 1/4 cycle (the midpoints of 0.5-cycle ∠P_EC steps, per Stinson, 1985a; Chan and Geisler, 1990). Data at the identified nodal frequencies were collected from all measurement locations and arranged into longitudinal maps.

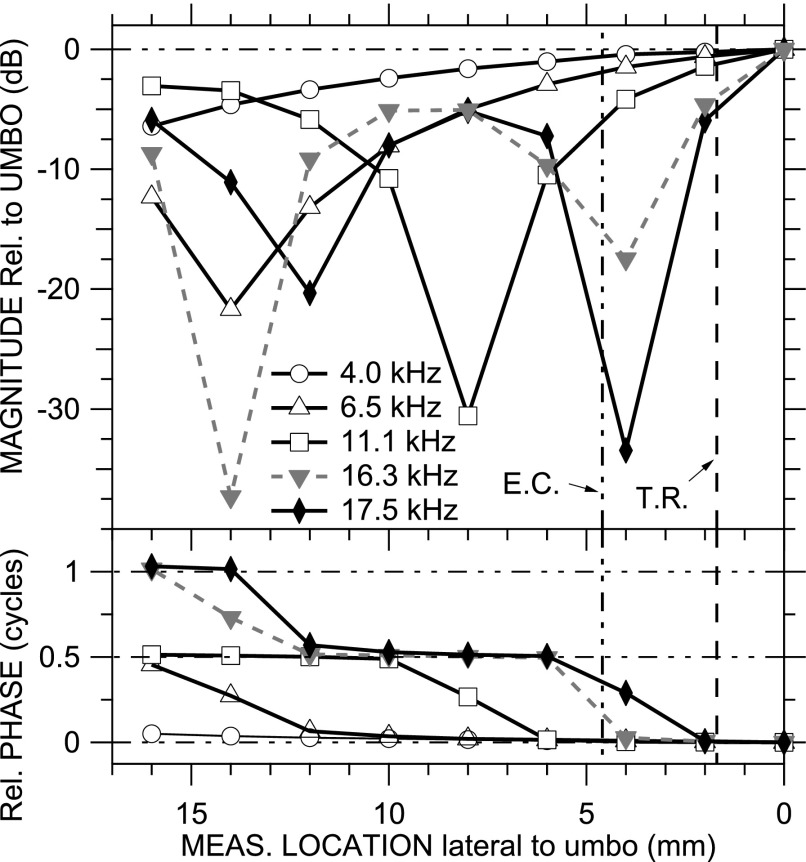
Such a map is shown in Fig. 7 for ear TB12 (natural EC) at five representative frequencies: 4.0, 6.5, 11.1, 16.3, and 17.5 kHz. The P_EC patterns are consistent with those observed previously and predicted by EC models (see Secs. IV A and IV B). At low frequencies (e.g., 4 kHz), P_EC magnitude and phase are approximately constant along the EC; at higher frequencies, P_EC shows a magnitude notch and 0.5-cycle phase step, the location of which moves medially as frequency increases (e.g., 6.5, 11.1 kHz). And, at still higher frequencies, a second |P_EC| notch and ∠P_EC step were observed (e.g., 16.3, 17.6 kHz). In the longer artificial ECs, the frequencies of the first and second notches were lower, and a third notch was observed at the highest frequencies.

FIG. 7.

P_EC maps along the natural EC in ear TB12 at five selected frequencies (4.0, 6.5, 11.1, 16.3, and 17.5 kHz) relative to P_TM at the umbo, constructed from spectra at measurement locations with a 2-mm spacing. (Top) magnitude; (bottom) phase. TR plane 1.7 mm from umbo (dashed vertical line); EC transverse plane 4.6 mm from umbo (double-dotted-dashed vertical line).

As for P_TM and P_TR, we developed a simple metric to describe longitudinal P_EC variations: The locations of P_EC standing-wave nodes predicted by a simple uniform-tube model at the nodal frequencies observed at the measurement locations (e.g., Stinson, 1985a; Chan and Geisler, 1990). This simple uniform-tube model has rigid walls and a rigid termination perpendicular to the tube axis. The predicted nodal locations are at odd multiples of 1/4 wavelength λ from the EC termination (e.g., λ/4, 3 λ/4, 5 λ/4) at the nodal frequencies.

Figure 8 shows scatter plots of the predicted node location vs the measured location for each ear and EC type (similar to Chan and Geisler, 1990, Fig. 2). In these plots, nodal locations close to or far from the umbo correspond to nodes produced at higher or lower frequencies, respectively (see right-hand vertical scale). A perfect prediction of the nodal locations (assuming that the effective EC termination is at the umbo) would fall on the unity line of slope +1 (dotted-dashed line). A constant upward or downward offset of the predicted nodal locations from the measured locations (while maintaining a slope of +1) suggests that the EC length was misestimated. A difference in slope from unity could indicate that (i) the termination is nonrigid and reactive and produces a phase shift in the reflected sound wave, (ii) the standing-wave pattern is compressed or stretched (as observed by Stinson, 1985b; Lawton and Stinson, 1986), (iii) the line of probe tube measurements deviates from the EC axis (Stinson, 1985b), or (iv) the effective length of the EC varies because the TM does not terminate the EC perpendicular to the EC axis. [Because the distance between the TR plane and the TM varied somewhat between ears with artificial ECs (see Sec. II B), the total EC length also varies in these ears.]

FIG. 8.

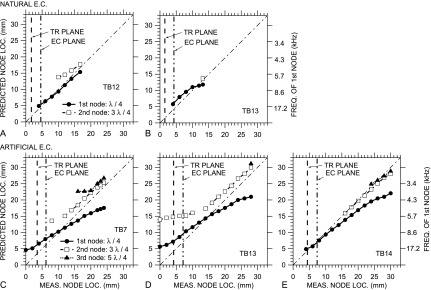
Comparison of the longitudinal P_EC distribution along the EC axis to that predicted from a simple uniform-tube model of the EC. Horizontal axis: Distance between the P_EC measurement locations and the umbo; Vertical left-hand axes: Distance from the EC termination to a standing-wave node predicted from the frequencies of standing-wave node(s) at the measurement locations (right-hand axes), assuming that the distance is an odd multiple of 1/4 wavelength λ. 1st node (λ/4): filled circles; 2nd node (3 λ/4): open squares; 3rd node (5 λ/4): filled triangles. Natural EC: (A) TB12; (B) TB13; artificial EC: (C) TB7, (D) TB13, (E) TB14. A perfect match between measurements and model is shown by the thin dotted-dashed line with slope +1. The locations of the TR plane and transverse EC plane are shown by vertical dashed and dotted-dashed lines, respectively. In all ears, a node was seen at the location of the transverse EC plane, and with an artificial EC, a node was seen at the TR plane as well.

In the natural ECs [TB12, TB13; Figs. 8(A) and 8(B)], the simple uniform-tube EC model provides fairly good predictions of the locations of the standing-wave nodes. In TB13, the predicted loci of the first nodes close to the umbo are ∼1 mm further from the umbo than the measurements, and in TB12, the predicted 2nd-node loci are ∼1 mm further from the umbo. This suggests that our estimate of the effective EC length is slightly low, perhaps indicating that the EC vertex (antero-inferior to the umbo) has an effect. (If the mismatch were due to a phase change in the reflected wave at the TM, we would expect the slope of the locus line to be different from unity.) For the 2nd node, predicted locations are further from the umbo than measurement locations, suggesting that the standing-wave pattern is compressed at higher frequencies.

In the artificial ECs [TB7, TB13, TB14; Figs. 8(C)–8(E)], there are still several similarities between the predicted and measured node locations, but the correspondence is not always as tight as in the natural EC. (1) The slopes of the 2nd and 3rd node loci (where present) are approximately unity except closest to the umbo (highest frequencies). In ear TB14, the predicted loci are nearly on the unity line, implying that the measured EC length corresponds closely to the effective EC length. In ears TB7 and TB13, the predicted loci are ∼3 mm more lateral to the umbo than the measured loci, implying that the effective EC length is underestimated by about 3 mm in these ears. (2) In all artificial ECs, the loci of the 2nd and 3rd nodes track very closely.

There are also differences between the predicted and measured node locations, especially for the first node. (1) The slope of the loci for the 1st node is shallower than unity in all of these ears, which suggests that the standing-wave pattern is stretched. (2) At medial locations (higher frequencies), the slope of the 2nd node loci in TB13 also flattens. Similarities and differences between standing-wave patterns in the natural and artificial ECs and those predicted by simple tube models will be discussed in Sec. IV B.

IV. DISCUSSION

A. A simple description of the sound field in the EC

A goal of this study was to investigate simple descriptions of the EC sound field to enable comparisons of the sound field at different locations, in different frequency ranges, among ears, and with modifications to the EC. This study emphasizes the sound field within a few mm of the TM. The simple descriptors we present here (gradient direction, nodal line location, sound pressure maxima and minima or range, and deviation of longitudinal variations from a simple uniform-tube model; see Sec. III C) provide both a fairly good description of the EC sound field and a means for these comparisons.

This study includes data from two ears with (shortened) natural ECs and three with artificial ECs whose dimensions mimic the natural EC (but are longer by ∼10 mm). With this small sample, only limited conclusions can be drawn about mean properties and the distribution of variations, but this sample provides a good indication of which features are common among ears and what sorts of variations might be observed in a larger population. Similarly, the spatial resolution of our measurements is much coarser than the resolution of tens of microns for TM motion studies (e.g., Rosowski et al., 2009), but is adequate to establish general trends in sound pressure distribution.

At low frequencies, the EC sound field is fairly uniform, as would be expected, since the sound wavelength greatly exceeds the EC dimensions at low frequencies (e.g., Beranek, 1986). Longitudinal variations arise at frequencies above a few kHz (Fig. 7), as expected for any tube of EC dimensions (e.g., Stinson, 1985a). Longitudinally, sound pressure varies smoothly along the EC below the frequency of the first resonance, the frequency and location of which are generally consistent with a quarter-wave resonance. Transverse variations are greatest near the TM or TR plane and are smaller several mm lateral to the TM (Fig. 6). As frequency increases, transverse variations increase smoothly at the TM, as well as in the TR and transverse EC planes (Fig. 6). |P_TM| variations are nearly completely described by a pressure gradient that increases from the postero-superior edge of the TM and EC to the antero-inferior edge (Fig. 4), but ∠P_TM is nearly uniform except at high frequencies (Fig. 5). The direction of the gradient is oriented along the projection of the EC axis on the TR plane (Fig. 4). Spatial variations in |P_TM| of ≥2 dB are detectable at 5 kHz and can be substantial (≥20 dB) by 15 kHz (Fig. 5).

At higher frequencies, around 14–15 kHz in most of the ears but as low as 11 kHz in one ear (TB13 with artificial EC), a nodal line appears on the TM, as evidenced by a |P_TM| minimum and a half-cycle increase in ∠P_TM range (Fig. 5). The nodal line is oriented approximately perpendicular to the projection of the EC axis on the TR plane (Fig. 2). As frequency increases, this node moves from the posterior-superior edge of the TM to its anterior-inferior edge. In one ear (TB13 with artificial EC), the node was coincident with the umbo at ∼15 kHz. In this ear, a second nodal line at a different orientation appeared at still higher frequencies and moved posteriorly across the TM.

Transverse sound pressure variations were generally higher in the TR plane than at the TM, especially in artificial ECs, and lower in a more lateral EC plane than at the TM (Fig. 6). The variations are probably not due to errors in measurement position, as we were able to define the TR and EC planes fairly closely (±0.3 mm at most; see Sec. II C). These variations and the similarities between (a) P_TR and P_TM and (b) the sound fields in natural and artificial ECs are discussed more below.

B. Comparison of EC sound field to a simple uniform-tube model

1. Similarities

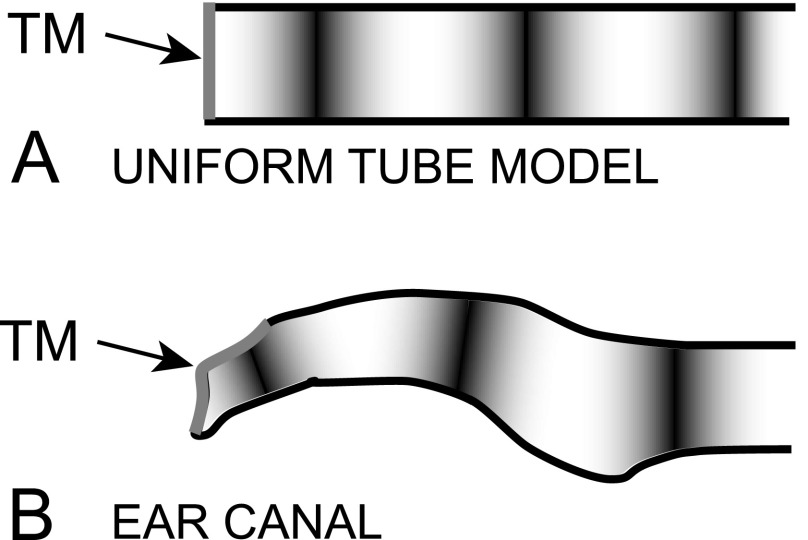
We compare the sound field measured in natural and artificial ECs to that predicted by a uniform-tube model with a rigid termination perpendicular (normal) to the tube axis [Fig. 9(A); see Stinson, 1985a]. The longitudinal P_EC variations described in Fig. 7 and the relative locations of standing-wave nodes and their movement toward the EC termination as frequency increases are very similar to those predicted by such a uniform-tube model (Fig. 8).

FIG. 9.

Schematic of (A) a simple uniform-tube model with a rigid perpendicular termination at the TM and (B) a transverse section of the human EC (after Stinson, 1985b). Local sound pressure maxima and minima (nodes) of a standing-wave pattern are shown by light and dark regions, respectively.

2. Differences and their relation to differences in geometry

The primary difference between the measured EC sound field and that predicted by a simple tube model is sound pressure variations across the TM, TR plane, and transverse EC plane (Figs. 2–6). A rigid normal termination in a uniform tube produces no transverse variation. The transverse variations we observe could be due, in part, to the differences in EC geometry from such a simple tube. The TM terminates the EC obliquely such that the TM can be considered part of the EC wall [Fig. 9(B)], and the nonrigid TM can allow sound energy to leave the EC (e.g., Stinson, 1985b; Stinson and Khanna, 1989).

If the EC axis is considered to extend to the umbo (as in Fig. 8) or the EC vertex, then the TM forms part of the EC wall [Stinson, 1985b; see Fig. 9(B)], and standing-wave nodes in the EC can be present on the TM at high frequencies. Figure 8 also shows the locations of the TR and the transverse EC plane (solid or dotted-dashed vertical lines, respectively) in each ear relative to the EC termination at the umbo. The plots show that, in all ears, a standing-wave node appears in the EC plane at one or more high frequencies and, in the artificial EC, a standing-wave node appears in the TR plane as well. This result is consistent with our observations of nodal lines in the TR plane and, in some ears, at the TM (Figs. 2–6).

The explanation of standing-wave nodes at the TM or TR plane above implies that the nodal lines should be perpendicular to the projection of the EC axis on the TR plane, yet we observed deviations (Figs. 2 and 4). A possible explanation is that, since the manubrium is oriented asymmetrically relative to the projection of the EC axis on the TM (Figs. 1, 2, and 4), variations in mechanical properties between different parts of the TM can influence the degree to which sound is absorbed or reflected from the TM and therefore produce local transverse variations in the sound field near the TM (“nonplanar” modes, e.g., Rabbitt and Holmes, 1988; Fletcher, 1992).

A uniform-tube EC model also predicts that sound pressure variations should be of the same size along the tube. In contrast, we observed a larger range of P_TR variations than P_TM variations (Fig. 6). Nonplanar modes excited at the TM and propagating laterally (e.g., Rabbitt and Holmes, 1988; Fletcher, 1992) might explain the existence of P_TR variations, but not why they are larger than P_TM variations. The larger P_TR variations could include a contribution from an effective EC curvature in this region (Stinson, 1990). Similar, transverse P_EC variations could be lower because the EC is straight in this more lateral region and/or because nonplanar modes from medial locations have dissipated (Rabbitt and Holmes, 1988; Fletcher, 1992; see Sec. IV C below).

C. Possible effects of experimental conditions

In this study, sound pressure was measured in human temporal bones rather than live human subjects. It is unlikely that post-mortem changes in the EC or middle-ear acoustical properties affected our results, as the EC walls are effectively rigid in both live and cadaver adult ears, and comparisons of middle-ear acoustic (Rosowski et al., 1990) and mechanical properties in live subjects or patients (e.g., Goode et al., 1993; Chien et al., 2006, 2009; Rosowski et al., 2007) have shown no appreciable post-mortem differences.

Acquiring a set of measurements took 45–60 min (Sec. II B), long enough that stiffening of the TM due to drying could confound pressure maps. P_TR and P_EC measured at the beginning and end of a measurement session were very similar, and stapes velocity measured before and after acoustic measurements was near the normal criterion (Rosowski et al., 2007), which indicates that the effects of drying during measurements were negligible.

One potential source of variations in the transverse sound field is the difference in how sound is provided to the artificial EC (through a tube in the EC wall) vs the natural EC (approximately axially at the lateral opening). Analyses of the role of geometric asymmetries in the lateral EC in generating transverse inhomogeneities in the EC sound field near the EC opening due to nonplanar sound modes (Rabbitt and Friedrich, 1991) suggest that transverse variations due to asymmetries in sound delivery decrease by ∼20 dB within 4 mm of the point of sound introduction at 15 kHz and below (which implies a space constant for a decrease by 1/e of ∼2 mm). The narrow isthmus in the natural EC also inhibits the propagation of nonplanar modes (Rabbitt and Friedrich, 1991). An examination of the artificial EC using a uniform-tube assumption and the major diameter (Fletcher, 1992) suggests that the first nonplanar mode propagates at frequencies >18.1 kHz, but at 17.1 kHz is still attenuated by 20 dB at the P_EC measurement plane, ∼23 mm from the sound delivery tube. Consequently, we expect that transverse P_EC variations due to the sound delivery tube location will be insignificant by the time they reach the transverse P_EC measurement plane at all but the highest frequency. [Similarly, the probe tube diameter is small enough that its presence and off-center location have no significant effect on the EC sound field (Rabbitt and Friedrich, 1991).] The observations that transverse P_EC variations are small, less than transverse P_TR variations, and no larger in artificial ECs than in natural ECs (Fig. 6) support this conclusion.

D. Comparison of results to previous studies

1. Longitudinally along the EC

Longitudinal standing-wave patterns along the human EC have been measured in several previous studies (e.g., Lawton and Stinson, 1986), and Stinson and colleagues compared the spacing of standing-wave nodes to that predicted by both simple tube models (Stinson, 1985b; Lawton and Stinson, 1986) and more complicated models that take EC curvature, the straight probe tube trajectory, and variations in EC cross-section area into account (Stinson, 1990). Both stretching and compression of the standing-wave patterns were observed, depending on changes in EC cross-section area and the transverse location of the probe tube in the EC. A study by Chan and Geisler (1990), on which our Fig. 8 is based, also showed stretching of the standing-wave pattern close to the TM in natural ECs, while, in our study, this stretching was most pronounced in artificial ECs. Chan and Geisler attributed this stretching, in part, to the discrepancy between the curvature of the EC and the straight trajectory of their probe tube. They estimated the effective EC termination midway between the “top” of the TM (perhaps corresponding to our TR plane) and the umbo (assuming a rigid EC termination). Finite-element (e.g., Gan et al., 2006) and boundary-element models of the EC sound field (Stinson and Daigle, 2005) also predict longitudinal EC sound field variations. Our results generally support these previous studies and provide a more comprehensive description of the sound field near the TM.

2. Transversely across the medial EC

To our knowledge, only one other set of measurements and two models of transverse sound pressure variations in human ECs exist. Sound pressure measured along a line in the TR plane in scaled models of several human ECs (“y”-axis and triangles in Figs. 9–12 of Stinson, 1985b) showed a null and were used to support an estimate of a standing-wave node at 15 kHz at a point ∼2/3 of the way from the umbo up the manubrium (Fig. 13 of Stinson, 1985b). In using measurements from a single line, that study assumed that isobars are perpendicular to the manubrium; we show that, in fact, they are perpendicular to the EC direction.

The boundary-element EC model of Stinson and Daigle (2005) predicted 5–25 dB sound pressure variations across the EC; predictions only at locations 15 or 25 mm lateral to the EC vertex were shown. We observed a 30-dB |P_EC| range and 0.5-cycle ∠P_EC range ∼5 mm from the umbo (∼9 mm from the vertex) in one intact ear (TB12), but |P_EC| variation was otherwise ∼15 dB at most. A finite-element model of the EC and middle ear (Koike et al., 2002, Fig. 15) predicted a nearly uniform TM sound pressure distribution at 100 Hz and slightly higher sound pressure near the umbo at 7 kHz. Our measurements support the model predictions at low frequencies, but show a much different |P_TM| distribution at higher frequencies (Fig. 2).

3. In other species

The longitudinal P_EC variations and standing-wave patterns we present are qualitatively similar to those observed in cat (Khanna and Stinson, 1985; Stinson and Khanna, 1994) and gerbil (Ravicz et al., 2007; Bergevin and Olson, 2014), and most of the differences in the frequencies of standing-wave nulls between human and gerbil can be explained by the shorter gerbil EC (∼4 mm vs 13–35 mm in our study). Similarly, sound pressure variations ±1 mm transversely across the TR in gerbil (Ravicz et al., 2007, Fig. 9) are much smaller (<3 dB) than variations in the direction of the EC axis (30 dB), similar to our results (see Figs. 2 and 3) and extending to higher frequencies (80 kHz). Sound variations measured by Bergevin and Olson (2014) in intermediate directions may include contributions from variations in both the EC axis and transverse directions and so are difficult to interpret in the context of this study.

E. Uniformity of the transverse sound field near the TM

As discussed above, the sound field over the TM surface is uniform at low frequencies (<5 kHz) and shows considerable variation at higher frequencies. (|P_TM| variations in some ears <3 kHz are believed to be due to a leak between the artificial EC and the temporal bone and so are an artifact of our measurement technique.)

At higher frequencies, |P_TM| is lower over the postero-superior part of the TM than at the umbo. In ears with a natural EC [Figs. 4(A) and 4(B)], this decrease exceeds 10 dB above 11 kHz (Fig. 5). Above 14 kHz, a |P_TM| minimum and half-cycle ∠P_TM step [Fig. 2(D)] indicate the presence of a standing-wave node on the TM (see also Figs. 4 and 5). The total |P_TM| range at the standing-wave frequency is 25–30 dB. Above the standing-wave frequency, P_TM over a substantial portion of the measured TM area is not in-phase with P_TM over the umbo. The story is very similar in ears with an artificial EC, though |P_TM| variations generally arise at slightly higher frequencies with the artificial EC than with the natural EC. In one ear (TB13), an additional transverse variation was seen near 15 kHz, which may be related to a transition between two standing-wave patterns. In another ear (TB14), no standing-wave pattern was observed even at the highest frequency measured (19 kHz), although |P_TM| varied by more than 25 dB in a narrow frequency range [Fig. 6(E)]. These results show that, with both natural and artificial ECs, substantial P_TM variations occur at even moderate frequencies, and standing waves are present on the TM at frequencies well within the human auditory range.

The low-frequency uniformity of the sound field near the TM, simple variations at high frequencies, and the smooth transition between them are in contrast to the much more complicated TM motion distributions (e.g., Tonndorf and Khanna, 1972; Chang et al., 2013; Cheng et al., 2013) that can be divided into distinct regimes in discrete frequency ranges with easily evident transitions (Rosowski et al., 2009; Cheng et al., 2010). The P_TM measurements presented here are an essential part of understanding the origin and importance of the TM motion distributions and suggest that the complicated TM motion may be due mostly to the TM mechanical properties and have little relation to local sound pressure distributions.

The existence of standing-wave nodes on the TM surface at high frequencies also raises the question of whether the upper frequency limit of human hearing (∼20 kHz) is influenced by the sound pressure distribution over the TM. If P_TM over most of the TM contributes to high-frequency middle-ear input, cancellation by regions with out-of-phase ∠P_TM might reduce the summed |P_TM|. If much of the TM is effectively decoupled from the malleus at high frequencies (e.g., Zwislocki, 1962; Shaw and Stinson, 1983; Shera and Zweig, 1991), such that P_TM near the umbo provides the primary middle-ear input (e.g., Khanna and Stinson, 1985, p. 588), a standing-wave node at the umbo could greatly reduce the middle-ear input and could contribute to the rolloff of hearing sensitivity at high frequencies that determines the upper frequency limit of hearing.

F. Sound pressure at more lateral locations as a predictor of TM sound pressure

1. In the TR plane

In ears with a natural or artificial EC, there are many similarities between the sound field at the TM and in the TR plane. Differences between P_TR and P_TM occur mostly at high frequencies and are manifested primarily as a downward shift in the frequency of dominant features. For instance, |P_TM| and |P_TR| gradient directions and nodal line orientations are similar, and standing waves appear in the TR plane at frequencies 1–2 kHz lower than at the TM surface (Fig. 4).

With a natural EC, P_TR and P_TM ranges are very similar at nearly all frequencies [Figs. 6(A) and 6(B)]. In one ear (TB13), the P_TR range is slightly higher than the P_TM range between 8 and 15 kHz, and the standing-wave node appears at a slightly lower frequency in the TR plane than on the TM (13 vs 15 kHz); in the other (TB12), the |P_TR| range is slightly lower than the |P_TM| range above 16 kHz.

With an artificial EC, the differences between P_TR and P_TM are more pronounced, but can still be described simply. In these ears, the |P_TR| range is greater than the |P_TM| range above 6–8 kHz [Figs. 6(C)–6(E)], but shows the same increase with frequency to a peak denoting a standing wave. The standing-wave frequency is lower for P_TR than for P_TM, but the variations in P_TR range can be described well by a shift of the P_TM range variations to slightly lower frequencies [Fig. 6(B)]. In TB14, evidence of a standing wave is seen in the P_TR range, while the P_TM range shows only the increase in magnitude and phase range that is a precursor to the appearance of a standing wave.

The similarity of most features in P_TM and P_TR in ears with an intact EC means that P_TR is a good predictor of P_TM. Even in ears with an artificial EC, in which P_TR variations are larger than P_TM variations and occur at a lower frequency, P_TR provides an upper bound to P_TM variability and predicts P_TM extrema with an appropriate downward frequency shift. In this way, P_TR provides a useful estimate of P_TM.

2. In the transverse EC plane

In most ears, the transverse variations in P_EC were smaller than P_TM or P_TR variations at nearly all frequencies (Fig. 6). The result that P_EC variations were smaller than P_TR variations means that variations that arise at or near the TM or TR are sufficiently small and/or do not propagate far laterally up the EC. However, standing waves in the EC produce longitudinal P_EC variations of at least 30 dB (Figs. 7 and 8), which limits the usefulness of P_EC as a predictor of P_TM.

Even simple transverse P_TM variations complicate the idea of an input impedance at the TM (e.g., Stinson, 1985b), just as the oblique termination of the EC by the nonrigid TM makes the TM termination and effective EC length difficult to describe. The existence of these complications points out the need and use for other descriptors of EC power flow at high frequencies such as reflectance (e.g., Stinson, 1985b; Keefe et al., 1993) or estimates of stimulus intensity (Neely and Gorga, 1998) that can be computed from measurements at a single EC location far from the TM, where transverse variations are minimal.

G. Similarity of the sound field near the TM in artificial and natural ECs

In Secs. IV E and IV F above, we discuss how P_TM and P_TR variations are similar among both natural and artificial ECs, and in Sec. III B 3 and III C above, we discuss how P_EC variations are similar among natural and artificial ECs, taking into account the greater distance between the transverse EC plane or the TR plane and the TM in artificial ECs compared to natural ECs. In comparisons both in the same ear (TB13) and between ears, the robustness of these results indicates that the artificial EC mimics the natural EC for most important features. This artificial EC is suitable for studies of the sound field in natural ECs.

V. SUMMARY AND CONCLUSIONS

• (1)The sound field within either the natural human EC or an artificial EC can be described fairly well by a few simple parameters: sound pressure gradient direction, standing-wave nodal line orientation and location, magnitude and phase maximum and minimum or range, and locations of longitudinal standing-wave nodes along the EC axis relative to those predicted by a uniform-tube model with a rigid termination.
• (2)With a natural or artificial EC, sound pressure across the TM surface varies by at least 10 dB at 11 kHz and more at higher frequencies. Standing-wave nodes are present on the TM at frequencies ≳14 kHz. In one ear, the standing-wave node was located over the umbo within the frequency range of measurements. The nodal lines on the TM surface that first appear near 15 kHz are generally perpendicular to the EC axis, but their orientation changes slightly as frequency increases.
• (3)The sound pressure distribution in the TR plane is similar to that on the TM surface. The sound pressure distribution in a transverse EC plane is more uniform than in the TR plane, which indicates that P_TM and P_TR variations do not propagate far up the EC.
• (4)Longitudinal P_EC variations are similar to those predicted by a simple uniform-tube model, with a few differences. The measured nodal locations are offset and stretched (scaled) compared to the model predictions, as seen previously (e.g., Stinson, 1990). The degree of stretching is comparable to that observed previously in model ECs (Stinson, 1985b) and human subjects (Lawton and Stinson, 1986; Stinson, 1990).
• (5)The sound pressure distribution in the TR plane is a useful predictor of P_TM. P_TR variations are larger and occur at a lower frequency than P_TM variations, but other features are similar [see (3) above].
• (6)The artificial EC is a useful model of the natural EC. Transverse variations in the TR plane are higher in the artificial EC than in the natural EC, but other features are similar.
• (7)The sound pressure distribution over the TM surface is not well correlated to complex patterns of TM motion.