Multibody correlations in the hydrophobic solvation of glycine peptides

Abstract

Protein collapse during folding is often assumed to be driven by a hydrophobic solvation energy (ΔG_vdw) that scales linearly with solvent-accessible surface area (A). In a previous study, we argued that ΔG_vdw, as well as its attractive (ΔG_att) and repulsive (ΔG_rep) components, was not simply a linear function of A. We found that the surface tensions, γ_rep, γ_att, and γ_vdw, gotten from ΔG_rep, ΔG_att, and ΔG_vdw against A for four configurations of deca-alanine differed from those obtained for a set of alkanes. In the present study, we extend our analysis to fifty decaglycine structures and atomic decompositions. We find that different configurations of decaglycine generate different estimates of γ_rep. Additionally, we considered the reconstruction of the solvation free energy from scaling the free energy of solvation of each atom type, free in solution. The free energy of the isolated atoms, scaled by the inverse surface area the atom would expose in the molecule does not reproduce the γ_rep for the intact decaglycines. Finally, γ_att for the decaglycine conformations is much larger in magnitude than those for deca-alanine or the alkanes, leading to large negative values of γ_vdw (−74 and −56 cal/mol/Ų for CHARMM27 and AMBER ff12sb force fields, respectively). These findings imply that ΔG_vdw favors extended rather than compact structures for decaglycine. We find that ΔG_rep and ΔG_vdw have complicated dependencies on multibody correlations between solute atoms, on the geometry of the molecular surface, and on the chemical identities of the atoms.

I. INTRODUCTION

Computing accurate solvation energies (ΔG) is a major goal of computational chemistry. If such calculations could be made simple and routine, then they would allow more complicated chemical transformations to be computed in vacuum, where such calculations are often easier to perform.^1,2 One common approach to computing ΔG is to divide it into two components: the energy of inserting an uncharged molecule (cavity) into solution (ΔG_vdw) and the energy of turning on the atomic partial charges (ΔG_el).^3,4 Several theories have been developed to predict ΔG_el, including approaches based on the Poisson equation (Poisson-Boltzmann⁵ and generalized Born⁶ methods), integral equations,⁷ and structured continuum approaches.^8–10 Here, we tested various theories for computing ΔG_vdw.

Many researchers have assumed^2,11–13 that ΔG_vdw = γ_vdwA, where A is the solvent-accessible surface area of the molecule and γ_vdw is a positive surface tension that is independent of the properties of the molecule. This behavior is expected for macroscopic interfaces with and cavities in solvent.¹⁴ Because a solvation free energy that increased with A would favor compact conformations, the notion that ΔG_vdw drives the initial collapse during protein folding and aggregation is widely held.^2,15,16

Other researchers have, however, noted that the arguments that lead to the idea that ΔG_vdw = γ_vdwA only account for the energy of expelling the water from the molecular cavity and do not account for the formation of favorable dispersive interactions between the solute and solvent.^17–25 These studies have therefore proposed to split ΔG_vdw into purely repulsive (ΔG_rep) and attractive (ΔG_att) components. Also, several other studies^26–29 have claimed that ΔG_rep should be proportional to the solvent-accessible volume (V) rather than A for sufficiently small solutes. Following these ideas, several studies have attempted to compute ΔG_vdw by assuming that ΔG_rep is a linear function of A and V and that ΔG_att can be computed from other means.^20,21,24

Two other methods that have been used to estimate ΔG_vdw or ΔG_rep are to assign separate γ_vdw or γ_rep to different atom types³⁰ and in an analogy with macroscopic interfaces to add a correction term to γ_vdw to account for the curvature of the molecular surface.^31,32

Recent work seems to contradict some of the assumptions underlying these models.^25,33–35 These studies demonstrated that ΔG_vdw decreases with the number of monomers for glycine and alanine peptides and that it also decreases with increasing A and V for decaalanine.³⁴ These findings appear to contradict the common hypothesis^2,15,16 that ΔG_vdw drives aggregation and collapse during peptide aggregation and protein collapse and folding. By decomposing ΔG_vdw into ΔG_rep and ΔG_att according to a Weeks-Chandler-Andersen (WCA) decomposition,^17,18 we showed that ΔG_vdw decreased with A for deca-alanine because although ΔG_rep did increase with A, this increase was more than matched by increasingly favorable ΔG_att.²⁵ This finding appears to support studies^17–24 that argue that ΔG_att should be computed separately from ΔG_rep. However, γ_vdw for a series of alkanes differed from that for four configurations of decaalanines, and the derivatives (∂ΔG_rep/∂x_i) of ΔG_rep with respect to the coordinates (x_i) of the atomic centers were not linear in ∂A/∂x_i, as would be expected if γ_vdw were a well-defined quantity. These findings may help explain such apparent anomalies as the observation that ΔG increases at different rates with A for cyclic or branched, rather than linear, alkanes.³⁶ They also indicate that γ_rep is probably not universally well defined and that how ΔG_rep changes when an atom is moved depends not just on how A changes but also on multibody interactions with neighboring atoms and the local structure of the molecular surface.

In a recent study, we considered the decomposition of ΔG_vdw into ΔG_rep and ΔG_att for a series of alkanes and four conformers of deca-alanine.²⁵ The study raised questions about both variation with respect to chemistry and the sensitivity of the results to model parameters. In the present study, we extend our analysis to 50 sampled conformations of decaglycine taken over a few hundred nanoseconds and examine the sensitivity of our conclusions to the choice of force field by comparing two different force fields, CHARMM27^37,38 and AMBER ff12sb (models (1) and (2), respectively). Although the model force fields produce different quantitative results, the basic findings are consistent with our previous studies of decaalanines and alkanes. The values of γ_rep, γ_att, and γ_vdw differ significantly from those we found for deca-alanine and the alkanes, implying that these are not universally well-defined quantities, and that ∂ΔG_rep/∂x_i is not correlated with ∂A/∂x_i for some atom types.

Additionally, here we consider ΔG_rep of each isolated atom type in the decaglycine to test atom-scaling models of hydrophobicity. We find the repulsive component of the free energy of the isolated atoms, scaled by the surface the atom would exposed in the molecule does not reproduce ∂ΔG_rep/∂x_i versus ∂A/∂x_i for each atom type. This finding, combined with the poor correlations between ∂ΔG_rep/∂x_i and ∂A/∂x_i for some atom types and the finding that the slopes of such plots for some atom types differed from the slopes obtained for the same atom types in decaalanine imply that using a separate surface tension for each atom type is not able to explain our results.

In the Results section, we obtain estimates of γ_vdw for decaglycines (−74 and −56 cal/mol/Ų for models (1) and (2)) that are larger and more negative than what we found for decaalanines (−3 cal/mol/Ų) or alkanes (5 cal/mol/Ų), implying that ΔG_vdw favors extended rather than compact structures for decaglycine.^25,34,35 We consider the implication of these results and the inability of area scaling the solvation free energy of isolated atoms to reproduce that for a molecule in the context of available models.

II. THEORY

Decomposing free energies into components can be challenging, as path dependencies in energy definitions can lead to difficulties in interpreting the results. Our chosen decomposition of ΔG_vdw into ΔG_rep and ΔG_att according to a WCA decomposition,^17,18 in contrast, is a well-defined decomposition with a strictly defined path. Because ΔG_rep is well-defined, we can examine its sensitivity to the molecular structure by computing its derivatives with respect to the atomic coordinates.²⁵

A. Free energy definitions

We define ΔG_vdw to be the free energy required to go from a system where the solute and solvent do not interact to one where the interaction potential between solute and solvent atoms is given only by a Lennard-Jones potential,

$$U_{\mathrm{vdw}}^{ij}={\varepsilon }_{ij}\left[{\left(r_{ij}^{\min }/r_{ij}\right)}^{12}-2{\left(r_{ij}^{\min }/r_{ij}\right)}^6\right],$$ (1)

where r_ij is the distance between the atoms, $r_{ij}^{\min }$ is the distance to the minimum of U_vdw, and ε_ij is the energy at the minimum of U_vdw. As we are computing ΔG_vdw and not ΔG, the electrostatic interaction between solute and solvent is not included. We define ΔG_rep to be the free energy required to go from a system where the solute and solvent did not interact to one where the interaction potential between solute and solvent atoms is given by the repulsive component of a Weeks-Chandler-Andersen^17,18 breakdown of ΔG_vdw

$$U_{\mathrm{rep}}^{ij}={\varepsilon }_{ij}\left\{\begin{array}{cc}\hfill {\left(\frac{r_{ij}^{\min }}{r_{ij}}\right)}^{12}-2{\left(\frac{r_{ij}^{\min }}{r_{ij}}\right)}^6+1& \hfill \text{if}{r}_{ij}<r_{ij}^{\min }\\ \hfill 0& \hfill \text{otherwise}.\end{array}\right.$$ (2)

We define ΔG_att ≡ ΔG_vdw − ΔG_rep and $U_{\mathrm{att}}^{ij}\equiv U_{\mathrm{vdw}}^{ij}-U_{\mathrm{rep}}^{ij}$.

B. Computation of free energies and free energy derivatives

To compute the energy ($\Delta G_{\mathrm{rep}}^i$) of inserting a single atom of each atom type i in the force field, we used free energy perturbation (FEP).^39,40 A λ-dependent potential with a soft core was used,

$$U\left(\lambda \right)=\lambda {\varepsilon }_{ij}\sum \left\{\begin{array}{cc}\hfill {\left(\frac{r_{ij}^{\min }}{r_{ij}\left(\lambda \right)}\right)}^{12}-2{\left(\frac{r_{ij}^{\min }}{r_{ij}\left(\lambda \right)}\right)}^6+1& \hfill \text{if}{r}_{ij}<r_{ij}^{\min }\\ \hfill 0& \hfill \text{otherwise},\end{array}\right.$$ (3)

where $r_{ij}\left(\lambda \right)={(r_{ij}^2+(1-\lambda ){\left(r_{ij}^{\min }\right)}^2)}^{1/2}$.

Linear response theory (LRT) estimates of ΔG_att ($\Delta G_{\mathrm{att}}^{\mathrm{lrt}}$) were computed by

$$\Delta G_{\mathrm{att}}^{\mathrm{lrt}}=1/2[{⟨U_{\mathrm{att}}⟩}_0+{⟨U_{\mathrm{att}}⟩}_1],$$ (4)

where ⟨…⟩₀ signifies an average over an ensemble where the solute and solvent interaction potential is $U_{\mathrm{rep}}^{ij}$, ⟨…⟩₁ signifies an average over an ensemble where the potential is $U_{\mathrm{vdw}}^{ij}$, and $U_{\mathrm{att}}=\sum U_{\mathrm{att}}^{ij}$, where this summation was taken over all solute-solvent atom pairs.

As in our previous study,²⁵ ∂ΔG_rep/∂x_i was computed by

$$\partial \Delta G_{\mathrm{rep}}/\partial x_i={⟨\partial U_{\mathrm{rep}}/\partial x_i⟩}_0,$$ (5)

where $U_{\mathrm{rep}}=\sum U_{\mathrm{rep}}^{ij}$, again taken over all solute-solvent atom pairs.

Once estimates of ∂ΔG_rep/∂x_i had been obtained, perturbative estimates (${\gamma }_{\mathrm{rep}}^{\mathrm{der}}$) of γ_der could be obtained by computing the slopes of best-fit lines of plots of ∂ΔG_rep/∂x_i against ∂A/∂x_i.

III. METHODS

The simulations used to obtain the configurations of decaglycine in models (1) and (2) were run with NAMD 2.9.⁴¹ To create the conformations of decaglycine in model (1), a simulation was run with the CHARMM27 force field.^37,38 First, an extended decaglycine was created with the MOLEFACTURE plugin in VMD⁴² and placed in a 45×45×45 Å water box. It was then minimized for 10 000 steps and equilibrated for 20 ps. We then simulated for 300 ns, and configurations were saved every 10 ps. The structures with the largest and smallest A were taken from these configurations. The remaining 48 structures were selected to ensure an even spacing in A between the structures with the largest and smallest A. To create the conformations of decaglycine in model (2), the same protocol was followed except that the initial extended decaglycine was created with xleap⁴³ and the force field parameters were taken from the AMBER ff12sb force field.

To compute $\Delta G_{\mathrm{att}}^{\mathrm{lrt}}$ and ∂G/∂x_i, each selected decaglycine structure was placed in a water box 20 Å larger than the molecule in each dimension, and these systems were minimized for 5000 steps. Two copies of each system were then created, one where the interaction potential between the solute and solvent was $U_{\mathrm{rep}}^{ij}$ and the other where it was $U_{\mathrm{vdw}}^{ij}$. The temperatures of these systems were then increased from 25 to 300 K in increments of 25 K, with 2 ps simulations at each temperature. Next, each system was simulated for 1 ns, snapshots were taken every 0.2 ps, and these frames were used to compute the averages in Eq. (4). We computed ∂ΔG_rep/∂x_i from the same simulations we used to compute $\Delta G_{\mathrm{att}}^{\mathrm{lrt}}$.

ALPHASURF in the PROGEOM package⁴⁴ was used to compute A and ∂A/∂x_i. As in our previous work, A was defined to be the solvent-accessible surface area of the molecule,⁴⁵ defined with a probe radius of 1.7682 Å (the van der Waals radius of a water oxygen in the CHARMM27 force field) rather than the more normal 1.4 Å. The traditional choice of a radius of 1.4 Å is due to the OO peak in the water-water radial distribution function. However, this exceptionally close approach between water molecules (more than 0.5 Å closer than the minimum in their $U_{\mathrm{vdw}}^{ij}$) is caused by the strong favorable hydrogen-bonding energy between neighboring molecules. In our calculations, the solute molecules contained no charges, so there were no similar strong attractive forces between the solute and solvent to change the effective radius in $U_{\mathrm{vdw}}^{ij}$. For this reason and because it yielded slightly better correlations between ΔG_rep and A in our previous study on decaalanines we made this area defining choice.^25,35

Another approach that might be considered would be to use alternative surface definitions, and curvature corrections such as those explored by Honig and co-workers.³¹ However, many alternative surfaces are often approximated with triangulated or other meshes. We did attempt to use other surface definitions in our previous work on decaalanines,²⁵ but we did not include the analysis because the resulting estimates of ∂A/∂x_i were frequently not consistent with finite-difference estimates of these derivatives. The type of analysis performed in the present study, where we compare ∂A/∂x_i to ∂ΔG_rep/∂x_i to test the proposition that ΔG_rep is linear in A, would not converge well with such triangulated surface definitions.

To compute the repulsive component ($\Delta G_{\mathrm{rep}}^{\mathrm{i}}$) of the ΔG_vdw of inserting a single atom of type i into solution, λ-space was divided into 10 equally spaced windows. A single solute atom of each type was placed in a water box 20 Å on a side, and this structure underwent 50 000 steps of minimization. From this minimized structure, initial structures for each λ value were created by increasing the temperature of this box from 25 to 300 K in 25 K increments. At each temperature, the system was simulated for 2 ps. Each of the resulting systems was then run for 1 ns, configurations were taken every 0.2 ps, and these frames were used in the FEP calculations. Although FEP is more accurate when a particle is being inserted rather than removed from solution,⁴⁶ the differences between the estimates obtained from forward FEP and those from backward FEP provided rough estimates of the errors in these calculations.

IV. RESULTS

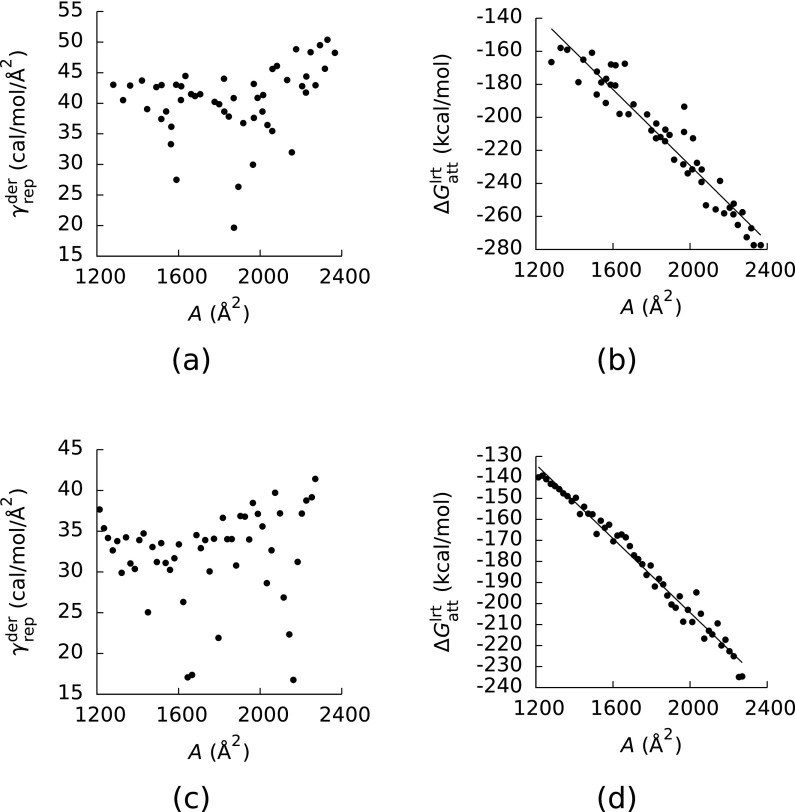
Panels (a) and (c) of Figure 1 show ${\gamma }_{\mathrm{rep}}^{\mathrm{der}}$ as a function of A for models (1) and (2). Rather than being a constant, ${\gamma }_{\mathrm{rep}}^{\mathrm{der}}$ ranged from 19.7 to 50.3 and 15.8 to 41.4 cal/mol/Ų for models (1) and (2), and the correlations between $\partial \Delta G_{\mathrm{rep}}^{\mathrm{der}}/\partial x_i$ and ∂A/∂x_i were weak for many of the configurations of decaglycine. (The Pearson's correlation coefficients (R²) between these two quantities ranged from 0.53 to 0.84 and 0.33 to 0.78 for models (1) and (2), respectively.) The average values of ${\gamma }_{\mathrm{rep}}^{\mathrm{der}}$ from models (1) and (2) (40.4 and 32.2 cal/mol/Ų) differed from what we found for decaalanine (43 cal/mol/Ų), but the range of ${\gamma }_{\mathrm{rep}}^{\mathrm{der}}$ in model (1) did at least contain the value of γ_rep we found for decaalanine. The values of γ_rep obtained here also differed significantly from what we found for a series of alkanes (69 cal/mol/Ų), implying that γ_rep is not a well-defined quantity.

FIG. 1.

(a) The slope (${\gamma }_{\mathrm{rep}}^{\mathrm{der}}$) of the least-squares lines between the derivatives ($\partial \Delta G_{\mathrm{rep}}^{\mathrm{der}}/\partial x_i$) of the repulsive component (ΔG_rep) of the van der Waals component (ΔG_vdw) of the solvation free energy with respect to the coordinates (x_i) of the atomic centers and the derivative (∂A/∂x_i) of the solvent-accessible surface area (A) with respect to the x_i as a function of A. (b) Linear response theory estimates ($\Delta G_{\mathrm{att}}^{\mathrm{lrt}}$) of the attractive component of ΔG_vdw as a function of A. The values in (a) and (b) were computed with the CHARMM27 force field and configurations taken from a simulation run with CHARMM27. (c) and (d) The same as (a) and (b), respectively, but the values in these plots were computed with AMBER ff12sb and configurations taken from a simulation run with AMBER ff12sb. The slopes of the least-squares lines in (c) and (d) were −114 and −88 cal/mol/Ų, and the Pearson's correlation coefficients of these lines were R² = 0.92 and 0.98.

To verify that the estimates of ${\gamma }_{\mathrm{rep}}^{\mathrm{der}}$ had converged, we also computed these quantities from estimates of ∂ΔG_rep/∂x_i obtained from the first halves of the trajectories used to generate our estimates of ${\gamma }_{\mathrm{rep}}^{\mathrm{der}}$ and estimates of ∂A/∂x_i obtained from finite difference derivatives computed by moving each atom 0.001 Å in each direction. These coarser estimates of ${\gamma }_{\mathrm{rep}}^{\mathrm{der}}$ differed from those in Figure 1 by less than 1.1 cal/mol/Ų.

Panels (b) and (d) of Figure 1 show $\Delta G_{\mathrm{att}}^{\mathrm{lrt}}$ plotted as a function of A for models (1) and (2). As in our previous study, this energy was roughly linear in A, although here the correlations between $\Delta G_{\mathrm{att}}^{\mathrm{lrt}}$ and A (R² = 0.92 and 0.98 for models (1) and (2)) were weaker than that between ΔG_att and A for decaalanine in our previous study (R² = 0.99). The weaker correlations in the present study may be a consequence of the larger number of diverse configurations, which allowed us to better test the proposition that ΔG_att should be linear in A. Furthermore, the estimates of ${\gamma }_{\mathrm{att}}^{\mathrm{lrt}}$ obtained from this data (−114 and −88 cal/mol/Ų for models (1) and (2)) differed from either what we observed for the decaalanine peptides (γ_att = −48 cal/mol/Ų) or what we observed for the alkanes (γ_att = −64 cal/mol/Ų).

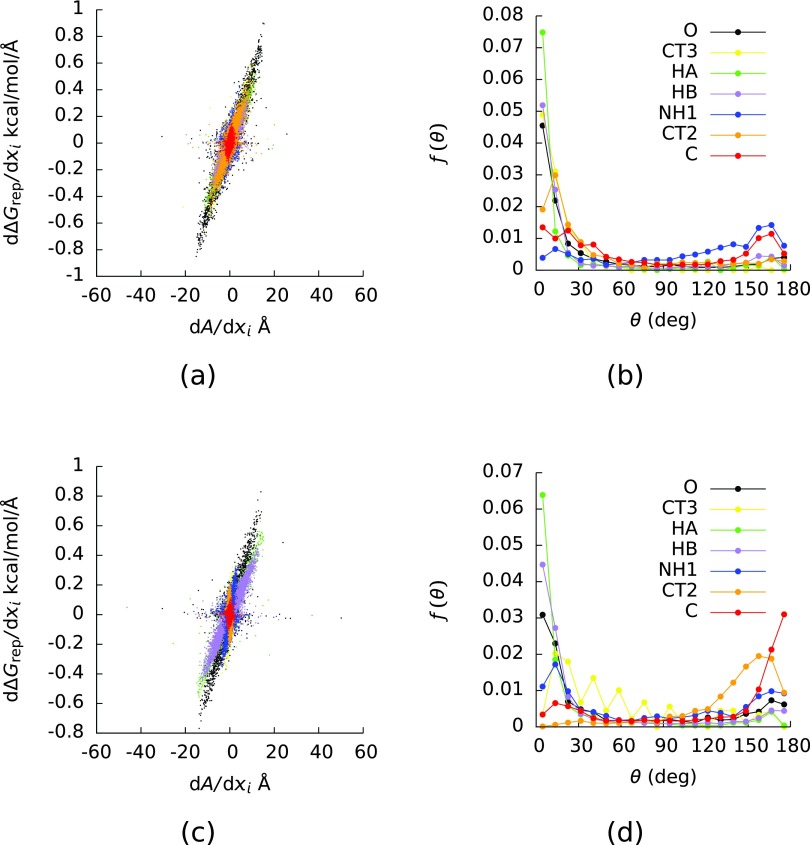
As in our previous study, whether ∂ΔG_rep/∂x_i was proportional to ∂A/∂x_i depended on the atom type considered. In panels (a) and (c) of Figure 2, ∂ΔG_rep/∂x_i is plotted as a function of ∂A/∂x_i for models (1) and (2), and the points are colored by their atom types in the CHARMM27 force field. Atoms of type C were the carbonyl carbons, atoms of type CT2 were the α-carbons, atoms of type CT3 were the terminal carbons, atoms of type HA were the hydrogens bound to the terminal carbons, atoms of type HB were the hydrogens bound to the α-carbons, atoms of type NH1 were the nitrogens, and atoms of type O were the oxygens. The atom types in AMBER ff12sb do not exactly match those in the CHARMM27 force field (AMBER ff12sb groups the α- and terminal carbons into the same atom type (CT), it groups the hydrogens bound to the α-carbons with those that bind to the N-terminal carbons into the same atom type (H), and it gives a separate atom type (HC) to hydrogens that bind to the C-terminal carbons), but because the α- and terminal carbons had different relationships between ∂ΔG_rep/∂x_i and ∂A/∂x_i in both models (Figure 2 and Table I), we classified the atoms according to the CHARMM27 force field. Given this difference in classification, the estimates of ∂ΔG_rep/∂x_i and ∂A/∂x_i in model (2) were computed with the parameters from the AMBER ff12sb force field.

FIG. 2.

(a) The derivative (∂ΔG_rep/∂x_i) of the repulsive (ΔG_rep) component of the van der Waals component (ΔG_vdw) of the solvation free energy with respect to the coordinates (x_i) of the atomic centers as a function of the derivative (∂A/∂x_i) of the solvent-accessible surface area (A) with respect to the x_i. (b) The probability densities (f) of the angle (θ) between ∇_iA and ∇_iΔG_rep where ∇_i = (∂/∂x_i, ∂/∂y_i, ∂/∂z_i) and (x_i, y_i, z_i) were the coordinates of the center of atom i. The points in (a) and the curves in (b) are colored by the atom type in the CHARMM27 force field. The values in (a) and (b) were computed with the CHARMM27 force field and configurations taken from a simulation run with CHARMM27. (c) and (d) The same as (a) and (b), respectively, but the values in these plots were computed with AMBER ff12sb and configurations taken from a simulation run with AMBER ff12sb.

Table I.

FEP estimates of ${\gamma }_{\mathrm{rep}}^{\mathrm{der},i}$ for each atom type, Pearson's correlation coefficients (R²) of the corresponding least-squares lines of plots of ∂ΔG_rep/∂x_i versus ∂A/∂x_i, and estimates of $\Delta G_{\mathrm{rep}}^i/A$ obtained by inserting a single atom of each type into solvent and dividing by the solvent-accessible surface areas of these atoms. All ${\gamma }_{\mathrm{rep}}^{\mathrm{der}}$ and ΔG_rep/A were in units of (cal/mol/Ų).

	CHARMM27			AMBER ff12sb
Atom type	$\Delta G_{\mathrm{rep}}^i/A$	${\gamma }_{\mathrm{rep}}^{\mathrm{der},i}$	R2	${\gamma }_{\mathrm{rep}}^{\mathrm{der},i}$	R2
C	32	18	0.11	−4	0.01
CT2	32	38	0.69	−54	0.15
CT3	32	48	0.86	12	0.44
HA	21	38	0.89	32	0.89
HB	22	34	0.78	28	0.83
NH1	33	8	0.02	22	0.14
O	30	45	0.85	38	0.69

Table I contains the slopes (${\gamma }_{\mathrm{rep}}^{\mathrm{der},\mathrm{i}}$) of plots of ∂ΔG_rep/∂x_i against ∂A/∂x_i for each atom type in the CHARMM27 force field, computed on both models (1) and (2), along with the R² of these plots. Also shown in Table I are $\Delta G_{\mathrm{rep}}^i$ of each atom type i in the CHARMM force field divided by A. If γ_rep did not depend on the chemical environment of the atom, then $\Delta G_{\mathrm{rep}}^i/A$ would equal ${\gamma }_{\mathrm{rep}}^{\mathrm{der},\mathrm{i}}$. Clearly, ΔG_rep/A differs significantly from ${\gamma }_{\mathrm{rep}}^{\mathrm{der},\mathrm{i}}$. This observation further indicates that γ_rep depends on the molecular environment of the atom in question and is therefore not really a well-defined quantity.

As can be seen in Figure 2, the value of ${\gamma }_{\mathrm{rep}}^{\mathrm{der}}$ is determined primarily by atoms of types HA, HB, and O, both because these atom types had the largest ∂ΔG_rep/∂x_i and because their ∂ΔG_rep/∂x_i were roughly proportional to ∂A/∂x_i. Table I shows that the correlations between ∂ΔG_rep/∂x_i and ∂A/∂x_i were significant for these three atom types in each model. Additionally, ∂ΔG_rep/∂x_i was significantly correlated with ∂A/∂x_i for atoms of type CT2 and CT3 in model (1), but not in model (2).

Some of the statistics in Table I differ from those in our previous work on decaalanine and various alkanes.²⁵ In that study, ∂ΔG_rep/∂x_i was correlated with ∂A/∂x_i for the oxygens and hydrogens, as in the present study. These two quantities were significantly correlated for the α-carbons in model (1), whereas ∂ΔG_rep/∂x_i was not significantly correlated with ∂A/∂x_i for the α-carbons in the decaalanines. Additionally, in our previous study ∂ΔG_rep/∂x_i was correlated with ∂A/∂x_i for the nitrogens and carbonyl carbons, but the ${\gamma }_{\mathrm{rep}}^{\mathrm{der},i}$ were negative. In contrast, ∂ΔG_rep/∂x_i and ∂A/∂x_i were not correlated for these atom types in the present study. These findings demonstrate how the relationship between ∂ΔG_rep/∂x_i and ∂A/∂x_i for an atom type can change when the surrounding atoms in the solute molecule change.

Panels (b) and (d) of Figure 2 show the probability densities (f(θ)) of the angle (θ) between ∇_iΔG_rep and ∇_iA, where ∇_i = (∂/∂x_i, ∂/∂y_i, ∂/∂z_i) and (x_i, y_i, z_i) were the coordinates of the center of the atom i. If ΔG_rep were perfectly linear in A, then θ would equal 0°. For atom types HA, HB, and O, f(θ) was peaked at 0°, and these were the atom types noted above that determined ${\gamma }_{\mathrm{rep}}^{\mathrm{der}}$. Interestingly, some of the other atom types had significantly different f(θ) in the two models; (θ) was peaked at 180° for atom types C and CT2 in model (2) but not in model (1). In our previous study, we suggested that atom types for which f(θ) were peaked at 180° might tend to lie at the bottom of valleys in the solvent-accessible surface.²⁵ Additionally, some of these f(θ) differ from those we found for decaalanine. In that case, f(θ) was peaked at 180° for atoms of type NH1 and C, whereas in the present study f(θ) showed no clear peak for atoms of type NH1 and was only peaked at 180° for atoms of type C in model (2). These findings further emphasize the effects of the local molecular geometry and chemical environment on solvation free energy.

V. CONCLUSIONS

By examining 50 conformations of decaglycine, we were able to test the propositions that ΔG_rep, ΔG_att, and ΔG_vdw are linear functions of A more extensively than in our previous works.^25,33–35 The different configurations of decaglycine produced ${\gamma }_{\mathrm{rep}}^{\mathrm{der}}$ that covered a large range of values, implying that γ_rep may not be a well defined quantity at the molecular scale we are investigating. Additionally, the correlations between $\Delta G_{\mathrm{att}}^{\mathrm{lrt}}$ and A in this study were weaker than those between ΔG_att and A for either decaalanine or alkanes, and the magnitude of γ_att was significantly larger than those we observed for either decaalanine or alkanes. As a result, the estimates of γ_vdw obtained in the present study (−74 and −56 cal/mol/Ų for CHARMM27 and AMBER ff12sb) were larger than what we observed previously. These findings, in combination with our previous findings, seem to imply that none of ΔG_rep, ΔG_att, and ΔG_vdw is a simple linear function of A for a wide range of molecules and molecular shapes.

That the full γ_vdw for decaglycine was large and negative confirmed previous findings on shorter glycine oligomers.^33,34 Previously, we found that γ_vdw was negative for decaalanine because −γ_att > γ_rep and γ_att < 0, but in that case, the magnitude of γ_vdw was fairly small.²⁵ One could have argued that ΔG_vdw could simply be neglected for that system. In contrast, the large γ_vdw for these decaglycines is probably not negligible and that it is negative implies that ΔG_vdw favors extended over compact states for these peptides. Apparently, whether ΔG_vdw favors extended or compact conformations and how strongly will have to be determined on a case-by-case basis.

We found that the relationship between ∂ΔG_rep and ∂A/∂x_i was different for different types of atoms. Overall ${\gamma }_{\mathrm{rep}}^{\mathrm{der}}$ was apparently largely determined by the well exposed hydrogen and oxygen atoms in the peptides. Additionally, the relationships between ∂ΔG_rep/∂x_i and ∂A/∂x_i for some of these atom types differed from what we saw for decaalanines. In our previous study, we found that f(θ) was peaked at 180° for the carbonyl carbons and nitrogens in decaalanine, whereas in these decaglycines f(θ) for the nitrogens had no clear peak and it was only peaked for the carbonyl carbons when the AMBER ff12sb force field was used. Furthermore, for several atom types ∂ΔG_rep/∂x_i was not correlated with ∂A/∂x_i. These observations could not be explained by assigning different surface tensions to different atom types.

Collectively, these findings imply that none of ΔG_rep, ΔG_att, and ΔG_vdw can be assumed to be linear in A with well-defined surface tensions (γ_rep, γ_att, and γ_vdw). Instead, each atom's contribution to these free energies appears to depend on its chemical identity and multibody interactions with neighboring solute atoms. These contributions therefore appear to contain nontrivial dependencies on the local structure of the molecular surface. Successful hydrophobic theories will have to account for such interactions.