Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2015 Nov 1.
Published in final edited form as: Eur J Cancer. 2014 Oct 8;50(17):3068–3075. doi: 10.1016/j.ejca.2014.08.019

A filter-flow perspective of haematogenous metastasis offers a non-genetic paradigm for personalised cancer therapy

Jacob G Scott a,b,*, Alexander G Fletcher b, Philip K Maini b, Alexander RA Anderson a, Philip Gerlee a
PMCID: PMC4258103  NIHMSID: NIHMS631837  PMID: 25306188

Abstract

Research into mechanisms of haematogenous metastasis has largely become genetic in focus, attempting to understand the molecular basis of ‘seed–soil’ relationships. Preceding this biological mechanism is the physical process of dissemination of circulating tumour cells (CTCs) in the circulation. Patterns of metastatic spread have been previously quantified using the metastatic efficiency index, a measure quantifying metastatic incidence for a given primary-target organ pair and the relative blood flow between them. We extend this concept to take into account the reduction in CTCs which occurs in organ capillary beds connected by a realistic vascular network topology. Application to a dataset of metastatic incidence reveals that metastatic patterns depend strongly on assumptions about the existence and location of micrometastatic disease which governs CTC dynamics on the network, something which has heretofore not been considered – an oversight which precludes our ability to predict metastatic patterns in individual patients.

Keywords: Mathematical model, Metastasis, Oligometastasis, Circulating tumour cells

1. Introduction

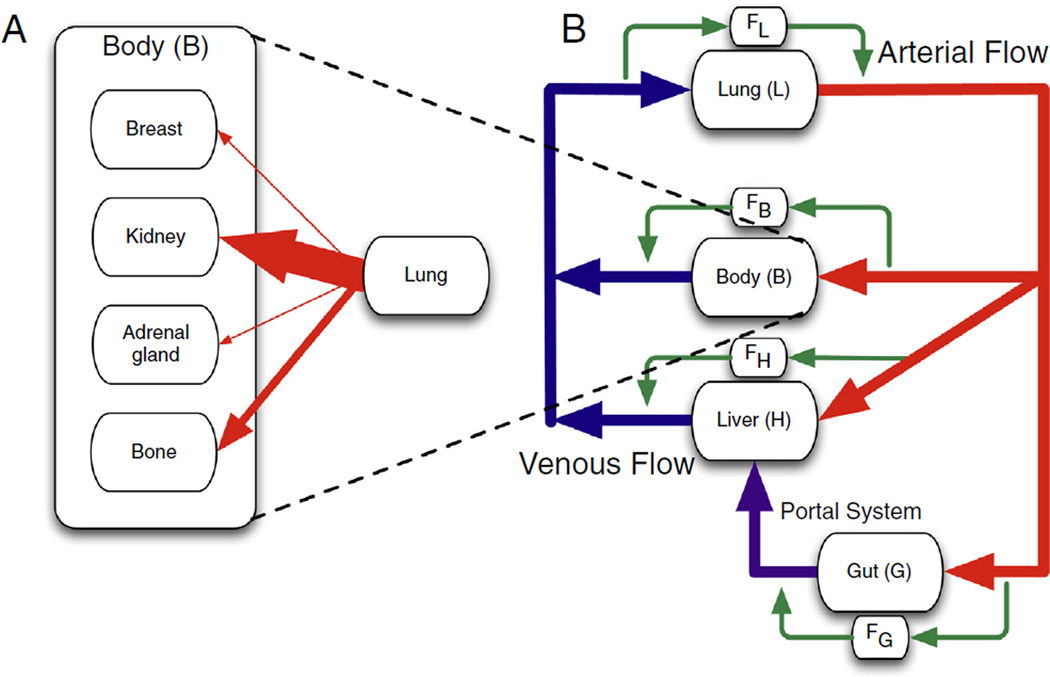
Nearly 150 years after Ashworth’s discovery of the circulating tumour cell (CTC) [1], the putative vector of haematogenous metastatic disease, the mechanisms driving this process remain poorly understood and unstoppable [2]. For over a century the dominant paradigm has been the seminal, yet qualitative, seed–soil hypothesis proposed by Paget in 1889 [3]. This idea was challenged by the ‘mechanical hypothesis’ put forward by Ewing in the 1920s [4], that postulated that metastatic incidence is due to differential blood flow. These two opposing views were merged in 1992, when a quantification of the contribution of mechanical and seed–soil effects was attempted by Weiss [5], who considered the ‘metastatic efficiency index’ (MEI) of individual primary tumours and metastatic sites [6] (see Fig. 1A). The MEI captures the compound inefficiency of all processes acting between the cancer cells leaving the primary tumour and forming clinically detectable metastases. He calculated MEI as the ratio of metastatic involvement to blood flow through an organ and three classes of organ pairs emerged: low, where the soil-organ relationship is hostile; high, where it is friendly and medium, where blood flow patterns to a large extent explain patterns of metastatic spread.

Fig. 1.

Fig. 1

Open in a new tab

Schematic of (A) Weiss conceptual framework for calculating the metastatic efficiency index (MEI) and (B) our extension of the framework. (A) Weiss used the relative arterial blood flow to normalise the metastatic incidence and calculate the MEI (the width of the arrows is proportional to blood flow). (B) In our framework we consider both relative arterial blood flow and venous flow. This forces us to consider the loss of circulating tumour cells (CTCs) that occurs in capillary beds of different organs. It is evident by inspection of the network diagram that tumours originating in the gut and lung experience significantly different flow patterns and a different order in which they experience filtration at capillary beds than tumours originating in other parts of the ‘body’ [15]. The alternate pathways (green) represent the fraction of cells which evade arrest (filtration) at a given capillary bed. There are scant measurements of this fraction in the literature, and none in clinical studies that evaluate outcomes. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

The utility of Weiss’ classification method largely ended there, and has since been put aside in favour of genetic investigations [7], an exception being work in prostate cancer by Pienta and Loberg [8] showing a lack of correlation between blood flow and incidence, suggesting strong seed–soil effects. While illuminating, the gene-centric approach to understanding patterns of metastatic spread has yet to offer any actionable conclusions, and its applicability is threatened by the growing understanding that genetic heterogeneity, not clonality, is the rule in cancer [9,10]. Our aim is to revisit the pre-genetic model and show that a physical perspective of metastatic spread can lead to new and actionable insights into this enigmatic disease process.

While primary tumour and lymph node metastases are carefully described in the clinic, metastatic disease is considered to be a binary change of state, a patient being diagnosed either with or without metastasis, MO or Ml. Until recently, this was appropriate, as even perfect information about the existence and distribution of metastatic disease would have done little to affect treatment choice, the options being limited to the use of systemic chemotherapies. Recent years, however, have witnessed the advent of more effective and tolerable localised therapies for metastatic involvement, in the form of liver-directed therapy [11], bone-seeking radionuclides [12] and stereotactic body radiation therapy [13]. These recently adopted modalities have allowed for targeted therapy to specific parts of the body with minimal side-effects and high eradication potential. Further, trials offering treatment with curative intent to patients with limited, ‘oligometastatic’ disease have shown promise [13], although it is not yet possible to identify such patients in an objective manner [14]. The time is therefore ripe for a quantitative framework that can analyse and guide these and similar efforts.

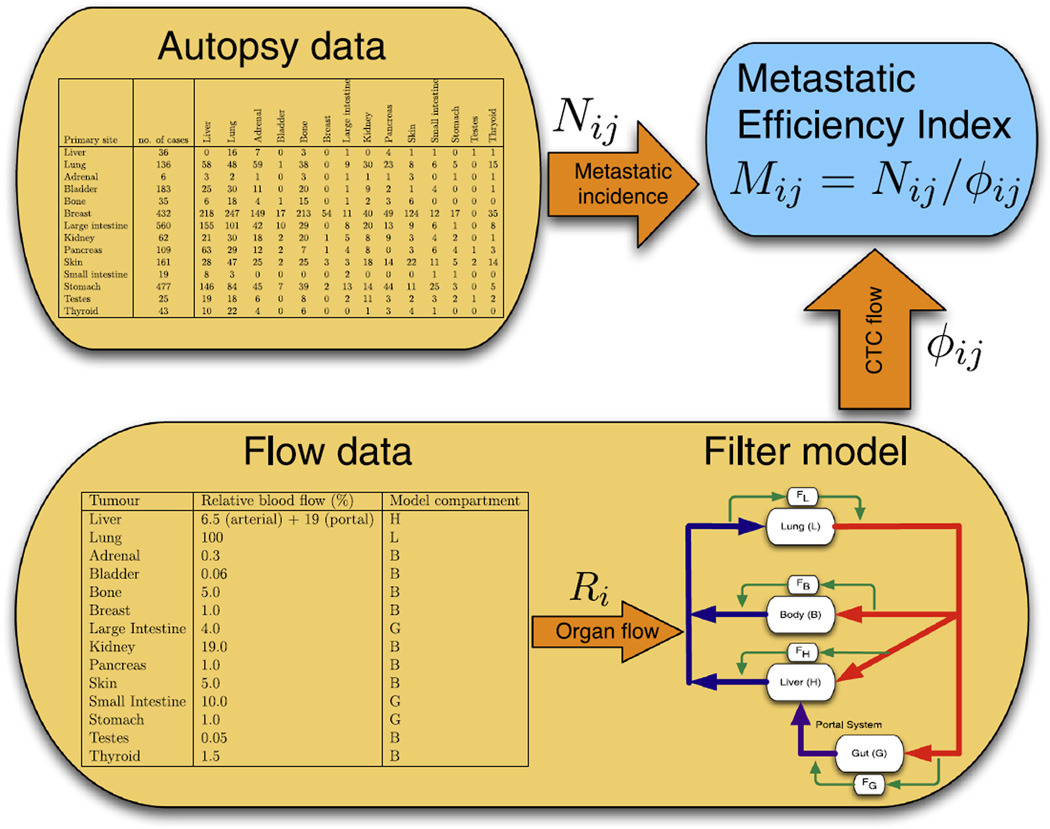
In this paper we apply a recently published framework for understanding haematogeneous metastates [15,16] to an existing dataset of metastatic spread [17] in an attempt to draw new conclusions and suggest novel therapeutic options (see Fig. 2). Specifically we seek to use Weiss’ MEI and the filter-flow model of CTC dynamics (summarised in Fig. 1B) to understand how micrometastatic disease influences calculations of metastatic efficiency. This synthesis presents a way to utilise ‘personalised’ patient CTC measurements to assay for the burden and distribution of metastatic disease (Fig. 4). These measurements represent a novel class of patient-specific data by which any pattern of metastasis can be understood. This allows for a new way to dissect out the heterogeneous groups from population level data, and hence represents a non-genetic, translatable method by which to alter staging and subsequently, treatment strategies.

Fig. 2.

Fig. 2

Open in a new tab

Schematic of our modelling framework. Autopsy data are used in order to calculate metastatic incidence for different organ pairs [17], while flow data [18] are used in order parametrise a filter-flow model of circulating tumour cell (CTC) flow, whose output is the relative flow of CTCs between organ pairs. Both these quantities are then used in order to estimate the metastatic efficiency index for a number of organ pairs.

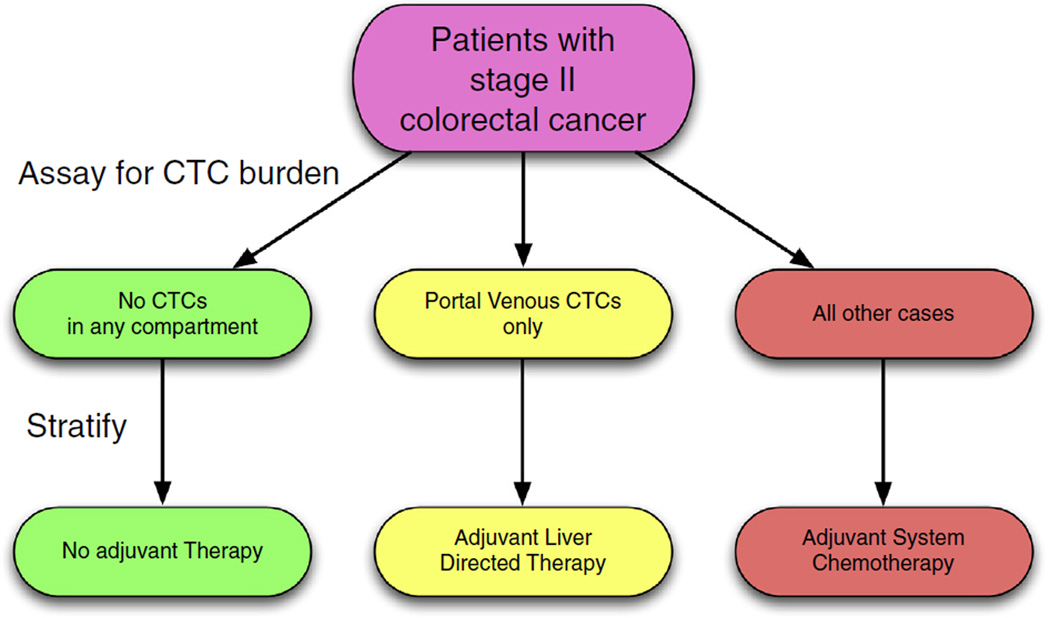
Fig. 4.

Fig. 4

Open in a new tab

An example of clinical trial stratification based on circulating tumour cell (CTC) localisation. Stage II colon cancer remains enigmatic, with no clear guidelines for adjuvant therapy after surgery [38]. We propose that stratifying by CTC presence or absence in specific vascular compartments, information about subclinical metastatic disease could be brought to light, and recommendations for location specific treatment, if appropriate, could be made. A first approximation would be to collect this information prospectively in the setting of existing trials.

To do this, we consider blood flow between organs [18], filtration in capillary beds (see Fig. 1) and distribution of metastatic involvement in a series of untreated patients at autopsy [17]. For each organ-organ pair we calculate the MEI by normalising incidence by putative CTC flow between the two organs, taking into account the reduction that occurs in capillary beds [19,20,15,16]. This post-capillary bed reduction in CTC numbers can be altered by the presence of micrometastases, which can amplify CTC numbers downstream of their location through shedding. Thus, by adjusting filtration rates throughout the network, we can represent different configurations of metastatic disease and hence capture different organ-organ metastatic efficiencies.

2. Materials and methods

2.1. Calculation of metastatic efficiency index (MEI)

The autopsy dataset used in the analysis covers 3827 patients presenting with primary tumours in 30 different anatomical sites [17]. For each primary tumour the number of metastases are reported according to anatomical site (in total 9484 metastases). As we focus on the effect of blood flow patterns, we consider only the organs for which blood flow has been measured. For each organ-organ pair we calculate the metastatic involvement as

Nij=#Metastases in organjgiven primary ini#Primary tumorurs in organi. (1)

We have that 0 ⩽ Nij < 1 and this number corresponds to the fraction of cases where a primary tumour in organ i gave rise to a metastasis in organ j. The metastatic efficiency index (MEI) from organ i to j is then defined by

Mij=Nij/φij, (2)

where φij is the relative flow of CTCs from organ i to j. This quantity takes into account the relative blood flow Ri that each target organ receives [18], and the reduction in CTCs that occurs en route between the two organs.

For the sake of simplicity we consider the blood flow to be stationary (i.e. not affected by postural changes) and we only include the effects of capillary bed passage on CTCs. Further we assume that cancer cells extravasate into the systemic venous side of circulation, which is known to be the dominant mechanism of dissemination, even for lung cancers [21]. It has been shown in mouse model studies that approximately 1% of cancer cells injected into the portal vein passes through the liver in a viable state [19]. This is probably an overestimate of the process in humans, since cancer cell lines often are highly transformed. Clinical studies suggest that CTC numbers are reduced by two orders of magnitude when passing through capillary beds [20]. This rough estimate is arrived at by taking the ratio of the CTC concentration in the pulmonary venous blood and in a peripheral blood sample from the arm (taking into account the fact that the arm receives on the order of 1% of cardiac output). In line with these observations we assume that there occurs a reduction of CTC number by a factor F when the cells pass through the capillary bed of an organ. As a baseline, we set the pass rate F = 10−2 for all organs. This is likely an oversimplification as each organ could well have its own pass rate. However, as there are no published data to this effect, we choose to use a single parameter value, any change in which, as it is applied across calculations, would not change the qualitative results.

It is well known that metastases in the lung and liver have the ability to shed cells into the bloodstream and hence give rise to ‘second order’ metastases [22], and it has been shown that even ‘dormant’ micrometastatic disease can shed CTCs [23]. If one were to measure the CTC concentration downstream of an organ containing metastases then, it would be higher than in the case of a disease-free organ. For our purposes, this implies that the presence of metastatic disease can be represented in the model as a lower reduction of CTCs in the capillary bed of the affected organ. This simplification is only valid if we disregard the biological properties of the CTCs (since CTCs originating from metastases might have different genotypes and phenotypes compared to cells from the primary tumour), but is sufficient for our purposes. The effect of micrometastases naturally depends on their number and size, but as a crude estimate we assume that the ratio of the mass of the primary tumour to the micrometastases, and therefore shed CTCs, is 100:1 (a primary tumour weighing on the order of 100 grams and an undetectable metastatic lesion being smaller than 1 cm in diameter thus weighing ~1 g). This assumption then allows the prediction that the relative concentration of CTCs downstream of the afflicted organ would be 10−2 + 10−2 = 2 × F (CTCs from primary + CTCs from micromets), a doubling of the pass rate, a change which should be measurable. To simulate the presence of micrometastases in the lung and liver we therefore change the pass rates to FL = 2 × 10−2 and FH = 2 × 10−2 respectively.

To calculate the relative flow between two organs we consider the shortest path transversed by the blood between the two sites. As an example of our methodology, we now present the calculations for the MEI for breast to adrenal gland. The cancer cells leaving a breast tumour enter the circulation on the venous side and are transported via the heart to the lung capillary bed, through which only a fraction FL pass as viable cells. These cells then flow into the arterial side of the circulation and are distributed to the different organs of the body according to blood flow, of which the adrenal gland receives 0.3% [18]. In the absence of micrometastases, the relative flow of CTCs from breast to adrenal gland is therefore given by φbreast,adrenal = FL × 0.3 = 0.3 × 10−2, and in the presence of micrometastases in the lung φbreast,adrenal = 0.3 × 2 × 10−2 = 0.006.

2.2. Comparison to Weiss

In Weiss’ original publication the MEI was calculated as the ratio between metastatic incidence and target organ blood flow (in units ml/min). In order to make our index more physically meaningful (Weiss’ index has units min/ml to which it is impossible to attach a physical interpretation) we instead use ‘percent of cardiac output’ defined as organ blood flow divided by the total cardiac output (6500 ml/min as reported in [18]) giving us a dimensionless measure. Further it should be noted that Weiss did not consider any loss of CTCs en route, and therefore to make the two indices comparable we scale Weiss’ index to compensate for the loss of CTCs that occurs in the lung capillary bed. Also, Weiss did not account for CTC loss in the liver, although a number of gut malignancies (colorectal, pancreatic and stomach cancer) were included in his calculation of MEIs, which means that these MEIs were systematically underestimated.

2.3. Patient group decomposition

The incidence, Nij, relative flow of CTCs, φij and the MEI, Mij are related according to Mij = Nij/φij, or equivalently φij = Mij / Nij To understand the impact of flow in this relationship, we will assume a fixed MEI while the flow φij varies across patients. We consider four patient groups: no micrometastases, micrometastases in the lung, micrometastases in the liver and micrometastases in both. If we now let nk denote the fraction of patients in each group, k, where n1 + n2 + n3 + n4 = 1, then we can write

n1φij1+n2φij2+n3φij3+n4φij4+Mij/Nij, (3)

where φij1,2,3,4 is the relative flow of CTCs in the different patient groups. The problem of finding the nk’s is under-determined, and the solution is given by any point on a surface defined by (3), such that nk > 0 for all patient groups and n1 +n2 + n3 + n4 = 1. This implies that aggregated incidence data can be explained by many different patient group compositions, each with its distinct pattern of metastatic progression.

3. Results

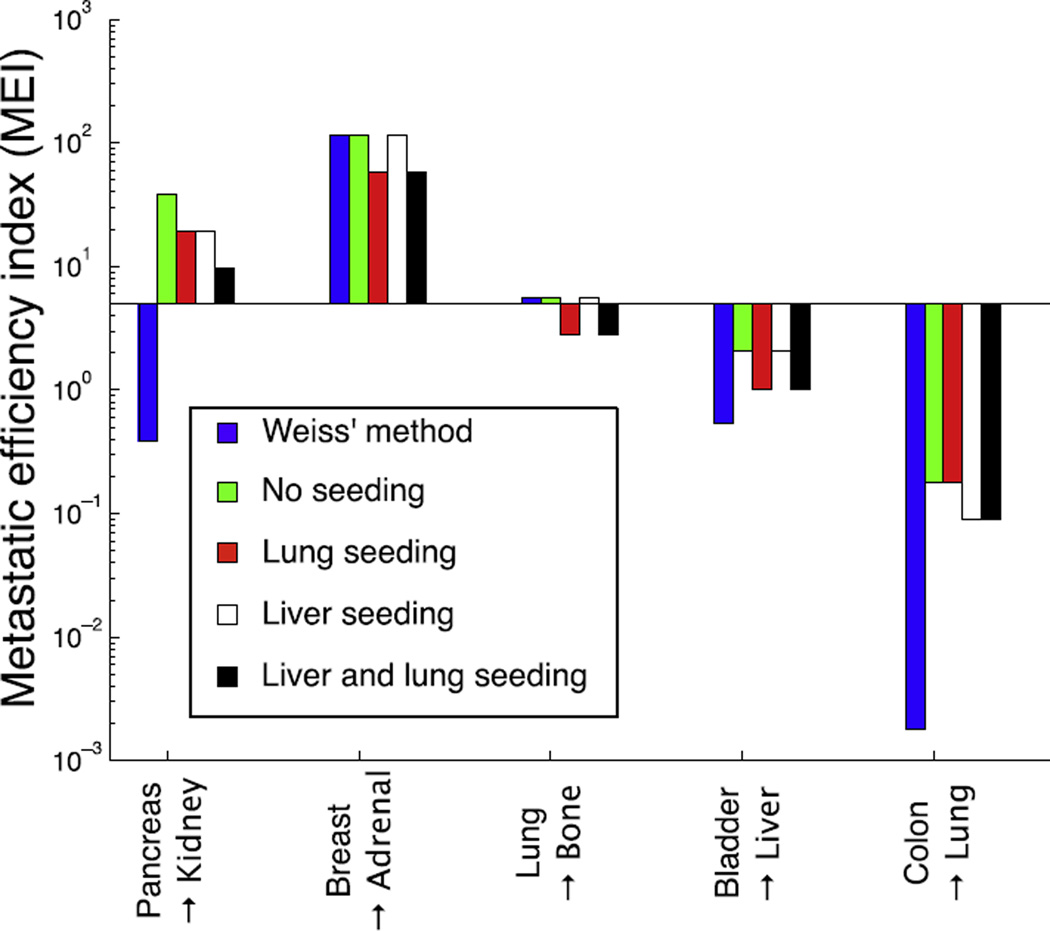
To illustrate the effect of micrometastatic disease on MEIs, we have compared Weiss’ original method with MEIs calculated using the filter-flow framework in four different regimes: no micrometastases, micrometastases present in the lung, in the liver or in both locations. Fig. 3 shows the result of this comparison for five organ pairs.

Fig. 3.

Fig. 3

Open in a new tab

The impact of filter and flow characteristics on estimation of the metastatic efficiency index (MEI). We have compared Weiss’ original method (rescaled to be comparable, see Section 2) with our filter-flow framework under the assumption of no micrometastases, micrometastases in the lung, in the liver, and in both locations. The comparison is carried out for five organ pairs that cover the canonical pathways of spread (gut → body, body → body, lung → body, body → liver and gut → lung). We see that because Weiss’ method only considers the dynamics on the arterial side (and disregards the filtration in the liver) it provides a smaller MEI in three of the cases (pancreas → kidney, bladder → liver and colon → lung). From the comparison it is also evident that assumptions about the presence or absence of micrometastases heavily influences the results, in the case of pancreas → kidney shifting the MEI two orders of magnitude.

The differences seen across the organ pairs for a given seeding scenario reflect the differential ability of cancer cells from different organs to form metastases in these target organs. In other words the MEI quantifies ‘seed–soil effects’, where the effects of flow and filtration have been factored out. For example, the high MEI of breast to adrenal indicates the predilection of carcinomas of the breast to preferentially spread to the adrenal gland [24]. Weiss’ metric differs strikingly from ours, e.g. in the case of colon to lung, since it does not consider filtration, and therefore severely underestimates the efficiency compared to our approach.

However, more importantly, our results highlight that the metastatic efficiency depends on the current disease state. For example, our estimate of the efficiency with which cells originating from a primary pancreatic tumour can form kidney metastases varies over two orders of magnitude, depending on whether micrometastatic lesions are present, and their location. The variations in MEI due to seeding scenario highlight an opportunity to go a step further in disease characterisation than presence or absence of CTCs at staging – we need to include information about where in the vascular network, and in what relative quantities, these CTCs reside.

The preceding analysis assumes that the filtration rate for each organ is identical for all patients in the data set. This is likely a gross oversimplification, but no clinical trial has yet determined the intrapatient heterogeneity in this (currently absent) parameter set. Above, we used incidence data to calculate MEIs, but we may also reverse the process and calculate the prevalence of micrometastatic disease given incidence data and organ-pair MEIs (see Section 2 for details). We now show how this can be used as a means to suggest possible patient group decompositions.

Consider the population incidence of metastases in the adrenal gland arising from primaries in the large intestine, which equals 7.5%. By fixing the MEI, the incidence rate can be explained by a subdivision according to 25% in the no metastasis group, 20% in the liver metastases group, 9% in the lung metastases group and 54% of the patients harbouring metastases in both liver and lung. However the incidence can also be explained by a subdivision of 5%, 25%, 9% and 69% into each patient group respectively. This highlights the fact that population-based measures of incidence hide a rich heterogeneity of individual patient metastatic dynamics [25] and cannot be used to predict individual patient outcomes.

4. Discussion

Metastasis is a complex and multifactorial process and much recent progress has been made towards understanding its relevant biological aspects. We posit however, that the exclusion of the physical aspects of metastasis has slowed our understanding of the process as a whole, and therefore our ability to intervene. We have presented a simple model of physical flow of CTCs within the human vascular network and extended early attempts by Weiss [21] to quantify the disparate contributions of biological and physical processes to the metastatic process. Weiss’ early attempts at quantification represented a major step forward in our thinking about metastasis that has largely, since his death, been forgotten.

In this first extension of Weiss’ MEI, we have purposefully excluded a significant amount of biological heterogeneity and complexity such as: heterogeneity in CTC size [26], half life [23,27], dormancy [28], clonogenic potential or sternness [29,30], phenotypic status [31] and other physical properties like deformability [32]. While this heterogeneity is important, the first step should always be to understand a model’s baseline behaviour before adding further complexity; we therefore leave their inclusion for future work. Additionally, recent work towards understanding patterns of spread of breast cancer [33] has utilised dimensional measures of metastatic risk. This sort of temporal risk prediction could be made using our framework by adding dimensionality to our index in the form of tumour-CTC shedding rates and coupling it to appropriate growth laws [34].

We have presented a number of novel predictions and methods by which individual patient information can be gleaned from currently measurable, but overlooked, phenomena. To enable these insights and their translation to the clinic, systematic testing of individual patient filter-flow parameters is required. While several research groups have successfully interrogated this step of the metastatic cascade in animals [35–37], it has yet to be done in humans. To effect this, measurement of CTCs from each of the individual vascular compartments (see Fig. 4) before surgical manipulation of the primary, at initial staging needs to be undertaken. Subsequent correlation with outcomes would yield initial information with which more complete models could be built, and from which rational prospective trials could be designed. Importantly, observations would have to be made both between patients with identical histologies (inter-patient) in addition to within given patients over time (intra-patient). This level of understanding of an individual patient’s disease state constitutes a new type of personalised medicine, which seeks to assay not just the collection of mutations that a patient’s cancer cells have accumulated, but also their physical distribution through time. This would allow for more accurate staging and the rational inclusion of organ directed therapy in clinical trials, a concept which is gaining popularity with recently approved methods existing for bone and liver [12,11].

We present an example of how this methodology could be implemented using technology that exists, but is not yet in widespread use, in Fig. 4. Here, patients presenting with stage II colorectal cancer are stratified after resection of their primary tumour according to CTC burden in different compartments of the circulatory system. We have chosen stage II colon cancer as a first Japproach as there are no clear guidelines [38] as to which patients should receive adjuvant therapy, and further because we have effective liver-directed therapies which could be used in the adjuvant setting. Specifically, we suggest that the absence of CTCs in any compartment would suggest a situation in which no adjuvant therapy would be indicated, as the primary could not yet have metastasized. The presence of CTCs in the portal venous circulation only, would represent risk of metastasis only to the liver, and therefore, in this limited situation, liver directed therapy could serve as an effective adjuvant therapy. In the case of CTCs being present in any (or all) other compartments, our framework would predict that the primary tumour had already seeded relevant metastases which themselves were shedding CTCs, making systemic therapy most appropriate. In this example, our methodology offers a rational method of treatment allocation - offering a way to spare patients from systemic therapy and its risks. While we have chosen to highlight colorectal cancer, we stress that this sort of approach, and the information gleaned from it, could be useful for any primary cancer.

5. Conclusion

We have presented a fresh look at old data on metastatic patterns inspired by a physical science perspective and shown that there is a deep gap in our understanding. Specifically, we show that our lack of knowledge of the dynamics of CTCs in foreign organ capillary beds prevents us from making further progress towards predicting patterns of spread. We suggest some simple steps to fill in these gaps, and a simple trial design to take advantage of currently obtainable, yet overlooked, patient specific information: CTC distribution throughout the patient’s vascular network.

By further elucidating the principles underlying haematogenous metastasis, we hope to make inroads toward therapeutic strategy changes that would otherwise be impossible. Our results highlight the importance of addressing not only genetic factors, but also physical and anatomical aspects of the metastatic process, which in this gene-centric era have been largely forgotten.

Acknowledgements

The authors would like to thank the reviewers for their time and effort. J.G.S. would like to thank the NIH Loan Repayment Program for support. A.G.F. is funded by the EPSRC and Microsoft Research, Cambridge through grant EP/I017909/1. PG, A.R.A.A. and J.G.S. gratefully acknowledge funding from the NCI Integrative Cancer Biology Program (ICBP) grant U54 CA113007 and they and P.K.M. also thank the NCI Physical Sciences in Oncology Centers U54 CA143970 grant.

Footnotes

Conflict of interest statement

None declared.

References

  • 1.Ashworth TR. A case of cancer in which cells similar to those in the tumours were seen in the blood after death. Australian Medical Journal. 1869;14(3–4):146–147. [Google Scholar]
  • 2.Plaks V, Koopman CD, Werb Z. Circulating tumor cells. Science. 2013;341(6151):1186–1188. doi: 10.1126/science.1235226. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Paget S. The distribution of secondary growths in cancer of the breast. 1889. Cancer Metastasis Rev. 1989;8(2):98–101. [PubMed] [Google Scholar]
  • 4.Ewing James. Neoplastic diseases. A treatise on tumors. Am J Med Sci. 1928;176(2):278. [Google Scholar]
  • 5.Rapp DG. In memoriam Leonard L. Weiss, Sc.D., M.D., Ph.D. Cancer Res. 2001;61:5663. [Google Scholar]
  • 6.Weiss L. Comments on hematogenous metastatic patterns in humans as revealed by autopsy. Clin Exp Metastasis. 1992;10(3):191–199. doi: 10.1007/BF00132751. [DOI] [PubMed] [Google Scholar]
  • 7.Bos PD, Zhang XHF, Nadal C, Shu W, Gomis RR, Nguyen DX, et al. Genes that mediate breast cancer metastasis to the brain. Nature. 2009;459(7249):1005–1009. doi: 10.1038/nature08021. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Pienta Kenneth J, Loberg Robert. The emigration, migration, and immigration of prostate cancer. Clin Prostate Cancer. 2005;4(1):24–30. doi: 10.3816/cgc.2005.n.008. [DOI] [PubMed] [Google Scholar]
  • 9.Gerlinger M, Rowan AJ, Horswell S, Larkin J, Endesfelder David, Gronroos E, et al. Intratumor heterogeneity and branched evolution revealed by multiregion sequencing. N Engl J Med. 2012;366(10):883–892. doi: 10.1056/NEJMoa1113205. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Navin N, Kendall J, Troge J, Andrews P, Rodgers L, Mclndoo J, et al. Tumour evolution inferred by single-cell sequencing. Nature. 2011;472(7341):90–94. doi: 10.1038/nature09807. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Seront E, Van den Eynde M. Liver-directed therapies: does it make sense in the current therapeutic strategy for patients with confined liver colorectal metastases? Clin Colorectal Cancer. 2012;11(3):177–184. doi: 10.1016/j.clcc.2011.12.004. [DOI] [PubMed] [Google Scholar]
  • 12.Harrison MR, Wong TZ, Armstrong AJ, George DJ. Radium-223 chloride: a potential new treatment for castration-resistant prostate cancer patients with metastatic bone disease. Cancer Manag Res. 2013;5:1–14. doi: 10.2147/CMAR.S25537. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Milano MT, Katz AW, Zhang H, Okunieff P. Oligometastases treated with stereotactic body radiotherapy: long-term follow-up of prospective study. Int J Radiat Oncol Biol Phys. 2012;83(3):878–886. doi: 10.1016/j.ijrobp.2011.08.036. [DOI] [PubMed] [Google Scholar]
  • 14.Weichselbaum RR, Hellman S. Oligometastases revisited. Nat Rev Clin Oncol. 2011;8(6):378–382. doi: 10.1038/nrclinonc.2011.44. [DOI] [PubMed] [Google Scholar]
  • 15.Scott JG, Kuhn P, Anderson ARA. Unifying metastasis—integrating intravasation, circulation and end-organ colonization. Nat Rev Cancer. 2012;12:1–2. doi: 10.1038/nrc3287. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Scott JG, Basanta D, Anderson ARA, Gerlee P. A mathematical model of tumour self-seeding reveals secondary metastatic deposits as drivers of primary tumour growth. J R Soc Interface. 2013;10:1–10. doi: 10.1098/rsif.2013.0011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Disibio G, French SW. Metastatic patterns of cancers: results from a large autopsy study. Arch Pathol Lab Med. 2008;132(6):931–939. doi: 10.5858/2008-132-931-MPOCRF. [DOI] [PubMed] [Google Scholar]
  • 18.Williams LR, Leggett RW. Reference values for resting blood flow to organs of man. Clin Phys Physiol Meas. 1989;10(3):187–217. doi: 10.1088/0143-0815/10/3/001. [DOI] [PubMed] [Google Scholar]
  • 19.Weiss Leonard, Ward Pamela M, Holmes Janet C. Liver-to-lung traffic of cancer cells. Int J Cancer. 1983;32(1):79–83. doi: 10.1002/ijc.2910320113. [DOI] [PubMed] [Google Scholar]
  • 20.Okumura Y, Tanaka F, Yoneda K, Hashimoto M, Takuwa T, Kondo N, et al. Circulating tumor cells in pulmonary venous blood of primary lung cancer patients. Ann Thorac Surg. 2009;87(6):1669–75. doi: 10.1016/j.athoracsur.2009.03.073. [DOI] [PubMed] [Google Scholar]
  • 21.Weiss Leonard. Principles of metastasis. Orlando (FL), USA: Academic Press; 1985. [Google Scholar]
  • 22.Bross I, Viadana W, Pickren J. Do generalized metastases occur directly from the primary? J Chronic Dis. 1975;28(3):149–159. doi: 10.1016/0021-9681(75)90003-x. [DOI] [PubMed] [Google Scholar]
  • 23.Meng Songdong, Tripathy Debasish, Frenkel Eugene P, Shete Sanjay, Naftalis Elizabeth Z, Huth James F, et al. Circulating tumor cells in patients with breast cancer dormancy. Clin Cancer Res. 2004;10(24):8152–8162. doi: 10.1158/1078-0432.CCR-04-1110. [DOI] [PubMed] [Google Scholar]
  • 24.Cifuentes Nestor, Pickren John W. Metastases from carcinoma of mammary gland: an autopsy study. J Surg Oncol. 1979;11(3):193–205. doi: 10.1002/jso.2930110303. [DOI] [PubMed] [Google Scholar]
  • 25.Gallaher Jill, Babu Aravind, Plevritis Sylvia, Anderson Alexander RA. Bridging population and tissue scale tumor dynamics: a new paradigm for understanding differences in tumor growth and metastatic disease. Cancer Res. 2014;74(2):426–435. doi: 10.1158/0008-5472.CAN-13-0759. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Marrinucci Dena, Bethel Kelly, Bruce Richard H, Curry Douglas N, Hsieh Ben, Humphrey Mark, et al. Case study of the morphologic variation of circulating tumor cells. Hum Pathol. 2007;38(3):514–519. doi: 10.1016/j.humpath.2006.08.027. [DOI] [PubMed] [Google Scholar]
  • 27.Stott Shannon L, Lee Richard J, Nagrath Sunitha, Yu Min, Miyamoto David T, Ulkus Lindsey, et al. Isolation and characterization of circulating tumor cells from patients with localized and metastatic prostate cancer. Sci Transl Med. 2010;2(25):25ra23. doi: 10.1126/scitranslmed.3000403. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 28.Allan Alison L, Vantyghem Sharon A, Tuck Alan B, Chambers Ann F. Tumor dormancy and cancer stem cells: implications for the biology and treatment of breast cancer metastasis. Breast Dis. 2007;26(1):87–98. doi: 10.3233/bd-2007-26108. [DOI] [PubMed] [Google Scholar]
  • 29.Shiozawa Yusuke, Nie Biao, Pienta Kenneth J, Morgan Todd M, Taichman Russell S. Cancer stem cells and their role in metastasis. Pharmacol Ther. 2013;138(2):285–293. doi: 10.1016/j.pharmthera.2013.01.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30.Baccelli Irene, Schneeweiss Andreas, Riethdorf Sabine, Stenzinger Albrecht, Schillert Anja, Vogel Vanessa, et al. Identification of a population of blood circulating tumor cells from breast cancer patients that initiates metastasis in a xenograft assay. Nat Biotechnol. 2013 doi: 10.1038/nbt.2576. [DOI] [PubMed] [Google Scholar]
  • 31.Yu Min, Bardia Aditya, Wittner Ben S, Stott Shannon L, Smas Malgorzata E, Ting David T, et al. Circulating breast tumor cells exhibit dynamic changes in epithelial and mesenchymal composition. Science. 2013;339(6119):580–584. doi: 10.1126/science.1228522. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Harouaka Ramdane A, Nisic Merisa, Zheng Si-Yang. Circulating tumor cell enrichment based on physical properties. J Lab Autom. 2013;18(6):455–468. doi: 10.1177/2211068213494391. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.Coumans Frank AW, Siesling Sabine, Terstappen Leon WMM. Detection of cancer before distant metastasis. BMC Cancer. 2013;13(1):283. doi: 10.1186/1471-2407-13-283. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 34.Gerlee Philip. The model muddle: in search of tumor growth laws. Cancer Res. 2013;73(8):2407–2411. doi: 10.1158/0008-5472.CAN-12-4355. [DOI] [PubMed] [Google Scholar]
  • 35.Al-Mehdi AB, Tozawa K, Fisher AB, Shientag L, Lee A, Muschel RJ. Intravascular origin of metastasis from the proliferation of endothelium-attached tumor cells: a new model for metastasis. Nat Med. 2000;6(1):100–102. doi: 10.1038/71429. [DOI] [PubMed] [Google Scholar]
  • 36.Dianne Cameron M, Schmidt Eric E, Kerkvliet Nancy, Nadkarni Kishore V, Morris Vincent L, Groom Alan C, et al. Temporal progression of metastasis in lung: cell survival, dormancy, and location dependence of metastatic inefficiency. Cancer Res. 2000;60(9):2541–2546. [PubMed] [Google Scholar]
  • 37.Chambers Ann F, MacDonald Ian C, Schmidt Eric E, Koop Sahadia, Morris Vincent L, Khokha Rama, et al. Steps in tumor metastasis: new concepts from intravital videomicroscopy. Cancer Metastasis Rev. 1995;14(4):279–301. doi: 10.1007/BF00690599. [DOI] [PubMed] [Google Scholar]
  • 38.NCCN. National cancer center network guidelines version 1. 2014 [Google Scholar]

RESOURCES