Rotation to a Partially Specified Target Matrix in Exploratory Factor Analysis in Practice

Abstract

The purpose of the current study was to explore the influence of the number of targets specified on the quality of exploratory factor analysis solutions with a complex underlying structure and incomplete substantive measurement theory. Previous research in this area was extended by (a) exploring this phenomenon in situations in which both the common factor model and the targeted pattern matrix contained specification errors and (b) comparing the performance of target rotation to an easier to use default rotation criterion (i.e., geomin) under conditions commonly observed in practice. A Monte Carlo study manipulated target error, number of targets, model error, overdetermination, communality, and sample size. Outcomes included bias (i.e., accuracy) and variability (i.e., stability) with regard to the rotated pattern matrix. The effects of target error were negligible for both accuracy and stability, while small effects were observed for the number of targets for both outcomes. Further, target rotation outperformed geomin rotation with regard to accuracy but generally performed worse than geomin rotation with regard to stability. These findings underscore the potential importance (or caution in the case of stability) of using extant, even if incomplete and somewhat inaccurate, substantive measurement theory to inform the rotation criterion in a non-mechanical way.

MacCallum (2003) argued that the mathematical models used in practice (i.e., theoretical model) often only approximate a more complex reality (i.e., population model). Monte Carlo studies that assume that the theoretical model is identical to the population model (i.e., an absence of model error), “might be of interest to theorists, [but] they are of limited value to users of methods. A more realistic and relevant question is: How do our methods behave and perform when the model in question is not correct in the population?” (MacCallum, p. 135). The current study extended the literature by (a) investigating the performance of exploratory factor analysis with target rotation under conditions (e.g., model and target error) commonly observed in practice, and then (b) comparing the performance of target rotation to the performance of an easier to use default rotation criterion (i.e., geomin).

Factor analysis has been closely linked with investigations of construct validity in the social sciences for several decades (Nunnally, 1978). Investigations of construct validity have frequently occurred in studies where only factor analytic measurement models, exploratory (EFA) and/or confirmatory (CFA), were specified – typically guided by incomplete substantive measurement theory (DiStefano & Hess, 2005; Henson & Roberts, 2006). Incomplete measurement theory often manifests as model error and offers an explanation as to why nearly all construct validity studies fail the test of exact fit under a CFA approach (Jackson, Gillaspy, & Purc-Stephenson, 2009). Incomplete measurement theory may be better handled by EFA with rotation of the pattern matrix rather than a more restrictive CFA approach that relies on post hoc modifications (MacCallum, Roznowski, & Necowitz, 1992). EFA with target rotation can be conceptualized as “situated between CFA and EFA” (Asparouhov & Muthén, p. 399, 2009).

Direct analytic rotation of the pattern matrix is based on several decades of research within the EFA framework (e.g., Jennrich, 2007; Jennrich & Sampson 1966) as detailed in Browne (2001). Rotation of the pattern matrix is accomplished via post-multiplication of the pattern matrix by the inverse of an optimal transformation matrix:

$${\mathbf{\Lambda }}_{p\times r}^{\ast }={\mathbf{\Lambda }}_{p\times r}{\left({\mathbf{H}}_{r\times r}^{\ast }\right)}^{-1}.$$ (1)

An optimal transformation matrix, H^*, is determined by minimizing a continuous complexity function of the elements in the pattern matrix, f (Λ). A mechanical rotation criterion can be thought of as being relatively easy to implement but providing little to no opportunity to incorporate a priori measurement theory into the f (Λ).Various rotation techniques define f (Λ) differently but each was typically designed to provide the simplest solution.

For decades a simple solution has often been interpreted as having one non-zero pattern coefficient per row (variable complexity, vc, = 1, for each “pure” variable); though this “perfect simple structure” is a more restrictive approach than advocated by Thurstone (1947). For example, Thurstone’s conceptualization of simple structure allowed for r − 1 non-zero elements per row (i.e., vc ≤ = r – 1). Complex structures where r ≥ 2 and vc ≥ 2 for one or more variables are not uncommon in practice, though commonly used rotation criterion (e.g., direct quartimin) typically do not perform well in such situations (Yates, 1987). The failure of most rotation criteria to perform well with complex structures is not surprising given that most f (Λ) were designed in such a way that a (perfect) simple structure is sought (Browne, 2001).

Geomin rotation (Yates, 1987) minimizes row (e.g., variable) complexity in a way that is more consistent with Thurstone’s (1947) conceptualization of simple structure as compared to the more restrictive perfect simple structure. Accordingly, geomin has performed relatively well when vc > 1 both in empirical examples (e.g., Marsh et al., 2009; McDonald, 2005) and in a simulation study when compared to other mechanical rotation criteria (Sass & Schmitt, 2010). Currently geomin is the default rotation criterion in Mplus (Muthén & Muthén, 1998–2012) and, therefore, may be used frequently in practice. The f(Λ) for geomin implemented in Mplus is:

$$\sum _{i=1}^p{\left(\prod _{j=1}^r\left({\lambda }_{ij}^2+\epsilon \right)\right)}^{1/r},$$ (2)

where

ε is a small positive constant added by Browne (2001) to reduce the problem of indeterminacy.

In Asparouhov and Muthén (2009), geomin performed well when vc was moderate (vc ≤ 2), m was small (m = 2), and the factors were moderately correlated. Geomin, however, “…fails for more complicated loading matrix structures involving three or more factors and variables with complexity 3 and more;… For more complicated examples the Target rotation criterion will lead to better results” (Asparouhov & Muthén, p. 407). The performance of target rotation as compared to geomin rotation, however, has yet to be systematically studied. For example, the previous quote from the seminal work of Asparouhov and Muthén seemed to be based on results where the outcome was either bias (p. 427) or coverage (p. 428) and not directly on variability for complex loading matrix structures. Additional studies are important, in part, because target rotation requires more from the user than a mechanical rotation criterion does. This additional demand on the user is especially noteworthy because a solution will be mathematically equivalent under competing rotation criterion.

Target rotation has been developed over several decades and can be thought of as “a non- mechanical exploratory process, guided by human judgment” (Browne, 2001, p.125). Early versions of target rotation were indirect and based on a fully specified target matrix (e.g., Horst, 1941; Tucker, 1944). Later versions of target rotation in EFA were direct and could be based on only a partially specified target matrix, B_pxr (Browne, 1972a, 1972b; Gruvaeus, 1970). The f(Λ) for target rotation can be written as:

$$\sum _{i=1}^p\sum _{j=1}^r{a}_{ij}{\left({\lambda }_{ij}-b_{ij}\right)}^2,$$ (3)

where

• a_ij = 1 if λ_ij is a target and 0 if λ_ij is not a target, and

• b_ij = the targeted value.

Note that the user must provide a_ij and b_ij, and therefore, helps to define f (Λ) for target rotation. Thus, target rotation does not seek a (perfect) simple structure unless specified to do so.

Target rotation was designed to rotate Λ to a least squares fit to a targeted pattern matrix, B, which can utilize incomplete a priori measurement theory without fixing coefficients to particular values as in CFA. For example, Figure 1 provides a matrix A that designated whether each pattern coefficient was (1) or was not (0) a target, and a B that provided correct values (i.e., b_ij = λ_ij) that targeted elements would be rotated towards. Under the assumption that the targeted values are correct the observed rotated pattern matrix, Λ̂*, generally should more accurately and reliably recover Λ as the number of targets increase. Target error (i.e., b_ij ≠ λ_ij) would likely be present in practice because the true value of any particular λ_ij would likely be unknown. It has long been believed that target rotation may be relatively robust to such misspecification due to the least squares fit to B (Browne, 2001). However, the potential role for target error to influence the quality of the rotated solution has yet to be systematically studied. For example, all of the relevant previous studies of which we are aware have either assumed the absence of target error and/or have set all targets to a single value (e.g., 0) often consistent with a pure variable approach.

Figure 1.

Matrix A designated whether each pattern coefficient was (1) or was not (0) a target. Matrix B provided values that targeted elements would be rotated towards and denoted non-targeted elements with a ? symbol. Matrix Λ provided population values.

The role for systematically increasing the number of error-free targets specified per factor to influence the quality of the rotated solution with a complex underlying structure and incomplete measurement theory has been studied by Myers, Ahn, and Jin (2013). A positive effect of the number of targets specified on the accuracy and stability of Λ̂* was observed but the magnitude of this effect varied by level of communality (h; where h_i is the proportion of variance in the i^th variable accounted for by the common factors) and overdetermination of Λ (i.e., the ratio of the number of observed variables to the number of underlying factors, p:r). The effect of the number of targets specified generally was strongest when h = .20 to .40 (i.e., low) and p = 10 (i.e., small) or 20 (i.e., average) and r = 3 (i.e., average). For all levels of h and p:r, however, a positive effect of the number of targets specified on the accuracy and stability of Λ̂* generally was observed. Further, only a small number of targets (e.g., r) per factor needed to be specified in order to achieve good accuracy when p:r = 10:3 or 20:3, h > low, and N ≥ 100. Limitations of the Myers et al. study included the absence of: (a) model and target error and (b) a comparison of the performance of target rotation to an easier to use mechanical rotation criterion.

A strength of Myers et al. (2013) was conceptualizing the performance of target rotation within MacCallum and Tucker’s (1991) broader mathematical framework for identifying sources of error in factor analysis. This framework informed hypotheses in the current study and is summarized below with an emphasis on model error. The purpose of the emphasis on model error was to inform expectations (which will be stated in the hypotheses section) regarding the degree to which the findings of Myers et al. may hold under the presence of model error.

Model error is the discrepancy between the true covariance matrix for the observed variables, Σ_yy, and the implied covariance matrix that would result from fitting the theoretical model to Σ_yy, Σ̃_yy (θ), where θ is a vector of parameter values If the theoretical model is fit to sample data, S_yy, the covariance matrix implied from the fitted model is Σ̂yy (θ̂), where θ̂ is a vector of parameter estimates. The discrepancy between Σ̃ _yy (θ), and Σ̂_yy (θ̂), is due to sampling error. Overall discrepancy is the difference between Σ̂_yy (θ̂), and Σ_yy, which under model misspecification and sufficiently large N is given by the sum of model error and sampling error (Cudeck & Henly, 1991).

Under standard assumptions of the common factor model the structure for both Σ_yy and S_yy in the presence of model error can be made explicit. The structure for Σ_yy is given by:

$${\mathbf{\sum }}_{yy}=\mathbf{\Lambda }\mathbf{\Phi }{\mathbf{\Lambda }}^{\prime }+{\mathbf{\Theta }}^2+{\mathbf{\Delta }}_{ME(P)},$$ (4)

where

• Φ = population correlation matrix for the common (and standardized) major factors,

• Θ = diagonal matrix of unique pattern coefficients, and

• Δ_{ME (P)} = model error in the population covariance structure.

The structure of S_yy is given by:

$${\mathbf{S}}_{yy}=\mathbf{\Lambda }\mathbf{\Phi }{\mathbf{\Lambda }}^{\prime }+{\mathbf{\Theta }}^2+{\mathbf{\Delta }}_{ME(S)}+{\mathbf{\Delta }}_{SE},$$ (5)

where

• Δ_{ME (S)} = model error in the sample covariance structure, and

• Δ_SE = sampling error.

Holding estimation method constant, differences between θ and θ̂ are due to the differences between the error terms in Equation 4, Δ_{ME (P)}, and Equation 5, Δ_{ME (S)} +Δ_SE. MacCallum, Widaman, Preacher, and Hong (2001) demonstrated that Δ_{ME (S)} ≈ Δ_{ME (P)} over repeated sampling, and thus, Δ_SE is the primary unique factor accounting for differences between θ and θ̂.

Sampling error introduces differences between the sample, C_xx, and population, Σ_xx, covariance matrix for the common and unique factor scores (MacCallum, Widaman, Zhang, & Hong, 1999). Submatrices of C_xx can be viewed as weights for the S_yy implied by the common factor model by expanding Equation 5 (while ignoring Δ_{ME (S)}):

$${\mathbf{S}}_{yy}=\mathbf{\Lambda }{\mathbf{C}}_{cc}{\mathbf{\Lambda }}^{\prime }+\mathbf{\Lambda }{\mathbf{C}}_{cu}{\mathbf{\Theta }}^{\prime }+\mathbf{\Theta }{\mathbf{C}}_{uc}{\mathbf{\Lambda }}^{\prime }+\mathbf{\Theta }{\mathbf{C}}_{uu}{\mathbf{\Theta }}^{\prime },$$ (6)

where subscripts c and u denote common and unique factors, respectively. Equation 6 is useful for identifying some key consequences of Δ_SE (e.g., Σ_uu ≠ C_uu ≠ I; Σ_cu ≠ C_cu ≠ 0) that provide a general framework to explain why fitting S_yy to a reduced form of Equation 5, ΛΦΛ′ + Θ², generally results in a θ̂ that differs from θ.

MacCallum et al. (1999) hypothesized and then demonstrated in a Monte Carlo study that some key specific factors affecting the quality of an EFA solution include N, h, and p:r. Outcomes included a measure of accuracy and a measure of stability with regard to Λ̂*. The problematic effects of Δ_SE decreased under conditions when the right-hand side of Equation 6 moved toward a reduced, yet familiar, form: ΛΦΛ′ + Θ². Movement toward this reduced form of the right-hand side of Equation 6 occurred when Θ approached a null matrix (e.g., level of h = high) and/or submatrices of C_xx approached population values, Σ_uu ≈ C_uu ≈ I, Σ_cu ≈ C_cu ≈ 0,(e.g., N was large), and/or the common factors became more overdetermined (e.g., moving from p:r = 20:7 to p:r = 20:3) decreasing the size, and hence the influence, of C_cu and C_uc.

The major findings of MacCallum et al. (1999) summarized in the previous paragraph were also observed in MacCallum et al. (2001) who extended the earlier study by demonstrating the same general patterns in the presence of model error in addition to sampling error. A feature of the MacCallum et al. (2001) study was that population pattern matrices were used as target matrices following direct quartimin rotation. The role for systematically increasing the number and/or the accuracy of targets specified to influence the quality of the rotated solution after controlling for the influence of other well-known factors (e.g., model error) was not studied.

Hypotheses for the Current Study

Myers et al. (2013) provided evidence for the unique role of the number of targets specified and replicated the findings of MacCallum et al. (1999) with regard to N, h, and p:r. Based on MacCallum et al. (2001), the findings of Myers et al. with regard to the number of targets should be observed in the presence of model error in addition to sampling error. Hypotheses unique to this study in regard to the accuracy and stability of Λ̂* are provided below.

Hypothesis 1

Target error would not exert a meaningfully large impact due to the flexibility afforded by the least squares fit to B.

Hypothesis 2

There would be an effect for the number of targets specified. As the number of targets increased Λ̂* would become more accurate and more stable because each Λ̂ would be rotated toward a common B that was increasingly overdetermined (i.e., more targets) and thereby reduce the effect of sampling error.

Hypothesis 3

There would be an interactive effect between h and the number of targets specified. Specifically, when h was high the effect of the number of targets would be smaller because Θ would approach a null matrix and thereby reduce the effect of sampling error.

Hypothesis 4

Target rotation would perform at least as well as geomin rotation with regard to accuracy, particularly as the number of targets specified increased, due to the ability of target rotation to be specified in such a way as to search for a complex underlying structure. An a priori hypothesis regarding the performance of target rotation versus geomin rotation with regard to stability was not put forth due to a lack of directly related research.

Method

The design consisted of two studies. Study 1 tested Hypothesis 1 through Hypothesis 3. Study 2 tested Hypothesis 4 under some of the conditions imposed in Study 1. Both studies used the same 18 population models.

Eighteen population models were specified for the purpose of achieving the desired characteristics with regard to overdetermination of Λ, h, and model error (detailed in the Manipulated Factors section). Nine of the 18 Λ were nearly identical to nine of the Λ used in MacCallum et al. (2001) where p = 20, r = 3.¹ The remaining nine Λ in the current study were specified in order to achieve the desired characteristics for population models where p = 10, r = 3 because MacCallum et al. did not study population models where p = 10, r = 3.

The set of population models in the current study was selected for three reasons. First, the population models logically followed previous research regarding target rotation by Myers et al. (2013). Second, the population models had a link to two seminal studies in the factor analysis area as the population model generation approach taken in MacCallum et al. (2001) closely followed the approach taken by Tucker, Koopman, and Linn (1969). Third, the population models had some key characteristics that were similar to EFA in practice (Henson & Roberts, 2006). For example, each Λ was realistic in the sense that there was “variation in importance of major factors as well as numerous small to moderate secondary loadings” (MacCallum, et al., p. 620). As an example, values within a Λ are provided in Figure 1. Table 1 summarizes some key characteristics of the common factors for each of the 18 Λ. Population correlation values between the common factors equaled zero which was consistent with MacCallum et al.

Table 1.

Some Key Characteristics of the Common Factors by p:r

key characteristics	p:r = 20:3 ≈ 7:1
	ε = .025			ε = .065			ε = .090
	h = high	h = wide	h = low	h = high	h = wide	h = low	h = high	h = wide	h = low
average number of high pattern coefficients per r	6.67	3.33	0.33	6.00	4.33	0.00	6.33	3.33	0.00
number of pure variables	0	0	0	0	0	0	0	0	0
	p:r = 10:3 ≈ 3:1
average number of high pattern coefficients per r	3.33	1.67	0.00	3.00	2.33	0.33	3.33	2.33	0.00
number of pure variables	0	0	0	0	0	0	0	0	0

Note. ε = population RMSEA value; h = communality; p = number of observed variables; r = number of factors; high pattern coefficient = λ ≥ .63 (Comrey & Lee, 1992); pure variable = observed variable has only one non-zero pattern coefficient.

Study 1

Manipulated Factors

Six factors were manipulated: overdetermination of Λ (p:r; two conditions), model error (three conditions), h (three conditions), N (three conditions), number of targets (nine or four conditions depending on the level of p:r), and target error (four conditions). Manipulation of the first three factors was accomplished via specification of 18 population models. Table 2 provides an overview of the experimental design, which had a total of 1404 cells. The p:r = 20:3 (i.e., Model 1 – Model 9) and the p:r = 10:3 (i.e., Model 10–18) conditions contributed 972 (3*3*3*9*4) and 432 cells (3*3*3*4*4), respectively.

Table 2.

Overview of Experimental Design for Study 1

Population model	Overdetermination of Λ (p:r)	Model error (me)	Communality (h)	N	Number of targets (t)	Target error (te)	cells
Model 1	20:3	fair	high	100, 300, 500	r−1 thru r+7	exact thru poor	1–108
Model 2	20:3	fair	low	100, 300, 500	r−1 thru r+7	exact thru poor	109–216
Model 3	20:3	fair	wide	100, 300, 500	r−1 thru r+7	exact thru poor	217–324
Model 4	20:3	poor	high	100, 300, 500	r−1 thru r+7	exact thru poor	325–432
Model 5	20:3	poor	low	100, 300, 500	r−1 thru r+7	exact thru poor	433–540
Model 6	20:3	poor	wide	100, 300, 500	r−1 thru r+7	exact thru poor	541–648
Model 7	20:3	very good	high	100, 300, 500	r−1 thru r+7	exact thru poor	649–756
Model 8	20:3	very good	low	100, 300, 500	r−1 thru r+7	exact thru poor	757–864
Model 9	20:3	very good	wide	100, 300, 500	r−1 thru r+7	exact thru poor	865–972
Model 10	10:3	fair	high	100, 300, 500	r−1 thru r+2	exact thru poor	973–1020
Model 11	10:3	fair	low	100, 300, 500	r−1 thru r+2	exact thru poor	1021–1068
Model 12	10:3	fair	wide	100, 300, 500	r−1 thru r+2	exact thru poor	1069–1116
Model 13	10:3	poor	high	100, 300, 500	r−1 thru r+2	exact thru poor	1117–1164
Model 14	10:3	poor	low	100, 300, 500	r−1 thru r+2	exact thru poor	1165–1212
Model 15	10:3	poor	wide	100, 300, 500	r−1 thru r+2	exact thru poor	1213–1260
Model 16	10:3	very good	high	100, 300, 500	r−1 thru r+2	exact thru poor	1261–1308
Model 17	10:3	very good	low	100, 300, 500	r−1 thru r+2	exact thru poor	1309–1356
Model 18	10:3	very good	wide	100, 300, 500	r−1 thru r+2	exact thru poor	1357–1404

Note. p = number of observed variables; r = number of factors.

Overdetermination of Λ (p:r)

Two conditions were specified for p:r: highly overdetermined (i.e., p:r = 20:3) or weakly overdetermined (i.e., p:r = 10:3). The highly overdetermined condition was consistent with EFA models in practice where the median p is ~20 and median r is ~3.00 (Henson & Roberts, 2006). The weakly overdetermined condition (i.e., relatively small p:r) was consistent the questionable, but often observed, practice of discarding complex, yet substantively important, items (Marsh, Hau, Balla, & Grayson, 1998).

Model error (me)

Three conditions were specified for me: low (i.e., population RMSEA, ε, = .025) moderate (ε = .065), or high (ε, = .090), These values were equal to those reported in MacCallum et al. (2001) and were conceptualized in the same way: very good fit, fair fit, and poor fit, respectively (Browne & Cudeck, 1993; Steiger, 1989). Model error conditions were consistent with levels commonly observed in practice (Jackson et al., 2009).

Model error was integrated into the simulation of the current study through the use of minor factors (n=180) as described in Hong (1999).² For each of the 18 population models a pattern matrix for the minor factors, Λ_m, was generated. Each Λ_m was initially generated by using multivariate random normal deviates. The standard deviation of the first minor factor was equal to 1. The standard deviation of each successive minor factor was .9 times the standard deviation of the preceding minor factor. After generating random pattern values for the minor factors the rows of Λ_m were rescaled to achieve a specific amount of variance accounted by the minor factors. The specific amount of total variance accounted by the minor factors ranged from 12.5% (i.e., ε = .025 and communality equaled high) to 60.6% (i.e., ε = .090 and communality equaled low) and was manipulated so that the desired level of me (i.e., ε, = .025 or .065 or .090) was integrated into each of the 18 population correlation matrices. The population correlation matrices were formed from Λ_m, Λ and unique variances and were used for data generation.

Communality (h)

Three conditions were specified for h: high (i.e., h_i = .60 to .80; h̄ _high = .70 ), wide (i.e., h_i = .20 to .80; h̄ _wide = .50 ), or low (i.e., h_i = .20 to .40; h̄ _low = .30 ).³ These values were consistent with those used in MacCallum et al. (2001). Henson and Roberts (2006) reported that for EFA models in practice, the average total variance explained by the extracted factors (R² ) ≈ 52% (R²_min ≈ 17% and R²_max ≈ 87%).

Sample size (N)

Three conditions were specified for N: 100, 300, or 500. Henson and Roberts (2006) reported that the distribution of sample size for EFA models in practice is positively skewed (minimum = 42, median = 267, M = 436, maximum = 3113).

Number of targets per factor (t)

Two sets of conditions were specified for t based on level of p:r (see Table 3). For all 18 population models, t was increased systematically from a minimum number necessary for rotation identification, r − 1 per column, up to 50% of targeted elements in each column of B (i.e., r + 7 when p:r = 20:3 and r + 2 when p:r = 10:3). Fifty percent of targeted elements in each column of B was selected as the maximum to reflect the incomplete measurement theory commonly observed in practice (Myers et al., 2013).

Table 3.

Target Conditions by p:r

t	p:r = 20:3			p:r = 10:3
	t per r (%)	nt per r (%)	nt	t per r (%)	nt per r (%)	nt
r − 1	2 (10%)	18 (90%)	54	2 (20%)	8 (80%)	24
r	3 (15%)	17 (85%)	51	3 (30%)	7 (70%)	21
r + 1	4 (20%)	16 (80%)	48	4 (40%)	6 (60%)	18
r + 2	5 (25%)	15 (75%)	45	5 (50%)	5 (50%)	15
r + 3	6 (30%)	14 (70%)	42
r + 4	7 (35%)	13 (65%)	39
r + 5	8 (40%)	12 (60%)	36
r + 6	9 (45%)	11 (55%)	33
r + 7	10 (50%)	10 (50%)	30

Note. p = number of observed variables; t = number of targets per factor; r = number of factors; nt = number of non-targets.

A total of 117 unique B (holding target error = 0) were specified across all 18 population models (i.e., 81 B in p:r = 20:3 case and 36 B in p:r = 10:3 case). For all B, the first t condition (i.e., r − 1) included two small pattern coefficients in each column (M = .00, SD = .08). From there the smallest non-targeted pattern coefficient in each column was specified as a target as t increased (e.g., from r − 1 to r).⁴ See Figure 1 for an example of a B where 50% of the elements were targeted. Specifying many small valued pattern coefficients as targets was consistent with previous research (Browne, 1972a, 1972b; Gruvaeus, 1970). A conceptual rationale for targeting only small valued pattern coefficients is that for any particular indicator the targeted value(s) may frequently be more accurate if the column(s) that the indicator is(are) not intended to measure is(are) targeted (e.g., values near zero) than if the column(s) that the indicator is(are) intended to measure is(are) targeted.

Target error (te)

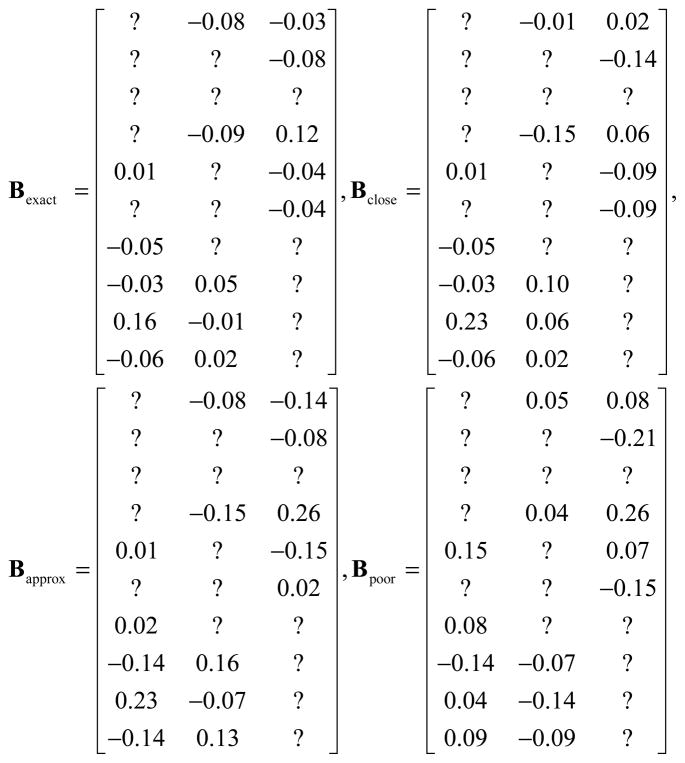
Four conditions were specified for te: exact, B_exact (b_ij = λ_ij), close, B_close, (b_ij = λ_ij or b_ij = λ_ij ± 1SE), approximate, B_approx (b_ij = λ_ij or b_ij = λ_ij ± 1SE or b_ij = λ_ij ± 2SE), or poor, B_poor (b_ij = λ_ij ± 2SE). Within each B condition, the assignment of each b_ij to a particular value was systematic and continuous (from factor 1 to factor 3) as t increased. For example, when B = B_approx and t = r − 1, the first target in the first column was specified as b_i1 = λ_i1, the second target in the first column was specified as b_i1 = λ_i1 + 1SE, the first target in the second column was specified as b_i2 = λ_i2 − 1SE,..., the second target in the third column was specified as b_i3 = λ_i3. Continuing with t = r for B = B_approx, the additional target in the first column was specified as b_i1 = λ_i1 + 1SE,..., and so forth.

Empirical standard errors for each λ_ij within each of the 18 Λ were estimated in 18 Monte Carlo studies (i.e., one for each population model) where, N = 300, the number of replications, N_R, = 10,000, and the rotation criterion was direct quartimin. A modest N was selected to reflect sample sizes in practice, while a relatively large N_R was selected to increase the accuracy of the empirical standard errors (Hoogland & Boomsma, 1998). For each λ_ij, the average of the estimated standard error over the replications was used as the empirical standard error. Figure 2 provides the four te conditions for the Λ previously depicted in Figure 1. A total of 468 unique B were specified (i.e., 117 for each of the four te conditions).

Figure 2.

Four target error conditions for the Λ depicted in Figure 1. Non-targeted elements were denoted with a ? symbol.

Rotation Identification

Some known conditions for rotation identification in factor analysis exist (e.g., Algina, 1980; Hayashi & Marcoulides, 2006). Under oblique rotation H* is a non-symmetric square matrix that results in r² indeterminacies. Imposing r² constraints on Λ and Ψ is a necessary condition for rotation identification. Fixing the variance for each of the common factor to 1 provided r constraints. A set of sufficient conditions for imposing the remaining r(r – 1) constraints included: (a) each column of Λ has r – 1 elements specified as zeros, and (b) each submatrix Λ_s, where s = 1,…,r, of Λ composed of the rows of Λ that have fixed zeros in the r^th column must have rank r – 1. For each t specification, it was confirmed that both conditions were met with regard to the population values.⁵

Population-level rotation

In each of the 18 population models the parameter values represented one possible rotated solution. In order to operate under the assumption that the particular set of parameter values in Λ was the simplest in each case, population-level rotation, Λ^*, was obtained from a Monte Carlo study where N =1,000,000 and N_R, = 1 (Asparouhov & Muthén, 2009). This was done for each t condition (because each t condition represented a unique rotation criterion) in each of the 18 population models when B = B_exact. Across all 117 Monte Carlo studies the average difference between each element within the relevant Λ* and the relevant Λ was −.02 with SD = .04.

Data Generation

The experiment was performed within the exploratory structural equation modeling framework (ESEM; Asparouhov & Muthén, 2009) as implemented in Mplus 7 (Muthén & Muthén, 1998–2012). Data were drawn from a multivariate normal distribution (0, Σ). Number of iterations was set to 10000 for both the unrotated and the rotated solution. Parameter values were provided in the model statement to define the alignment criteria in order to avoid factor order switching and reduce the likelihood of negative factors (Asparouhov & Muthén, 2009).

Within each cell N_R = 100 for each initial run though it was expected that non-convergence and/or inadmissible solutions would frequently be observed in some cells (e.g., Velicer & Fava, 1998). Consistent with the goal of maximizing the representativeness of the results to practice, replications that did not converge to a (rotated) solution or that converged to an improper solution were discarded (Bandalos, 2006). Each replication was screened because the program retained all completed replications – even if the solution was improper. Taking this approach was a primary reason that N_R was relatively small. Replications were added as necessary to achieve 100 acceptable solutions in each cell.

Outcomes

To investigate the similarity between Λ and Λ̂* mean bias, δ, was calculated for each replication:

$$\delta =\frac{{\displaystyle \sum _{i=1}^p}{\displaystyle \sum _{j=1}^r}\left({\lambda }_{ij}-{\widehat{\lambda }}_{ij}^{\ast }\right)}{pr},$$ (7)

where

• ${\widehat{\lambda }}_{ij}^{\ast }$ is the observed rotated pattern coefficient for variable i on factor j, and

• λ_ij is the true pattern coefficient for variable i on factor j.

Bias was used to assess the accuracy of Λ̂*.

To investigate the stability of Λ̂* a measure of variability for the entire matrix, V, was calculated for each replication:

$$V={\left[\frac{\mathit{Trace}\left[{\left({\widehat{\mathbf{\Lambda }}}^{\ast }-\overline{{\widehat{\mathbf{\Lambda }}}^{\ast }}\right)}^{\prime }\left({\widehat{\mathbf{\Lambda }}}^{\ast }-\overline{{\widehat{\mathbf{\Lambda }}}^{\ast }}\right)\right]}{pr}\right]}^{1/2},$$ (8)

where

• $\overline{{\widehat{\mathbf{\Lambda }}}^{\ast }}$ = was the mean observed rotated solution over 100 replications in a given cell. V was used to assess the stability of Λ̂*.

Testing Hypotheses 1 through Hypothesis 3

A six-way ANOVA modeled δ and then V by p:r, me, h, N, t, and te. All main and interaction effects were modeled and α was set .05 from this point forward. Effect size was emphasized over statistical significance and was categorized as small, .01 < ω̂² < .05, medium, .05 ≤ ω̂² < .13, and large, ω̂² ≥ .13, consistent with general guidelines from Cohen (1988).

Study 2

Study 2 tested Hypothesis 4 under some of the conditions imposed in Study 1. The manipulated factor t was re-conceptualized as rotation criterion, rc, and geomin rotation was added as a condition (where ε = .001; the default value in Mplus for three factors). Target error was reduced from four conditions to one condition, B_poor, for textual parsimony and to potentially provide a more conservative test with regard to target rotation. All other manipulated factors, data generation procedures, and outcomes were identical to Study 1.

Testing Hypothesis 4

A five-way ANOVA modeled δ and then V by p:r, me, h, N, and rc. All main and interaction effects were modeled but the focus was on post hoc comparisons within rc factor (i.e., geomin versus levels of t) by h. Thus, there was a total of 54 post hoc comparisons (27 for each outcome). Effect size was categorized as small, .1 ≤ |d| < .5, medium, .5 ≤ |d| < .8, and large, |d| ≥ .8, consistent with general guidelines from Cohen (1988). A somewhat liberal definition of small was considered reasonable given that both target and geomin rotation are somewhat flexible in that neither f (Λ) was confined to search for a perfect simple structure, and, that rotation occurs after estimation of the unrotated solution.

Results

The number of acceptable solutions from the first 100 replications in each cell was consistent with results from Velicer and Fava (1998). The percentage of acceptable solutions when p:r ≥ 20:3 was high (i.e., ≥ 83% in each of these cells; M = 98% across these cells), while the percentage of acceptable solutions when p:r = 10:3 was more variable (i.e.,≥ 45% in each of these cells; M = 86% across these cells). A total of 152,056 datasets were generated in order to achieve 140,400 datasets that yielded an acceptable solution.

Study 1

Bias (δ) summary

Average (across the 100 replications within each of the 1404 cells of the design) mean bias, δ̄, was small: M = −0.02, SD = 0.03. The small amount of δ observed in the current study was consistent with result reported in MacCallum et al. (2001). Given the small amount of δ and its location around zero, the absolute value of δ (i.e., unsigned bias) was calculated for each replication because the magnitude of δ was viewed as more important than the direction of δ, and, to avoid cancelling due to δ of opposite signs in subsequent analyses.

Effects from the six-way ANOVA that were greater than small and not directly related to the hypotheses in the current study were: h (ω̂² = .16 ), p:r (ω̂² = .10), p:r*h (ω̂ ² = .05 ).⁶ These main and interaction effects were consistent with MacCallum et al. (1999) and are not discussed further. The major patterns (e.g., statistically significant but small effects) found in MacCallum et al. (2001) with regard to the main and interaction effects of me were replicated and are not discussed further in the main text. The smaller main and interaction effects of N in the current study (as compared to MacCallum et al. 2001) was likely attributable to the omission of a very small N (e.g., = 60 as in MacCallum et al. 2001) condition in the current study.

Variability (V) summary

Average (across replications within each of the 1404 cells of the design) mean variability, V̄, was: M = 0.31, SD = 0.14. Effects from the six-way ANOVA that were greater than small and not directly related to the hypotheses in the current study were: p:r (ω̂ ² = .09) and h (ω̂ ² = .07 ). Both of these main effects, along with the statistically significant but small main and interaction effects for me and N, were consistent with MacCallum et al. (2001) and are not discussed further. Hypotheses unique to this study are discussed below.

Hypothesis 1

Effect size for the main effect of te, and all interaction effects involving te, on both δ and V was ω̂ ² ≤ .01 and in the vast majority (58 out of 64) cases ω̂ ² = .00. Thus, there was support for Hypothesis 1 in that target rotation was relatively robust to the target error conditions studied.

Hypothesis 2 and Hypothesis 3

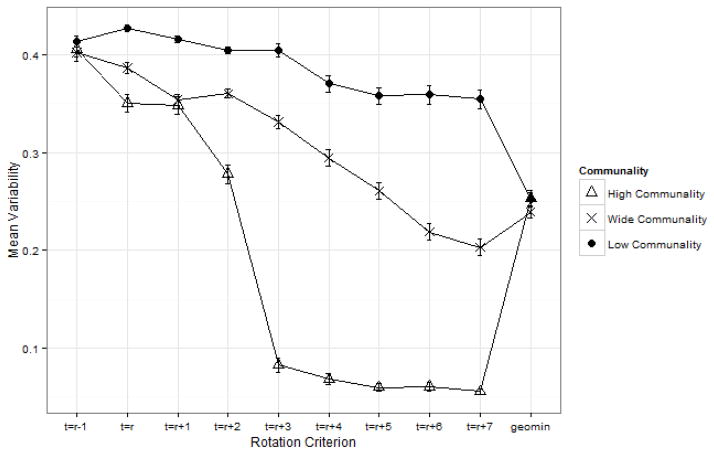
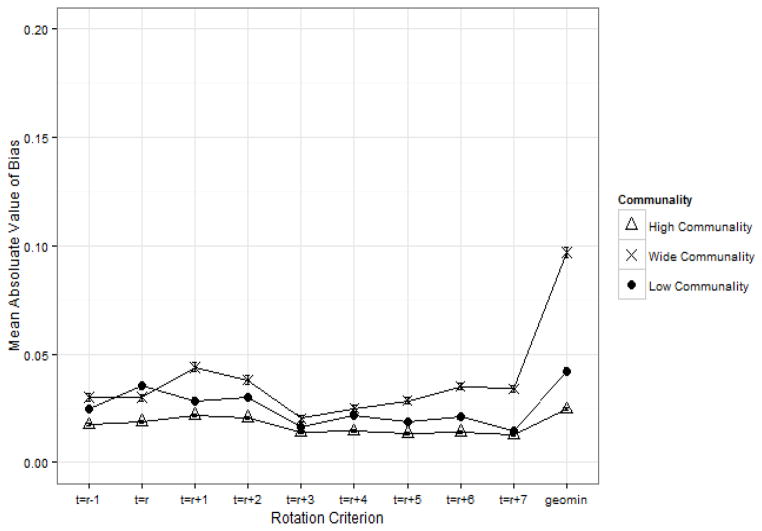
There was a small main effect for t on both δ (i.e., ω̂ ² = .01) and V (i.e., ω̂ ² = .04 ) but in both cases the magnitude of this effect depended somewhat on level of h (i.e., ω̂² = .01 and ω̂ ² = .01, respectively). For example, as can be viewed in Figure 3, the negative effect of t on V was strongest/weakest when h was high/low. For example, as can be viewed in Figure 4, the negative effect of t on δ was weakest/strongest when h was high/low. The negative effect of t on δ was weaker and likely due to a floor effect previously described in the bias summary. Thus, there was some support for both Hypothesis 2 and Hypothesis 3 in that the negative effect of t on both δ and V depended somewhat on level of h.

Figure 3.

The effect of rotation criterion, where t = the number of targets per factor and implies target rotation, on variability by communality (h) when target error was poor. Symbols represent an average variability while error bars represent the 95% confidence interval around this average.

Figure 4.

The effect of rotation criterion, where t = the number of targets per factor and implies target rotation, on mean absolute value of bias by communality (h) when target error was poor. Symbols represent an average absolute bias value while error bars represent the 95% confidence interval around this average.

Study 2

Hypothesis 4

Target rotation outperformed geomin rotation in each of the 27 post hoc comparisons within levels of rc by h in regard to δ (see Figure 3). The magnitude of the effect tended to differ somewhat by level of h and t. When h = high, d ranged from 0.21 to 0.98 and was consistently large (i.e., d ≥ .84) when t ≥ r + 3. When h = wide, d was consistently large and ranged from 1.10 to 1.76. When h = low, d ranged from 0.17 to 0.99 and was consistently moderate to large (i.e., d ≥ .74) when t ≥ r + 3. For all comparisons, the magnitude of d was heavily influenced by the by the precision of the pooled SD as the largest mean difference for any comparison was 0.08. Similarly, and as can be viewed in Figure 4, both rotation criteria tended to produce solutions of relatively good accuracy as δ̄ ≤ .10.

Geomin rotation outperformed target rotation in 20 of the 27 post hoc comparisons within levels of rc by h in regard to V (see Figure 4). The magnitude of the effect tended to differ somewhat by level of h and t. When h = high and t ≥ r +2, d ranged from 0.13 to 0.86 in favor of geomin rotation and this effect tended to shrink as t increased. When h = high and t > r +2, d ranged from 1.01 to 1.25 in favor of target rotation. When h = wide and t ≥ r +5, d ranged from 0.17 to 1.19 in favor of geomin rotation and this effect tended to shrink as t increased. When h = wide and t > r + 5, d ranged from 0.16 to 0.29 in favor of target rotation. When h = low, geomin rotation always outperformed target rotation and d ranged from 0.74 (t = r + 7) to 1.58 (t = r). An a priori hypothesis regarding the performance of target rotation versus geomin rotation with regard to stability was not put forth due to a lack of directly related research; results from these comparisons will be tentatively discussed in relation to the partially specified target matrix.

Discussion

The purpose of the current Monte Carlo study is to explore the influence of the number of targets specified on the quality of EFA solutions with a complex underlying structure and incomplete substantive measurement theory. Study 1 extends previous research by exploring this phenomenon in situations in which specification errors are present in both the common factor model (i.e., model error) and the targeted pattern matrix (i.e., target error). Study 2 extends previous research by comparing the performance of target rotation to geomin rotation under some of the conditions imposed in Study 1. Established sources of error in factor analysis manipulated in both studies include overdetermination of the pattern matrix, communality, and sample size. Outcomes are a measure of accuracy and a measure of stability with regard to the rotated pattern matrix. Findings are discussed with respect to the hypotheses tested with an emphasis on potential implications for applied research.

There is support for Hypothesis 1 in that the magnitude of the main effect of target error, and all interactive effects involving target error, on both the accuracy and stability of the rotated solution is negligible. This finding is consistent with long held methodological speculation that target rotation may be relatively robust to such misspecification due to the inherent flexibility of the least squares fit to the targeted pattern matrix. This finding also may have important implications for practice given that the true value of any particular pattern coefficient, let alone the true value for each of the several pattern coefficients necessary for rotation identification, is likely to be unknown in any particular application. More broadly, the fact that target rotation may be relatively unaffected by both model and target error suggests that this rotation criterion may be useful under conditions frequently observed in practice: important substantive measurement theory is available yet it is both incomplete and less than perfectly accurate.

There is some support for both Hypothesis 2 and Hypothesis 3 in that the magnitude of the effect of the number of targets specified on both the accuracy and stability of the rotated solution depends somewhat on level of communality (but not on target error). Like in the Myers et al. (2013) study, these findings can be viewed as analogous to the interactive effect of communality and degree of overdetermination of the pattern matrix (substituting the number of targets per factor for p:r) predicted and found in both MacCallum et al. (1999) and MacCallum et al. (2001). In general, when communality is high, the effect of the number of targets on increasing accuracy is smaller (likely due to a floor effect) than when communality is not high. From an applied perspective, these findings make clear the potential importance of using extant, even if incomplete and somewhat inaccurate, substantive measurement theory to specify the target matrix to the full extent possible – particularly when the observed variables are not uniformly highly reliable indicators of the underlying factors.

There is some support for Hypothesis 4 in that target rotation outperforms geomin rotation in regard to accuracy. While the size of the effect generally is at least medium it should be noted that both rotation criteria tend to produce solutions of relatively good accuracy thus the effect size was largely achieved by the precision of the pooled SD. From a methodological perspective the accuracy findings are consistent with the fact that neither rotation criterion is restricted to search for a perfect simple structure, and, that target rotation can be specified in such a way as to search for a complex underlying structure. From an applied perspective, the potential importance of using extant, even if incomplete and somewhat inaccurate, substantive measurement theory to inform the rotation criterion in a non-mechanical way may be worthwhile in general with regard to accuracy. Most simply, the additional demand placed on the user under target rotation versus geomin rotation may be worthwhile with regard to accuracy.

Geomin rotation outperforms target rotation in most conditions of this study in regard to stability. As can be viewed in Figure 1, the target matrix typically is only partially specified and thus the complexity function that is minimized is based on partial information. For this reason, target rotation may yield relatively less stable results as compared to rotation criterion whose complexity function is based on fuller information, particularly when only a small percentage of possible targets are specified. As can be viewed in Figure 3, instability tended to decrease as the number of targets increased but the magnitude of this decrease tended to depend on level of communality. From an applied perspective, when the observed variables are less than uniformly reliable indicators of the underlying factors, geomin rotation may be expected to outperform target rotation. When, however, the observed variables are uniformly reliable indicators of the underlying factors and several targets are specified, target rotation may be expected to outperform geomin rotation. In summary, using incomplete substantive measurement theory to inform the rotation criterion in a non-mechanical way may be worthwhile only in limited circumstances, as compared to a fuller information mechanical approach, with regard to stability.

The ability to broadly generalize results from this study is constrained by the conditions imposed. Specific conditions in this study that are restrictive include the exclusion of: large pattern matrices, structural coefficients in the latent variable model, and egregiously incorrect targeted values. Subsequent studies that examine the performance of the number of targets per factor for large pattern matrices (e.g., several factors) under conditions commonly observed in practice (e.g., model and target error), and compare this performance to mechanical rotation criteria, could advance the literature. Subsequent studies also could expand the form of the structural equation to include structural coefficients in the latent variable portion of the model, while examining the performance of target rotation as compared to other rotation criteria. Subsequent studies that examine the performance of the number of targets per factor when the targets are more incorrect than in the current study could advance the literature. Finally, the correct number of factors always is specified in the current study, which is a limitation consistent with known limits of factor analysis (e.g., Fava & Velicer, 1996). The potential studies proposed in this paragraph may be timely as the recently proposed ESEM framework (and by extension potential specification of a rotation criterion) appears to offer a viable alternative to CFA in some instances in theory (Asparouhov & Muthén, 2009) and in practice (e.g., Marsh et al., 2009; Morin & Maïano, 2011; Myers, Chase, Pierce, & Martin, 2011).