Phase I/II adaptive design for drug combination oncology trials

Abstract

Existing statistical methodology on dose finding for combination chemotherapies has focused on toxicity considerations alone in finding a maximum tolerated dose combination to recommend for further testing of efficacy in a phase II setting. Recently, there has been increasing interest in integrating phase I and phase II trials in order to facilitate drug development. In this article, we propose a new adaptive phase I/II method for dual-agent combinations that takes into account both toxicity and efficacy after each cohort inclusion. The primary objective, both within and at the conclusion of the trial, becomes finding a single dose combination with an acceptable level of toxicity that maximizes efficacious response. We assume that there exist monotone dose–toxicity and dose–efficacy relationships among doses of one agent when the dose of other agent is fixed. We perform extensive simulation studies that demonstrate the operating characteristics of our proposed approach, and we compare simulated results to existing methodology in phase I/II design for combinations of agents.

1. Introduction

1.1. Background information

In general, the primary objective of phase I clinical trials is to identify the maximum tolerated dose (MTD) of the agent or agents being investigated. In a subsequent phase II trial, the agent is evaluated for efficacy at the recommended dose (MTD). In oncology trials of chemotherapeutic agents, identification of the MTD is usually determined by considering dose-limiting toxicity (DLT) information only, with the assumption that the MTD is the highest dose that satisfies some safety requirement, so that it provides the most promising outlook for efficacy. Usually, phase I and phase II trials are performed independently, without formally sharing information across the separate phases. There has been a recent shift in the paradigm of drug development in oncology to integrate phase I and phase II trials so that drug development process may be accelerated, while potentially reducing costs [1]. To this end, several published phase I/II methods have extended dose-finding methodology to allow for the modeling of both toxicity and efficacy ([2–7], among others).

In general, the principal assumption driving the design of phase I trials is that the administration of higher doses can be expected to result in DLT in a higher percentage of patients and that higher doses will be more efficacious. These relationships are typically characterized by dose–toxicity and dose–efficacy patterns in which the probability of toxicity and the probability of efficacy increase monotonically with increasing dose. Situations in which the monotonicity assumption, for both toxicity and efficacy, may fail are becoming increasingly common in cancer research practice. Most notably, these studies are phase I trials that involve combinations of agents. Dose finding for multi-drug combinations can be broadened to the more general problem of partial ordering in clinical trials. Other partial order problems include patient heterogeneity and different treatment schedules [8, 9]. By partial ordering, we mean that it may be possible to identify the ordering of DLT probabilities for only a subset of the available combinations. This relaxes the assumption of monotonicity among all doses (i.e. combinations) in terms of their toxicity (and efficacy).

Various methods have been suggested by authors to handle the problem of dose finding in drug combination trials ([10–15], among others). These methods determine combinations to which to allocate patients solely on the basis of toxicity considerations, without accounting for efficacy. There has been limited research on early-phase designs for drug combination trials that account for both toxicity and efficacy. Huang et al. [16] proposed a parallel phase I/II design for combinations of agents. The phase I part of the design utilizes the ‘3 + 3’ dose-finding design [17] to identify a set of combinations with ‘acceptable’ toxicity. Once the initial dose-escalation process is completed, a response adaptive randomization procedure based on efficacy is performed using all combinations in the set found to be acceptable in the dose-finding portion. Li et al. [18] presented a dose-schedule finding method for partially ordered phase I/II clinical trials. Yuan and Yin [19] also proposed phase I/II design for combinations, in which the phase I component establishes a set of admissible doses on the basis of copula-type regression outlined in [20]. The phase II component takes the set of admissible doses and implements a novel procedure, known as moving-reference adaptive randomization, in order to compare efficacy among admissible treatments. Both of these phase I/II designs for combinations take a fixed set of admissible doses into the phase II portion of the study in order to assess efficacy. We contrast these designs with the one we propose here in that, throughout the duration of the trial, we continuously monitor safety data in order to adaptively update our set of acceptable dose combinations with which to make allocation decisions based on efficacy.

In this article, we propose a new phase I/II adaptive design that takes into account both toxicity and efficacy in order to make allocation decisions and find the optimal dose combination (ODC). The ODC is defined as the most efficacious dose combination with a tolerable toxicity profile. Because of the partial ordering among combinations, this may not be the combination with the highest DLT rate in the set of acceptable combinations. The overall strategy of the method proposed in this article is to use two binary responses, one for toxicity and one for efficacy, from each entered patient to adaptively identify a set of ‘acceptable’ toxicity combinations and allocate the next entered cohort to the combination in the set that the data indicate to be most efficacious. Simulation results will demonstrate that the new design will gravitate towards acceptable toxicity combinations with high efficacy. In the remainder of this section, we briefly describe the problem of partial ordering in dose-finding trials. In the following section, we outline the models and inference for the proposed design. In Section 4, we present simulation results that illustrate the operating characteristics of the proposed work and compare them to those of Yuan and Yin [19]. Finally, we conclude with some discussion and directions for future research.

1.2. The problem of partial ordering

1.2.1. Toxicity

As an example, consider a FDA-approved drug combination trial designed at the University of Virginia Cancer Center. The example is a phase I/II trial designed to find an ODC of two agents, which we label agent A and agent B. Both agents have three dose levels, resulting in a total of nine combinations, {d₁, d₂, …, d₈, d₉} under consideration, creating a 3 × 3 matrix order, and the treatments are labeled as in Table I. A reasonable assumption to be made in these type of studies is that toxicity increases monotonically with dose of an agent, if the other agent is held fixed (i.e., across and up columns of the matrix). The DLT probabilities follow a complete order in that the relationship between all DLT probabilities for one of the agents, when the other agent is fixed, is completely known. Denoting the probability of a DLT at combination d_i by π_T (d_i), if agent A is fixed at dose level 2, then we know π_T (d₄) ≤ π_T (d₅) ≤ π_T (d₆). It may not be possible to arrive at a complete ordering among the combinations along the diagonals of the drug combination matrix. Moving from d₄ to d₂ corresponds to decreasing the dosage of agent A from 2 to 1, while increasing the dosage of agent B from 1 to 2. Therefore, the conditions

$${\pi }_T(d_1)\le {\pi }_T(d_2),{\pi }_T(d_1)\le {\pi }_T(d_4)$$

hold without it being possible to order π_T (d₂) and π_T (d₄) with respect to one another, creating a partial order between π_T (d₁), π_T (d₂), and π_T (d₄). Taking into account known and unknown relationships between combinations, we proceed by laying out possible complete orders of the dose–toxicity relationship. Considering all possibilities in studies such as the example provided is not feasible because of the large number. We rely on the practical approach of Wages and Conaway [21] by formulating a reasonable subset of possible orders according to the rows, columns, and diagonals of the matrix of combinations. The resulting orderings, index by m, are as follows:

1. across rows [m = 1]

   π_T (d₁) ≤ π_T (d₂) ≤ π_T (d₃) ≤ π_T (d₄) ≤ π_T (d₅) ≤ π_T (d₆) ≤ π_T (d₇) ≤ π_T (d₈) ≤ π_T (d₉)

2. up columns [m = 2]

   π_T (d₁) ≤ π_T (d₄) ≤ π_T (d₇) ≤ π_T (d₂) ≤ π_T (d₅) ≤ π_T (d₈) ≤ π_T (d₃) ≤ π_T (d₆) ≤ π_T (d₉).

3. up diagonals [m = 3]

   π_T (d₁) ≤ π_T (d₂) ≤ π_T (d₄) ≤ π_T (d₃) ≤ π_T (d₅) ≤ π_T (d₇) ≤ π_T (d₆) ≤ π_T (d₈) ≤ π_T (d₉)

4. down diagonals [m = 4]

   π_T (d₁) ≤ π_T (d₄) ≤ π_T (d₂) ≤ π_T (d₇) ≤ π_T (d₅) ≤ π_T (d₃) ≤ π_T (d₈) ≤ π_T (d₆) ≤ π_T (d₉)

5. alternating down-up diagonals [m = 5]

   π_T (d₁) ≤ π_T (d₂) ≤ π_T (d₄) ≤ π_T (d₇) ≤ π_T (d₅) ≤ π_T (d₃) ≤ π_T (d₆) ≤ π_T (d₈) ≤ π_T (d₉) and

6. alternating up-down diagonals [m = 6]

   π_T (d₁) ≤ π_T (d₄) ≤ π_T (d₂) ≤ π_T (d₃) ≤ π_T (d₅) ≤ π_T (d₇) ≤ π_T (d₈) ≤ π_T (d₆) ≤ π_T (d₉)

Table I.

Combination labels for two agents forming a 3 × 3 matrix order.

Doses of A	Doses of B
	1	2	3
3	d7	d8	d9
2	d4	d5	d6
1	d1	d2	d3

1.2.2. Efficacy

In the most common of cases, there exists a monotone efficacy relationship among doses of one of the agents when the other agents are fixed. Therefore, we focus our discussion of partially ordered dose–efficacy relationships under the assumption that single-agent efficacy profiles are monotone for the agents being investigated. If we assume, as we did with toxicity, that efficacy increases monotonically across rows and up columns of the matrix, then we can formulate possible orderings in the same way we described earlier with regard to DLT probabilities. Therefore, denoting the probability of efficacious response at combination d_i as π_E(d_i), the possible dose–efficacy relationships can be expressed according to rows, columns, and diagonals as above, with π_E’s replacing the π_T ’s. Our pro-posed design has the ability to accommodate other subset sizes for toxicity, efficacy, or both, should we have more or less ordering information available. We do not make the assumption that the most likely ordering of probabilities for the combinations will be the same with regard to both toxicity and efficacy. For instance, suppose that along the diagonal in Table I π_T (d₈) = 0.25 and π_T (d₆) = 0.20. In single-agent trials, it would be reasonable to assume that higher toxicity is associated with higher efficacy so π_E (d₈) > π_E (d₆). This may not be a reasonable assumption in drug combination trials because of the unknown interactions between the drugs. It could be the case that π_E(d₈) < π_E(d₆) even though d₈ has a slightly higher toxicity. Therefore, we formulate the subset of orderings for both toxicity and efficacy separately, allowing the observed data to tell us which toxicity ordering and which efficacy ordering are most likely.

2. Models and inference

Consider a trial investigating I drug combinations, {d₁, …, d_I}. Suppose there are M complete toxicity orders and K complete efficacy orders available for investigation, either in total or a chosen subset. For instance, if we choose to use the ‘default’ subset of orderings described earlier, then M = K = 6. Toxicity and efficacy are modeled as binary endpoints, so that for each subject j, we measure

$$Y_j=\{\begin{array}{cc}0\hfill & \text{if no toxicity},\hfill \\ 1\hfill & \text{if toxicity}\hfill \end{array}{Z}_j=\{\begin{array}{cc}0\hfill & \text{if no response},\hfill \\ 1\hfill & \text{if response}.\hfill \end{array}$$

The combination, X_j for the j th entered patient, j = 1, …, n, can be thought of as random, taking values x_j ∈ {d₁, …, d_k}.

2.1. Toxicity

Suppose that the doses follow a partial order with respect to toxicity for which there are M possible complete orders under consideration. For a particular ordering, m; m = 1, …, M, we model π_T (d_i), the true probability of DLT response at d_i by

$${\pi }_T(d_i)=\text{Pr}(Y_j=1|d_i)\approx F_m(d_i,\beta );m=1,\dots ,M$$

for a class of working dose–toxicity models, F_m(d_i, β), corresponding to each of the possible dose–efficacy orderings, and β ∈ ℬ. For instance, the power model, $F_m(d_i,\beta )=p_{im}^{\text{exp}(\beta )}$, is common to CRM designs [22], where ℬ = (−∞, ∞) and 0 < p_1m < ⋯ < p_Im < 1 are the standardized units (skeleton) representing the combinations d_i. Further, we may wish to take account of any prior information concerning the plausibility of each ordering and so introduce τ(m) = {τ(1), …, τ(M)}, where τ(m) ≥ 0 and where ∑_m τ(m) = 1. Even when there is no prior information available on the possible orderings, we can formally proceed in the same way by specifying a discrete uniform for τ(m). After inclusion of the first j patients into the trial, we have toxicity data in the form of 𝒟_j = {(x₁, y₁), …, (x_j, y_j)}. Under ordering m, we obtain an estimate, β̂_jm, for the parameter β.

In the Bayesian framework, we assign a prior probability distribution g(β) for the parameter β of each model, and a prior probability τ(m) to each possible order. In order to establish running estimates of the probability of DLT at the available combinations, we need an expression for the likelihood for the parameter β. After inclusion of the first j patients into the study, the likelihood under ordering m is given by

$$L_m(\beta |{𝒟}_j)=\prod _{\ell =1}^j{\{F_m(x_{\ell },\beta )\}}^{y_{\ell }}{\{1-F_m(x_{\ell },\beta )\}}^{(1-y_{\ell })},$$ (1)

which, for each ordering, can be used in order to generate a summary value, β̂_jm, for β. Given the set 𝒟_j and the likelihood, the posterior density for β is given by

$$P_k(\beta |{𝒟}_j)=\frac{L_m(\beta |{𝒟}_j)g(\beta )}{{\int }_{\beta }{L}_m(\beta |{𝒟}_j)g(\beta )d\beta }.$$

This information can be used to establish the posterior probabilities of the orderings given the data as

$$\omega (m|{𝒟}_j)=\frac{\tau (m){\int }_{\beta }{L}_m(\beta |{𝒟}_j)g(\beta )d\beta }{\sum _{m=1}^M\tau (m){\int }_{\beta }{L}_m(\beta |{𝒟}_j)g(\beta )d\beta }.$$

The prior probabilities, τ(m), for the ordering are updated by the toxic response data, 𝒟_j. It is expected that the more the data support ordering m, the greater its posterior probability will be. Thus, we appeal to sequential Bayesian model choice to guide allocation decisions. When a new patient is to be enrolled, we choose a single ordering, m*, with the largest posterior probability such that

$$m^{*}=\text{arg}\underset{m}{\text{max}}\omega (m|{𝒟}_j);m=1,\dots ,M.$$

We then take the working model, F_m*(d_i, β), associated with this ordering to generate toxicity probability estimates at each dose. Beginning with the prior for β and having included the j th subject, we can compute the posterior probability of a DLT for d_i so that

$${\mathrm{\pi ̂}}_T(d_i)=F_{m^{*}}(d_i,{\mathrm{\beta ̂}}_{j{m}^{*}});{\mathrm{\beta ̂}}_{j{m}^{*}}={\int }_{\beta }\beta P_k(\beta |{𝒟}_j)d\beta ,$$

which we can use to define a set of acceptable (safe) combinations based on a maximum toxicity tolerance, ϕ_T.

2.2. Efficacy

Much of the modeling notation and convention is similar to the preceding section on toxicity. Suppose we have some class of models, G, corresponding to each of the possible dose–efficacy orderings, that model the true probability of efficacy at dose X_j = x_j such that

$${\pi }_E(d_i)=\text{Pr}(Z_j=1|d_i)\approx G_k(d_i,\theta )$$

for k = 1, …, K and θ ∈ Θ. Like toxicity, for efficacy, we appeal to the simple power model, $G_k(d_i,\theta )=q_{ik}^{\text{exp}(\theta )}$, which has shown itself to work well in practice in single-agent CRM designs [22]. Here again, Θ = (−∞, ∞) and 0 < q_1k < ⋯ < q_Ik < 1 is the skeleton of the model. Let ξ(k) be a set of prior probabilities placed on each of the orderings and h(θ) be a prior distribution placed on θ. Using the accumulated toxicity data from j patients, Ω_j = {(x₁, z₁), …, (x_j, z_j)}, the posterior mean θ̂_jk and the posterior probabilities of k are generated for each ordering, based on the likelihoods L_k (θ | Ω_j), which takes a similar form as (1). The procedure for choosing an ordering then follows as described earlier for toxicity on the basis of adaptive Bayesian model selection. The order k* with the largest posterior probability is chosen for the next cohort, and the estimate θ̂_jk* is used to estimate the efficacy probabilities for each combinations under ordering k* so that π̂_E(d_i) = G_k*(d_i, θ̂_jk*); i = 1, …. I. The efficacy probability estimates, π̂_E(d_i), are used to make decisions regarding combination allocation as described in Section 3.

3. Dose-finding algorithm

Overall, we are going to allocate each entered patient to the dose combination estimated to be the most efficacious, among those with acceptable toxicity. After obtaining the DLT probability estimates, π̂_T (d_i), for each combination, we are going to first restrict our attention to those combinations with estimated probabilities less than a maximum acceptable toxicity rate, ϕ_T.

In general, after j entered patients, we define the set of ‘acceptable’ combinations as

$${𝒜}_j=\{d_i:{\mathrm{\pi ̂}}_T(d_i)\le {\varphi }_T;i=1,\dots ,I\}.$$

We then allocate the next entered patient to a combination in 𝒜_j on he basis of estimated efficacy probabilities, π̂_E(d_i). By incorporating an acceptable set, 𝒜_j, we exclude overly toxic dose combinations. The allocation algorithm depends upon the amount of data that have been observed so far in the trial. If a limited amount of data exist, we will rely on an adaptive randomization phase to allocate future patients to acceptable combinations. In the latter portion of the trial, when a sufficient amount of data have been observed, we will utilize a maximization phase in which we allocate according to the most efficacious treatment among the set of acceptable dose combinations.

3.1. Adaptive randomization phase

Early in the trial, there may not be enough data to rely entirely on maximization of estimated efficacy probabilities within 𝒜_j to accurately assign patients to the most efficacious combination with acceptable toxicity. There may be doses in 𝒜_j that have never been tried, and information on these can only ever be obtained through experimentation. Added randomization allows for information to be obtained on competing dose combinations and prevents the method from ‘locking in’ on a combination that has been tried early in the trial. Therefore, we do not rely entirely on the maximization of estimated efficacy probabilities for guidance as to the most appropriate treatment but rather implement adaptive randomization to obtain information more broadly. On the basis of the estimated efficacy probabilities, π̂_E(d_i), for combinations in 𝒜_j, calculate a randomization probability R_i,

$$R_i=\frac{{\mathrm{\pi ̂}}_E(d_i)}{\sum _{d_i\in {𝒜}_j}{\mathrm{\pi ̂}}_E(d_i)}$$

and randomize the next patient or cohort of patients to combination d_i with probability R_i. We are going to rely on this randomization algorithm for a subset of n_R patients in order to allow information to accumulate on untried combinations, before switching to a phase in which we simply allocate according to the maximum estimated efficacy probability among the acceptable doses. The number of patients on which to implement the adaptive randomization (AR) phase can vary from trial to trial. Some may involve randomization for the entirety of the study, whereas others do not randomize any patients and treat according to which dose combination the data indicate is the most efficacious. We found that performance, in terms of choosing desirable combinations, is optimized when some mixture of randomization and maximization is utilized. In the simulation results in the subsequent discussions, we explore performance of our method under various values of n_R. The subsequent simulated results will demonstrate that the size of the adaptive randomization phase can be expanded or contracted according to the desire of the clinician/statistician team and operating characteristics, with regard to dose recommendation, will be relatively unaffected.

3.2. Maximization phase

Upon completion of the AR phase, the trial design switches to a maximization phase in which maximized efficacy probability estimates guide allocation. Among the doses contained in 𝒜_j, we allocate the (j + 1)th patient cohort to the combination x_j+1 according to the estimated efficacy probabilities, π̂_E(d_i), such that

$$x_{j+1}=\underset{d_i\in {𝒜}_j}{\text{arg max}{\widehat{\pi }}_E(d_i)}.$$

Continuing in this way, the ODC is the recommended combination d_i = x_N+1 for the hypothetical (N + 1)th patient after the inclusion of the maximum sample size of N patients or some stopping rule takes effect.

3.3. Starting the trial

In order to get the trial underway, we will choose the toxicity and efficacy ordering with the largest prior probability, τ(m) and ξ(k), respectively, among the orderings being considered. If several, or all, of the orderings have the same maximum prior probability, then we will choose at random from these orderings. Given the starting orderings, m* and k*, for toxicity and efficacy, respectively, the starting dose, x₁ ∈ {d₁…,d_I}, is then chosen. Specifically, on the basis of the toxicity skeleton, p_im*, for ordering m*, we define the acceptable set, a priori, to be

$${𝒜}_j=\{d_i:p_{i{m}^{*}}\le {\varphi }_T;i=1,\dots ,I\}.$$

On the basis of the efficacy skeleton, q_ik*, corresponding to ordering k* for doses in 𝒜_j, we calculate the randomization probability R_i,

$$R_i=\frac{q_{i{k}^{*}}}{\sum _{d_i\in {𝒜}_j}{q}_{i{k}^{*}}},$$

and randomize the first patient or cohort of patients to combination x₁ = d_i with probability R_i.

3.4. Stopping the trial

Safety

Investigators will want some measure by which to stop the trial in the presence of undesirable toxicity. At any point in the trial, we can calculate an exact binomial confidence interval for toxicity $({\pi }_T^{-}(d_1),{\pi }_T^{+}(d_1))$ at the lowest combination, d₁. The value of ${\pi }_T^{-}(d_1)$ provides a lower bound for the probability of toxicity at d₁, above which we are 95% confident that the true toxicity probability for d₁ falls. We want to compare this lower bound to our maximum acceptable toxicity rate, ϕ_T. If our lower bound exceeds this threshold, we can be confident that the new treatment has too high of a DLT rate to warrant continuing the trial. Therefore, if ${\pi }_T^{-}(d_1)>{\varphi }_T$, stop the trial for safety, and no treatment is identified as the ODC.

Futility

If the new treatment is no better than the current standard of care, we would also like for the trial to be terminated. After j inclusions, we calculate an exact binomial confidence interval for efficacy $({\pi }_E^{-}(x_j),{\pi }_E^{+}(x_j))$ at the current combination, x_j. The value of ${\pi }_E^{+}(x_j)$ provides an upper bound for the probability of efficacy at the current treatment, below which we are 95% confident that the true efficacy probability for that combination falls. We want to compare this upper bound to some futility threshold, ϕ_E, that represents the efficacy response rate for some current standard of care. If our upper bound fails to reach this threshold, we can be confident that the new treatment does not have a sufficient response rate to warrant continuing the trial. Therefore, if ${\pi }_E^{+}(x_j)<{\varphi }_E$, stop the trial for futility, and no treatment is identified as the ODC. This stopping rule will only be assessed in the maximization phase, not the adaptive randomization phase, so that here j ≥ n_R. The reason for this is that the upper bound will be calculated on the current treatment, which is based on the maximum estimated efficacy probability. We can be confident that if the maximum of the estimated probabilities did not reach the futility threshold, then none of the other acceptable toxicity combinations would reach it, because they are presumed to have lower efficacy than the selected treatment. In the adaptive randomization phase, when we randomize, there may exist a more efficacious treatment in the set 𝒜_j that was not selected purely because of randomization. Consequently, another treatment may have reached the futility threshold had it been selected, so we would not want to stop the trial in this case.

4. Simulated results

4.1. Design specifications

We examined the operating characteristics of the proposed design via simulation studies. Under each of the true probability scenarios provided in Table II, 1000 trials were simulated. The proposed design embodies characteristics of the CRM so we can utilize these features in specifying design parameters. It has been shown [23] that CRM designs are robust and efficient with the implementation of ‘reasonable’ skeletons. Simply defined, a reasonable skeleton is one in which there is adequate spacing between adjacent values. The toxicity and efficacy probabilities were modeled via the power models described in Section 2. The models correspond to multiple skeletons that represent the varying possible orderings of dose–toxicity (dose–efficacy) curves with the skeleton values for both models generated according to the algorithm of Lee and Cheung [25] using the getprior function in R package dfcrm [26]. For each ordering, we implemented a normal prior with mean 0 and variance 1.34 on the parameters so that g(β) = h(θ) = 𝒩(0, 1.34) [24]. We assumed, a priori, that each of the six dose–toxicity/dose–efficacy orderings were equally likely and set τ(m) = ξ(k) = 1/6. The maximum sample size for each simulated trial was set to N = 40, and we assessed the impact of various sizes, n_R, for the adaptive randomization phase, the values of which can be found in the table of simulation results. Another design parameter that must be addressed is the association between toxicity and efficacy responses. The models and inference presented in Section 2 ignore the correlation between toxicity and efficacy, and thus model their respective probabilities independently without regard to an association parameter ψ. In the simulated studies, we initially assumed that ψ = 0 so that toxicity and efficacy are simulated independently with probability (π_T (d_i), π_E(d_i)) at each dose level d_i. Bivariate binary outcomes were generated using function ranBin2 in R package binarySimCLF [26]. We then evaluated the sensitivity of using two independent models with nonzero values for the association ψ. We fit the independent models using correlated binary data, generated according to various association (ψ) values. We ran simulations using outcomes generated with four fixed values of ψ used in Thall and Cook [6]; ψ = {−2.049,−0.814, 0.814, 2.049}. We present results for two of these values, ψ = {−2.0049, 0.814}, with results for remaining values omitted for the sake of brevity. Overall, the following results will demonstrate our method’s robustness to the misspecification of the association parameter.

Table II.

True (toxicity, efficacy) probabilities for scenarios 1–6 for nine treatment combinations.

Scenario	Doses of A	True (toxicity, efficacy) rates
		Doses of B
		1	2	3
1	3	(0.08, 0.15)	(0.10, 0.20)	(0.18, 0.40)
	2	(0.04, 0.10)	(0.06, 0.16)	(0.08, 0.20)
	1	(0.02, 0.05)	(0.04, 0.10)	(0.06, 0.15)
2	3	(0.16, 0.20)	(0.25, 0.35)	(0.35, 0.50)
	2	(0.10, 0.10)	(0.14, 0.25)	(0.20, 0.40)
	1	(0.06, 0.05)	(0.08, 0.10)	(0.12, 0.20)
3	3	(0.24, 0.40)	(0.33, 0.50)	(0.40, 0.60)
	2	(0.16, 0.20)	(0.22, 0.40)	(0.35, 0.50)
	1	(0.08, 0.10)	(0.14, 0.25)	(0.20, 0.35)
4	3	(0.33, 0.50)	(0.40, 0.60)	(0.55, 0.70)
	2	(0.18, 0.35)	(0.25, 0.45)	(0.42, 0.55)
	1	(0.12, 0.20)	(0.20, 0.40)	(0.35, 0.50)
5	3	(0.45, 0.55)	(0.55, 0.65)	(0.75, 0.75)
	2	(0.20, 0.36)	(0.35, 0.49)	(0.40, 0.62)
	1	(0.15, 0.20)	(0.20, 0.35)	(0.25, 0.50)
6	3	(0.65, 0.60)	(0.80, 0.65)	(0.85, 0.70)
	2	(0.55, 0.55)	(0.70, 0.60)	(0.75, 0.65)
	1	(0.50, 0.50)	(0.55, 0.55)	(0.65, 0.60)

Combinations with acceptable toxicity (i.e., ≤ ϕ_T = 30%) and high efficacy (i.e., ≥ ϕ_E = 30%) are defined as ‘binations’ and are indicated in boldface type.

Software in the form of R code is available on request from the corresponding author. For each scenario in Table II, ‘target’ combinations are defined as any treatment with a true DLT rate less than 30% that has true response rate larger than 30%. Overall, the simulations study the operating characteristics of six sets of design specifications, which we describe subsequently.

1. Skeleton values for the DLT probabilities are generated using getprior(0.045, 0.30, 5, 9) and ϕ_T = 0.30. Skeleton values for efficacy probabilities are generated using getprior(0.045, 0.50, 5, 9). The location of these values was then adjusted to correspond to each of the possible orderings considered in each subset, creating M = 6 different skeletons for toxicity and K = 6 different skeletons for efficacy. The data were generated as independent binary responses (i.e., ψ = 0), and the AR phase size was n_R = 20.

2. Skeleton values for the DLT and efficacy probabilities are the same as A and ϕ_T = 0.30. The data were generated as correlated binary responses with ψ = −2.049, and the AR phase size was n_R = 20.

3. Skeleton values for the DLT and efficacy probabilities are the same as A and ϕ_T = 0.30. The data were generated as correlated binary responses with ψ = 0.814, and the AR phase size was n_R = 20.

4. Skeleton values for the DLT probabilities are generated using getprior(0.06, 0.30, 4, 9) and ϕ_T = 0.30. Skeleton values for efficacy probabilities are generated using getprior(0.06, 0.50, 4, 9). The data were again generated as independent binary responses (ψ = 0), and the AR phase size was n_R = 20.

5. Skeleton values for the DLT and efficacy probabilities are the same as A and ϕ_T = 0.30. The data were again generated as independent binary responses (ψ = 0), and the AR phase size was n_R = 10.

6. Skeleton values for the DLT and efficacy probabilities are the same as A and ϕ_T = 0.30. The data were again generated as independent binary responses (ψ = 0), and the AR phase size was n_R = 30.

4.2. Operating characteristics

Tables III and IV provide summary statistics for the performance of the proposed design. The full distribution of selected combinations for the first set of design specifications can be found in the Supporting information. The distribution for the other sets of specifications was similar. Table III reports the proportion of trials in which three categories ((i) safe but ineffective, (ii) acceptable toxicity/high efficacy (i.e., target), and (iii) overly toxic combinations were selected as the ODC after the conclusion of the trial. Table III also gives the mean sample size after 1000 trial runs, and the proportion of patients enrolled on target combinations. Table IV reports the percent of trials stopped early for both safety and futility on the basis of the stopping rules described earlier, the overall observed DLT rate, and the overall observed response rate. The futility threshold was set at ϕ_E = 0.20. We also simulated trials with larger ϕ_E values, and as expected, the design stopped for futility more often than for ϕ_E = 0.20. We wanted to confirm that the method would indeed stop quicker and more often, although we do not report these results here. All simulations were carried out using R. The scenarios reflect a range of situations, with target combinations beginning at the highest level of the drug combination matrix in scenario 1 and moving down and left in the dose space as we go to scenario 5. There are no acceptable combinations in scenario 6, and all combinations are too toxic. We want to observe how often the design stops the trial in this situation and how frequently it recommends one of these overly toxic combinations.

Table III.

Summary statistics for six specifications of the proposed design.

	Scenario
Design specifications	1	2	3	4	5	6
	Probability of recommending safe/ineffective combinations as ODC
$p_i^{*},q_i^{*}$, ψ = 0, nR = 20	0.266	0.333	0.125	0.013	0.041	n/a
$p_i^{*},q_i^{*}$, ψ = −2.049; nR = 20	0.281	0.353	0.132	0.013	0.035	n/a
$p_i^{*},q_i^{*}$, ψ = 0.814; nR = 20	0.248	0.353	0.133	0.013	0.032	n/a
$p_i^{**},q_i^{**}$, ψ = 0, nR = 20	0.319	0.395	0.188	0.033	0.066	n/a
$p_i^{*},q_i^{*}$, ψ = 0, nR = 10	0.248	0.317	0.132	0.014	0.035	n/a
$p_i^{*},q_i^{*}$, ψ = 0, nR = 30	0.307	0.399	0.157	0.021	0.046	n/a
	Probability of recommending target combinations as ODC
$p_i^{*},q_i^{*}$, ψ = 0, nR = 20	0.685	0.534	0.704	0.577	0.796	n/a
$p_i^{*},q_i^{*}$, ψ = −2.049; nR = 20	0.679	0.518	0.680	0.581	0.776	n/a
$p_i^{*},q_i^{*}$, ψ = 0.814; nR = 20	0.709	0.545	0.669	0.579	0.764	n/a
$p_i^{**},q_i^{**}$, ψ = 0, nR = 20	0.608	0.449	0.649	0.625	0.766	n/a
$p_i^{*},q_i^{*}$, ψ = 0, nR = 10	0.700	0.533	0.666	0.603	0.745	n/a
$p_i^{*},q_i^{*}$, ψ = 0, nR = 30	0.663	0.484	0.687	0.578	0.759	n/a
	Probability of recommending overly toxic combinations as ODC
$p_i^{*},q_i^{*}$, ψ = 0, nR = 20	n/a	0.078	0.146	0.397	0.146	0.279
$p_i^{*},q_i^{*}$, ψ = −2.049; nR = 20	n/a	0.076	0.157	0.383	0.157	0.286
$p_i^{*},q_i^{*}$, ψ = 0.814; nR = 20	n/a	0.065	0.173	0.397	0.179	0.267
$p_i^{**},q_i^{**}$, ψ = 0, nR = 20	n/a	0.061	0.117	0.320	0.111	0.276
$p_i^{*},q_i^{*}$, ψ = 0, nR = 10	n/a	0.080	0.175	0.365	0.184	0.312
$p_i^{*},q_i^{*}$, ψ = 0, nR = 30	n/a	0.094	0.146	0.391	0.172	0.297
	Mean # of patients enrolled
$p_i^{*},q_i^{*}$, ψ = 0, nR = 20	39.55	39.50	39.74	39.85	39.83	26.96
$p_i^{*},q_i^{*}$, ψ = −2.049; nR = 20	39.63	39.48	39.62	39.65	39.53	26.95
$p_i^{*},q_i^{*}$, ψ = 0.814; nR = 20	39.67	39.68	39.60	39.88	39.64	26.89
$p_i^{**},q_i^{**}$, ψ = 0, nR = 20	39.39	38.40	39.40	39.70	39.24	27.35
$p_i^{*},q_i^{*}$, ψ = 0, nR = 10	39.53	39.13	39.64	39.71	39.71	27.71
$p_i^{*},q_i^{*}$, ψ = 0, nR = 30	39.84	39.84	39.95	39.94	39.81	27.54
	Proportion of patients allocated to true ODC(s)
$p_i^{*},q_i^{*}$, ψ = 0, nR = 20	0.389	0.353	0.537	0.521	0.643	n/a
$p_i^{*},q_i^{*}$, ψ = −2.049; nR = 20	0.375	0.347	0.529	0.506	0.642	n/a
$p_i^{*},q_i^{*}$, ψ = 0.814; nR = 20	0.390	0.349	0.526	0.517	0.641	n/a
$p_i^{**},q_i^{**}$, ψ = 0, nR = 20	0.395	0.341	0.512	0.534	0.631	n/a
$p_i^{*},q_i^{*}$, ψ = 0, nR = 10	0.476	0.409	0.538	0.517	0.652	n/a
$p_i^{*},q_i^{*}$, ψ = 0, nR = 30	0.271	0.287	0.485	0.523	0.606	n/a

Combinations with acceptable toxicity (i.e., ≤ ϕ_T = 30%) and high efficacy (i.e., ≥ ϕ_E = 30%) are defined as ‘target combinations’.

$p_i^{*}=\mathtt{\text{getprior}}(0.045,0.30,5,9);q_i^{*}=\mathtt{\text{getprior}}(0.045,0.50,5,9),p_i^{**}=\mathtt{\text{getprior}}(0.06,0.30,4,9);q_i^{**}=\mathtt{\text{getprior}}(0.06,0.50,4,9).$.

Table IV.

Summary statistics for six specifications of the proposed design.

	Scenario
Design specifications	1	2	3	4	5	6
	Proportion stopped for safety
$p_i^{*},q_i^{*}$, ψ = 0, nR = 20	0.000	0.000	0.000	0.000	0.000	0.721
$p_i^{*},q_i^{*}$, ψ = −2.049, nR = 20	0.000	0.000	0.000	0.000	0.000	0.714
$p_i^{*},q_i^{*}$, ψ = 0.814, nR = 20	0.000	0.000	0.000	0.000	0.000	0.733
$p_i^{**},q_i^{**}$, ψ = 0, nR = 20	0.000	0.000	0.000	0.000	0.000	0.722
$p_i^{*},q_i^{*}$, ψ = 0, nR = 10	0.000	0.000	0.000	0.000	0.001	0.684
$p_i^{*},q_i^{*}$, ψ = 0, nR = 30	0.000	0.000	0.000	0.000	0.001	0.701
	Proportion stopped for futility
$p_i^{*},q_i^{*}$, ψ = 0, nR = 20	0.049	0.055	0.025	0.013	0.017	0.000
$p_i^{*},q_i^{*}$, ψ = −2.049, nR = 20	0.040	0.053	0.031	0.023	0.032	0.000
$p_i^{*},q_i^{*}$, ψ = 0.814, nR = 20	0.043	0.037	0.030	0.011	0.025	0.000
$p_i^{**},q_i^{**}$, ψ = 0, nR = 20	0.073	0.095	0.046	0.022	0.057	0.000
$p_i^{*},q_i^{*}$, ψ = 0, nR = 10	0.052	0.070	0.027	0.018	0.035	0.000
$p_i^{*},q_i^{*}$, ψ = 0, nR = 30	0.030	0.023	0.010	0.010	0.022	0.000
	Observed DLT rate
$p_i^{*},q_i^{*}$, ψ = 0, nR = 20	0.116	0.177	0.212	0.245	0.248	0.512
$p_i^{*},q_i^{*}$, ψ = −2.049, nR = 20	0.113	0.175	0.211	0.249	0.247	0.511
$p_i^{*},q_i^{*}$, ψ = 0.814, nR = 20	0.115	0.174	0.211	0.244	0.247	0.516
$p_i^{**},q_i^{**}$, ψ = 0, nR = 20	0.118	0.175	0.214	0.241	0.242	0.508
$p_i^{*},q_i^{*}$, ψ = 0, nR = 10	0.127	0.189	0.225	0.257	0.255	0.507
$p_i^{*},q_i^{*}$, ψ = 0, nR = 30	0.104	0.163	0.201	0.235	0.237	0.511
	Observed response rate
$p_i^{*},q_i^{*}$, ψ = 0, nR = 20	0.256	0.272	0.340	0.411	0.399	0.508
$p_i^{*},q_i^{*}$, ψ = −2.049, nR = 20	0.256	0.271	0.342	0.411	0.402	0.503
$p_i^{*},q_i^{*}$, ψ = 0.814, nR = 20	0.259	0.267	0.343	0.419	0.400	0.509
$p_i^{**},q_i^{**}$, ψ = 0, nR = 20	0.264	0.271	0.340	0.406	0.389	0.507
$p_i^{*},q_i^{*}$, ψ = 0, nR = 10	0.283	0.290	0.361	0.427	0.414	0.507
$p_i^{*},q_i^{*}$, ψ = 0, nR = 30	0.230	0.251	0.323	0.399	0.381	0.510

Combinations with acceptable toxicity (i.e., ≤ ϕ_T = 30%) and high efficacy (i.e., ≥ ϕ_E = 30%) are defined as ‘target combinations’.

$p_i^{*}=\mathtt{\text{getprior}}(0.045,0.30,5,9);q_i^{*}=\mathtt{\text{getprior}}(0.045,0.50,5,9),p_i^{**}=\mathtt{\text{getprior}}(0.06,0.30,4,9);q_i^{**}=\mathtt{\text{getprior}}(0.06,0.50,4,9).$

It is clear from examining results from Tables III and IV that the proposed design is performing well in terms of recommending target combinations, as well as treating patients at these combinations. In scenario 1, the proposed design selects, as the ODC, the target combination in approximately 70% of simulated trials, while assigning between 38% and 39% of patients to the target combination in situations in which n_R = 20. In scenario 2, recommendation of target combinations as the ODC occurs in approximately half of simulated trials. About 35% of the patients enrolled are treated at one of the two target combinations in scenario 2. In scenario 3, there are three target combinations. The proposed design identifies one of these three treatments as the ODC in approximately 70% of simulated trials for the first set of design specifications, while allocating more than 50% of patients to target dose combinations. In scenario 4, target combinations are recommended in 58–60% of simulated trials, and about half of the enrolled patients are allocated to target treatments, in situations in which n_R = 20, which again indicates strong performance after only 40 patients. When looking at the percentage of patients treated on overly toxic combinations, one may notice that this percentage is higher in scenario 4 than in any other scenario, with the exception of scenario 6 in which all combinations are too toxic. For the first set of specifications, overly toxic combinations are selected as ODC in 39.7% of simulated trials. In 36.7% of trials (see Supporting information for full distribution), combinations with true DLT probabilities of 33% and 35% are selected, meaning that in only 3% does the method recommend a combination with DLT rate larger than 35%. Plus, with that extra toxicity, we were able to obtain a bit more efficacy for the patients enrolled on those combinations. Similar conclusions can be made in regard to scenario 5, although the selection of target combinations is higher than in scenario 4. In fact, in scenario 5, we again a see strong performance for the method in recommending and allocating patients to target combinations. In scenario 6, there are no acceptable combinations, and the design demonstrates its ability to stop for safety by doing so in approximately 72% of trials. Overall, the simulation results indicate that the proposed design is a practical design for dose finding in a matrix of combination therapies on the basis of both toxicity and efficacy.

The recommendation percentages remain fairly consistent for n_R = 10 and n_R = 30, while the allocation percentages for true ODC’s are higher for n_R = 10 and lower for n_R = 30 in scenarios 1 and 2. This makes sense when thinking about the true dose–toxicity/efficacy curve. In scenario 1, there is only one combination considered a target combination (d₉). Therefore, in the AR phase, there is a higher chance of a patient being randomized to a sub-optimal combination in scenario 1 than in other scenarios in which there is more than one target combination. For instance, in scenario 3, in the AR phase, a patient has a very good chance of being randomized to one of the three target combinations. On the other hand, Table IV illustrates that in situations in which n_R = 10, the methods tend to stop for futility slightly more often than larger values for n_R. This is due to the amount of information available at the start of the maximization phase, at which point the futility stopping rule is triggered. With information on only 10 patients to make a stopping decision, it is possible that the trial could incorrectly stop for futility. Overall, it is difficult to recommend a single value for n_R because optimal performance will depend upon the true, unknown dose–toxicity/efficacy curve, as well as the maximum sample size N. In some cases, clinician/statistician teams may choose to set n_R according to their personal preference. However, simulation results demonstrate that our method, across a broad range of scenarios, is fairly robust to the choice of n_R. As a general rule of thumb, adaptively randomizing for half of the maximum sample size seems to work well in a wide variety of scenarios, including those discussed in the following section.

4.3. Comparison to alternative method

In this section, we compared the performance of the proposed approach with that of Yuan and Yin [19] for finding target dose combinations in a melanoma clinical trial investigating three doses of one agent (drug A) and two doses of another agent (drug B), for nine true toxicity/efficacy scenarios contained in their paper. These scenarios are contained in Table V and have the property that both toxicity and efficacy increase with dose levels of each agent, which, as Yuan and Yin pointed out, ‘represent the most common cases’ [19]. All scenarios, with the exception of scenario 5, have a single target dose combination that is placed in various locations throughout the drug combination space. Scenario 5 contains two target doses that represent a toxicity and efficacy equivalence contour. In each set of 1000 simulated trials, the maximum sample size was N = 80 patients, with n₁ = 20 for phase I and n₂ = 60 for phase II of the Yuan and Yin design. For the proposed method, the size of the AR phase was set equal to half the maximum sample size; that is, n_R = 40. The prior specifications for the Yuan and Yin design can be found in their paper. For our proposed method, we again used skeletons chosen via the getprior function in R package dfcrm. For toxicity, we implemented getprior(0.04, 0.25, 4, 6) and for efficacy getprior(0.09, 0.50, 4, 6). We again assumed, a priori, that each of the dose–toxicity/dose–efficacy orderings was equally likely. The maximum acceptable toxicity was ϕ_T = 0.33 and the minimum efficacy threshold was ϕ_E = 0.20. For each scenario, the target dose combination is defined as the most efficacious combination that is contained in the set of acceptable combinations. User-friendly R-code for implementing the proposed design can be downloaded at http://faculty.virginia.edu/model-based_dose-finding/.

Table V.

True (toxicity, efficacy) probabilities for scenarios 1–9 for six treatment combinations.

Scenario	Doses of A	True (toxicity, efficacy) rates
		Doses of B
		1	2	3
1	2	(0.10, 0.20)	(0.15, 0.40)	(0.45, 0.60)
	1	(0.05, 0.10)	(0.15, 0.30)	(0.20, 0.50)
2	2	(0.10, 0.20)	(0.20, 0.40)	(0.50, 0.55)
	1	(0.05, 0.10)	(0.15, 0.30)	(0.40, 0.50)
3	2	(0.10, 0.20)	(0.15, 0.30)	(0.20, 0.50)
	1	(0.05, 0.10)	(0.10, 0.20)	(0.15, 0.40)
4	2	(0.10, 0.30)	(0.40, 0.50)	(0.60, 0.60)
	1	(0.05, 0.20)	(0.20, 0.40)	(0.50, 0.55)
5	2	(0.10, 0.20)	(0.20, 0.40)	(0.50, 0.50)
	1	(0.05, 0.10)	(0.15, 0.30)	(0.20, 0.40)
6	2	(0.40, 0.44)	(0.72, 0.58)	(0.90, 0.71)
	1	(0.23, 0.36)	(0.40, 0.49)	(0.59, 0.62)
7	2	(0.24, 0.40)	(0.56, 0.60)	(0.83, 0.78)
	1	(0.13, 0.32)	(0.25, 0.50)	(0.42, 0.68)
8	2	(0.15, 0.30)	(0.25, 0.41)	(0.40, 0.54)
	1	(0.11, 0.15)	(0.15, 0.22)	(0.20, 0.31)
9	2	(0.15, 0.17)	(0.19, 0.33)	(0.23, 0.55)
	1	(0.12, 0.10)	(0.15, 0.22)	(0.19, 0.39)

Combinations with acceptable toxicity (i.e., ≤ ϕ_T = 30%) and high efficacy (i.e., ≥ ϕ_E = 20%) are defined as ‘target combinations’ and are indicated in boldface type.

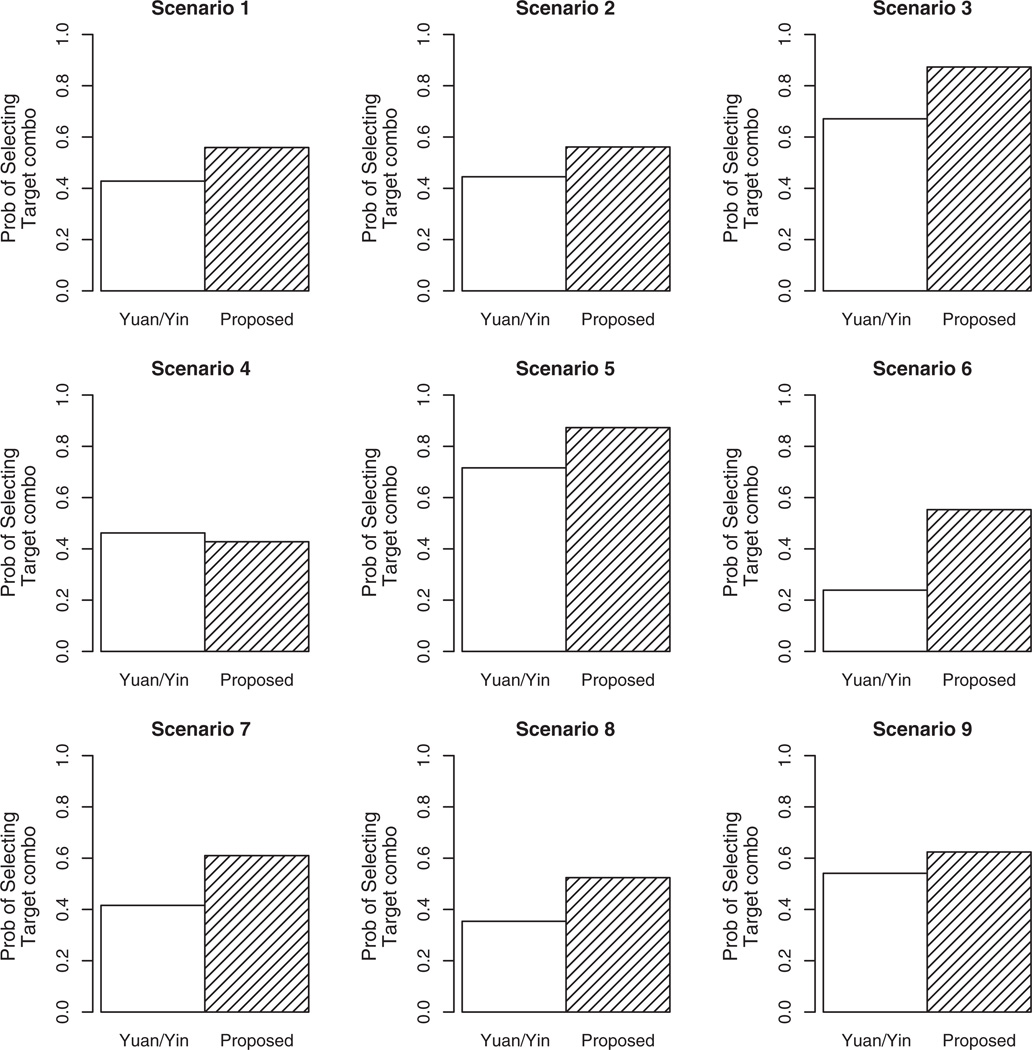
The results of the comparison are summarized in Figure 1, and the results of the full distribution of combination selection can be found in the Supporting information. Each bar in the Figure 1 represents the proportion of simulated trials that each method selected a target combination as the ODC. Overall, the proposed method is performing quite well in comparison to that of Yuan and Yin [19]. In scenario 1, the proposed method improves the recommendation percentage of Yuan and Yin by approximately 13% (55.9 vs. 42.8%). A similar improvement can be observed in scenario 2 (56.1 vs. 44.5%). In scenario 3, the target dose is located at the highest combination (e.g., d₆) and is selected by the proposed design in 87.3% of simulated trials, which is approximately 20% higher than the selection percentage of Yuan and Yin (67.1%). Scenario 4 provides a case in which the Yuan and Yin method slightly outperforms the proposed method by a few percentage points (46.2% vs. 42.8%). As was mentioned earlier, in scenario 5, there are two target dose combinations, each with true (toxicity, efficacy) rates of (0.20, 0.40), representing an equivalence contour. We want to assess how often each method selects either of these two combinations. Yuan and Yin selects combination d3 at the conclusion of 29.8% of simulated trials, and d5 at the end of 41.8% of trials, for a total of 71.6%. Our design selects d₃ in 41.9% of trials, and d5 in 45.4% of trials, for a total of 87.3%. In scenario 6, there is only one acceptable combination (d₁), with regard to safety. The Yuan and Yin method selected d₁ as the ODC in 23.9% of trials and stopped for safety in 71.9% of trials. This is a high stopping percentage for a true scenario that does in fact contain a target dose combination. By contrast, the proposed design stops for safety in only 0.6% of simulated trials, while selecting d₁ as the ODC 55.3% of the time. The final three scenarios demonstrate similar performance in terms of improvement of our method over that of Yuan and Yin, with the proposed approach selecting target combinations as the ODC in approximately 20%, 17%, and 8% more trials than Yuan and Yin in scenarios 7–9, respectively. Overall, the strong showing of our method against published work in the area in extensive simulation studies makes us feel confident in recommending it as a viable alternative in phase I/II combination studies.

Figure 1.

Operating characteristics of the proposed design and Yuan and Yin [19]. Each bar represents the proportion of times that each method recommended target combination(s) as the ODC at the conclusion of a simulated phase I/II trial with a maximum sample size of N = 80 patients.

5. Conclusions and directions for future research

In this article, we have outlined a new phase I/II design for multi-drug combinations that accounts for both toxicity and efficacy. The simulation results demonstrated the method’s ability to effectively recommend target combinations, defined by acceptable toxicity and high efficacy, in a high percentage of trials with manageable sample sizes. The assumption made with regard to efficacy is that it increases with dose as one agent is being held fixed, which we feel is appropriate for chemotherapeutic agents. There certainly exist situations where this assumption would need to be relaxed, but we have not addressed them here. We feel that monotonicity across rows and up columns of the drug combination matrix in terms of efficacy represents the most common cases encountered in oncology dose-finding trials. The proposed design is most appropriate when both toxicity and efficacy outcomes can be observed in a reasonably similar time frame. In some practical situations, this may not be possible because of the fact that efficacy may occur much later than toxicity. This would create a situation where we would be estimating DLT probabilities on the basis of more patient observations than efficacy probabilities. As we are ignoring their association in modeling these responses, we can fit the likelihood for each response on the basis of different amounts of data, and simply utilize the efficacy data that we have available, even though it may be less than that of the toxicity data. This idea requires further study, and we are exploring modifications to the proposed methodology to handle such practical issues. Along these same lines, incorporating time-to-event outcomes may be an effective extension of the method as a means of handling delayed response.