Inference from presence-only data; the ongoing controversy

Abstract

Presence-only data abounds in ecology, often accompanied by a background sample. Although many interesting aspects of the species’ distribution can be learned from such data, one cannot learn the overall species occurrence probability, or prevalence, without making unjustified simplifying assumptions. In this forum article we question the approach of Royle et al. (2012) that claims to be able to do this.

Modelling of species distributions is most convincing when presence–absence data is sampled in a systematic way. For example, researchers survey a collection of equal sized quadrats and record the presence or absence of a particular species of plant. They also record other features of the quadrat, such as annual precipitation, soil salinity, altitude, and so on. These features are then used in a statistical model such as logistic regression to build a model for the probability of species occurrence. Using this fitted model, species occurrence probability is predicted and can be projected onto a map of the region, if the features are available at each geographical unit. See Guisan and Zimmerman (2000) for a review of such methods.

Often the only species data available are the geographical coordinates of sites where the species was observed – so-called presence-only data – as recorded by observers. Also available is a large collection of background data, consisting of geographical coordinates and associated geographical features such as those available from GIS data. In many cases this background data is available at every geographical unit of area in a map of the region, and hence also at the presence sites. Apart from those locations where the species were observed, no species information is available for the background data.

For animal species, sampling time as well as area is relevant, since the species may wander around. Other complicating factors exist, such as the species being present but are not observed, and sampling bias (e.g. proximity to roads). For the purposes of this article, we keep the discussion simple and avoid these other sampling issues.

The question is what can one learn from such presence–background data? There are many approaches to this problem, which has become an active area of research. Our current favorite approach is to model the species occurrence rate (as in number of times the focal species is seen per unit area, per unit time). To this end the inhomogeneous Poisson point process (IPP) (Wharton and Shepard 2010, Aarts et al. 2012) is attractive. Other popular approaches are: 1) MAXENT (Phillips and Dudik 2008) which models the feature density for the presence data. 2) Naive logistic regression, which treats the background data as absence data, and fits logistic regression models. 3) Manly's exponential model (Manly et al. 2010), a precursor to the IPP model in this context. Fithian and Hastie (unpubl.) survey these methods, and shows that they are all equivalent to the IPP model, in particular for an exhaustive sample of background data. Similar conclusions appear in Aarts et al. (2012) as well as Warton and Shepherd (2010). The conclusion to be drawn from these comparisons is that while absolute occurrence rates are typically elusive, relative rates are more accessible and available from these type of data.

This forum article will step away from these sampling considerations, and address a simpler question. We can think of sampling units as geographical sites x ∈ χ; each x represents a cell or unit of area, and χ represents the domain of interest, or entire collection of such cells. At each site the vector z = z(x) records the values of som geographical attributes or features. Let the binary variable y denote presence (1) or absence (0) sites. We denote the marginal density of z by π(z), and the (conditional) density of z at presence sites by π₁(z), and absence sites by π₀(z). If the overall presence occurrence probability is Ψ(y = 1) and hence absence Ψ(y = 0) = 1 – Ψ(y = 1), then basic probability theory tells us two things:

1. the conditional occurrence probability at a site, given we observe feature z, is given by

   $$\psi (y=1\mid z)=\frac{\psi (y=1){\pi }_1\left(z\right)}{\pi \left(z\right)}$$ (1)
2. The marginal feature density π(z) is a mixture of the two class-conditional densities:

   $$\pi \left(z\right)={\pi }_1\left(z\right)\psi (y=1)+{\pi }_0\left(z\right)(1-\psi (y=1))$$ (2)

Presence–background data consists of a random sample of values of z from π₁(z), as well as a separate sample from π(z) (possibly the entire background distribution), which directly inform us about the densities π₁ and π. However, even if both of these distributions were fully known, we can see from Eq. (1) that this would not be enough information to estimate Ψ(y = 1|z). We are missing the overall occurrence probability Ψ(y = 1), or at least some data that allow us to estimate this.

The reader might think that Eq. (2) offers some hope, but it does not. We know or have data on π(z) and π₁(z) – this leaves a lot of flexibility in choosing somewhat arbitrary values for Ψ(y = 1) and π₀(z) to make Eq. (2) work out – unless, that is, we impose strong parametric restrictions on some of the ingredients. But then we are manufacturing information via these assumptions when none exists in the data. We will see more of this in the next section. Ward et al. (2009) discuss this problem and the lack of identifi-ability of Ψ(y = 1) from such data. They warned of the folly in relying on arbitrary parametric assumptions to squeeze out estimates of Ψ(y = 1). Phillips et al. (2009) raise similar issues. Most recently Phillips and Elith (2013) address the same issue, and reinforce some of the points we make here.

The parametric approach of Royle et al

Royle et al. (2012) discuss methods for estimating species occurrence probabilities from presence-only data – the same problem we outline above. They cite Ward et al. (2009), yet proceed to impose parametric assumptions on Ψ(y = 1|z) to enable estimation of Ψ(y = 1) – exactly what we warned against. Here we will strengthen our argument in the context of their model, and using their notation. We will also simplify the discussion further, as they did, and focus attention on geographic features x rather than environmental features z = z(x); in the appendix we show that this transition is benign.

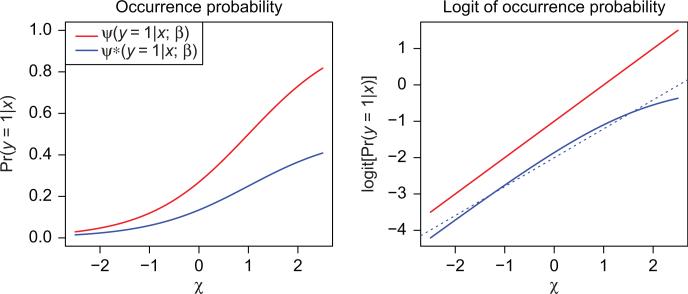
Figure 1 (left panel, red) shows a plot of a very simple model for occurrence probability

$$\psi (y=1\mid x;\beta )$$ (3)

This corresponds to a logistic regression model linear in x,

$$\mathrm{logit}\left[\psi (y=1\mid x;\beta )\right]={\beta }_0+x{\beta }_1$$ (4)

Figure 1.

Left panel: two different models for occurrence probabilities. The blue curve is half the red curve, and hence has exactly half the prevalence (marginal occurrence probability) of the red curve. The implied likelihood (Eq. 9) of the presence-data x_i is identical for these two models. Right plot: the logits of the two models on the left. The broken blue curve is the best linear approximation to the solid blue curve – the approximation that would be imposed by a linear logistic regression model. Since the solid logit curves (red and blue) are indistinguishable with respect to the likelihood (Eq. 9), distinguishing the dotted blue line from the red is no easier than distinguishing it from the solid blue. Determining whether or not this slight curvature is present is the entire basis upon which the Royle et al. (2012) procedure would estimate the prevalence at either 34% (solid red) or 17% (dotted blue).

In this case β₀ = 21 and β₁ = 1. We assume here that the marginal distribution π(x) is uniform on [–2.5, 2.5], which makes the overall prevalence Ψ(y = 1) = ∫Ψ(y = 1|x; β) π(x)dx ≈ 0.33 in this case, and the values of Ψ(y = 1|x; β) range between 0.03 and 0.83. Royle et al. (2012) use a linear logistic model similar to Eq. (4) for modeling occurrence probability.

With such a parametric assumption, one can perform inference on the data. As they point out, using Eq. (1) we can write

$$\psi (y=1){\pi }_1\left(x\right)=\psi (y=1\mid x)\pi \left(x\right)$$ (5)

$$=\psi (y=1,x)$$ (6)

If π(x) is uniform, as it typically is in the geographic domain, and since Σ_x∈cχ Ψ(y = 1, x) = Ψ(y = 1), we can write

$${\pi }_1\left(x_i\right)=\frac{\psi (y_i=1\mid x_i)}{{\Sigma }_{x\in \chi }\psi (y=1\mid x)}$$ (7)

This is a model for the density of the observed data x_i at the presence sites, and it is expressed in terms of the parameters of our logistic regression model if we replace Ψ(y|x) in Eq. (7) with Ψ(y|x; β). On the basis of this Royle et al. (2012) do maximum-likelihood estimation for β see Eq. (9) below. Note that the presence observations x_i appear in the numerator; the background data are used to compute the sums in the denominator.

This sounds like statistical alchemy: why don't we need to know Ψ(y = 1) anymore? Note that β₀ is playing a similar role as Ψ(y = 1) was before (Ψ(y = 1) multiplied all occur-rence probabilities, whereas e^β₀ multiplies the odds). Therefore, it should be surprising that suddenly we can estimate it from the data. The reason β₀ = –1 vs β₀ = +1 are distinguishable from each other in this model is that if we hold β₁ fixed and change β₀, it increases all of the probabilities Ψ(y = 1|x) in Eq. (7), increasing the numerator and the denominator. But because it changes some a little more than others, it subtly changes the density π₁(x_i) – ‘subtly’ being the operative word. The problem is that other things can subtly change π₁ too – such as the linear logistic model (Eq. 4) being subtly misspecified, as we see next.

The blue curve in this left hand plot of Fig. 1 corresponds to a different model for the occurrence probability,

$${\psi }^{\ast }(y=1\mid x;\beta )=\frac{1}{2}\times \psi (y=1\mid x;\beta )$$ (8)

For this model (Eq. 8) the overall prevalence Ψ*(_y = 1) = 1/2 × Ψ(y = 1), i.e. 0.17 or exactly half of the prevalence for model (Eq. 3). Although Ψ*(y = 1|x) does not correspond to a linear logistic model, it is nearly linear on the logit scale (see the solid blue curve in the right plot of Fig. 1), and is still a simple parametric model; but more on that to come.

The critical point of this example is that the joint likelihood of the presence data (i.e. Eq. 4 in Royle et al. (2012))

$$\mathcal{L}\left(\beta \right)=\prod _{i=1}^n\frac{\psi (y_i=1\mid x_i;\beta )}{{\Sigma }_{x\in \chi }\psi (y=1\mid x;\beta )}$$ (9)

$$=\prod _{i=1}^n\frac{{\psi }^{\ast }(y_i=1\mid x_i;\beta )}{{\Sigma }_{x\in \chi }{\psi }^{\ast }(y=1\mid x;\beta )}$$ (10)

is identical for these two models. In other words, the likelihood would have nothing to say about whether model (Eq. 3) or model (Eq. 8) was preferred – two models, both with two parameters, but with one having prevalence half the other. We could change the 1/2 in (Eq. 8) to any 0 = C ≥ 1 and the same statement would be true (with ‘half’ changed to ‘fraction C ’). We note that this lack of identifi-ability with propotional models that we exploit was pointed out by Lele and Keim (2006, p. 3023, top left), who originally proposed the approach used by Royle et al. (2012).

Now the second model is not a linear logistic model, so it would not be up for comparison in the Royle et al. (2012) framework. The right hand panel shows the logit transforms of each of these two models. Indeed, the second model is not a linear logistic model, but it is almost one. The dotted blue curve shows the best linear approximation to this logit in the population. Since the solid red line and solid blue curve are indistinguishable from each other with respect to the likelihood Eq. (9), distinguishing the dotted blue line from the red is no easier than distinguishing it from the solid blue. Determining whether or not this slight curvature is present is the entire basis upon which the Royle et al. (2012) procedure would estimate the prevalence at either 34% (solid red) or 17%. One would need an awfully large amount of data to be able to detect a difference between the two blue lines, even with presence–absence data.

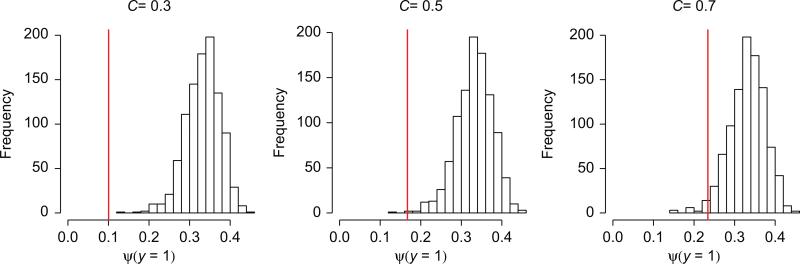
We now present a simulation to reinforce the points we have made. We simulate data from model (Eq. 8) (nearly linear logistic), and fit a linear logistic model using the likelihood (Eq. 9). In detail, we generate a large sample of values of x via the uniform distribution π, generate 0/1 ‘presence/absence’ data using the probabilities (Eq. 8), and then take a random subset of 1000 values of x from those that came up as ‘present’. This sample of 1000 is fed into (Eq. 9), which is then maximized with respect to the two linear logistic parameters. Rather than show the parameter estimates ${\widehat{\beta }}_0$ and ${\widehat{\beta }}_1$ that result, we instead compute the implied estimated prevalence value $\widehat{\psi }(y=1)=\int \psi (y=1\mid x;\widehat{\beta })\pi \left(x\right)dx$. This was repeated B = 1000 times. The middle histogram in Fig. 2 shows the results. The histogram is peaked around 0.33 (the value from Eq. (3), not the true value 0.17). The flanking histograms repeat these simulations using 3/10 and 7/10 rather than the 1/2 in (Eq. 8). In all cases the estimated $\widehat{\psi }(y=1)$ bear no relationship to the true values (red lines).

Figure 2.

Results of three separate simulation runs. The center histogram shows the estimated value $\widehat{\psi }(y=1)$ when a linear logistic regression model is fit to data generated from model (Eq. 8). The histogram summarizes B = 1000 different runs, each consisting of 1000 presence samples. The true value of Ψ(y = 1) is given by the vertical red line. The two flanking histograms change the 1/2 in (Eq. 8) to C = 3/10 (left) and C = 7/10 (right), with again the red line showing the true value of Ψ(y = 1). In all cases, irrespective of the true value of Ψ(y = 1), the histograms indicate that the value being estimated is centered around Ψ(y = 1) ≈ 0.33, the value from Eq. (3).

The take-home message here is that: a) two perfectly good and parsimonious probability models are indistinguishable with respect to the likelihood (Eq. 9) for the presence data, despite the fact that one has half the prevalence of the other; i.e. prevalence is not identifiable in this extended family. b) By insisting on a particular parametric form, e.g. linear logistic, we are on extremely flimsy ground, as the subtle distinction in this example shows. c) When presence-only data arise via models that are nearly linear on the logistic scale, maximum likelihood using Eq. (9) and a linear logistic regression model can be incapable of estimating the correct parameter values, and in particular the correct implied prevalence. This is not trickery with data simulations or abstract ideas; it cuts to the core of how Royle et al.'s model estimates probabilities. They say you can estimate probabilities from presence-only data by using their model, which relies on a linear logistic framework. The problem is that in the real world, functional forms are almost never linear; linearity is just a useful approximation. We have shown here that data distributed just slightly differently to that allowed in their framework will lead to incorrect estimates of prevalence, and therefore incorrect estimates of probability of presence.

Stepping back a bit, we remake our earlier point. It should be clear that a sample of n₁ sites, along with a sample of n₀ unclassified samples (i.e. a mix of presence and absence), tells you nothing about the overall probability of occurrence, absent strong parametric assumptions about the form of the underlying densities. In other words, there is no information on prevalence in the data itself; it all comes from the model assumptions. Using such assumptions as the basis for estimating overall prevalence is not a good idea; as shown here, they are too fragile and arbitrary, and will not be robust in practical settings.

Appendix

Geographic vs environmental features

Usually we parameterize our conditional occurrence model in terms of environmental features z_i = z(x_i) rather than the geographic features x_i themselves. For ease of exposition here, we treat z as discrete rather than continuous.

Then along the lines of Eq. (7) we would have

$${\pi }_1\left(z_i\right)=\frac{\psi (y_i=1\mid z_i)\pi \left(z_i\right)}{{\Sigma }_{z\in Z}\psi (y=1\mid z)\pi \left(z\right)}$$ (11)

Here π(z) is the marginal environmental feature distribution, and is not uniform. However,

$$\pi \left(z\right)=\sum _{x\in \chi ;z\left(x\right)=z}\pi \left(x\right)$$ (12)

and so the denominator in Eq. (11) can be written

$$\sum _{z\in Z}\psi (y=1\mid z)\pi \left(z\right)=\sum _{x\in \chi }\psi (y=1\mid z\left(x\right))\pi \left(x\right)$$

So then we have

$${\pi }_1\left(z_i\right)=\frac{\psi (y_i=1\mid z\left(x_i\right))}{\sum _{x\in \chi }\psi (y=1\mid z\left(x\right))\pi \left(x\right)}\times \pi \left(z_i\right)$$ (14)

So if π(x) is uniform, and we parameterize Ψ(y_i = 1|z(x_i); β), then the log-likelihood contribution from presence site i for β is

$$\log \left[\frac{\psi (y_i=1\mid z\left(x_i\right);\beta )}{\sum _{x\in \chi }\psi (y=1\mid z\left(x\right);\beta )}\right]+C_i$$ (15)

where C_i can be discarded, since it does not depend on β.