Abstract
Statistical modeling of presence-only data has attracted much recent attention in the ecological literature, leading to a proliferation of methods, including the inhomogeneous Poisson process (IPP) model, maximum entropy (Maxent) modeling of species distributions and logistic regression models. Several recent articles have shown the close relationships between these methods. We explain why the IPP intensity function is a more natural object of inference in presence-only studies than occurrence probability (which is only defined with reference to quadrat size), and why presence-only data only allows estimation of relative, and not absolute intensity of species occurrence.
All three of the above techniques amount to parametric density estimation under the same exponential family model (in the case of the IPP, the fitted density is multiplied by the number of presence records to obtain a fitted intensity). We show that IPP and Maxent give the exact same estimate for this density, but logistic regression in general yields a different estimate in finite samples. When the model is misspecified—as it practically always is—logistic regression and the IPP may have substantially different asymptotic limits with large data sets. We propose “infinitely weighted logistic regression,” which is exactly equivalent to the IPP in finite samples. Consequently, many already-implemented methods extending logistic regression can also extend the Maxent and IPP models in directly analogous ways using this technique.
Key words and phrases: Presence-only data, logistic regression, maximum entropy, Poisson process models, species modeling, case-control sampling
1. Introduction
In recent years ecologists have devoted significant attention to the problem of estimating the geographic distribution of a species of interest from records of where it has been found in the past. There are many motivations for solving this problem, including planning wildlife management actions, monitoring endangered or invasive species, and understanding species' response to different habitats. A great variety of experimental designs and statistical methods exist for tackling this problem, and can be found in the literature on resource-selection functions [Manly et al. (2002), Lele and Keim (2006)], case-augmented designs [Lee, Scott and Wild (2006), Dorazio (2012)] and site occupancy modeling [MacKenzie (2006)].
Ecologists have proposed many statistical methods for modeling such data, including the inhomogeneous Poisson process (IPP) model [Warton and Shepherd (2010)], maximum entropy (Maxent) modeling of species distributions [Phillips, Dudík and Schapire (2004), Phillips, Anderson and Schapire (2006), Phillips and Dudík (2008)] and the logistic regression model along with its various generalizations such as GAM, MARS and boosted regression trees [Hastie, Tibshirani and Friedman (2009)]. See Elith et al. (2006) for discussion and comparison of these and other methods in common use.
In recent years several articles have emerged detailing connections between the three modeling methods above. Each method takes as its input a presence-only data set along with a set of background points consisting of a regular grid or random sample of locations in some geographic region of interest. Warton and Shepherd (2010) showed that logistic regression estimates converge to the IPP estimate when the size of the presence-only data set is fixed and the background sample grows infinitely large. Aarts, Fieberg and Matthiopoulos (2012) additionally described a variety of models for presence-only and other data sets whose likelihoods may all be derived from the IPP likelihood. Renner and Warton (2013) further explore the connection between Maxent and the IPP, taking up the important issue of how we might check the IPPs modeling assumptions.
Our primary aim in writing this paper is to provide additional clarity to this topic, recapitulating and deriving the results in a unified framework and extending them in several directions. We view all three major methods as solutions to the same parametric density estimation problem.
1.1. Presence-only data
Modeling of species distributions is simplest and most convincing when the observations of species presence are collected systematically. In a typical design, a surveyor visits a one-square-kilometer patch of land for one hour and records how many specimens she discovers in that interval. The records of unsuccessful surveys are called absence records, a mild misnomer since ecologists recognize that specimens could be present but go undetected. A data set reflecting presence or absence of a species in each sampling unit is called presence–absence data.
Unfortunately, dedicated surveys recording sampling effort are expensive, especially for rare or elusive species. For many species of interest, the only data available are museum or herbarium records of locations where a specimen was found and reported, for instance, by a motorist or hiker. Typically these presence-only records are collected haphazardly and frequently suffer from unknown sampling bias such as that illustrated in Figure 1. The clustering of koala sightings near roads and cities probably has more to do with the behavior of people than of koalas.
Fig. 1.

Sampling bias in presence-only data for koalas. Taken from Margules et al. (1994).
In recent years many such presence-only data sets have become available electronically, and geographic information systems (GIS) enable ecologists to remotely measure a variety of geographic covariates without having to visit the actual locations of the observations. As a result, presence-only data has become a popular object of study in ecology [Elith et al. (2006)].
1.2. What should we estimate?
Before we can sensibly decide how to model presence-only data, we must address the issue of what it is we are modeling in the first place. How should we think of “species occurrence,” the scientific phenomenon nominally under study? This issue arises with presence-only and presence–absence data alike.
1.2.1. Occurrence probability
Figure 2 is a typical “heat-map” output of a study of the willow tit in Switzerland using count data [Royle, Nichols and Kéry (2005)]. The map reveals which locations are more or less favored by the species (in this case, high elevation and moderate forest cover appear to be the bird's habitat of choice). The legend tells us that the color of a region reflects the local probability of “occurrence.”
Fig. 2.
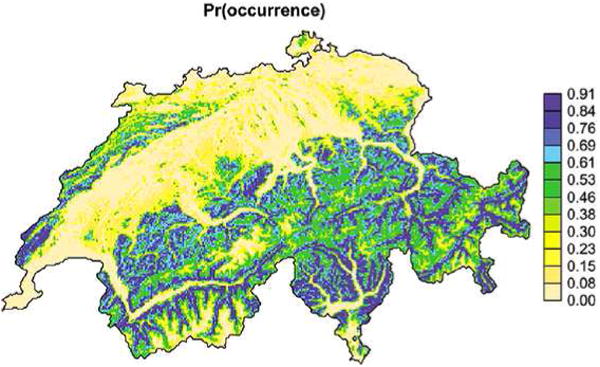
Heat map of occurrence probabilities. Taken from Royle, Nichols and Kéry (2005).
But precisely what event has this probability? Reading the paper, we discover that occurrence means that there is at least one willow tit present on a survey path through a 1 km × 1 km quadrat of land. In this case, the authors analyze a presence–absence data set using a hierarchical model that explicitly accounts for the possibility that a bird was present but not detected at the time of the survey.
Because the survey path length varies across sampling units, the authors use it in their model as a predictor of presence probability. It is not specified which value of this predictor is used in generating the heat map, which makes the map difficult to interpret.
Even if we could interpret the heat map as the probability of a bird being present anywhere in the quadrat (not just along a path of unspecified length), this probability would still be larger in a 2 km × 2 km sampling unit and smaller in a 100 m × 100 m one. Therefore, the very definition of “occurrence probability” in a presence–absence study depends crucially on the specific sampling scheme used to collect the presence–absence data. Consequently, interpreting the legend of such a heat map can only make sense in the context of a specific quadrat size, namely, whatever size was used in the study. We would recommend that this information always be displayed alongside the plot to avoid conveying the false impression (suggested by a heat map) that occurrence probability is an intrinsic property of the land, when it is really an extrinsic property.
Though the choice of quadrat size used to define occurrence probability is ecologically arbitrary, it can in principle yield estimates with meaningful interpretations. By contrast, estimating occurrence probability in a presence-only study is a murkier proposition. Any method purporting to do so without reference to quadrat size would be predicting the same occurrence probability within a large or small quadrat, which cannot make sense.
1.2.2. Occurrence rate
Since occurrence probability is only meaningful with reference to a specific quadrat size, it is a somewhat awkward quantity to model in a presence-only study. In this context it is more natural to estimate an occurrence rate or intensity: that is, a quantity with units of inverse area (e.g., 1/km2) corresponding to the expected number of specimens per unit area. Under some simple stochastic models for species occurrence, including the Poisson process model considered here, specifying the occurrence rate is equivalent to specifying occurrence probability simultaneously for all quadrat sizes.
Unfortunately, a presence-only data set only affords us direct knowledge of the expected number of specimen sightings per unit area. The absolute sightings rate is reflected in the number of records in our data set, but, at best, this rate is only proportional to the occurrence rate discussed above, which typically is the real estimand of interest. We must assume that our sightings only constitute a small fraction of the species' population over our study region, possibly with repeated sightings of the same specimen. Without other data or assumptions we would have no way of knowing what this constant of proportionality might be.
In other words, the absolute sightings rate is observable but usually not of direct interest, while the absolute occurrence rate is interesting but not observable without another source of information. Using presence-only data alone, we can at best hope to estimate a relative, not absolute, occurrence rate. Even assuming that the sightings and occurrence rates are proportional is optimistic, since it rules out sampling bias like that in Figure 1, an issue we take up again in Section 2.5.
1.3. Notation
We now introduce notation we will use for the remainder of the article. We begin with some geographic domain of interest
 , typically a bounded subset of ℝ2. If the time of an observation is an important variable, we might alternatively take
, typically a bounded subset of ℝ2. If the time of an observation is an important variable, we might alternatively take
 ⊆ ℝ3 so that our observations haveboth space and time coordinates. Associated with each geographic location z ∈
⊆ ℝ3 so that our observations haveboth space and time coordinates. Associated with each geographic location z ∈
 is a vector x(z) of measured features.
is a vector x(z) of measured features.
Our presence-only data set consists of n1 locations of sightings Zi ∈
 for i = 1,2,…, n1, accompanied by n0 “background” observations zt for i = n1+ 1,…, n1+ n0 (typically a regular grid or uniformly random sample from
for i = 1,2,…, n1, accompanied by n0 “background” observations zt for i = n1+ 1,…, n1+ n0 (typically a regular grid or uniformly random sample from
 ). Finally, let xi = x(zi) be the features for observation i, and yt be a 0/1 indicator that i is a presence sample. Our treatment of these data as random or fixed will vary throughout the article.
). Finally, let xi = x(zi) be the features for observation i, and yt be a 0/1 indicator that i is a presence sample. Our treatment of these data as random or fixed will vary throughout the article.
1.4. Outline
The rest of the paper is organized as follows. In Section 2 we define the log-linear inhomogeneous Poisson process (IPP) model and its application to presence-only data, with special focus on interpreting its parameters and their maximum likelihood estimates. In particular, the estimate of the intercept α reflects nothing more than the total number of presence samples and, as such, is typically not of scientific relevance for the reasons discussed in Section 1.2.2. In fact, IPP model estimation amounts to parametric density estimation in an exponential family model, followed by multiplication of the fitted density by n1. The density thus obtained reflects the relative rate of sightings as a function of geographic coordinates z.
Aarts, Fieberg and Matthiopoulos (2012) showed that many methods in species distribution modeling can be motivated by the IPP model. We review these connections and generalize them for several illuminating examples. In Section 3 we consider a particularly important example, showing that the popular Maxent method of Phillips, Dudík and Schapire (2004) follows immediately from partially maximizing the IPP log-likelihood with respect to α, a result which is explored further in Renner and Warton (2013). Hence, given any set of presence and background points, the Maxent and IPP methods obtain identical estimates for the slope β̂ and for the density.
In Section 4 we discuss so-called “naive” logistic regression and its connections to the IPP model. We derive its likelihood as a conditional form of the IPP likelihood, but show that if the log-linear model is misspecified this convergence may not occur until the background sample is quite large. The need for a large background sample is due not only to variance, but also to bias that persists until the proportion n1/n0 becomes negligibly small. We show, however, that if we upweight all the background samples by large weight W ≫ 1, we can use logistic regression to recover the IPP estimate β̂ precisely with any finite presence and background sample. This procedure, which we call “infinitely weighted logistic regression,” is a device for using GLM software to maximize the IPP log-likelihood. Section 5 recapitulates the relationships and contains discussion.
2. The inhomogeneous Poisson process model
The IPP is a simple model for a random set of points Z falling in some domain
 . Both the number and locations of points are random. It can be defined by its intensity function
. Both the number and locations of points are random. It can be defined by its intensity function
| (1) |
which indexes the likelihood that a point falls at or near z. For A ⊆
 , write
, write
| (2) |
and assume Λ(
 ) <∞.
) <∞.
There are two main ways to formally characterize an IPP with intensity λ. One simple definition is that the total number of points is a Poisson random variable with mean Λ(
 ) and, conditionally on the number of points, their locations are independent and identically distributed with density pλ (z) = X(z)/Λ(
) and, conditionally on the number of points, their locations are independent and identically distributed with density pλ (z) = X(z)/Λ(
 ). That is, an IPP is an i.i.d. sample from pλ whose size is itself random.3
). That is, an IPP is an i.i.d. sample from pλ whose size is itself random.3
Alternatively we can think of an IPP as a continuous limit of an independent Poisson count model for ever-finer discretizations of
 . If N(A) = #(Z ∩ A), the number of points falling in set A, then
. If N(A) = #(Z ∩ A), the number of points falling in set A, then
| (3) |
with N(A) and N(B) independent for disjoint sets A and B. For more on the IPP and other point process models, see Gaetan and Guyon (2009) or Cressie (1993).
In the case of a finite discrete domain
 = {z1, z2,…, zm}, the IPP model reduces to a discrete Poisson model, with N(zi) ∼ Poisson(λ(zi)). In this sense, the IPP model may be seen as a limit of finer and finer discretizations of
= {z1, z2,…, zm}, the IPP model reduces to a discrete Poisson model, with N(zi) ∼ Poisson(λ(zi)). In this sense, the IPP model may be seen as a limit of finer and finer discretizations of
 . We discuss this connection further in Section 2.4.
. We discuss this connection further in Section 2.4.
Warton and Shepherd (2010) proposed modeling species sightings z1,…,zn1 as arising from an IPP whose intensity is log-linear in the features x(z):
| (4) |
The formal linearity assumption is less restrictive than it seems, since our features x(z) could include polynomial terms, interactions, splines or other basis expansions, which substantially broaden the space of possible λ(z).
Interpreting the IPP as an i.i.d. sample with random size, we see that α and β play very different roles. Since α only multiplies λ(z) by a constant, it has no effect on pλ(z) = λ(z)/Λ(
 ). The “slope” parameters β completely determine pλ, while α scales the intensity up or down to determine the expected sample size Λ(
). The “slope” parameters β completely determine pλ, while α scales the intensity up or down to determine the expected sample size Λ(
 ).
).
2.1. Geographic space and feature space
In the context of logistic regression, it can be more natural to think of the xi as a sample of points in “feature space” [i.e., the range of x(z)] rather than as the features corresponding to a sample in the geographic domain
 . There is no real distinction between these two viewpoints, so long as we adjust for the fact that some values of x are more common in
. There is no real distinction between these two viewpoints, so long as we adjust for the fact that some values of x are more common in
 than others.
than others.
Let Ax = {z: x(z) = x} and h(x) =∫Ax 1 dz. Then if the set Z is an IPP with intensity λ(x(z)), the corresponding set x(Z) is an IPP with intensity λx(x) = λ(x) ·h(x) and, conditionally on n1, their distribution is px(x) ∝ pλ(x)·h(x). For more detailed discussion see Elith et al. (2011) and Johnson et al. (2006).
2.2. Maximum likelihood for the IPP
The score equations for the log-linear IPP are simple and enlightening. The IPP log-likelihood in terms of the presence samples is
| (5) |
Differentiating with respect to α, we obtain the score equation
| (6) |
That is, whatever β̂ is, α̂ plays the role of a “normalizing” constant guaranteeing that λ(z) integrates to n1, the number of total presence records. Hence, if n1 is not of scientific interest, then neither is α̂.
Solving for α in (6) and ignoring constants, we obtain the partially maximized log-likelihood
| (7) |
which is the same log-likelihood we would obtain by conditioning on n1 and treating the zi as a random sample with density .
Finally, differentiating (7) with respect to β and dividing by n1 gives the remaining score equations:
| (8) |
Solving (8) amounts to finding β for which the expectation of x(z) under Pλ(z) matches the empirical mean over the presence samples.
Hence, maximum likelihood for a log-linear IPP may be thought of as an algorithm with two discrete steps:
Estimate the density pλ: find β̂ for which
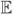 p̂λ
x(z) matches the empirical means of the presence sample xi.
p̂λ
x(z) matches the empirical means of the presence sample xi.Multiply p̂λ by n1: find α̂ for which λ̂(z) = n1 ⋅ p̂λ (z).
Unless n1 is meaningful, then, the IPP is essentially density estimation. In our view, it is rare that n1 merits much scientific interest, but there are important cases where it might. For instance, if we are comparing multiple species, study areas or periods of study, and if we believe that sampling effort is comparable across the different studies, then comparing the n1 from each data set may teach us something.
Note, however, that in each of these cases our inference target can be viewed as a relative intensity across the different data sets. If we wish to make such comparisons, the right approach may simply be to expand the survey area
 to include multiple regions or time periods and add region identity or species identity as a feature, then perform a combined analysis. n1 for the combined analysis (the total number of sightings across all the different data sets) would then typically not be of much interest.
to include multiple regions or time periods and add region identity or species identity as a feature, then perform a combined analysis. n1 for the combined analysis (the total number of sightings across all the different data sets) would then typically not be of much interest.
2.3. Numerical evaluation of the integral
When we cannot evaluate the integrals in equations (5)–(8) analytically, we replace them with numerical integrals based on the background samples. Hence, (5) becomes
| (9) |
where |
 | = ∫
| = ∫ 1 dz represents the total area of the region.
1 dz represents the total area of the region.
The background points may be either a uniform sample from
 or a regular grid. Quadrature weights may also be assigned to the background points to approximate the integral with a weighted sum, instead of the unweighted sum represented above.
or a regular grid. Quadrature weights may also be assigned to the background points to approximate the integral with a weighted sum, instead of the unweighted sum represented above.
We could repeat the derivation of Section 2.2 to obtain the criteria
| (10) |
Throughout, we will refer to (9) as the numerical IPP log-likelihood to distinguish it from (5). In practice, fitting the IPP means solving (10) for some background sample.
2.4. Connection to Poisson log-linear model
If the background zi comprise a regular grid, we can discretize
 into n0 pixels Ai, each of roughly the same size
and centered at zi. If x(z) is continuous, then
into n0 pixels Ai, each of roughly the same size
and centered at zi. If x(z) is continuous, then
| (11) |
The IPP model implies that the counts N(Ai) arise independently via
| (12) |
Hence, the approximate log-likelihood is
| (13) |
Let Si = {k:zk ∈ Ai,yk = 1} contain the presence samples in pixel i. Then
| (14) |
Hence, the only difference between (9) and (13) is that in the latter we also discretize the location of each presence sample to match its nearest background point.
Berman and Turner (1992) proposed using this approximation to fit the IPP model using Poisson GLM software, and Baddeley and Turner (2000) show how to generalize it to other point-process models including generalized additive models. This device provides a simple means of accessing the modeling flexibility of GLM methods at a cost of some loss of data, since it effectively replaces the covariate vector xi for each presence sample with that of its nearest background sample.
Baddeley et al. (2010) discuss the bias incurred by the discretization, showing in particular that it vanishes in the small-pixel limit. They also propose a strategy for improving the bias, which splits pixels into subpixels whose covariates are closer to constant.
As we will see later, this discretization is not really necessary. In Section 4 we propose a different procedure, infinitely weighted logistic regression, that also allows us to fit an IPP model using GLM software but produces exactly the same estimates we would obtain by maximizing (9) on the original presence and background data.
2.5. Identifiability and sampling bias
Sampling bias poses a serious challenge to valid inference in presence-only studies. Scientifically, we are interested in the occurrence process consisting of all specimens of the species of interest. However, our data set consists of what we might call the sightings process, consisting only of the occurrences observed and reported by people.
We can model the sightings process as an occurrence process thinned by incomplete observation, as proposed by Chakraborty et al. (2011) and Renner and Warton (2013). That is, suppose that specimens occur with intensity λ̃(z), but that most occurrences go unobserved. Each occurrence is observed with probability s(z), which may depend on features of the geographic location z (e.g., proximity to the road network). If detection is independent across occurrences, then the observation process is an IPP with intensity
| (15) |
The trouble is that our presence-only data set only directly reflects A, the intensity of sightings, and not λ̃.
Optimistically, we might assume that s is constant (no sampling bias). In that case, by estimating λ(z) we are also estimating λ̃(z) up to an unknown constant of proportionality s, so pλ̃= pλ but λ̃ ≠ λ. Even in this optimistic scenario we can only estimate relative, not absolute, occurrence intensities. Phillips and Elith (2013) also elaborate the same point in the context of logistic regression models.
Slightly less optimistically, we might assume that s is an unknown function of z, but that s and λ̃ are known to depend on z through two disjoint feature sets. For instance, we could model λ̃ and s as log-linear in features x1(z) and x2(z), respectively:
| (16) |
| (17) |
Then the sightings process follows the log-linear model λ(z) = eα+β′x(z) with and . Note that α̃ and β̃ are the quantities of primary scientific interest, whereas α and β are the parameters governing the process we actually observe. Nevertheless, β̃ is still identifiable from the data because β is.4
As n0,n1 → ∞, our estimate β̂ converges to the true value of β̃, the slope coefficients of λ̃. However, α̃ will converge not to α̃ but rather to α̃ + γ. Without knowing γ, we have no way of estimating α̃. By the same token, if some features appear both in x1 and x2—or if x1 and x2 are not linearly independent—the model is unidentifiable.
To be concrete, suppose koala occurrence is known to depend only on elevation (x1), and that sampling bias is known to depend only on proximity to roads (x2). Then, despite the obvious sampling bias in Figure 1, we could still estimate what elevations koalas tend to frequent, by making the correct adjustments for road proximity. By contrast, we could not estimate from presence-only data alone whether koalas tend to avoid roads, since that is confounded by sampling bias.
Whether or not s is constant, our estimate for α = α̃ + γ carries no real information about α̃ unless we have independent knowledge of γ. Indeed, we have already seen that the only role α̂ plays in estimation is to make λ integrate to n1.
The distinction between β and β̃ may be very important for some problems, but for the remainder of this article we focus on estimation of β, the slope parameters of the process we get to observe.
3. Maximum entropy
Another popular approach to modeling presence-only data, which we will see is equivalent to the IPP, is the Maxent method proposed by Phillips, Dudík and Schapire (2004). The authors begin by assuming that the presence samples z1,…,zn1 are a random sample from some probability distribution p(z), called the species distribution.
The authors adopt the view, inspired by information theory that our estimate p̂ should have large entropy H(p) =−∫ p(z) log(p(z)) dz. Large H(p) means roughly that p is close to the uniform density 1/|
p(z) log(p(z)) dz. Large H(p) means roughly that p is close to the uniform density 1/|
 |, the species distribution we would observe if the species were indifferent to all geographic features. The idea is that p̂ should be “nearly geographically uniform,” subject to constraints that make it resemble the observed data.
|, the species distribution we would observe if the species were indifferent to all geographic features. The idea is that p̂ should be “nearly geographically uniform,” subject to constraints that make it resemble the observed data.
Phillips, Dudík and Schapire (2004) propose to choose the p which maximizes H(p) subject to the constraint that the expectation of the features x(z) under p̂ matches the sample mean of those features, that is,
| (18) |
They show that this criterion is equivalent to maximizing the likelihood of the parametric exponential family density:
| (19) |
This is exactly the form of pλ for our log-linear IPP, and its log-likelihood is exactly the partially maximized log-likelihood ℓ*(β), the log-likelihood for an IPP conditioned on n1. The constraint (18) is precisely the score criterion (8) for β in an IPP, so the Maxent β̂ is the same as the IPP β̂. This result may also be found in Appendix A of Aarts, Fieberg and Matthiopoulos (2012).
The popular software package Maxent implements a method slightly more complex than the one originally proposed in 2004. First, it automatically generates a large basis expansion of the original features into many derived features: quadratic terms, interactions, step functions and hinge functions of the original features. Then, it fits a model by optimizing an ℓ1-regularized version of the conditional IPP likelihood (7):
| (20) |
The regularization parameters rj are chosen automatically according to rules based on an empirical study of various presence-only data sets [Phillips and Dudík (2008)].5
Mathematically, the basis expansion increases the dimension of x(z) but changes nothing else. Moreover, the ℓ1 regularization scheme does not constitute an essential difference with the other methods considered here. One could (and often should) regularize β when fitting an IPP model as well especially if x(z) contains many features resulting from a large basis expansion.
Penalizing the Maxent log-likelihood does not change the equivalence between the two models, so long as α is left unpenalized. If we add a penalty term J(β) to the IPP log-likelihood (5), we still obtain (6) after differentiating with respect to α. Then, partially maximizing ℓ(αβ) –J(β) gives us ℓ*(β) – J(β), the penalized Maxent log-likelihood. This equivalence depends on our not penalizing α in (5).
This argument generalizes immediately to a generic penalized likelihood method with any parametric form for log λ(z). We have established the following general proposition:
Proposition 1. Given some parametric family of real-valued functions {fθ: θ ∈ ℝd} with penalty function J(θ), consider the penalized log-likelihood g1 for an IPP with intensity eα+fθ(x(z)),
| (21) |
and the penalized log-likelihood g2 for a sample with density ∝eα+fθ(x(z)):
| (22) |
Then θ maximizes g2 iff (θ, β) maximize g1 for some α. The same applies if we replace the integrals in (21)–(22) with sums over the background sample.
Proof. Partially maximize g1 over α as in (7) to obtain g2.
Thus, we see that, while Maxent and the IPP appear to be different models with different motivations, they result in the exact same density estimate p̂ (z). In terms of the two-step algorithm we derived in Section 2.2, Maxent is identical to step 1, but it skips step 2. The IPP fit λ̂ is n1 times the Maxent fit λ̂.
4. Logistic regression
Another ostensibly different model for presence-only data is so-called “naive” logistic regression, which casts presence-only modeling as a problem of classifying points as presence (y = 1) or background (y = 0) on the basis of their features. The logistic regression model treats n1, n0 and the xi as fixed and the yi as random with
| (23) |
Superficially, this approach may appear ad hoc and unmotivated compared to IPP or Maxent. Nevertheless, it has enjoyed some popularity, in part because logistic regression is an extremely mature method in statistics, enjoying myriad well-understood and already-implemented extensions such as GAM, MARS, LASSO, boosted regression trees and more.
Logistic regression modeling of presence-only data has often been motivated by analogy to logistic regression for presence-absence data. Since it is not known whether the species is present at or near the background examples, these are sometimes referred to as “pseudo-absences,” and the supposed naivete of the method is that it appears to treat background samples as actual absences. For instance, Ward et al. (2009) introduced latent variables coding “true” presence or absence and proposed fitting this model via the EM algorithm.
This interpretation raises once again the troublesome question of what it would mean for one of our randomly sampled background points to be a “true presence.” Need there be a specimen sitting directly on the location, or is it enough for it to be within 100 m? 1 km?
Fortunately, we can sidestep these concerns, since connections between the logistic regression and IPP models yield a more straightforward interpretation.
4.1. Case-control sampling
Suppose the background data are a uniform random sample, and the presence data arise from a log-linear IPP. Then if we condition on n1, the zi are a mixture of two i.i.d. samples, one from density eα+β′x(z)/Λ(
 ) and the other from density 1/|
) and the other from density 1/|
 |. By Bayes' rule, for a random index i,
|. By Bayes' rule, for a random index i,
| (24) |
| (25) |
| (26) |
with . Since ℙ(yi = 1|zi) depends only on xi = x(zi), we could just as well condition on xi instead, giving (23). Therefore, if the log-linear IPP model is correct, it implies the individual yi|xi follow a logistic regression with the same slope parameters β.6
Thus, given any finite sample of presence and background points, if we believe in the IPP model, then we could either maximize the numerical IPP likelihood or the logistic regression likelihood, and in either case we would be estimating the same population parameter β. This does not guarantee we will obtain the same estimates β̂ in any given finite sample, but if the model is correct, then either method gives a consistent estimator of β.
Note that if we change the marginal class ratio n1/n0 by some factor ec, the only effect will be to multiply the odds of yi = 1 given xi by the same factor, that is, add c to η and leave β unchanged. Hence, under correct specification, β̂ → β regardless of the limiting ratio n1/n0.
4.2. Case-control sampling under misspecification
Now, suppose that λ(z) is not really log-linear in our features x. Then, the fitted slopes β̂ for logistic regression and the numerical IPP will not converge to the same limiting β if n1 and n0 grow large together. In fact, the limiting logistic regression parameters depend on the limiting ratio of n1/n0 [Xie and Manski (1989)].
To gain some intuition for why this is so, suppose we have a single covariate x, with λ(z) = eα+x(z)2. Then the derivation of (24)–(26) gives
| (27) |
with η as before. In the large-sample limit, then, our estimation problem amounts to finding η̂, β̂ for which
| (28) |
in the population from which we are sampling. Now, since changing n1/n0 only adds a vertical shift to the right-hand side of (28), it may seem rather counterintuitive that this should have any impact on the slope β̂ of our approximation on the left-hand side.
To understand why, we must come to grips with the sense in which we make the approximation in (28). The logistic regression log-likelihood is
| (29) |
Its first derivatives with respect to η and β can be written in terms of the fitted conditional probabilities ŷi (η, β) = ℙη,β(y = 1| x = xi):
| (30) |
| (31) |
If we define ri = yi − ŷi, then η̂, β̂ maximize the likelihood if and only if Σi ri = 0 and x ⊥ r. The crucial point is that the residuals of our approximation, yi − ŷi, are measured on the probability scale, and not the log-odds scale.
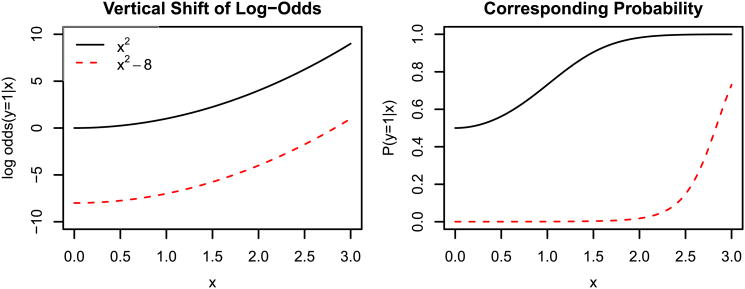
The black and red curves in the left panel of Figure 3 show the conditional log-odds for our misspecified model with two different values of η, 0 and -8 respectively. On the log-odds scale, one is no steeper than the other. But when we look at the same two curves on the conditional probability scale (right panel), now the red looks steeper than the black. This is due to a “ceiling” effect for the black curve: in the region where the log-odds x2 is changing fast, the probability has already saturated at 1. The actual estimates of η̂ and β̂ depend on the background density of x as well as n1/n0; see Section 4.5 for a full simulation.
Fig. 3.
The dashed red curve in the left panel is a vertical shift of the solid black curve. However, vertically shifting the log-odds changes the conditional probability in a more complex way.
As Warton and Shepherd (2010) prove, this ceiling effect vanishes in the limit where n1/n0 → 0; in that case η̂ → − ∞, , and the logistic regression and IPP estimates are identical. Hence, there is no difference when the background sample grows so large that it dwarfs the presence records in the population from which we are sampling. Dorazio (2012) considers a similar framework, called the case-augmented design, and proves a similar equivalency to the IPP as n0 → ∞.
4.3. Infinitely weighted logistic regression
If we modify the logistic regression procedure a bit, we can resolve the discrepancy in the previous section and recover the same β̂ that we would estimate with an IPP using the same presence and background samples.
We can remove the ceiling effect of the previous section if we add case weights to the samples
| (32) |
for some large number W. We then obtain the weighted log-likelihood
| (33) |
| (34) |
Proposition 2. Let J(β) be any convex penalty, and suppose ℓIPP (α,β)–J(β) has a unique maximizer (α〲IPP, β̂IPP). Then if (η̂W, β̂W) maximize ℓWLR(η,β)–J(β) for weight W,
| (35) |
Proof. Reparameterizing (33) with α= η + log(Wn0/|
 |) and ignoring constants, we obtain
|) and ignoring constants, we obtain
| (36) |
Fixing (α,β) and taking W → ∞, each term in the second sum converges to while the third sum converges to 0. Hence, ignoring constants, (36) converges to the numerical IPP log-likelihood (9), and this convergence occurs uniformly on compact subsets of the parameter space.
Now, both ℓWLR(α,β) – J(β) and ℓIPP(α,β) – J(β) are concave, and the latter is strictly concave by assumption; hence, the maximizer of the first converges to the maximizer of the second.
From the above, we see that IWLR is not really a new statistical method, but rather a technical device for optimizing the IPP/Maxent log-likelihood using already-implemented GLM software.
Although technically β̂W ≠β̂IPP for any finite W (hence the name “infinitely weighted”), in practice, we only need W large enough that the approximation of ℓWLR(α,β) to ℓIPP(α,β) is good near (α̂, β̂).
Essentially, if for each i (say, all are less than 0.001), then the Taylor approximation should be good. We can assess this easily if we observe that
| (37) |
when all of the above are small. To rephrase, then, if maxi ŷi from the logistic regression is less than 0.001 or so, it seems to us that W should be sufficiently large. If not, we can set and check that the fitted ŷi are now small enough. If any uncertainty remains whether W is large enough, one can always increase it by (say) another factor of 100 and check that the estimates do not change appreciably.
4.4. Logistic regression as density estimation
One interpretation of the results we have just reviewed is that in the context of presence-only data, logistic regression solves the same parametric density estimation problem as Maxent and the IPP do. Moreover, our infinitely weighted logistic regression yields an identical estimate of the density.
Using logistic regression for density estimation has been proposed before. For example, Hastie, Tibshirani and Friedman (2009) discuss it as a means for turning an unsupervised density estimation problem into a supervised classification problem. Their proposal uses a different weighting scheme (assigning half the total weight to the presence samples) which, unlike infinitely weighted logistic regression, does not give exactly the IPP solution.
4.5. Simulation study: Weighted vs unweighted logistic regression
We have seen that both infinitely weighted logistic regression (a.k.a. numerical IPP) and unweighted logistic regression estimate the same β parameter of the same log-linear IPP model, and when the background sample is much larger than the presence sample the estimates β̂ are close to each other.
However, the infinitely weighted logistic regression estimate can converge much faster to the large-background-sample limit if the linear model is misspecified, as we illustrate here with a simulation study.
Consider a geographic region with a single covariate x whose background density is p0(x) = N(0,1). Now, suppose a species follows our log-linear IPP model with slope β, so that λ(x(z)) ∝ eβx. Then the density of presence samples in feature space is P1(x) = eβxp0(x)/(∫eβup0(u) du) = N(β, 1).
Suppose our species is in fact a mixture of two subspecies, one of which comprises 95% of the population and prefers x large, while the remaining 5% prefer x small. If each subspecies follows our model with coefficients 1.5 and -2, respectively, then
| (38) |
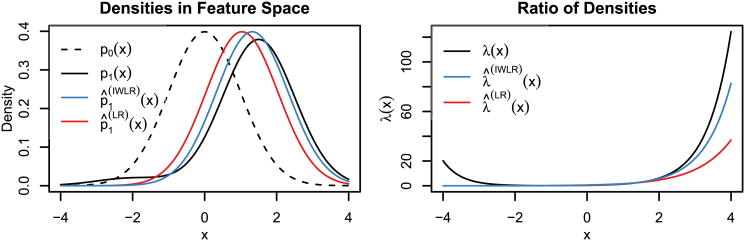
which no longer follows the log-linear model. p0(x) and p1(x) are depicted in the upper panel of Figure 4 as the dashed and solid black lines. The black line in the left panel shows λ(x) = P1(x)/p0(x), the relative intensity as a function of the covariate x. In the left panel all the curves have been normalized so that Λ(
 ) = ∫ λ(x)p0(x) dx =1.
) = ∫ λ(x)p0(x) dx =1.
Fig. 4.
Large-sample estimates for the simulation study, misspecified case. The black curves represent the true presence density (left panel) and intensity (right panel). The blue and red curves show the fitted densities using IWLR and standard logistic regression with n0 = n1.
If we fit an infinitely-weighted logistic regression (or, equivalently, a log-linear IPP) to a large presence and background sample, our fitted β̂(IWLR)will tend to μ1 =
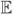 p1 (x) = 1.325. We have plotted the corresponding large-sample estimates λ̂(IWLR)(x) and p̂1 (x) as blue lines in the respective panels of Figure 4.
p1 (x) = 1.325. We have plotted the corresponding large-sample estimates λ̂(IWLR)(x) and p̂1 (x) as blue lines in the respective panels of Figure 4.
If, alternatively, we fit an unweighted logistic regression to the same data set with large n0 = n1, the estimate β̂(LR) will tend to roughly 1.04. The resulting large-sample estimates p̂(LR)(x) and λ̂(LR)(x) are plotted in red.
If we fit an unweighted logistic regression to a large sample with a different ratio n1/n0, we would get a different estimate, which would tend toward the IPP estimate of 1.325 if and only if this ratio tended to 0. By the same token, when n1 and n0 are fixed, the ratio between them can play a significant role in determining the estimated β. In contrast, the IWLR/IPP estimate tends to 1.325 in large samples no matter what the ratio n1/n0.
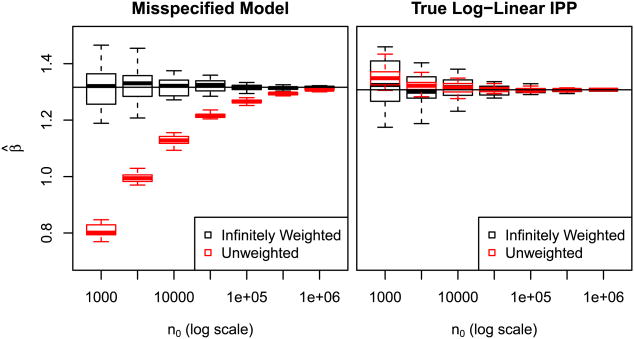
The left panel of Figure 5 illustrates this with a simulation study of the example just discussed. We first generate a single presence sample of size n1 = 3000 from this species, then generate 20 sets of n0 background samples from p0 = N(0,1) for each of a range of values n0 ranging from 103 to 106.
Fig. 5.
β̂ estimates for simulation study with n1 = 3000 and varying n0. Unweighted logistic regression may require a very large background sample before convergence when the model is misspecified.
For each background sample, we fit both an “infinitely” weighted (W = 104) and unweighted logistic regression to the combination of presence and background points. For relatively large sizes of background sample, there is very little sampling variability, but the logistic regression estimates carry a large bias that depends greatly on the size of the background sample. The limiting β̂, to which both methods would converge given an infinite background sample, is depicted with a horizontal line.
In the right panel, we repeat this study with a presence sample from N(μ1,1), the correctly-specified model with the same mean as our misspecified model. Now the situation is very different; no matter what the mix of presence and background samples, the log-odds are truly linear with slope β = μ1. Consequently, as n0 → ∞ and n1 → ∞, regardless of the limiting ratio n1/n0.
Since the choice of background sample size is primarily a matter of convenience, it is preferable to use an estimator that depends on it as little as possible. When the linear model is misspecified (which is nearly always the case), we recommend the infinitely weighted logistic regression over unweighted logistic regression for this reason.
We emphasize here that although IWLR resolves the issue of bias that we discussed in Section 4.2, using IWLR does not guarantee that we will obtain a good estimate for small n0. The smaller n0 is, the larger the variance of our estimate, so a larger background set is always better unless computational constraints apply.
What is more, the variability in our estimate due to the background sample is not reflected in the default standard error outputs from GLM software—only the variability due to the presence records is. Because ℓIWLR (α,β) ≈ ℓIPP (α,β) for large W, its Hessian will also converge to the Hessian of the IPP.
Even if our background sample was extremely large, the standard error estimates for any of the models we have discussed are based on asymptotic normal approximations that hold when the log-linear model is correctly specified. Resampling methods such as the bootstrap are more generally reliable, but even the bootstrap will depend crucially on the assumption that presence records (and in the case of logistic regression, background records) are independent observations. In terms of the IPP model, this assumption rules out spatial clustering of presence records. Renner and Warton (2013) provide evidence that this assumption may not hold for presence-only data. Therefore, model-based estimates of standard error should be viewed with suspicion no matter what method we choose.
5. Discussion
We have discussed several closely related models for a single presence-only sample. In this section we collect them all in one place and review their relationships:
Inhomogeneous Poisson process
The “mother” model, from which the others can be derived, is the inhomogeneous Poisson process (IPP), whose log-likelihood is
| (39) |
In practice, (39) is approximated numerically via
| (40) |
Fitting this model amounts to solving for the density pλ(z)∝ eβ′x(z) for which the expected features
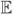 pλx(z) match the empirical mean
, then multiplying that density by n1.
pλx(z) match the empirical mean
, then multiplying that density by n1.
Maxent
Conditioning on n1, we obtain the exponential family density model p (z)∝ eβ′x(z), resulting in the log-likelihood
| (41) |
or its numerical counterpart. This is the log-likelihood maximized by Maxent, and it corresponds exactly to the log-likelihood (39) partially maximized with respect to α. Hence, both procedures give exactly the same estimates of β and p.
Logistic regression
The logistic regression log-likelihood is
| (42) |
When the log-linear IPP model is correctly specified, this model is as well (aside from the fact that the yi|xi are only approximately independent), with the same true β as in the IPP model. However, in finite samples the estimates for β given by maximizing (42) instead of (40) may be substantially different.
Infinitely weighted logistic regression
We can resolve this difference by upweighting all the background points by W ≫ 1, obtaining weighted log-likelihood
| (43) |
In the limit where W → ∞, we recover exactly the same β̂ as we would by maximizing (40).
Discretized Poisson LLM
Another means for approximating the IPP log-likelihood with a GLM log-likelihood is the Berman and Turner method, which simply discretizes geographic space into pixels and assigns each presence point to a bin belonging to its nearest background point:
| (44) |
This discretization of presence features is unnecessary given that we can exactly fit the IPP likelihood using the infinitely weighted approach of (43).
5.1. Extending the IPP model
Logistic regression is one of the most widely applied methods in statistics. For decades, applied statisticians have been developing, studying and using variations on logistic regression to solve classification problems in statistics. R packages exist for fitting generalized additive models (GAMs), boosted regression trees, MARS and every manner of tailored regularization schemes [see, e.g., Hastie, Tibshirani and Friedman (2009)].
All of these methods are well understood within the context of logistic regression. We believe that the most important practical implication of the finite-sample equivalence between the IPP model and infinitely weighted logistic regression is that all of these methods can now be equally well understood and easily applied within the context of the IPP model.
For instance, we can fit an IPP / Maxent version of boosted regression trees with the following single line of R:
boosted.ipp <- gbm(y∼., family=“bernoulli,” data=dat, weights=1E3^(1-y)).
For an IPP / Maxent version of LASSO, ridge, or the elastic net:7
lasso.ipp <- glmnet(dat.x, dat.y, family=“binomial,” weights=1E3^(1-y)).
For an IPP GAM:
gam.ipp <- gam(y∼s(x1)+x2, family=binomial, data=dat, weights=1E3^(1-y)).
This added flexibility promises to provide a powerful tool to modelers of presence-only data.
5.2. Model selection
Regardless of which of the various related likelihoods we choose, there remains the issue of model selection. With the use of geographic information systems, ecologists often have access to a large number of predictor variables and may wish to winnow the field before modeling to avoid overfitting. Conversely, if some continuous variables are known to be important predictors, assuming a linear effect on the log-intensity may be too restrictive, and we may wish to expand the basis using splines, interactions, wavelets, etc. In either case, regularization may be called for.
Though it would be impossible to give a full treatment here of the many important considerations governing model selection, we note that these choices need not be governed by which likelihood we take as our starting point. In particular, the large set of derived features and ℓ1 regularization used by Maxent software can just as well be applied to the IPP model or, for that matter, to logistic regression. Using the infinitely weighted logistic regression method, we can implement the exact loss function used by the Maxent with software for penalized GLMs.
Acknowledgments
The authors are grateful to Jane Elith for helpful discussions and suggestions. We were also very fortunate to have had very thorough and thoughtful reviewers; the current manuscript has benefited greatly from their attention.
Footnotes
Cressie (1993) and Aarts, Fieberg and Matthiopoulos (2012) refer to an IPP conditioned on n1 as a “Conditional IPP”; this is exactly an i.i.d. sample of size n1 from the density pλ(z).
As with any regression adjustment scheme, we should proceed with caution here. If our linear model is misspecified (perhaps we should have included ) and x1 is correlated with the missing variables, even regression adjustment will not remove all bias. In perverse situations it could even make the situation worse.
The notation of the Maxent papers uses λ and β to denote what we call β and r, respectively.
The yi are technically not conditionally independent (if we knew the other n1 + n0 -1 labels, we would know the last as well). This is always true in case-control studies, but it is typically ignored since the dependence is weak for large samples.
The user should be warned that glmnet automatically re-normalizes the weights so they sum to n0 + n1. To avoid issues, set glmnet.control(pmin=1.0e-8, fdev=0) in your R session, and keep in mind this renormalization when setting the Lagrange parameter λ.
Contributor Information
William Fithian, Email: wfithian@stanford.edu.
Trevor Hastie, Email: hastie@stanford.edu.
References
- Aarts G, Fieberg J, Matthiopoulos J. Comparative interpretation of count, presence–absence and point methods for species distribution models. Methods in Ecology and Evolution. 2012;3:177–187. [Google Scholar]
- Baddeley A, Turner R. Practical maximum pseudolikelihood for spatial point patterns (with discussion) Aust N Z J Stat. 2000;42:283–322. MR1794056. [Google Scholar]
- Baddeley A, Berman M, Fisher NI, Hardegen A, Milne RK, Schuhmacher D, Shah R, Turner R. Spatial logistic regression and change-of-support in Poisson point processes. Electron J Stat. 2010;4:1151–1201. MR2735883. [Google Scholar]
- Berman M, Turner TR. Approximating point process likelihoods with GLIM. J Appl Stat. 1992;41:31–38. [Google Scholar]
- Chakraborty A, Gelfand AE, Wilson AM, Latimer AM, Silander JA. Point pattern modelling for degraded presence-only data over large regions. J R Stat Soc Ser C Appl Stat. 2011;60:757–776. MR2844854. [Google Scholar]
- Cressie NAC. Statistics for Spatial Data. Wiley; New York: 1993. Revised reprint of the 1991 edition. MR1239641. [Google Scholar]
- Dorazio RM. Predicting the geographic distribution of a species from presence-only data subject to detection errors. Biometrics. 2012;68:1303–1312. doi: 10.1111/j.1541-0420.2012.01779.x. MR3040037. [DOI] [PubMed] [Google Scholar]
- Elith J, Graham CH, Anderson RP, Dudik M, Ferrier S, Guisan A, Hijmans RJ, Huettmann F, Leathwick JR, Lehmann A, et al. Novel methods improve prediction of species' distributions from occurrence data. Ecography. 2006;29:129–151. [Google Scholar]
- Elith J, Phillips SJ, Hastie T, Dudík M, Chee YE, Yates CJ. A statistical explanation of MaxEnt for ecologists. Diversity and Distributions. 2011;17:43–57. [Google Scholar]
- Gaetan C, Guyon X. Spatial Statistics and Modeling. Springer; New York: 2009. [Google Scholar]
- Hastie T, Tibshirani R, Friedman J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. 2nd. Springer; New York: 2009. MR2722294. [Google Scholar]
- Johnson CJ, Nielsen SE, Merrill EH, McDonald TL, Boyce MS. Resource selection functions based on use-availability data: Theoretical motivation and evaluation methods. Journal of Wildlife Management. 2006;70:347–357. [Google Scholar]
- Lee AJ, Scott AJ, Wild CJ. Fitting binary regression models with case-augmented samples. Biometrika. 2006;93:385–397. MR2278091. [Google Scholar]
- Lele SR, Keim JL. Weighted distributions and estimation of resource selection probability functions. Ecology. 2006;87:3021–3028. doi: 10.1890/0012-9658(2006)87[3021:wdaeor]2.0.co;2. [DOI] [PubMed] [Google Scholar]
- MacKenzie DI. Occupancy Estimation and Modeling: Inferring Patterns and Dynamics of Species Occurrence. Academic Press; New York: 2006. [Google Scholar]
- Manly BFJ, McDonald LL, Thomas DL, McDonald TL, Erickson WP. Resource Selection by Animals: Statistical Analysis and Design for Field Studies. Kluwer Academic; Dordrecht: 2002. [Google Scholar]
- Margules CR, Austin MP, Mollison D, Smith F. Biological models for monitoring species decline: The construction and use of data bases (with discussion) Philosophical Transactions of the Royal Society of London Series B: Biological Sciences. 1994;344:69–75. [Google Scholar]
- Phillips SJ, Anderson RP, Schapire RE. Maximum entropy modeling of species geographic distributions. Ecological Modelling. 2006;190:231–259. [Google Scholar]
- Phillips SJ, Dudík M, Schapire RE. Proceedings of the Twenty-First International Conference on Machine Learning. Vol. 83. ACM; New York: 2004. A maximum entropy approach to species distribution modeling. [Google Scholar]
- Phillips SJ, Dudík M. Modeling of species distributions with Maxent: New extensions and a comprehensive evaluation. Ecography. 2008;31:161–175. [Google Scholar]
- Phillips SJ, Elith J. On estimating probability of presence from use-availability or presence-background data. Ecology. 2013;94:1409–1419. doi: 10.1890/12-1520.1. [DOI] [PubMed] [Google Scholar]
- Renner IW, Warton DI. Equivalence of MAXENT and Poisson point process models for species distribution modeling in ecology. Biometrics. 2013;69:274–281. doi: 10.1111/j.1541-0420.2012.01824.x. [DOI] [PubMed] [Google Scholar]
- Royle JA, Nichols JD, Kéry M. Modelling occurrence and abundance of species when detection is imperfect. Oikos. 2005;110:353–359. [Google Scholar]
- Ward G, Hastie T, Barry S, Elith J, Leathwick JR. Presence-only data and the EM algorithm. Biometrics. 2009;65:554–563. doi: 10.1111/j.1541-0420.2008.01116.x. MR2751480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warton DI, Shepherd LC. Poisson point process models solve the “pseudo-absence problem” for presence-only data in ecology. Ann Appl Stat. 2010;4:1383–1402. MR2758333. [Google Scholar]
- Xie Y, Manski CF. The logit model and response-based samples. Sociol Methods Res. 1989;17:283–302. [Google Scholar]