Determining the Origins of Superoxide and Hydrogen Peroxide in the Mammalian NADH: Ubiquinone Oxidoreductase

Abstract

NADH: ubiquinone oxidoreductase (Complex I) is a proton pump in the electron transport chain that can produce a significant amounts of superoxide and hydrogen peroxide. While the flavin mononucleotide (FMN) is the putative site for hydrogen peroxide generation, sites responsible for superoxide are less certain. Here, data on Complex I kinetics and ROS generation are analyzed using a computational model to determine the sites responsible for superoxide. The analysis includes all the major redox centers: the FMN, iron-sulfur cluster N2, and semiquinone. Analysis reveals that the fully reduced FMN and semiquinone are the primary sources of superoxide, and the iron-sulfur cluster N2 produces none. The FMN radical only produces ROS when the quinone reductase site is blocked. Model simulations reveal ROS generation is maximized during reverse electron transport with both the FMN and semiquin one producing similar amounts of superoxide. In addition, the model successfully predicts the increase in ROS generation when the membrane potential is high and matrix pH is alkaline. Of the total ROS produced by Complex I, the majority originates from the FMN.

Introduction

NADH: ubiquinone oxidoreductase (Complex I) is a large, multi-subunit complex that forms part of the electron transport chain (ETC) in mitochondria and some bacteria [1, 2]. The complex consists of a hydrophilic domain involved in electron transport and a hydrophobic domain responsible for proton pumping. The hydrophilic domain contains NADH oxidase activity at the proximal end and quinone (Q) reductase activity as the distal end. It encompasses a flavin mononucleotide (FMN) and a series of redox-active iron-sulfur (Fe-S) clusters that guide electrons from NADH to quinone (or a feasible electron acceptor). In the mammalian isoform, there are seven Fe-S clusters involved with electron transport. The hydrophobic domain contains up to four, active proton pumps that are responsible for proton translocation coupled to quinone reduction. The precise pumping mechanics are unknown but most likely involve either a piston-like mechanism or sequence of tightly coupled, nudge-like interactions to drive protein conformational changes [3, 4].

The reaction is extremely exergonic, but the energetic cost of trans locating four protons against an electrochemical potential makes this the first enzyme in the ETC to reach equilibrium. Under physiological conditions, this circumstance does not happen. It requires a very large proton electrochemical potential and a highly reduced Q pool. However, during ischemia, electron-flow through Complex I can transiently reverse until equilibrium conditions are met. This phenomenon is known as reverse electron transport (RET) and is strongly correlated with significant increases in reactive oxygen species (ROS) generation [5]. During forward electron transport (FET), ROS generation is low.(ROS is an ambiguous term generally used to describe any chemically reactive molecule that contains oxygen. Here we use ROS to specifically mean superoxide and hydrogen peroxide.)

The type and origin of ROS produced by mammalian Complex I are controversial. Some argue that the FMN is the sole source of ROS generation via the fully reduced FMN[6, 7]. And of the ROS produced, a vast majority is superoxide for the mammalian protein [8]. Others contend either the Fe-S clusterN2 or a semiquinone (SQ) bound to the Q reductase site is responsible for the majority of ROS generation [9–11]. And yet it has also been argued that ROS generation from Complex I originate from either a FMN radical or SQ[12]. It’s likely that each claim has some validity, and type and origin of ROS produced is variable and depends strongly on the experimental/environmental conditions.

Herein, we’ve developed a kinetic model of Complex I that is thermodynamically consistent and simulates the ability of this enzyme to produce ROS under a variety of conditions. The model simulates the redox state of the major redox centers: the FMN, Fe-S cluster N2, and semiquinone bound to the quinone reductase site. Also, the effects of membrane potential and pH are explicitly modeled. ROS is produced by the FMN moiety but is also generated from a SQ bound at the Q reductase site. In general, ROS output is less than 2% of total electron flux through the complex. However, the exact percentage is variable and depends on the redox state, membrane potential and pH. During RET, the amount of electrons that leak to oxygen is significantly increased relative to FET conditions. In nearly all cases, the major source of ROS is found to originate from the FMN. As such, the model is well suited for integration into larger scale models of mitochondrial bioenergetics, and enables the exploration of ROS production from the ETC under a variety of conditions.

Material and Methods

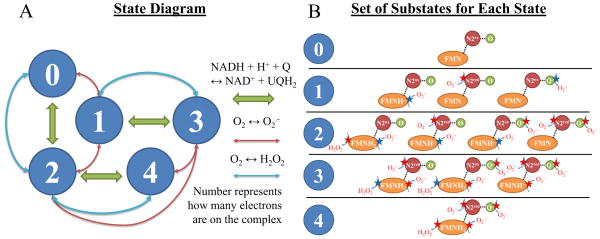
The state-diagram of the model of Complex I is depicted in Figure 1A. The model is constructed using the same framework for our Complex III model [13]. In short, the model is constructed using a set of rules that govern when the enzyme is capable of undergoing various redox transitions. Global thermodynamic consistency is ensured by constraining the reverse rate of each half-reaction. We assume that substrate and product binding only depend on the redox state of the nearest redox center. And for simplicity, we only consider the redox states for the FMN, Fe-S cluster N2, and SQ. Stopped-flow analysis reveals that electron dwell time on the other FeS clusters is negligible compared to those of the FMN and N2 [14]. Incorporating additional Fe-S clusters would unnecessarily increase the model complexity. Substates are shown in Figure 1B with possible sites of ROS generation depicted by a red or blue star. Blue stars highlight sites identified by model analysis that are the most important/significant for ROS production. All model equations are presented in the Supporting Material.

Figure 1. Model state diagram and ROS leak pathways.

A) The 5-state model is shown with green arrows representing the NADH + H⁺ + Q ↔ NAD⁺ + QH₂ reaction, blue arrows representing O₂ ↔ H₂O₂ reaction, and red arrows representing the O₂ ↔ O₂^·− reaction. B) For each state, the substates and their possible ROS leak sites are shown as stars (right). Green stars signify the most relevant sites identified after model analysis.

Reactant binding

For simplicity, we assume binding of substrates, products and protons is rapid with respect to state transition rates. This allows for the use of binding polynomials to calculate the fraction a given state is bound with a given reactant. For further details, see [13]. For the NADH oxidase site, we allow for the differential binding of NAD⁺ and NADH to various redox states of the FMN. For the Q reductase site, this is not necessary to explain the data. As an example, $[\mathit{NADH}]/K_{\mathit{NADH}}^o/P_{No}$ represents the fraction of a given oxidized FMN state with NADH bound. Equations 1–11 in the Supporting Material show the binding polynomial expressions for the FMN and Q reductase sites for each redox state.

Midpoint potentials

The thermodynamics associated with the redox biochemistry dictate the fractional occupancies of a given state. The midpoint potentials included in the model exhibit a pH dependence that is captured in equations 12–21 in the Supporting Material. All midpoint potentials were taken from the literature or directly fit to redox-titration data. See Table S1 for these values.

Substates

Within each oxidation state (number of electrons on the complex), there exists the possibility of multiple substates. Since electron transfer between these states is fast (O(μs)), we model these substates as rapidly interconverting species governed by the thermodynamics of electron transfer. For example, when the complex is reduced with only one electron, it can reside on either of three redox centers: the flavin, N2, or SQ. (See Figure 1B for details.) The reduction potentials for these species are used to compute the relative fraction of these species. Equations 21–50 in the Supporting Material give the equilibrium constants for each possible couple and the substate fractions.

Primary state transitions

The state transitions follow a 2e- reduction, 2e- oxidation or 1e-oxidation of the enzyme by NADH, Q or O₂, or O₂, respectively. Although NADH binding and hydride transfer are fast, these processes are not treated as rapid equilibrium reactions because some of the experimental conditions contain 0 NAD⁺. In order to apply the rapid equilibrium assumption, both the substrate and the product must be present to avoid a mathematical singularity. These rates are computed using equations 51–96 in the Supporting Material.

Flux expressions

The rate of net substrate/product consumption is computed as the sum of the net flux for each branch in the cycle involving that substrate/product. The rate of electrons entering from oxidation of either NADH or QH₂ is balance by the rate of electrons leaving via reduction of NAD⁺, Q, or oxygen. The rate of electron input via superoxide or hydrogen peroxide is negligible and can be ignored; however, they are included in the model to maintain thermodynamic consistency. Equations 97–101 in the Supporting Material are used to calculate net NADH oxidation, Q reduction, superoxide production, and hydrogen peroxide production.

Experimental Data

Most of the data are from the same source, bovine heart mitochondria, with a few data from rat heart mitochondria. Of all the data, the kinetic data and the ROS data from bovine heart mitochondria are the most reliable and have all relevant variables measured or known. The ROS data from intact rat mitochondria are less complete. All variables were not measured and certain approximations had to be made that are important for parameter estimation. For these data, we were only concerned with matching the trends and simulating fluxes in the neighborhood of what was reported.

Purification of Complex I for kinetic studies is non-trivial. Yoshikawa reports the need for a tightly bound Q₁₀ prosthetic group for catalytically active Complex I [15]. When they attempted to improve the purity, the stoichiometry of Q₁₀: FMN dropped below unity, and the enzyme became catalytically deficient. In addition, the enzyme requires an activation step that includes incubation with a small amount of NADH to properly function [6, 16]. This results in a variable mixture of active and inactive enzyme across all preparations. To account for this observation, we tuned the enzyme activities no more than a few-fold change for each dataset during parameter estimation. (Note that this variation did not apply to individual simulations within a given dataset.)

Model Simulations

In our simulations, we included all relevant experimental details reported in the original reference such as enzyme concentration, temperature, and type of reactants used for the kinetic analyses. Also, we assumed both superoxide and hydrogen peroxide were kept low enough to ignore by the ROS detection systems described in the experimental papers (e.g. Amplex Red and horseradish peroxidase, superoxide dismutase, and acetyl-cytochrome c).

The model was developed, parameterized and simulated on an HP desktop PC with an Intel i7–3770 CPU at 3.40 GHz and 16.0 GB of RAM using MATLAB ver. 2013b (Mathworks, Natick, MA). The steady-state equation for the five-state model was analytically solved using MATLAB’s symbolic toolbox. A parallelized simulated annealing algorithm was used to globally search for feasible parameters before employing a local, gradient-based optimization algorithm. A standard deviation of 10% of the max value was used during parameter estimation unless given in the original data set.

Results and Discussion

The model was challenged with a wide array of data from the literature: i) kinetics that includes various substrate product combinations at different pH, iii) kinetics in the presence of a membrane potential, iii) kinetics at temperatures from 20 °C to 37 °C, and iv) conditions that favored ROS generation from the either the FMN, semiquinone or both. In each case, the model is able to reproduce the experimental data within a small margin of error. This is a significant achievement considering that the data contain electron fluxes that range from high to low through the NADH oxidase site to the Q reductase site and low electron flux through the NADH oxidase site to oxygen with Q-site reactions inhibited by rotenone. In all simulations, the NAD⁺ and NADH dissociation constants, NADH- and Q-associated state transition rates, and ROS rate constants were identical. Only the Q-analogue dissociation constants and related stability constants were allowed to vary. Better fits are obtained when Q-related rate constants are allowed to be substrate specific. But we feel that this adds unnecessary complexity to the model. See Table S2 for kinetic parameter details.

In general, most of the kinetic parameters are identifiable and are in the range of previously reported values. An identifiable parameter is defined as one having high sensitivity and low correlation with other parameters. (See Table S4 for the correlation coefficients.) The most sensitive parameters are the ones associated with NADH oxidation and those related to Q reduction rates. Several of the NADH and NAD⁺ dissociation and rate constants are in the top ranked set of identifiable parameters. This is not surprising considering that NADH and/or NAD⁺ are perturbed in all the data used for parameter estimation. A few parameters are highly correlated with others. For example, the stability constants and Q dissociation constants are highly correlated with each other. Of the ROS parameters, five parameters are sensitive and relatively uncorrelated with other parameters. They are $k_{f,1\to 0}^{{SQ}^{.-}/O_2^{.-}},k_{f,2\to 1}^{{\mathit{FMNH}}_2/O_2^{.-}},k_{f,1\to 0}^{{\mathit{FMNH}}^{.-}/O_2^{.-}},k_{fa,3\to 1}^{{\mathit{FMNH}}_2/{\mathrm{H}}_2{O}_2}$, and $k_{fb,3\to 1}^{{\mathit{FMNH}}_2/{\mathrm{H}}_2{O}_2}$. These parameters are associated with the minimal set of ROS producing states required to reproduce the data. Most of the ROS parameters are insensitive which implies that the associated states are not significant sources of ROS. And the correlation among these parameters suggests the need for more data and/or the need for further model simplification. See Table S3 for ROS parameter details.

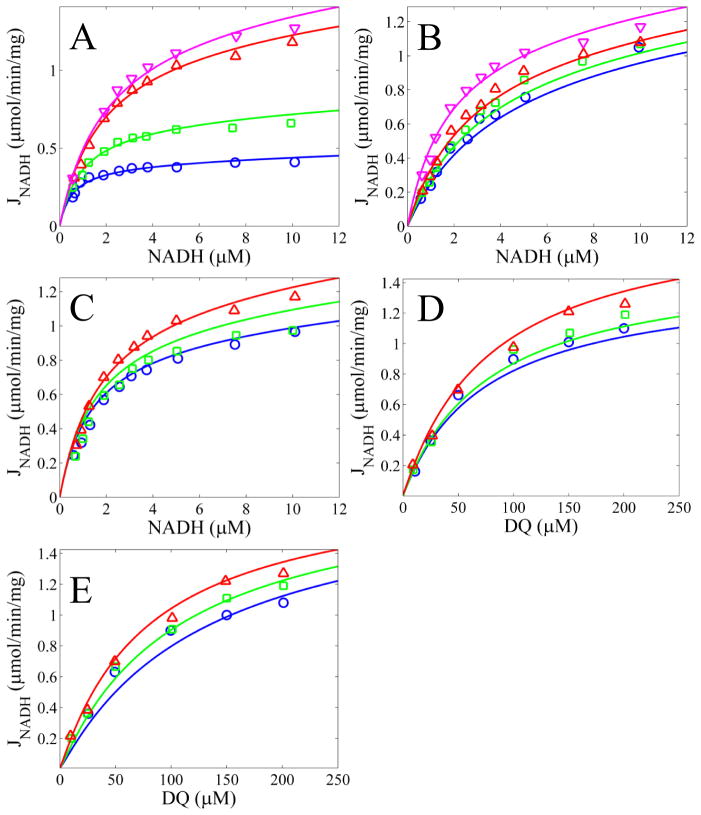
Figure 2 shows model simulations reproducing data obtained using decylubiquinone as the electron acceptor. The data were obtained from purified bovine enzyme. The simulations reveal the model’s ability to capture the NADH oxidation kinetics for a variety of substrate and product combinations. We also fit kinetic data from bovine heart sub mitochondrial particles obtained by ultrasonic irradiation; freeze-thawed mitochondria; and intact, uncoupled mitochondria as shown in Figures S1 and S2. These fits also show that the model can reproduce kinetic data from a wide range of experimental conditions. For simulation details, see figure legends.

Figure 2. Model simulations of NADH oxidation rates as a function of DQ compared to data.

A) NADH concentrations are varied for fixed DQ concentrations of 25, 50, 100, and 200 μM for blue, green, red, and magenta lines and circles, respectively. B) NADH concentrations are varied for a fixed DQ concentration of 100 μM and fixed NAD⁺ concentrations of 0, 200, 400, and 600 μM for blue, green, red, and magenta lines and circles, respectively. C) NADH concentrations are varied for a fixed DQ concentration of 100 μM and fixed DQH₂ concentrations of 200, 100, and 0 μM for blue, green, and red lines and circles, respectively. D) DQ concentrations are varied for a fixed NADH concentration of 10 μM and fixed NAD⁺ concentrations of 600, 400, and 0 μM for blue, green, and red lines and circles, respectively. E) DQ concentrations are varied for a fixed NADH concentration of 10 μM and fixed DQH₂ concentrations of 200, 100, and 0 μM for blue, green, and red lines and circles, respectively. The pH was 8.0 and ΔΨ was 0 for all simulations. All data from [32].

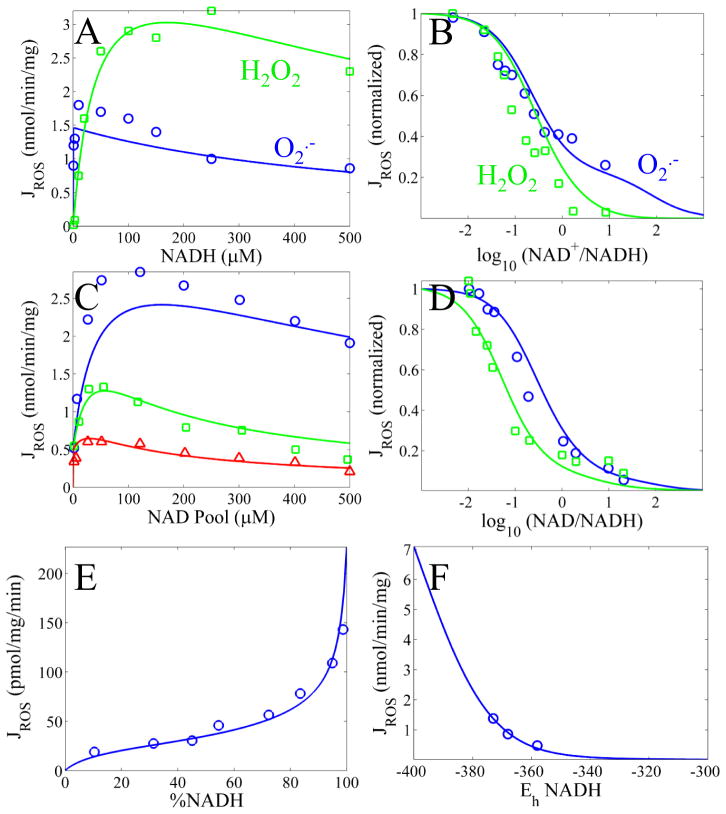
Figure 3 shows model simulations of ROS generation from various sites compared to experimental data. When rotenone was present, we assumed no interaction at the Q reductase site. The simulations reveal that the model is captures the NADH dependence of ROS production quite well and also is able to simulate ROS production under RET conditions. Data in Figure 3A–D were obtained from bovine SMPs incubated with rotenone to block electron flow at the Q reductase site [11, 17]. The rate of NADH oxidation was monitored under a variety of experimental conditions. For Figure 3A, only NADH was changed while measuring the production rate of superoxide (blue) and hydrogen peroxide (green). For Figure 3B, the NAD⁺/NADH was manipulated while measuring the production rate of superoxide (blue) and hydrogen peroxide (green). In Figure 3C, the total rate of ROS production (superoxide plus hydrogen peroxide) was measured as the NAD(H) pool size was changed at various ratios of NAD⁺:NADH (blue, 0:1; green, 1:5, red 1:1). Data in Figure 3E and F were obtained from intact rat skeletal muscle [9, 18]. The mitochondria were inhibited with stigmatellin and energized with ATP. Figure 3E shows the rate of total ROS production at the FMN site by blocking the Q reductase site with rotenone. The percent of NADH was titrated with malonate and succinate. Figure 3F shows the rate of total ROS production at the Q reductase site at specified NADH redox poises. The Q pool was assumed to be in equilibrium with the NADH redox poise and proton motive force as described in the original paper [9].

Figure 3. Model simulations of superoxide (O₂^·−), hydrogen peroxide (H₂O₂) or total ROS production.

A) Rates of simulated O₂^·− (blue) or H₂O₂ (green) production as a function of NADH concentration are compared to data from [11]. B) Normalized rates of simulated O₂^·− (blue) or H₂O₂ (green) production as a function of NAD⁺/NADH are compared to data from [11]. C) Rates of simulated ROS (O₂^·− + H₂O₂) production as a function of NADH concentration at a 0:1 (blue), 1:5 (green) and 1:1 (red) NAD⁺:NADH ratios are compared to data from [17]. D) Normalized rates of simulated O₂^·− ROS (O₂^·− + H₂O₂) production as a function of NAD⁺/NADH for a 50 (blue) and 500 (green) μM NADH pool size are compared to data from [17]. E) Rates of simulated ROS (O₂^·− + H₂O₂) production from the flavin as a function of %NADH[18]. F) Rates of simulated ROS (O₂^·− + H₂O₂) production from the SQ as a function of redox potential. Q₁₀ redox values, ΔΨ, and matrix pH are set as reported in [9].

We found that the best fits were obtained when the FMN site was nucleotide free before any ROS could be generated. In addition, we found that the model fit the data better when this site was deprotonated for the superoxide producing reactions. Based on model analysis, the primary source of ROS originates from several key states. The fully reduced FMN in state 2 and the FMN radical in state 1 are responsible for the majority of superoxide at the NADH oxidase site. For RET conditions, state 1 produces superoxide from the bound SQ at the Q reductase site. Hydrogen peroxide is produced by the fully reduced FMN in state 3, with states 2 and 4 contributing little. That said, in the forward mode, the superoxide is primarily produced right after the 1^st NADH is oxidized followed by a production of hydrogen peroxide after another NADH oxidation step. In the reverse mode, superoxide is generated at both the Q reductase and NADH oxidase sites after QH₂ is oxidized. In fact, we find that the contribution to superoxide from the FMN and the SQ is about equal in nearly all cases examined.

The ability of a SQ to reduce oxygen to for superoxide in Complex I is still debated [6, 9]. It has been argued that only the reduced FMN is responsible for ROS in either FET or RET operating conditions [6]. But others have contended that there exists two sites of superoxide production [9]. In the former study, the authors concluded that they only observed ROS from the reduced FMN and the SQ did not produce any ROS. However, the bovine SMPs that they used were relatively uncoupled. It is well known from a thermodynamic perspective that there must be a high ΔΨ and a highly reduced Q pool in order for an appreciable amount of SQ to form. So it is likely that in the study by Pryde and Hirst, the experimental conditions were not optimal to observe ROS from the SQ. Another group showed that superoxide production is closely correlated with the amount of SQ and not the fully reduced FMN or FMN radical [12]. Moreover, the model requires superoxide production from SQ in order to explain the data in a consistent manner. Therefore, there are at least two sites on Complex I capable of producing ROS.

Interestingly, we found the model best reproduced the data when superoxide from the Fe-S cluster N2 was excluded. This is surprising considering that several investigators have argued the contrary [10, 11]. But in a recent report, Ohnishi et al. show that in the presence of a Q substrate, superoxide levels produced by isolated complex I is more correlated with the EPR signal of the SQ than the reduced N2 [12]. In the absence of a Q substrate, superoxide levels are highly correlated with the FMN radical. They interpret these results as evidence for the 1e- reduced FMN and the SQ as the source of ROS from complex I. These findings are in direct support of our model simulations. Furthermore, model analysis reveals that the FMN radical is only a significant source of ROS when Q is absent or Q reductase site inhibitors are present. This is consistent with the findings of Kussmaul and Hirst [7]. For example, in Figure 3B, it was concluded that the Fe-S cluster N2 was the likely source of superoxide since the rate of superoxide production did not follow the NAD⁺ Nernst potential as did the rate of hydrogen peroxide. Model analysis uncovers that the source of superoxide is a mixture of the fully reduced FMN and the FMN radical. The model is capable of explaining much of the available ROS data, but multiple sites of potential ROS generation do limit the ability to identify the precise mechanism. We considered many scenarios that included many of the putative sources of ROS, but the most parsimonious model only included ROS production from the 2e-/1e- reduced FMN and SQ species. That said, these species constitute the minimum number of redox species required to reproduce the data which is in full agreement with previous findings.

Table 1 shows that the model is quite capable of simulating NADH oxidation rates under a wide range of conditions, including physiological ones. The experiments include uncoupled bovine SMP preparations and intact isolated mitochondria from porcine heart. The intact isolated mitochondrial data are particularly relevant when identifying the model components involving proton motive force (Δp)-dependent steps. The proton motive force is the proton electrochemical potential defined in millivolts. Based on thermodynamic principles, only part of the reaction cycle is capable of supporting proton pumping. In particular, the final reduction step at the Q-site is the favored step that is responsible for proton pumping. In a recently published mechanism, T reberg et al. argue that this is indeed the case [19]. In the model, this corresponds to states transitions 2→0, 3→1, and 4→2 that involve Q. We find that doing so results in a feasible mechanism that can explain the data. However, model analysis uncovers a potential kinetic issue that must be addressed before this determining the true nature of the proton pumping mechanism.

Table 1.

Model Simulation Results of Various Oxidase and ROS Rates Compared to Data

Model Conditions	Model	Experiment	Ref.
NADH=100 μM, Q=50%, ΔΨ=0 mV, pHn=pHp= 8a	1661	1600 ± 150 nmol/min/mg	[11]b
NADH=100 μM, Q=80 μM, ΔΨ=0 mV, pHn=pHp= 8	901	900 ± 70 nmol/min/mg	[11]b
NADH=100 μM, Q=Ø, 33=0 mV, pHn=pHp= 8c	4.13	4 ± 0.2 nmol/min/mg	[11]b
NADH=60%, Q=18.7%, ΔΨ=172 mV, pHn = 7.14e	30.8	30.8 ± 0.9 nmol O2/min/nmolCyta	[33]d
NADH=76%, Q=77.4%, ΔΨ=194 mV, pHn = 7.13e	40.0	40 ± 3.4 nmol O2/min/nmolCyta	[33]d
NADH=45%, Q=1.2%, ΔΨ=148 mV, pHn = 7.16e	27.4	24.6 ± 4.4 nmol O2/min/nmolCyta	[33]d
NADH=29%, Q=99.9%, ΔΨ=163 mV, pHn = 7.14e	245	256 ± 20 nmol O2 /min/nmolCyta	[33]d

^aAssuming max NADH-oxidase activity when Q pool is 50% reduced.

^bSMP experimental system.

^cRotenone inhibited.

^dIsolated mitochondria experimental system. Assumed all oxygen reduced by NADH.

^epH_p = 7.1. %Q was fit to match experimental rates. For further experimental details, see associated references. NAD and Q pool sizes given in Table S1.

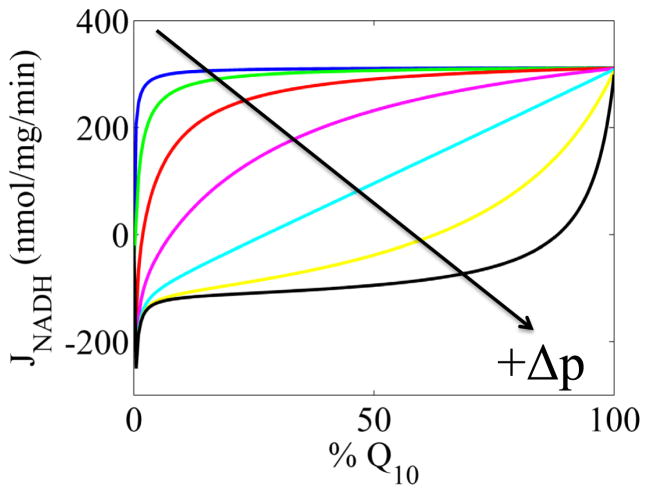
In Figure 4, the dependence of the rate of NADH oxidation on the Q pool redox state at various fixed Δp is presented. As the Δp is decreased, the rate becomes more and more insensitive to the Q pool redox state. This is a consequence of stacking the entire Δp-dependence on a single step whereby the rate constant for this step changes 6-orders of magnitude when the Δp changes from 0 to 200 mV. With this dependence, the model is hypersensitive to Δp, and at Δp< 100 mV the rate of NADH oxidation is increasingly insensitive to the Q pool redox state and only depends on the NAD(H) pool redox state. For example, at a Δp of 0 mV, the half-maximum rate of NADH oxidation is achieved at a Q pool poise of −390 mV. But at 180 mV, the Q pool poise reaches a more oxidized potential of 40 mV at the half-maximum rate. During the parameter estimation process, we could also fit the data by invoking an asymmetric energy barrier at this step or a more distributed Δp-dependence at the cost of additional parameters. For the latter, an example would be to allow some of the processes involving NADH oxidation to help take part in proton pumping. Many have argued that since the free energy drop from NADH oxidation to Fe-S cluster N2 reduction is close to zero, there isn’t enough energy to pump any protons [3, 19–21]. While true, this argument fails to consider the chemical potential energy buildup of enzyme oxidoreduction states that could compensate for this lack of free energy via mass action. That said, we do not have sufficient data to conclusively determine how the energetic cost of proton pumping is distributed in the reaction mechanism. From an experimental design perspective, it would be informative to compare NADH oxidation rates vs the Q pool (endogenous) redox state in both uncoupled mitochondria and energized mitochondria. These types of data would allow us to infer which steps in the reaction mechanism are coupled to proton pumping. So until more data become available on this matter, nothing more can be said about the nature of the Δp-dependence.

Figure 4. Model simulations of NADH oxidation rates as a function of Q pool redox state at various fixed Δp’s.

The Δp increased from 140 mV to 200 mV in 10 mV increments starting from the top, blue line. The arrow indicates the direction of Δp decrease. The Q-reductase site parameters are the Q₁₀ ones listed in Table S2. For all curves NADH is 50% of the NAD(H) pool. Both matrix and cytosolic pH equal 7.1, so the Δp is equivalent to the ΔΨ.

The manner in which Complex I produces ROS as a function of electron input from either NADH or QH₂ is complex. While it depends on several factors that control electron flow, it is most correlated with elevated ΔΨ and matrix pH[22, 23]. This relationship can be written as the following biochemical equation:

$$\mathit{NADH}+(1-n)Q+n{\mathrm{O}}_2+H^{+}\rightleftharpoons {\mathit{NAD}}^{+}+(1-n){QH}_2+{nH}_2{O}_2.$$ Eq. 1

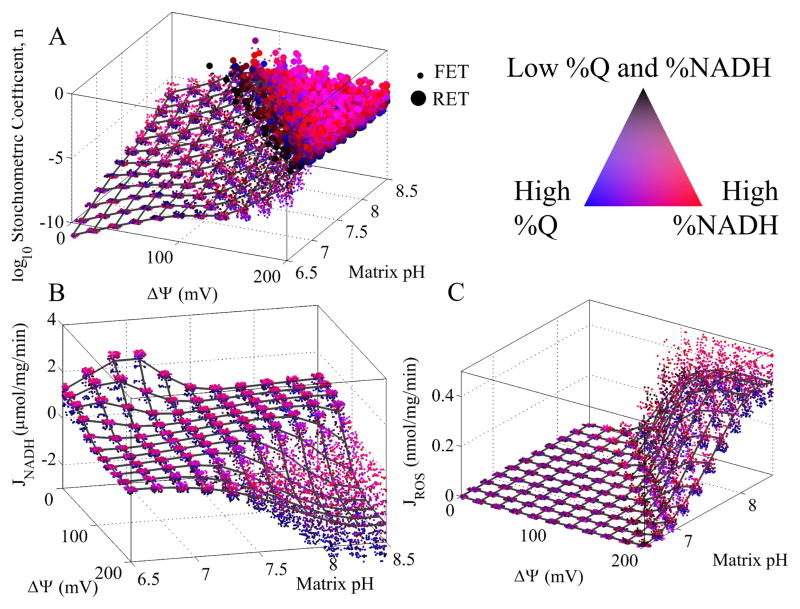
Without loss of generality, we only consider hydrogen peroxide as the final ROS product. We assume that any superoxide formed is quickly converted to hydrogen peroxide. When the reaction reverses, the coefficient 1-n is moved from the Q and QH₂ to NAD⁺ and NADH. The stoichiometric coefficient, n, determines how much of the reduction potential of NADH or QH₂is leaked to oxygen. This coefficient is not static and depends on a range of conditions. In Figure 5A, n is plotted as a function of ΔΨ, matrix pH, %NADH, and %Q. The ΔΨ and matrix pH are plotted on the main independent axes, and the %NADH and %Q are depicted using a color scheme. Cytosolic pH was fixed at 7.1 in all simulations. In addition, small points corresponding to FET and large circles represent RET operating conditions. For details, see the figure legend. At low ΔΨ and pH, n is small and nearly all of the electrons from NADH reach their intended target, Q. As both ΔΨ and pH increase, not only does n increase, but also, the amount of RET increases as well. In agreement with previous studies [9], the model predicts that ROS are produced in greater excess during RET versus FET. Most notably, the fraction of electrons reducing oxygen becomes quite significant when both the NAD(H) and Q pools are highly reduced. This is a direct result of electrons having nowhere else to go except to oxygen.

Figure 5. Model simulation of ROS stoichiometric coefficient, n, NADH oxidation, and ROS production as a function of ΔΨ, matrix pH, %NADH, and %Q.

The ΔΨ and pH are plotted on the main independent axes, and the %NADH and %Q are depicted using a color scheme. The legend for the color scheme is indicated in the figure. Blue indicates high %Q, red indicates high %NADH, magenta indicates both high %Q and %NADH, and black indicates low %Q and %NADH. In A), small points corresponding to forward electron transport (FET) and large circles represent reverse electron transport (RET) operating conditions. FET is defined as NADH-induced reduction of Q. RET is defined as QH₂-induced reduction of NAD⁺. The mesh represents the average value at a given ΔΨ and pH value. In C, J_ROS is equal to J_O2^·−/2 + J_H2O2. Cytosolic pH was set to 7.1 in all simulations.

Figure 5B shows the rate of NADH oxidation as a function ΔΨ, matrix pH, %NADH, and %Q. The maximum rate is observed at 0 mV and a pH near 7. As either ΔΨ or pH increases, the rate of NADH oxidation decreases until the reaction reverses when the Δp crosses ~200 mV. Also, higher rates are observed when the NAD(H) pool is reduced and the Q pool is oxidized. The figure shows that there exists a large, flat plane of physiological NADH oxidation rates (100s of nmol/mg/min) at various combinations of ΔΨ and matrix pH. These combinations correspond to Δp values near 150 mV and demonstrate that ETC is capable of maintaining physiological rates under a range of ΔΨ and matrix pH conditions.

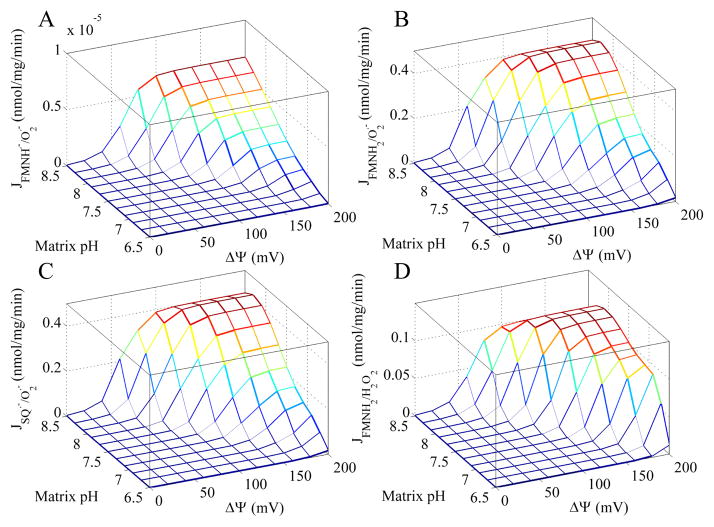
Figure 5C shows that the amount of ROS produced only becomes significant as the reaction shown in Eq. 1 reaches equilibrium and after it reverses. In particular, the majority of ROS arises when both the NAD(H) and Q pools are highly reduced. The origin of this ROS is elucidated in Figure 6. In all cases, the rate of ROS production increases at every potential site when both ΔΨ and matrix pH is elevated. But the ROS from the FMN radical is insignificant compared to the fully reduced FMN and SQ. Surprisingly, superoxide from the fully reduced FMN and SQ are near equal in all conditions. And their contribution to the total ROS (as defined as 2e⁻ equivalents) is greater than hydrogen peroxide formation from the fully reduced FMN. Thus, the FMN is a major source of ROS and conditions that favor its reduction will tend to increase ROS from Complex I.

Figure 6. Simulated ROS production rate for each redox center under the conditions described in the legend of Figure 5.

For each ΔΨ and matrix pH combination, the maximum ROS production rate is shown for each redox center.

Studies have shown that depletion of the mitochondrial NAD(H) pool is associated with elevated ROS and cell death [24–26]. The model supports these findings in that increased ROS production is simulated when the NAD(H) pool is lowered (see Figure 3D). This excess ROS originates from the FMN and is corroborated by the experimental studies from Vinogradov’s lab [11, 17]. In their studies, they show that ROS production decreases with an increasing NAD(H) pool size. Moreover, comparing the ROS production from the FMN measured in the Vinogradov lab to those measured in the Brand lab substantiates these findings [18]. Brand observes a ROS production rate that is roughly 20 times less than that reported by the Vinogradov lab. This is due to a variety of factors, but primarily results from the endogenous NAD(H) pool. In Brand’s studies, isolated skeletal rat mitochondria were used. In this system, the NAD(H) pool is in the mM range and there exists a residual amount of ROS scavenging unaccounted for. So despite the difference in magnitude of ROS production measured by both labs, factoring in the above details places them into parity.

To date, few thermodynamically consistent models of Complex I exist. The models range in complexity from simple linear, flux-force [27], nonlinear mass action [28], extensively detailed, large systems of ordinary differential equations [29, 30], and kinetic models [31]. While each of these models has their own strengths and weaknesses, none are able to simulate ROS generation. The model discussed herein is able to reproduce a wide range of experimental observations that includes NADH oxidation and ROS production rates in a thermodynamically consistent manner. As such, it is an ideal model to integrate into existing models of the mitochondrial electron transport system and oxidative phosphorylation.

Overall, our study helps resolve a critical issue pertaining to the origins of ROS from Complex I. By analyzing independent data sets on Complex I kinetics and ROS generation, we show that the primary source of ROS is the FMN. However, the SQ also plays an important role in ROS generation when the electron flow reverses. Surprisingly, the Fe-S cluster N2 does not produce ROS at a significant level and only acts as an electron intermediary between NADH and Q. We also show that the pumping mechanism that is directly coupled to the reduction of the SQ in the reaction scheme is thermodynamically and kinetically feasible.

Abbreviations

Complex I, NADH

ubiquinone oxidoreductase

ETC

electron transport chain

Q

quinone

FMN

Flavin mononucleotide

Fe-S

iron-sulfur

RET

reverse electron transport

ROS

reactive oxygen species

FET

forward electron transport

SQ

semiquinone