Recent Advances in Computational Epidemiology

Public health epidemiology aims to understand the spatio-temporal spread of diseases and to develop methods to control such spread. The threat of pandemic outbreaks across multiple continents and the associated economic and social costs is a key societal concern, and continues to demand significant resources for modeling, detection, and control efforts (case in point: the recent influenza outbreak caused by H7N9 in China).

Computational epidemiology has become increasingly multidisciplinary (borrowing techniques from epidemiology, molecular biology, applied mathematics, theoretical computer science, machine learning, and high performance computing) and has led to novel computational methods for understanding and controlling spatio-temporal disease spread. Here, we highlight some recent advances, focusing specifically on modeling, data mining, and inferential and planning questions. We focus on infectious diseases, primarily involving humans.

1 Modeling Epidemics: An Interaction Based Approach

Traditionally mathematical epidemiology has focused on rate-based differential equation models. In this approach, one partitions the population into subgroups based on various criteria (e.g., demographic characteristics and disease states), and uses differential equation models to describe the disease dynamics across these groups. Models such as [17] characterize disease dynamics by a parameter, R₀, the basic reproduction number. R₀ is defined as the number of secondary infections caused by a single infective individual into a wholly susceptible population. It determines whether an epidemic can occur at all; if R₀ < 1, the epidemic will die out, while if R₀ > 1, then we will have an epidemic. This approach has been tremendously successful in informing public health policy. Nevertheless, a potential weakness is its inability to capture the complexity of human interactions and behaviors.

Effective planning and response in the event of epidemics is not about just prediction, but anticipation and adaptation. The typical workflow of a public health analyst involves the measure-project-analyze-intervene cycle. Diverse data is collected via surveys, social media, sensors and policy documents, which are then analyzed to yield contextual situational representations. Dynamic models in the form of computer simulations are then used to interpolate as well as extrapolate from the data. Simulations are also used to evaluate various what-if scenarios (counterfactual experiments). This information is used by a policy analyst to make specific policy decisions, potentially leading to changes in epidemic dynamics. The measure-project-analyze-intervene cycle motivates an ‘interaction based approach’ for developing informatics platforms. Here we aim to accurately model the social interactions that form the basis of disease transmission. The approach uses endogenous representations of individuals together with explicit interactions between these agents to generate and capture the disease spread across the social interaction network.

However, this approach is fraught with new technical difficulties. It is impossible to obtain an accurate, detailed, time-varying urban-scale human social contact network by simple measurements. Nevertheless, recent advances in machine learning, data mining and network science make it possible to develop new approaches for producing reasonable estimates of such networks. We have developed one such computational approach, the synthetic information environments approach.

2 Synthetic Information Environments

A Synthetic Information Environment (SIE) consists of four components: 1) a statistical model of the population of interest, which we refer to as a synthetic population, 2) an activity based model of the social contact network, 3) models of disease progression, and 4) models for representing and evaluating interventions, public policies and individual behavioral adaptations [5].

First, a synthetic population is generated by integrating census data with other demographic and geographic data to create a population of individual agents. Synthetic populations are statistically identical to the data sources that are used to construct them but preserve individual privacy and maintain anonymity. Second, we generate a detailed minute-by-minute schedule for each individual in the synthetic population, using time-use surveys combined with machine learning techniques (e.g. CART). Activities are then geo-located using business survey information and, using a gravity model, each individual is associated with particular activity locations over the course of the day. The availability of modern datasets collected via phone call logs and social media sites such as Foursquare provide new opportunities to refine the methodology and improve the quality of the assignment.

A time-varying, spatially explicit person-location network can now be constructed using the synthetic data. The synthesis of such networks is an ongoing research theme in computational social science and is sometimes referred to as generative social science [12]. Recently, researchers have explored other methods to synthesize smaller social contact networks using smart phones, RFID tags and other digital devices combined with social media; examples include synthesis of social contact networks for among high school students when attending schools and college students. These methods provide valuable data sources to create smaller subnetworks that can be used for validation purposes [16, 25, 28, 21].

In the third step, each individual is endowed with a within-host disease model represented using probabilistic timed transition systems (PTTS). Individual level demographic variations (immunity, age, etc.) can be incorporated within the framework. Individual PTTS are coupled via the social contact network described earlier. High performance computer simulations are used to understand the spread of the contagion over the network of PTTS.

The final step involves representing and analyzing public policies, individual behavioral adaptations, and the efficacy of various intervention strategies. A key concept here is that of implementable policies and interventions, i.e., policies that are realizable in the real world. For example, an optimal vaccination policy based on computational models might specify a set of k-individuals who are super-spreaders and hence should be vaccinated. But in the real world, it is not easy to identify these individuals explicitly. Data mining and machine learning techniques are used to identify surrogates (i.e., combinations of demographic and social attributes) that can redescribe the super-spreader property.

The biggest strengths of the SIE approach are its scalability and its extensibility. An epidemiologist using the system can easily design a new intervention and carry out an appropriate computer experiment for a large urban area like Los Angeles in minutes to uncover critical individuals and pathways and evaluate the indirect effects (e.g. economic impact) of certain policies.

Simdemics is an integrated modeling environment that embodies the SIE approach to aid state, local and federal public health officials in pandemic planning, response and control [3]. As an example, in [4] we used Simdemics to estimate the social and economic impact of the various public and private intervention strategies aimed at controlling influenza-like illness. We developed a synthetic social contact network for the New River Valley (NRV) area of Virginia¹. We evaluated a range of realistic individual behavioral strategies as well as public policies to control a “flu-like” epidemic. The study showed that a combination of school closure, individual context-based behavioral adaptation and targeted anti-viral distribution can reduce the number of infections by 87% and income loss by 82% as compared to the base case with no intervention.

3 Big Data driving Real-time Epidemiology

Real-time epidemiology, a rapidly developing area within public health epidemiology seeks to support policy makers in near real-time as the epidemic is unfolding [13]. A natural use of real-time epidemiology is in disease surveillance, i.e., the problem of monitoring the space-time progression of disease. Traditional tools for surveillance include sentinel clinics and serological sampling [8]. Recently, social media data [11, 24] has been used to obtain disease outbreaks and progression, an excellent example of how computational advances are changing public health epidemiology.

Perhaps the most celebrated example of social media surveillance is Google FluTrends (http://www.google.org/flutrends/) that uses search engine queries as an indicator of health-seeking behavior, and thus an indicator of disease (flu) activity among a population [15]. Not long after Google FluTrends was introduced, techniques for nowcasting flu rates using Twitter became prominent [19]. Researchers have paid careful attention to content modeling of tweets. For instance, Lamb et al. [18] have developed methods to separate tweets that report actual flu infections from others that exhibit mere awareness/concern about the flu. Broader uses of Twitter for syndromic surveillance, in particular for capturing spatio-temporal distributions of symptoms and medications, have also been explored [22]. In general, social media is a fertile resource for exploring many epidemiological questions, e.g., sentiment propagation about vaccination [26].

The above methods are focused on gross estimation of disease activity over a region. In line with our earlier discussion about synthetic populations, researchers have also explored unraveling patterns of online communication from Twitter with a view to uncovering social interactions. Sadilek et al. [23] use geolocation and machine learning methods to estimate physical interactions between healthy and sick individuals and, in turn, estimate the likelihood of the healthy individual getting infected at some point in the future.

More recent research has focused on identifying social network sensors, i.e., identifying a subset of individuals whose infection states can be monitored to serve as an early indicator of an emerging epidemic. Christakis and Fowler [10] propose a design of social network sensors for monitoring flu based on the friendship paradox: your friends have more friends than you do. Alternatively it can be said that a friend of a random person has higher expected degree than that of the random person. Christakis and Fowler use the set of friends nominated by randomly chosen people as a sensor set. After a field study on randomly selected students at Harvard during the flu season in 2009, they found that the peak of the daily incidence curve in the sensor set occurs 3.2 days earlier than that of a random set of students.

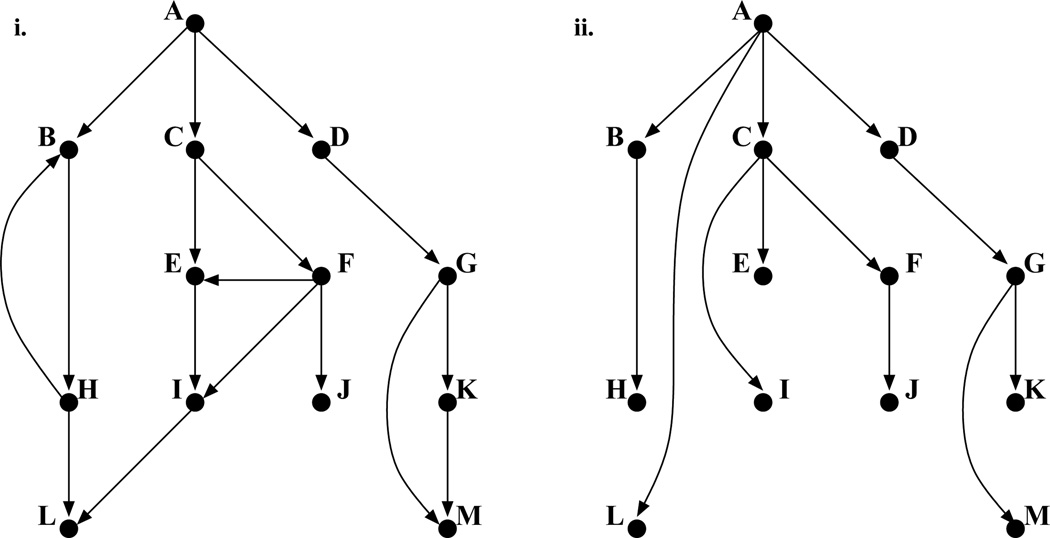
In [27], we have formalized the idea of social network sensors using the notion of graph dominators [20]. In a given graph, a node x is said to dominate a node y if all paths from a designated start node to y must go through x. In our case, the start node indicates the source of the infection or disease. In Fig. 1 (left), which describes a social contact network with nodes as people, all paths from node A (the designated start node) to H must pass through B; therefore B dominates H. Note that a person can be dominated by many other people. For instance both C and F dominate J (further C dominates F). To simplify such transitive situations, we say that node x is the unique immediate dominator of y iff x dominates y and there does not exist a node z such that x dominates z and z dominates y. This enables us to uncover an underlying tree of dominator relationships, as shown in Fig. 1 (right), with a much smaller number of edges than the original graph.

Figure 1.

(i) An example graph and (ii) its dominator tree.

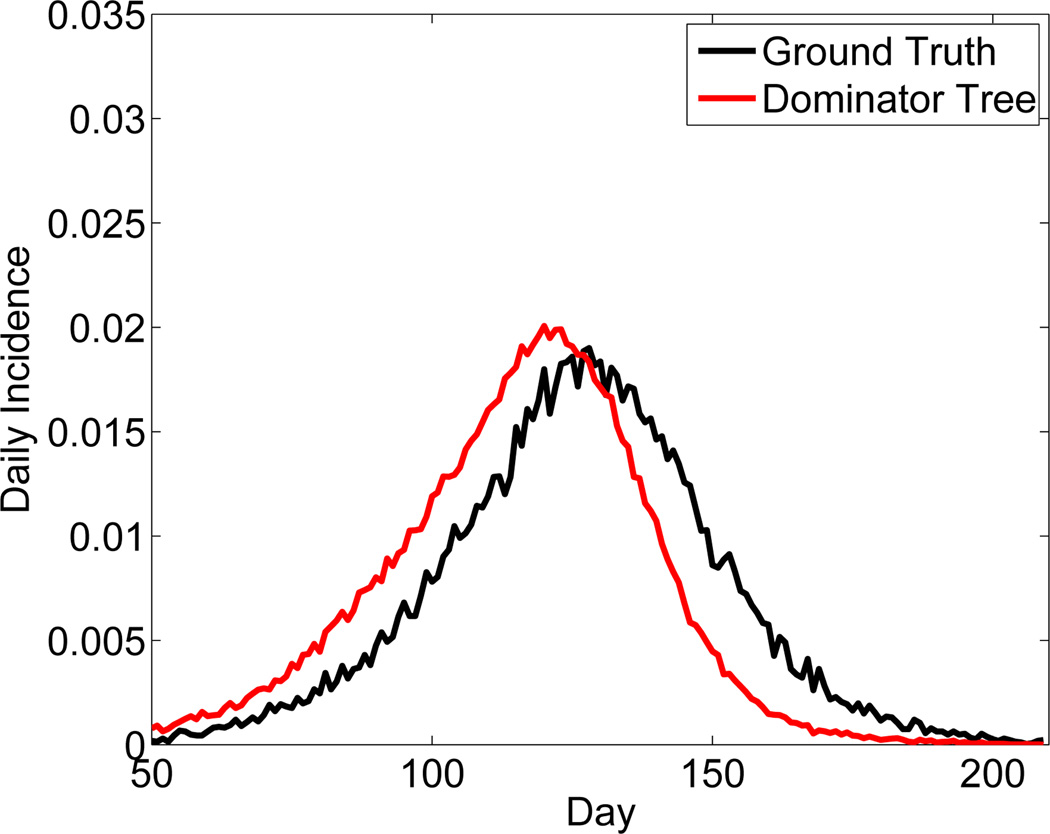
If we were to reconstruct the social contact network, therefore, we can readily compute the dominator tree and capture critical junctures in the transmission of epidemics. Using city-scale datasets generated by extensive microscopic epidemiological simulations involving millions of individuals, we have shown how the notion of dominators can provide up to 10 days more lead time compared to the friend-of-friends approach (see Fig. 2). Most importantly, as we show in [27], we can develop surrogates/proxies for policy makers for designing social network sensors that do not require intrusive knowledge of people and their relationships. For instance, we can identify demographic properties that best redescribe the dominator relationship, and use these properties to help form the sensor set in practice.

Figure 2.

Monitoring an epidemic using a social network sensor based on the dominator heuristic enables earlier detection, i.e., the peak in the sensor curve occurs ahead of the peak in the general population.

4 Resource Allocation, Behavior Modeling, and Inference

Computational models and machine learning are important for broader policy questions in epidemiology as well. When applying these techniques in practice, one faces the usual challenges: the data is noisy and insufficient, resources are scarce, there are multiple objective functions, and most importantly time to decision making is short.

Resource optimization problems arise in epidemiology when scarce public health resources need to be expended to respond to epidemic outbreaks. Examples of such problems include: (i) allocation of vaccines and anti-virals, (ii) medical equipment such as facemasks, hospital beds, ventilators, etc., (iii) staffing problems at hospitals, and (iv) allocation of pharmaceuticals. The objective functions are complex, including economic costs, health costs, and social disruptions. Moreover the objectives are usually conflicting, thus making the decision-making process harder.

Inference problems in epidemics arise from the need to understand the spatio-temporal characteristics of an epidemic especially at the start of the epidemic. Examples include: (i) inferring the index case, (ii) inferring the disease properties, (iii) inferring the social contact network and (iv) inferring the transmission tree.

A prototypical and important problem is vaccine allocation for controlling influenza outbreaks. Even the basic problem is computationally challenging. It is complicated by the fact that due to various logistical complications, vaccines become available in batches. Moreover, just like in the social network sensors problem, it is important to develop an implementable strategy for assigning vaccines. Classical work has focused either on optimal strategies that are not implementable or on allocating vaccines to predefined groups. In [1], we combine data mining techniques and dynamical properties of networks to design a near-optimal vaccination strategy that compares very well with known strategies.

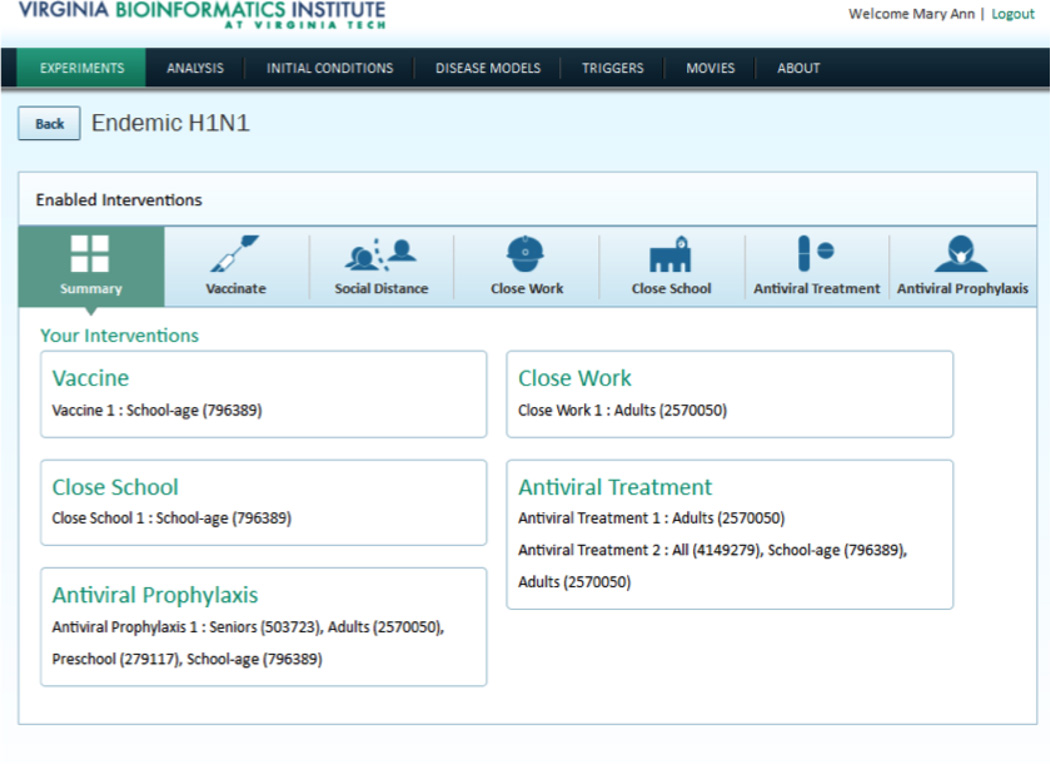
It is important to note that the application of interventions, guided by public policy, will in turn induce behavioral changes in individuals. A computational representation theory of behaviors as it pertains to epidemiology thus needs to be developed. Health scientists have developed verbal or conceptual behavioral models [6, 2] to understand the role of behaviors in public health. But these models are typically informal and it is quite demanding to identify the data necessary to instantiate in-silico behavioral models. Recent advances in social media, crowd sourcing (e.g., Computational Turk), online games, online surveys, and digital traces all form the basis of potentially very exciting methods to make progress in this direction [14]. In [7], we have developed a computational modeling environment wherein complex behaviors and interventions can be represented and analyzed. Fig. 3 presents the interface to our system that enables the analyst to set up complex statistical experiments (interventions) and analyze their effects on the underlying population. The experiments are then executed using a high performance computing oriented simulation, and the results are summarized and presented to the user.

Figure 3.

Isis is a web-based decision support environment that allows public health epidemiologists to analyze various counter-factual scenarios related to epidemic planning.

As a case study, we have explored an important policy problem in epidemiology: is there an optimal strategy to distribute a limited supply of anti-viral (AV) doses between the public stockpile administered through hospitals and private stockpiles distributed through a market mechanism? In modeling this problem, we considered a number of measures of effectiveness, including number of people infected, peak number of infections, cost of recovery, and equitable allocation. We were broadly interested in understanding how disease dynamics, individual behavior, network structure, and AV demand co-evolve. We developed and instantiated several behavioral models based on published literature and data. These models spanned individual behaviors (e.g., reporting of symptoms by infected persons), family behaviors (e.g., purchasing behaviors and isolation precautions), and organizational behaviors (including behavior of markets as well as entities such as hospitals). See [9, 7] for more details.

Key findings based on our experiments include: (i) Market based distribution is inherently inequitable, (ii) Prevalence of elastic demand leads to inequitable distribution (due to price increase); this provides ways to evaluate government investment, (iii) There is an optimal allocation strategy of AVs between public and private stockpiles, (iv) Natural behavior adaptations in conjunction with well established logistics (markets + public distribution) reduce and delay the peak infection rate.

5 Conclusions

The use of machine learning and reasoning methods in support of computational epidemiology is a rich area with many significant research challenges. Key areas for future research include:

New methods and data sources for extending synthetic populations

This is a relatively understudied problem, and formal characterization of the difficulty of the problem as well as efficient and effective algorithm development needs to be undertaken.

Integrating model-driven methods with data mining approaches

We have hinted at some possibilities here but more opportunities abound, e.g., using a combination of approaches to design quarantine policies from field data, behavioral models, and a theory-driven statement of epidemiological objectives.

Social network sensors

Can we develop new methods and surrogates for identifying sentinel populations from both massive passive data (twitter) and for use in clinics and hospitals?

Fine-grained modeling of social media datasets

As techniques for content modeling and text mining become increasingly sophisticated, we believe there will be a greater carryover of such methods to syndromic surveillance with real-time epidemiological applications.

Active data collection, leading to co-evolving policy, simulation, and mining

There is increasing interest in conducting cell phone surveys and integrating such survey data with more passively gathered information. Active data can help ‘fill in the gaps’ that traditional data mining of passive datasets. For instance, a survey of disease symptoms in a targeted region combined with mining of tweets can give lead time advantages in detecting an emerging epidemic.