Cherenkov Excited Phosphorescence-based pO₂ Estimation during Multi-beam Radiation Therapy: Phantom and Simulation Studies

Abstract

Megavoltage radiation beams used in External Beam Radiotherapy (EBRT) generate Cherenkov light emission in tissues and equivalent phantoms. This optical emission was utilized to excite an oxygen-sensitive phosphorescent probe, PtG4, which has been developed specifically for NIR lifetime-based sensing of the partial pressure of oxygen (pO₂). Phosphorescence emission, at different time points with respect to the excitation pulse, was acquired by an intensifier-gated CCD camera synchronized with radiation pulses delivered by a medical linear accelerator. The pO₂ distribution was tomographically recovered in a tissue-equivalent phantom during EBRT with multiple beams targeted from different angles at a tumor-like anomaly. The reconstructions were tested in two different phantoms that have fully oxygenated background, to compare a fully oxygenated and a fully deoxygenated inclusion. To simulate a realistic situation of EBRT, where the size and location of the tumor is well known, spatial information of a prescribed region was utilized in the recovery estimation. The phantom results show that region-averaged pO2 values were recovered successfully, differentiating aerated and deoxygenated inclusions. Finally, a simulation study was performed showing that pO₂ in human brain tumors can be measured to within 15mmHg for edge depths less than 10-20mm using the Cherenkov Excited Phosphorescence Oxygen imaging (CEPhOx) method and PtG4 as a probe. This technique could allow non-invasive monitoring of pO₂ in tumors during the normal process of EBRT, where beams are generally delivered from multiple angles or arcs during each treatment fraction.

1. Introduction

Tissue partial pressure of oxygen (pO₂) is well known to affect the efficacy of radiation therapy because radiation-induced reactive oxygen species are the dominant mediator of the biological tissue damage (1-3). The ratio of cell killing efficacy by radiation in tissue varies about 3 fold with and without oxygen (1, 2), while tumors are known to frequently contain highly hypoxic regions. Therefore, the ability to quantify tissue pO₂ in tumors could benefit tumor treatment and dose delivery planning. However, all currently existing methods of tissue oxygen measurements have significant limitations. The most established method relies on needle-type oxygen electrodes to acquire point measurements at multiple locations (3). Unfortunately, such invasive probing is not feasible during the course of a standard radiation therapy treatment, while non-invasive methods, such as reflectance spectroscopy (4) or pulse oximetry, relay information about tissue oxygenation via oxygen saturation of hemoglobin. In normal tissue, under steady state conditions, average tissue pO₂ and hemoglobin (Hb) saturation are usually correlated. However, in diseased tissue the balance between the hemoglobin-(Hb) bound oxygen and oxygen that is seen directly by the cells can be compromised due to impaired delivery and/or consumption. Furthermore, Hb-based measurements are limited by the excitation light delivery, which may be inefficient for relatively deep-seated tumors.

Here we present our efforts to develop a new non-invasive method to quantitatively image regional tissue pO₂ during routine application of external beam radiation therapy with multiple beam treatment. This method is referred to as Cherenkov Excited Phosphorescence Oxygen (CEPhOx) imaging. It is based on phosphorescence lifetime imaging (5, 6) with probes whose phosphorescence lifetimes report on local oxygen concentration.

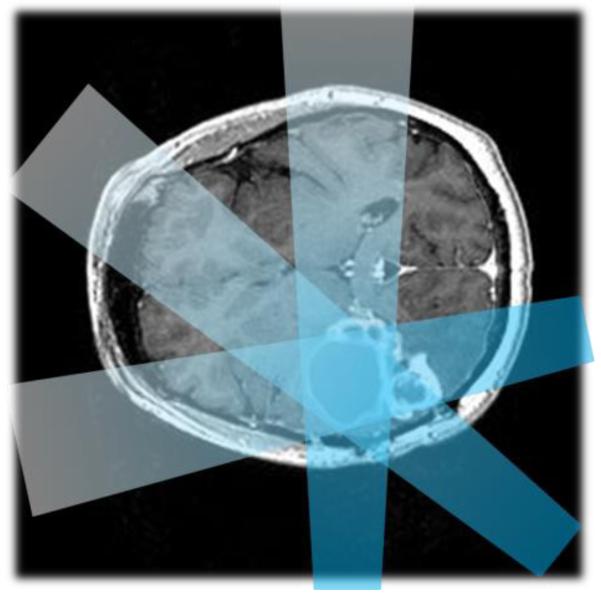
Radiation therapy is performed by directing ionizing radiation to a prescribed volume. In order to maximize the radiation dose in the tumor region and to minimize the dose to benign tissue, multiple crossing beams at different incident angles are used (figure 1). This treatment occurs by moving the beam of a linear accelerator or rotating the patient bed, or both. CEPhOx imaging makes use of these multiple beams to perform tomographic recovery of the pO₂ in the targeted region relative to the surrounding tissue.

Figure 1.

A schematic of a multi-beam radiation treatment plan for a brain tumor is shown.

Cherenkov radiation occurs when charged particles move in a dielectric medium (such as water or biological tissue) at a phase velocity greater than the speed of light in that medium, and it is regularly emitted throughout the volume of tissue subjected to therapeutic beams of even relatively low intensities (tens of nW/cm³) (7-15), and tissues which have been injected with radiotracers(16, 17). The spectrum of Cherenkov emission is highly weighted to the ultraviolet/blue spectral region. However, due to the high absorption of UV/blue light in biological tissue, it is challenging to detect Cherenkov photons directly, especially when emanating from deep tissue. In the past, we have shown that Cherenkov light can be used to excite fluorescent and phosphorescent probes that emit in the near infrared (NIR) region. The endogenous absorption of biological tissue is much lower in this region (18,19), which allows detection of optical signals originating from larger depths (18). The key concept of CEPhOx imaging is to utilize multiple angles of the incident radiation beams to facilitate tomographic reconstruction of phosphorescence as a function of location. Through inclusion of prior information about the beam direction, object (e.g. tumor) location, and the exponential decay of phosphorescence, it is possible to solve the inverse phosphorescence lifetime problem (6) and thus obtain oxygen distribution in the tumor region.

Platinum(II)-G4 (PtG4) was used in our CEPhOx experiments as a phosphorescent probe (20-22). The relationship between the phosphorescence lifetime of PtG4 and the local oxygen concentration is described by the Stern-Volmer equation:

$$\frac{1}{\tau }=\frac{1}{{\tau }_0}+k_q\times \mathrm{p}{\mathrm{O}}_2,$$ (1)

where τ is the phosphorescence lifetime at partial oxygen pressure pO₂, τ₀ is the phosphorescence lifetime in a deoxygenated medium, and k_q is the oxygen quenching constant. For PtG4, τ₀ and k_q are well suited for the measurements in the biologically relevant range of oxygen concentrations (0-160 mmHg) and they do not change when the probe is placed in a biological environment.

Previously, Cherenkov emission from megavoltage beams has been used to excite and tomographically recover fluorescent or phosphorescent targets (18, 19, 23-25). However, only the simplest situation with irradiation of the entire phantom by a single radiation beam has been investigated to date. CEPhOx has also been investigated in a previous study using a fiber bundle-based system by combining conventional diffuse optical tomography (DOT) (19, 26), similar to Cherenkov Luminescence Tomography(17, 27, 28), with phosphorescence lifetime tomography (6, 29, 30). The accuracy of equation 1 with respect to recovered phosphorescence lifetimes has been previously validated (18, 19, 31). Since conventional DOT does not make use of any prior anatomical information, defining the location of a tumor is less accurate than image-guided image recovery. Following our previous studies, the CEPhOx imaging scheme proposed here is different because it utilizes multiple radiation beams and a fixed imaging system, which consists of an intensified charge couple device (ICCD) camera and a standard optical macro lens. The theoretical and experimental approach presented here is similar to that employed in X-ray induced fluorescence imaging, previously described by Pratx and Carpenter (32, 33). However, here this approach is adapted specifically for the case of targeted beams and is applied to emission lifetime recovery, rather than just intensity.

In this paradigm, the measured phosphorescent light intensity is modeled as a function of time as:

$$d(r_b,t)=E_c{\int }_0^t\int {\Phi }^{ch}(r,r_b,t-t^{\prime })qc\left(r\right)e^{\frac{t^{\prime }}{\tau \left(r\right)}}{\Phi }^d(r,t^{\prime })d^{3}rd{t}^{\prime },$$ (2)

where Φ^{c h}(r, r_b, t) is the Cherenkov light profile for beam location r_b at time t, r denotes the vector coordinate throughout the volume, c(r) is the probe distribution, τ(r) is the phosphorescence lifetime map, Φ^d(r, t) is the sensitivity of the detection (i.e. the spatial probability density of a detected photon’s origin) at location r and time t, q is a constant proportional to the probe’s extinction coefficient and quantum yield of formation of the phosphorescent triplet state, and E_c is the efficiency of the detector. For the purposes of this study, the detection sensitivity Φ^d has been calculated using a diffusion model with the NIRFAST software package(34, 35). The characteristic time of the propagation of the light through the tissue (on the order of ns) is much shorter than the phosphorescence lifetime of the probe (microseconds, μs). Therefore, the characteristic time change of Φ^ch and Φ^d is much less than that of the exponential term, meaning that on the time scale of phosphorescent measurement these functions can be treated using steady state approximation, and the additional constants from the integration will be rolled into E_c (6, 36). Using this model, we can define a forward model operator for measurement i at position r:

$$A(i,r)=\int {\Phi }^{ch}(r,r_b){\Phi }^d\left(r\right)d^{3}r.$$ (3)

Characteristic representations of the fields and the resulting operator from Eq. 3 are shown in Fig. 2. The spatially integrated datum, corresponding to a measurement resulting from a beam at r_b at moment t_k can then be modeled as:

$$E_{c}q{\Sigma }_{j=1}^n{A}_{ij}{c}_j{e}^{-t∕{\tau }_j}=d(r_b,t_k),$$ (4)

where j is an index denoting the spatial location and n is the number of voxels or finite element nodes in the model. This equation can be represented in a more compact form as:

$$\mathit{A}p=d,$$ (5)

where p_j = E_cqc_je^−t/τ_j is the weighted phosphorescence emission distribution.

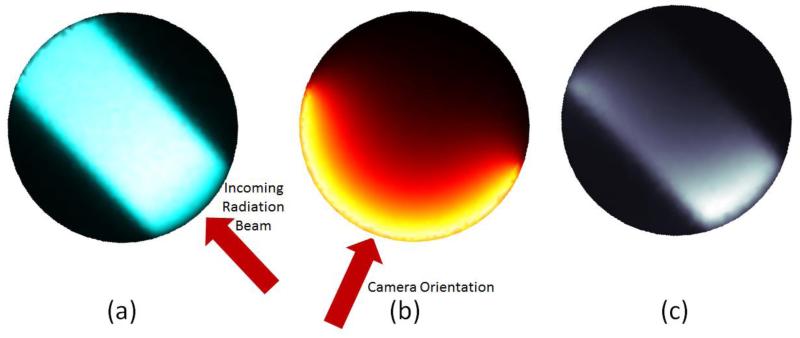
Figure 2.

Visual representations of the components of the forward model matrix. (a) Monte Carlo-derived Cherenkov emission profile, Φ^ch. (b) Optical detection sensitivity Φ^d. (c) Resulting forward model sensitivity distribution.

The inverse problem in tomographic optical imaging, including phosphorescence lifetime imaging, is severely ill-posed. In order to improve the accuracy of image recovery, it is possible to use an n-by-m mapping matrix to reduce the number of free parameters in the problem to the number of distinct regions (with the number of regions given by m). The matrix elements are defined as:

$$K_{ij}=\{\begin{array}{cc}\frac{1}{n_j},\hfill & ifnodeiisinregionj\hfill \\ 0,\hfill & otherwise\hfill \end{array}\phantom{\}},$$ (6)

where n_j is the number of elements in region j. These distinct regions are typically segmented from structural medical images, such as ultrasound, x-ray CT, or MRI. Typically, anatomical medical imaging is performed prior to radiation treatment planning. Using the information from these images, the system may be reduced to:

$$\mathit{AK}\tilde{p}=d,$$ (7)

where $\tilde{p}$ is the r-by-1 vector representing mean phosphorescence light emission density in each region.

In summary, the imaging scheme can be broken down into the following steps. First, a radiation beam is directed onto the imaging domain, which in turn emits Cherenkov radiation. The Cherenkov light then excites the phosphorescent agent, PtG4, whose phosphorescence lifetime is related to the local oxygen levels. The phosphorescence light is measured at the surface of the subject. Time resolved area maps of the phosphorescence internal to the subject are recovered using image-guided tomographic methods, ensuring that a uniform phosphorescence value is recovered for each region. Finally, these phosphorescence maps are used to determine local oxygenation levels by lifetime fitting and by inversion of Equation 1.

2. Phantom Experiments

Two phantom experiments were performed to verify the validity of theCEPhOx image recovery scheme outlined above. A cylindrical liquid phantom 65 mm in diameter and 50 mm-tall was filled with 1% v/v solution of intralipid, containing 0.0025% v/v Indian ink and a 1 μM concentration of PtG4 (figure 3). The solution was fully oxygenated (i.e. with pO₂~160 mmHg) by being equilibrated with air. A 25 mm diameter cylindrical inclusion was placed inside the vial such that the edge of the inclusion was 5 mm away from the external boundary of the phantom. The inclusion contained 1% v/v solution of intralipid, 0.002%v/v Indian ink, and a 5 μM concentration of PtG4. The phantom thus had optical absorption of 0.033 mm⁻¹ and a reduced scatter coefficient of 1.8 mm⁻¹ at the dominant Cherenkov wavelength, and an optical absorption and reduced scatter of 0.002 mm⁻¹ and 1.033 mm⁻¹ at the phosphorescence emission wavelength(37, 38). The concentration of the probe was constructed to reflect realistic, non-toxic values(39-41). Further, the concentration of the probe was higher in the inclusion than in the background to reflect realistic clinical conditions: the macromolecular probe PtG4 will accumulate at a tumor site due to the Enhanced Permeability and Retention (EPR) effect. For the first experiment, the inclusion was fully oxygenated. For the second experiment, the inclusion was fully deoxygenated using a glucose/glucose oxidase/catalase enzymatic system (42).

Figure 3.

Schematic diagram of imaging experiments. (a) Diagram of imaging system with camera and time gating. (b) Overhead schematic of phantom geometry and beam locations with respect to the camera. (c) Cherenkov radiation profile from Monte Carlo Simulations. (d) Composite map of summed Cherenkov radiation for all beam locations, which is known to be a surrogate of the radiation dose map (43-47).

In both experiments, to simulate the situation typically encountered in the established stereotactic tumor treatment, the phantom was irradiated by 20 uniquely-placed radiation beams along the central arc of the cylindrical phantom, covering an angle range of 95°. The resulting phosphorescence was measured by gated ICCD camera (PI-MAX3, Princeton Instrument) with a commercial lens (f = 2.0) trained at the side surface of the phantom. The linear accelerator (CLINAC 2100CD, Varian) delivered 6 MV, 3.25 μs radiation pulses at 200 Hz. The camera operation was synchronized with the radiation pulses (24). Collection of the phosphorescence began at delays varying from 3.25 μs (right after the radiation pulse) to 203.25 μs with 5 μs increments. For each delay, phosphorescence from 100 radiation pulses was accumulated and stored as one image frame. Thus, 40 images with different initial delays were acquired for each incident angle, with a total of 20 incident angles. As a benchmark for recovery accuracy, the bulk phosphorescent lifetime was calculated based on the integrated intensity measurements without performing tomographic reconstruction. These values are shown in Table 1.

Table 1. Bulk Properties Estimates.

Inclusion Type	Recovered Volume-Averaged Phosphorescent Lifetime (μs)	Recovered Volume-Averaged pO2 (mmHg)
Aerated	24.6	107
Deoxygenated	36.1	34.8

The imaging domain was separated into two regions: the bulk of the phantom and the inclusion (figure 3). This separation improved the conditioning of the problem sufficiently, so that a simple least-squares method could be used to reconstruct the image. For each frame, the normal system of equations (Eq. 7) was inverted using QR decomposition and Gaussian elimination to recover the volumetric phosphorescence distribution. The lifetime values were then used to calculate the phosphorescence lifetime map, which in turn allowed recovery of the pO₂ distribution using the Stern-Volmer model (Eq. 1).

The phantom was discretized into 1440 nodes corresponding to 2789 2-D triangular finite elements. Based on the concentration of intralipid, the optical absorption at 780 nm (the wavelength of the phosphoresced light) was set to be 0.0025 mm⁻¹, while the reduced scattering coefficient was set to 1.033mm⁻¹. The orientation of the camera with respect to the phantom was known, allowing for the construction of an optical sensitivity profile. The NIRFAST software package was used to build the integrated-field ICCD sensitivity function (Fig. 2) (34, 35). The gamma ray excitation profiles and subsequent Cherenkov photons were simulated using GAMOS, a Geant4-based Monte Carlo toolbox (48,49). For the purposes of this simulation, the phantom was discretized into a set of uniform voxels with an edge size of 0.2 mm and modeled using water-equivalent energy response values in GAMOS. For each simulated beam location, one hundred million primary photons were injected into the phantom and tracked. In order to exploit the cylindrical symmetry of the imaging domain, and in order to be expressed on the 2-D finite elements representation of the phantom, all the 3-D Cherenkov profiles from GAMOS were summed into a 2-D distribution. These are the 2-D Cherenkov profiles referred to in Eq. 2 (Fig. 3).

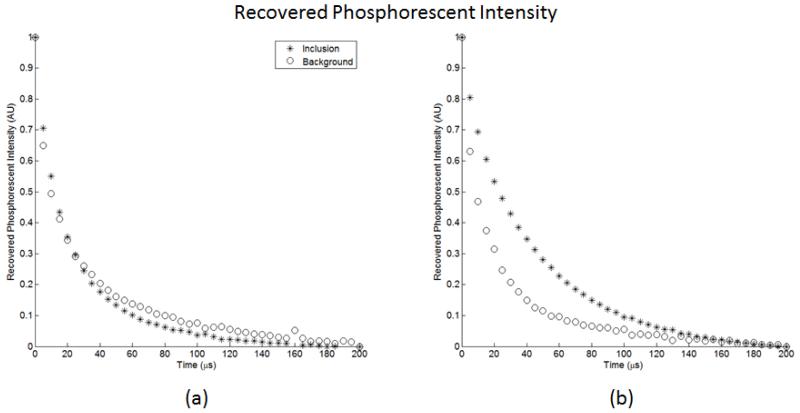
The recovered phosphorescence intensity values for are shown in figure 4, and the pO₂ values recovered using the proposed framework are shown in Table 2.

Figure 4.

Phosphorescence intensity recovered for both the inclusion and background regions for: (a) the oxygenated inclusion experiment and (b) the deoxygenated inclusion experiment.

Table 2.

Tomographic Recovery of Oxygen Distribution

Inclusion Type	Recovered Phosphorescent Lifetime in Inclusion (μs)	Recovered Phosphorescent Lifetime in Background (μs)	Recovered pO2 in Inclusion (mmHg)	Recovered pO2 in Background (mmHg)
Aerated	23.9	26.3	113	92.4
Deoxygenated	41.2	21.3	15.4	142

In the current implementation, the method was only capable of distinguishing high versus low oxygenation. However, image guidance permitted the use of far fewer data points. Table 3 shows the oxygenation recovery when the results from only four beam excitations are used, indicating how robust this approach is to sparse data.

Table 3.

Tomographic Recovery of Oxygen Distribution: Reduced Number of Measurements

Inclusion Type	Recovered Phosphorescent Lifetime in Inclusion (μs)	Recovered Phosphorescent Lifetime in Background (μs)	Recovered pO2 in Inclusion (mmHg)	Recovered pO2 in Background (mmHg)
Aerated	21.3	28.1	141	78.6
Deoxygenated	42.8	21.2	10.5	143

The intensity of the recovered phosphorescence signal is linear with respect to the concentration of the phosphorescent probe in a given location, based on Eq. 5. A higher concentration of the probe would improve the fidelity of the signal. The concentration of PtG4 used in this phantom study is 1 and 5 μM, while higher concentrations (over 10 μM) has been shown to be safe for in vivo studies (20, 50, 51). However, recovery of oxygenation in principle only requires the presence of the probe, since it is the lifetime of the phosphorescence, but not the intensity, that is used for pO₂ recovery. Thus, it is not necessary to calibrate the intensity measurements of the imaging system, but only to make sure that the system response is consistent throughout the experiment. Similarly, it is not necessary that the phosphor be uniformly distributed. However, the intensity and hence the probe concentration define the signal-to-noise ratio (SNR) in the data.

For each incident angle, the data acquisition time was approximately 20 s, which is similar to the irradiation time for each beam in an actual medical setting, although dose per beam varies considerably with different treatment plans. For each incident angle, the data was acquired at 40 different time points. However, it has been shown that 5 to 10 time points should be sufficient for the fitting of a single-exponential decay, provided sufficient SNR in the data (6). Thus, the data acquisition time could be easily reduced to be within 5 s without affecting the normal treatment process.

3. Feasibility Study of Human Brain Tumor Imaging with CEPhOx

A simulation study was also performed to examine the possibility of CEPhOx monitoring during the treatment of human brain cancer with EBRT. A representative human head MRI from the NIRFAST software package release was segmented into five regions (Figure 5a) and assigned realistic optical properties (34). An elliptical ‘tumor site’ was added to the imaging domain as a target region (figure 5a). For the purposes of this simulation study, the imaging domain was further divided into three regions of interest: tumor region, scalp, and the remaining normal brain tissue. The tumor was assigned lateral axis sizes ranging from 5mm to 20mm in steps of 1mm and proximal axis sizes ranging from 7.5mm to 30mm in steps of 1.5mm. The tumor was also assigned an array of edge depths from 5mm to 25mm in steps of 1mm. The ratio of the probe concentration at the tumor site to that in the normal brain was assumed to be 4:1 and the corresponding scalp to brain ratio 5:1. These numbers reflect the expected in vivo probe partitioning as follows from the preliminary animal studies (20) and available information about the blood-brain barrier. The imaging domain was discretized into a finite element mesh with 21,974 nodes corresponding to 43,533 triangular elements. The same targeted EBRT treatment, which was previously applied to the phantom, was applied to this domain, using the same integrated surface data collection method. Thus, obtained data were used to recover the phosphorescence distribution as a function of time on a finite element mesh with 5169 nodes corresponding to 10910 triangular elements, which were further mapped onto the previously described four regions with the same approach that was used in the phantom study. A 2D simulation series was performed in this case as a proof of concept to demonstrate the principles of the proposed method. The recovered pO₂ values for the scalp and bulk tissue did not show significant errors. However, the recovered pO₂ values for the tumor region were found to be dependent upon the tumor size, depth, and oxygenation.

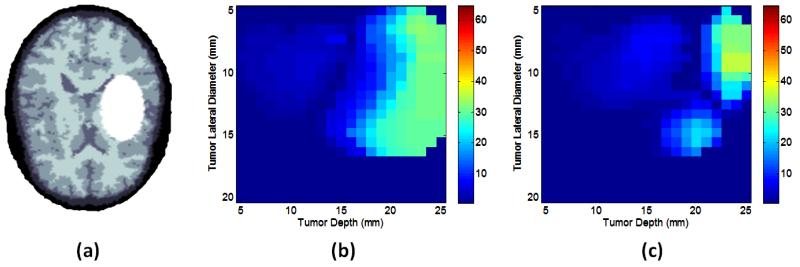
Figure 5.

(a) A sample head CT scan used for image testing with skull (dark) grey and white matter, and with target irradiation site is shown (white). In (b) the targeted region oxygenation recovery absolute error (mmHg) is shown for a well-oxygenated region. In (c) the region oxygenation recovery error is shown, for the case of a deoxygenated target region.

The results of the simulation study are shown in Figure 5, where Figures 5b and 5c show oxygenation recovery error in the tumor with respect to an increasing tumor depth (moving from left to right in Figures 5b and 5c) and increasing tumor size (moving from the top to the bottom of Figures 5b and 5c). These results indicate that CEPhOx recovery could be an effective means for pO₂ estimation in tumors of all sizes, as long as they are located at depths less than 10-20mm, depending upon the oxygenation value. With these constraints, the oxygen recovery error is within 15mmHg. It is possible that the efficacy of this form of imaging can be improved by varying locations and angles of the excitation beams. A deoxygenated tumor will produce a longer and a stronger decay than a normoxic one, due to the effect of phosphorescence quenching by oxygen. At late time points, the overall signal will be greatly dominated by the hypoxic tumor, thereby improving the accuracy of recovery (6).

4. Discussion

Traditional optical excitation fields are generally delivered from outside of the object and have limited penetration depth, due to the high optical absorption of tissue. In contrast, Cherenkov emission is generated locally by the beam radiation and can serve as internal excitation source even when the region of interest is deeply seated. Additionally, it has been shown that the intensity of local Cherenkov emission is proportional to the delivered radiation dose (8, 10, 11). Since the dose map calculation is a significant part of the treatment planning, and the treatment is constructed to maximize the dose at the target site, the Cherenkov light will maximize the signal emanating from the target.

The use of image guidance in the recovery of phosphorescence greatly improves accuracy, based on the comparison of the bulk characteristics in Table 1 to the region-based characteristics in Table 2, but also allows for the use of fewer beam excitations. If a diffuse recovery is used, every time point will have a number of free parameters equal to the number of discretized nodes in the imaging domain. However, when region-based recovery is used, the number of free parameters is decreased to the distinct number of regions. Since a great deal of spatial information is encoded in the Cherenkov profiles, and since the image recovery is mapped into uniform regions, it is no longer necessary to discretize the optical measurements at the surface; an integrated signal is now sufficient for accurate recovery. Furthermore, since the optical signal can be integrated, this vastly improves the quality of the data for reconstruction. In effect, each data point was constructed by summing thousands of pixels, thus lowering the noise significantly.

It is true that a complete, continuous map of the oxygenation of the tumor would be extremely valuable and interesting. With the proposed method, this is not a feasible goal given that there is limited probing of the tumor site. There are a limited number of beams used in EBRT, which correspondingly limits the amount of information which can be collected about the imaging domain. In short, it is not probed enough to get continuous maps. However, the authors suggest that a mean value across a region would be of sufficient use for treatment efficacy prediction. Further, if there were large regions of the tumor known to be necrotic, and if this were visible during the treatment planning stages, this could be information which is included in the spatial discretization of the imaging domain. The necrotic section of the tumor could become its own region in this recovery scheme, thus improving the information content. The proposed imaging scheme could, with little modification, be used in a non-tomographic sense. If the tumor were seated superficially (e.g. a skin or shallow neck cancer), then the tomographic recovery approach would not be necessary. Further, this would allow for continuous oxygenation map recovery.

5. Conclusion

In summary, we have proposed the CEPhOx method to perform monitoring of oxygenation in tumors during external radiation beam therapy. Our method only requires the addition of a non-toxic, biologically compatible, excretable phosphorescent tracer PtG4 and the presence of a camera in the treatment room. It is, therefore, a minimally invasive method and is compatible with the established work flow of radiation therapy in situations where tumor pO₂ measurement is a pertinent dosimetric need.