GRID-ENABLED TREATMENT PLANNING FOR PROTON THERAPY USING MONTE CARLO SIMULATIONS

Abstract

Grid computing is an emerging technology that enables computational tasks to be accomplished in a collaborative approach by using a distributed network of computers. The grid approach is especially important for computationally intensive problems that are not tractable with a single computer or even with a small cluster of computers, e.g., radiation transport calculations for cancer therapy. The objective of this work was to extend a Monte Carlo (MC) transport code used for proton radiotherapy to utilize grid computing techniques and demonstrate its promise in reducing runtime from days to minutes. As proof of concept we created the Medical Grid between Texas Tech University and Rice University. Preliminary computational experiments were carried out in the GEANT4 simulation environment for transport of 25 ×10⁶ 200 MeV protons in a prostate cancer treatment plan. The simulation speedup was approximately linear; deviations were attributed to the spectrum of parallel runtimes and communication overhead due to Medical Grid computing. The results indicate that ~3 × 10⁵ to 5 × 10⁵ proton events with processor core would result in 65 to 83% efficiency. Extrapolation of our results indicates that about 10³ processor cores of the class used here would reduce the MC simulation runtime from 18.3 days to ~1 h.

I. INTRODUCTION

External-beam radiotherapy treatment planning (RTP) is a process in which radiation fields are custom designed to maximize dose to the tumor while minimizing dose to surrounding healthy tissues. Dose calculations for proton RTP are usually performed with analytical methods¹ because of these methods’ high computational speed and adequate accuracy. However, some cases call for dose predictions using the Monte Carlo (MC) method,² which provides superior accuracy³ and additional capabilities, such as absolute dosimetry⁴ and predictions of doses from stray and leakage radiation.⁵ Several studies suggested that the MC technique will become possible for routine RTP (Refs. 6 through 10) once the obstacle of long computation times is overcome. The MC approach is particularly powerful when the tumor is surrounded by healthy critical organs that must be spared from radiation exposure and traditional analytical approaches are not sufficiently accurate.

In the MC-based RTP process, complex microscopic interactions between protons and the tumor medium are randomly sampled. Many proton trajectories are simulated in order to obtain small random statistical variations in radiation dose predictions in the patient. Ideally, for clinical implementation, the MC simulations are to be accomplished in minutes or seconds. Currently, the major obstacle is the limited availability of computing power and capacity in a single hospital. Multihospital collaborations are a promising avenue for increasing computing capacity. However, secure and fast data movement technologies would be necessary for collaborations among organizations. Grid computing^11,12 is an emerging collaborative computing environment that securely connects computing, storage, visualization, and database resources across several organizational and administrative domains. In addition, the grid security supports proprietary standard and privilege-based resource and data access and their seamless integration, especially when multihospital collaborations are the goal. Multihospital collaborative efforts are also gaining substantial importance in efforts to address challenges in cancer biomedicine such as Campbell and Dellinger¹³ and Kanup et al.¹⁴ The Cancer Bioinformatics Grid¹⁵ (caBIG) and Biomedical Informatics Research Network¹⁶ (BIRN) efforts of the National Institute of Health substantiate this vision.

Processing for MC simulations is embarrassingly parallel, and this feature is expected to exhibit linear speedup with an increase in the number of cores. Since there is no interprocess communication in MC simulations, grid computing environments should be ideal for overcoming computational challenges in these types of computations. Downes et al.¹⁷ found that was the case in their preliminary studies on grid computing for intensity-modulated radiotherapy using Radio Therapy Grid¹⁸ (RTGrid).

Despite the promise of grid computing, there is not sufficient evidence that it can mitigate the currently insurmountable clinical challenge of reducing MC simulation runtimes from days to minutes or seconds. Therefore, our goal in this analysis was to demonstrate the scope and power of grid computing for MC simulations in RTP. For this proof-of-concept study, we set up the Medical Grid by connecting three Linux clusters, two from Texas Tech University (TTU) and one from Rice University.

II. METHODS

II.A. Database and Materials Information

We have used a proton field phase-space that was used to treat a prostate cancer patient who was treated at MD Anderson Cancer Center (MDACC), Houston. The treatment technique was described previously by Fontenot et al.¹⁹ A simulation of the passive-scattering proton therapy treatment unit was implemented previously.²⁰ The final beam-shaping components of the treatment unit, the collimating aperture, and the range compensator were included. The proton phase-space was generated using the MCNPX code,²¹ version 2.7a. The phase-space was input to the GEANT4 (version 4.8.3)toolkit,^22,23 which simulated the transport of protons through the final elements of the treatment unit and into the patient phantom, as described previously.¹⁰

In this proof-of-concept study, we chose a well-characterized prostate treatment plan that was anonymized previously. About 25 × 10⁶ 200-MeVprotons with realistic phase-space distributions were used to simulate the RTP. The number of proton events in the MC simulation was chosen such that the resulting uncertainty in the dose matrix would be <2%. The number of simulation events was chosen so that (a) the serial runtime would be large enough to demonstrate parallel speedup and (b) the least amount of parallel runtime due to heterogeneity in the Medical Grid, when maximum processor cores are employed for the simulation, would be sufficiently large. By virtue of criterion (b), the runtime overhead due to scheduling policies for cluster-specific batch schedulers in the Medical Grid could be ignored without significant loss of accuracy in the total job runtime. To account for processor heterogeneity and communication overhead for the Medical Grid, we defined an aggregate speedup S_Agg and efficiency ε_Agg.

II.B. Aggregate Speedup and Efficiency

The total events in the simulation were divided equally across the available cores in the Medical Grid. The amount of work assigned to each cluster in the Medical Grid depends on the cluster’s size (number of cores). Therefore, the serial runtimes for the clusters may differ from one another.

Let there be N Linux clusters (L₁, L₂, etc.) in the Medical Grid. Let τ₁, τ₂, etc., be the respective serial runtimes for L₁, L₂, etc. Then, the total serial runtime for the entire work is given by $\tau ={\sum }_{i=1}^N{\tau }_i$. Further, the parallel runtimes may differ among processor cores due to processor heterogeneity and application-specific input conditions, such as phase-space in this problem. Let (T_P)_i be the maximum parallel runtimes for each L_i. Then, the parallel runtime across the grid T_P = max[(T_p)_i]. There-fore, grid-wide speedup S_Agg and efficiency ε_Agg are given by S_Agg = τ/(T_P + δ)and ε_Agg = S_Agg/P, where P is the number of cores in the Medical Grid and δ is the overhead due to grid security (see Sec. II.C).

II.C. Medical Grid Simulation Environment

The Medical Grid represented a typical grid computing environment with strong heterogeneity. The clusters (shown in Table I) in the Medical Grid ran the Virtual Data Toolkit²⁴–based grid services through the Globus toolkit²⁵ (GTK) 4.2.x. The Grid Security Infrastructure²⁶ (S) and Web Services (WS) Grid Resource Allocation and Management²⁷ (GRAM) are the main components in the GTK. Pertinent details of other components can be found in Ref. 11. The GSI provides implementations for both the message-level²⁸ and transport-level^26,28 securities via X.509-based resource and user certificates. In the present work, these certificates were generated by using Simple Authority²⁹ Certificate Authority issued by TTU. These certificate settings were internally modified to conform to the Open Grid Forum profile standard.³⁰ At TTU, we used the Grid User Management System³¹ to map user accounts dynamically to a pool of local accounts created for grid operations. At Rice University, the grid users were mapped to local accounts through the grid mapfile.

TABLE I.

Technical Specifications of the Clusters in the Medical Grid^*

Institution	Cluster Name	Number of Cores	Architecture	Physical Memory(GB/core)	Storage (TB)	Batch Scheduler	Interconnect
TTU	Antaeus	200	Xeon 3.2 and 2.4 GHz Dual-quad; dual-dual core	2	46	SGE	Gigabit Ethernet
TTU	Weland	100	Nehalem 3.0 GHz Dual-quad	2	46	LSF	Infiniband
Rice University	Osg-Gate	8	Intel 2.66 GHz Core duo	2	10	Condor	Gigabit Ethernet

^*TTU clusters were connected through the Lustre file system.

The grid job management was accomplished through WS-GRAM in GTK 4.2.x. This feature allows writing job submission scripts in extensible markup language (XML). The GTK WS translates the XML scripts into target cluster-specific batch schedulers such as Sun Grid Engine (SGE), Load Sharing Facility (LSF), and Condor³² in the Medical Grid. High-bandwidth file transfer protocols, such as gridftp and uberftp, were used for staging files in and out of the target machine. The gsissh service, for grid-enabled remote login, was used to access and debug programs on the target machine.

The input database was made available in all clusters in the Medical Grid. This step eliminated the communication overhead due to staging input database files. The simulations were conducted using up to 250 cores across the TTU clusters in the Medical Grid. Postprocessing was carried out using the osg-gate cluster at Rice University. We used uberftp to securely stage-out all outputs as a postprocessing step. This approach substantially reduced the impact of communication latency on the speedup, reported by Downes et al.,¹⁷ and our estimates for S_Agg and ε_Agg are reasonably accurate.

II.D. Runtime Studies

Several input files covering the spectrum of proton energies that might be used in a typical prostate cancer treatment plan were used in the present work. A customized shell script was used to generate input-specific XML scripts for WS-GRAM, their scheduling, and their management in the Medical Grid. To compute S_Agg and.ε_Agg, the 25 × 10⁶ proton events in the simulation were equally divided into 50 to 250 subjobs per job set. Each subjob was allocated to a core. To investigate the dependence of parallel runtimes on input conditions, a profile run was conducted using 200 subjobs in a job set. We have used a power function of the form f(T_p) = cP^−b to fit the parallel runtime in the present work.

III. RESULTS AND DISCUSSION

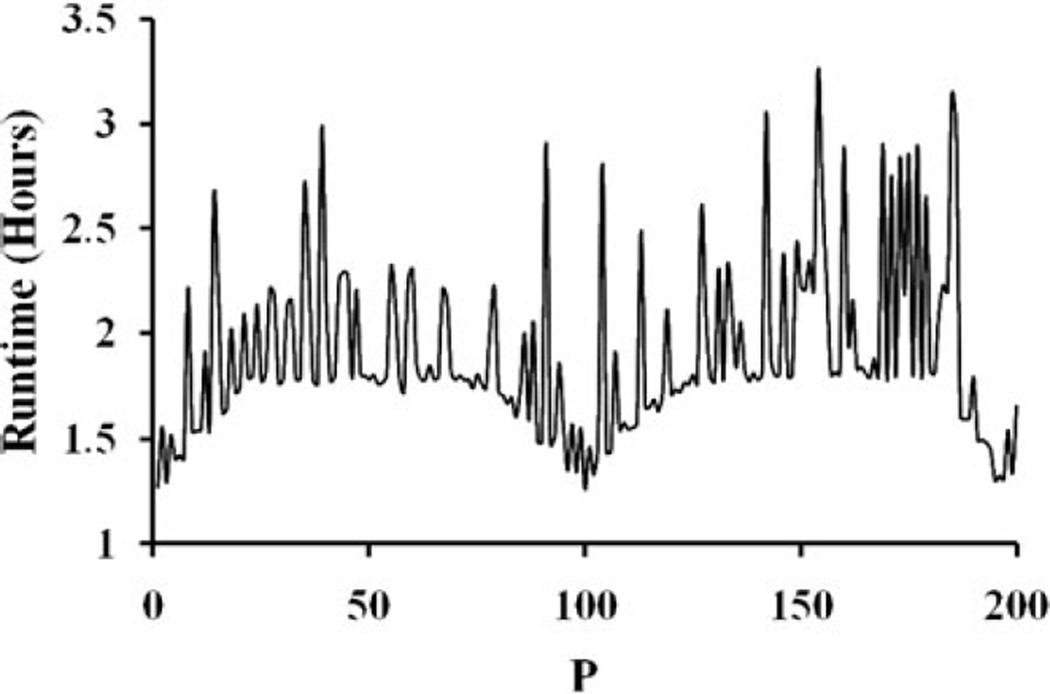
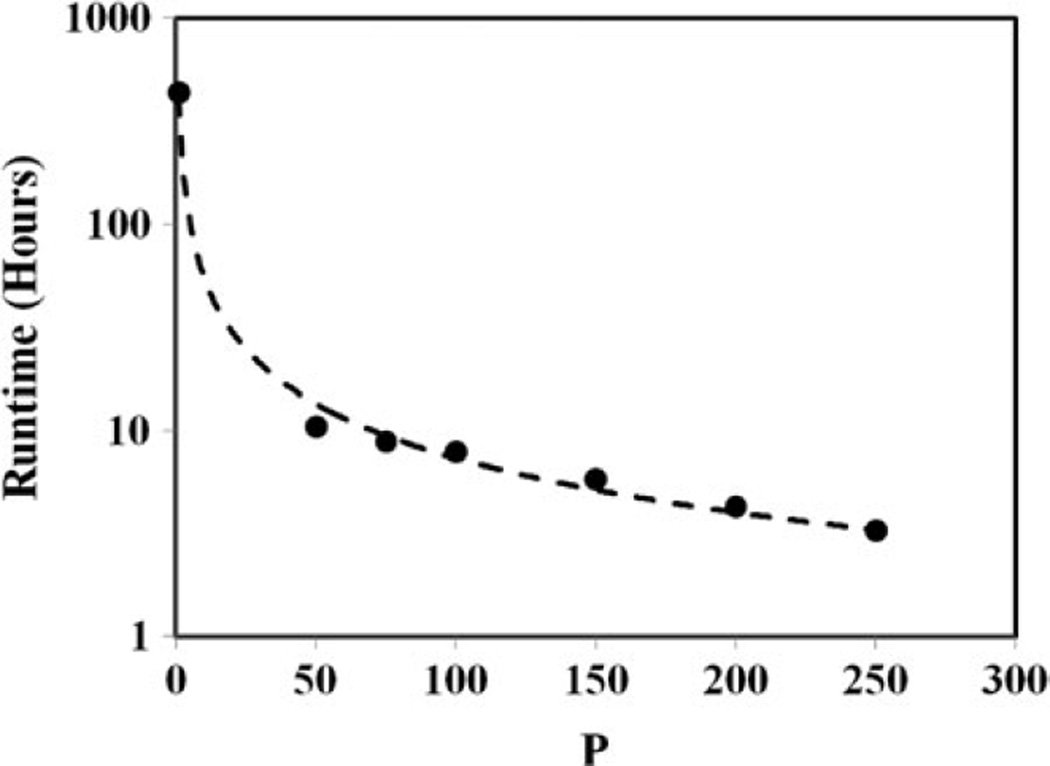
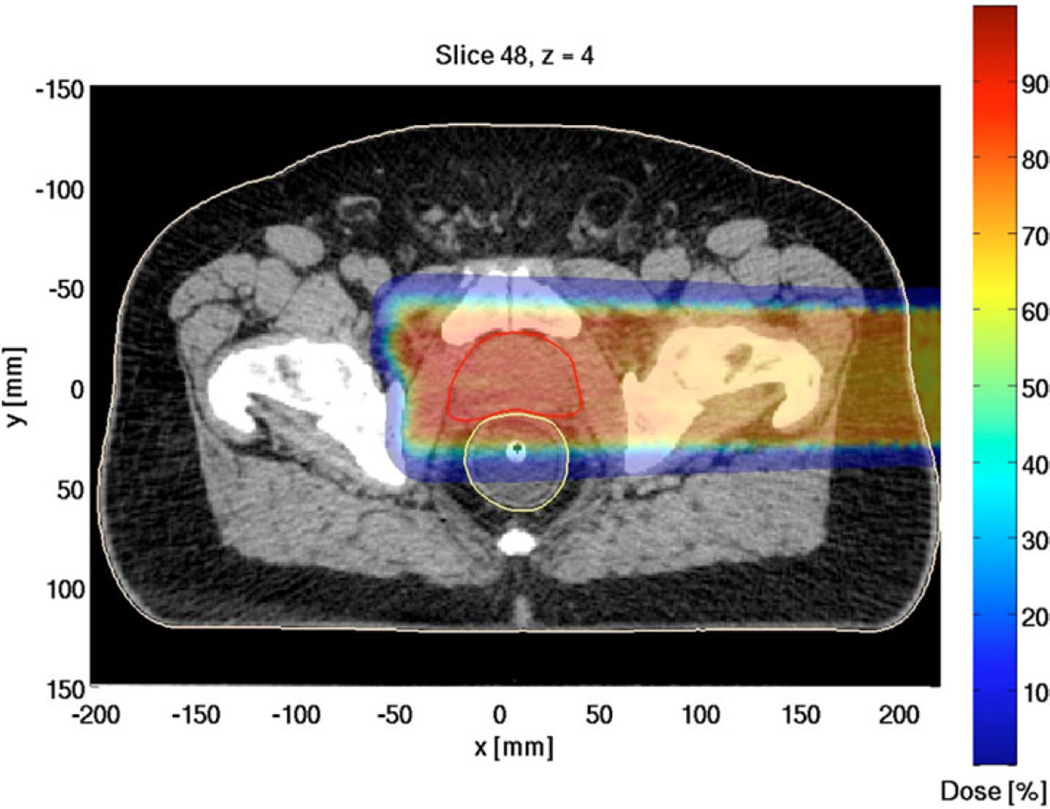
The serial runtime for the entire simulation was τ = 434.9 h (18.3 days). Figure 1 shows that the parallel runtimes for a job set with 200 subjobs varied in the interval [1.21, 3.26] hours. In addition to the processor heterogeneity, significant spread in parallel runtimes due to the phase-space conditions in input files could have affected S_Agg and ε_Agg. Table II shows the computed S_Agg and ε_Agg for several job sets with 50 to 250 subjobs per job set, and cluster site specific runtime efficiencies for computations in the present work. The results indicate that S_Agg was approximately linear (Table II). As shown in Fig. 2, extrapolation of the results for S_Agg indicate that the simulation runtime can be reduced to ~1 h when P ≈ 10³ with ε_Agg of ~50%. Figure 3 shows the proton therapy treatment plan constructed from the present work.

Fig. 1.

Typical distribution of runtimes across the processor cores.

TABLE II.

Aggregated Speedup S_Agg and Efficiency ε_Agg in GEANT4-Based Monte Carlo Simulations Using the Medical Grid for 200-MeV Proton Distributions for Prostate Cancer^*

Job Set Size (Number of Cores)	Subjob Size (protons/core)	τ(h) 25 × 106 Protons	TP (h)	SAgg	εAgg	εA	εW
50	500 000	434.9	10.47	41.54	0.83	0.79	0.93
75	333 333	434.9	8.86	49.09	0.65	0.74	0.83
100	250 000	434.9	7.90	55.05	0.55	0.67	0.79
150	166 667	434.9	5.79	75.12	0.50	0.63	0.69
200	125 000	434.9	4.28	101.61	0.54	0.59	0.55
250	100 000	434.9	3.26	133.4	0.53	0.58	0.59

^*Respectively, ε_A and ε_W are efficiencies of the clusters Antaeus and Weland shown in Table I.

Fig. 2.

Medical Grid–wide speedup. Extrapolation of the results indicated that the parallel runtime T_P would be ~1 h if the number of cores P ≈ 10³. (The serial runtime is included in the plot.)

Fig. 3.

Proton therapy treatment plan for prostate cancer resulting from the simulation runs in the current study (with appropriate adjustments).

The ε_Agg was ~83% for ~5 × 10⁵ proton simulation events per core and decreased to ~53% for 1 × 10⁵ proton simulation events per core. Since there is no interprocess communication in MC simulations, we hypothesize that the loss in efficiency was largely due to the distribution of parallel runtimes. In addition, communications over the Internet in grid computing have low bandwidth and high communication latency; therefore, the overhead due to the message-level and transport-level securities in GSI could also have been a factor in the computed ε_Agg. Our preliminary studies also indicate that the number of simulation events of ~3 × 10⁵ to 5 × 10⁵ that result in ε_Agg of 65 to 83% may be optimal for current cluster configurations in the Medical Grid. It would be interesting to investigate load-balancing strategies for improving S_Agg and ε_Agg.

In the present work, we have employed two cluster sites to best represent a minimal configuration required for the grid computing environment. Therefore, the present work is a true test for grid computing. Extension of this work to involve more cluster sites, which are well controlled and secure, would be a relatively straightforward approach. In the MC method, there is no communication between the subjobs (or cores). Therefore, the impact of the type of the processor interconnect fabric—Infiniband or Gigabit Ethernet shown in Table I—is minimal, if any.

IV. CONCLUSIONS

Our simulations showed that S_Agg exhibits an approximately linear trend as the number of cores increases, and by extrapolation of S_Agg, we conclude that it is feasible to reduce total simulation runtimes from several days to 1 h when using about 1000 cores. Although this increase in speedup was accompanied by a loss in processing efficiency, we attributed that loss mainly to the spectrum of parallel runtimes due to the input conditions and processor heterogeneity; the communication overhead due to GSI may also have contributed.

Accurate simulations require ~50 × 10⁶ to 100 × 10⁶ proton events per treatment plan, and several such treatment plans may be necessary for accurate prediction of dose to the tumor geometry. Clusters with about 256 to 512 cores are now common in many hospital environments. By grid-enabling the clusters across several hospitals with related interests in RTP, clinically infeasible MC simulations can be undertaken. In addition, grid computing provides an excellent platform for knowledge sharing through multihospital collaborations.

V. FUTURE WORK

In the present work, we have used user-controlled shell scripts for job management across the Medical Grid. In the future, we plan to deploy a metascheduler that supports dynamic resource management and strategies for load balancing across the Medical Grid. The current effort has helped us better understand the dependence of grid speedup and efficiency on cluster heterogeneity, GSI, and input conditions due to phase-space and will assist us and others in identifying strategies for improvements. We will employ load-balancing strategies to reduce the spread in parallel runtime and improve grid speedup and efficiency. It would be interesting to extend the simulations using 1000 or more cores and validate the observations in the present work.