EFFECT OF BREASTFEEDING ON GASTROINTESTINAL INFECTION IN INFANTS: A TARGETED MAXIMUM LIKELIHOOD APPROACH FOR CLUSTERED LONGITUDINAL DATA

Abstract

The PROmotion of Breastfeeding Intervention Trial (PROBIT) cluster-randomized a program encouraging breastfeeding to new mothers in hospital centers. The original studies indicated that this intervention successfully increased duration of breastfeeding and lowered rates of gastrointestinal tract infections in newborns. Additional scientific and popular interest lies in determining the causal effect of longer breastfeeding on gastrointestinal infection. In this study, we estimate the expected infection count under various lengths of breastfeeding in order to estimate the effect of breastfeeding duration on infection. Due to the presence of baseline and time-dependent confounding, specialized “causal” estimation methods are required. We demonstrate the double-robust method of Targeted Maximum Likelihood Estimation (TMLE) in the context of this application and review some related methods and the adjustments required to account for clustering. We compare TMLE (implemented both parametrically and using a data-adaptive algorithm) to other causal methods for this example. In addition, we conduct a simulation study to determine (1) the effectiveness of controlling for clustering indicators when cluster-specific confounders are unmeasured and (2) the importance of using data-adaptive TMLE.

1. Introduction

The PROmotion of Breastfeeding Intervention Trial (PRO-BIT) [Kramer et al. (2001, 2002)] was undertaken in order to obtain randomized control trial evidence of the health effects of longer breastfeeding. This was done by cluster randomizing a breastfeeding support intervention which encouraged exclusivity and duration. The effect of the PROBIT intervention on gastrointestinal tract infection in the newborns was originally evaluated using a stratified intention-to-treat analysis. The results indicated a significant reduction in infection incidence for infants whose mothers had been assigned to the intervention group [Kramer et al. (2001)]. The intervention was presumably effective because it successfully encouraged breastfeeding, which subsequently improved infant health. However, because breastfeeding itself was not randomized, the estimated effect obtained in the study can at best be considered a biased assessment of the effect of breast-feeding on infection. Due to the ethical and practical impossibility of randomizing breastfeeding, estimation of the causal effect of breastfeeding must be obtained through statistical methods.

Our goal is therefore to estimate the causal effect of breastfeeding duration on the number of infections a newborn is expected to experience in their first year. One of the challenges involved in analyzing this effect is the confounding presence of intermediate infections (occurring at any time during the year). The presence of an infection affects both the continuation of breastfeeding and the outcome (since it deterministically increases the outcome by one). Therefore, intermediate infection is a time-dependent confounder. Since infection is also hypothesized to be affected by previous breastfeeding status, standard regression methods (including or excluding the time-dependent confounder) may produce a biased estimate of the causal parameter [Robins (1986)]. Causal methods are therefore required to isolate the desired effect. Additional confounding also occurs due to baseline differences in the study group and by informative participant dropout.

Many longitudinal methods have been developed that correctly take into account time-dependent confounders predicted by past exposure. One such method is inverse probability of treatment weighting (IPTW) for marginal structural models [Hernán, Brumback and Robins (2000), Robins, Hernán and Brumback (2000)]. However, IPTW is not semiparametric efficient [Robins and Rotnitzky (1992)] and has poor performance under certain common scenarios [Petersen et al. (2012)]. The shortcomings of simple weighting methods have since spurred the development of new estimators with better properties. Efficient estimating equation methodology [Bang and Robins (2005), Robins and Rotnitzky (1992), van der Laan and Robins (2003)] produces estimators that are double robust (consistent under partial model misspecification) and efficient when correctly specified. Targeted maximum likelihood estimation (TMLE) [van der Laan and Rubin (2006)] shares these properties, but because it is a substitution estimator, it can be made to be stable and produce estimates bounded within the parameter space in some situations where IPTW performs poorly [Gruber and van der Laan (2010)]. In addition, TMLE is often implemented fully nonparametrically, which avoids modeling errors caused by incorrect parametric assumptions.

van der Laan (2010) established a TMLE procedure for longitudinal data based on a binary decomposition of the intermediate variables (the time-dependent confounders). This method has been described and implemented by Rosenblum and van der Laan (2010a) and Schnitzer, Moodie and Platt (2013) for two time points, and Stitelman, De Gruttola and van der Laan (2012) for a survival outcome. However, the implementation of this method for large numbers of time points results in heavy computational requirements and a restriction on the form of the data (specifically, requiring discretized intermediate covariates). More recently, van der Laan and Gruber (2012) developed a simpler and more flexible implementation of TMLE for longitudinal data based on the ideas of Bang and Robins (2005).

An initial causal analysis of the PROBIT study using different double-robust causal methods was performed by Schnitzer, Moodie and Platt (2013) but was limited to two time points. In this paper, after giving more details about the PRO-BIT study and the scientific question of interest (Section 2), we describe several options for potentially unbiased estimation of the effect of breastfeeding on infection: (a) G-computation [Robins (1986)], (b) a variant of G-computation that we call sequential G-computation [Bang and Robins (2005)], and (c) a longitudinal TMLE based on sequential G-computation [van der Laan and Gruber (2012)] (Section 3). The subsection on the longitudinal TMLE demonstrates a 6 time-point implementation for estimation of the effect of breastfeeding duration on gastrointestinal tract infection, with modified variance estimation reflecting the clustered design of the PROBIT. In Section 4 we present the results of analyzing the PRO-BIT data with each of these methods in addition to IPTW. Finally, we compare this TMLE approach to the other causal techniques for longitudinal data in a simulation study designed to imitate the analysis of the PROBIT data.

2. The PROBIT data

The PROBIT study paired participating maternal hospitals according to (1) geographic region in Belarus, (2) urban or rural status, (3) number of deliveries per year and (4) breastfeeding rates upon discharge. One hospital of each pair was then assigned to receive a breastfeeding support intervention that involved retraining all midwives, nurses and physicians involved in labor, delivery and the postpartum hospital stay. The control hospitals were assigned to continue their current practice. Thirty-four hospitals were initially randomized, but three were dropped from the study due to eventual refusal to follow the assignment or falsification of data.

The PROBIT study enrolled healthy, full-term, singleton infants of mothers who intended to breastfeed, weighing at least 2500 g, soon after birth. Follow-up visits were scheduled at 1, 2, 3, 6, 9 and 12 months of age to record various measures of health and size, including number of gastrointestinal infections over each time interval. At each follow-up visit, it was established whether the mother continued to breastfeed.

Within the 31 hospitals, 17,046 mother/infant pairs were recruited into the trial. Of these, ten were missing necessary baseline information and were removed from the analysis. The remaining 17,036 subject pairs were used in the analysis. Characteristics of the complete data set (including missing data summaries) are presented in Table 1. Within the hospitals, the number of recruited patients varied between 232 and 1180 with median 471.

Table 1.

Characteristics at baseline of the 17,046 mother-infant pairs in the PROBIT data set

Characteristic	Summary		N. missing
Numeric variables	Median	IQRa
Age of mother (years)	23	(21, 27)
N. previous children	0	(0, 1)
Gestational age (months)	40	(39, 40)
Infant weight (kg)	3.4	(3.2, 3.7)
Infant height (cm)	52.00	(50.00, 53.00)
Apgar scoreb	9	(8, 9)	5
Head circumference (cm)	35	(34, 36)	3
Binary variables	N.	%
Smoked during pregnancy	389	2.28
History of allergy	750	4.40
Male child	8827	52
Cesarean	1974	12
Mother’s education			2
Some high school	663	4
High school	5497	32
Some university	8568	50
University	2316	14
Geographic region
East Belarus, urban	5615	33
East Belarus, rural	2706	16
West Belarus, urban	4380	26
West Belarus, rural	4343	25

^aIQR: inter-quartile range.

^bThe Apgar score is an assessment of newborn health (range 1–10) where 8+ is vigorous, 5–7 is mildly depressed and 4- is severely depressed [Finster and Wood (2005)]. A range of 5–10 was observed in PROBIT due to entry restrictions on weight and health at baseline.

Measured baseline potential confounders of the effect of breastfeeding on infection (and predictors of outcome) were chosen to be mother’s education, mother’s smoking status during pregnancy, mother’s age, family history of allergy, number of previous children, whether the birth was by cesarean section, gender of child, gestational age, Apgar score for health of the newborn, geographic region, and the weight, height, head circumference at birth, and hospital. The hospital (or cluster) was included in the set of potential confounders because the conditions of the hospital frequented by a patient can affect both their infant’s health outcome and their decision to continue breastfeeding. In addition, since similar patients may be clustered within a hospital, hospital may act as a proxy for unmeasured baseline characteristics.

The hypothetical intervention of interest for this analysis was breastfeeding up until a given time. The binary intermediate variable at a given time was whether or not gastrointestinal infection occurred in the interval immediately preceding the time point. The outcome is the total number of infections occurring up until 12 months of age.

A subject was defined as censored at the first visit where information required in the analysis was missing. The number of censored subjects at each time point is described in Table 2. Absenteeism or study drop-out are often dependent on subject-specific characteristics and current health, which is why adjustment for censoring was considered necessary.

Table 2.

Censoring, number of infections and mothers still breastfeeding by time point

Time point	1	2	3	4	5	6
Month	1	2	3	6	9	12
N. censored	284	500	326	491	717	139
Cumulative N.	284	784	1110	1601	2318	2457
Cumulative %	1.66	4.60	6.52	9.40	13.61	14.42
N. with infections	171	232	230	443	518	408
N. of infections	173	235	236	472	544	439
N. breastfeeding	15,392	13,128	10,765	6893	4717	–

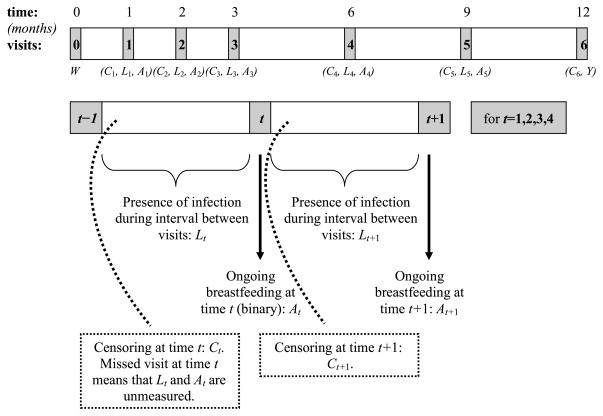
At each visit, the number of gastrointestinal infections since the last visit were counted. In addition, breastfeeding status at that time was obtained. There is therefore uncertainty about exact time-ordering of each infection and breastfeeding cessation within a time interval. By defining the exposure as breastfeeding status at time-point t, we can consider that this intervention point occurs after infection counts measured over the previous interval. With six visits, and the outcome assessed at the sixth visit, this means that only the first five exposure nodes are considered in the analysis. However, we observe six censoring times (occurring before each of the six follow-up times). Figure 1 gives a graphic display of the time-ordering of the observed data.

Fig. 1.

Time-ordering of the variables in the PROBIT study. Data were collected at baseline and six follow-up times. At each follow-up time point, breastfeeding status (A_t) and presence of infection over the past interval (L_t) were noted. Censoring occurring at time t (C_t = 1) indicates that later breastfeeding and infection status were not observed.

Intermediate infections were considered to be an important time-varying confounder because mothers were less likely to continue breastfeeding when their infant became ill. Therefore, even if breastfeeding has absolutely no effect on infection, ignoring this confounding effect would make it seem like infants who experienced infections were also breastfed for shorter periods of time. Table 2 also shows a summary of the infection counts at each time point. Few children experienced more than one infection during a given time interval, so the time-dependent confounder was summarized as a binary indicator of infection. However, we used the true number of infection counts for the outcome.

3. Estimation for longitudinal data

As in the PROBIT study, suppose we observe longitudinal information from n individuals of the form O = (W, C₁, L₁, A₁, C₂, L₂, …, L_K−1, A_K−1, C_K, Y). Let K be the total number of follow-up visits, and the subscripts on each variable indicate the visit at which that variable was measured. The variable W is the collection of potentially confounding variables at baseline. The variables C_t, t = 1, …, K, indicate whether a subject has been censored before the tth time point. Intermediate infection was represented by L_t, t = 1, …, K − 1, indicating whether the infant had any gastrointestinal infections between time-points t − 1 and t. If a subject has been censored, define their missing L_t and Y values to be zero. The variables A_t, t = 1, …, K − 1, denote breastfeeding status at time-point t (A_t = 1 means continued breastfeeding). The outcome Y is the total number of infections accrued up until and including visit K. For any time-dependent variable X, we will use X̄_t = (X₁, …, X_t) to denote the history of X up to and including X_t.

Let ā = (a₁, a₂, …, a_K−1) denote a fixed breastfeeding regimen. For instance, breastfeeding past the first time period, then stopping before the second would be written as (1, 0, 0, …, 0). Because breastfeeding is approximately monotone, the regimens of interest are equivalent to a corresponding duration of breastfeeding. Following the Neyman–Rubin model [Rubin (1974)], define the counterfactual variable $L_t^{\overline{a}}$ as the observation L_t that an individual would have had if they had followed the breastfeeding regimen ā and remained uncensored. Similarly, Y^ā is the counterfactual number of infections that would have been observed under breastfeeding regimen ā. The target of inference is the marginal mean counter-factual outcome, denoted ψ_ā = E(Y^ā). The standard causal missing data problem arises from observing each individual under only one breastfeeding regimen.

3.1. The G-computation method

G-computation [Robins (1986), Snowden, Rose and Mortimer (2011)] is a likelihood-based approach to estimating a causal parameter. It is often described as a substitution estimator because it takes a fit of the likelihood and substitutes it into a function to get an estimate of the parameter of interest. Suppose our observed data O consist of n independently and identically distributed draws from a true underlying distribution f(O). This density may be decomposed corresponding to the time-dependent structure of the data as

$$\begin{array}{l}f(O)=\underset{Q}{\underbrace{Q_Y(Y\mid {\overline{C}}_K,{\overline{A}}_{K-1},{\overline{L}}_{K_1})\prod _{t=1}^{K-1}{Q}_{L_t}(L_t\mid {\overline{C}}_t,{\overline{A}}_{t-1},{\overline{L}}_{t-1},W)Q_W(W)}}\\ \times \underset{g}{\underbrace{\prod _{t=1}^{K-1}{g}_{A_t}(A_t\mid {\overline{L}}_t,{\overline{C}}_t,{\overline{A}}_{t-1},W)\prod _{t=1}^K{g}_{C_t}(C_t\mid {\overline{A}}_{t-1},{\overline{L}}_{t-1},{\overline{C}}_{t-1},W)}},\end{array}$$

where Q is the joint conditional distribution of the Y, L_t and W variables that can be decomposed into conditional distributions Q_Y, Q_Lt, t = 1, …, K, and Q_W. Similarly, g is the conditional distribution of the exposure and censoring variables that can be decomposed into g_At, t = 1, …, K − 1, and g_Ct, t = 1, …, K.

Given a fixed breastfeeding regimen, ā, we can define the distribution Q^ā of the corresponding counterfactual variables Y^ā, ${\overline{L}}_K^{\overline{a}}$, W (under the causal assumptions of consistency and sequential ignorability discussed in Section 4.1) as

$$Q^{\overline{a}}(Y^{\overline{a}},{\overline{L}}_K^{\overline{a}},W)=Q_Y(Y\mid {\overline{C}}_K=0,{\overline{A}}_{K-1}={\overline{a}}_{K-1},{\overline{L}}_{K-1},W)\times \prod _{t=1}^{K-1}{Q}_{L_t}(L_t\mid {\overline{C}}_t=0,{\overline{A}}_{t-1}={\overline{a}}_{t-1},{\overline{L}}_{t-1},W)Q_W(W),$$

where ā_t = (a₁, …, a_t) is the component of the fixed regime up until time-point t. The targeted parameter of interest, specifically the marginal mean under a fixed breastfeeding regimen ā, can then be described as ψ̂_ā = E_QY^ā where the expectation is taken under Q^ā.

Because the intermediate variables L_t, 1 ≤ t ≤ K − 1, are binary, the expression for ψ_ā = E_QY^ā simplifies to

$$\begin{array}{l}{\psi }_{\overline{a}}={\int }_W\sum _{l_1=\{0,1\}}\cdots \sum _{l_{K-1}=\{0,1\}}E(Y\mid C_K=0,{\overline{A}}_{K-1}=\overline{a},{\overline{L}}_{K-1}={\overline{l}}_{K-1},W)\\ \times Pr(L_{K-1}=l_{K-1}\mid {\overline{C}}_{K-1}=0,\\ {\overline{A}}_{K-2}={\overline{a}}_{K-2},{\overline{L}}_{K-2}={\overline{l}}_{K-2},W)\cdots \\ \times Pr(L_1=l_1\mid C_1=0,W)Q_W(W)dW.\end{array}$$ (1)

Each component of the above expression can be estimated from the observed data. Only the conditional mean of Y and the conditional probabilities for L_t, 1 ≤ t ≤ K, must be fit to produce a G-computation estimate. The mean and the conditional probabilities can be estimated using any parametric method as desired.

To obtain an estimate of the parameter using G-computation, first get a prediction of each conditional expectation and probability in equation (1) for each subject, i. The Q_W can be estimated using the empirical density so that Q_W (w_i) = 1/n for each subject (with baseline variables w_i). Then, the predicted values for the conditional expectation and probabilities are combined according to equation (1), where the integral is replaced by summation over all subjects, i.

G-computation does not rely on the full specification of the density Q. However, it requires correct specification of the conditional models for the mean and each of the probabilities in order to obtain unbiased estimation of the parameter ψ_ā. No closed form or asymptotic result is available for the G-computation standard error, so using a nonparametric bootstrap is often suggested [Snowden, Rose and Mortimer (2011)]. To properly assess the variance in the clustered design, the analyst might use the pairs clustered bootstrap [Cameron, Gelbach and Miller (2008)] by resampling clusters instead of individuals.

3.2. Sequential G-computation formulation

As suggested by Bang and Robins (2005) and used by van der Laan and Gruber (2012), an alternative decomposition of the parameter of interest, and therefore an alternative to the standard likelihood G-computation, can be constructed by taking sequential expectations of the outcome. Their result is an application of the property of iterated expectations.

Under the causal assumptions of sequential exchangeability and consistency, the marginal mean under breastfeeding regime ā and no censoring can be reexpressed as

$$\begin{array}{l}{\psi }_{\overline{a}}=E(Y^{\overline{a}})\\ =E\{E(Y\mid C_K=0,{\overline{A}}_{K-1}={\overline{a}}_{K-1},{\overline{L}}_{K-1},W)\}\\ =E[E\{E(Y\mid C_K=0,{\overline{A}}_{K-1}={\overline{a}}_{K-1},{\overline{L}}_{K-1},W)\mid C_K=0,{\overline{A}}_{K-2}={\overline{a}}_{K-2},{\overline{L}}_{K-2},W\}]\end{array}$$ (2)

by sequentially breaking up the expectations into nested conditional expectations. This decomposition of the expectations is continued until the outermost expectation is only conditional on W.

In order to obtain an estimate of the parameter using this decomposition, a model must be fit for each level of conditioning, beginning with the innermost expectation. To more easily refer to each model fit, van der Laan and Gruber (2012) described the conditional models of the counterfactuals iteratively. Let

$${\overline{Q}}_K=E(Y\mid C_K=0,{\overline{A}}_{K-1}={\overline{a}}_{K-1},{\overline{L}}_{K-1},W)$$

be the outcome expectation conditional on the full history, for those who followed the regime ā and were fully observed. The fit Q̄_K is obtained using a conditional modeling method. Then, recursively define

$$\begin{array}{l}{\overline{Q}}_t=E({\overline{Q}}_{t+1}\mid C_t=0,{\overline{A}}_{t-1}={\overline{a}}_{t-1},{\overline{L}}_{t-1},W),t=K-1,\dots ,2,\\ {\overline{Q}}_1=E({\overline{Q}}_2\mid W)\end{array}$$

for each successive nested expectation. The overbar in Q̄_t denotes a mean.

This alternative decomposition of the parameter can be used to compute an estimate of the parameter of interest using the following algorithm. It is done by producing model fits for each of the Q̄_t’s, obtaining predictions for each individual, and then taking a mean of Q̄₁ over all participants. Specifically, the estimation algorithm proceeds as follows:

1. First, model the outcome Y given all of the covariate history, for only those completely uncensored subjects with observed breastfeeding regime Ā_K−1 = ā_K−1. This can be done using logistic regression or any appropriate prediction method. (Alternatively, a general conditional expectation conditional on Ā_K−1 can be fit using all uncensored subjects and then evaluated at ā_K−1 in order to smooth over all observations.)

2. Then, using the model produced in (1), predict the conditional outcome for all subjects (including those censored), resulting in the fit Q̄_K,n.

   Then, iteratively for t = K, …, 2,

3. Fit a model for Q̄_t,n from the previous step conditional on covariates L̄_t−1 using only subjects uncensored up until time t − 1 (i.e., subjects with C_t−1 = 0) with observed breastfeeding status Ā_t−2 = ā_t−2. (Again, this model can be alternatively fit using all uncensored subjects, conditioning on Ā_t−2, and then evaluating at ā_t−2.)

4. For all subjects, predict a new conditional outcome from this last model, producing the fit Q̄_t−1,n.

Repeat steps 3 and 4 for each time point (going backward in time) until predictions Q̄_1,n are obtained for the outcome conditional on only the baseline covariates, W. The parameter estimate is then obtained by taking a mean of Q̄_1,n over all observations. As in the previous G-computation method, variance estimates are computed using bootstrap cluster resampling. Note that the above procedure does not depend on the type or dimension of the variables L_t and W, and fits one model per time point (where there is an intervention or censoring).

3.3. Efficient estimation for longitudinal data

Both G-computation algorithms described here require correct specification of different decompositions of the underlying data generating form. Alternatively, efficient semiparametric estimation allows for root-n consistent estimation with the added benefit of double robustness [Tsiatis (2006), van der Laan and Robins (2003)]. Briefly, influence curves are weighted score functions that contain all of the information about the asymptotic variance of the related estimator. The efficient influence curve for a given parameter is the influence curve that reaches the minimal variance bound. One possible way of obtaining efficient semiparametric inference is to estimate the components of the efficient influence curve and then use it as an estimating equation by setting it equal to zero and solving for the target parameter.

Corresponding to the original G-computation factorization of the likelihood, van der Laan (2010) derived a representation of the efficient influence curve for a longitudinal form with binary intermediate variables. Similarly, Stitelman, De Gruttola and van der Laan (2012) modified the corresponding theory for survival data. The alternative formulation for the efficient influence curve was developed by Bang and Robins (2005) and used by van der Laan and Gruber (2012), allowing for a general longitudinal form and much easier estimation procedures for higher-dimensional or more complex longitudinal data.

Let ḡ_t, t = 2, …, K, be the probability associated with obtaining a given history of breastfeeding ā up until time t − 1 and no censoring up until time-point t, conditional on the observed history L̄_t−1 and W. Specifically, let

$$\begin{array}{l}{\overline{g}}_t({\overline{L}}_{t-1},W)\\ =Pr(C_1=0\mid W)\\ \times \prod _{k=2}^t\{Pr(C_k=0\mid {\overline{A}}_{k-1}={\overline{a}}_{k-1},C_{k-1}=0,{\overline{L}}_{k-1},W)\\ \times Pr(A_{k-1}=a_{k-1}\mid {\overline{A}}_{k-2}={\overline{a}}_{k-2},C_{k-1}=0,{\overline{L}}_{k-1},W)\end{array}$$ (3)

for t = 2, …, K, and where A₀ and a₀ are null sets. Further, let ḡ₁(W) = Pr(C₁ = 0 | W) be the probability of being uncensored at the first time point, conditional on baseline covariates, W. These probabilities can be estimated using logistic regression, for instance. As derived and explained for a general longitudinal structure in van der Laan and Gruber (2012), the efficient influence curve D(O) for a fixed ā can then be written recursively for the PROBIT data as the sum of the components

$$\begin{array}{l}{D}_t=\frac{I({\overline{A}}_{t-1}={\overline{a}}_{t-1},C_t=0)}{{\overline{g}}_t}({\overline{Q}}_{t+1}-{\overline{Q}}_t)\text{for}t=K,\dots ,2,\\ D_1=\frac{I(C_1=0)}{{\overline{g}}_1}({\overline{Q}}_2-{\overline{Q}}_1)\text{and}\\ D_0=({\overline{Q}}_1-{\psi }_{\overline{a}}),\end{array}$$ (4)

where Q̄_K+1 = Y is defined for notational convenience (and the dependencies of some components repressed). I (·) is an indicator function.

With each of the ḡ_t and Q̄_t components estimated using any given prediction method, the parameter ψ_ā can be estimated by setting the sum of the K + 1 components equal to zero and solving for ψ̂_ā. In addition to being efficient, such an estimator is double robust: it is consistent if either the models for Q̄_t, t = 1, …, K, or the models for ḡ_t, t = 1, …, K, contain the truth.

3.4. TMLE using the alternative G-computation formulation

The sequential G-computation method described in Section 3.2 is a substitution estimator because it is a function of a component of the likelihood, specifically the nested conditional expectations, Q̄_t. The general TMLE procedure begins with some choice of substitution estimator, but modifies this estimator by updating the fits of the conditional expectations in order to produce a parameter estimate that satisfies the equation of the efficient influence curve set equal to zero. This parameter estimate is efficient and double robust. The general TMLE procedure has been described previously, for example, by Gruber and van der Laan (2010), Rosenblum and van der Laan (2010b), van der Laan and Rubin (2006).

Details regarding the construction of the sequential longitudinal estimator are given by van der Laan and Gruber (2012). The first step in the TMLE procedure is to fit the conditional densities {Q̄_t, t = 1, …, K} using a method of choice. For the update step, the logistic loss function is chosen even for our case of an integer-valued outcome (which is reduced to proportions by shifting and scaling the vector to [0, 1]) due to the boundedness properties of the inverse of its canonical link function. The logistic loss becomes particularly valuable when there is sparsity at certain levels of the covariates or exposure [Gruber and van der Laan (2010)].

The next step is to fluctuate each of the initial density estimates {Q̄_t,n, t = K, …, 1}, starting at t = K, with respect to a new parameter, ε_t. A subscript n will be used to denote a fitted value. The fluctuation function for each Q̄_t (ε_t) can be described as

$$\text{logit}{\overline{Q}}_t^1({\epsilon }_t)=\text{logit}{\overline{Q}}_t+{\epsilon }_t{G}_t,t=1,\dots ,K,$$ (5)

for some expression G_t. Again letting Q̄_K+1 = Y, the estimate for ε_t is found by minimizing the empirical mean of the logistic loss function

$$\mathcal{L}\{{\overline{Q}}_t^1({\epsilon }_t)\}=-[{\overline{Q}}_{t+1}log\{{\overline{Q}}_t^1({\epsilon }_t)\}+(1-{\overline{Q}}_{t+1})log\{1-{\overline{Q}}_t^1({\epsilon }_t)\}],$$ (6)

which is equivalent to solving the empirical mean score (or derivative of the loss function) at zero. This requires that the function G_t be defined and estimated.

According to the general TMLE procedure, the above fluctuation function in equation (5) is required to satisfy two conditions: (1) the fluctuation function must reduce to the original density when ε_t = 0, and (2) the derivative with respect to ε_t of the loss function at ε_t = 0 must linearly span the efficient influence curve. The first condition is clearly satisfied when ε_t = 0. Taking the derivative of the loss function in equation (6) with respect to ε_t gives

$${\frac{d\mathcal{L}({\overline{Q}}_{t,n}^1({\epsilon }_t))}{d{\epsilon }_t}|}_{{\epsilon }_t=0}=G_t\times ({\overline{Q}}_{t+1}-{\overline{Q}}_t),t=1,\dots ,K.$$

Therefore, the score spans the efficient influence curve when G_t is defined as

$$G_t(C_t,{\overline{A}}_{t-1},{\overline{L}}_{t-1},W)=\frac{I(C_t=0,{\overline{A}}_{t-1}={\overline{a}}_{t-1})}{{\overline{g}}_t}.$$

The covariate G_t is often described as “clever” because it allows the score to span the efficient influence curve.

The update step is carried out by minimizing the empirical mean of the loss function, $\mathcal{L}\{{\overline{Q}}_{t,n}^1({\epsilon }_t)\}$, with respect to ε_t. This is equivalent to running the logistic regression in equation (5): no intercept, with offset logit(Q̄_t,n) and unique covariate G_t (C_t, Ā_t−1, L̄_t−1, W). Let ε̂_t be the estimate of the coefficient for G_t, which is the maximum likelihood estimate (or, equivalently, the minimum loss-based estimate) for ε_t.

Once all of the densities have been updated to give { ${\overline{Q}}_{t,n}^1$, t = K, …, 1}, the parameter ψ_ā is estimated as the mean of ${\overline{Q}}_{1,n}^1$ over all subjects, that is, ${\widehat{\psi }}_{\overline{a}}=\frac{1}{n}{\sum }_i{\overline{Q}}_{1,n}^1(W=w_i)$ (where w_i is the observed baseline vector for subject i).

This TMLE is double robust: it is consistent if either the models for Q̄_t, t = 1, …, K, or the models for ḡ_t, t = 1, …, K, contain the truth. In addition, because of the usage of the logistic loss function and the corresponding fluctuation function in equation (5), the parameter estimates are bounded, regardless of the size of the weights, ${\overline{g}}_t^{-1}$. This makes TMLE robust to certain kinds of data sparsity that cause large weights. A comparison of the fundamental qualities of the G-computation estimators, TMLE and IPTW, can be found in Table 3.

Table 3.

Comparison of methods

Method	Required for consistency	Robust to data sparsity	Variance estimate	Respects parameter boundaries
G-comp.	CE	✓	BS	✓
G-comp. seq.	NE	✓	BS	✓
IPTW	propensity	×*	EIC/BS	×
TMLE	propensity or NE	✓	EIC	✓

CE: conditional expectations; NE: nested expectations; BS: bootstrap; EIF: efficient influence curve; propensity: the conditional probabilities of intervention (e.g., breastfeeding) and censoring.

^*Improvement under weight stabilization.

3.4.1. TMLE procedure for the PROBIT data

We observed the following procedure in our estimation of the parameter ψ_ā, for a given breastfeeding regimen ā. As described above, our interpretation of the structure of the PROBIT data set is O = (W, C₁, L₁, A₁, C₂, L₂, …, A₅, C₆, Y). There are six intervention nodes: censoring can occur at any of them and breastfeeding status is assessed at t = 1, …, 5. All subjects are initially breastfeeding, so breastfeeding regimen is equivalent to the total duration of breastfeeding. If a subject has been censored, impute their missing L_t and Y variables with zero values:

1. Fit models predicting breastfeeding and censoring (resp.) at each time point, conditional on all previous history. For each model, compute a predicted probability for each subject conditional on Ā_t = ā_t and C_t = 0.

   • Given the monotone nature of breastfeeding, if ā = (1, 0, 0, 0, 0), for instance, the predicted probability of not breastfeeding at time 3 will be one for all participants, since it is conditional on stopping before time 2.

2. Using the predictions from step 1, calculate the propensity score ḡ_t,n from equation (3) for each subject.

3. Set Q̄_7,n = Y, where Y is rescaled to [0, 1]. Then, for t = 6, …, 1,

   • For the subset of subjects with Ā_t−1 = ā_t−1 and C_t = 0, fit a model for E(Q̄_t+1,n | L̄_t−1). Using this model, predict the conditional outcome for all subjects and let this vector be denoted Q̄_t,n.

   • Construct the “clever covariate” G_t (C_t, Ā_t−1, L̄_t−1, W) = I (C_t = 0, Ā_t−1 = ā_t−1)/ḡ_t,n.

   • Update the expectation by running a no-intercept logistic regression with outcome Q̄_t+1,n, the fit logit(Q̄_t,n) as an offset and clever covariate G_t as the unique covariate. Let ε̂_t be the estimated coefficient of G_t.

   • Update the fit of Q̄_t by setting

     $${\overline{Q}}_{t,n}^1=\text{expit}\{\text{logit}({\overline{Q}}_{t,n})+{\widehat{\epsilon }}_t{G}_t(A_{t-1}={\overline{a}}_{t-1},C_t=0,{\overline{L}}_{t-1})\}$$

     and then obtain a predicted value of ${\overline{Q}}_{t,n}^1$ for all subjects.

     Note that the model for Q̄₁ is modeled using only subjects with C₁ = 0. The resulting fit Q̄_1,n is only conditional on W and is estimated for all subjects.

4. Having fit ${\overline{Q}}_{1,n}^1$ for each subject, take the mean. Rescale the mean (do the inverse of the original scaling of Y). This is the TMLE for ψ_ā.

The standard errors can be calculated using a sandwich estimator, which uses the influence curve to approximate the asymptotic variance. First, the value of the influence curve D(O) is estimated for each subject. The clusters Z_m are indexed by m = 1, …, M. Let ρ_m = E(D_i D_j) for two elements in the cluster Z_m and let ${\sigma }_m^2=\text{Var}(D_i)=E(D_i^2)$ be the common variance for subjects in cluster Z_m.

Assuming independence between the clusters and common variance for elements in a cluster, the large sample variance of the estimator is approximated using

$$\begin{array}{l}{\sigma }^2=1/n^{2}E{\left(\sum _{i=1}^n{D}_i\right)}^2=\frac{1}{n^2}\sum _{m=1}^M\sum _{i,j\in Z_m}E(D_i{D}_j)I(i\ne j)+E(D_i^2)I(i=j)\\ =\frac{1}{n^2}\sum _{m=1}^M{n}_m(n_m-1){\rho }_m+n_m{\sigma }_m^2,\end{array}$$

where n_m is the size of cluster Z_m. The supplemental article Schnitzer et al. (2014) contains details about the form of the influence curve under clustering. The expectations can be estimated by taking the empirical covariance and variance within each of the clusters. Confidence intervals are calculated assuming Normality of the estimator, using the estimate plus and minus 1.96 times the estimated standard error.

4. Analysis of the PROBIT

The PROBIT data were analyzed by both G-computation methods; TMLE with parametric modeling of the sequential conditional means and conditional probabilities of breastfeeding and censoring (logistic main terms regression for binary breastfeeding status and censoring, and for the outcome shifted and scaled to [0, 1]); TMLE with Super Learner to model the conditional expectations and probabilities; and a stabilized IPTW estimator. All models were implemented directly in R Statistical Software [R Development Core Team (2011)] with the exception of Super Learner which we fit using the R library SuperLearner [Polley and van der Laan (2011)]. Super Learner calculates predictions using each method in a library, and then estimates the ideal combination of these results based on the k-fold cross-validated error. The library we chose included main terms logistic regression, generalized additive modeling [Hastie (2011)], the mean estimate, a nearest neighbor algorithm [Peters and Hothorn (2011)], multivariate adaptive regression spline models [Milborrow (2011)] and a stepwise AIC procedure [stepAIC from Venables and Ripley (2002)].

A stabilized IPTW estimator was computed by obtaining the solution of the empirical mean of

$$(Y-{\widehat{\psi }}_{\overline{a}}^{\text{IPTW}})\frac{I({\overline{A}}_5=\overline{a},C_6=0)(1/n)\sum {\overline{g}}_{6,n}}{{\overline{g}}_{6,n}}$$

set equal to zero. To be consistent, IPTW relies on correct modeling of the breast-feeding and censoring probabilities in ḡ₆. IPTW was implemented using logistic regressions to fit each of these conditional probabilities.

The standard errors for all methods except the G-computations were calculated using the sandwich estimator, adjusting for clustering as described in Section 3.4.1. The standard errors for the G-computation methods were estimated using pairs cluster bootstrap [Cameron, Gelbach and Miller (2008)] by resampling the 31 clusters with replacement, repeating 200 times, recalculating the estimates, and taking the standard error of the estimates. Confidence intervals were calculated by taking the 2.5th and 97.5th quantiles of the resampled estimates.

Both G-computations were found to be sensitive to modeling choices when fitting the conditional expectations. In particular, we implemented both G-computations with Poisson regressions and with logistic regressions using a rescaled outcome. For the standard G-computation, both parametric specifications produced very similar point estimates, but the Poisson model was found to be highly unstable through the cluster bootstrapping while the logistic model was more stable. For the sequential G-computation, the Poisson model produced uninterpretable point estimates that deviated substantially from the other models, while the point estimates of the logistic model conformed more or less to the other results. Only the logistic results are therefore presented in the table.

The estimates of three comparisons of interest are presented in Table 4. The first parameter of interest is the difference between the marginal expected number of infections (in the first year or life) for infants who were breastfed for between 3 and 6 months compared to infants who were breastfed for between 1 and 2 months. The second parameter compares infants who were breastfed for greater than 9 months to those breastfed for 3 to 6 months. The third parameter compares greater than 9 months to between 1 and 2. The table presents the estimates, standard errors and 95% confidence intervals for each parameter of interest as calculated by each method.

Table 4.

Differences in marginal expected number of infections under different breastfeeding durations

Method	Estimate	S.E.	95% C.I.
	3–6 months vs 1–2 months
G-comp. (likelihood)	−0.032	0.008	(−0.046, −0.019)
G-comp. (sequential)	−0.039	0.013	(−0.062, −0.016)
IPTW	−0.021	0.011	(−0.042, 0.000)
Parametric TMLE	−0.027	0.010	(−0.045, −0.008)
TMLE with SL	−0.039	0.010	(−0.058, −0.020)
	9+ months vs 3–6 months
G-comp. (likelihood)	−0.013	0.004	(−0.020, −0.005)
G-comp. (sequential)	−0.014	0.013	(−0.027, 0.004)
IPTW	−0.013	0.010	(−0.032, 0.007)
Parametric TMLE	−0.021	0.013	(−0.047, 0.004)
TMLE with SL	−0.024	0.007	(−0.038, −0.010)
	9+ months vs 1–2 months
G-comp. (likelihood)	−0.045	0.010	(−0.065, −0.027)
G-comp. (sequential)	−0.053	0.018	(−0.084, −0.020)
IPTW	−0.034	0.014	(−0.061, −0.007)
Parametric TMLE	−0.048	0.018	(−0.084, −0.012)
TMLE with SL	−0.063	0.013	(−0.088, −0.038)

G-comp.: G-computation, using both methods described in the text, likelihood in Section 3.1 and sequential in Section 3.2; TMLE: targeted maximum likelihood estimation; SL: Super Learner; IPTW: inverse probability of treatment weighting (stabilized).

All of the methods estimated a negative parameter value for the difference, corresponding with the interpretation that longer durations of breastfeeding reduce the expected number of gastrointestinal infections. TMLE with Super Learner and likelihood G-computation found a statistically significant difference for each comparison. Only IPTW found an insignificant estimate for the first comparison. Sequential G-computation, IPTW and parametric TMLE found an insignificant estimate for the second comparison. All methods determined that there is a true difference between the marginal mean infection counts for breastfeeding for over nine months versus between one and two months.

The estimates of the difference parameters varies substantially between methods. In two of the comparisons, TMLE with Super Learner produced higher estimates than all of the other methods (almost twice the size of the smallest estimates). IPTW gave the smallest estimates of the differences. Likelihood G-computation consistently produced the smallest standard errors and TMLE with Super Learner produced the second smallest.

4.1. The validity of a causal interpretation

A causal interpretation of the analysis of the PROBIT data requires several important but untestable assumptions, including the sequential randomization assumption. In other words, all confounders are assumed to have been measured and included in W, including all prognostic factors of infection that also predict censoring. The complexities of the substantive matter make it challenging to believe that we identified all the common causes of breastfeeding cessation and infections [Kramer et al. (2011)]. However, we argue that by controlling for cluster as a baseline variable, much of this confounding effect may have been alleviated (this is investigated in Section 5).

In addition, we must assume no interference between study units (mother/infant pairs) and that only one version of the treatment (i.e., breastfeeding) is applied to all units [together referred to as the stable unit treatment variable assumption, or SUTVA; Rubin (1978)]. The assumption of no interference requires that the breastfeeding status of one mother does not influence the outcome of another’s child. We believe this to be very plausible because mothers spent short periods of time in the hospital which limited their interaction. For the second assumption, due to the discretization of the study design, different durations of breastfeeding are grouped together. We must assume that it does not matter when a mother ceases to breastfeed within an interval.

5. Simulation study

A simulation study was performed where data were generated as a simplified version of the PROBIT data set. Five hundred subjects were generated in each of 31 clusters. The baseline covariates W and U were generated as Gaussian variables with cluster-specific means drawn from separate Gaussian distributions. The time-dependent variables (C₁, L₁, A₁, C₂, L₂, A₂, C₃, L₃) were generated independently for each subject conditional on the subject’s history, including baseline variables W and U (and not otherwise clustered). Binary variables A_t, t = 1, 2, indicate continued breastfeeding, C_t, t = 1, 2, 3, are censoring indicators, and L_t, t = 1, 2, 3, indicate the presence of infections. The outcome $Y={\sum }_{t=1}^3{L}_t$ is a count variable. Breastfeeding status was generated as conditional on the baseline variables and immediate preceding covariates at every time point. In particular, breastfeeding was specifically made to be less likely to continue when infection was indicated at the current time point. Breastfeeding (like censoring) is a monotone process, and so A₂ = 1 is only possible if A₁ = 1. The probability of censoring was conditional on baseline covariates and most recent infection status; censoring was less likely if breastfeeding continued at the previous time point and more likely if an infection occurred at the previous time point. Infections were generated conditional on baseline variables and breastfeeding for the past two visits, so that longer duration of breastfeeding decreased the probability of infection. The strengths of the associations between exposure/censoring and intermediate infections were designed to reflect the true PROBIT results. Details of the data generation can be found in the supplemental article Schnitzer et al. (2014).

The parameter ψ_ā = E(Y_ā) was estimated for ā = (0, 0) and ā = (1, 1). The parameter of interest, reflecting the first parameter of interest in the PROBIT study, was δ = ψ_(1,1) − ψ_(0,0).

A concern we had during the planning of the PROBIT study was that we may be missing some important confounders of the effect of breastfeeding on infection. Therefore, we attempt to explore this issue in the simulation study by omitting the variable U from the modeling. In a second modeling scenario, we illustrate how adjusting for the cluster like a baseline confounder can successfully adjust for unmeasured confounding that is characterized by the cluster itself. In addition, we test the scenario where U is included in the modeling so that the results could be compared. Finally, we test a scenario where we suppose that the analyst is given transformed versions of W and U [using two of the transformations in Kang and Schafer (2007)] and the models are run using these transformed variables.

One thousand data sets of 500 × 31 = 15,500 observations were generated. Under each of the four modeling scenarios (unmeasured U, adjusting for cluster, adjusting for U and transformed confounders), the performance of the TMLE was compared to G-computation, the sequential formulation of the G-computation formula and a stabilized IPTW estimator. TMLE was implemented in two ways: with main terms logistic regressions to estimate all probabilities and with Super Leaner, using only main terms logistic regression and a nearest neighbors algorithm in its library (a small subset of the library used in the PROBIT analysis). Standard errors were computed using influence curve inference where available and nonparametric bootstrap resampling otherwise (details in the footnote of Table 5). Due to the way the data were generated, the sequential G-computation was always incorrectly specified (in the model form), as were the outcome models for the TMLE.

Table 5.

Difference between marginal expected outcomes, by scenario. True value = −0.030

Method	δ̂	% bias	SE (δ̂)	rMSE (δ̂)	Coveragea
	Unmeasured confounder
G-comp. (likelihood)	−0.060	−99	0.017	0.035	49
G-comp. (sequential)	−0.062	−105	0.018	0.037	44
IPTW	−0.054	−77	0.021	0.023	100
Parametric TMLE	−0.058	−90	0.017	0.027	63
SL TMLE	−0.054	−79	0.019	0.024	78
	Unmeasured confounder, adjusting for cluster
G-comp. (likelihood)	−0.033	−11	0.008	0.009	92
G-comp. (sequential)	−0.035	−16	0.009	0.011	94
IPTW	−0.032	−6	0.010	0.009	94
Parametric TMLE	−0.032	−7	0.009	0.009	94
SL TMLE	−0.030	1	0.008	0.009	90
	Adjusting for all confounders
G-comp. (likelihood)	−0.032	−4	0.008	0.009	91
G-comp. (sequential)	−0.034	−12	0.018	0.010	43
IPTW	−0.031	−1	0.010	0.009	93
Parametric TMLE	−0.031	−1	0.009	0.009	92
SL TMLE	−0.029	5	0.009	0.010	88
	Transformed confounders
G-comp. (likelihood)	−0.068	−125	0.017	0.042	29
G-comp. (sequential)	−0.075	−147	0.023	0.050	20
IPTW	−0.062	−106	0.109	0.125	55
Parametric TMLE	−0.067	−121	0.041	0.045	36
SL TMLE	−0.033	−9	0.032	0.013	95

SE(δ): the average standard error is the square-root of the mean of the variances, with each variance calculated using the influence curve for TMLE and IPTW and the nonparametric boostrap^b for G-comp. (likelihood) and G-comp. (sequential); rMSE: root mean squared error calculated over the simulated data sets; Coverage: mean coverage; TMLE: targeted maximum likelihood estimator; G-comp.: G-computation; IPTW: (stabilized) inverse probability of treatment weighting.

^aThe estimated coverage is the % of data sets where the true value falls between (i) the estimate plus and minus 1.96 times the standard error of the estimate for TMLE and IPTW or (ii) the 2.5th and 97.5th bootstrap percentiles for the G-computation methods;

^bThe bootstrap standard error was computed using 200 resamples from the data set of size n = 15,500.

As a small departure from the real data, the simulated data allowed only one infection at each time interval (as opposed to more than one event). The G-computation used the information that the outcome was a sum of the first two binary infection variables and the additional binary variable, L₃, measured at time t = 3. Thus, $Y={\sum }_{t=1}^2{L}_t+L_3$, so that the G-computation simplified to the empirical mean of

$$\begin{array}{l}\sum _{l_1=\{0,1\}}\cdots \sum _{l_K=\{0,1\}}[\left\{\sum _{t=1}^2{L}_t+E(L_3\mid C_3=0,{\overline{A}}_2={\overline{a}}_2,{\overline{L}}_2={\overline{l}}_2,W)\right\}\\ \times \{p(L_2=l_2\mid C_2=0,{\overline{A}}_1={\overline{a}}_1,{\overline{L}}_1={\overline{l}}_1,W)\}\\ \times p(L_1=l_1\mid C_1=0,W)].\end{array}$$

Note that using the information regarding the number of infections at each time interval for the PROBIT data analysis would have required fitting multinomial models in the likelihood G-computation. With so few subjects having more than one infection at any given time, we did not feel that substantial information could be added by increasing the complexity of the model for the applied example using a similar approach.

5.1. Simulation results

The results of each of the models under each modeling scenario are displayed in Table 5. With an unmeasured confounder related to cluster, both G-computation models performed the most poorly in terms of bias, root mean-squared error (rMSE) and coverage. TMLE produced an improvement in these measures, and adding Super Learner improved all measures of performance except for the standard error. IPTW had the lowest bias, but higher standard errors, resulting in overcoverage. When cluster was used as a surrogate for the unmeasured confounder, all of the methods produced results with much lower bias and standard errors. When all confounders were measured and adjusted for, G-computation, parametric TMLE and IPTW all had a reduction in bias compared to the previous scenario and performed ideally, despite parametric TMLE being model-misspecified in the outcome models. TMLE with Super Learner produced slight undercoverage. The sequential G-computation was model-misspecified and produced high bias and standard error, leading to poor coverage (since it is not double robust). When the confounders were transformed, all of the parametric models were incorrectly specified, leading to high bias and low coverage. Among the parametric models, IPTW had the lowest bias and the highest root mean-squared error. TMLE with Super Learner (using only one data adaptive algorithm in its library) was essentially unbiased with ideal coverage.

6. Discussion

In this article we applied five different causal methods to the PROBIT data to obtain estimates of the differences in the marginal expected number of infection counts for different breastfeeding durations. All methods agreed that extending the duration of breastfeeding significantly lowers the expected number of gastrointestinal infections. TMLE with Super Learner produced much larger effect estimates, for example, its estimate was almost double the IPTW estimate for the comparison between 1–2 and 9+ months of breastfeeding. This represents a clinically important difference in the estimated effect. Super Learner also reduced the higher standard error of the TMLE procedure to a level comparable to that of the G-computation (which is an efficient parametric estimator).

Using the mean estimate from TMLE with Super Learner, altering the breast-feeding durations of 16 mothers from between one and two months to over nine months will avoid one infant infection (i.e., the Number Needed to Treat or NNT) on average in this population. This can roughly be compared with the intention-to-treat result in the original PROBIT study [Kramer et al. (2001)], where they obtained a NNT of 24 for the presence ofany gastrointestinal infection over the first year when contrasting subjects who did and did not receive the breastfeeding intervention. We have therefore shown that breastfeeding itself might have a larger impact on childhood infections than suggested by the original PROBIT analysis.

In the simulation study we generated baseline confounders from a distribution with a cluster-specific mean. The simulation results demonstrated that bias (and inflated standard error) incurred by cluster-specific unmeasured confounders can be adjusted for using the cluster indicators themselves as baseline covariates. We also showed that under the plausible scenario of being given transformed versions of the confounders, only TMLE with Super Learner was able to unbiasedly estimate the parameter of interest.

TMLE is a double-robust method, as it only requires correct specification of the conditional probabilities of the intervention (here, breastfeeding and censoring) or of the nested conditional expectations of the outcome (theQ̄_t’s) to be consistent. Contrastingly, IPTW relies on correct specification of the probabilities of the intervention, and the G-computations rely on correct specification of the outcome models. When the probabilities of intervention are modeled in the same way for IPTW and TMLE, in absence of data sparsity, and when the outcome models are incorrectly specified, these two methods are expected to perform similarly (as seen in the simulation study and possibly in the PROBIT results). In many other contexts, advantages of longitudinal TMLE over IPTW and G-computation have been established through simulation study in van der Laan and Gruber (2012), Petersen et al. (2014), Stitelman, De Gruttola and van der Laan (2012), and Schnitzer, Moodie and Platt (2013).

It is important to note that for longitudinal data with time-dependent confounding, there may not exist a data generating distribution that corresponds to the way the outcome is modeled in the TMLE (i.e., in the sequential G-computation). Therefore, we recommend that data adaptive methods like Super Learner always be used with TMLE in the longitudinal setting. Because TMLE with Super Learner is arguably the most reliable estimator (assessed through theory and simulation studies), we have reason to believe that the magnitude of the effect of breastfeeding is actually larger than suggested by the methods that use parametric modeling and larger than the effect reported in the original PROBIT analysis.