SELECTION BIAS MODELING USING OBSERVED DATA AUGMENTED WITH IMPUTED RECORD-LEVEL PROBABILITIES

Abstract

PURPOSE

Selection bias is a form of systematic error that can be severe in compromised study designs such as case-control studies with inappropriate selection mechanisms or follow-up studies that suffer from extensive attrition. External adjustment for selection bias is commonly undertaken when such bias is suspected, but the methods used can be overly simplistic, if not unrealistic, and fail to allow for simultaneous adjustment of associations of the exposure and covariates with the outcome, when of interest. Internal adjustment for selection bias via inverse-probability-weighting allows bias parameters to vary with levels of covariates but has only been formalized for longitudinal studies with covariate data on patients up until loss-to-follow-up.

METHODS

We demonstrate the use of inverse-probability-weighting and externally obtained bias parameters to perform internal adjustment of selection bias in studies lacking covariate data on unobserved participants.

RESULTS

The ‘true’ or selection-adjusted odds ratio for the association between exposure and outcome was successfully obtained by analyzing only data on those in the selected stratum (i.e. responders) weighted by the inverse probability of their being selected as function of their observed covariate data.

CONCLUSIONS

This internal adjustment technique using user-supplied bias parameters and inverse-probability-weighting for selection bias can be applied to any type of observational study.

INTRODUCTION

Selection bias is a form of systematic error that can be severe in compromised study designs as in case-control studies with inappropriate selection of cases or control series (e.g., Berksonian bias or non-response bias) or in follow-up studies that suffer from extensive loss of contact with participants (e.g., loss to follow-up, follow-up bias). Adjusting for selection bias in a study requires knowledge of, or plausible assumptions about the factors that affect the selection mechanism. If the parameters of the selection mechanism are known or can be assumed reasonably, a selection factor can be used to adjust the biased measure of association, typically the sample odds ratio [1–5]. This method is formulaic, requiring external adjustment of crude and adjusted outcome models in a bias analysis [6]. In studies affected by follow-up bias (as opposed to response bias), inverse probability of censoring weighted (IPCW) fitting of the target model can be used to create a pseudo-population that mimics the underlying cohort (including those who were lost to follow up) [7–10]. This form of internal adjustment entails modeling censoring as a function of the last fully observed exposure and measured risk factor history that affect both censoring and the endpoint under study, which requires having said factors measured for both the censored and uncensored. This method generates record-level selection probabilities and their inverse can be used as a weighting factor incorporated into the analytical dataset before any outcome models are run. A distinct advantage of record-level estimation of the selection probabilities is that internal adjustment allows for the bias parameters to vary with individual covariate levels. Additionally, this approach allows end-users to conduct different analyses without and with adjustment for selection bias for different association or effect measures of interest using any statistical software and conventional regression modeling methods. In many epidemiologic studies, data on censored or non-selected participants are unknown, limiting IPCW methods to longitudinal studies that document data on everyone up until loss-to-follow-up.

In this paper, we formalize and demonstrate a method of internal adjustment for selection bias without the need for data on censored patients. This can be done using externally obtained bias parameters combined with data on respondents, or uncensored participants, to simulate or impute the corresponding selection probability for each respondent under the assumed selection and data generating mechanism, as would be depicted in a directed acyclic graph (DAG). Selection bias can then be adjusted using IPCW fitting of any planned outcome regression. Unlike IPCW, this technique is applicable to any observational study. This work is an extension of IPCW, because rather than reliance on data from a censored population, the relationships depicted in the causal diagram can be used to inform specification of selection bias parameters. Externally derived parameters (i.e., from a validation study) can also be used to generate selection probabilities. We formalize our method using probability and illustrate its use with a series of simulations.

NOTATION AND METHODS

Let X be a binary exposure, Y a binary disease outcome, Z be a set of confounding variables that are common causes of both X and Y, and S be a binary selection factor affected by both X, Y and at least one Z, such that exposure in the population can be represented by the probability of P(X=1 | Z=z), prevalence of disease among the unexposed can be represented by the probability P(Y=1 | X=0, Z=z), and those selected into the study population can be represented by the probability P(S=1 | X=x, Y=y, Z=z). Assuming no unmeasured confounding, the causal odds ratio can be represented by the conditional odds ratio, OR_YX|Z.

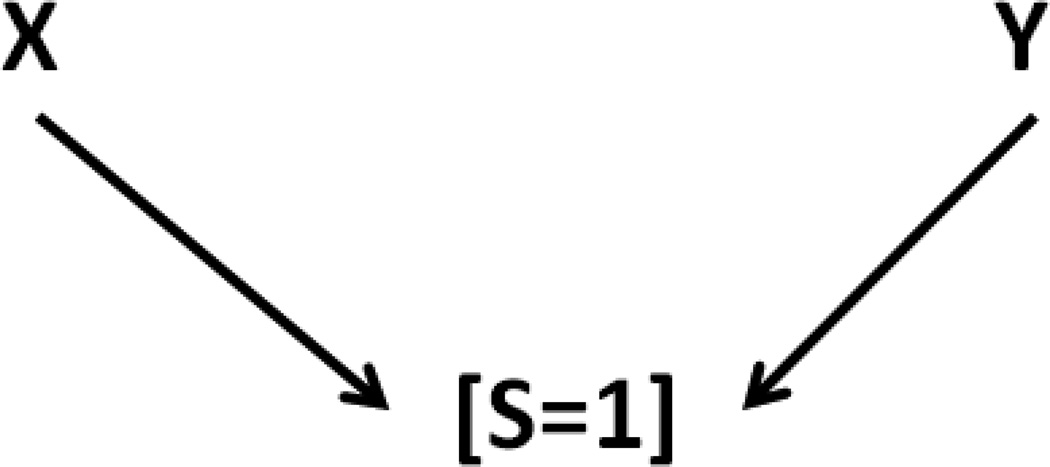
In the language of DAGs, selection bias is the result of collider bias, which occurs when the exposure (or cause of the exposure) and outcome (or cause of the outcome) both directly or indirectly affect selection into the study. The use of DAGs to express these causal relationships imparts a basic set of rules that have been extensively described elsewhere [11–16]. The minimal structure for collider bias is depicted in Figure 1.

Figure 1.

A DAG representing marginally independent but conditionally (on S=1) dependent X and Y; a simple example of collider-stratification bias.

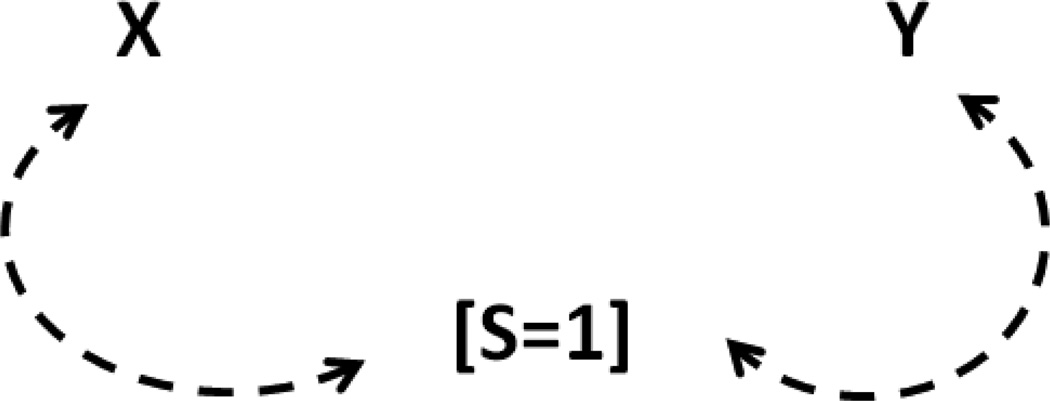
This figure shows that the marginally independent exposure X and outcome Y can become conditionally dependent given selection S=1. Figure 2 shows another example.

Figure 2.

A DAG representing marginally independent but conditionally (on S=1) dependent X and Y, another example of collider-stratification bias in the presence of uncontrolled common causes of X-S and Y-S

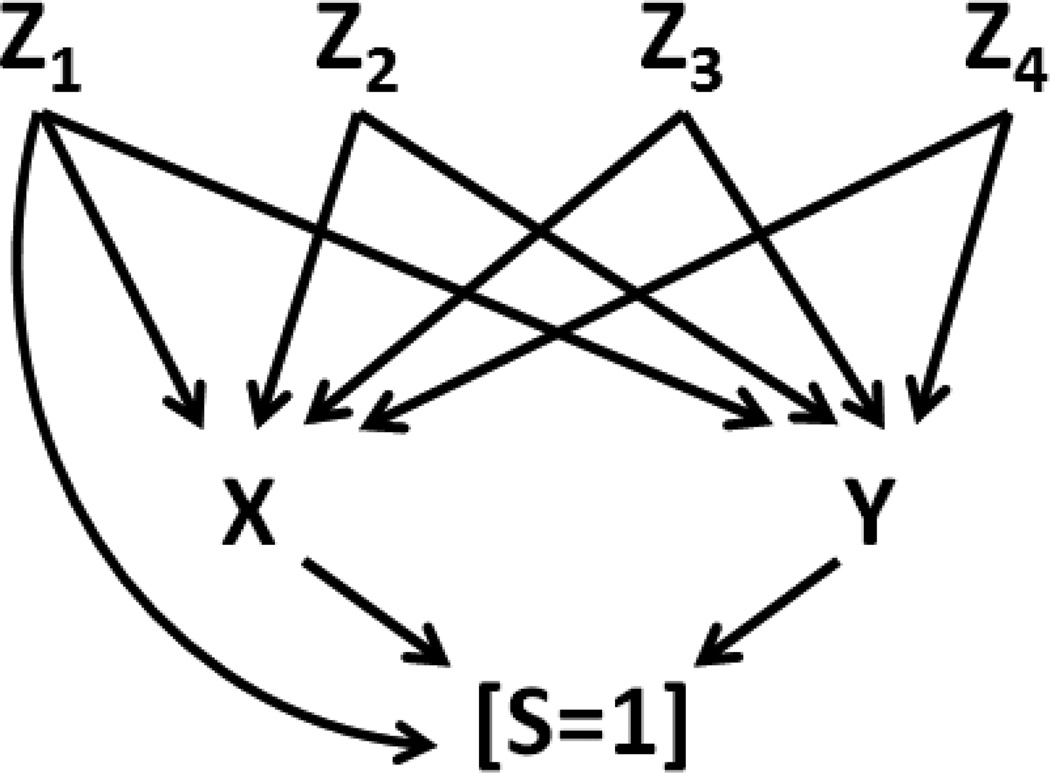
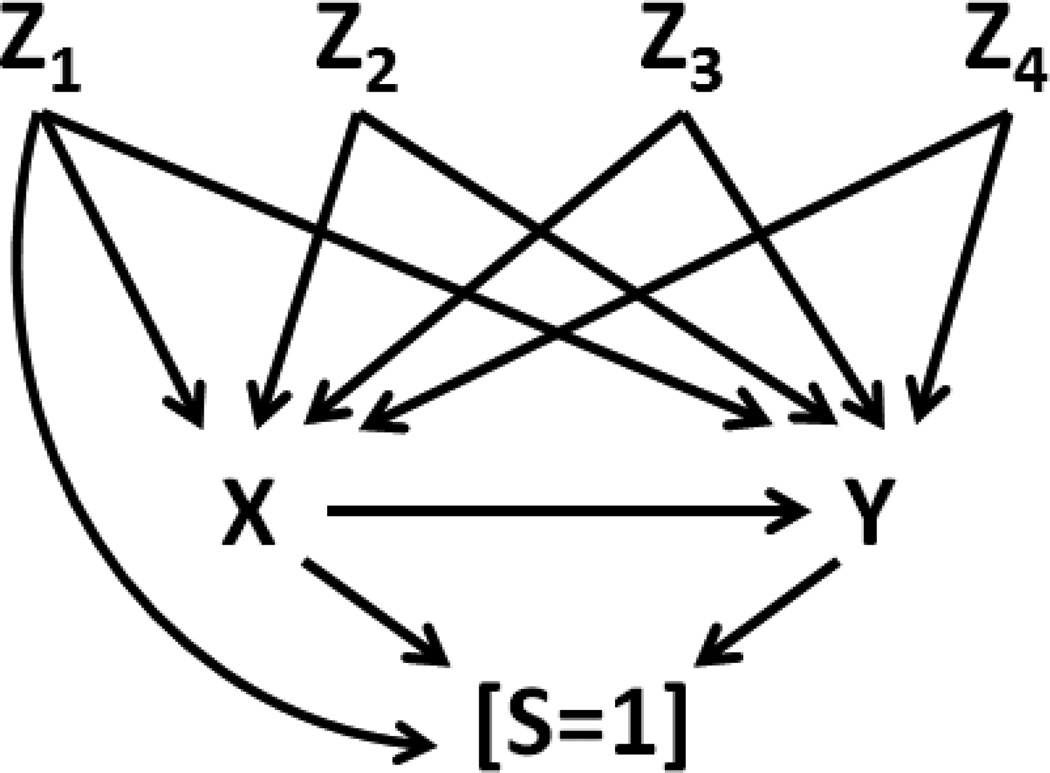
Figures 3 and 4 show scenarios 1 and 2, respectively, where selection is cause by exposure X, confounding variable set Z = [Z₁, Z₂, Z₃, and Z₄] and outcome Y. In either scenario, the joint probability of S=1, y, x, and z is given by:

$$P(S=1,y,x,z)=P(S=1|y,x,z)P(y|x,z)P(x|z)P(z)$$ (1)

Figure 3.

Scenario 1 – A DAG representing marginally independent but conditionally (on S=1) dependent X and Y, with four confounding variables Z₁, Z₂, Z₃, and Z₄, one of which directly affects S.

Figure 4.

Scenario 2 – A DAG representing marginally dependent X and Y with additional conditional (on S=1) dependency and four confounding variables Z₁, Z₂, Z₃, and Z₄, one of which directly affects S.

The term P(S=1|y,x,z) is the probability of selection given the observed data on Y, X and Z. To obtain the selection-bias-free joint probability P(y, x, z) or P(S=1)P(y, x, z), we re-weight the observed P(S=1, y, x, z) by the inverse of P(S=1 | y, x, z) or P(S=1 | y, x, z)/P(S=1). This entails weighting all records in the S=1 sample by either 1/P(S=1 | y, x, z) or P(S=1)/P(S=1 | y, x, z) (the latter being the stabilized version of the inverse probability weight) in a procedure known as inverse-probability-weighting. We will call this procedure inverse-probability-of-selection-weighting (IPSW), a generalization of IPCW.

The conditional probability of selection P(S=1 | y, x, z) is unknown, but it can be modeled using a logistic equation with bias parameter set β as follows:

$$\mathit{\text{logit}}(P(S=1|y,x,z;\mathit{\beta })={\beta }_S+{\beta }_{SY}y+{\beta }_{SX}x+{\beta }_{SZ}z+{\beta }_{SYX}yx+{\beta }_{SYZ}yz+{\beta }_{SXZ}xz+{\beta }_{SYXZ}yxz$$ (2)

Where:

1. β_S is the log odds of selection S=1 when Y=0, X=0 and Z=0 (indicating a degree of selection that is independent of Y, X, and Z);

2. β_SY is the log odds ratio (OR) relating selection S and Y when X=Z=0;

3. β_SX is the log odds ratio relating S and X when Y=Z=0;

4. β_SZ is the log odds ratio relating S and Z when Y=X=0;

5. β_SYX is the logarithm of the ratio of (i) the odds ratio relating S and Y among X=1 and Z=0 to (ii) the odds ratio relating S and Y among X=0 and Z=0 (that is, log(OR_SY|X=1,Z=0/OR_SY|X=0,Z=0) = log(OR_SX|Y=1,Z=0/OR_SX|Y=0,Z=0), by the symmetry of the odds ratio);

6. β_SYZ is the logarithm of the ratio of (i) the odds ratio relating S and Y when Z=1 and X=0 to (ii) the odds ratio relating S and Y when Z=0 and X=0 (that is, log(OR_SY|Z=1,X=0/OR_SY|Z=0,X=0) = log(OR_SZ|Y=1,X=0/OR_SZ|Y=0,X=0));

7. β_SYZ is the logarithm of the ratio of (i) the odds ratio relating S and X when Z=1 and Y=0 to (ii) the odds ratio relating S and X when Z=0 and Y=0 (that is, log(OR_SX|Z=1,Y=0/OR_SX|Z=0,Y=0) = log(OR_SZ|X=1,Y=0/OR_SZ|X=0,Y=0)); and

8. β_SYXZ is the logarithm of the ratio of two ratios, namely the ratio of (i) the ratio of the odds ratio relating S and Y when X=1 and Z=1 and the odds ratio relating S and Y when X=0 and Z=1 to (ii) the ratio of the odds ratio relating S and Y when X=1 and Z=0 and the odds ratio relating S and Y when X=0 and Z=0 (that is, log[(OR_SY|X=1,Z=1/OR_SY|X=0,Z=1)/(OR_SY|X=1,Z=0/OR_SY|X=0,Z=0)]). This β_SYXZ is alternatively given by log[(OR_SX|Y=1,Z=1/OR_SX|Y=0,Z=1)/(OR_SX|Y=1,Z=0/OR_SX|Y=0,Z=0)] = log[(OR_SZ|Y=1,X=1/OR_SZ|Y=0,X=1)/(OR_SZ|Y=1,X=0/OR_SZ|Y=0,X=0)].

The expit transform, expit(logit(P(S=1|y,x, z))), yields the selection probability P(S=1|y,x,z) for each actually selected (S=1) record in the dataset conditional on their Y, X and Z values and given the externally obtained β above. An important advantage of using the logistic model to estimate the selection probability is that it will be bounded by 0 and 1, as a probability should be. In some scenarios, the product term parameters might be presumed to be null, but if a selection mechanism involves product terms this might result in insufficient bias adjustment.

Bias parameters should be defined using knowledge of the selection process, or the underlying source population. In most cases, however, these parameters will not be known, and the selection bias adjustment should use a range of plausible bias parameters to conduct robust bias analysis. We reiterate that the key difference between this technique (IPSW) and the now-conventional IPCW used in longitudinal data with censoring is that the betas, or bias parameters, are externally estimated (either using validation data, similar studies, etc.) and supplied to the dataset in our technique while they are estimated from observed data in IPCW. In most epidemiologic studies, data are rarely collected on non-respondents; hence, the specification of a bias model from a range of assumed parameters using our technique or something similar is often the only option.

ILLUSTRATION 1: PROOF OF CONCEPT SIMULATION USING “CORRECT” BIAS PARAMETERS

Illustration 1 provides a proof of principle using a valid, empirically derived set of bias parameters from a hypothetical cohort in which both strata S=1 and S=0 were simulated. Using the equation in expression (2), and IPSW techniques, we demonstrate the ability to recovery of the true OR_YX in an analysis involving only the S=1 stratum. To do this, we simulated a large cohort (N=100,000) with one dichotomous exposure variable (X), two dichotomous confounders (Z₁ and Z₂), one continuous confounder (Z₃), one trichotomous confounder (Z₄), and a dichotomous outcome (Y). The data generating mechanism was based on the relationships between these variables as depicted in the causal structures in Figures 3 and 4. In scenario 1 (Figure 3), after control for the sufficient set of Z confounders, Y is marginally independent of X; in scenario 2 (Figure 4), X causes Y.

Z₁ and Z₂ were generated by random draws from independent Bernoulli distributions with success probability of P(Z₁=1) = 0.3 and P(Z₂=1) = 0.3. Z₃ was generated from the normal distribution such that Z₃ ~N (0, 1). Z₄ was generated from two conditional Bernoulli distributions such that the resulting two indicator variables combined make an exclusive categorization with mean population distributions P(Z₄=1) = 0.4, P(Z₄=2) = 0.3 and P(Z₄=0) = 0.3. The probability of exposure was generated as a function of variables Z₁…Z₄, and the exposure variable was generated from random draws from a corresponding Bernoulli distribution.

The disease variable was generated from random draws from a Bernoulli distribution as a function of the background risk of disease (P(Y=1 | X=0, Z₁=0, Z₂=0, Z₃=0, Z₄=0) = 0.3), the exposure status, and Z₁…Z₄.

Finally S was generated by drawing from a Bernoulli distribution as a function of X, Y, and Z₁ with varying levels of P(S=1 | Y=0, X=0, Z₁=0, Z₂=0, Z₃=0, Z₄=0).

Next, we ran logistic regression of Y on X, Z₁, Z₂, Z₃, and Z₄ for the entire cohort to estimate the “true” OR relating Y and X conditional on Z₁, Z₂, Z₃, and Z₄ (OR_YX|z). We then fit a binary logistic model for S=1 as a function of the other DAG variables in the full cohort, including all 2-way, 3-way, 4-way and 5-way product terms according to expression (2). We then restricted the cohort to those subjects where S=1 and ran a logistic regression of Y on X, Z₁, Z₂, Z₃, Z₄ to estimate the biased OR relating Y and X conditional on Z among the S=1 records, OR_YX|z,S=1. Finally, we generated each selected records’ P(S=1 | y, x, z) using the bias parameters β estimated from the full data as described above.

We then ran logistic regression of Y on X, Z₁, Z₂, Z₃, and Z₄ using data on the S=1 records, with 1/P(S=1 | y, x, z) as the regression weight to estimate the “adjusted” OR_YX|z,S-adj. We repeated this illustration for different hypothetical selection bias scenarios. Trials A1-A8 correspond to Figure 3, trials B1-B8 correspond to Figure 4 with no modification of the S-Y relationship by X, and trials C1-C4 correspond to Figure 4 with an added parameter for the modification by X on the S-Y relationship in the data generation process. We evaluated model performance by calculating bias and RMSE comparing “true” OR_YX|z and “adjusted” OR_YX|z,S-adj.

ILLUSTRATION 2: PERFORMANCE OF A REDUCED ALGORITHM

Illustration 2 assesses the performance of the algorithm applied in illustration 1 under less flexible equations not accounting for any 2-way, 3-way-, 4-way, or 5-way interaction coefficients other than β_SYX in the bias parameter set (β). To do this, we repeated the DAG-directed simulation of our selection weights for the hypothetical population described in illustration 1, excluding all interaction terms in our modeling of P(S=1 | y, x, z) from the full cohort, using the following modified version of equation (2):

$$\mathit{\text{logit}}(P(S=1|y,x,z;{\mathit{\beta }}_{\mathit{r}})={\beta }_S+{\beta }_{SY}y+{\beta }_{SX}x+{\beta }_{SZ}z+{\beta }_{SYX}yx$$ (3)

This resulted in a reduced bias parameter set β_r which was used in the IPSW process to weight the outcome model in the S=1 stratum. As in illustration 2, we ran logistic regression of Y on X, Z₁, Z₂, Z₃, and Z₄ using data on the S=1 records, with 1/P(S=1 | y, x, z) as the regression weight to estimate the “adjusted” OR_YX|z,S-adj. We repeated this illustration for the same selection bias scenarios as illustration 1, varying the effect of X and Y on selection.

Trials A1-A8 correspond to Figure 3, trials B1-B8 correspond to Figure 4 with no modification by X on the S-Y relationship, and trials C1-C4 correspond to Figure 4 with an added parameter for the modification by X on the S-Y relationship in the data generation process. We evaluated the reduced model algorithm performance by calculating bias and RMSE comparing “true” OR_YX|z and “adjusted” OR_YX|z,S-adj.

ILLUSTRATION 3: MISSPECIFIED PARAMETERS

Illustration 3 demonstrates the performance of the algorithm using external bias parameters that are an imperfect measure of the true bias. We repeated the DAG-directed simulation of our probability of selection weights for a hypothetical population (N=100,000) corresponding to the DAG in Figure 4, with OR_YX|Z = 2. This time we applied bias parameters with slight misspecification (−20% to +20%) of the empirical bias parameters. For illustration, true prevalences in the hypothetical population were held constant as follows: P(S=1 | Y=0, X=0, Z=0) = 0.2, P(X=1 | Z=0) = 0.3 and P(Y=1 | X=0, Z=0) = 0.5. The trials were performed twice, once with a strong level of selection bias: e^β_SX = 5.0, e^β_SY = 5.0, e^β_SZ1 = 5.0 and e^{β_{SY X}} = 5.0 (trials D1-D21), and once with a weak to moderate level of selection bias: e^β_SX = 2.0, e^β_SY = 2.0, e^β_SZ1 = 2.0, and e^{β_{SY X}} = 0.8 (trials E1-E21). In both sets of trials, these parameters were “misspecified” by multiplying or dividing by 0.1 and 0.2 to represent the bias adjustment under incorrect externally applied bias parameters. As in illustrations 1 and 2, we evaluated model performance by calculating bias and RMSE comparing “true” OR_YX|z and “adjusted” OR_YX|z,S-adj.

RESULTS

Tables 1 and 2 include results from simulated populations based on the DAGs pictured in Figures 3 and 4 and used IPW to correct for the selection bias effect that was the result of conditioning on the collider at the S node. All bias parameters were empirically derived from the underlying hypothetical population. Generally, we observed a downward bias in any model that included a positive relationship between exposure and selection and disease and selection. If for the relationship of interest at least one of these direct effects were negative, the bias was upward. As has been demonstrated in the literature [8, 9], bias adjustment using IPSW was adequate in all models. Variation in the population characteristics P(S=1 | Y=0, X=0, Z=0), P(X=1 | Z=0), and P(Y=1 | X=0, Z=0) did not result in any discernible pattern of bias adjustment accuracy. Increasing the e^β_SX and e^β_SY resulted in slightly reduced accuracy of the bias adjustment. Addition of the interaction parameter, e^{βSY X}, also slightly degraded bias adjustment performance.

Table 1.

Correctly specified parameters for adjustment of collider-stratification bias in a cohort (N=100,000) defined by the DAGs in Figures 3¹ and 4¹

Trial	P(S=1|Y=0,X=0,Z=0)	eβSX	eβSY	eβSYX	True ORYX|z	Biased ORYX|z,S=1	Bias adjusted ORYX|z,S-adj	Bias	RMSE
A1	0.10	5.0	5.0	1.0	1.01 (0.97, 1.04)	0.59 (0.55, 0.63)	1.01 (0.97, 1.04)	−0.0023	0.0176
A2	0.20	5.0	5.0	1.0	1.01 (0.97, 1.04)	0.62 (0.59, 0.65)	1.00 (0.97, 1.03)	−0.0099	0.0200
A3	0.50	5.0	5.0	1.0	1.01 (0.97, 1.04)	0.75 (0.72, 0.78)	1.00 (0.97, 1.04)	−0.0036	0.0178
A4	0.70	5.0	5.0	1.0	1.01 (0.97, 1.04)	0.83 (0.80, 0.87)	1.01 (0.97, 1.04)	−0.0013	0.0174
A5	0.10	0.7	0.7	1.0	1.01 (0.97, 1.04)	1.00 (0.88, 1.14)	1.03 (0.99, 1.06)	0.0192	0.0260
A6	0.10	10.0	0.5	1.0	1.00 (0.96, 1.03)	1.25 (1.12, 1.39)	0.99 (0.95, 1.02)	−0.0073	0.0196
A7	0.10	10.0	5.0	1.0	1.00 (0.96, 1.03)	0.44 (0.41, 0.48)	0.99 (0.95, 1.02)	−0.0073	0.0195
A8	0.10	10.0	10.0	1.0	1.00 (0.96, 1.03)	0.33 (0.30, 0.35)	0.98 (0.95, 1.02)	−0.0133	0.0224
B1	0.10	5.0	5.0	1.0	1.97 (1.90, 2.05)	1.16 (1.09, 1.24)	1.95 (1.88, 2.03)	−0.0200	0.0275
B2	0.20	5.0	5.0	1.0	1.97 (1.90, 2.05)	1.22 (1.16, 1.29)	1.95 (1.87, 2.02)	−0.0279	0.0336
B3	0.50	5.0	5.0	1.0	1.97 (1.90, 2.05)	1.47 (1.41, 1.53)	1.97 (1.90, 2.04)	−0.0063	0.0198
B4	0.70	5.0	5.0	1.0	1.97 (1.90, 2.05)	1.63 (1.57, 1.70)	1.97 (1.90, 2.04)	−0.0022	0.0189
B5	0.10	0.7	0.7	1.0	1.97 (1.90, 2.05)	1.99 (1.73, 2.29)	2.02 (1.95, 2.10)	0.0465	0.0502
B6	0.10	10.0	0.5	1.0	1.97 (1.90, 2.04)	2.54 (2.32, 2.78)	1.99 (1.92, 2.07)	0.0261	0.0322
B7	0.10	10.0	5.0	1.0	1.97 (1.90, 2.04)	0.92 (0.85, 0.98)	1.93 (1.86, 2.01)	−0.0330	0.0381
B8	0.10	10.0	10.0	1.0	1.97 (1.90, 2.04)	0.82 (0.77, 0.87)	1.90 (1.83, 1.97)	−0.0668	0.0694
C1	0.20	5.0	5.0	0.4	1.97 (1.90, 2.05)	1.05 (1.00, 1.11)	1.94 (1.87, 2.01)	−0.0368	0.0413
C2	0.20	5.0	5.0	0.8	1.97 (1.90, 2.05)	1.19 (1.13, 1.25)	1.94 (1.87, 2.02)	−0.0286	0.0342
C3	0.20	5.0	5.0	2.0	1.97 (1.90, 2.05)	1.29 (1.22, 1.36)	1.94 (1.87, 2.01)	−0.0313	0.0365
C4	0.20	5.0	5.0	5.0	1.97 (1.90, 2.05)	1.34 (1.27, 1.41)	1.95 (1.88, 2.02)	−0.0218	0.0288

¹Simulated prevalences in the hypothetical population were held constant as follows: P(X=1 | Z=0) = 0.3 and P(Y=1 | X=0, Z=0) = 0.5.

Table 2.

Reduced models with correctly specified parameters for adjustment of collider-stratification bias in a cohort (N=100,000) defined by the DAGs in Figures 3¹ and 4¹

Trial	P(S=1|Y=0,X=0,Z=0)	eβSX	eβSY	eβSYX	True ORYX|z	Biased ORYX|z,S=1	Bias adjusted ORYX|z,S-adj	Bias	RMSE
A1	0.10	5.0	5.0	1.0	1.01 (0.97, 1.04)	0.59 (0.55, 0.63)	1.01 (0.98, 1.05)	0.0055	0.0182
A2	0.20	5.0	5.0	1.0	1.01 (0.97, 1.04)	0.62 (0.59, 0.65)	1.01 (0.98, 1.05)	0.0019	0.0175
A3	0.50	5.0	5.0	1.0	1.01 (0.97, 1.04)	0.75 (0.72, 0.78)	1.01 (0.97, 1.04)	−0.0001	0.0174
A4	0.70	5.0	5.0	1.0	1.01 (0.97, 1.04)	0.83 (0.80, 0.87)	1.01 (0.97, 1.04)	−0.0008	0.0174
A5	0.10	0.7	0.7	1.0	1.01 (0.97, 1.04)	1.00 (0.88, 1.14)	1.02 (0.98, 1.05)	0.0067	0.0187
A6	0.10	10.0	0.5	1.0	1.00 (0.96, 1.03)	1.25 (1.12, 1.39)	0.99 (0.96, 1.03)	−0.0027	0.0183
A7	0.10	10.0	5.0	1.0	1.00 (0.96, 1.03)	0.44 (0.41, 0.48)	0.99 (0.96, 1.03)	−0.0012	0.0181
A8	0.10	10.0	10.0	1.0	1.00 (0.96, 1.03)	0.33 (0.30, 0.35)	0.99 (0.96, 1.03)	−0.0018	0.0182
B1	0.10	5.0	5.0	1.0	1.97 (1.90, 2.05)	1.16 (1.09, 1.24)	1.98 (1.91, 2.05)	0.0077	0.0203
B2	0.20	5.0	5.0	1.0	1.97 (1.90, 2.05)	1.22 (1.16, 1.29)	1.98 (1.90, 2.05)	0.0030	0.0190
B3	0.50	5.0	5.0	1.0	1.97 (1.90, 2.05)	1.47 (1.41, 1.53)	1.97 (1.90, 2.05)	0.0000	0.0188
B4	0.70	5.0	5.0	1.0	1.97 (1.90, 2.05)	1.63 (1.57, 1.70)	1.97 (1.90, 2.05)	−0.0014	0.0188
B5	0.10	0.7	0.7	1.0	1.97 (1.90, 2.05)	1.99 (1.73, 2.29)	2.01 (1.94, 2.09)	0.0365	0.0410
B6	0.10	10.0	0.5	1.0	1.97 (1.90, 2.04)	2.54 (2.32, 2.78)	1.97 (1.90, 2.05)	0.0062	0.0199
B7	0.10	10.0	5.0	1.0	1.97 (1.90, 2.04)	0.92 (0.85, 0.98)	1.97 (1.90, 2.04)	0.0002	0.0189
B8	0.10	10.0	10.0	1.0	1.97 (1.90, 2.04)	0.82 (0.77, 0.87)	1.97 (1.90, 2.04)	0.0027	0.0191
C1	0.20	5.0	5.0	0.4	1.97 (1.90, 2.05)	1.05 (1.00, 1.11)	1.98 (1.90, 2.05)	0.0023	0.0189
C2	0.20	5.0	5.0	0.8	1.97 (1.90, 2.05)	1.19 (1.13, 1.25)	1.98 (1.90, 2.05)	0.0033	0.0191
C3	0.20	5.0	5.0	2.0	1.97 (1.90, 2.05)	1.29 (1.22, 1.36)	1.98 (1.90, 2.05)	0.0029	0.0190
C4	0.20	5.0	5.0	5.0	1.97 (1.90, 2.05)	1.34 (1.27, 1.41)	1.98 (1.90, 2.05)	0.0031	0.0190

¹Simulated prevalences in the hypothetical population were held constant as follows: P(X=1 | Z=0) = 0.3 and P(Y=1 | X=0, Z=0) = 0.5.

In Table 3 we carried forward the simulation from DAG 4, this time including a varying degree of misspecification of the bias parameters (−20% to +20%). We did this twice, once for a strong selection bias (trials D1-D21) and once for a moderate to weak selection bias (trials E1-E21). In both scenarios, misspecification of the β_S or the e^β_SYX parameters did not greatly inhibit bias adjustment. Misspecification of the e^β_SX and e^β_SY resulted in inadequate bias adjustment in the presence of strong selection bias (trials D1-D21).

Table 3.

Misspecified parameters for adjustment of collider-stratification bias in a cohort (N=100,000) defined by the DAG in Figure 4¹

Trial	Misspecified parameter2,3	Degree of misspecification	True ORYX|z	Biased ORYX|z,S=1	Bias adjusted ORYX|z,S-adj	Bias	RMSE
D1	None	None	1.97 (1.90, 2.05)	1.34 (1.27, 1.41)	1.98 (1.90, 2.05)	0.0031	0.0190
D2	βS	−20%	1.97 (1.90, 2.05)	1.34 (1.27, 1.41)	1.97 (1.89, 2.05)	−0.0042	0.0203
D3	βS	−10%	1.97 (1.90, 2.05)	1.34 (1.27, 1.41)	1.98 (1.90, 2.05)	0.0036	0.0197
D4	βS	+10%	1.97 (1.90, 2.05)	1.34 (1.27, 1.41)	1.97 (1.90, 2.04)	−0.0067	0.0194
D5	βS	+20%	1.97 (1.90, 2.05)	1.34 (1.27, 1.41)	1.95 (1.88, 2.02)	−0.0263	0.0317
D6	eβSX	−20%	1.97 (1.90, 2.05)	1.34 (1.27, 1.41)	1.75 (1.69, 1.82)	−0.2186	0.2194
D7	eβSX	−10%	1.97 (1.90, 2.05)	1.34 (1.27, 1.41)	1.87 (1.80, 1.94)	−0.1065	0.1081
D8	eβSX	+10%	1.97 (1.90, 2.05)	1.34 (1.27, 1.41)	2.08 (2.01, 2.16)	0.1089	0.1106
D9	eβSX	+20%	1.97 (1.90, 2.05)	1.34 (1.27, 1.41)	2.18 (2.10, 2.27)	0.2101	0.2110
D10	eβSY	−20%	1.97 (1.90, 2.05)	1.34 (1.27, 1.41)	1.75 (1.69, 1.82)	−0.2230	0.2238
D11	eβSY	−10%	1.97 (1.90, 2.05)	1.34 (1.27, 1.41)	1.86 (1.80, 1.93)	−0.1088	0.1104
D12	eβSY	+10%	1.97 (1.90, 2.05)	1.34 (1.27, 1.41)	2.08 (2.01, 2.16)	0.1115	0.1131
D13	eβSY	+20%	1.97 (1.90, 2.05)	1.34 (1.27, 1.41)	2.19 (2.11, 2.27)	0.2155	0.2163
D14	eβSZ1	−20%	1.97 (1.90, 2.05)	1.34 (1.27, 1.41)	2.00 (1.93, 2.07)	0.0250	0.0312
D15	eβSZ1	−10%	1.97 (1.90, 2.05)	1.34 (1.27, 1.41)	1.99 (1.92, 2.06)	0.0137	0.0232
D16	eβSZ1	+10%	1.97 (1.90, 2.05)	1.34 (1.27, 1.41)	1.97 (1.89, 2.04)	−0.0067	0.0200
D17	eβSZ1	+20%	1.97 (1.90, 2.05)	1.34 (1.27, 1.41)	1.96 (1.89, 2.03)	−0.0156	0.0245
D18	eβSYX	−20%	1.97 (1.90, 2.05)	1.34 (1.27, 1.41)	2.00 (1.93, 2.07)	0.0269	0.0328
D19	eβSYX	−10%	1.97 (1.90, 2.05)	1.34 (1.27, 1.41)	1.99 (1.91, 2.06)	0.0138	0.0233
D20	eβSYX	+10%	1.97 (1.90, 2.05)	1.34 (1.27, 1.41)	1.97 (1.90, 2.04)	−0.0057	0.0197
D21	eβSYX	+20%	1.97 (1.90, 2.05)	1.34 (1.27, 1.41)	1.96 (1.89, 2.03)	−0.0130	0.0228
E1	None	None	1.97 (1.90, 2.05)	1.62 (1.52, 1.73)	1.98 (1.91, 2.05)	0.0049	0.0194
E2	βS	−20%	1.97 (1.90, 2.05)	1.62 (1.52, 1.73)	1.96 (1.89, 2.04)	−0.0104	0.0230
E3	βS	−10%	1.97 (1.90, 2.05)	1.62 (1.52, 1.73)	1.97 (1.90, 2.05)	−0.0021	0.0197
E4	βS	+10%	1.97 (1.90, 2.05)	1.62 (1.52, 1.73)	1.98 (1.91, 2.05)	0.0105	0.0208
E5	βS	+20%	1.97 (1.90, 2.05)	1.62 (1.52, 1.73)	1.99 (1.92, 2.06)	0.0149	0.0227
E6	eβSX	−20%	1.97 (1.90, 2.05)	1.62 (1.52, 1.73)	1.95 (1.88, 2.02)	−0.0269	0.0325
E7	eβSX	−10%	1.97 (1.90, 2.05)	1.62 (1.52, 1.73)	1.96 (1.89, 2.03)	−0.0112	0.0217
E8	eβSX	+10%	1.97 (1.90, 2.05)	1.62 (1.52, 1.73)	1.99 (1.92, 2.07)	0.0212	0.0285
E9	eβSX	+20%	1.97 (1.90, 2.05)	1.62 (1.52, 1.73)	2.01 (1.94, 2.09)	0.0378	0.0424
E10	eβSY	−20%	1.97 (1.90, 2.05)	1.62 (1.52, 1.73)	1.95 (1.88, 2.02)	−0.0252	0.0313
E11	eβSY	−10%	1.97 (1.90, 2.05)	1.62 (1.52, 1.73)	1.96 (1.89, 2.04)	−0.0103	0.0214
E12	eβSY	+10%	1.97 (1.90, 2.05)	1.62 (1.52, 1.73)	1.99 (1.92, 2.07)	0.0203	0.0277
E13	eβSY	+20%	1.97 (1.90, 2.05)	1.62 (1.52, 1.73)	2.01 (1.94, 2.08)	0.0360	0.0407
E14	eβSZ1	−20%	1.97 (1.90, 2.05)	1.62 (1.52, 1.73)	1.98 (1.91, 2.06)	0.0089	0.0207
E15	eβSZ1	−10%	1.97 (1.90, 2.05)	1.62 (1.52, 1.73)	1.98 (1.91, 2.05)	0.0068	0.0199
E16	eβSZ1	+10%	1.97 (1.90, 2.05)	1.62 (1.52, 1.73)	1.98 (1.90, 2.05)	0.0029	0.0191
E17	eβSZ1	+20%	1.97 (1.90, 2.05)	1.62 (1.52, 1.73)	1.97 (1.90, 2.05)	0.0011	0.0189
E18	eβSZ1	−20%	1.97 (1.90, 2.05)	1.62 (1.52, 1.73)	1.92 (1.85, 1.99)	−0.0522	0.0555
E19	eβSYX	−10%	1.97 (1.90, 2.05)	1.62 (1.52, 1.73)	1.95 (1.88, 2.02)	−0.0241	0.0306
E20	eβSYX	+10%	1.97 (1.90, 2.05)	1.62 (1.52, 1.73)	2.01 (1.94, 2.08)	0.0346	0.0394
E21	eβSYX	+20%	1.97 (1.90, 2.05)	1.62 (1.52, 1.73)	2.04 (1.96, 2.11)	0.0652	0.0679

¹Simulated prevalences in the hypothetical population were held constant as follows: P(S=1|Y=0,X=0,Z=0)= 0.2, P(X=1|Z=0) = 0.3 and P(Y=1|X=0, Z=0) = 0.5. The true OR_YX|Z was simulated as 2.

²For trials D1-D21, each hypothetical population, the true bias parameters were specified as follows: β_S = 0.2, e^β_SX = 5.0, e^β_SY = 5.0, e^β_SZ1 = 5.0, and e^β_SYX = 5.0.

³For trials E1-E21 each hypothetical population, the true bias parameters were specified as follows: β_S = 0.2, e^β_SX = 2.0, e^β_SY = 2.0, e^β_SZ1 = 2.0, and e^β_SYX = 0.8.

DISCUSSION

We have demonstrated a method of sensitivity analysis for selection bias adjustment using record level data augmentation, which is based on the recoverability of the joint distribution given data on the S=1 stratum and prior knowledge or beliefs about the S=0 stratum [17], and can be implemented in absence of data on the S=0 stratum. In our simulations, we used imputed probabilities with IPSW and were able to produce unbiased estimates of the causal odds ratio using only the selected stratum. This method is distinct from IPCW because it need not be based on data from censored individuals in the underlying cohort, and thus may be applicable to case-control studies. As has been done previously, we used DAGs to visualize the selection bias mechanisms and considered selection (or collider) bias to be a form of nonignorable missing data [15, 18, 19].

We found via our simulation scenarios that this method provided adequate adjustment of selection bias under empirically derived priors, but the framework of the method can be adapted to the use of external bias parameters. We found that performance was optimal using fully saturated models, but the reduced model forms performed comparably well, and with much simpler computational execution. Application of this method under misspecification demonstrated that (as would be expected intuitively) reweighting the population according to invalid bias parameters produces invalid results.

Although this method performs adequately in our simulation scenarios, it is highly dependent on plausible characterization of the magnitude and direction of the bias, most of which we derived empirically from the underlying source population. If input data are not available from empirical sources, arriving at a set of bias parameters that plausibly characterize a completely unknown population of individuals (i.e., the S=0 stratum) may be a difficult undertaking. To this end, we suggest (as others have) to always present selection bias adjustments as part of a detailed bias analysis [20]. Additionally, using this method under extreme levels of selection bias, upon even slight misspecification of these parameters the bias adjustment would degrade considerably. Although we did not present examples of it, as can be expected, gross misspecification, or misspecification of multiple parameters could result in entirely invalid adjusted estimates.

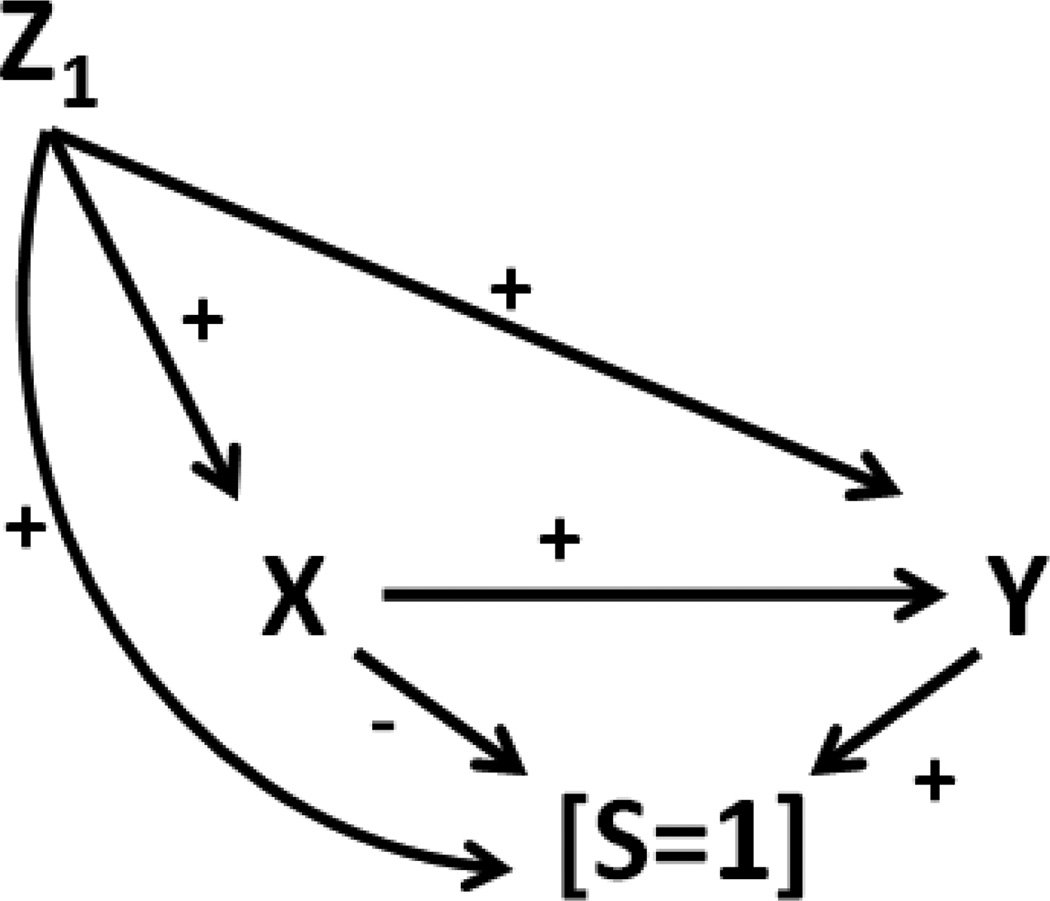
Assignment of bias parameters (i.e., in the absence of a validation sub-study) could be aided by the use of signed DAGs. In a signed DAG, edges are marked with the direction (positive or negative) of the average effect for each pair of directly connected variables, conditional on other relevant variables. The use of signed DAGs for characterizing the directionality of relationships in the diagram and in understanding confounding bias has been described in detail [21, 22]. For example, as depicted in Figure 5, if Y increased the probability of selection conditional on X and Z₁, then the odds ratio e^β_SY would be assigned a positive value(> 1). Similarly, e^β_SX could be assigned a negative value (<1) on the X→S path whereby other paths connecting X and S are blocked by conditioning on Y and Z₁. Assignment can proceed similarly for e^β_SZ1 by considering the net sign of all open paths between Z₁ and S conditional on X and Y. More work is needed to formalize these insights.

Figure 5.

A hypothetical selection bias mechanism with signed edges indicating the direction of effect between each pair of connected variables.

In simulating varying scenarios of selection bias in hypothetical populations, we detected a discernible pattern of bias direction that may warrant further investigation. When both the exposure and disease were positively associated with selection, the bias direction was downward. When one was positive and the other was negative, the bias direction was upward. If the overall magnitude of bias was small, this rule of directionality was not as evident. A thorough evaluation of the expected magnitude and direction of selection bias has not yet been published in the epidemiologic literature. Suspected examples of severe Berksonian bias have been shown to cause extreme downward bias, to 10-fold decrease in effect estimate [23, 24]. Exploration of the potential impact of selection bias in the electromagnetic fields (EMF) and leukemia literature has found that this type of bias could result in a 2-fold increase in effect estimates [25]. Some theoretical work has been done to predict the magnitude of expected bias from controlling on a collider, when bias parameters are known [14]. Further research including simulation studies may be warranted in this area.

ABBREVIATIONS AND ACRONYMS

DAG

directed acyclic graph

IPCW

inverse probability of censoring weight(ed/ing)

IPSW

inverse probability of selection weight(ed/ing)

OR

odds ratio

RMSE

root mean squared error