Bias in identification of the best treatment in a Bayesian network meta-analysis for binary outcome: a simulation study

Abstract

Network meta-analysis (NMA) has emerged as a useful analytical tool allowing comparison of multiple treatments based on direct and indirect evidence. Commonly, a hierarchical Bayesian NMA model is used, which allows rank probabilities (the probability that each treatment is best, second best, and so on) to be calculated for decision making. However, the statistical properties of rank probabilities are not well understood. This study investigates how rank probabilities are affected by various factors such as unequal number of studies per comparison in the network, the sample size of individual studies, the network configuration, and effect sizes between treatments. In order to explore these factors, a simulation study of four treatments (three equally effective treatments and one less effective reference) was conducted. The simulation illustrated that estimates of rank probabilities are highly sensitive to both the number of studies per comparison and the overall network configuration. An unequal number of studies per comparison resulted in biased estimates of treatment rank probabilities for every network considered. The rank probability for the treatment that was included in the fewest number of studies was biased upward. Conversely, the rank of the treatment included in the most number of studies was consistently underestimated. When the simulation was altered to include three equally effective treatments and one superior treatment, the hierarchical Bayesian NMA model correctly identified the most effective treatment, regardless of all factors varied. The results of this study offer important insight into the ability of NMA models to rank treatments accurately under several scenarios. The authors recommend that health researchers use rank probabilities cautiously in making important decisions.

Background

Meta-analysis is a statistical procedure that can be used to synthesize evidence from multiple studies to determine the common effect when effect sizes are consistent, or to identify reasons for variation between studies when effects are inconsistent.^1,2 The traditional meta-analysis method allows comparison of two interventions. In practice, there are often multiple therapies for a particular disease.³ Sound decision making requires comparisons of all available, relevant competing interventions.^4,5 The comparative effectiveness of a range of interventions requires statistical methodology beyond classical meta-analysis methods.

Network meta-analysis (NMA), also called multiple treatments meta-analysis or mixed treatment comparison, is an extension of the traditional pairwise meta-analysis that enables comparisons between multiple interventions simultaneously,⁶ respecting the randomization in the evidence.⁷ In practice, direct evidence may not be available for every pair of treatments. NMA enables researchers to obtain the relative efficacy of a particular intervention versus any competing intervention even when direct evidence is not present, via a common comparator.⁸ NMA yields more precise estimates by combining direct and indirect evidence versus direct evidence alone.^4,6,7,9,10 In addition to relative effects, when conducted in a Bayesian framework, NMA generates the probability that each treatment is ranked first, second, and so on.^11,12 It has been applied in clinical research areas such as diabetes,¹³ cardiovascular safety,¹⁴ cancer,¹⁵ anatomy,^16–20 and drug development,²¹ and is gaining considerable favor among clinicians, guideline decision makers, and health technology agencies.^22–24

Considerable research focused on methodological issues of NMA has been published in recent years; however, a limited number of simulation studies have been conducted. In particular, few simulations have explored the operating characteristics of rank probabilities obtained from an NMA. Some concern has been raised about the use of rank probabilities in decision making. Researchers argue that rank probability is sensitive to various factors and it is biased when there is a paucity of direct comparisons. Because of this fragility, researchers claim that decisions based on rank probabilities should not be trusted unless accompanied with effect sizes of pairwise comparisons, such as means and their credible intervals, as in some cases individual treatments may be disqualified on the basis of cost or clinical contraindication.^11,24–26 If there are few trials per comparison, as in the study by Haas et al²⁷ for neonatal mortality outcome, it may lead to the problem of overestimating rates, suggesting extra caution should be exercised when interpreting the treatment rankings. This study aims to investigate how rank probabilities obtained from a Bayesian NMA are affected by characteristics of the network, including network configuration, number of studies per comparison, individual study sample sizes, and effect sizes. The simulation was conducted for a binary outcome.

Motivating example

A recently published article shared the results from pair-wise comparisons of four treatments in the reduction of heavy menstrual bleeding,²⁸ including analysis of individual patient data. The authors conducted a wide-range search for studies that compared hysterectomy (hyster), endometrial destruction (both first-generation hysteroscopic [1gen] and second-generation nonhysteroscopic [2gen] techniques), and the levonorgestrel releasing intrauterine system (Mirena) from the Cochrane Library, MEDLINE, Embase, and CINAHL databases and reference lists. The authors found that the level of satisfaction with treatment was the most commonly measured outcome across all identified studies, with 21 out of 30 using this measure, and used it as their primary outcome measure. Direct and indirect comparisons among the four treatments were made without an NMA approach. The binary outcome data from 20 of these two-arm studies were available, and the resulting network is shown in Figure 1.

Figure 1.

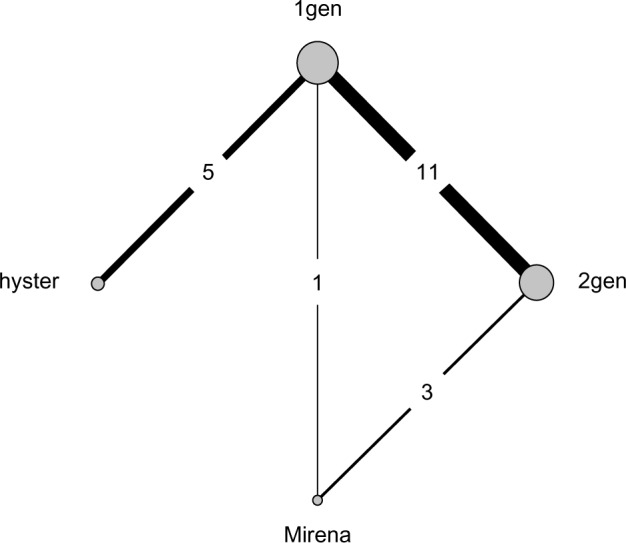
Network configuration.

Note: Copyright © 2010. BMJ. Adapted from Middleton LJ, Champaneria R, Daniels JP, et al. Hysterectomy, endometrial destruction, and levonorgestrel releasing intrauterine system (Mirena) for heavy menstrual bleeding: systematic review and meta-analysis of data from individual patients. 2010;341:c3929.²⁸

Abbreviations: 1gen, first-generation hysteroscopic endometrial destruction technique; 2gen, second-generation nonhysteroscopic endometrial destruction technique; hyster, hysterectomy.

The network plot reveals an unequal number of studies per comparison and the absence of direct evidence between some of the pairs of treatments (eg, hyster and Mirena). An NMA synthesizing all evidence simultaneously was not conducted and rank probabilities were not estimated.

Using the available raw data (from the identified studies), a Bayesian NMA was performed for the purpose of yielding probabilistic conclusions. It was possible to determine estimates for both relative effect sizes and rank probabilities through Markov chain Monte Carlo (MCMC) simulation sampling using an R package called gemtc. The pairwise estimates are available in Table 1. Based on this table, hysterectomy is the treatment yielding the greatest reduction of patients’ dissatisfaction regarding heavy menstrual bleeding, with the remaining three treatments relatively indistinguishable. These estimates are very similar to their findings despite the methods applied.

Table 1.

Relative treatment effects of all possible comparisons

	1gen	2gen	Mirena	hyster
1gen	–	1.14 (0.78–1.61)	1.16 (0.54–2.50)	2.72* (1.51–5.05)
2gen	0.88 (0.62–1.28)	–	1.02 (0.50–2.09)	2.38 (1.23–4.95)
Mirena	0.86 (0.40–1.84)	0.98 (0.48–2.01)	–	2.34 (0.89–6.17)
hyster	0.37 (0.20–0.66)	0.42 (0.20–0.82)	0.43 (0.16–1.12)	–

Notes:

^*The figures in the table show estimated odds ratios along with 95% credible interval (CrI) for the treatment shown in the row relative to the treatment in the corresponding column. For example, we can see that more women were dissatisfied at 12 months after first generation endometrial destruction than after hysterectomy: odds ratio (95% CrI) 2.72 (1.51 to 5.05).

Abbreviations: 1gen, first-generation hysteroscopic endometrial destruction technique; 2gen, second-generation nonhysteroscopic endometrial destruction technique; hyster, hysterectomy.

The rank probabilities of the four treatments are provided in Table 2. This ranking supports the conclusion that hysterectomy is the most effective treatment. However, when working with real data, there is no way to know if any bias is present in the findings. This paper will consider what factors might influence these rank probabilities. The focus will be on the first rank probability (ie, the first column of Table 2). Using comprehensive simulations, possible sources of bias in networks similar to this one (eg, the effect of unequal studies per comparison) will be assessed.

Table 2.

The treatment rank probabilities

	Rank probability
	1st	2nd	3rd	4th
1gen	0.00020	0.12555	0.31260	0.56165
2gen	0.00355	0.35570	0.50455	0.13620
Mirena	0.04245	0.47750	0.17830	0.30175
hyster	0.95380	0.04125	0.00455	0.00040

Note: Copyright © 2010. BMJ. Adapted from Middleton LJ, Champaneria R, Daniels JP, et al. Hysterectomy, endometrial destruction, and levonorgestrel releasing intrauterine system (Mirena) for heavy menstrual bleeding: systematic review and meta-analysis of data from individual patients. 2010;341:c3929.²⁸

Abbreviations: 1gen, first-generation hysteroscopic endometrial destruction technique; 2gen, second-generation nonhysteroscopic endometrial destruction technique; hyster, hysterectomy.

The rest of this article is organized as follows. First, a brief description of the NMA method is provided. Next, the simulation approach is described, results are presented, and a discussion and limitations of the simulation are given. Finally, a conclusion is provided.

Methods

The NMA method relies on the fundamental assumptions of homogeneity, similarity, and consistency.²⁹ Homogeneity requires the effect of treatments to be similar across trials,³⁰ similarity (or transitivity) requires that relative treatment effects are assumed to be exchangeable, and consistency (or coherence) requires that evidence from both direct and indirect comparisons is in agreement.^4,29,31,32 Assumptions can prove difficult to verify.³³

In NMA, a network’s geometry uses nodes to represent interventions and edges to represent the direct comparisons between interventions. The amount of available information is often represented in network plots by varying the sizes of nodes and thickness of edges. The visual depiction of a network can reveal that some treatments are included in significantly more studies than others. This disparity may come from comparator preference bias, sponsorship bias, selective reporting bias, and time lag bias.⁴ Network geometries range from simple (a network with only three treatments) to very complex (a network with multiple treatments).³⁴ In this simulation study, graphical networks that often result from systematic reviews were considered: star,^35,36 loop, one closed loop,^25,36,37 and ladder (linear)^25,36,37 (Figure 2). All of the four network patterns also exist together in the paper published by Lu and Ades.²³ Each network comprises four nodes representing four interventions (treatments one to four labeled T₁, T₂, T₃, and T₄). Except for the star pattern, each configuration has both direct and indirect evidence.

Figure 2.

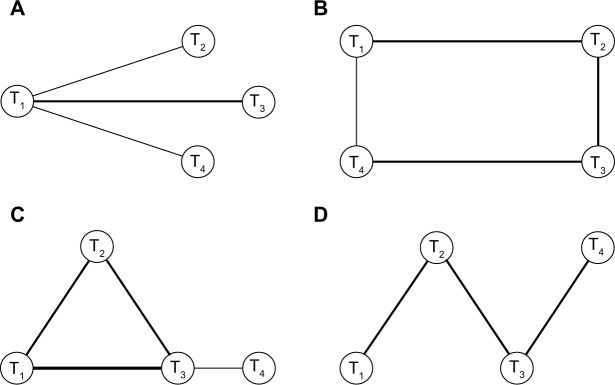
Type of network geometry considered in our simulation.

Notes: (A) Star geometry. (B) Loop geometry. (C) One closed loop geometry. (D) Ladder or linear geometry. T₁ denotes a reference treatment and T₂ to T₄ are treatments that are compared relative to the reference.

Statistical details

In NMA, input data are summary statistics gathered from published literature. The aggregate input data might be available in two formats: arm-level summaries (eg, odds, absolute risk, hazard, mean) or contrast-level summaries (eg, odds ratio, risk ratio, hazard ratio, mean difference). Arm-level data, which is modeled with the exact likelihood rather than its normal approximation,⁶ were adopted in this simulation study. Both frequentist and Bayesian frameworks can suitably fit models for either of the two data formats.³⁸

Although inference based on NMA can be made in both frequentist and Bayesian frameworks, Bayesian NMA is more common and provides two advantages. First, it allows researchers to incorporate prior knowledge for parameters of interest and a rich and flexible family of models can be fitted. Second, treatment rank probabilities can be calculated easily. Employing a Bayesian framework requires the calculation of posterior distributions using MCMC methods. Procedures are described in detail by Salanti et al.¹¹ Furthermore, Bayesian inferences are exact for finite samples when appropriate priors are used (unlike frequentist inference, which relies on a normality assumption) and, hence, are more appealing, especially with small samples.

The calculation of rank probabilities is also straightforward in the Bayesian framework. For every MCMC run, each treatment in the study is ranked based on the relative effect estimates. The proportion of MCMC cycles in which the treatment ranks first gives the probability that it is the best among all competing treatments in the study. Similarly, rank probabilities of being second best, third best, and so on are computed for every treatment.

The general linear model for NMA has been proposed by several researchers.^32,39 The model can be fitted for different types of data, including normal, binomial, Poisson, and multinomial. The following sections will review how the Bayesian NMA model can be fitted for arm-level study summaries of binary outcomes.

Fixed effects models in NMA

This section describes both fixed and random effects NMA models confined to binary outcomes. Suppose that there are N randomized controlled trials that compare K treatments. Let r_ik be the number of events of the ith clinical trial in the arm representing treatment k. Let n_ik represent the number of observations and p_ik denote the corresponding success probability for treatment k in study i. Then the distribution of the number of events is given by:

$${\mathrm{r}}_{\text{ik}}~\text{Bin}\left({\mathrm{p}}_{\text{ik}},{\mathrm{n}}_{\text{ik}}\right),\mathrm{i}=\mathrm{1},\dots ,\mathrm{N};\mathrm{k}=\mathrm{1},\mathrm{2},\dots \mathrm{K}$$ (1)

where p_ik represents the corresponding probability of a successful outcome for treatment k and is modeled on the logit scale as:

$$\log \text{it}({\mathrm{p}}_{\text{ib}})=\log \frac{{\mathrm{p}}_{\text{ib}}}{1-{\mathrm{p}}_{\text{ib}}}={\mathrm{\mu }}_{\mathrm{i}}\mathrm{i}=\mathrm{1},\mathrm{2},\dots ,\mathrm{N};\mathrm{b}=\mathrm{k}=1,\dots ,\mathrm{K}$$ (2)

$$\log \text{it}({\mathrm{p}}_{\text{ik}})=\log \frac{{\mathrm{p}}_{\text{ib}}}{1-{\mathrm{p}}_{\text{ib}}}={\mathrm{\mu }}_{\mathrm{i}}+{\mathrm{d}}_{\mathrm{i},1\mathrm{k}}\iff {\mathrm{p}}_{\text{ik}}=\log {\text{it}}^{-1}\left({\mathrm{\mu }}_1+{\mathrm{d}}_{1,1\mathrm{k}}\right)$$ (3)

with i =1, 2, …, N; k =2, …, k; b < k where μ_i are the trial specific baselines representing the log odds of an event occurring in the referent treatment group (k = b). Then, d_i,1k are the fixed trial-specific log odds of event occurrence in group k compared with the referent treatment. The logit link function maps the probabilities onto the real number line.

Random effects models in NMA

In a random effects model, each study i provides an estimate of the study-specific log odds, δ_i,1k which are assumed to be independent of the order in which they were carried out (exchangeable). Then, the random effects model is obtained by replacing d_i,1k in the above fixed effects model by δ_i,1k, ie,

$$\begin{array}{c}\log \text{it}\left({\mathrm{p}}_{\text{ik}}\right)=\log \frac{{\mathrm{p}}_{\text{ik}}}{1-{\mathrm{p}}_{\text{ik}}}={\mathrm{\mu }}_{\mathrm{i}}+{\delta }_{\mathrm{i},1\mathrm{k}},\\ \mathrm{i}=1,2,\dots \mathrm{N};\mathrm{k}=2,\dots ,\mathrm{k};\mathrm{b}<\mathrm{k}.\end{array}$$ (4)

It is typically assumed that δ_i,bk ~ N(d_bk = d_1k −d1b, σ²). The notation k > b indicates that k is after b and d₁₁ =0. Prior distributions for basic parameters (d₁₂, d₁₃, d₁₄, …) need to be assumed in the Bayesian framework while the remaining contrasts, called functional parameters, are defined in terms of those treatments compared with the baseline treatment directly assuming consistency. The functional parameters are written as:

$${\mathrm{d}}_{\text{st}}={\mathrm{d}}_{\text{bt}}-{\mathrm{d}}_{\text{bs}},\mathrm{b}=1,\mathrm{2},\dots ,\mathrm{K};\mathrm{s}=2,3,\dots ,\mathrm{K};\mathrm{t}=3,4,\dots ,\mathrm{K};\mathrm{s}<\mathrm{t}.$$ (5)

With regard to choice of priors for hyperparameters, it is common to set weakly informative priors that let the data speak, usually μ_i,d_bk, β ~ N(0, 10⁴).^4,32,39 For the likelihood of binomial outcomes with logit link models, a uniform flat prior for the standard deviation (ie, σ ~ Uniform (0,5))⁴⁰ is usually used. A flat γ prior on the precision (ie, 1/σ² ~ γ(0.001, 0.001)) is another alternative. It assigns small weights to a large standard deviation. This feature may be useful particularly when data are sparse to improve numerical stability and speed convergence of MCMC sampling.

The dramatic increase of interest in the Bayesian analysis is primarily because of the emergence of MCMC methods. While the MCMC method provides a convenient way to draw inference from complicated statistical models, there are some problems associated with this method. One of these problems is that convergence in MCMC sampler is a complex issue. It usually needs a large number of iterations to reach convergence. In addition, early MCMC iterations are highly sensitive to starting values of parameters and do not provide good information about the target distribution and, hence, are required to be thinned. The basic idea is that although the chains look divergent at early iterations due to different starting points, when the MCMC algorithm is converged, the chains should mix together and become indistinguishable from each other as they converge to the same posterior distribution. In this study, the package gemtc (http://cran.r-proct.org/web/packages/gemtc/index.html) from the R library, was used to implement the Bayesian NMA through MCMC simulation nicely, and is compatible with other packages that can conduct convergence diagnostics.

Simulation studies

In this section, the simulation design and results are provided. As outlined in the Background section, this simulation study addresses how an unequal number of studies per comparison affects the ranking of treatments and the influence of network configuration.

Simulation design

In this study, four treatments were considered and two-arm level binary data were simulated. The treatments were denoted T₁ (placebo), T₂, T₃, and T₄. The parameters varied during simulation are given in Table 3. Three scenarios were considered. The first two scenarios used the success probability conditions (0.1, 0.5, 0.5, 0.5) for (T₁, T₂, T₃, T₄). In both scenarios, three equivalent treatments were compared with a reference treatment, T₁. The difference between the two scenarios was the position of the reference treatment within the network configuration, ie, T₁ and T₃ were interchanged. The third scenario with success probabilities (0.2, 0.2, 0.2, 0.8) for (T₁, T₂, T₃, T₄) compared a superior treatment with the remaining equally inferior treatments. Under each of the three scenarios, four different network patterns, seven different numbers of studies per comparison, and three different study-level sample sizes were used to simulate arm-level data.

Table 3.

Parameters varied during simulations

Parameters	Values
Probability of success for T1 T2, T3, T4	(0.1, 0.5, 0.5, 0.5), (0.5, 0.5, 0.1, 0.5), (0.2, 0.2, 0.2, 0.8)
Study sample size	50, 100, 200
Network pattern	Star, ladder, loop, one closed loop
Number of studies per comparison
Network	Equal:	Unequal:
Star, ladder	(1, 2, 3, 5, 10, 15)	(1, 5, 15)
Loop, one closed loop	(1, 2, 3, 5, 10, 15)	(1, 3, 5, 15)

For the ladder and star geometries, the unequal number of studies (1, 5, 15) denoted the number of studies for the comparisons between treatments (T₁ and T₂, T₂ and T₃, T₃ and T₄) and (T₁ and T₂, T₁ and T₃, T₁ and T₄), respectively. Likewise, the unequal number of studies (1, 3, 5, 15) for loop and one closed loop geometries denoted the number of studies comparing the pairs of treatments (T₁ and T₂, T₂ and T₃, T₃ and T₄, T₁ and T₄), respectively. Lastly, for the completely connected loop geometry, the number of studies between (T₁ and T₂, T₁ and T₃, T₁ and T₄, T₂ and T₃, T₂ and T₄, T₃ and T₄) were set at (1, 2, 3, 5, 10, 15), respectively.

Using the parameters described above, binary data were generated from an appropriate binomial distribution. Then, the hierarchical Bayesian NMA model was fitted to perform statistical inference. In each MCMC simulation, the first 5,000 iterations were discarded as a burn-in to minimize the effect of initial values on the posterior distribution. Moreover, to minimize poor mixing (or slow convergence), chains were thinned by keeping every tenth simulated draw from each MCMC sequence. After burn-in and thinning, 2,000 iterations were used to estimate posterior distributions and make inferences about rank probabilities. For each simulation setting, this process was repeated 1,000 times. Convergence was assessed using the Brooks–Rubin diagnostic test where a potential scale reduction factor of 1.05 or lower was considered sufficient for convergence.⁴¹

The first rank probability estimates yielded from the MCMC process were averaged over the 1,000 simulations for each setting to create mean first rank probabilities. Two measures of performance, the bias for estimates of first rank probabilities and the standard deviation of the estimates over 1,000 samples, were calculated.

Simulation results

In this section, estimates of the mean, bias, and standard deviation of first rank probabilities for each simulation setting are given. For the first two sets of success probabilities, no difference between the average first rank probabilities of T₂, T₃, and T₄ were expected. Table 4 shows results for a star geometry. For an equal number of studies per comparison, the star geometry identified treatments as expected with minimal bias. However, with an unequal number of studies per comparison, the star geometry showed large bias and large standard deviation.

Table 4.

Star network pattern with success probabilities (0.1, 0.5, 0.5, 0.5) and n=200

Number of studies	Rank probability				Bias				Standard deviation
	T1	T2	T3	T4	T1	T2	T3	T4	T1	T2	T3	T4
(1, 1, 1)	0.00	0.33	0.33	0.34	0.00	0.00	0.00	0.00	0.00	0.10	0.10	0.10
(2, 2, 2)	0.00	0.34	0.32	0.34	0.00	0.00	−0.01	0.00	0.00	0.19	0.20	0.20
(3, 3, 3)	0.00	0.34	0.32	0.33	0.00	0.01	−0.01	0.00	0.00	0.23	0.22	0.23
(5, 5, 5)	0.00	0.33	0.34	0.33	0.00	0.00	0.01	0.00	0.00	0.23	0.24	0.24
(10, 10, 10)	0.00	0.35	0.33	0.33	0.00	0.01	−0.01	−0.01	0.00	0.25	0.24	0.24
(15, 15, 15)	0.00	0.34	0.32	0.34	0.00	0.01	−0.01	0.01	0.00	0.25	0.24	0.25
(1, 5, 15)	0.00	0.43	0.31	0.26	0.00	0.09	−0.02	−0.07	0.00	0.27	0.23	0.21
(15, 5, 1)	0.00	0.26	0.30	0.44	0.00	−0.07	−0.03	0.10	0.00	0.22	0.23	0.27
(15, 1, 5)	0.00	0.27	0.43	0.31	0.00	−0.07	0.09	−0.02	0.00	0.21	0.27	0.24
(1, 15, 5)	0.00	0.43	0.26	0.31	0.00	0.10	−0.07	−0.02	0.00	0.27	0.21	0.24
(5, 15, 1)	0.00	0.30	0.26	0.44	0.00	−0.03	−0.08	0.11	0.00	0.23	0.21	0.27
(5, 1, 15)	0.00	0.30	0.44	0.25	0.00	−0.03	0.11	−0.08	0.00	0.23	0.27	0.21

Note: T₁ is reference treatment and T₂ to T₄ are treatments in comparison relative to this reference.

The upward bias of the first rank probability corresponds to the treatment with the smallest number of studies in the network. All possible permutations of the unbalanced number of studies were checked and showed that the overestimation of the first rank probability always aligns with the treatment used in the fewest number of studies.

Table 5 shows results for the loop geometry. Here, T₃ was consistently underestimated, albeit slightly, though it was expected to be equivalent in efficacy with T₂ and T₄.

Table 5.

Loop network pattern with success probabilities (0.1, 0.5, 0.5, 0.5) and n=200

Number of studies	Rank probability				Bias				Standard deviation
	T1	T2	T3	T4	T1	T2	T3	T4	T1	T2	T3	T4
(1, 1, 1, 1)	0.00	0.35	0.29	0.35	0.00	0.02	−0.04	0.02	0.00	0.13	0.12	0.13
(2, 2, 2, 2)	0.00	0.34	0.31	0.35	0.00	0.01	−0.03	0.02	0.00	0.22	0.20	0.21
(3, 3, 3, 3)	0.00	0.36	0.29	0.35	0.00	0.03	−0.05	0.02	0.00	0.24	0.21	0.24
(5, 5, 5, 5)	0.00	0.36	0.28	0.36	0.00	0.02	−0.05	0.03	0.00	0.25	0.22	0.25
(10, 10, 10, 10)	0.00	0.36	0.28	0.36	0.00	0.02	−0.06	0.03	0.00	0.27	0.23	0.26
(15, 15, 15, 15)	0.00	0.35	0.30	0.36	0.00	0.02	−0.04	0.02	0.00	0.25	0.23	0.25
(1, 3, 5, 15)	0.00	0.38	0.27	0.35	0.00	0.04	−0.06	0.02	0.00	0.25	0.21	0.25
(15, 3, 5, 1)	0.00	0.37	0.28	0.35	0.00	0.04	−0.05	0.02	0.00	0.25	0.21	0.24

Note: T₁ is reference treatment and T₂ to T₄ are treatments in comparison relative to this reference.

In order to determine the impact of direct evidence, an additional simulation was conducted using a complete network. When direct evidence was available for all treatment comparisons, the model correctly estimated the ranks of treatments. These results are provided in Table 6.

Table 6.

Loop (complete) network pattern with success probabilities (0.1, 0.5, 0.5, 0.5) and n=200

Number of studies	Rank probability				Bias				Standard deviation
	T1	T2	T3	T4	T1	T2	T3	T4	T1	T2	T3	T4
(1, 1, 1, 1, 1, 1)	0.00	0.33	0.33	0.34	0.00	0.00	0.00	0.00	0.00	0.19	0.19	0.19
(2, 2, 2, 2, 2, 2)	0.00	0.32	0.33	0.35	0.00	−0.01	0.00	0.01	0.00	0.23	0.23	0.23
(3, 3, 3, 3, 3, 3)	0.00	0.33	0.33	0.34	0.00	0.00	−0.01	0.00	0.00	0.23	0.23	0.24
(5, 5, 5, 5, 5, 5)	0.00	0.35	0.32	0.32	0.00	0.02	−0.01	−0.01	0.00	0.25	0.24	0.24
(10, 10, 10, 10, 10, 10)	0.00	0.32	0.33	0.35	0.00	−0.01	0.00	0.01	0.00	0.24	0.25	0.25
(15, 15, 15, 15, 15, 15)	0.00	0.34	0.33	0.33	0.00	0.01	−0.01	0.00	0.00	0.26	0.25	0.25
(1, 2, 3, 5, 10, 15)	0.00	0.37	0.33	0.29	0.00	0.04	0.00	−0.04	0.00	0.26	0.25	0.23
(15, 10, 5, 3, 2, 1)	0.00	0.29	0.34	0.38	0.00	−0.05	0.00	0.04	0.00	0.23	0.25	0.26

Note: T₁ is reference treatment and T₂ to T₄ are treatments in comparison relative to this reference.

The results from the one closed loop geometry are provided in Table 7. As with the loop geometry, the rank probability of T₃ was underestimated while those of T₂ and T₄ were overestimated. The underestimation by the one closed loop configuration was more extreme than with the loop configuration. This appears to be related to the additional direct evidence in the one closed loop configuration; T₃ was compared with T₁, T₂, and T₄ as opposed to only T₂ and T₄ in loop geometry.

Table 7.

One closed loop network pattern with success probabilities (0.1, 0.5, 0.5, 0.5) and n=200

Number of studies	Rank probability				Bias				Standard deviation
	T1	T2	T3	T4	T1	T2	T3	T4	T1	T2	T3	T4
(1, 1, 1, 1)	0.00	0.36	0.24	0.39	0.00	0.03	−0.09	0.06	0.00	0.14	0.10	0.14
(2, 2, 2, 2)	0.00	0.35	0.26	0.38	0.00	0.02	−0.07	0.05	0.00	0.22	0.19	0.22
(3, 3, 3, 3)	0.00	0.35	0.26	0.39	0.00	0.02	−0.08	0.06	0.00	0.23	0.19	0.24
(5, 5, 5, 5)	0.00	0.37	0.25	0.37	0.00	0.04	−0.08	0.04	0.00	0.25	0.20	0.25
(10, 10, 10, 10)	0.00	0.36	0.25	0.39	0.00	0.03	−0.09	0.06	0.00	0.26	0.21	0.27
(15, 15, 15, 15)	0.00	0.36	0.24	0.40	0.00	0.03	−0.09	0.07	0.00	0.26	0.21	0.27
(1, 3, 5, 15)	0.00	0.42	0.25	0.33	0.00	0.08	−0.08	0.00	0.00	0.27	0.21	0.24
(15, 3, 5, 1)	0.00	0.31	0.25	0.44	0.00	−0.02	−0.08	0.11	0.00	0.23	0.20	0.26

Note: T₁ is reference treatment and T₂ to T₄ are treatments in comparison relative to this reference.

Table 8 displays the results of when the position of the reference treatment for the one closed loop network geometry was changed. This result shows that T₄, the treatment that was compared only with the placebo, was favored as compared to the other two equivalent treatments, which were compared to one another.

Table 8.

One closed loop network pattern with success probabilites (0.1, 0.5, 0.5, 0.5) and n=200

Number of studies	Rank probability				Bias				Standard deviation
	T3	T2	T1	T4	T3	T2	T1	T4	T3	T2	T1	T4
(1, 1, 1, 1)	0.30	0.29	0.00	0.41	−0.04	−0.04	0.00	0.08	0.12	0.12	0.00	0.15
(2, 2, 2, 2)	0.28	0.28	0.00	0.44	−0.06	−0.05	0.00	0.10	0.20	0.20	0.00	0.24
(3, 3, 3, 3)	0.29	0.29	0.00	0.42	−0.04	−0.05	0.00	0.09	0.22	0.22	0.00	0.26
(5, 5, 5, 5)	0.30	0.29	0.00	0.41	−0.03	−0.05	0.00	0.08	0.23	0.22	0.00	0.27
(10, 10, 10, 10)	0.29	0.30	0.00	0.41	−0.05	−0.03	0.00	0.08	0.22	0.23	0.00	0.27
(15, 15, 15, 15)	0.28	0.30	0.00	0.42	−0.06	−0.03	0.00	0.09	0.22	0.24	0.00	0.28
(1, 3, 5, 15)	0.35	0.33	0.00	0.32	0.02	−0.00	0.00	−0.01	0.25	0.24	0.00	0.24
(15, 3, 5, 1)	0.25	0.26	0.00	0.49	−0.08	−0.08	0.00	0.16	0.21	0.22	0.00	0.28

Note: T₁ is reference treatment and T₂ to T₄ are treatments in comparison relative to this reference.

Table 9 shows results for the ladder geometry. The first rank probability for T₃ was underestimated as with the loop geometry, with even stronger bias.

Table 9.

Ladder network pattern success probabilities (0.1, 0.5, 0.5, 0.5) and n=200

Number of studies	Rank probability				Bias				Standard deviation
	T1	T2	T3	T4	T1	T2	T3	T4	T1	T2	T3	T4
(1, 1, 1)	0.02	0.36	0.24	0.37	0.02	0.03	−0.09	0.04	0.00	0.09	0.07	0.09
(2, 2, 2)	0.00	0.37	0.25	0.38	0.00	0.04	−0.09	0.05	0.00	0.20	0.16	0.20
(3, 3, 3)	0.00	0.38	0.25	0.38	0.00	0.04	−0.09	0.05	0.00	0.23	0.18	0.23
(5, 5, 5)	0.00	0.37	0.25	0.38	0.00	0.04	−0.08	0.04	0.00	0.24	0.20	0.24
(10, 10, 10)	0.00	0.39	0.24	0.37	0.00	0.05	−0.09	0.04	0.00	0.26	0.21	0.26
(15, 15, 15)	0.00	0.37	0.25	0.38	0.00	0.04	−0.09	0.05	0.00	0.26	0.21	0.26
(1, 5, 15)	0.00	0.41	0.25	0.34	0.00	0.08	−0.08	0.00	0.00	0.26	0.21	0.25
(15, 5, 1)	0.00	0.32	0.25	0.43	0.00	−0.01	−0.09	0.09	0.00	0.22	0.19	0.25

Note: T₁ is reference treatment and T₂ to T₄ are treatments in comparison relative to this reference.

Table 10 shows results for the final scenario, when T₄ is superior in efficacy compared to three equally less effective treatments. Here, as expected, T₄ was identified by the model under each simulation setting as the most effective treatment with highest rank probability, regardless of the network geometry or placement of the superior treatment within it. The impact of the number of studies on the rank probability was negligible. In this scenario, bias and standard deviations were generally very small in all cases. The results were presented with a sample size of 50 for the star network pattern since the results were not markedly different for other network configurations or sample sizes, regardless of the position of the superior treatment.

Table 10.

Star network pattern success probabilities (0.2, 0.2, 0.2, 0.8) and n=200

Number of studies	Rank probability				Bias				Standard deviation
	T1	T2	T3	T4	T1	T2	T3	T4	T1	T2	T3	T4
(1, 1, 1)	0.01	0.08	0.08	0.83	0.01	0.08	0.08	−0.17	0.00	0.04	0.04	0.04
(2, 2, 2)	0.00	0.01	0.01	0.98	0.00	0.01	0.01	−0.02	0.00	0.01	0.01	0.02
(3, 3, 3)	0.00	0.00	0.00	1.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
(5, 5, 5)	0.00	0.00	0.00	1.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
(10, 10, 10)	0.00	0.00	0.00	1.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
(15, 15, 15)	0.00	0.00	0.00	1.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
(1, 5, 15)	0.00	0.00	0.00	1.00	0.00	0.00	0.00	0.00	0.00	0.01	0.00	0.01
(15, 5, 1)	0.00	0.00	0.00	1.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00

Discussion

NMA offers a set of methods to model, visualize, analyze, and interpret a comprehensive picture of the evidence involving multiple treatments and to understand the relative merits of each intervention. In NMA, the Bayesian approach is becoming more popular than the frequentist approach. It provides a simple process for calculating the rank probabilities of interventions, incorporates prior knowledge, and fits more flexible models.

The primary purpose of this article was to examine the effect of various factors on rank probabilities of treatments in NMA through simulation. For the treatments compared in loop, one closed loop, and ladder network structures with an equal number of studies per comparison, the model-estimated rank probabilities exhibited bias. The model favored the treatment that was directly compared with the fewest number of treatments in the network patterns. The rank probability of the treatment that was compared with the largest number of treatments was always underestimated.

The simulations also showed that when two equally effective treatments in the same network are included in the same number of direct comparisons, the effectiveness of the treatments to which they are compared will affect the rankings. Treatments that are compared directly with inferior treatments yield ranks that are overestimated, while treatments that are exclusively compared with equal or superior treatments yield ranks that are underestimated. When there is an unequal number of studies per comparison for a given network structure, the model overestimated the rank probability of the treatment associated with smaller number of studies. The first rank probability’s overestimation when it is the least-studied treatment is an artifact of a larger estimated variance for that treatment. The rank probabilities obtained from Bayesian NMA for loop, one closed loop, and ladder geometry can be reliable only when there is direct evidence for every treatment involved in the analysis or when there is an obvious superiority in efficacy. In other words, rank estimates for treatments that have never been directly compared should not be trusted. The position of the reference treatment in the network may affect conclusions from rank probabilities. Increasing the sample size of individual studies did not help to adjust the over/underestimation of the rank probabilities. These findings validate the concerns of Mills et al²⁴ about using rank probabilities for decision making.

There are some limitations of this simulation that must be noted. Although the Bayesian NMA model can be used broadly, only a binary outcome was considered in this simulation study. This study was also confined to only two-arm studies. In practice, multi-arm studies in NMA are often encountered where correlation is induced among contrasts that involve a common comparator and must be modeled.^38,42 Furthermore, this study only focused on the rank probabilities that each treatment is best, but the authors might be interested in investigating all of the ranks of available treatments.

Conclusion

This simulation study revealed several occasions of bias of rank probabilities obtained from a Bayesian NMA. For example, for an unequal number of studies per comparison, the rank probability of the treatment with more studies was underestimated. In addition, the rank probability of the treatment that was directly compared with the placebo and an equivalent treatment simultaneously (eg, T₂ and T₄ in loop, ladder, and one closed loop geometries) gained spurious rank probabilities, whereas the rank probability of a treatment that was compared with two equivalent treatments (eg, T₃ in loop, ladder, and one closed loop) was underestimated. In summary, decisions should not be made based on rank probabilities especially when treatments are not directly compared (ie, ladder, one closed loop, star) as they may be ill-informed.