Genetic Association Analysis under Complex Survey Sampling: The Hispanic Community Health Study/Study of Latinos

Abstract

The cohort design allows investigators to explore the genetic basis of a variety of diseases and traits in a single study while avoiding major weaknesses of the case-control design. Most cohort studies employ multistage cluster sampling with unequal probabilities to conveniently select participants with desired characteristics, and participants from different clusters might be genetically related. Analysis that ignores the complex sampling design can yield biased estimation of the genetic association and inflation of the type I error. Herein, we develop weighted estimators that reflect unequal selection probabilities and differential nonresponse rates, and we derive variance estimators that properly account for the sampling design and the potential relatedness of participants in different sampling units. We compare, both analytically and numerically, the performance of the proposed weighted estimators with unweighted estimators that disregard the sampling design. We demonstrate the usefulness of the proposed methods through analysis of MetaboChip data in the Hispanic Community Health Study/Study of Latinos, which is the largest health study of the Hispanic/Latino population in the United States aimed at identifying risk factors for various diseases and determining the role of genes and environment in the occurrence of diseases. We provide guidelines on the use of weighted and unweighted estimators, as well as the relevant software.

Introduction

The cohort design allows for rigorous investigation into a range of diseases and conditions in a single study while reducing important biases inherent in the case-control design.^1–3 Most cohort studies employ multistage, unequal probability, and cluster sampling to select participants, with the intention of achieving particular population profiles or to enrich the cohort with exposed individuals or those affected by conditions of interest. Such studies include the Family Heart Study,⁴ the MONICA Augsburg Surveys,⁵ the National Health and Nutrition Examination Survey (NHANES),⁶ the National Longitudinal Study of Adolescent Health (Add Health),⁷ and the National Children’s Study,⁸ among many others. These cohorts provide a valuable and indispensable resource for identifying genetic variants affecting measured risk factors, indicators of subclinical diseases, and clinical manifestations of diseases.^1–3,7–13 However, the implications of the complex sampling design in genetic data analysis have not been well appreciated.

Sampling was particularly complex in the Hispanic Community Health Study (HCHS)/Study of Latinos (SOL), which is an ongoing multicenter cohort study of 16,415 Hispanic/Latino individuals with various countries of origin to identify risk factors for multiple diseases and determine the role of genes and environment, including acculturation, in the occurrence of diseases. The HCHS/SOL cohort was selected through a stratified multistage cluster sampling design.¹⁴ The community areas in four field centers—Bronx, Chicago, Miami, and San Diego—were delineated by census tracts from the 2000 decennial census. The field centers selected the tracts to target noninstitutionalized Hispanic/Latino adults aged 18–74 years. At the first stage of sample selection, a stratified simple random sample of census block groups (BGs) was selected for each field center; four strata were formed by cross-classifying BGs by socioeconomic status (SES) (2 levels) and the proportion of individuals who were Hispanic/Latino (2 levels). At the second stage, separate samples of household addresses in each of the sampled BGs were selected from lists of postal addresses stratified by Hispanic/Latino surnames versus all others. Afterward, Bernoulli subsampling was used to oversample 45- to 74-year-old Hispanic/Latino residents within selected households.

The HCHS/SOL participants underwent a clinic exam that included blood collection (from which DNA was extracted and analytes measured), an electrocardiogram, and assessments of ankle-brachial index, anthropometry, blood pressure, spirometry, dental, and neurocognitive phenotypes. Participants also completed extensive socio-demographic, medical, behavioral, and lifestyle questionnaires. Annual follow-up interviews have been conducted, and endpoints in cardiovascular and lung diseases have been collected. As part of the Population Architecture using Genomics and Epidemiology (PAGE) Consortium,¹¹ the HCHS/SOL participants were genotyped on the MetaboChip¹⁵ and will soon be genotyped on a new Illumina chip for low-frequency and rare exomic variants in ethnically diverse samples. Recently, the Omics in Latinos (OLa) project was launched to conduct genome-wide association analysis in the HCHS/SOL participants.

Genetic association analysis in the HCHS/SOL poses two major challenges. First, because of unequal selection probabilities and considerable levels of differential nonresponse, the participants are not a simple random sample of the target population, so genetic associations might be distorted in the selected cohort. Second, there is a complex pattern of relatedness: individuals in the same household are probably related and in addition there is endogamous mating within the Hispanic/Latino community,¹⁶ such that some households are connected into large pedigrees that extend beyond the primary sampling units (i.e., BGs).

In this article, we develop a weighted version of the generalized estimating equations (GEEs)¹⁷ to account for unequal inclusion probabilities and complex patterns of relatedness. Our approach does not require modeling the correlation structures of complex pedigrees and is applicable to any trait, including quantitative and binary traits. We construct two weighted estimators that properly control the type I error. The first weighted estimator uses the inverse inclusion probabilities as the weights and provides unbiased estimation of the overall association in the target population even when the strength of the association depends on the sampling variables. The second weighted estimator accounts only for the aspect of the sampling process that is not determined by the covariates in the association model and tends to be more powerful than the first one because of the reduced variation of the weights. We derive variance estimators that are accurate even for low-frequency SNPs. We compare, both analytically and numerically, the performance of the proposed weighted estimators with unweighted estimators that either ignore the sampling design or include the sampling variables or inclusion probability as additional covariates. We implement both types of estimators in a user-friendly software program and report preliminary results from our ongoing analysis of MetaboChip data in the HCHS/SOL. We make recommendations on the choice of weighted versus unweighted estimators under various scenarios.

Material and Methods

To address the issue of relatedness, we first perform an identity by descent (IBD) analysis of study participants by using genome-wide markers from a GWAS chip or some other chip. We use the IBD information to identify pairs of individuals who are first-degree or second-degree relatives. We then create (extended) families by connecting the households who share first-degree relatives or either first- or second-degree relatives. The trait values are assumed to be correlated within families but independent between families. In our experience, it is sufficient to account for the first-degree relatedness in association analysis.

Suppose that there are a total of K families in the target population, with N_k members in the k^th family (k = 1,..., K). For k = 1,..., K and i = 1,..., N_k, let Y_ki denote the trait of interest for the i^th member of the k^th family, and X_ki the corresponding set of covariates, which can include SNP genotypes, principal components (PCs) for ancestry, and demographic variables. We relate Y_ki to X_ki through a regression model characterized by the density function $f\left(y|x;\theta \right)$, where θ is a set of regression parameters. If all of the individuals in the target population were selected, we would estimate θ through the following generalized estimating function:¹⁷

$$U\left(\theta \right)=\sum _{k=1}^K\sum _{i=1}^{N_k}{U}_{ki}\left(\theta \right),$$

where $U_{ki}\left(\theta \right)=\partial \text{log}f\left(Y_{ki}|X_{ki};\theta \right)/\partial \theta$.

The individuals are selected with unequal probabilities, and some selected individuals decline to participate in the study. Suppose that a total of $\tilde{K}$ families participate in the study, with n_k participants in the k^th family. For $k=1,\dots ,\tilde{K}$ and i = 1,..., n_k, let π_ki denote the inclusion probability of the i^th member of the k^th family. Then a Horvitz-Thompson¹⁸ type “estimator” of U(θ) is

$$\hat{U}\left(\theta \right)=\sum _{k=1}^{\tilde{K}}\sum _{i=1}^{n_k}{w}_{ki}{U}_{ki}\left(\theta \right),$$

where w_ki = 1 / π_ki. Denote the resulting estimator of θ by ${\hat{\theta }}_w$.

We show in Appendix A that ${\hat{\theta }}_w$ is approximately normal with mean θ and a covariance matrix that can be estimated by ${\hat{V}}_w={\hat{A}}^{-1}\left({\hat{\theta }}_w\right)\hat{B}\left({\hat{\theta }}_w\right){\hat{A}}^{-1}\left({\hat{\theta }}_w\right)$ or ${\tilde{V}}_w={\hat{A}}^{-1}\left({\hat{\theta }}_w\right)\tilde{B}\left({\hat{\theta }}_w\right){\hat{A}}^{-1}\left({\hat{\theta }}_w\right)$, where

$$\begin{array}{l}\hat{A}\left(\theta \right)=\sum _{k=1}^{\tilde{K}}\sum _{i=1}^{n_k}{w}_{ki}\frac{\partial U_{ki}\left(\theta \right)}{\partial \theta },\hfill \\ \hat{B}\left(\theta \right)=\sum _{k=1}^{\tilde{K}}\sum _{i=1}^{n_k}\sum _{j=1}^{n_k}{w}_{ki}{w}_{kj}{U}_{ki}\left(\theta \right)U_{kj}^{\prime }\left(\theta \right)+\sum _{k=1}^{\tilde{K}}\sum _{i=1}^{n_k}\sum _{l\ne k,l=1}^{\tilde{K}}\sum _{j=1}^{n_l}\frac{w_{ki}{w}_{lj}\left({\pi }_{kilj}-{\pi }_{ki}{\pi }_{lj}\right)}{{\pi }_{kilj}}{U}_{ki}\left(\theta \right)U_{lj}^{\prime }\left(\theta \right)\hfill \\ \tilde{B}\left(\theta \right)=-\sum _{k=1}^{\tilde{K}}\sum _{i=1}^{n_k}{w}_{ki}^2\frac{\partial U_{ki}\left(\theta \right)}{\partial \theta }+\sum _{k=1}^{\tilde{K}}\sum _{i=1}^{n_k}\sum _{j\ne i,j=1}^{n_k}{w}_{ki}{w}_{kj}{U}_{ki}\left(\theta \right)U_{kj}^{\prime }\left(\theta \right)+\sum _{k=1}^{\tilde{K}}\sum _{i=1}^{n_k}\sum _{l\ne k,l=1}^{\tilde{K}}\sum _{j=1}^{n_l}\frac{w_{ki}{w}_{lj}\left({\pi }_{kilj}-{\pi }_{ki}{\pi }_{lj}\right)}{{\pi }_{kilj}}{U}_{ki}\left(\theta \right)U_{lj}^{\prime }\left(\theta \right),\hfill \end{array}$$

and π_kilj is the probability that the i^th member of the k^th family and the j^th member of the l^th family are both included. Note that $\tilde{B}\left(\theta \right)$ differs from $\hat{B}\left(\theta \right)$ in that the within-subject covariance matrix of U_ki(θ) is estimated by the Fisher information matrix $-\partial U_{ki}\left(\theta \right)/\partial \theta$ rather than the empirical covariance matrix $U_{ki}\left(\theta \right)U_{ki}^{\prime }\left(\theta \right)$. The former estimator is more accurate than the latter for low-frequency SNPs; however, the latter is (asymptotically) valid even when the association model is misspecified whereas the former might not be. We refer to ${\hat{V}}_w$ and ${\tilde{V}}_w$ as the robust and model-based variance estimators, respectively.

The calculations of ${\hat{\theta }}_w$ and its covariance matrix estimators ${\hat{V}}_w$ and ${\tilde{V}}_w$ involve only the data from the study participants. This weighted analysis fully accounts for unequal probabilities of inclusion among study participants and thus produces unbiased estimation of the regression parameters. The correlations among related individuals are not modeled parametrically but rather are adjusted for empirically in the variance estimation. Because different participants receive different weights in the estimating function, the weighted estimator is statistically inefficient. To improve statistical efficiency (at the cost of inducing some bias), we can trim the extreme values of w_ki. We might also trim the pairwise selection probabilities π_kilj in the denominator of the last term of $\hat{B}$ or $\tilde{B}$ so as to improve stability.

A statistically more efficient and computationally simpler approach is to ignore unequal inclusion probabilities and perform the conventional unweighted analysis. The unweighted analysis is a special case of the weighted analysis in which all w_ki are set to 1, and it corresponds to the standard GEE method.¹⁷ In that case, ${\hat{V}}_w$ reduces to the covariance matrix estimator of the standard GEE whereas ${\tilde{V}}_w$ is different in that the within-subject contributions to the covariance matrix of the estimating function are estimated by the Fisher information matrices rather than the empirical covariance matrices of the score functions. This modification greatly improves variance estimation for low-frequency SNPs.

By the arguments of Lin et al.,¹⁹ we can show that the unweighted analysis produces biased estimation of the genetic association if the sampling variables (i.e., the variables that determine the selection probabilities and response rates) are correlated with both the trait of interest and the SNP of interest. This will be the case in the HCHS/SOL if the proportion of Hispanic/Latino individuals or SES is correlated with the trait of interest, say, BMI, and also with the test SNP. There are unlikely to be many such SNPs, so the unweighted analysis would not produce a large-scale inflation of false-positive results; however, the unweighted analysis is not guaranteed to yield valid p values for all traits and all SNPs.

One might account for the sampling design by including the sampling variables in the regression model;²⁰ however, the conditional association for a SNP given the sampling variables is generally different from the unconditional (i.e., marginal) association. In the HCHS/SOL, the conditional association of a trait, say BMI, with a test SNP given the proportion of Hispanic/Latino individuals or SES might well be different from the marginal association. In many applications, the sampling variables are difficult to define or unavailable to the data analyst. The sampling probability can be used as a surrogate for the sampling variables;²¹ however, the conditional association given the sampling probability might not be the same as the marginal association, either. We refer to the unweighted estimators of θ that include the sampling variables and sampling probability in the model as UW-C and UW-P, respectively, and to the unweighted estimator that does not include such covariates as UW-M.

If the sample selection depends only on the covariates in the regression model, then the sampling process is ignorable and the UW-M estimator is valid (and efficient). To protect against nonignorable sampling, it is necessary only to account for the aspect of the sampling process that is not determined by the covariates. Thus, we replace w_ki by $q_{ki}=w_{ki}/E\left(w_{ki}|X_{ki}\right)$, where $E\left(w_{ki}|X_{ki}\right)$ is the conditional expectation of w_ki given X_ki.²² We might estimate the conditional expectations by the sample means of the observed w_ki in the cells formed by the discretized X_ki or by the predicted values under a gamma regression model.²³ We denote the resulting estimator of θ by ${\hat{\theta }}_q$. The modified weights (q_ki) account for the net sampling effects on the conditional distribution of Y given X, whereas the original sampling weights (w_ki) account for the sampling effects on the joint distribution of Y and X. Thus, the q_ki tend to be less variable than the w_ki, such that ${\hat{\theta }}_q$ is expected to be more efficient than ${\hat{\theta }}_w$. Indeed, if w_ki is a deterministic function of X_ki, then q_ki = 1 and ${\hat{\theta }}_q$ reduces to the UW-M estimator. It is important to point out that the modified weighted estimator ${\hat{\theta }}_q$ is valid even if the conditional expectation $E\left(w_{ki}|X_{ki}\right)$ is misspecified because the estimated conditional expectation is a function of covariates only. We estimate the covariance matrix of ${\hat{\theta }}_q$ by ${\hat{V}}_q$ and ${\tilde{V}}_q$, which are obtained from ${\hat{V}}_w$ and ${\tilde{V}}_w$, respectively, by replacing w with q everywhere. We name ${\hat{\theta }}_w$ and ${\hat{\theta }}_q$ the W-HT and W-PS estimators (after Horvitz and Thompson¹⁸ and Pfeffermann and Sverchkov²²), respectively.

Thus far we have assumed that the association model $f\left(y|x;\theta \right)$ is correctly specified. If that is not the case, then W-HT will be an approximately unbiased estimator of θ^∗, which is the solution to the finite-population estimating equation U(θ) = 0. For the quantitative trait, θ^∗ pertains to the slope in the target population. The other methods might yield biased estimation of θ^∗ even if the SNP of interest is not correlated with the sampling variables. Specifically, if the SNP association with a particular trait (e.g., BMI) varies with a sampling variable (e.g., age), then W-HT will still be an unbiased estimator of the overall association in the target population whereas the other estimators will be driven by the individuals who are oversampled (e.g., older individuals).

Results

Simulation Studies

We conducted extensive simulation studies to evaluate the performance of the weighted and unweighted methods by mimicking the HCHS/SOL sampling scheme. Specifically, we set the number of families in the population at 500,000 and mimicked the family structures in the HCHS/SOL cohort. We simulated a standard normal random variable S_k to represent the ancestry of the k^th family. We set the minor allele frequency (MAF) to $e^{-0.5+0.1S_k}/\left(1+e^{-0.5+0.1S_k}\right)$ and generated the genotype G_ki for the i^th member of the k^th family under Mendelian inheritance. We considered two sampling variables: W_ki is a discrete uniform random variable with values {18,19,...,74} that represents a variable such as age that is independent of G_ki, and Z_ki = τG_ki + ϕ_ki is a variable, such as proportion of Hispanic/Latino individuals or SES, that is possibly correlated with G_ki, where τ is a parameter controlling the degree of correlation and ϕ_ki is standard normal. We generated the values of a quantitative trait under the linear mixed model

$$Y_{ki}=\beta G_{ki}+0.1S_k+0.01W_{ki}+{\psi }_k+{\mathit{ϵ}}_{ki},$$

where ${\psi }_k$ is a zero-mean normal random variable with variance 0.1 that induces the within-family correlations, and ${\mathit{ϵ}}_{ki}$ is an independent standard normal variable. We allowed Y_ki and Z_ki to be correlated by generating $\left({\varphi }_{ki},{\mathit{ϵ}}_{ki}\right)$ from a bivariate normal distribution with correlation ρ.

To mimic the stratified cluster sampling of the HCHS/SOL, we defined four strata of families according to the means of Z_ki in the families, such that the first stratum has the smallest means and the fourth stratum has the largest means; and the second stratum is twice as large as the first one, the third one is twice as large as the second, and the fourth one is twice as large as the third. In each stratum, we selected 2,600 families through simple random sampling. To mimic the oversampling of older individuals (i.e., 45–74 years of age) in the HCHS/SOL, we selected, from those 10,400 families, the individuals with W_ki ≥ 45 with certainty and other individuals with probability 0.5. In this way, we obtained a total of ∼15,000 individuals, which is the size of the HCHS/SOL cohort. The distribution of the sampling probabilities is similar to that of the HCHS/SOL.

We considered the two weighted estimators, W-HT and W-PS, and the three unweighted estimators, UW-M, UW-C, and UW-P. For the first three methods, we fit the (marginal) linear regression model with covariates G_ki, S_k, and W_ki. For W-PS, we estimated q_ki by the sample mean of w_ki in the genotype × age (18–44 versus 45–74 years) category. For UW-C, we added Z_ki to the model; for UW-P, we added a cubic function of log(π_ki). We varied the value of ρ, which represents the correlation between the sampling variable Z and the trait of interest Y, and we also varied the value of τ to create a range of correlation between the sampling variable Z and the genotype G.

The results under the null hypothesis (H₀ : β = 0) and the alternative hypothesis (H₁ : β = 0.06) are displayed in Figures 1 and 2, respectively. The W-HT and W-PS estimators are virtually unbiased, and their variance estimators are very accurate. Thus, the corresponding association tests have correct control of the type I error. The three unweighted estimators (UW-M, UW-C, and UW-P) are biased and the corresponding association tests have inflated type I error unless the sampling is independent of the genotype or the trait. The reasons for the bias depend on the estimator: UW-M is biased when the sampling process is nonignorable; UW-C and UW-P are biased because the conditional associations are different from the marginal association. The standard errors of the unweighted estimators are considerably lower than those of the weighted estimators, such that the unweighted estimators tend to be more powerful than the weighted estimators; however, they can be less powerful when the estimators are biased substantially toward 0. The W-PS estimator has smaller standard error than the W-HT estimator and is thus more powerful than the latter.

Figure 1.

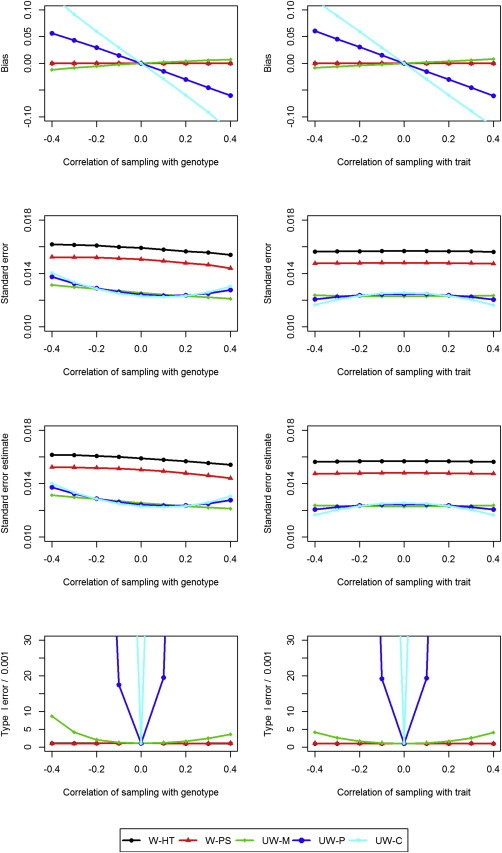
Simulation Results under the Null Hypothesis

Bias, standard error, mean standard error estimate, and type I error (divided by the nominal significance level 0.001) for weighted and unweighted methods as a function of the correlation between the sampling variable and the genotype when the correlation between the sampling variable and the trait of interest is 0.2 (left side) and as a function of the correlation between the sampling variable and the trait of interest when the correlation between the sampling variable and the genotype is 0.2 (right side). The estimates of the bias and type I error are indistinguishable between W-HT and W-PS.

Figure 2.

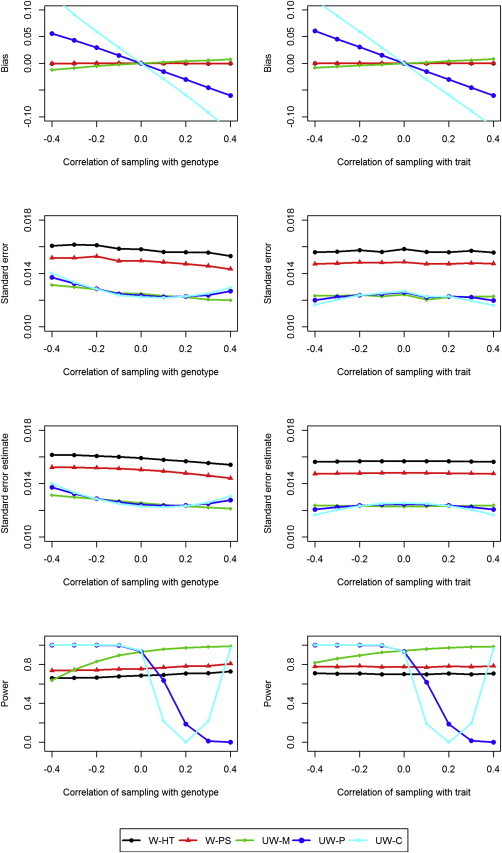
Simulation Results under the Alternative Hypothesis

Bias, standard error, mean standard error estimate, and power (at the nominal significance level of 0.001) for weighted and unweighted methods as a function of the correlation between the sampling variable and the genotype when the correlation between the sampling variable and the trait of interest is 0.2 (left side) and as a function of the correlation between the sampling variable and the trait of interest when the correlation between the sampling variable and the genotype is 0.2 (right side). The estimates of the bias are indistinguishable between W-HT and W-PS.

To investigate the consequences of model misspecification, we generated the quantitative trait values under the following model

$$Y_{ki}=\beta G_{ki}+0.1S_k+0.01W_{ki}+\gamma G_{ki}\left(W_{ki}-45\right)+{\psi }_k+{\mathit{ϵ}}_{ki},$$

but we omitted the product term (and the random effect) in the analysis. This corresponds to the situation in which one is interested in the overall genetic association in the population when the association varies with age. The results under τ = 0 (i.e., independence of the sampling variable and the genotype) are displayed in Figure 3. The W-HT estimator is virtually unbiased; all other estimators are biased when there is model misspecification because they are not properly calibrated to the population totals. The mean square error of W-HT is lower than those of the other estimators under severe model misspecification.

Figure 3.

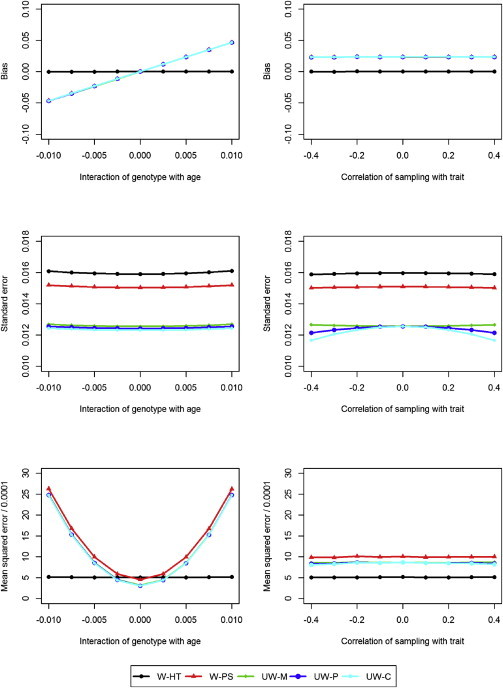
Simulation Results under Misspecified Models

Bias, standard error, and mean square error for weighted and unweighted methods as a function of the interaction between the genotype and age when the correlation between the sampling variable and the trait of interest is 0.2 (left side) and as a function of the correlation between the sampling variable and the trait of interest when the interaction between the genotype and age is 0.005 (right side). The estimates of the bias are indistinguishable among W-PS, UW-M, UW-C, and UW-P, and the estimates of the mean square error are indistinguishable among UW-M, UW-C, and UW-P.

HCHS/SOL

The HCHS/SOL, which began in 2006, is a landmark study of 16,415 Hispanic/Latino adults in the United States. As described earlier, individuals were selected into the HCHS/SOL through a multistage cluster sampling design with unequal selection probabilities. The probabilities of selection were adjusted by household-level and individual-level nonresponse. The calculations of the nonresponse-adjusted marginal inclusion probabilities π_ki and pairwise inclusion probabilities π_kilj are detailed in Appendix B. The distributions of these probabilities are displayed in Figure S1 available online. We trimmed the marginal inclusion probabilities according to Equation A1 of Appendix A with π₀ = 0.01 and c = 10.

Recently, 12,472 HCHS/SOL participants were genotyped on the MetaboChip array, which contains replication targets and fine-mapping regions for metabolic and atherosclerotic-cardiovascular traits.¹⁵ The genotyping was performed at the Human Genetics Center of the University of Texas, Houston, and genotypes were called with the GenCall 2.0 algorithm in Illumina’s GenomeStudio. A total of 12,121 participants remained after excluding duplicates and individuals with genotyping call rates <95% or sex discordance. Of the 196,725 SNPs that were genotyped, 182,917 remained after applying various SNP quality-control criteria, including call rate, calling score, clustering score, Mendelian inconsistency, and Hardy-Weinberg equilibrium.

In order to accommodate the relatives in the HCHS/SOL when calculating the PCs, we created 20 eigenvectors of genotypes by using six of the 1000 Genomes reference samples (CEU, YRI, MXL, PUR, CLM, and CHB) with a panel of 44,883 SNPs in low linkage disequilibrium (LD) and then projected the HCHS/SOL sample along each of the 20 eigenvectors. We performed an IBD analysis of the 12,121 HCHS/SOL participants by using a subset of 13,290 MetaboChip SNPs with MAF > 5% and pairwise r² ≤ 0.1 within any 50-SNP window. We identified pairs of individuals with $0.35<\hat{\pi }<0.98$ as first-degree relatives and $0.2<\hat{\pi }\le 0.35$ as second-degree relatives, where $\hat{\pi }$ is the estimated IBD proportion. After connecting households who shared first-degree relatives, we obtained 4,969, 1,930, 555, 206, 62, 34, and 35 extended families of sizes 1, 2, 3, 4, 5, 6, and ≥7, respectively. With second-degree relatives added, the corresponding numbers are 4,856, 1,865, 554, 219, 68, 37, and 42. We decided to account for relatedness according to the first-degree relatedness and disregard the second degree and beyond because the latter did not unduly influence the test statistics.

In order to minimize the influence of the densely fine-mapped regions of the MetaboChip on our quantile-quantile plots and other comparisons, we pruned the set of 182,917 SNPs that passed our quality control. Specifically, we used a window of 50 base pairs and an incremental step of five SNPs in PLINK²⁴ to prune any SNP in strong pairwise LD (r² > 0.8) with another SNP in a given window. This process excluded an additional 59,653 SNPs and resulted in a final set of 123,264 SNPs. Of those SNPs, there are 91,019 with MAF > 1%, 19,976 with MAF between 0.1% and 1%, and 5,131 with MAF between 0.01% and 0.1%.

We used the weighted estimators, W-HT and W-PS, and unweighted estimators, UW-M, UW-C, and UW-P, to assess SNP associations with 16 cardiovascular traits. We included age, gender, the top ten PCs, field center, and (self-reported) Hispanic/Latino background (Dominican Republican, Central American, Cuban, Mexican, Puerto Rican, South American, others) as covariates. For UW-C, we added the stratification variables. For UW-P, we added a cubic spline of logπ_ki with two interior knots (at the 33^th and 67^th percentiles). For W-PS, we estimated q_ki under the gamma regression model with the log link function that includes age, age-square, gender, field center, and Hispanic/Latino background, as well as all product terms with p values < 0.1. We winsorised q_ki to the 95^th percentile. The UW-C results are almost identical to those of UW-P (Figure S2) and thus will not be shown.

Figure 4 compares the performance of the robust and model-based variance estimators in the association tests for BMI. For SNPs with MAF > 1%, the two variance estimates are very similar. For low-frequency SNPs, the robust variance estimates yield some very extreme p values whereas the model-based variance estimates produce much more reasonable p values. It is remarkable that the model-based variance estimates are stable even for SNPs with MAF of 0.01%, which corresponds to a minor allele count of 2 or 3.

Figure 4.

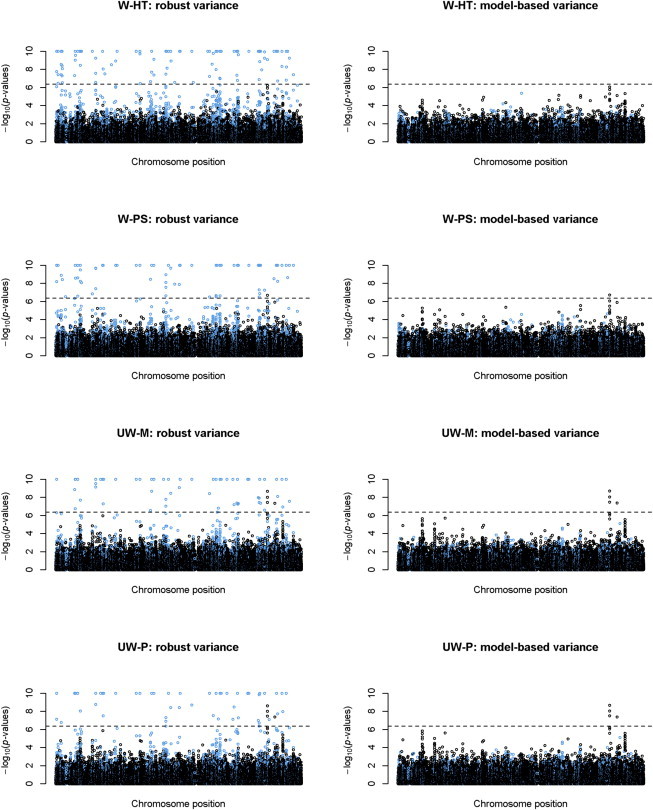
Manhattan Plots from the Genome-wide Association Analysis of BMI in the HCHS/SOL

Plots of −log₁₀(p values) for weighted and unweighted methods with robust versus model-based variance estimators are shown. The log-transformation was applied to BMI. SNPs with MAF < 0.01% were excluded. The Bonferroni threshold for genome-wide significance is indicated by the dashed line.

Figure S3 compares the effect estimates and standard error estimates for the four methods in the association analysis of BMI. The results for UW-M and UW-P are very similar. The W-HT and W-PS effect estimates can be appreciably different from each other and even more different from the UW-M and UW-P estimates. The standard error estimates of W-HT are larger than those of W-PS, which are larger than those of UW-M and UW-P.

Figure 5 presents the p values for the four methods in the association tests for BMI, fasting glucose, height, and total cholesterol. The results for UW-M and UW-P are highly similar. W-HT and W-PS tend to produce smaller λ values than UW-M and UW-P. The p values generated by W-PS tend to lie between those of W-HT and UW-M (or UW-P). The p values from the association tests that assume independence of households and independence of BGs are shown in Figures S4 and S5, respectively. When relatedness beyond the original households or BGs is ignored, the observed test statistics deviate more from the global null hypothesis of no association (yielding larger λ values).

Figure 5.

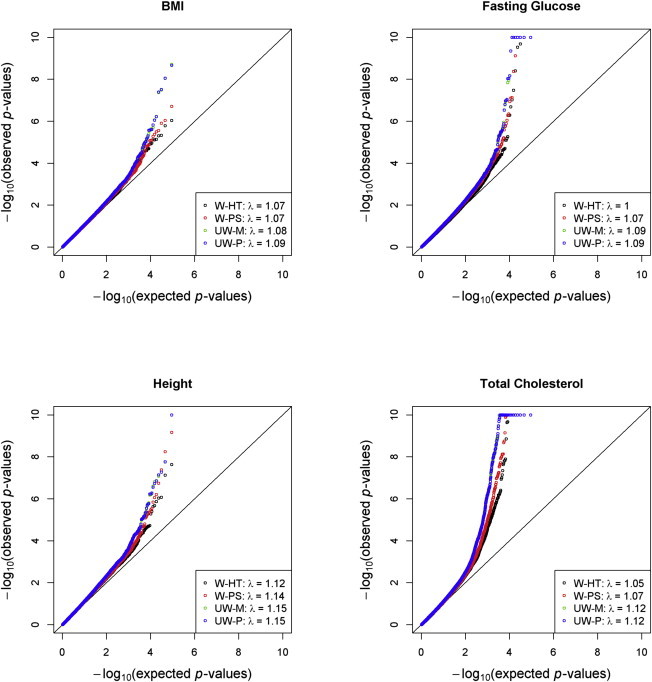
Quantile-Quantile Plots from the Genome-wide Association Analysis of BMI, Fasting Glucose, and Total Cholesterol in the HCHS/SOL

Quantile-quantile plots of −log₁₀(p values) for weighted and unweighted methods with model-based variance estimators are shown. The log-transformation was applied to BMI and total cholesterol, and the inverse normal transformation was applied to fasting glucose. SNPs with MAF < 1% were excluded. Most of the p values are indistinguishable between UW-M and UW-P.

As discussed, if the SNP association with a trait varies with age, then the W-HT estimator still provides unbiased estimation of the overall association in the target population whereas the other estimators are unduly driven by older individuals, who were oversampled in the HCHS/SOL. To demonstrate this phenomenon, we analyzed 28 known BMI loci in the younger age group (18–44 years), the older age group (45–74 years), and the entire cohort (18–74 years); some results are displayed in Figure 6. For the SNP rs2241423, which has similar effect estimates between the younger and older age groups, the four methods yield similar estimates of the overall association. For the other three SNPs shown in Figure 6, the effect estimates in the younger age group are considerably different from those of the older age group. In such cases, the W-HT estimate of the overall association tends to be driven more by the estimate of the younger age group as compared to the UW-M or UW-P estimate because the older age group was oversampled and is thus downweighted by W-HT.

Figure 6.

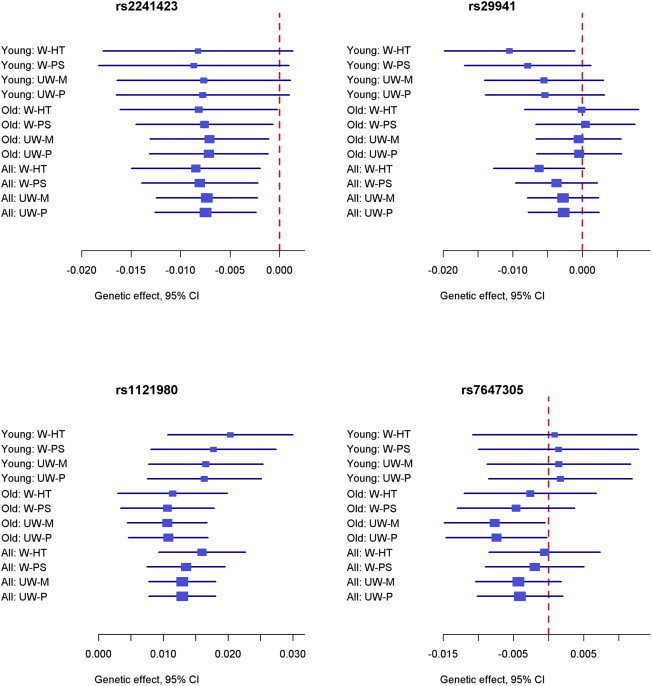
Forest Plots for Four Known BMI Loci in the HCHS/SOL

The effect estimates and 95% confidence intervals for weighted and unweighted methods with robust variance estimators are shown for the younger age group (young), older age group (old), and all individuals (all). The log-transformation was applied to BMI.

Discussion

The cohort design offers many advantages over the case-control design for exploring the genetic basis of complex human diseases and gene-environment interactions. However, cohort studies are exceedingly expensive and time intensive;^1–3 for example, the National Children’s Study has cost $1 billion for the groundwork alone. Thus, it is imperative to analyze cohort studies with the best practices in statistical methodology. Our work is highly relevant to the analysis of existing cohorts, as well as the design and analysis of future cohort studies.

We have presented five methods for genetic association analysis under complex survey sampling. We would not recommend UW-C or UW-P because the conditional association (given the sampling variables or sampling probability) can be quite different from the marginal association, as shown in the simulation studies. The remaining three methods have pros and cons. W-HT correctly controls the type I error and provides unbiased estimation of the overall genetic association in the target population even when the association model is misspecified, as shown by the simulated and empirical data. However, this estimator is inefficient, especially when the sampling weights are highly variable. W-PS also correctly controls the type I error and tends to be more powerful than W-HT, but it does not provide unbiased estimation of the association in the target population under misspecified models. UW-M has the highest power but yields inflated type I error when the sampling is correlated with both the trait of interest and the test SNP. Thus, we recommend UW-M in the discovery stage, especially when there is a plan to confirm significant findings; W-PS should be used if proper control of the type I error is paramount; W-HT should be used if the primary interest lies in unbiased estimation of the association in the target population.

There are two major approaches to handling within-family correlations: mixed and marginal models. The former approach characterizes the dependence of individuals by normal random effects and provides efficient maximum likelihood estimation; the latter formulates the marginal distribution of each individual and accounts for the dependence empirically in the variance estimation. We adopted the latter approach because it does not require modeling the dependence structures and can easily handle any type of trait. For simplicity, we used the independence working correlation matrix. It is possible to improve efficiency by incorporating the kinship relationships into the working correlation matrix.²⁵

The prevailing approach to analysis of survey data is finite-population inference, under which the target population is considered fixed and the only randomness stems from the sampling of individuals from the target population, such that the variance of any estimator would be zero if all individuals in the target population were selected.²⁰ We adopted the super-population approach, under which the target population is considered a random sample from an infinite population and the variance estimation accounts for the variabilities induced by the sampling of individuals from the target population as well as the sampling of the target population from the infinite population.^20,26 For association analysis, super-population inference is more sensible because we are interested in statistical associations rather than finite-population quantities.

Existing survey regression methodology cannot be applied to the HCHS/SOL because endogamous mating induces relatedness of participants among the primary sampling units. To tackle this challenge, we created extended families by connecting the households who shared first-degree relatives, and we accounted for the sampling design in the variance estimation by using pairwise inclusion probabilities. With the super-population approach, pairwise inclusion probabilities appear only in the last terms of $\hat{B}$ and $\tilde{B}$, for individuals from different families. These probabilities are determined by sampling fractions and response rates (see Appendix B). The last terms of $\hat{B}$ and $\tilde{B}$ are small compared to the overall values of $\hat{B}$ and $\tilde{B}$ and thus can be omitted when pairwise inclusion probabilities are not available.

Our work provides several important contributions. First, we developed two weighted estimators that properly account for complex sampling designs and intricate patterns of relatedness. Second, we compared, both theoretically and empirically, the performance of weighted and unweighted estimators in the context of genetic association analysis and offered practical recommendations. Third, we provided a modification to the robust variance estimator that substantially improves the performance of both weighted and unweighted methods for low-frequency SNPs. Fourth, we developed a software program that implements all the methods.

Although Hispanics represent one out of every six people in the U.S., our knowledge about Hispanic health has been limited. The HCHS/SOL seeks to investigate many diseases and conditions of particular importance to the Hispanic/Latino community in the U.S. and to understand risk factors that could lead to improved prevention/intervention strategies in all communities. Several working groups have recently formed to analyze MetaboChip and GWAS data in the HCHS/SOL. Each group has focused on a particular type of trait (e.g., anthropometry, cardiovascular disease, diabetes, lipid, lung function). These groups have adopted our methods and software, and their results will be communicated in future manuscripts.

Our methods are also useful to other complex surveys, such as those mentioned in the Introduction,^4–8 all of which involve multistage cluster sampling with unequal probabilities. In the MONICA Augsburg Surveys, three study populations were recruited in 1984–1985 (subjects aged 25–64 years), 1989–1990 (subjects aged 25–74 years), and 1994–1995 (subjects aged 25–74 years) by a two-stage cluster sampling, with random sampling for the city of Augsburg and a random selection of 16 communities by community size in the two adjacent counties.⁵ NHANES is a four-stage, national area probability survey with fixed sample-size targets for sampling domains defined by race and Hispanic origin, sex, age, and low-income status.⁶ Add Health is a nationally representative longitudinal study of more than 20,000 adolescents in the United States in 1994–1995 who have been followed for 15 years into adulthood, and the design included oversamples of more than 3,000 pairs of individuals with varying genetic resemblance, including monozygotic twins, dizygotic twins, full siblings, half siblings, and unrelated siblings who were raised in the same household.⁷ The NHANES and Add Health data, along with design information and sample weights, are publicly available.

Our article investigates the implications of complex survey sampling in genetic association analysis. There is a growing body of literature on the related issue of extreme-trait sampling.^19,27–33 With extreme-trait sampling, the variance formulas for weighted estimators take simple forms, and efficient likelihood-based methods are available. With complex survey sampling, the variance estimation for weighted estimators is delicate, and the construction of valid and efficient estimators remains an open problem.

Appendix A: Theoretical Properties of Weighted Estimators

For k = 1,..., K and i = 1,..., N_k, let ${\xi }_{ki}$ indicate, by the values 1 versus 0, whether the i^th individual of the k^th family is included in the study, and let π_ki be the corresponding inclusion probability. Then the weighted estimating function can be rewritten as

$$\hat{U}\left(\theta \right)=\sum _{k=1}^K\sum _{i=1}^{N_k}\frac{{\xi }_{ki}}{{\pi }_{ki}}{U}_{ki}\left(\theta \right).$$

Clearly,

$$\hat{U}\left(\theta \right)=\sum _{k=1}^K\sum _{i=1}^{N_k}{U}_{ki}\left(\theta \right)+\sum _{k=1}^K\sum _{i=1}^{N_k}\frac{{\xi }_{ki}-{\pi }_{ki}}{{\pi }_{ki}}{U}_{ki}\left(\theta \right).$$

The two terms on the right side of the above equation are uncorrelated. By the standard central limit theorem, the first term is approximately zero-mean normal with covariance matrix

$$B_1\left(\theta \right)=\sum _{k=1}^K\sum _{i=1}^{N_k}\sum _{j=1}^{N_k}{U}_{ki}\left(\theta \right)U_{kj}^{\prime }\left(\theta \right).$$

By the finite-population central limit theorem,^34–36 the second term is approximately zero-mean normal with covariance matrix

$$B_2\left(\theta \right)=\sum _{k=1}^K\sum _{i=1}^{N_k}\sum _{l=1}^K\sum _{j=1}^{N_l}\frac{{\pi }_{kilj}-{\pi }_{ki}{\pi }_{lj}}{{\pi }_{ki}{\pi }_{lj}}{U}_{ki}\left(\theta \right)U_{lj}^{\prime }\left(\theta \right),$$

where π_kilj is the probability that the i^th member of the k^th family and the j^th member of the l^th family are both included. The covariance matrix of $\hat{U}\left(\theta \right)$ is the sum of B₁(θ) and B₂(θ), which is

$$B\left(\theta \right)=\sum _{k=1}^K\sum _{i=1}^{N_k}\sum _{j=1}^{N_k}\frac{{\pi }_{kij}}{{\pi }_{ki}{\pi }_{kj}}{U}_{ki}\left(\theta \right)U_{kj}^{\prime }\left(\theta \right)+\sum _{k=1}^K\sum _{i=1}^{N_k}\sum _{l\ne k,l=1}^K\sum _{j=1}^{N_l}\frac{{\pi }_{kilj}-{\pi }_{ki}{\pi }_{lj}}{{\pi }_{ki}{\pi }_{lj}}{U}_{ki}\left(\theta \right)U_{lj}^{\prime }\left(\theta \right),$$

where π_kij is the probability that the i^th and j^th members of the k^th family are both included.

A Horvitz-Thompson estimator of B(θ) is

$$\hat{B}\left(\theta \right)=\sum _{k=1}^K\sum _{i=1}^{N_k}\sum _{j=1}^{N_k}\frac{{\xi }_{ki}{\xi }_{kj}}{{\pi }_{ki}{\pi }_{kj}}{U}_{ki}\left(\theta \right)U_{kj}^{\prime }\left(\theta \right)+\sum _{k=1}^K\sum _{i=1}^{N_k}\sum _{l\ne k,l=1}^K\sum _{j=1}^{N_l}\frac{{\xi }_{ki}{\xi }_{lj}\left({\pi }_{kilj}-{\pi }_{ki}{\pi }_{lj}\right)}{{\pi }_{kilj}{\pi }_{ki}{\pi }_{lj}}{U}_{ki}\left(\theta \right)U_{lj}^{\prime }\left(\theta \right).$$

If π_kilj = π_kiπ_lj, then the second term on the right side of the above equation is zero, such that pairwise selection probabilities are not needed.

By the Taylor series expansion, ${\hat{\theta }}_w$ is approximately normal with mean θ and covariance matrix ${\hat{V}}_w={\hat{A}}^{-1}\left({\hat{\theta }}_w\right)\hat{B}\left({\hat{\theta }}_w\right){\hat{A}}^{-1}\left({\hat{\theta }}_w\right)$, where

$$\hat{A}\left(\theta \right)=\sum _{k=1}^K\sum _{i=1}^{N_k}\frac{{\xi }_{ki}}{{\pi }_{ki}}\frac{\partial U_{ki}\left(\theta \right)}{\partial \theta }.$$

If the inclusion probabilities are all equal to 1, then ${\hat{V}}_w$ reduces to the usual covariance matrix estimator for GEE.¹⁷ Replacing $U_{ki}\left(\theta \right)U_{ki}^{\prime }\left(\theta \right)$ in $\hat{B}\left(\theta \right)$ by $-\partial U_{ki}\left(\theta \right)/\partial \theta$ yields

$$\tilde{B}\left(\theta \right)=-\sum _{k=1}^K\sum _{i=1}^{N_k}\frac{{\xi }_{ki}}{{\pi }_{ki}^2}\frac{\partial U_{ki}\left(\theta \right)}{\partial \theta }+\sum _{k=1}^K\sum _{i=1}^{N_k}\sum _{j\ne i,j=1}^{N_k}\frac{{\xi }_{ki}{\xi }_{kj}}{{\pi }_{ki}{\pi }_{kj}}{U}_{ki}\left(\theta \right)U_{kj}^{\prime }\left(\theta \right)+\sum _{k=1}^K\sum _{i=1}^{N_k}\sum _{l\ne k,l=1}^K\sum _{j=1}^{N_l}\frac{{\xi }_{ki}{\xi }_{lj}\left({\pi }_{kilj}-{\pi }_{ki}{\pi }_{lj}\right)}{{\pi }_{kilj}{\pi }_{ki}{\pi }_{lj}}{U}_{ki}\left(\theta \right)U_{lj}^{\prime }\left(\theta \right).$$

The corresponding covariance matrix estimator of ${\hat{\beta }}_w$ is denoted by ${\tilde{V}}_w$. The estimators ${\hat{V}}_w$ and ${\tilde{V}}_w$ are asymptotically equivalent (under correctly specified models), but the latter estimator is more stable and more accurate for low-frequency SNPs. Under misspecified models, ${\hat{V}}_w$ continues to provide valid covariance estimation for ${\hat{\theta }}_w$ whereas ${\tilde{V}}_w$ might not.

Under the linear regression model

$$Y_{ki}={\theta }^{\prime }{X}_{ki}+{\mathit{ϵ}}_{ki},$$

where ${\mathit{ϵ}}_{ki}\sim N\left(0,{\sigma }^2\right)$, we have

$$U_{ki}\left(\theta \right)=\left(1/{\sigma }^2\right)\left(Y_{ki}-{\theta }^{\prime }{X}_{ki}\right)X_{ki},$$

and

$$\partial U_{ki}\left(\theta \right)/\partial \theta =-\left(1/{\sigma }^2\right)X_{ki}{X}_{ki}^{\prime },$$

where σ² is estimated by

$${\hat{\sigma }}^2=\sum _{k=1}^K\sum _{i=1}^{N_k}\frac{{\xi }_{ki}}{{\pi }_{ki}}{\left(Y_{ki}-\widehat{{\theta }^{\prime }}{X}_{ki}\right)}^2/\sum _{k=1}^K\sum _{i=1}^{N_k}\frac{{\xi }_{ki}}{{\pi }_{ki}}.$$

Under the logistic regression model

$$\text{logit}\left\{\mathrm{Pr}\left(Y_{ki}=1\right)\right\}={\theta }^{\prime }{X}_{ki},$$

we have

$$U_{ki}\left(\theta \right)=\left(Y_{ki}-\frac{e^{{\theta }^{\prime }{X}_{ki}}}{1+e^{{\theta }^{\prime }{X}_{ki}}}\right)X_{ki},$$

and

$$\partial U_{ki}\left(\theta \right)/\partial \theta =-\frac{e^{{\theta }^{\prime }{X}_{ki}}}{{\left(1+e^{{\theta }^{\prime }{X}_{ki}}\right)}^2}{X}_{ki}{X}_{ki}^{\prime }.$$

Similar expressions are available for the proportional hazards model with age-at-onset data.²⁶

To improve efficiency of estimation (at the cost of inducing some bias), we trim the marginal inclusion probabilities according to the following formula

$${\pi }_{ki}^{\ast }=\{\begin{array}{ll}{\pi }_0+\left({\pi }_{ki}-{\pi }_0\right)/c_0\hfill & \text{if}{\pi }_{ki}<{\pi }_0,\hfill \\ {\pi }_{ki}\hfill & \text{otherwise},\hfill \end{array}$$ (Equation A1)

where π₀ and c₀ are constants. Likewise, we trim the joint inclusion probabilities as follows

$${\pi }_{kilj}^{\ast }=\frac{{\pi }_{ki}^{\ast }{\pi }_{lj}^{\ast }}{{\pi }_{ki}{\pi }_{lj}}{\pi }_{kilj}.$$

The joint probabilities appear only in the last terms of $\hat{B}$ and $\tilde{B}$. With our trimming strategy,

$$\frac{{\pi }_{kilj}^{\ast }-{\pi }_{ki}^{\ast }{\pi }_{lj}^{\ast }}{{\pi }_{kilj}^{\ast }}=\frac{{\pi }_{kilj}-{\pi }_{ki}{\pi }_{lj}}{{\pi }_{kilj}}.$$

Thus, it is not necessary to explicitly trim the joint probabilities provided that both the trimmed and untrimmed versions of the marginal probabilities are available.

Appendix B: Calculating Inclusion Probabilities for the HCHS/SOL

Suppose that there are a total of G BGs in a given field center. For g = 1,..., G, let K_g denote the number of households in the g^th BG. For g,h = 1,..., G and k,l = 1,..., K_g, we define the following selection probabilities:

$${\pi }_g=\text{probability}\text{of}\text{selecting}\text{the}{\text{g}}^{\text{th}}\text{BG},$$

$${\pi }_{gh}=\text{joint}\text{probability}\text{of}\text{selecting}\text{the}{\text{g}}^{\text{th}}\text{and}{\text{h}}^{\text{th}}\text{BGs},$$

$${\pi }_{k|g}=\text{probability}\text{of}\text{selecting}\text{the}{\text{k}}^{\text{th}}\text{household}\text{from}\text{the}{\text{g}}^{\text{th}}\text{BG},$$

$${\pi }_{kl|g}=\text{joint}\text{probability}\text{of}\text{selecting}\text{the}{\text{k}}^{\text{th}}\text{and}{\text{l}}^{\text{th}}\text{households}\text{from}\text{the}{\text{g}}^{\text{th}}\text{BG}.$$

In the first stage of sampling, BGs were selected by stratified simple random sampling without replacement (SRSWOR). Suppose that there are S strata. For s = 1,..., S, let N_s denote the total number of BGs in the s^th stratum, and n_s the corresponding number of BGs that are selected. Then π_g = n_s / N_s if the g^th BG lies in the s^th stratum. In addition,

$${\pi }_{gh}=\{\begin{array}{ll}\frac{n_s}{N_s}\frac{n_s-1}{N_s-1}\hfill & \text{if}\text{the}{g}^{\text{th}}\text{and}{h}^{\text{th}}\text{BGs}\text{lie}\text{in}\text{the}{s}^{\text{th}}\text{stratum},\hfill \\ \frac{n_s}{N_s}\frac{n_t}{N_t}\hfill & \text{if}\text{the}{g}^{\text{th}}\text{and}{h}^{\text{th}}\text{BGs}\text{lie}\text{in }\text{the}{s}^{\text{th}}\text{and}{t}^{\text{th}}\text{strata},s\ne t.\hfill \end{array}$$

In the second stage, the households were selected by stratified SRSWOR within BGs. Suppose that there are T strata in the g^th BG. For t = 1,..., T, let M_t denote the total number of households in stratum t, and m_t the corresponding number of households that are selected. Then ${\pi }_{k|g}=m_t/M_t$ if the k^th household lies in the t^th stratum. In addition,

$${\pi }_{kl|g}=\{\begin{array}{ll}\frac{m_s}{M_s}\frac{m_s-1}{M_s-1}\hfill & \text{if}\text{the}{k}^{\text{th}}\text{and}{l}^{\text{th}}\text{households}\text{lie}\text{in}\text{the}{s}^{\text{th}}\text{stratum},\hfill \\ \frac{m_s}{M_s}\frac{m_t}{M_t}\hfill & \text{if}\text{the}{k}^{\text{th}}\text{and}{l}^{\text{th}}\text{households}\text{lie}\text{in}\text{the}{s}^{\text{th}}\text{and}{t}^{\text{th}}\text{strata},s\ne t.\hfill \end{array}$$

After sampling at the BG and household levels, independent Bernoulli subsampling was used to oversample individuals 45–74 years of age. Two methods were used: method 1 (used during initial fieldwork) retained with certainty eligible households that contained only 45- to 74-year-old Hispanic/Latino residents and randomly selected all other households; method 2 (used during later fieldwork) divided each household into one or two age subclusters (18–44 versus 45–74 years of age) and selected the older subclusters with certainty and the younger subclusters with lower probabilities. Let ${\pi }_{gk}^{\left(HB\right)}$ denote the probability of selecting the k^th household of the g^th BG under method 1, and let ${\pi }_{u|gk}^{\left(SB\right)}$ denote the probability of selecting the u^th subcluster of the k^th household in the g^th BG under method 2.

Adjustments for nonresponse were made at the household and individual levels. The household-level adjustments were determined by jointly grouping the selected households by center, BG stratum, and household list source (Hispanic surname or not); the individual-level adjustments were determined by a joint grouping of each center’s selected individuals by age group, gender, and Hispanic/Latino background to form adjustment cells. Let r_gk denote the household-level response rate for the k^th household of the g^th BG. For method 1, let p_gki be the individual-level response rate for the i^th individual belonging to the k^th household of the g^th BG; for method 2, let p_gkui be the individual-level response rate for the i^th individual belonging to the u^th subcluster of the k^th household of the g^th BG.

The overall inclusion probabilities are determined by the two-stage stratified SRSWOR and the third-stage Bernoulli subsampling, as well as the household- and individual-level nonresponse. Under method 1, the inclusion probability for the i^th individual belonging to the k^th household of the g^th BG is ${\pi }_g{\pi }_{k|g}{\pi }_{gk}^{\left(HB\right)}{r}_{gk}{p}_{gki}.$ Under method 2, the inclusion probability for the i^th individual belonging to the u^th subcluster of the k^th household of the g^th BG is ${\pi }_g{\pi }_{k|g}{\pi }_{u|gk}^{\left(SB\right)}{r}_{gk}{p}_{gkui}$.

The joint probability of inclusion for a pair of individuals depends on which Bernoulli subsampling method is applied to each member of the pair. Specifically, the joint probability for including the i^th individual belonging to the k^th household of the g^th BG under method 1 and the j^th individual belonging to the v^th subcluster of the l^th household of the h^th BG under method 2 is

$$\{\begin{array}{l}{\pi }_g{\pi }_{kl|g}{\pi }_{gk}^{\left(HB\right)}{\pi }_{v|gl}^{\left(SB\right)}{r}_{gk}{r}_{gl}{p}_{gki}{p}_{glvj}\text{if}g=h,\hfill \\ {\pi }_{gh}{\pi }_{k|g}{\pi }_{l|h}{\pi }_{gk}^{\left(HB\right)}{\pi }_{v|hl}^{\left(SB\right)}{r}_{gk}{r}_{hl}{p}_{gki}{p}_{hlvj}\text{if}g\ne h.\hfill \end{array}$$

Under method 1, the joint probability for including the i^th individual belonging to the k^th household of the g^th BG and the j^th individual belonging to the l^th household of the h^th BG is

$$\{\begin{array}{l}{\pi }_g{\pi }_{k|g}{\pi }_{gk}^{\left(HB\right)}{r}_{gk}{p}_{gki}{p}_{gkj}\text{if}g=h\text{and}k=l,\hfill \\ {\pi }_g{\pi }_{kl|g}{\pi }_{gk}^{\left(HB\right)}{\pi }_{gl}^{\left(HB\right)}{r}_{gk}{r}_{gl}{p}_{gki}{p}_{glj}\text{if}g=h\text{but}k\ne l,\hfill \\ {\pi }_{gh}{\pi }_{k|g}{\pi }_{l|h}{\pi }_{gk}^{\left(HB\right)}{\pi }_{hl}^{\left(HB\right)}{r}_{gk}{r}_{hl}{p}_{gki}{p}_{hlj}\text{if}g\ne h.\hfill \end{array}$$

Under method 2, the joint probability for including the i^th individual belonging to the u^th subcluster of the k^th household of the g^th BG and the j^th individual belonging to the v^th subcluster of the l^th household of the h^th BG is

$$\{\begin{array}{l}{\pi }_g{\pi }_{k|g}{\pi }_{u|gk}^{\left(SB\right)}{r}_{gk}{p}_{gkui}{p}_{gkuj}\text{if}g=h,k=l\text{and}u=v,\hfill \\ {\pi }_g{\pi }_{k|g}{\pi }_{u|gk}^{\left(SB\right)}{\pi }_{v|gk}^{\left(SB\right)}{r}_{gk}{p}_{gkui}{p}_{gkvj}\text{if }g=h,k=l\text{but}u\ne v,\hfill \\ {\pi }_g{\pi }_{kl|g}{\pi }_{u|gk}^{\left(SB\right)}{\pi }_{v|gl}^{\left(SB\right)}{r}_{gk}{r}_{gl}{p}_{gkui}{p}_{glvj}\text{if}g=h\text{but}k\ne l,\hfill \\ {\pi }_{gh}{\pi }_{k|g}{\pi }_{l|h}{\pi }_{u|gk}^{\left(SB\right)}{\pi }_{v|hl}^{\left(SB\right)}{r}_{gk}{r}_{hl}{p}_{gkui}{p}_{hlvj}\text{if}g\ne h.\hfill \end{array}$$

Web Resources

The URLs for data presented herein are as follows:

• Add Health, http://www.cpc.unc.edu/projects/addhealth

• NHANES, http://www.cdc.gov/nchs/nhanes.htm

• Online Mendelian Inheritance in Man (OMIM), http://www.omim.org/

• SUGEN, http://dlin.web.unc.edu/software/SUGEN/