Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Dec 9;4:7391. doi: 10.1038/srep07391

Sequence dependence of electron-induced DNA strand breakage revealed by DNA nanoarrays

Adrian Keller 1,2,*, Jenny Rackwitz 3, Emilie Cauët 4, Jacques Liévin 4, Thomas Körzdörfer 3, Alexandru Rotaru 5, Kurt V Gothelf 1, Flemming Besenbacher 1, Ilko Bald 1,3,6,a
PMCID: PMC4260214  PMID: 25487346

Abstract

The electronic structure of DNA is determined by its nucleotide sequence, which is for instance exploited in molecular electronics. Here we demonstrate that also the DNA strand breakage induced by low-energy electrons (18 eV) depends on the nucleotide sequence. To determine the absolute cross sections for electron induced single strand breaks in specific 13 mer oligonucleotides we used atomic force microscopy analysis of DNA origami based DNA nanoarrays. We investigated the DNA sequences 5′-TT(XYX)3TT with X = A, G, C and Y = T, BrU 5-bromouracil and found absolute strand break cross sections between 2.66 · 10−14 cm2 and 7.06 · 10−14 cm2. The highest cross section was found for 5′-TT(ATA)3TT and 5′-TT(ABrUA)3TT, respectively. BrU is a radiosensitizer, which was discussed to be used in cancer radiation therapy. The replacement of T by BrU into the investigated DNA sequences leads to a slight increase of the absolute strand break cross sections resulting in sequence-dependent enhancement factors between 1.14 and 1.66. Nevertheless, the variation of strand break cross sections due to the specific nucleotide sequence is considerably higher. Thus, the present results suggest the development of targeted radiosensitizers for cancer radiation therapy.

DNA exhibits nucleotide sequence dependent electronic properties, which affect its charge transport properties, UV stability, and sensitivity toward radiation1,2,3. These properties manifest themselves in quantities such as the ionization potential4,5, in the dynamics of the electronic states (excitonic coupling, lifetime of excited states)1,6, but also in the reactivity for instance towards low-energy electrons3,7,8.

A large number of secondary electrons is formed along the radiation track of high-energy radiation, which is routinely applied in radiation therapy to kill tumor tissue. These low-energy electrons (LEEs) have a most probable energy around 10 eV9 and are able to directly induce DNA single and double strand breaks (SSBs and DSBs) via dissociative electron attachment through the formation of negative ion resonances10,11,12. Although it is experimentally extremely challenging to quantify the LEE induced DNA strand break (SB) yield of oligonucleotides of specific nucleotide sequence, a number of studies suggested a sequence dependence of electron-induced DNA strand breakage. In electron transmission through self-assembled DNA monolayers it was demonstrated that the number of electrons trapped in the DNA film depends strongly on the guanine (G) content3. These experiments did not yield any information on the damage of the DNA film, but the SSB yield upon irradiation with 1 eV electrons was later quantified using microarrays of DNA SAMs and fluorescence detection of the hybridisation efficiency7. It was found that the SSB yield increases linearly with the number of G bases present in the oligonucleotide. This behaviour is explained by the relative instability of G compared to the other DNA bases13, which is also reflected in the low ionization potential (IP) of G14. However, in addition to the base-dependent damage, it was also demonstrated that the specific base sequence has a strong effect on the DNA damage. In electron transmission experiments the human telomeric repeat TTAGGG turned out to be particularly prone to LEE capture15. The particular role of the telomere sequence was confirmed by ab initio calculations showing that the IP of a TTAGGG sequence is smaller than the IP of a TTGGGG sequence, although isolated G has a lower IP than A16. Despite the particular role of G it was recently demonstrated by using HPLC analysis of oligonucleotide trimers irradiated with 10 eV electrons, that the total DNA damage was largest for TTT and smallest for TGT8. Nevertheless, the ratio of strand breaks (C-O cleavage) to nucleobase loss (C-N cleavage) was found to be highest for TGT8.

The investigation of LEE induced strand breakage of specific oligonucleotides longer than a few nucleobases is very challenging due to the small penetration depth of LEEs resulting in small amounts of damaged material8. Recently, we demonstrated the detection of LEE-induced bond cleavage in DNA origami based DNA nanoarrays on the single molecule level using atomic force microscopy (AFM)17,18,19. The visualization of DNA strand breakage by AFM using DNA nanoarrays has several advantages: (i) Due to the detection of DNA strand breaks at a single-molecule level only miniscule amounts of material are required to establish sub-monolayer surface coverage. (ii) Two or more different oligonucleotide sequences can be irradiated within a single experiment to efficiently compare a number of different DNA structures. (iii) Absolute strand break cross sections (σSSB) are readily accessible (vide infra) thus providing benchmark values for further experimental and theoretical studies. (iv) The DNA nanoarray technique is not limited to single strands, but can be extended to quantify double strand breaks and to investigate higher-order DNA structures. Here, we compare the absolute strand break cross sections of different 13 mer oligonucleotide sequences. We compare the sequences 5′-TT(XTX)3TT with X = A, C or G to evaluate the role of the different DNA nucleobases for DNA strand breakage. In a next step, we study the sensitizing effect of the incorporation of 5-bromouracil (BrU) by comparing the absolute strand break cross sections of the sequences 5′-TT(XBrUX)3TT with X = A, C or G.

Results and Discussion

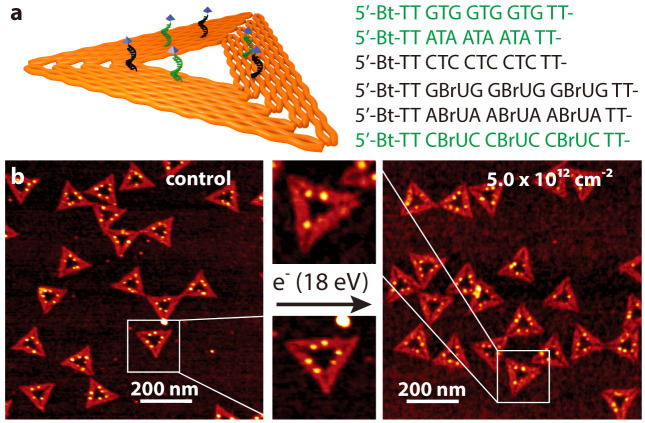
Fig. 1a shows a scheme of a triangular DNA origami platform carrying six target sequences, which represents the DNA nanoarray. Three biotinylated target sequences are situated in the center of the trapezoids, and three are located on the sides of the trapezoids. Basically, the nucleotide sequence of each of the six target oligonucleotides can be freely chosen. In the present study the three central target strands (green in Fig. 1a), and the three side positions (black in Fig. 1a) cannot be distinguished in the AFM images and are hence chosen to have the same sequence. Thus, two different target sequences are studied within one irradiation experiment, and the specific sequences and their positions are indicated in Fig. 1a. In Fig. 1b typical AFM images from DNA origami samples after incubation with streptavidin (SAv) which binds to biotin (Bt) are shown. The left image shows a control sample that was not irradiated while the image on the right was obtained from a sample irradiated with 18 eV electrons at a fluence of 5.0 × 1012 cm−2. The energy of 18 eV was chosen due to its relevance for the damage induced by secondary electrons originating from the ionization track of high-energy radiation. For secondary electrons the damage probability has a global maximum around 18 eV, i.e. the damage induced mainly by ionization and electronic excitation weighted by the LEE distribution in aqueous samples irradiated with high-energy radiation20. In the AFM image on the right-hand side of Fig. 1 the number of specifically bound SAv is reduced compared to the non-irradiated control sample indicating that a number of target sequences have been damaged by electron-induced strand breakage. To determine the absolute cross section for strand breakage (see Methods section), the relative number of SBs (NSB) was recorded as a function of the electron fluence. The fluence dependence of NSB for the target sequences TT(XTX)3TT with X = A, C, G is displayed in Fig. 2a. From the linear fit in the low-fluence regime σSSB is determined, which is shown in Fig. 2b. The oligonucleotide TT(GTG)3TT shows the lowest response to 18 eV electrons. To ensure for an accurate linear fit, a smaller fluence increment and thus more data points were chosen for TT(GTG)3TT.

Figure 1. Illustration of the procedure for determination of absolute cross sections for DNA strand breakage using the DNA origami based DNA nanoarrays.

Figure 1

Open in a new tab

(a) Scheme showing protruding DNA strands of different nucleotide sequence. On the right-hand side the sequences are shown, which are investigated here. Green sequences are placed onto the center of the trapezoids, and black sequences are placed onto the side positions of the trapezoids. (b) After SAv incubation the two positions can be distinguished in AFM images. On the left a typical AFM image of non-irradiated DNA origami samples carrying TT(GTG)3TT and TT(GBrUG)3TT oligonucleotides is shown. On the right, a typical AFM image after irradiation with 18 eV electrons is shown. The number of specifically bound SAv is reduced due to strand breaks in the protruding sequences.

Figure 2. The cross sections for DNA strand cleavage are determined by recording the fluence dependence of the relative number of strand breaks (left) upon irradiation with 18 eV electrons.

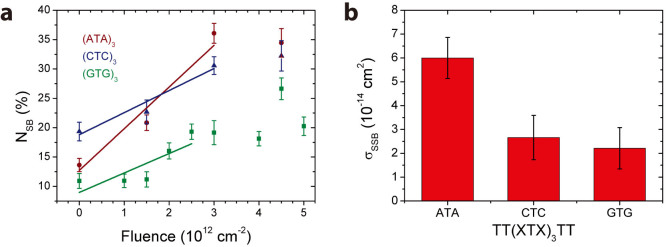
Figure 2

Open in a new tab

On the right the sequence dependence of the strand break cross section is shown. The highest σSSB was observed with the TT(ATA)3TT nucleotide sequence.

In general, there are three basic mechanisms that could account for the electron-induced DNA strand cleavage at 18 eV (in the following the general form TT(XYX)3TT of the DNA sequences is used):

  1. Dissociative ionization: TT(XYX)3TT + e−(18 eV) → [TT(XYX)3TT]+ + 2e− → SB. The cross sections for the first step, electron impact ionization, for isolated nucleobases at 18 eV are of the order of 10−16 cm2,21. For the components of the DNA backbone, i.e. the phosphate group and the deoxyribose sugar, the corresponding cross sections are even slightly higher22.

  2. Dissociative electron attachment (DEA): TT(XYX)3TT + e−(≤18 eV) → TT(XYX)3TT− → SB. Direct electron attachment at 18 eV is very unlikely, but the initial incoming electron might undergo inelastic scattering in the surrounding of the target sequence and might attach at lower energies with higher cross sections. DEA cross sections for instance for the loss of hydrogen from the thymine anion at 1.0 eV have been previously determined to be 7.8 · 10−17 cm2,23. Alternatively, low energy secondary electrons can be generated either from the substrate, or by electron impact ionization according to (i), which can induce a SB by DEA.

  3. Neutral dissociation: TT(XYX)3TT + e−(18 eV) → TT(XYX)3TT** + e−(<18 eV) → SB. The transfer of electronic energy from the incoming electron to the oligonucleotide might be associated with a dissociative state resulting in a SB. The inelastic electron scattering cross section is comparable with the cross section for electron impact ionization and is e.g. for pyrimidine of the order of 10−16 cm2,24. Bond breaking by a catalytic electron is a similar mechanism that involves transient negative ions and neutral fragmentation products25.

Judging from the magnitude of cross sections it is most likely that the initial step in strand breakage is either ionization or electronic excitation of the target strands. For a DNA strand break to occur a bond within the phosphate–sugar backbone needs to be cleaved. A direct SB without the involvement of the nucleobases as it was suggested previously is thus feasible26,27. The IP of the phosphate-sugar backbone is with about 11.7 eV considerably higher than the IPs of the nucleobases, nevertheless electron impact ionization cross sections of the DNA backbone are calculated to be higher than that of the nucleobases due to the higher number of electrons in the sugar-phosphate backbone22.

However, the absolute strand break cross sections determined here (Fig. 2) show a strong dependence on the specific nucleotide sequence with the TT(GTG)3TT sequence having the lowest σSSB and TT(ATA)3TT having the highest σSSB. This indicates that the nucleobases have a strong influence on the strand breakage and a damage mechanism involving only the DNA backbone is not likely.

The absolute cross sections for strand breakage vary from (2.21 ± 0.87) · 10−14 cm2 to (6.00 ± 0.86) · 10−14 cm2 depending on the specific nucleotide sequence (see table 1 for details). The cross sections are comparable with the cross sections found for electron induced strand breakage in plasmid DNA. Boudaiffa et al. found an effective cross section for SSBs at 10 eV electron energy of 2.6 · 10−15 cm2 using the plasmid pGEM 3Zf(−) with 3199 base pairs28. Later, Panajotovic et al. reported effective SSB cross sections of 10.8 · 10−15 cm2 (at 10 eV) and 24.8 · 10−15 cm2 (at 1 eV) using the same plasmid29. Very recently the absolute cross section for loss of supercoiled plasmid DNA was determined at 10 eV to be 3.0 · 10−14 cm2,30, which is in accordance with the values found in the present study. In the previous studies agarose gel electrophoresis has been used to detect SSBs in plasmid DNA. This method and the present DNA nanoarray based method both detect the first SSB that occurs upon electron irradiation. Subsequent SSBs that occur due to the impact of additional electrons are no more detected. Since the geometrical cross sections of DNA with more than a few nucleotides (1 nm2 = 10−14 cm2 corresponds to about three nucleotides) are larger than the SSB cross sections, the reported cross sections should be independent of the size of the system (plasmid DNA vs. oligonucleotides).

Table 1. Absolute strand break cross sections determined for the different oligonucleotide sequences for 18 eV electron irradiation in units of 10−14 cm2. The last row shows the enhancement factors upon BrU incorporation.

  X = A X = C X = G
TT(XTX)3TT 6.00 ± 0.86 2.66 ± 0.93 2.21 ± 0.87
TT(XBrUX)3TT 7.06 ± 2.4 3.04 ± 0.85 3.67 ± 0.90
Enhancement factor 1.18 1.14 1.66
Open in a new tab

The trend of σSSB with respect to the nucleotide sequence is surprising since G containing sequences are generally assumed to be particularly fragile due to the small ionization potential of G. Both, the vertical and adiabatic IPs of the isolated nucleobases increase in the order of G < A < C < T14. A similar order is found for the total electron impact ionization cross sections at low energy (20 eV): G ≈ A > T ≈ C21. The IP can be considered an important quantity in this context since at an energy of 18 eV the electron ionization cross section is presumably orders of magnitude higher than the DEA cross section (vide supra). However, the absolute strand break cross sections found in the present study for the different sequences cannot be explained with the electron impact ionization properties of the individual nucleobases.

The adjacent nucleobases interact via stacking interactions between the aromatic systems, and it was previously found that the strength of π-π interaction depends strongly on the type of nucleobases. Stacking interactions are strongest between the purine bases A and G, and in the case of A nucleobases the stacking interactions further increase by a propeller twist of the A bases. This effect plays also a role for AT base stacks, but is not relevant for GG and GT interactions31. In DFT calculations it was also found that the IP of G stacks decreases more with the number of bases than in the case of A stacks5. Nevertheless it was found that the difference between vertical and adiabatic IP, i.e. the reorganization energy, is smaller for A stacks. A smaller reorganization energy facilitates hole delocalization. On the other hand the large nuclear reorganization energy results in hole localization in G stacks5. This is consistent with the observation that G stacks act as hole traps in DNA.

In order to find out whether the nucleotide sequences studied here give rise to specific modifications of their electronic structure we have computed the IPs of stacked oligonucleotide trimers. The IPs obtained with two different theoretical methods (MP2 and GW) are presented in Table 2. According to the results obtained by MP2 calculations the ATA stack has an IP of 8.01 eV, which is indeed lower than the IP of the GTG stack (8.19 eV) and thus does not follow the same trend as the IPs of the isolated nucleobases14. The vertical IP of isolated A is about 0.4 eV higher than that of isolated G14. Nevertheless the IP of the ATA stack is 0.18 eV lower than the IP of GTG according to the MP2 calculations, which is a considerable shift compared to what is expected from the isolated nucleobases. According to the GW method, however, the trend of IPs reflects the trend observed for the isolated nucleobases, i.e. the GTG stack has the lowest IP (7.96 eV). This difference between MP2 and GW method might be explained when considering also the excited states of the system by means of CASPT2. A detailed comparison of the MP2 and GW methods is presented in the supporting information. As a consequence, a correlation of the observed absolute strand break cross sections and the computed IPs for the stacked trimers is not straight-forward. Here it should be noted that in the calculations only a single conformation of the stacked trimers is considered and environmental effects are not included. Furthermore, the experimental SB cross sections are determined for oligonucleotide 13 mers, but due to limited computing resources we could only consider the trimers listed in table 2. Consequently, further detailed investigations have to be performed on complex systems to elucidate possible connections between the sequence-dependence of strand breakage and the respective IPs.

Table 2. Ionization potentials (in eV) of stacked nucleobase trimers calculated by two different methods (MP2 and GW).

  ATA CTC GTG ABrUA CBrUC GBrUG
MP2 8.01 8.58 8.19 8.52 8.60 8.19
GW 8.11 8.40 7.96 8.14 8.43 7.97
Open in a new tab

A particular role of the electronic states of A containing oligonucleotides was found already in previous studies. It was demonstrated that due to electronic coupling between A molecules in an A homopolymer excitons in the VUV (190 nm) spectral region are extended over up to eight nucleobases6. However, the electronic coupling can be eliminated by a single T spacer32. On the other hand, by using HPLC analysis of oligonucleotide trimers irradiated with 10 eV electrons the damage due to strand breaks was found to increase in the row of sequences TCT ≈ TGT < TAT, which is consistent with the trend of σSSB values determined here33.

5-Bromouracil (BrU) is a well-known radiosensitizer, whose incorporation into DNA by replacing T increases the SSB and DSB yields upon irradiation with electrons and photons34,35,36. We have studied the effect of BrU incorporation on the strand break cross sections by using the sequences discussed above and replacing the three central T bases by BrU. The absolute strand break cross sections determined for 18 eV electron irradiation are shown in Fig. 3a. Again, the TT(ABrUA)3TT sequence exhibits the highest σSSB, whereas the TT(CBrUC)3TT sequence has the lowest σSSB. There is only a small difference between TT(CBrUC)3TT and TT(GBrUG)3TT, but the cross section of TT(ABrUA)3TT is about twice as high as that of TT(CBrUC)3TT. The exact values of σSSB of the different sequences are summarized in Table 1.

Figure 3.

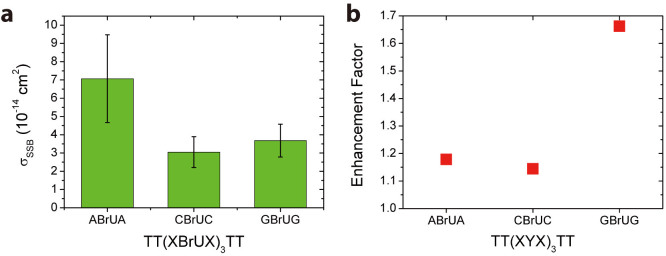
Figure 3

Open in a new tab

(a) DNA strand break yields of similar sequences as shown above (Figure 2), only the central T bases have been replaced by BrU. The incorporation of BrU leads to a slight increase in σSSB, but the A containing sequence remains the most fragile one. (b) The enhancement factor is displayed, which is largest for the G containing sequences. The results indicate that the variation of σSSB due to different nucleotide sequences is stronger than the enhancement upon BrU incorporation.

The similarity of σSSB for oligonucleotides with and without BrU indicates that σSSB is much more sensitive to the nucleotide sequence than to the presence of BrU. The influence of BrU on σSSB might be higher at lower electron energies, since DEA to gas phase BrU shows the highest cross sections for Br− formation close to zero eV37.

In Table 2 the computed IPs of the BrU containing stacked trimers are listed. With both methods of calculation, MP2 and GW, the same trend of IPs is observed, i.e. the IP of GBrUG is the lowest and CBrUC is the highest. There are basically no differences between the IPs of stacked trimers with and without BrU. The only exception is the IP of AYA calculated by MP2, which is 8.01 eV for Y = T, and 8.52 eV for Y = BrU.

Fig. 3b shows the enhancement factors for BrU incorporation (EF = σSSB(XTX)/σSSB(XBrUX)), which are found to be the highest for TT(GYG)3TT (1.66) and the lowest for TT(CYC)3TT (1.14), see Table 1 for details. Thus, the effect of BrU incorporation is highest when BrU is directly adjacent to G. In a recent study using femtosecond laser spectroscopy, the observation of anionic transients suggested that the effect of BrU should be the strongest in close proximity to A. A similar effect but slightly weaker was inferred to G, since G was assumed to be the major damaging site38. However, in this particular study, only mixtures of BrdU and dAMP/dGMP were investigated instead of oligonucleotides so that no information about the occurrence of strand breaks could be obtained. In contrast, we directly probe σSSB of different oligonucleotide sequences in our experiments.

In a recent study using HPLC analysis of trimers irradiated with 10 eV electrons it was found that the total damage of TBrUT was about 50% higher than that of TTT. However, most of the damage was associated with formation of TUT39. In another study using the same technique it was found that the amount of fragments associated with strand breaks is approximately the same for TBrUT and TUT, i.e. no increase of strand breaks was observed with TBrUT33. Therefore, when comparing our results with previous studies, the different sequences, lengths of oligonucleotides and the electron energy must be taken into account. The present study represents a starting point for a global assessment of the sequence dependence of LEE induced DNA damage, for which a large number of DNA sequences at a range of electron energies must be studied in the future. The DNA nanoarray technique is suitable for that since different oligonucleotides can be probed in a single irradiation experiment and absolute strand break cross sections serving as benchmark values are obtained.

Conclusions

We have determined the absolute cross sections for DNA single strand breakage induced by 18 eV electrons using DNA origami based DNA nanoarrays. Since the analysis of irradiated samples is performed by atomic force microscopy at a single molecule level this novel method represents a simple way to access absolute strand break cross sections. The absolute single strand break cross sections depend strongly on the nucleotide sequence and we find values varying between (2.21 ± 0.87) · 10−14 cm2 and (6.00 ± 0.86) · 10−14 cm2 for the oligonucleotide sequences TT(XTX)3TT with X = A, C, G. Furthermore, we find that exchange of the central T bases by 5-bromouracil increases the strand break cross section in a sequence-dependent manner by a factor of 1.14 to 1.66.

The observed trend in the absolute strand break cross sections agrees qualitatively with previous HPLC studies investigating the fragmentation of oligonucleotide trimers of the sequence TXT with X = A, C, G irradiated with 10 eV electrons33. As in the here presented results, the authors observed almost identical yields of strand break fragments for the C- and G-containing trimers while the yield for the A-containing trimer was about twice as high. In addition, the absolute strand break cross sections measured here are comparable in magnitude with cross sections for strand breakage in different plasmid DNAs induced by 1–10 eV electrons as determined by agarose gel electrophoresis29,30. The DNA nanoarray technique thus bridges the gap between genomic dsDNA several kbp in size and very short oligonucleotides only few nt long, and enables the detailed investigation of sequence-dependent processes in DNA radiation damage. The observed sequence-specificity most likely results from the modification of electronic states by electronic coupling of the individual nucleobases. The sensitivity of the A containing sequences might be associated with the strong stacking interactions and pronounced hole delocalization in adjacent A bases. Further experimental and theoretical studies will be carried out covering a broad range of electron energies and DNA sequences to elucidate the most relevant damage mechanisms.

The present results suggest that radiosensitizers applied in tumor radiation therapy could operate more efficiently if they targeted specific nucleotide sequences that have the highest damage cross sections. Further extended experiments have to be performed to explore the electron energy dependence of radiosensitization and thus the physico-chemical mode of action of established and potential radiosensitizers40,41.

Methods

Preparation of DNA nanoarrays

Triangular DNA origami nanostructures have been prepared from the circular single-stranded viral DNA scaffold strand M13mp18 and 208 short artificial staple strands according to the original design and procedure by Rothemund42. Selected staple strands have been extended with a specific target sequence and a Bt modification at the 5′-end. The extended staple strands form a nanoscale array, and the individual target sequences can be visualized with AFM after incubation with SAv, which binds to the Bt modifications of the intact protruding strands. For each irradiation experiment two different target sequences have been selected and in total 6 staple strands per DNA origami structure have been modified (see Fig. 1).

The DNA origami structures are assembled by annealing of the scaffold strand with a 30-fold excess of staple stands from 65°C to 4° within approximately 2 hours (1 × TAE buffer, 10 mM MgCl2). The excess staple strands are separated from the assembled DNA origami structures by spinfiltering twice using Amicon Ultra centrifuge filters (100.000 Da MWCO).

Electron irradiation and AFM analysis

The detailed procedure of immobilization and LEE irradiation of the DNA nanoarrays is given in ref. 17. In brief, the DNA origami structures are bound electrostatically to Si/SiO2 by incubation in 10 × TAE and 100 mM MgCl2 for approximately one hour. Afterwards, the dry samples are transferred into ultrahigh vacuum (UHV), and irradiated with LEEs of defined fluence at a current of 1–10 nA. After irradiation the samples are removed from the UHV chamber and rinsed to remove fragmentation products. To identify the intact remaining target sequences the samples are exposed to a 50 nM solution of SAv for about 2–10 minutes. Then the solution is rinsed again and the dry samples are analysed by AFM. From the AFM images the relative number of DNA strand breaks of a given sequence NSB can be determined from the number of intact oligonucleotides after electron irradiation compared to the initial number of oligonucleotides prior to irradiation (i.e. three oligonucleotides per DNA origami triangle). From NSB the sequence-specific absolute cross section for strand breakage can be determined.

The cross section for DNA damage can be described by the following exposure-response relation29:

graphic file with name srep07391-m1.jpg

with N0 being the initial number of DNA oligonucleotides protruding from the DNA origami platform, σ the cross section for DNA damage, J the electron flux and t the irradiation time. The number of strand breaks NSB (i.e. the relative number of damaged oligonucleotides: 1 – N(t)/N0) can be approximated for short irradiation times by using a Taylor series:

graphic file with name srep07391-m2.jpg

with F = Jt being the electron fluence. Thus, the cross section σ can be determined from the slope of NSB(F) in the low-fluence regime. The determined cross section can be conceived as an absolute cross section since it is based on single molecule measurements, i.e. it is not effective for a specific DNA density or film thickness. The obtained absolute strand break cross sections are corrected for electron-induced damage to the biotin label, which was previously determined to be (1.1 ± 0.2) · 10−14 cm2 18.

To support the presented data the absolute strand break cross section for brominated sequences was determined also in a second, different design of DNA nanoarrays (see supporting information), and the obtained σSSB values agree with the ones shown here.

Calculation of IPs

The ground-state geometries of all the investigated structures (i.e. XTX and XBrUX with X = C, A and G) were first optimized in the gas phase at the density functional theory (DFT) level of theory using the B97-D functional43 and a 6-31+G(d,p) polarized basis set. Frequency calculations for each derivative have been performed with the same level of theory, verifying that all structures correspond to true minima of the potential energy surface. IPs were calculated using spin-restricted open-shell second-order Møller-Plesset perturbation theory (MP2)44 and a 6-311++G(d,p) basis set. Vertical IPs were obtained for all structures from the difference in total energy between the neutral species and the radical cation and anion, respectively, evaluated at the optimized geometry of the neutral species. All MP2 calculations have been achieved with the Gaussian 09 program suite. In addition, we employed many-body perturbation theory calculations in the GW approximation45,46. GW is considered as one of the most accurate electronic structure method for the calculation of charged excitations (such as IPs) feasible for the systems studied in this work. All GW calculations were performed in FHIaims47 using the consistent starting point scheme48 and a converged basis set (tier 4). More details on the calculations are provided in the SI.

Author Contributions

A.K. and I.B. designed and performed the experiments, analyzed the data and wrote the manuscript. J. R. was involved in AFM imaging and data analysis. E.C., J.L. and T.K. performed calculations. A.R. was involved in DNA origami design and synthesis. K.G. and F.B. advised on the research. All authors commented on the manuscript.

Supplementary Material

Supplementary Information

Supporting Information

srep07391-s1.doc (1.1MB, doc)

Acknowledgments

We thank Jakob Bach Knudsen for preparing the Scheme of the DNA origami triangle. This research was supported by a Marie Curie FP7 Integration Grant within the 7th European Union Framework Programme, by the Deutsche Forschungsgemeinschaft (DFG), the University of Potsdam, the Alexander von Humboldt Foundation, and the Danish National Research Foundation (DNRF81) and the Danish Research Agency. A.R. acknowledges financial support from the European Union's Seventh Framework Programme (FP7/2007–2013) under grant agreement n°264115 - STREAM. E.C. and J.L. thank the Communauté Française de Belgique (ARC contract).

References

  1. Crespo-Hernandez C. E., Cohen B. & Kohler B. Base stacking controls excited-state dynamics in A-T DNA. Nature 436, 1141 (2005). [DOI] [PubMed] [Google Scholar]
  2. Sidorov A. N. & Orlando T. M. Monolayer Graphene Platform for the Study of DNA Damage by Low-Energy Electron Irradiation. J. Phys. Chem. Lett. 4, 2328 (2013). [DOI] [PubMed] [Google Scholar]
  3. Ray S. G., Daube S. S. & Naaman R. On the capturing of low-energy electrons by DNA. Proc. Natl. Acad. Sci. U. S. A. 102, 15 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Rooman M. & Wintjens R. Sequence and conformation effects on ionization potential and charge distribution of homo-nucleobase stacks using M06-2X hybrid density functional theory calculations. J. Biomol. Struct. Dyn. 32, 532 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Kumar A. & Sevilla M. D. Density Functional Theory Studies of the Extent of Hole Delocalization in One-Electron Oxidized Adenine and Guanine Base Stacks. J. Phys. Chem. B 115, 4990 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Nielsen L. M., Hoffmann S. V. & Nielsen S. B. Electronic coupling between photo-excited stacked bases in DNA and RNA strands with emphasis on the bright states initially populated. Photochem. Photobiol. Sci. 12, 1273 (2013). [DOI] [PubMed] [Google Scholar]
  7. Solomun T., Seitz H. & Sturm H. DNA Damage by Low-Energy Electron Impact: Dependence on Guanine Content. J. Phys. Chem. B 113, 11557 (2009). [DOI] [PubMed] [Google Scholar]
  8. Li Z. J., Cloutier P., Sanche L. & Wagner J. R. Low-Energy Electron-Induced DNA Damage: Effect of Base Sequence in Oligonucleotide Trimers. J. Amer. Chem. Soc. 132, 5422 (2010). [DOI] [PubMed] [Google Scholar]
  9. Pimblott,. Simon M. & LaVerne,. Jay A. Production of low-energy electrons by ionizing radiation. Radiat. Phys. Chem. 76, 1244 (2007). [Google Scholar]
  10. Boudaiffa B. et al. Resonant formation of DNA strand breaks by low-energy (3 to 20 eV) electrons. Science 287, 1658 (2000). [DOI] [PubMed] [Google Scholar]
  11. Huels M. A. et al. Single, double, and multiple double strand breaks induced in DNA by 3-100 eV electrons. J. Amer. Chem. Soc. 125, 4467 (2003). [DOI] [PubMed] [Google Scholar]
  12. Baccarelli I. et al. Electron-induced damage of DNA and its components: Experiments and theoretical models. Phys. Rep.-Rev. Sec. Phys. Lett. 508, 1 (2011). [Google Scholar]
  13. Schyman P. & Laaksonen A. On the effect of low-energy electron induced DNA strand break in aqueous solution: A theoretical study indicating guanine as a weak link in DNA. J. Amer. Chem. Soc. 130, 12254 (2008). [DOI] [PubMed] [Google Scholar]
  14. Cauët E., Dehareng D. & Liévin J. Ab initio study of the ionization of the DNA bases: Ionization potentials and excited states of the cations. J. Phys. Chem. A 110, 9200 (2006). [DOI] [PubMed] [Google Scholar]
  15. Markus T. Z. Daube S. S. & Naaman R. Cooperative Effect in the Electronic Properties of Human Telomere Sequence. J. Phys. Chem. B 114, 13897 (2010). [DOI] [PubMed] [Google Scholar]
  16. Cauët, Emilie Unique Hole-Trapping Property of the Human Telomere Sequence. J. Biomol. Struct. Dyn. 29, 557 (2011). [DOI] [PubMed] [Google Scholar]
  17. Keller A. et al. Probing Electron-Induced Bond Cleavage at the Single-Molecule Level Using DNA Origami Templates. ACS Nano 6, 4392 (2012). [DOI] [PubMed] [Google Scholar]
  18. Keller A., Kopyra J., Gothelf K. V. & Bald I. Electron-induced damage of biotin studied in the gas phase and in the condensed phase at a single-molecule level. New J. Phys. 15, 083045 (2013). [Google Scholar]
  19. Bald I. & Keller A. Molecular Processes Studied at a Single-Molecule Level Using DNA Origami Nanostructures and Atomic Force Microscopy. Molecules 19, 13803 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Alizadeh E. & Sanche L. Precursors of Solvated Electrons in Radiobiological Physics and Chemistry. Chem. Rev. 112, 5578 (2012). [DOI] [PubMed] [Google Scholar]
  21. Mozejko P. & Sanche L. Cross section calculations for electron scattering from DNA and RNA bases. Rad. Environ. Bioph. 42, 201 (2003). [DOI] [PubMed] [Google Scholar]
  22. Vinodkumar M. et al. Electron impact total ionization cross sections for all the components of DNA and RNA molecule. Int. J. Mass Spectrom. 339, 16 (2013). [Google Scholar]
  23. Kopyra J., Koenig-Lehmann C. & Illenberger E. On the absolute value for the cross-section of dissociative electron attachment (DEA) to the DNA base thymine. Int. J. Mass Spectrom. 281, 89 (2009). [Google Scholar]
  24. Masin Z. et al. Elastic and inelastic cross sections for low-energy electron collisions with pyrimidine. J. Chem. Phys. 136, 14 (2012). [DOI] [PubMed] [Google Scholar]
  25. Davis D., Vysotskiy V. P., Sajeev Y. & Cederbaum L. S. Electron Impact Catalytic Dissociation: Two-Bond Breaking by a Low-Energy Catalytic Electron. Angew. Chem. Int. Ed. 50, 4119 (2011). [DOI] [PubMed] [Google Scholar]
  26. Bald I., Dabkowska I. & Illenberger E. Probing Biomolecules by Laser-Induced Acoustic Desorption: Electrons at Near Zero Electron Volts Trigger Sugar-Phosphate Cleavage. Angew. Chem. Int. Ed. 47, 8518 (2008). [DOI] [PubMed] [Google Scholar]
  27. Cauët E. et al. Electron-Attachment-Induced DNA Damage: Instantaneous Strand Breaks. J. Phys. Chem. B 117, 9669 (2013). [DOI] [PubMed] [Google Scholar]
  28. Boudaiffa B. et al. Cross sections for low-energy (10–50 eV) electron damage to DNA. Radiat. Res. 157, 227 (2002). [DOI] [PubMed] [Google Scholar]
  29. Panajotovic R. et al. Effective cross sections for production of single-strand breaks in plasmid DNA by 0.1 to 4.7 eV electrons. Radiat. Res. 165, 452 (2006). [DOI] [PubMed] [Google Scholar]
  30. Boulanouar O. et al. Absolute cross section for loss of supercoiled topology induced by 10 eV electrons in highly uniform/DNA/1,3-diaminopropane films deposited on highly ordered pyrolitic graphite. J. Chem. Phys. 139, 5 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Sponer J. et al. Nature of base stacking: Reference quantum-chemical stacking energies in ten unique B-DNA base-pair steps. Chem. Eur. J. 12, 2854 (2006). [DOI] [PubMed] [Google Scholar]
  32. Nielsen L. M., Holm A. I. S., Hoffmann S. V. & Nielsen S. B. Effect of introducing thymine spacers into an adenine strand: Electronic decoupling? J. Photochem. Photobiol. A-Chem. 220, 1 (2011). [Google Scholar]
  33. Park Y. et al. Fundamental Mechanisms of DNA Radiosensitization: Damage Induced by Low-Energy Electrons in Brominated Oligonucleotide Trimers. J. Phys. Chem. B 116, 9676 (2012). [DOI] [PubMed] [Google Scholar]
  34. Kinsella T. J., Dobson P. P., Mitchell J. B. & Fornace A. J. Enhancement of X-Ray-Induced DNA Damage by Pretreatment with Halogenated Pyrimidine Analogs. Int. J. Radiat. Oncol. Biol. Phys. 13, 733 (1987). [DOI] [PubMed] [Google Scholar]
  35. Iliakis G., Kurtzman S., Pantelias G. & Okayasu R. Mechanism of Radiosensitization by Halogenated Pyrimidines - Effect of BrdU on Radiation Induction of DNA- and Chromosome-Damage and its Correlation with Cell Killing. Radiat. Res. 119, 286 (1989). [PubMed] [Google Scholar]
  36. Cecchini S. et al. Single-strand-specific radiosensitization of DNA by bromodeoxyuridine. Radiat. Res. 162, 604 (2004). [DOI] [PubMed] [Google Scholar]
  37. Abdoul-Carime H., Huels M. A., Illenberger E. & Sanche L. Sensitizing DNA to Secondary Electron Damage: Resonant Formation of Oxidative Radicals from 5-Halouracils. J. Amer. Chem. Soc. 123, 5354 (2001). [DOI] [PubMed] [Google Scholar]
  38. Wang C. R. & Lu Q. B. Molecular Mechanism of the DNA Sequence Selectivity of 5-Halo-2′-Deoxyuridines as Potential Radiosensitizers. J. Amer. Chem. Soc. 132, 14710 (2010). [DOI] [PubMed] [Google Scholar]
  39. Li Z. J., Cloutier P., Sanche L. & Wagner J. R. Low-Energy Electron-Induced Damage in a Trinucleotide Containing 5-Bromouracil. J. Phys. Chem. B 115, 13668 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Kopyra J., Keller A. & Bald I. On the role of fluoro-substituted nucleosides in DNA radiosensitization for tumor radiation therapy. Rsc Advances 4, 6825 (2014). [Google Scholar]
  41. Chomicz L., Furmanchuk A., Leszczynski J. & Rak J. Electron induced single strand break and cyclization: a DFT study on the radiosensitization mechanism of the nucleotide of 8-bromoguanine. Phys. Chem. Chem. Phys. 16, 6568 (2014). [DOI] [PubMed] [Google Scholar]
  42. Rothemund P. W. K. Folding DNA to create nanoscale shapes and patterns. Nature 440, 297 (2006). [DOI] [PubMed] [Google Scholar]
  43. Grimme S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 27, 1787 (2006). [DOI] [PubMed] [Google Scholar]
  44. Headgordon M., Pople J. A. & Frisch M. J. MP2 Energy Evaluation by Direct Methods. Chem. Phys. Lett. 153, 503 (1988). [Google Scholar]
  45. Hedin L. New Method for Calculating 1-Particle Greens Function with Application to Electron-Gas Problem. Phys. Rev. 139, A796 (1965). [Google Scholar]
  46. Hybertsen M. S. & Louie S. G. Electron Correlation in Semiconductors and Insulators - Band Gaps and Quasi-Particle Energies. Phys. Rev. B 34, 5390 (1986). [DOI] [PubMed] [Google Scholar]
  47. Blum V. et al. Ab initio molecular simulations with numeric atom-centered orbitals. Comput. Phys. Commun. 180, 2175 (2009). [Google Scholar]
  48. Korzdorfer T. & Marom N. Strategy for finding a reliable starting point for G(0)W(0) demonstrated for molecules. Phys. Rev. B 86. 041110 (2012). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supporting Information

srep07391-s1.doc (1.1MB, doc)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES