Quantification of Myocardial Blood Flow in Absolute Terms u27sing ⁸²Rb PET Imaging: Results of RUBY-10—a multicenter study comparing ten computer analysis programs

Abstract

Objective

To compare myocardial blood flow (MBF) and myocardial flow reserve (MFR) estimates from 82Rb PET data using ten software packages (SPs): Carimas, Corridor4DM, FlowQuant, HOQUTO, ImagenQ, MunichHeart, PMOD, QPET, syngo MBF, and UW-QPP.

Background

It is unknown how MBF and MFR values from existing SPs agree for 82Rb PET.

Methods

Rest and stress 82Rb PET scans of 48 patients with suspected or known coronary artery disease (CAD) were analyzed in 10 centers. Each center used one of the 10 SPs to analyze global and regional MBF using the different kinetic models implemented. Values were considered to agree if they simultaneously had an intraclass correlation coefficient (ICC) > 0.75 and a difference < 20% of the median across all programs.

Results

The most common model evaluated was the one-tissue compartment model (1TCM) by Lortie et al. (2007). MBF values from seven of the eight software packages implementing this model agreed best (Carimas, Corridor4DM, FlowQuant, PMOD, QPET, syngoMBF, and UW-QPP). Values from two other models (El Fakhri et al. in Corridor4DM and Alessio et al. in UW-QPP) also agreed well, with occasional differences. The MBF results from other models (Sitek et al. 1TCM in Corridor4DM, Katoh et al. 1TCM in HOQUTO, Herrero et al. 2TCM in PMOD, Yoshida et al. retention in ImagenQ, and Lautamäki et al. retention in MunichHeart) were less in agreement with Lortie 1TCM values.

Conclusions

SPs using the same kinetic model, as described in Lortie et al. (2007), provided consistent results in measuring global and regional MBF values, suggesting they may be used interchangeably to process data acquired with a common imaging protocol.

Introduction

Measuring myocardial blood flow (MBF) in absolute terms with PET is nowadays possible in clinical routine practice (1). These measurements at rest and under stress can be completed fast (2,3), and the reconstructed dynamic images can be analyzed in few minutes by the majority of the available software packages (4). The analysis produces left ventricle (LV) absolute MBF values measured in mL/min/g at rest and under stress as well as the myocardial flow reserve (MFR)—the ratio of stress to rest MBF expressed as a unitless number. These values provide unique information regarding diagnosis and monitoring of coronary artery disease (CAD), micro-vascular health (5), multi-vessel CAD (6), and risk stratification (7). Although recent studies have shown the diagnostic and prognostic value of MBF quantification over the standard relative image analysis (6,8,9), and use of the generator-produced rubidium-82 (⁸²Rb) (10,11) has brought MBF quantification closer to clinic, its integration into clinical routine practice remains under-utilized (5).

To convert imaging data to quantitative MBF parameters, measured radioactivity concentration values need to be transformed into milliliters of blood per minute per gram of myocardial tissue (mL/min/g) by applying tracer kinetic modeling to dynamic PET images. Thus, any numerical value that any professional receives from ⁸²Rb PET is a result of this transformation. At least eight different models have been proposed (12-19) for ⁸²Rb. Although deKemp et al. (20) and Tahari et al. (21) had addressed the reproducibility of ⁸²Rb PET analysis methods for MBF quantification, they had focused on a limited number of methods; therefore, a comprehensive comparison study was needed to analyze the current situation in ⁸²Rb PET quantification to help establish common and robust methods to support collaborative multi-center clinical trials.

The objective of the RUBY project was to compare all currently available software packages that can analyze ⁸²Rb PET MBF studies. The criteria for inclusion were the presence of the software in the peer-reviewed literature and the willingness of the development team to collaborate according to same ground rules, including blind analysis of the same selected patient data sets. The ten software packages compared in the present study were Carimas (22), Corridor4DM (23), FlowQuant (24), HOQUTO (19), ImagenQ (25), MunichHeart (16), PMOD (26), QPET (26), syngo.MBF (26), and UW-QPP (18) (for the detailed treatment see The evaluated software packages in the Appendix; for the side-by-side comparison of the packages, see Table 1 in Saraste et al., 2012 (4)).

Table 1.

The eight kinetic models implemented in ten software packages of RUBY-10

	Retention		One-tissue compartment				Two-tissue compartment	Axially-distributed
	Yoshida et al. 1996	Lautamaki et al. 2009	Sitek et al. 2000	Lortie et al. 2007	El Fakhri et al. 2009	Katoh et al. 2012	Herrero et al.1992	Alessio et al 2013
Carimas				+
Corridor4DM			+	+	+
FlowQuant				+
HOQUTO						+
ImagenQ	+			+
MunichHeart		+
PMOD				+			+
QPET				+
syngo MBF				+
UW-QPP				+				+

Materials and methods

Image Acquisition

All ⁸²Rb PET studies were performed at the Department of Nuclear Medicine of the University Hospital of Lausanne (Switzerland), according to the routine clinical practice. The study protocol was approved by the local ethics committee. Written informed consent was obtained from each patient prior to the study. Forty-eight patients with suspected or known CAD underwent rest and adenosine-induced stress ⁸²Rb PET. Patients were studied after an overnight fast and were instructed to refrain from caffeine- or theophylline-containing products or medications for 24 h before the ⁸²Rb PET study. During the study, patients were instructed to breathe normally (for the detailed treatment of the PET image acquisition see the Appendix).

Image analysis

The reconstructed rest and stress images were delivered to 10 facilities located in 10 centers across seven countries. Each investigator used one software package and, by the rules of this project, had been blinded to results of the image analysis of the other readers before they shared their results (see Appendix for details of the Study design).

In general, all the 10 packages implemented variations of a one-tissue-compartment model (1TCM) (28). Seven packages implemented the modification of 1TCM suggested by Lortie et al. in 2007 (14). An eighth package (ImagenQ-Lortie) also used the Lortie et al. 1TCM, however with a shorter 2.5-minute dynamic sequence (8x12s, 2x27s) interpolated from the original image data. Additionally, one SP—UW-QPP—implemented an axially-distributed blood flow model (18), and another—PMOD—used a two-tissue-compartment model (2TCM) (12) (Table 1). The image analysis process in all the packages consisted of image reorientation, segmentation—of both LV myocardium and cavity—and tracer kinetic modeling. Several packages enabled automatic reorientation and segmentation; other depended on the operator to influence segmentation of regions where modeling would be done (See The evaluated software packages in the Appendix for the details of image analysis process).

Image analysis resulted in estimated values for three parameters: rest MBF, stress MBF and MFR on global and regional levels. Global presented the average LV value, and regional presented values for the three vascular territories in the regions of coronary arteries: the left anterior descending (LAD), left circumflex (LCx) and right coronary artery (RCA). The vascular territories were in agreement with the 17-segment AHA standard model (29).

Statistical analysis

The large number of models compared prohibited use of standard approaches to measure agreement between two methods (30), so, a custom linear mixed model for the repeated measures (31) was applied to the dataset. The statistical model output included two main agreement metrics—intraclass correlation coefficient (ICC) and difference between the values from the implemented kinetic models—both calculated pairwise. The pairwise agreement between models we considered sufficient if the difference was less than 20% of the median across all programs, and with the corresponding ICC being equal to or greater than 0.75. The criteria for ICC was based on (32), and the difference greater than the predefined 20% standard. We also expressed the values as a percent of corresponding medians to demonstrate the scale of differences.

The paired t-test (Microsoft Excel 2013) was used to evaluate the differences between hemodynamic parameters of patients at rest and at pharmacological stress.

Biplot analysis

To visualize the large number of results of the RUBY-10 comparisons, we developed a custom biplot, relating the two defined metrics—the differences and the ICC values of compared pairs. In this plot the X-axis shows pairwise differences between the model values and the Y-axis shows corresponding pairwise values of 1 minus ICC. In this biplot the origin (x=0 and y=0) is the point of identity between the compared values, where there is no difference and the intraclass correlation is equal to 1. Thus, values further from the origin are less in agreement: either showing increasing difference or reduced ICC. The predefined criteria of agreement were defined as a rectangular region on the biplot. Thus, this biplot visualizes in an intuitive way our predefined criteria of agreement— the pairs inside of these borders were considered to have high pre-defined agreement.

Results

Patient characteristics and hemodynamics

The study population demographic and hemodynamic characteristics are in Table 2. During the pharmacological stress test, heart rate increased (P<0.001) while blood pressure (BP) showed a mild decrease (P<0.05); resulting in a rate pressure product (RPP) net increase (P<0.01). All 48 patients—also the one with 70/30 mm Hg stress BP—tolerated the stress test well.

Table 2.

Patient characteristics

Number of subjects	48
Number of males (% of total)	35 (73%)
Age, yrs. (range)	63±12.7 (33-87)
Weight, kg (range)	79± 15.3 (48-116)
Body mass index, kg/m2 (range)	27.0±4.78 (16.0-41.7)
Symptoms	36 (75%)
Angina	28 (58%)
Dyspnoea	27 (56%)
Family history of cardiovascular disease	14 (29%)
Known CAD	24 (50%)
Previous myocardial infarction	15(31%)
Received procedures	20 (42%)
Coronary artery bypass graft surgery	5 (10%)
Percutaneous coronary intervention	17 (35%)
Hypercholesterolaemia	29 (60%)
Arterial hypertension	38 (79%)
Diabetes mellitus	10 (21%)
Currently smoking or ex-smoker	28 (58%)
Hemodynamics at rest
Heart rate, beats/min (range)	76±17.0 (49-135)
Systolic blood pressure, mm Hg (range)	136±22.3 (94-212)
Diastolic blood pressure, mm Hg (range)	71±13.3 (46-110)
Rate pressure product, mm/min (range)	10400±2870 (6000-18900)
Hemodynamics at pharmacological stress
Heart rate, beats/min (range)	85±15.6* (48-135)
Systolic blood pressure, mm Hg (range)	131±21.1† (70-183)
Diastolic blood pressure, mm Hg (range)	68±15.1† (30-115)
Rate pressure product, mm/min (range)	11200±2870‡ (6100-21600)

Values are number (%) or arithmetic mean ± SD

^*p<0.001 vs. rest

^†p<0.05 vs. rest

^‡p<0.01 vs. rest

Absolute values of MBF at rest and during adenosine stress and MFR

Average MBF and MFR values (Table 3) showed marked variation between models. Differences (at P<0.0001) between highest and lowest values for any studied parameter were always greater than a factor of 1.5 times. For rest MBF the ratios between extreme values were 1.7 globally, and ~1.8 regionally; for stress MBF the ratios ranged from 1.9 globally to ~2.2 regionally; for MFR the ratios were 1.5 globally and ranged from 1.9 to 2.3 regionally.

Table 3.

Myocardial blood flow and myocardial flow reserve (MFR) values

	Global			LAD			LCx			RCA
	Rest	Stress	MFR	Rest	Stress	MFR	Rest	Stress	MFR	Rest	Stress	MFR
Carimas (Lortie et al. 2007)	1.11±0.36	2.38±1.04	2.18±0.82	1.12±0.38	2.31±1.09	2.10±0.87	1.08±0.33	2.30±0.92	2.17±0.75	1.16±0.42	2.86±1.32	2.54±1.07
Corridor4DM (El Fakhri et al., 2009)	1.08±0.48	2.40±1.10	2.42±1.16	1.13±0.49	2.40±1.07	2.32±1.05	1.10±0.48	2.39±1.11	2.37±1.16	1.02±0.50	2.46±1.24	2.74±1.75
Corridor4DM (Lortie et al., 2007)	1.23±0.38	2.58±0.97	2.17±0.78	1.31±0.39	2.57±0.91	2.05±0.71	1.20±0.36	2.45±0.94	2.10±0.75	1.20±0.49	2.82±1.28	2.52±1.23
Corridor4DM (Sitek et al., 2000)	1.69±0.61	3.57±1.37	2.23±0.89	1.79±0.63	3.55±1.28	2.10±0.80	1.64±0.59	3.41±1.34	2.20±0.89	1.63±0.70	3.81±1.71	2.57±1.33
ImagenQ (Lortie et al., 2007)	1.22±0.58	2.32±0.99	2.02±0.75	1.23±0.58	2.35+1.04	2.02±0.71	1.23±0.64	2.27±1.00	1.98±0.76	1.19±0.58	2.33±1.00	2.10±0.88
ImagenQ (Yoshida et al., 1996)	1.01±0.38	1.85±0.67	1.93±0.71	1.00±0.39	1.80±0.70	1.90±0.69	1.03±0.43	1.84±0.73	1.89±0.68	1.03±0.37	1.94±0.68	2.01±0.82
FlowQuant (Lortie et al. 2007)	1.08±0.38	2.35±1.05	2.29±0.98	1.05±0.39	2.29±1.06	2.29±0.99	1.13±0.42	2.32±1.02	2.29±0.99	1.08±0.39	2.48±1.16	2.39±1.13
HOQUTO (Katoh et al., 2012)	1.43±0.49	2.11±0.71	1.58±0.84	1.45±0.28	1.66±0.36	1.19±0.44	1.47±0.32	1.64±0.35	1.18±0.45	1.48±0.32	1.67±0.40	1.19±0.52
MunichHeart (Lautamaki et al., 2009)	1.13±0.37	2.19±0.89	2.06±0.77	1.16±0.37	2.23±0.91	2.05±0.79	1.12±0.41	2.08±0.93	1.99±0.82	1.11±0.37	2.24±0.87	2.13±0.74
PMOD (Herrero et al., 1992)	1.15±0.38	2.22±1.18	1.98±0.85	1.23±0.47	2.34±1.30	1.99±1.01	1.23±0.37	2.51±1.45	2.06±0.96	0.96±0.40	1.79±1.14	2.02±1.18
PMOD (Lortie et al., 2007)	1.16±0.35	2.62±1.00	2.29±0.74	1.23±0.38	2.60±1.03	2.17±0.70	1.10±0.33	2.40±0.92	2.23±0.74	1.14±0.38	2.88±1.23	2.60±1.05
QPET (Lortie et al., 2007)	1.14±0.30	2.51±0.84	2.30±0.75	1.20±0.31	2.53±0.87	2.18±0.73	1.13±0.29	2.38±0.82	2.18±0.70	1.06±0.33	2.61±0.92	2.61±1.05
syngo MBF (Lortie et al., 2007)	1.22±0.38	2.57±0.95	2.23±0.81	1.27±0.39	2.60±1.01	2.14±0.83	1.17±0.37	2.42±0.91	2.19±0.79	1.19±0.45	2.68±1.00	2.46±1.05
UW-QPP (Alessio et al., 2013)	0.97±0.35	2.12±0.93	2.25±0.94	1.06±0.41	2.14±0.92	2.11±0.84	0.93±0.32	1.96±0.85	2.18±0.92	0.90±0.35	2.28±1.17	2.65±1.39
UW-QPP (Lortie et al., 2007)	1.20±0.37	2.42±0.89	2.09±0.76	1.30±0.43	2.46±0.87	1.96±0.67	1.14±0.34	2.22±0.81	2.02±0.75	1.10±0.40	2.58±1.13	2.48±1.19
Max/Min ratio	1,7	1,9	1,5	1,8	2,1	1,9	1,8	2,1	2,0	1,8	2,3	2,3
Average (all models)	1.19±0.45	2.41±1.04	2.14±0.86	1.23±0.46	2.39±1.06	2.04±0.83	1.18±0.44	2.31±1.03	2.06±0.85	1.15±0.47	2.49±1.22	2.33±1.18
99% CI	1.15-1.23	2.31-2.51	2.05-2.22	1.19-1.28	2.29-2.49	1.96-2.12	1.14-1.22	2.21-2.41	1.98-2.14	1.10-1.19	2.38-2.61	2.22-2.45
Median (all models)	1.11	2.20	2.01	1.16	2.16	1.94	1.11	2.08	1.94	1.06	2.27	2.14
Interquartile range (Q3-Q1)	1.44-0.87	3.00-1.67	2.55-1.51	1.48-0.90	2.98-1.61	2.48-1.43	1.44-0.86	2.90-1.57	2.52-1.44	1.43-0.80	3.14-1.62	2.84-1.48

Values are mean ± SD (n = 48); Average, 99% Confidence Interval (CI), Median values, and Interquartile range are calculated for n = 720. Minimum (Min) and maximum (Max) values in each column are in bold.

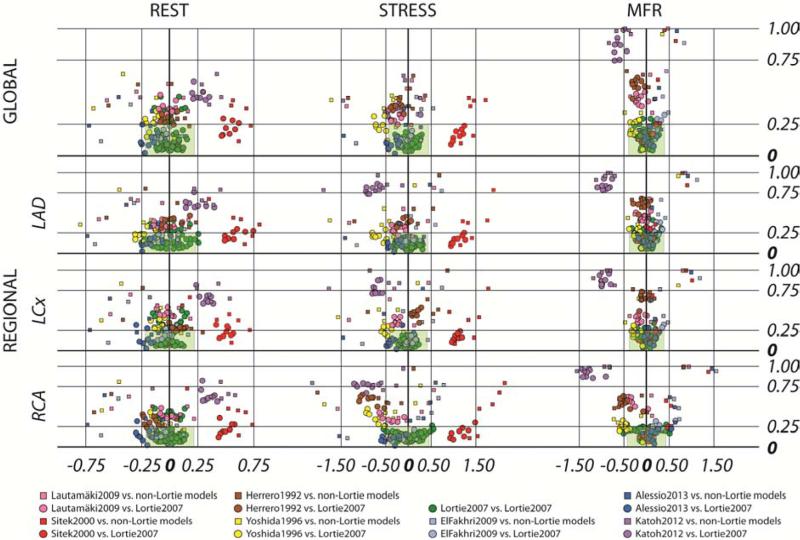
Agreement of global LV MBF measurements

The biplots (Figure 1) demonstrated several consistent patterns. The first pattern was that Lortie et al. (14) implementations (green elements) in eight software packages tended to concentrate close to the origin. The second pattern was that Katoh et al. (19) implemented in HOQUTO (purple elements) provided results that differed greatly from other models on all studied levels for both MBF and MFR. The third pattern was that Sitek et al. (17) implemented in Corridor4DM (red elements) provided MBF values much higher than the others, both at rest and stress. Note also that Yoshida et al. (13) implemented in ImagenQ (yellow elements) was within the predefined difference limits globally at rest (up to 19.8% of the median), but showed higher values for stress (up to 35.0% of the median) and for MFR (up to 24.5%).

Figure 1. Cross-comparison of results from all implemented models in 10 software tools.

The X-axis for REST and STRESS is difference in MBF values (mL/min/g), for MFR in unitless ratios; Y-axis is always 1-ICC. The x-range of the shaded green area represents ± 20% of the median value

Agreement of regional LV MBF measurements

Regional values generally showed larger differences; up to 41.5% of the median for RCA. Also, over half (60%) of ICC values did not fulfill the predefined criteria for agreement. Lautamäki et al. (16) as implemented in MunichHeart (pink elements) was within the predefined limits globally for MBF and MFR values, also regionally in the LAD and LCX, but had somewhat larger differences in RCA (up to 28.5%), and almost all (97%) of the ICC values did not fulfill the criteria of agreement.

Herrero et al. (12) implemented in PMOD (brown elements) exhibited similar pattern to the Lautamäki model: all the global differences were below the predefined limit, as well as the regional differences except for the RCA values, which were up to 48.3% of the median, yet again almost all the ICC values (97%) did not fulfill the criteria of agreement.

Differences using El Fakhri et al. (15) as implemented in Corridor4DM (light blue elements) were within the predefined limits globally and regionally, with the exception of MFR in the RCA where the difference was 30.0% of the median. ICC values in 38% of comparisons were below predefined limits; however, discarding Yoshida, Lautamäki and Herrero models, ICC values fulfilled the agreement criteria in 80% of remaining comparisons.

Differences between Alessio model (18), as implemented in UW-QPP, and the other models were generally within the predefined limits, yet occasionally were above: 23.5% of the median at rest and 22.5% at stress on the global level. Differences for MFR were low, yet in RCA, the difference was 25.7% of the median comparing to ImagenQ. Almost all (95%) of the ICC values were > 0.75.

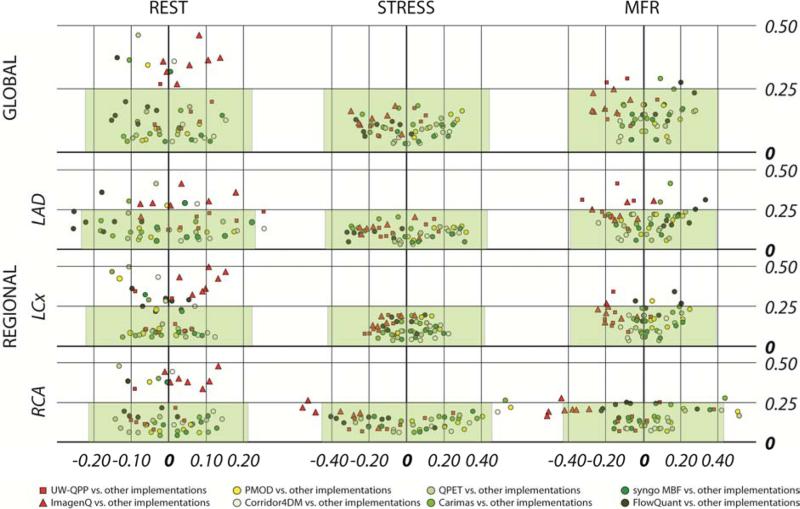
Agreement of LV MBF measurements for Lortie 1TCM

Since the Lortie model (14) was the most commonly applied model in the evaluated software packages, specific biplots for inter-Lortie comparisons were created and are displayed in Figure 2, red elements demonstrate the implementations of the model in UW-QPP (red squares) and ImagenQ (red triangles) that were added later to the RUBY project. Globally, all the stress differences were well within the pre-defined limits of agreement < 20% of the median value, and the majority of rest differences were also within this limit (except for the ICC values comparing with ImagenQ-Lortie). Similar patterns were observed regionally: the majority of stress MBF values were well within the predefined limits. However, in general, regional differences seemed to be larger in the RCA region. Values of the largest differences between implementations of the 1TCM of Lortie et al. (14) are shown in Table 4.

Figure 2. Cross-comparison of results from implemented Lortie models in eight software tools.

The X-axis for REST and STRESS is difference in MBF values (mL/min/g), for MFR in unitless ratios; Y-axis is always 1-ICC. The x-range of the shaded green area represents ± 20% of the median value.

Table 4.

Largest differences between software packages implementing Lortie et al. (2007)

		Difference (absolute)†	Difference (percent of median	SW name	SW name	at P value	ICC
GLOBAL	Rest	0.15	13.7	C4DM	FQ	0.0008	0.874
	Stress	0.30	13.5	PMOD	ImagenQ	0.0019	0.837
	MFR	0.28	13.7	QPET	ImagenQ	0.0068	0.835
LAD	Rest	0.25	22.0*	C4DM	FQ	<0.0001	0.869
	Stress	0.32	14.7	PMOD	FQ	0.0020	0.892
	MFR	0.33	17.0	FQ	UWQPP	0.0010	0.689
LCx	Rest	0.15	13.7	ImagenQ	C2	0.0016	0.533
	Stress	0.22	10.8	C4DM	UWQPP	0.0356	0.922
	MFR	0.25	12.6	PMOD	ImagenQ	0.0134	0.768
RCA	Rest	0.14	13.5	C4DM	QPET	0.0039	0.854
	Stress	0.56	24.5**	PMOD	ImagenQ	<0.0001	0.782
	MFR	0.51	24.0	QPET	ImagenQ	0.0001	0.834

^†Differences between MBF values are in units of mL/min/g; differences between MFR are in unitless ratios

^*In LAD there are two values > 20% of the corresponding median, both involving FQ

^**In RCA (both stress and MFR) there are three values > 20%; all three involve ImagenQ.

Discussion

RUBY-10 is the first and currently the only study aimed at comparing all existing software tools—used both in clinical cardiology and in research setting—for analyzing MBF and MFR with the most widely used cardiac PET tracer—⁸²Rb.

The positive finding of our study is that the 1TCM model described by Lortie et al. (14)— commonly found in most PET analysis programs—provided results generally close enough to be used interchangeably, if dynamic time binning protocols are the same. We must emphasize that without an absolute reference standard—such as microsphere data—we cannot infer the diagnostic or quantitative accuracy any of the methods considered. Despite this, our results do demonstrate that applying the same kinetic model to the same ⁸²Rb PET data, the received MBF and MFR values are independent of the software package within the specified agreement tolerances.

The negative finding is that different kinetic models currently used in ⁸²Rb PET produce different values for the same PET data. The finding is not new: in 2005, Khorsand et al. found differences comparing 1TCM with 2TCM for ¹³N-ammonia PET (33). New is the magnitude of possible differences: in the referred study, global differences were up to 13% for MBF and up to 26% for MFR, our results demonstrate that for ⁸²Rb PET global differences can be up to 90% for MBF and 50% for MFR. Regional differences can be up to 130% for both MBF and MFR.

The causes of differences can vary. In some cases, smoothing of the data can result in higher MBF (34) for factor-analysis-based methods such as Sitek et al. (17) and El Fakhri et al. (15) in Corridor4DM, and minimal filtering is recommended for improved MBF estimates. In other, the difference in prompt-gamma corrections (PGC) for ⁸²Rb between the PET-CT scanner used to perform the current study and the PET studies used originally to develop HOQUTO could be the cause of the difference (35). Notwithstanding the causes, the practical implication is clear: values of MBF or MFR presented without reference to the kinetic model cannot be directly compared, neither for pooling of patient data, nor for following up same patients.

Two metrics, derived from our statistical model, were used to indicate the agreement—ICC and differences between the compared MBF and MFR values. The benefit of using ICC was clear: it avoids the limitation of standard correlation coefficients—often met in comparison studies— when a linear relationship is mistaken for agreement. However, like other correlation coefficients, ICC depends on the range of variables measured, and this can explain its lower value for rest MBF and MFR compared to stress. The choice of limits of agreement is critical, and for ICC we used recommended (32) values—a cutoff for excellent agreement at over 0.75. For the differences, the choice of appropriate limit is not that straightforward, and we chose to use <20% difference in studied parameters as acceptable, as it is similar to the test-retest repeatability of 20-25% for rest MBF and MFR reported recently using ⁸²Rb PET (36). Increasing the number of compared models geometrically increases the results, which makes the analysis and display of these results challenging. For the measured global and regional values there were 2520 differences (210*(3+9)) and 1260 ICC values; listing all these values is impractical. The biplot binds these values, and with predefined cutoffs informs on the relative agreement of the model results. Therefore, the developed biplots enabled to handle the complexity of the data inherent in a cross-comparison of this scale.

The analysis of a dynamic PET scan goes through several steps—reorientation, myocardial segmentation, selection of the input function, kinetic modeling, and polar plot generation—each of which could significantly affect the results. We designed our study to simulate the clinical routine practice as much as possible and treated the workflow inside each software package as a “black box” being only interested in input—the patient PET images—and the output—the results in milliliters (MBF) or ratio units of MFR. As all the studied software packages were operated either by their developers or under their close supervision, we believe that the tools were used appropriately.

Limitations

The most significant limitation of this study is that there was no gold standard used and thus no claim of quantitative accuracy of a particular model can be inferred by these results. Another consideration is that the ImagenQ analysis used interpolated dynamic image frames to produce a dataset compatible with this implementation of the Lortie model. The shortened dynamic sequence used by ImagenQ may tend to exaggerate any differences from later uptake and washout frames that were used by the other Lortie models. Lastly, one of the limitations of the study can be considered the fact that one software tool, ImagenQ, was added after the preliminary results had been already received. The same approach led to inclusion of the two Lortie models: UW-QPP and ImagenQ, which were implemented after receiving preliminary (study average) results of RUBY. These decisions were made for the sake of comprehensiveness since it would have been practically impossible to repeat the study de novo, so we chose to include these analyses in the primary results. However, these analyses were still performed blinded to the individual results of the other software programs.

We do not consider a limitation the fact that we used only ⁸²Rb data coming from one centre, acquired on one scanner, reconstructed with one algorithm, etc., because introducing these new variables into our combinatorial study would have lead to practical impossibility to carry out the project.

Conclusions

Myocardial blood flow and myocardial flow reserve values obtained by ⁸²Rb PET must be interpreted together with information on their computational origin. The most important such information may not be the software program used to obtain these values, but rather the mathematical tracer kinetic model implemented within the software. The most widely implemented model for ⁸²Rb PET is the one-tissue-compartment model published by Lortie et al. (2007) available in eight software tools out of the studied ten. When different implementations of this kinetic model are used to analyze the same data, the results appear to be independent of the particular software program utilized. The quantitative blood flow results agree well between these analysis programs and may be used interchangeably for the benefit of large multi-center trials.

Abbreviations list

1TCM

one-tissue-compartment model

CAD

coronary artery disease

ICC

intraclass correlation coefficient

LAD

left anterior descending artery

LCx

left circumflex artery

LV

left ventricle

MBF

myocardial blood flow

MFR

myocardial flow reserve

RCA

right coronary artery

SP

software package