Abstract
The depauperate marine ecosystems of the Hawaiian Archipelago share a high proportion of species with the southern and western Pacific, indicating historical and/or ongoing connections across the large oceanic expanse separating Hawaii from its nearest neighbors. The rate and direction of these interactions are, however, unknown. While previous biogeographic studies have consistently described Hawaii as a diversity sink, prevailing currents likely offer opportunities for larval export. To assess interactions between the remote reefs of the Hawaiian Archipelago and the species rich communities of the Central and West Pacific, we surveyed 14 nuclear microsatellite loci (nDNA; n = 857) and a 614 bp segment of mitochondrial cytochrome b (mtDNA; n = 654) in the Yellow Tang (Zebrasoma flavescens). Concordant frequency shifts in both nDNA and mtDNA reveal significant population differentiation among three West Pacific sites and Hawaii (nDNA F′CT = 0.116, mtDNA ϕCT = 0.098, P < 0.001). SAMOVA analyses of microsatellite data additionally indicate fine scale differentiation within the 2600 km Hawaiian Archipelago (F′SC = 0.026; P < 0.001), with implications for management of this heavily-exploited aquarium fish. Mismatch analyses indicate the oldest contemporary populations are in the Hawaiian Archipelago (circa 318,000 y), with younger populations in the West Pacific (91,000 – 175,000 y). Estimates of Yellow Tang historical demography contradict expectations of Hawaii as a population sink, and instead indicate asymmetrical gene flow, with Hawaii exporting rather than importing Yellow Tang larvae.
Keywords: Acanthuridae, larval dispersal, larval retention, marine connectivity phylogeography, stock assessment
INTRODUCTION
The marine fauna of Hawaii is considerably less diverse than that of the tropical West and South Pacific but includes many of the same species (Randall 1998, Mundy 2005). Community similarities indicate the possibility of ongoing connections between the geographically remote Hawaiian Archipelago and the broader Indo-Pacific, but the rate of connectivity is difficult to assess. The broad distribution of many species similarly limits the identification of dispersal corridors and the directionality of colonization (Hourigan & Reese 1987, Jokiel 1987, Craig et al. 2010). Nevertheless, Hawaii’s marine fauna is widely regarded as a biogeographic “dead end”, with diversity flowing into but not out of the islands (Hourigan & Reese 1987, Jokiel 1987, Kay & Palumbi 1987, Randall 1998, Briggs 1999).
Dispersal corridors
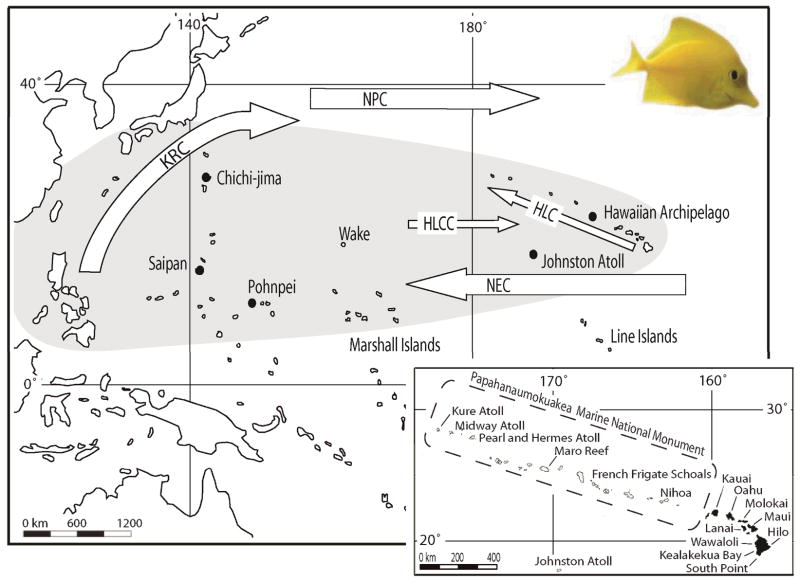
Affinities between reef fish communities in Hawaii and southern Japan have prompted the suggestion of larval exchange via the Kuroshio Current (KRC) and the North Pacific Current (NPC; Randall 1998), which encounters Kure and Midway Atoll in the recently established Papahânaumokuâkea Marine National Monument (PMNM; Figure 1). Sister taxa for two of Hawaii’s three endemic butterflyfishes (family Chaetodontidae) occur only in the West Pacific (including southern Japan), indicating likely colonization via the NPC (Craig et al. 2010). Drogues released off Japan have made their way to the PMNM (McNalley et al. 1983), though the drogues required more than a year to make the journey, which is far longer than most species’ pelagic larval duration (PLD). Formation of a land bridge between Taiwan and the southern Ryukyu Islands of Japan during recent glacial maxima deflected the Kuroshio Current eastward (Ujiie et al. 2003), potentially reducing travel time to Hawaii. Alternatively, dispersal may be aided by juvenile rafting with flotsam (Jokiel 1987, Randall 2007).
Figure 1.
Yellow Tang (Zebrasoma flavescens) collection sites. Sampling locations are identified with closed dots. Hawaiian sampling sites are detailed in the inset. Major currents are abbreviated as follows: KRC, Kuroshio Current; NPC, North Pacific Current; HLC, Hawaiian Lee Current; HLCC, Hawaiian Lee Counter Current; and NEC, North Equatorial Current. Collections were made from June 2004 to July 2005.
Dispersal to Hawaii may also occur along the eastward flowing Hawaiian Lee Countercurrent (HLCC), which attains speeds of up to 8 cm s−1 (Kobashi & Kawamura 2002) as it flows past Wake Atoll and northern portions of the Marshall Islands before terminating near Johnston Atoll, 800 km southwest of the Hawaiian archipelago (Figure 1). Johnston Atoll has been proposed as a link between Hawaii and other Central Pacific communities (Kobayashi 2006), though faunal affinities and recent genetic studies indicate Johnston is more likely an outpost of Hawaii rather than a link to the broader Pacific (Hourigan & Reese 1987, Skillings et al. 2011, Timmers et al. 2011). Johnston Atoll’s apparent inability to facilitate dispersal to Hawaii may be because dispersal to Johnston Atoll via the Hawaiian Lee Countercurrent is prohibitively long, and like contemporary dispersal via the North Pacific Current, would require a minimum journey of nearly a year (Kobayashi & Kawamura 2002).
The Line Islands, 1800 km south of Hawaii (Figure 1), have also been proposed as source for larvae dispersing to the archipelago (Myers 1989) and occasional strays and migrants have been observed (Randall 2007). Nonetheless, opportunities for exchange between the Line Islands and Hawaii are likely rare because of the need to cross the broad, fast and westward flowing North Equatorial Current (NEC), which regularly attains speeds greater than 25 cm s−1, and sometimes exceeds 60 cm s−1 (Kashino et al. 2009). These velocities are well beyond maximum sustainable swimming speeds for reef fishes (Fisher et al. 2005). Moreover, unlike the Southern Equatorial Current which can experience dramatic inter-annual changes in current velocity and direction in response to El Niño/La Niña conditions (Johnston & Merrifield 2000), the North Equatorial Current is considerably more stable, slowing only slightly during La Niña (Qui & Joyce 1992, Kashino et al. 2009).
While the consistency and velocity of the North Equatorial Current would appear to limit opportunities for larval exchange with the Line Islands, these same features may facilitate downstream export of Hawaiian born larvae (Jokiel & Martinelli 1992, Connolly et al. 2003). Anti-cyclonic eddies forming off the leeward shore of Hawaii Island have been recorded travelling as far west as the Marshall Islands under the influence of the NEC (Calil et al. 2008) and larvae from a diverse set of near shore taxa have been found entrained within the eddies (Lobel & Robinson 1988). The minimum estimated travel time along the NEC is 70 days, which is considerably shorter than dispersal estimates for other proposed corridors, and is within estimated larval durations for many fishes- particularly when considering the potential for many taxa to extend their pelagic period in the absence of suitable substrate (e.g. Toonen & Pawlik 2001) and that larval behavior may further reduce travel time (Fisher 2005, Cowen & Sponaugle 2009).
Genetic insights into larval dispersal
Recent phylogeographic assessments of Pacific reef fishes have revealed that larvae at least occasionally bridge Hawaii’s isolation (Craig et al. 2007, Reece et al. 2010, Eble et al. 2011). Connectivity rates and directionality have not explicitly been assessed, with one exception, a recently published survey of range-wide patterns of gene flow in the widely distributed Rubylipped Parrotfish (Scarus rubrioviolaceus) which revealed intriguing evidence of larval dispersal from Hawaii to reefs in the Central Pacific (Fitzpatrick 2010). Additional support for larval export from Hawaii can be found in the Bullethead Parrotfish (Chlorurus sordidus), which revealed Hawaiian derived mitochondrial lineages in West Pacific populations (Bay et al. 2004). Here we employ a multi-locus, range-wide genetic survey of the Indo-Pacific reef fish, the Yellow Tang (Zebrasoma flavescens) to assess connectivity patterns across the northern tropical and subtropical Pacific. A previous survey of Yellow Tang mitochondrial DNA (mtDNA) variation within the Hawaiian Archipelago revealed no population subdivisions (ϕCT = 0.001, P = 0.38; Eble et al. 2009), indicating the potential for high rates of population connectivity across long distances. We build on the previous mtDNA survey with range-wide coverage, larger sample sizes, and the inclusion of 14 microsatellite loci developed for Yellow Tang (Christie & Eble, 2009).
Yellow Tang are abundant reef herbivores in Hawaii (Walsh 1987, Tissot et al. 2004) but also occur in lower numbers throughout the tropical and subtropical North Pacific (Randall 1998). Juveniles and adults are relatively sessile (Claisse et al. 2009, Williams et al. 2009), restricting inter-population connectivity to the estimated 55 day planktonic larval phase (determined by otolith microdissection; Basch et al. 2003). In Hawaii, Yellow Tang comprise approximately 85% of the ornamental fish harvest, with an estimated 300,000 juveniles collected annually (Tissot & Hallacher 2003). Accordingly, one of the rationales for the recent establishment of the 360,000 km2 PMNM is that the region’s uninhabited islands and atolls may be an important source of larvae for the depleted reefs of the main Hawaiian Islands (MHI; McClanahan & Mangi 2000).
METHODS
Sample collection
To identify patterns of genetic structure and connectivity at multiple spatial scales, we sampled juvenile and adult Yellow Tang throughout its range, resulting in 857 fish from 19 locations (Fig. 1, Table 1). Previous collections from Hawaii and Johnston Atoll (Eble et al. 2009; n = 560) were supplemented with 297 additional specimens from the same locations, as well as collections at three locations in the West Pacific (Chichi-jima, Saipan, and Pohnpei). Hawaiian collections spanned the full 2600 km of the archipelago and included six sites within the newly established PMNM and nine sites within the MHI, including four sites on the largest island in the archipelago, Hawaii Island. Collections were made with pole-spears while using SCUBA, or snorkeling. Tissue specimens (fin clips) were stored in a saturated salt-dimethylsulfoxide (DMSO) buffer (Seutin et al. 1991), and total genomic DNA was extracted using a standard salting out protocol (Sunnucks & Hales, 1996).
Table 1.
Yellow Tang collection sites with sample size (N) for mtDNA sequencing (mtDNA) and microsatellite genotyping (nDNA). Haplotype diversity (h), nucleotide diversity (π, allelic richness (A) standardized for sample size, and observed (HO) and expected heterozygosity (HE) with standard deviations in parentheses.
| N | |||||||
|---|---|---|---|---|---|---|---|
| Site | mtDNA | nDNA | h | π | A | HO | HE |
| Chichi | 32 | 36 | 0.85 (0.06) | 0.003 (0.002) | 9.95 | 0.79 (0.02) | 0.84 (0.02) |
| Sai. | 33 | 35 | 0.85 (0.05) | 0.003 (0.002) | 10.40 | 0.75 (0.02) | 0.86 (0.02) |
| Poh. | 29 | 29 | 0.70 (0.10) | 0.002 (0.002) | 11.01 | 0.85 (0.02) | 0.87 (0.02) |
| Joh. | 32 | 47 | 0.79 (0.03) | 0.003 (0.002) | 9.02 | 0.79 (0.01) | 0.80 (0.04) |
| Kure | 35 | 55 | 0.80 (0.04) | 0.004 (0.002) | 8.73 | 0.76 (0.01) | 0.80 (0.04) |
| Mid. | 33 | 53 | 0.74 (0.04) | 0.004 (0.002) | 8.99 | 0.79 (0.01) | 0.81 (0.04) |
| PH | 29 | 55 | 0.77 (0.04) | 0.004 (0.002) | 8.70 | 0.78 (0.01) | 0.80 (0.04) |
| Maro | 26 | 29 | 0.70 (0.04) | 0.003 (0.002) | 8.37 | 0.74 (0.02) | 0.79 (0.04) |
| FFS | 40 | 50 | 0.73 (0.03) | 0.003 (0.002) | 8.72 | 0.76 (0.01) | 0.80 (0.05) |
| Nihoa | 20 | 32 | 0.81 (0.05) | 0.004 (0.002) | 8.64 | 0.77 (0.01) | 0.80 (0.04) |
| Kauai | 42 | 55 | 0.71 (0.04) | 0.003 (0.002) | 8.62 | 0.76 (0.01) | 0.79 (0.04) |
| Oahu | 35 | 50 | 0.70 (0.04) | 0.003 (0.002) | 8.56 | 0.78 (0.01) | 0.79 (0.04) |
| Mol. | 48 | 48 | 0.70 (0.04) | 0.004 (0.002) | 8.53 | 0.77 (0.01) | 0.79 (0.04) |
| Maui | 39 | 52 | 0.76 (0.03) | 0.003 (0.002) | 8.55 | 0.78 (0.01) | 0.80 (0.04) |
| Lanai | 35 | 33 | 0.69 (0.06) | 0.003 (0.002) | 8.53 | 0.73 (0.02) | 0.79 (0.04) |
| Waw. | 31 | 53 | 0.74 (0.05) | 0.003 (0.002) | 8.24 | 0.75 (0.02) | 0.78 (0.04) |
| Kea. | 36 | 45 | 0.78 (0.05) | 0.004 (0.003) | 8.79 | 0.77 (0.01) | 0.81 (0.04) |
| S.point | 37 | 50 | 0.70 (0.04) | 0.003 (0.002) | 8.78 | 0.76 (0.01) | 0.79 (0.04) |
| Hilo | 42 | 50 | 0.69 (0.04) | 0.003 (0.002) | 8.78 | 0.78 (0.01) | 0.81 (0.04) |
| Total/Mean | 654 | 857 | 0.75 (0.05) | 0.003 (0.002) | 8.94 | 0.77 (0.01) | 0.81 (0.04) |
Chichi Chichi-jima, Japan; Saipan Saipan, Northern Marianas Islands; Pohn. Pohnpei, Federated States of Micronesia; Joh. Johnston Atoll; Kure Kure Atoll; Mid. Midway Atoll; PH Pearl and Hermes Atoll; Maro Maro Reef; FFS French Frigate Atoll; Mol. Molokai; Waw. Wawaloli; Kea. Kealakekua; S. point South Point
Mitochondrial DNA
Fish isolates were sequenced to produce a 614 bp fragment of the mitochondrial cytochrome b gene with heavy strand primer (5′-GTGACTTGAAAAACCACCGTTG-3′) and light strand primer (5′-AATAGGAAGTATCATTCGGGTTTGATG-3′) designed by Song et al. (1998) and Taberlet et al. (1992), respectively. Polymerase chain reaction (PCR) and sequencing protocols are described in Eble et al. (2009). All specimens were sequenced in the forward direction, and rare or questionable haplotypes were sequenced in the reverse direction to confirm identity, with an ABI 3130×l automated sequencer (Applied Biosystems Inc., Foster City California).
Sequences were aligned in Mafft 6.62 (Katoh et al. 2002) and edited with Sequencher 4.6 (Gene Codes Corp., Ann Arbor, Michigan). Haplotype (h) and nucleotide (π) diversities were calculated in Arlequin 3.11 (Excoffier et al. 2005) which implements diversity index algorithms described in Nei (1987), and a statistical parsimony network was constructed using the software TCS 1.21 (Clement et al. 2000) with default settings.
Range-wide patterns of population structure were assessed with a spatial analysis of molecular variance (Samova 1.0; Dupanloup et al. 2002). Samova removes bias in group designation by implementing a simulated annealing procedure to identify maximally differentiated groupings without a priori assumptions about group identity. To ensure validity of the final K groupings, the simulated annealing process was repeated 100 times with a different random partition of samples into K groups. The configuration with the largest among group differentiation (ϕCT) is retained as the best sample grouping. Samova was run with values of K = 2 to 14 to identify the most likely number of sample groups. Deviations from random expectations were tested with 20,000 permutations. In Arlequin, patterns of genetic differentiation among individual sampling sites were estimated with pairwise ϕST values. A Mantel test implemented in ARLEQUIN with 10,000 simulations was used to test for an isolation-by-distance (IBD) signature (a positive correlation between genetic and geographic distance, measured as shortest route over water; Slatkin 1993). To provide insight into how the spatial scale of gene flow may differ across closely associated islands and large stretches of open ocean, IBD tests were conducted on the full data set and separately on Hawaii/Johnston Atoll samples (limited sampling within the West Pacific precluded testing for IBD).
Estimates of migration between populations were calculated with Migrate 2.1.3 (Beerli & Felsenstein 2001) on the University of Hawaii’s 96 node dual Xeon 3.2 GHz “Dell Cluster”. Migrate offers a robust framework for testing migration between more than two populations, whereas similar analyses are constrained by the assumption that a single population has split into two daughter populations (Hey & Nielsen 2007). RoyChoudhury & Stephen (2007) found Migrate-based estimates of gene flow were significantly different from expected for a simulated data set, however their analysis employed an earlier version of Migrate (1.7.3) with default settings. Subsequent tests of the same data set in Migrate 2.1 found bias and error was low and similar to that observed in other widely accepted programs (e.g. AMOVA; Beerli 2007). We employed the recommended Bayesian MCMC search strategy of a single, replicated, one million step chain (Beerli 2009). Chain convergence was assessed by ensuring 1) prior and posterior parameter estimates differed and 2) concordance in posterior parameter estimates over 10 replicate runs, with different random number seeds (Beerli 2004). Starting population parameters for diversity (Θ) and migration (M) were estimated from FST. Initial runs were conducted with default exponential priors and an unrestricted migration model. Resulting posterior distributions for Θ and M were used to inform priors for the final set of replicated runs. Estimates of the number of immigrants per generation (Nm) were calculated by multiplying final estimates (mode, 2.5%, and 97.5% quantile) of Θ and M.
To test for deviations from selective neutrality we generated F* and D* (Fu & Li 1993) in DnaSP 4.10.9 (Rozas et al. 2003). Female effective population sizes (Nef) were estimated from the equation θ = Nef2μt with θ estimated in Arlequin from the mean number of segregating sites (θS), μ is the estimated annual fragment mutation rate and t is the estimated generation time. Population ages in years were estimated from the population age parameter (τ), with τ = 2μT, where T is the time since the most recent bottleneck. We provisionally applied a generation time of five years for Yellow Tang (Claisse et al. 2009). Divergence estimates for cytochrome b have been obtained for a number of reef fishes though never specifically for an Acanthurid. We therefore employ within lineage mutation rates that encompass the range of cytochrome b evolutionary rates reported for reef fishes: 1% per 106 yr (Bowen et al. 2001) and 2.5% per 106 yr (Lessios 2008).
We tested for a signature of population expansion with Fs (Fu 1997) and by comparing observed and expected mismatch distributions (Rogers & Harpending 1992) in Arlequin with 90,000 simulated samples. Fu (1997) noted that Fs is particularly sensitive to deviations from a constant population size with population expansion resulting in a significant, negative Fs.
Nuclear DNA
Fish were genotyped at 14 microsatellite loci (Table 2) using the procedures described in Christie & Eble (2009). Unlabeled reverse primers were obtained from Integrated DNA Technologies, Inc. (Coralville, Indiana). Forward primers were labeled with 6-FAM, VIC, NED, and PET proprietary dyes (Applied Biosystems). PCR products were scored relative to a known size standard on an ABI 3100 automated sequencer and visualized using ABI PRISM GeneMapper 3.0 (Applied Biosystems).
Table 2.
Loci details, including: sample size (N), fragment size (reported as number of base pairs for mtDNA), number of alleles (A) or haplotypes (h), and observed heterozygosity (HO) or haplotype diversity (h) with standard deviations in parentheses.
| Locus | N | Fragment size | A or h | HO or h |
|---|---|---|---|---|
| mtDNA | 654 | 614 | 45 | 0.74 (0.07) |
| Zefl 01 | 810 | 129 – 243 | 33 | 0.83 (0.06) |
| Zefl 02 | 808 | 175 – 253 | 21 | 0.83 (0.05) |
| Zefl 08 | 814 | 133 – 195 | 12 | 0.75 (0.07) |
| Zefl 09 | 815 | 146 – 250 | 32 | 0.89 (0.05) |
| Zefl 10 | 818 | 198 – 246 | 14 | 0.67 (0.08) |
| Zefl 12 | 820 | 259 – 297 | 13 | 0.31 (0.10) |
| Zefl 14 | 811 | 170 – 300 | 50 | 0.89 (0.05) |
| Zefl 15 | 810 | 307 – 356 | 16 | 0.84 (0.05) |
| Zefl 17 | 814 | 275 – 396 | 21 | 0.80 (0.07) |
| Zefl 19 | 811 | 234 – 284 | 26 | 0.84 (0.05) |
| Zefl 20 | 814 | 131 – 189 | 20 | 0.77 (0.05) |
| Zefl 21 | 818 | 182 – 235 | 14 | 0.84 (0.04) |
| Zefl 22 | 814 | 182 – 250 | 29 | 0.87 (0.06) |
| Zefl 23 | 813 | 162 – 186 | 13 | 0.69 (0.05) |
Quality control followed Selkoe & Toonen (2006) and included tests for null alleles, loci scorability, linkage disequilibrium, and Mendelian inheritance. Departures from Hardy-Weinberg proportions (Guo & Thompson 1992) and linkage disequilibrium were tested using Genepop 3.2 (Raymond & Rousset 1995) with a Bonferroni correction for multiple pairwise comparisons (Bonferroni 1936). Tests of significance were combined over all loci using Fisher’s combined probability test (Sokal & Rohlf 1981). We employed Micro-Checker 2.2.3 (van Oosterhout et al. 2004) to infer scoring errors resulting from null alleles, large allele drop-out, and stutter peaks. In addition, a random subset of 10% of the samples were re-amplified, re-scored and compared to initial scores; which indicated a scoring error of less than 2% overall. Per locus estimates of allelic richness were standardized for sample size by rarefaction in Fstat 2.9.3 (Goudet 2001).
Estimates of genotypic population structure were conducted according to the methods described for sequence data. Estimates of population subdivision based on Wright’s fixation index (FST) are impacted by the amount of genetic variation within populations, with high levels of within population genetic variation leading to lower estimates of FST, without a corresponding effect on estimates of significance (Neigel 2002, Hedrick 2005). Therefore, microsatellite-based estimates of population differentiation were standardized (F′ST) relative to the maximum attainable value given observed within-population genetic variance using the standardization method of Hedrick (2005) as implemented in RecodeData 0.1 (Miermans 2006). A Mantel test implemented in ARLEQUIN was used to test for a relationship between pairwise F′ST and ϕST (mtDNA).
Population groupings were re-estimated in Structure 2.3.2 (Hubisz et al. 2009) which assigns individuals to one or more populations by minimizing deviations from Hardy-Weinberg and linkage equilibrium. Because of an expectation of weak genetic structure (Eble et al. 2009) sample locations were used as informative priors (Hubisz et al. 2009). For each run we conducted a 100,000 step burn-in followed by 100,000 Markov chain Monte Carlo iterations with the admixture model and correlated allele frequencies, as this configuration was determined to be best in cases of subtle population structure (Falush et al. 2003). We performed 10 runs for each estimated number of groups (K), from K = 1 to 10, and calculated the mean probability for each K over all replicate runs (Pritchard et al. 2007). Evanno et al. (2005) proposed calculating the change in mean probability for each K (ΔK) to identify the most likely number of groups. Because ΔK cannot be calculated for K = 1, we instead calculated the posterior probabilities of each K to identify the most appropriate number of groups (Pritchard et al. 2007). Where subdivision was indicated, we tested for further structure by running each of the subdivided groups independently as recommended by Pritchard et al. (2007).
Recent population contractions or founder events will confound estimates of population differentiation and migration; we therefore tested for bottlenecked populations by assessing a number of characteristic traits including reduced allelic richness, excess heterozygosity (Maruyama & Fuerst 1985; Cornuet & Luikart 1996), and a reduced value for the mean ratio of the number of alleles to the range of allele size (Garza & Williamson 2001). Allelic richness was compared among groups in Fstat 2.9.3. Heterozygosity excess relative to expectations under mutation-drift equilibrium was tested with the Wilcoxon’s signed-rank test of Bottleneck 1.2.02 (Cornuet & Luikart 1996) using the recommended two-phase mutational model (95% frequency of step-wise mutations; Piry et al. 1999). The mean ratio of the number of alleles to the range in allele size was calculated according to Garza & Williamson (2001). Significance was assessed by a comparison of the mean allele size/range ratio across all loci for each sample grouping, with values less than 0.68 indicating a recent bottleneck (Garza & Williamson 2001).
Estimates of migration rates were calculated in Migrate 2.1.3 with allele frequency data (in units of number of repeats). Runs were conducted with Migrate’s Brownian motion approximation of step-wise microsatellite evolution. Initial runs consisted of the recommended Bayesian MCMC search strategy of a single, replicated, 1 million step chain with five replicates (Beerli 2009). For allelic data, initial test runs indicated a lack of convergence after 1 million steps, however convergence was observed after 2 million steps with a 20,000 step burn-in and this setting was used on all subsequent runs. As with mtDNA sequence based runs, priors included an unrestricted migration model and initial estimates of Θ and M were used to inform priors for the final set of replicated runs.
RESULTS
Cytochrome b diversity
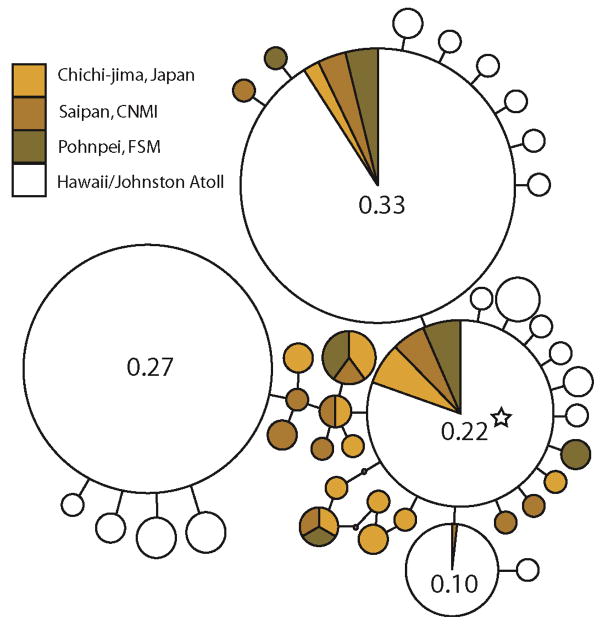
Sequences from 654 Yellow Tang revealed 39 haplotypes (Table 2; GenBank accession numbers FJ376767 – FJ376787 and GU320254 – GU320271) with the number of haplotypes per site ranging from 20 to 28. Haplotype and nucleotide diversity ranged from h = 0.69 – 0.85 and π = 0.002 – 0.004, respectively (Table 1). The statistical parsimony network indicated a cluster of closely related haplotypes (Fig. 2), a common outcome for marine fishes (Grant & Bowen 1998). Two of the three most common haplotypes were observed at every site and included the putative ancestral haplotype (Figure 2).
Figure 2.
Statistical parsimony network for Yellow Tang. Area of circle is proportional to the frequency of the respective haplotype (exact frequencies provided for the most common haplotypes), with the smallest circles representing haplotypes found in only one fish. Colors represent haplotype location (see key). Star indicates the putative ancestral haplotype, as identified by TCS analysis.
Microsatellite diversity
A sample of 857 Yellow Tang genotyped at 14 loci revealed 14 – 50 alleles per locus, and allelic richness per site ranging from A = 8.24 – 11.01 (Table 1). Mean expected heterozygosity ranged from HE = 0.79 – 0.87 and mean observed heterozygosity ranged from HO = 0.73 – 0.85. There were no significant deviations from Hardy-Weinberg proportions after applying a Bonferroni correction for multiple tests. Significant linkage disequilibrium was detected in only 27 of 2548 comparisons among the 14 loci after Bonferroni correction within populations. There was no consistent tendency towards linkage disequilibrium between any loci or within any population with the exception of Midway Atoll, where 7 out of 91 loci comparisons exhibited Bonferroni adjusted significance. While evidence of linkage disequilibrium within the Midway Atoll sample may be indicative of population natural history or selection, the pattern may instead be due to scoring errors. Although null alleles were detected in only four of 266 within sample comparisons (with no consistent pattern observed within loci or samples), locus Zefl 14 was found to contain null alleles in the Midway Atoll sample, and notably, was also present in four of the seven significant tests for linkage. Because the presence of null alleles can confound estimates of population differentiation and historical demography, we compared pairwise Fst estimates for Midway with and without locus Zefl 14. A paired t-test revealed no significant change in Fst due to the presence of null alleles (t = 2.11, P = 0.38), we therefore retain Zefl 14 in all subsequent analyses.
Population structure
Population genetic comparisons reveal shared microsatellite (nDNA) alleles and mtDNA haplotypes across the species range, though we observed significant pairwise differences in mtDNA haplotype distributions (ϕST) in 49 of 171 comparisons (Table 3) and in nDNA allele frequencies (F′ST) in 70 of 171 comparisons (Table 3). Significant estimates of pairwise population structure were ϕST = 0.037 – 0.291 and F′ST = 0.013 – 0.169. Pairwise differentiation was consistently greatest between Hawaii and West Pacific collection sites, though neither nDNA nor mtDNA exhibited a significant IBD correlation at this scale. A Mantel test comparing pairwise F′ST and ϕST values indicates strong agreement in estimates of range-wide nDNA and mtDNA population structure (r2 = 0.749; P < 0.001).
Table 3.
Results of pairwise tests for Yellow Tang population structure with mtDNA (ϕCT; above diagonal) and standardized microsatellites (F′ST; below diagonal).
| Joh. | Kure | Mid. | PH | Maro | FFS | Nihoa | Kauai | Oahu | Mol. | Maui | Lanai | Waw. | Kea. | S.point | Hilo | Chichi | Sai. | Poh. | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Joh. | ~ | −0.012 | −0.015 | −0.023 | −0.005 | −0.017 | −0.035 | −0.005 | −0.002 | 0.010 | −0.019 | 0.040 | 0.037 | 0.018 | 0.008 | 0.001 | 0.070* | 0.048* | 0.147† |
| Kure | 0.002 | ~ | −0.019 | −0.016 | −0.006 | −0.017 | −0.014 | −0.002 | −0.019 | −0.019 | −0.017 | −0.006 | 0.007* | −0.014 | −0.005 | −0.005 | 0.121† | 0.092† | 0.119† |
| Mid. | −0.010 | −0.004 | ~ | −0.002 | 0.021 | −0.007 | −0.006 | 0.023 | 0.005 | 0.001 | −0.003 | 0.003 | 0.140* | 0.011 | 0.027 | 0.023 | 0.109† | 0.096* | 0.230† |
| PH | 0.001 | −0.007 | −0.005 | ~ | −0.017 | −0.017 | −0.039 | −0.029 | −0.018 | −0.008 | −0.024 | 0.030 | 0.027 | −0.006 | −0.012 | −0.020 | 0.098† | 0.061* | 0.132* |
| Maro | −0.004 | 0.008 | −0.006 | 0.002 | ~ | −0.022 | −0.022 | −0.025 | −0.025 | −0.001 | −0.024 | 0.050 | 0.010 | 0.001 | −0.030 | −0.025 | 0.086* | 0.034 | 0.100* |
| FFS | 0.000 | 0.008 | −0.005 | −0.003 | 0.002 | ~ | −0.021 | −0.010 | −0.018 | −0.003 | −0.022 | 0.027 | 0.041 | 0.002 | −0.012 | −0.009 | 0.083* | 0.045* | 0.144* |
| Nihoa | 0.018 | 0.018 | 0.008 | 0.008 | 0.017 | −0.010 | ~ | −0.027 | −0.014 | 0.001 | −0.029 | 0.047 | 0.002 | 0.006 | −0.012 | −0.020 | 0.067* | 0.034 | 0.106* |
| Kauai | 0.006 | 0.024† | 0.006 | 0.013* | 0.014 | −0.010 | 0.002 | ~ | −0.017 | 0.001 | −0.018 | 0.051 | 0.013 | 0.002 | −0.020 | −0.022 | 0.103† | 0.053* | 0.101* |
| Oahu | 0.006 | 0.014 | 0.008 | −0.001 | 0.012 | −0.009 | −0.001 | 0.002 | ~ | −0.018 | −0.020 | 0.012 | 0.051 | −0.017 | −0.024 | −0.021 | 0.118† | 0.072* | 0.153* |
| Mol. | 0.002 | 0.022* | 0.000 | 0.003 | 0.003 | −0.001 | −0.003 | −0.008 | 0.006 | ~ | −0.006 | −0.006 | 0.087* | −0.019 | −0.006 | −0.005 | 0.147 | 0.108† | 0.189† |
| Maui | 0.000 | 0.007 | −0.010 | 0.000 | 0.003 | −0.005 | −0.003 | −0.002 | −0.003 | −0.005 | ~ | 0.030 | 0.029 | 0.000 | −0.016 | −0.017 | 0.090† | 0.052* | 0.129* |
| Lanai | 0.002 | 0.008 | −0.005 | −0.005 | −0.002 | −0.007 | 0.012 | 0.015* | 0.010 | −0.010 | 0.000 | ~ | 0.170 | −0.005 | 0.040 | 0.040 | 0.191‡ | 0.166† | 0.291† |
| Waw. | 0.015* | 0.026† | 0.012 | 0.001 | 0.010 | 0.001 | 0.004 | −0.001 | −0.002 | 0.000 | 0.017 | 0.012 | ~ | 0.087* | 0.030 | 0.025 | 0.076† | 0.021 | 0.008 |
| Kea. | 0.019* | 0.016 | 0.000 | 0.007 | 0.034† | 0.006 | 0.018 | 0.019* | 0.019* | 0.004 | −0.001 | −0.001 | 0.024† | ~ | −0.005 | −0.005 | 0.151‡ | 0.109† | 0.182† |
| S.point | 0.035‡ | 0.042‡ | 0.032‡ | 0.023† | 0.024* | 0.014 | 0.021* | 0.017* | 0.008 | 0.007 | 0.012 | 0.015* | 0.017* | 0.037‡ | ~ | −0.023 | 0.117† | 0.063* | 0.118* |
| Hilo | 0.009 | 0.012 | −0.006 | 0.001 | 0.008 | 0.003 | 0.007 | 0.011 | −0.003 | 0.002 | −0.007 | 0.006 | 0.007 | 0.001 | 0.029† | ~ | 0.114† | 0.063* | 0.112* |
| Chichi | 0.108‡ | 0.088‡ | 0.072‡ | 0.101‡ | 0.108‡ | 0.090‡ | 0.081‡ | 0.100‡ | 0.102‡ | 0.099‡ | 0.088‡ | 0.103‡ | 0.090‡ | 0.092‡ | 0.117‡ | 0.080‡ | ~ | −0.010 | 0.121† |
| Sai. | 0.123‡ | 0.101‡ | 0.108‡ | 0.127‡ | 0.138‡ | 0.133‡ | 0.118‡ | 0.134‡ | 0.140‡ | 0.151‡ | 0.137‡ | 0.142‡ | 0.146‡ | 0.125‡ | 0.169‡ | 0.139‡ | 0.018 | ~ | 0.054* |
| Poh. | 0.147‡ | 0.128‡ | 0.135‡ | 0.143‡ | 0.145‡ | 0.116‡ | 0.093‡ | 0.155‡ | 0.129‡ | 0.145‡ | 0.154‡ | 0.128‡ | 0.132‡ | 0.136‡ | 0.160‡ | 0.139‡ | 0.037 | 0.020 | ~ |
Significance represented by:
for P ≤ 0.05,
for P ≤ 0.01,
for P ≤ 0.001. Site abbreviations as in Table 1.
Tests for IBD in Hawaii were non-significant for both marker sets. However, exclusion of the Hawaii Island collections yielded a significant IBD signature in pairwise F′ST estimates across the remainder of the Hawaiian archipelago (r2 = 0.12; m = 4 × 10−6; P = 0.008). This is likely because collections around Hawaii Island, which were separated by as little as 50 km, exhibited genetic subdivision equivalent to comparisons between Hawaii Island and Midway Atoll, a distance of more than 2000 km (Table 3). Notably, exclusion of all the main Hawaiian Island samples increased the nDNA IBD correlation to r2 = 0.43 (slope = 1 × 10−5; P = 0.009). Although the rate of change in genetic distance with increasing geographic distance was small, genetic differentiation increased consistently and did not plateau, likely indicating drift-migration equilibrium and stable populations throughout the majority of the archipelago. Hierarchical spatial analysis of molecular variance (Samova) for both nDNA and mtDNA indicated K = 4 maximally differentiated groupings, those being: Chichi-jima, Saipan, Pohnpei, and Hawaii (Hawaii includes Johnston Atoll; Table 4). Among these groupings, estimates of differentiation were highly significant (P < 0.001) and remarkably similar between data sets (ϕCT = 0.098, F′CT = 0.116). Within group differentiation (ϕSC), however, differed markedly between nDNA and mtDNA. Where the mtDNA data set returned a non-significant estimate of within group differentiation at K = 4 (ϕSC = 0.002; P = 0.38), nDNA data indicates further population subdivision in Hawaii (F′SC = 0.026; P < 0.001). Tests for mtDNA cytochrome b selective neutrality (F* and D*) within the four SAMOVA populations were uniformly non-significant, indicating observed patterns of population structure are not the result of differential selection among collection sites (Table 5).
Table 4.
Structural analysis of molecular variance (SAMOVA) with maximally differentiated groupings for (a) mtDNA (K = 1 to 4) and (b) microsatellites (K = 1 to 4, 13). Degrees of freedom (df), variance components (Var.), percent variation (% Var.) and fixation indices for mtDNA (ϕ), standardized microsatellites (F′), and non-standardized microsatellites (F).
| (a) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Among groups | Among samples within groups | ||||||||
| Number of groups | Grouping | df | Var. | % Var. | ΦCT | df | Var. | % Var. | ΦSC |
| 1 | All | 18 | 0.03 | 2.43 | 0.024† | ||||
| 2 | Poh./Sai., Chichi, Hawaii | 1 | 0.13 | 10.99 | 0.110 | 17 | 0.02 | 1.67 | 0.019* |
| 3 | Poh./Sai./Chichi, Hawaii | 2 | 0.09 | 7.83 | 0.078* | 16 | 0.01 | 1.26 | 0.014 |
| 4 | Poh./Sai./Chichi/Hawaii | 3 | 0.11 | 9.80 | 0.098‡ | 15 | 0 | 0.18 | 0.002 |
| (b) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Among groups | Among samples within groups | ||||||||
| Number of groups | Grouping | df | Var. | % Var. | F′CT (FCT) | df | Var. | % Var. | F′SC (FSC) |
| 1 | All | 18 | 0.03 | 0.45 | 0.026‡ (0.005) | ||||
| 2 | Poh., Sai./Chichi, Hawaii | 1 | 0.11 | 1.99 | 0.095† (0.019) | 17 | 0.01 | 0.24 | 0.010‡ (0.002) |
| 3 | Poh./Sai./Chichi, Hawaii | 2 | 0.11 | 2.01 | 0.103† (0.020) | 16 | 0.01 | 0.24 | 0.011‡ (0.002) |
| 4 | Poh./Sai./Chichi/Hawaii Poh./Sai./Chichi/Joh./Kure, Mid., PH/Maro/ | 3 | 0.11 | 1.93 | 0.116‡ (0.022) | 15 | 0.01 | 0.13 | 0.005‡ (0.001) |
| 13 | FFS, Nihoa, Kauai, Oahu/Lanai/Maui, Mol./Waw./Kea./S. point/Hilo | 12 | 0.03 | 0.61 | 0.032‡ (0.006) | 6 | −0 | −0.12 | −0.011 (−0.002) |
Significance represented by:
for P ≤ 0.05,
for P ≤ 0.01,
for P ≤ 0.001. Site abbreviations as described in Table 1.
Table 5.
Estimates of Yellow Tang historical demography for the four SAMOVA populations, with theta (θs), estimates of female effective population size (Nef) for within lineage mutation rates of 1% and 2.5% per million years, test for deviations from the sudden expansion model of mismatch analysis (SSD) with associated significance, population age parameter (τ), population age in years (age), and tests for population expansion (Fs) and selective neutrality (F* and D*) for mtDNA haplotypes.
| Mismatch analyses | Selective neutrality | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Population | θs | Nef (1%) | Nef (2.5%) | SSD | t | age (1%) | age (2.5%) | Fs | F* | D* |
| Chichi-jima | 2.85 (1.64 – 4.06) | 46,416 (26,710 – 66,123) | 18,567 (10,684 – 26,450) | 0.002 (P = 0.73) | 2.15 (0.68 – 3.72) | 175,081 (55,375 – 302,932) | 70,033 (22,150 – 121,173) | −6.17‡ | 0.47 | 0.01 |
| Saipan | 3.14 (1.83 – 4.45) | 51,140 (29,804 – 72,475) | 20,456 (11,922 – 28,990) | 0.004 (P = 0.57) | 1.94 (0.48 – 3.13) | 157,980 (39,088 – 254,886) | 63,192 (15,635 – 101,954) | −6.67‡ | −1.67 | −1.85 |
| Pohnpei | 1.26 (0.51 – 2.01) | 20,521 (8,306 – 31,596) | 8,208 (3,322 – 13,094) | 0.015 (P = 0.62) | 1.12 (0.54 – 2.12) | 91,205 (43,974 – 172,638) | 36,482 (17,590 – 69,055) | −2.01† | −1.36 | −1.59 |
| Hawaii | 2.74 (1.94 – 3.54) | 44,625 (31,596 – 57,654) | 17,850 (12,638 – 23,061) | 0.044 (P = 0.16) | 3.90 (2.09 – 7.75) | 317,590 (170,196 – 631,107) | 127,036 (68,078 – 252,443) | 0.51 | 0.19 | 0.44 |
When not directly noted, significance represented by:
for P ≤ 0.05,
for P ≤ 0.01,
for P ≤ 0.001.
While Samova clearly identified K = 4 maximally differentiated groupings for both data sets, within Hawaii non-random allele frequency shifts provide further evidence of fine-scale genetic subdivision, with K = 13 being the smallest number of sample groups returning a non-significant estimate of within group differentiation (F′SC = −0.01; P = 0.13; Table 4). These groupings demonstrate subtle genetic divisions between all collection sites, with the exception of three undifferentiated sample groupings: 1) Kure, Midway, and Pearl and Hermes Atoll, 2) French Frigate Shoals, Nihoa, Kauai, and Oahu, and 3) Maui and Molokai. In contrast, Structure indicated only two populations (West Pacific and Hawaii), with posterior and mean probabilities highest for the full data set at K = 2, and for each region at K = 1. The discrepancy between Structure and S# is likely due to the inherent difficulty of resolving fine-scale population structure with individual clustering algorithms (Pritchard et al. 2007). Evanno et al. (2005) found the Bayesian clustering method of Structure was generally able to detect only the uppermost hierarchical levels of population structure, and did not detect more subtle (but significant) genetic subdivision. In contrast, Samova permutes samples among groups within the AMOVA framework, essentially testing every reasonable combination of sample sites (Dupanloup et al. 2002). The permutation based strategy offers an enhanced ability to resolve fine-scale structure because when predetermined sample sites correspond closely with actual populations, tests for allele frequency shifts are more powerful than individual clustering based on linkage disequilibrium and deviations from Hardy Weinberg equilibrium (Pritchard et al. 2007).
Historical demography
Microsatellite tests for recent population bottlenecks were uniformly non-significant (data not shown), however all sites demonstrated a high frequency of closely related mtDNA haplotypes (Fig. 2) consistent with the sudden expansion model of mismatch analysis (Table 5). Mismatch analyses indicate time since expansion to be on the order of 90,000 to 175,000 yrs in the West Pacific and 320,000 yrs in the Hawaiian group (assuming a within lineage mutation rate of 1% per million years; Table 5), which may explain our observation of non-significant Fs values in the Hawaii and significant negative values for Fs in the three West Pacific collections (Table 5). Simulations have shown Fs to be more sensitive to recent population expansion than other tests of demographic history (Fu 1997), so we place greater emphasis on Fs when interpreting each population’s most recent demographic trajectory. Coalescence estimates for individual sites in Hawaii (300,000 – 375,000 yrs) were similar to the average for the archipelago (320,000 yrs) indicating differences in the estimated age of extant West Pacific and Hawaiian populations were not an artifact of Hawaii biased sampling. Female effective population sizes derived from θs values were similar for all sites, with 95% confidence intervals ranging between approximately 20,000 and 70,000 individuals per region (for μ = 1%; Table 5). θs values for individual collection sites within Hawaii Island (1.19 – 2.17) were not significantly different from other sites in the archipelago (1.16 – 2.00; t = 2.78, P = 0.65) indicating the recent decline of Yellow Tang due to aquarium collections (Tissot & Hallacher 2003) has not led to a corresponding loss of genetic diversity. Coalescence based migration estimates for both mtDNA and nDNA reveal strongly asymetrical gene flow, with larval export from Hawaii at least 16 times greater than the reciprocal (Table 6). Migration rates (which are not scaled for population size) were likewise asymmetrical in favor of dispersal from Hawaii for both nDNA and mtDNA data sets. Assuming a within lineage mutation rate of 10−8 for mtDNA (1% per million years, Bowen et al. 2001) and an average per repeat mutation rate of 10−5 (Jarne & Lagoda 1996) for microsatellite loci, the migration rate from Hawaii was 4.2×10−4 – 5.8×10−4 (nDNA) and 2.1×10−5 to 1.4×10−5 (mtDNA), while the migration rate to Hawaii was 7.5×10−5 – 1.2×10−4 (nDNA) and 2.5×10−6 – 4.9×10−6 (mtDNA). Posterior distributions of parameter estimates consistently departed from priors, and results were consistent over multiple runs, indicating chain convergence (Beerli 2009). The exceptions to this pattern of convergence were migration estimates among West Pacific sites. Replicate migration estimates among these three sites varied from run to run but were consistently high, indicating that gene flow within this region is greater than can be resolved accurately (Beerli 2004).
Table 6.
Estimates of Yellow Tang larval dispersal (in units of migrants per generation) derived from Migrate for 14 microsatellites (nDNA) and mtDNA cytochrome b sequence data, with 95% confidence intervals in parentheses.
| West Pacific populations | nDNA | mtDNA | ||
|---|---|---|---|---|
| From Hawaii | To Hawaii | From Hawaii | To Hawaii | |
| Chichi-jima | 6.05 (3.16 – 8.42) | 0.26 (0.00 – 0.61) | 1.97 (0.00 – 29.25) | 0.00 (0.00 – 0.03) |
| Saipan | 4.60 (1.63 – 6.50) | 0.15 (0.00 – 0.51) | 2.49 (0.00 – 64.84) | 0.01 (0.00 – 0.08) |
| Pohnpei | 4.18 (0.98 – 6.39) | 0.25 (0.00 – 0.62) | 6.43 (0.53 – 22.31) | 0.00 (0.00 – 0.04) |
To test whether more extensive sampling of the Hawaiian Archipelago confounded migration estimates, Migrate was re-run 10 times with 50 randomly drawn individuals from Hawaii. Migration estimates derived from the randomly drawn Hawaiian samples concurred with estimates from the full data set demonstrating that the observed pattern of westward dispersal was not an artifact of intensive sampling in Hawaii.
DISCUSSION
Counter to expectations of Hawaii as exclusively a recipient of external biodiversity (Briggs 1999, Hourigan & Reese 1987, Randall 2007), nDNA and mtDNA migration estimates reveal a strong pattern of asymmetric gene flow between Hawaii and the West Pacific, with Hawaii exporting Yellow Tang alleles and haplotypes, presumably as larvae (Table 6). The frequency of larval export is, however, insufficient to homogenize populations across the range. SAMOVA tests for population structure reveal significant genetic differentiation between Hawaii and the West Pacific (ϕST = 0.008 – 0.230; F′ST = 0.072 – 0.169), as well as significant subdivision within the West Pacific (ϕST = 0.010 – 0.121; F′ST = 0.018 – 0.037) and fine-scale partitions within the Hawaiian Archipelago detected with microsatellites but not mtDNA (ϕSC = 0.002; P = 0.38; F′SC = 0.026; P < 0.001; Table 4). While nDNA and mtDNA markers differ in their resolution of population subdivisions within Hawaii, a Mantel test comparing pairwise F′ST and ϕST values indicates strong agreement in estimates of range-wide population structure (r2 = 0.749; P < 0.001). Yellow Tang are known to occasionally hybridize with congeners (Randall pers. comm.), and the presence of hybrids within the sample might confound interpretation of the data. However, the limited genetic distance between mtDNA haplotypes (Figure 2) and the ubiquity of admixed individuals (nDNA Structure plot, data not shown), indicates hybrids were not likely sampled.
Population structure within Hawaii
We observed microsatellite allele frequency shifts that provide clear evidence of an isolation-by-distance (IBD) signature across the majority of the Hawaiian Archipelago, indicating a general pattern of reduced larval exchange with increased distance. No IBD pattern, however, was observed in the mtDNA sequence data, likely because Hawaiian collections were dominated by the three most common haplotypes. The significance of the microsatellite based IBD relationship was confounded by inclusion of Hawaii Island samples (which were significantly differentiated across ≤ 50 km), indicating that factors other than IBD may be driving patterns of larval exchange at smaller spatial scales (e.g. near-shore currents; Selkoe et al. 2010, White et al. 2010).
The population structure of Yellow Tang in Hawaii has ramifications on at least two conservation fronts. First, the genetic resolution of populations indicates isolated stocks, with structure primarily corresponding to 1) the northern-most islands of the Hawaiian Archipelago (Kure, Midway, and Pearl and Hermes), 2) the broad region of the central archipelago from French Frigate Shoals to Oahu, 3) adjacent Maui and Molokai, and 4) multiple management units on Hawaii Island [though this latter designation deserves further research given recent indications of Yellow Tang larval exchange among Hawaii Island reefs (Christie et al. 2010)]. Population designations are consistent with the linear geography of the archipelago (Fig. 1) and are generally concordant with population discontinuities in other Hawaiian fishes, invertebrates, and marine mammals (Bird et al. 2007, Andrews et al. 2010, Polato et al. 2011, Toonen et al. in press).
Second, since one of the Yellow Tang populations defined above (French Frigate Shoals to Oahu) spans portions of both the PMNM and impacted reefs of the MHI, evidence of genetic connectivity between these regions indicates the potential for some larval spillover. Prevailing northwest surface currents (Hawaiian Lee Current; Fig. 1) may, however, limit opportunities for larval dispersal from the PMNM to the MHI (Calil et al. 2008, Rivera et al. 2011, DiBattista et al. 2011). Rather, it may be the impacted reefs of the main Hawaiian Islands that serve as a larval source for the PMNM (Bird et al. 2007). A recent assessment of parentage within Hawaii Island Yellow Tang identified four parent-offspring pairs, with larval dispersal from natal reefs consistently to the north (Christie et al. 2010). While the extrapolation of patterns from within a single island to the broader archipelago is questionable, observed northward dispersal matched predictions from the authors’ oceanographic model, and indicates the potential for dispersal downstream from the main Hawaiian Islands to PMNM.
Larval export from Hawaii
The geographic distribution of Yellow Tang nDNA and mtDNA diversity reveal a pattern of westward biased gene flow, with dispersal from Hawaii roughly 16 times greater than the reciprocal (Table 6). Because of the high likelihood of larval exchange with unsampled Yellow Tang populations in the Central and West Pacific, migration rates cannot be interpreted as direct estimates of larval exchange between Hawaii and West Pacific collection sites (Beerli 2004). Rather, migration estimates offer a qualitative assessment of the direction and tempo of gene flow across the large expanse of open ocean separating Hawaii from its nearest neighbors. Furthermore, coalescent based migration estimates represent a historic average over the time scale of genetic drift (e.g. 4Ne for diploid markers; Beerli 2004), and therefore may not reflect current conditions. Migration estimates derived from ten randomized subsamples of Hawaiian collections matched results from the full data set, demonstrating that evidence of westward dispersal was not an artifact of our extensive sampling in Hawaii.
Yellow Tang are particularly abundant among the southernmost islands of Maui Nui (Maui, Molokai, and Lanai) and Hawaii Island where they are the dominant herbivore (Walsh 1987). Yellow Tang are less common outside of Hawaii (J. Randall pers. comm.), raising the possibility that the observed pattern of asymmetrical larval export may in part result from differences in population size and corresponding reproductive output (Cowen & Sponaugle 2009). This, however, does not appear to be the case since migration rates (which are not scaled for population size) were likewise asymmetrical in favor of dispersal from Hawaii for both nDNA and mtDNA data sets.
Larval export from Hawaii does not appear to be restricted to Yellow Tang. Ember Parrotfish (Scarus rubroviolaceus) are common throughout the Indo-Pacific and East Pacific (Randall 2007) and estimates of the number of migrants per generation (m) derived from 15 microsatellite markers revealed a similar pattern of asymmetric larval export, with migration from Hawaii to the Central West Pacific [m = 1.70 (0.98 – 2.21)] approximately an order of magnitude greater than the reciprocal [m = 0.14 (0.03 – 0.49); Fitzpatrick 2010]. A similar, though substantially more balanced, pattern of larval export was revealed in an assessment of mtDNA (CO1) diversity in the Indo-Pacific sea cucumber, Holothuria atra (Skillings et al. 2011). Overall, H. atra larval export from Hawaii (m = 0.02 – 1.02) was marginally greater than larval import (m = 0.01 – 0.84), and indicates a pattern of bidirectional larval exchange. Evidence of larval export from Hawaii can also be found in a phylogenetic reconstruction of mtDNA control region sequences from the Bullethead Parrotfish (Chlorurus sordidus; Bay et al. 2004). Three highly differentiated, monophyletic lineages were resolved, with lineages corresponding to the Indian Ocean, the West Pacific, and Hawaii. However, several fish collected in the West Pacific contained haplotypes derived from the Hawaiian lineage, with the depth of the partitions between lineages indicating a period of extended isolation followed by more recent larval export (Bay et al. 2004).
Trans-Pacific biodiversity feedback
While it is clear that much of Hawaii’s marine biodiversity derives from the West Pacific (Hourigan & Reese 1987, Jokiel 1987, Kay & Palumbi 1987, Randall 1998, Briggs 1999, Craig et al. 2010), evidence of larval export in Yellow Tang and other reef species reveal Hawaii to be more than a simple diversity sink. Broader taxonomic sampling is required before we can determine the full extent of larval export versus import; nonetheless, the consistency of larval export in initial migration assessments begs the question of whether Hawaii may be exporting more than just genes.
Our phylogeographic assessment of the Yellow Tang reveals three lines of evidence that indicate Yellow Tang may have been a Hawaiian endemic that subsequently “escaped” to the west. First, mismatch analyses indicate more recent population coalescence in the West Pacific (91,000 – 175,000 yrs compared to 317,000 yrs in Hawaii; Table 5), an unexpected finding under a scenario of West Pacific origin, especially considering the likelihood of a population bottleneck upon colonization of Hawaii and the higher rates of population turnover in peripheral populations (Frankham 1996, Pardo et al. 2005). Second, Fs (Fu 1997; Table 5) indicates recent population expansion in the three West Pacific collection sites and stable populations in Hawaii. Third, the asymmetrical gene flow described above runs counter to expectations of a West Pacific origin. While we cannot rule out colonization of Hawaii from the West Pacific followed by the establishment of a prevailing pattern of westward dispersal, taken together findings point to a Hawaiian origin for Yellow Tang.
Regardless of Yellow Tang’s origins, evidence of larval export from Hawaii provides insights into evolutionary interactions between the remote reefs of the Hawaiian Archipelago and the species rich communities of the West Pacific. Rather than being a biogeographic “dead end”, biological and genetic diversity arising in Hawaii may be able to escape its remote origins- ultimately contributing to community diversity across the Indo-Pacific in a process of biodiversity feedback (sensu Rocha et al. 2008). Taken together with evidence of recent dispersal from Hawaii in other reef organisms, these findings indicate that the remote archipelagos of the central Pacific may function as both a source and recipient of Indo-Pacific marine diversity.
Acknowledgments
We thank the Papah naumoku kea Marine National Monument, US Fish and Wildlife Service, and Hawai’i Department of Land and Natural Resources for coordinating research activities and permitting procedures, and the crew of the NOAA Ship ‘Hi’ialakai’, M. Christie, J. Starmer, T. Donaldson, N. Yasuda, A. Alexander, B. Walsh, B. Carmen, I. Williams, S. Cotton, T. Daly-Engel, J. Claisse, M. Craig, L. Rocha, R. Kosaki, C. Musberger, S. Karl, D. White, C. Meyer, M. Gaither, M. Iacchei, G. Conception, M. Crepeau, Z. Szabo, D. Pence, K. Flanagan, and the UH Dive Safety Program for field collections, laboratory assistance, and valuable advice, and the University of Kansas Natural History Museum for providing specimens. This work was funded by US National Science Foundation grants to B.W.B. and R. J. T. (OCE-0454873, OCE-0453167, OCE-0623678, and OCE-0929031) and to the UH EECB program (OCE-0232016), in conjunction with the HIMB-NWHI Coral Reef Research Partnership (NMSP MOA 2005-008/6682), and the National Oceanic and Atmospheric Administration, Center for Sponsored Coastal Ocean Science, under awards #NA05NOS4261157 to the University of Hawai’i for the Hawai’i Coral Reef Initiative. We thank the staff of the HIMB Core Facility for sequencing and fragment analysis (EPS-0554657) and the UH Dell Computer Cluster for computing resources (grant number 5 P20 RR16467 and NSF-EPS02-37065). This is HIMB contribution No. 1433 and SOEST contribution No. 8087. This study complied with current laws in the United States and was conducted in accordance with the regulations of the University of Hawai’i Institutional Animal Care and Use Committee (IACUC).
References
- Andrews KR, Karczmarski L, Au WL, Bowen BW, Rickards S, Toonen RJ. Rolling stones and stable homes: social structure, habitat, diversity and population genetics of the spinner dolphin (Stenella longirostris) Mol Ecol. 2010;19:732–748. doi: 10.1111/j.1365-294X.2010.04521.x. [DOI] [PubMed] [Google Scholar]
- Bay LK, Choat JH, van Herwerden L, Robertson DR. High genetic diversities and complex genetic structure in an Indo-Pacific tropical reef fish (Chlorurus sordidus): evidence of an unstable evolutionary past? Mar Biol. 2004;144:757–767. [Google Scholar]
- Basch L, Shafer D, Walsh W, Eble J. Recruitment dynamics and early life history strategies of key herbivorous coral reef fishes in a Hawaiian MPA network. Abstracts 84th Meeting Western Society of Naturalists; Long Beach, CA. 2003. [Google Scholar]
- Beerli P. MIGRATE: documentation and program, part of LAMARC. Version 2.0. 2004 Revised December 23, 2004 Distributed over the Internet. [Google Scholar]
- Beerli P. Estimation of the population scaled mutation rate from microsatellite data. Genetics. 2007;177:1967–1968. doi: 10.1534/genetics.107.078931. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beerli P. How to use Migrate or why are Markov chain Monte Carlo programs difficult to use? In: Bertorelle G, Bruford MW, Hauffe HC, Rizzoli A, Vernesi C, editors. Population Genetics for Animal Conservation. Cambridge University Press; Cambridge: 2009. [Google Scholar]
- Beerli P, Felsenstein J. Maximum likelihood estimation of a migration matrix and effective population sizes in n subpopulations by using a coalescent approach. PNAS. 2001;98:4563–4568. doi: 10.1073/pnas.081068098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bird CE, Holland BS, Bowen BW, Toonen RJ. Contrasting phylogeography in three endemic Hawaiian limpets (Cellana spp.) with similar life histories. Mol Ecol. 2007;16:3173–3186. doi: 10.1111/j.1365-294X.2007.03385.x. [DOI] [PubMed] [Google Scholar]
- Bonferroni CE. Teoria statistica delle classi e calcolo delle probabilit a. Pubblicazioni del R Instituto Superiore di Scienze Economiche e Commerciali di Firenze. 1936;8:3–62. [Google Scholar]
- Bowen BW, Bass AL, Rocha LA, Grant WS, Robertson DR. Phylogeography of the trumpetfishes (Aulostomus): Ring species complex on a global scale. Evolution. 2001;55:1029–1039. doi: 10.1554/0014-3820(2001)055[1029:pottar]2.0.co;2. [DOI] [PubMed] [Google Scholar]
- Briggs JC. Coincident biogeographic patterns: Indo-West Pacific Ocean. Evolution. 1999;53:326–335. doi: 10.1111/j.1558-5646.1999.tb03769.x. [DOI] [PubMed] [Google Scholar]
- Calil PHR, Richards KJ, Jia YL, Bidigare RR. Eddy activity in the lee of the Hawaiian Islands. Deep-Sea Res Part II. 2008;55:1179–1194. [Google Scholar]
- Christie MR, Eble JA. Isolation and characterization of 23 microsatellite loci in the Yellow Tang, Zebrasoma flavescens (Pisces: Acanthuridae) Mol Ecol Res. 2009;9:544–546. doi: 10.1111/j.1755-0998.2008.02354.x. [DOI] [PubMed] [Google Scholar]
- Christie MR, Tissot BN, Albins MA, Beets JP, Yanli J, Thompson SE, Hixon MA. Larval connectivity in an effective network of marine protected areas. PLoS ONE. 2010;5:e15715. doi: 10.1371/journal.pone.0015715. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Claisse JT, Kienzle M, Bushnell ME, Shafer DJ, Parrish JD. Habitat- and sex-specific life history patterns of Yellow Tang Zebrasoma flavescens. Mar Ecol Prog Ser. 2009;389:245–255. [Google Scholar]
- Clement M, Posada D, Crandall KA. TCS: A computer program to estimates gene genealogies. Mol Ecol. 2000;9:1657–1660. doi: 10.1046/j.1365-294x.2000.01020.x. [DOI] [PubMed] [Google Scholar]
- Connolly SR, Bellwood DR, Hughes TP. Indo-Pacific biodiversity of coral reefs: deviations from a mid-domain model. Ecology. 2003;84:2178–2190. [Google Scholar]
- Cornuet JM, Luikart G. Description and power analysis of two tests for detecting recent population bottlenecks from allele frequency data. Genetics. 1996;144:2001–2004. doi: 10.1093/genetics/144.4.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cowen RK, Sponaugle S. Larval dispersal and marine population connectivity. Annu Rev Mar Sci. 2009;1:443–466. doi: 10.1146/annurev.marine.010908.163757. [DOI] [PubMed] [Google Scholar]
- Craig MT, Eble JA, Bowen BW, Robertson DR. High genetic connectivity across the Indian and Pacific Oceans in the reef fish Myripristis berndti (Holocentridae) Mar Ecol Prog Ser. 2007;334:245–254. [Google Scholar]
- Craig MT, Eble JA, Bowen BW. Origins, ages and population histories: comparative phylogeography of endemic Hawaiian butterflyfishes (genus Chaetodon) J Biogeo. 2010;37:2125–2136. [Google Scholar]
- DiBattista JD, Wilcox C, Craig MT, Rocha LA, Bowen BW. Phylogeography of the Pacific Blueline Surgeonfish Acanthurus nigroris reveals a cryptic species in the Hawaiian Archipelago. J Mar Bio. 2011;2011:1–17. doi: 10.1155/2011/839134. [DOI] [Google Scholar]
- Dupanloup I, Schneider S, Excoffier L. A simulated annealing approach to define the genetic structure of populations. Mol Ecol. 2002;11:2571–2581. doi: 10.1046/j.1365-294x.2002.01650.x. [DOI] [PubMed] [Google Scholar]
- Eble JA, Toonen RJ, Bowen BW. Endemism and dispersal: comparative phylogeography of three surgeonfishes across the Hawaiian Archipelago. Mar Biol. 2009;156:689–698. [Google Scholar]
- Eble JA, Rocha LA, Craig MT, Bowen BW. Not all larvae stay close to home: Insights into marine population connectivity with a focus on the Brown Surgeonfish (Acanthurus nigrofuscus) J Mar Biol. 2011;2011:1–12. doi: 10.1155/2011/518516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evanno G, Regnaut S, Goudet J. Detecting the number of clusters of individuals using the software STRUCTURE: a simulation study. Mol Ecol. 2005;14:2611–2620. doi: 10.1111/j.1365-294X.2005.02553.x. [DOI] [PubMed] [Google Scholar]
- Excoffier L, Laval LG, Schneider S. Arlequin ver 3.0: An integrated software package for population genetics data analysis. Evol Biol Online. 2005;1:47–50. [PMC free article] [PubMed] [Google Scholar]
- Falush D, Stephens M, Pritchard JK. Inference of population structure using multilocus genotype data: linked loci and correlated allele frequencies. Genetics. 2003;164:1567–1587. doi: 10.1093/genetics/164.4.1567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Felsenstein J. Accuracy of coalescent likelihood estimates: Do we need more sites, more sequences, or more loci? Mol Biol Evol. 2006;23:691–700. doi: 10.1093/molbev/msj079. [DOI] [PubMed] [Google Scholar]
- Fisher R. Swimming speeds of larval coral reef fishes: impacts on self-recruitment and dispersal. Mar Ecol Prog Ser. 2005;285:223–232. [Google Scholar]
- Fisher R, Leis JM, Clark DL, Wilson SK. Critical swimming speeds of late-stage coral reef fish larvae: variation within species, among species and between locations. Mar Biol. 2005;147:1201–1212. [Google Scholar]
- Fitzpatrick JM, Carlon DB, Lippe C, Robertson DR. The West Pacific diversity hotspot as a source or sink for new species? Population genetic insights from the Indo-Pacific parrotfish Scarus rubroviolaceus. Mol Ecol. 2010;20:219–234. doi: 10.1111/j.1365-294X.2010.04942.x. [DOI] [PubMed] [Google Scholar]
- Frankham R. Relationship of genetic variation to population size in wildlife. Con Biol. 1996;10:1500–1508. [Google Scholar]
- Fu YX, Li WH. Statistical tests of neutrality of mutations. Genetics. 1993;133:693–709. doi: 10.1093/genetics/133.3.693. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fu YX. Statistical tests of neutrality of mutations against population growth, hitchhiking and background selection. Genetics. 1997;147:915–925. doi: 10.1093/genetics/147.2.915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garza JC, Williamson EG. Detection of reduction in population size using data from microsatellite loci. Mol Ecol. 2001;236:305–318. doi: 10.1046/j.1365-294x.2001.01190.x. [DOI] [PubMed] [Google Scholar]
- Goudet J. FSTAT a program to estimate and test gene diversities and fixation indices. 2001 (version 2.9.3), p http://www.unil.ch/izea/softwares/fstat.html.
- Grant WS, Bowen BW. Shallow population histories in deep evolutionary lineages of marine fishes: insights from sardines and anchovies and lessons for conservation. J Hered. 1998;89:415–426. [Google Scholar]
- Guo SW, Thompson EA. A Monte-Carlo method for combined segregation and linkage analysis. Am J Hum Gen. 1992;51:1111–1126. [PMC free article] [PubMed] [Google Scholar]
- Hedrick PW. A standardized genetic differentiation measure. Evolution. 2005;59:1633–1638. [PubMed] [Google Scholar]
- Hey J, Nielsen R. Integration within the Felsenstein equation for improved Markov chain Monte Carlo methods in population genetics. PNAS. 2007;104:2785–2790. doi: 10.1073/pnas.0611164104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hourigan TF, Reese ES. Mid-ocean isolation and the evolution of Hawaiian reef fishes. TRENDS ECOL EVOL. 1987;2:187–191. doi: 10.1016/0169-5347(87)90018-8. [DOI] [PubMed] [Google Scholar]
- Hubisz MJ, Falush D, Stephens M, Pritchard JK. Inferring weak population structure with the assistance of sample group information. Mol Ecol Res. 2009;9:1322–1332. doi: 10.1111/j.1755-0998.2009.02591.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jarne P, Lagoda PJL. Microsatellites, from molecules to populations and back. TRENDS ECOL EVOL. 1996;11:424–429. doi: 10.1016/0169-5347(96)10049-5. [DOI] [PubMed] [Google Scholar]
- Johnston TMS, Merrifield MA. Interannual geostrophic current anomalies in the near-equatorial western Pacific. J Phys Ocean. 2000;30:3–14. [Google Scholar]
- Jokiel P. Ecology, biogeography and evolution of corals in Hawaii. TRENDS ECOL EVOL. 1987;2:179–182. doi: 10.1016/0169-5347(87)90016-4. [DOI] [PubMed] [Google Scholar]
- Jokiel P, Martinelli FJ. The vortex model of coral reef biogeography. J Biogeogr. 1992;19:449–458. [Google Scholar]
- Kashino Y, Espana N, Syamsudin F, Richards KJ, Jensen T, Dutrieux P, Ishida A. Observations of the North Equatorial Current, Mindanao Current, and Kuroshio current system during the 2006/07 El Niño and 2007/08 La Niña. J Oceanogr. 2009;65:325–333. [Google Scholar]
- Katoh M, Kuma M. MAFFT: a novel method for rapid multiple sequence alignment based on fast fourier transform. Nucleic Acids Res. 2002;30:3059–3066. doi: 10.1093/nar/gkf436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kay EA, Palumbi SR. Endemism and evolution in Hawaiian marine invertebrates. TRENDS ECOL EVOL. 1987;2:183–187. doi: 10.1016/0169-5347(87)90017-6. [DOI] [PubMed] [Google Scholar]
- Kobashi F, Kawamura H. Seasonal variation and instability nature of the North Pacific Subtropical Countercurrent and the Hawaiian Lee Countercurrent. J Geophys Res C. 2002:107. [Google Scholar]
- Kobayashi DR. Colonization of the Hawaiian Archipelago via Johnston Atoll: a characterization of oceanographic transport corridors for pelagic larvae using computer simulation. Coral Reefs. 2006;25:407–417. [Google Scholar]
- Lessios HA. The great American schism: Divergence of marine organisms after the rise of the Central American Isthmus. Annu Rev Ecol Evol Sytem. 2008;39:63–91. [Google Scholar]
- Lobel PS, Robinson AR. Larval fishes and zooplankton in a cyclonic eddy in Hawaiian waters. J Plank Res. 1988;10:1209–1223. [Google Scholar]
- Maruyama T, Fuerst PA. Population bottlenecks and nonequilibrium models in population-genetics. Genetics. 1985;111:675–689. doi: 10.1093/genetics/111.3.675. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McClanahan TR, Mangi S. Spillover of exploitable fishes from a marine park and its effect on the adjacent fishery. Ecol App. 2000;10:1792–1805. [Google Scholar]
- McNally GJ, Patzert WC, Kirwin AD, Vastano AC. The near-surface circulation of the north Pacific using satellite tracked drifting buoys. J Geophys Res C. 1983;88:507–518. [Google Scholar]
- Meirmans PG. Using the AMOVA framework to estimate a standardized genetic differentiation measure. Evolution. 2006;60:2399–2402. [PubMed] [Google Scholar]
- Mundy BC. Bishop Museum Bulletin in Zoology. Vol. 6. Bishop Museum; Honolulu: 2005. Checklist of fishes of the Hawaiian Archipelago. [Google Scholar]
- Myers RF. Micronesian Reef Fishes. Coral Graphics; Barridada, Guam: 1989. [Google Scholar]
- Nei M. Molecular Evolutionary Genetics. Columbia University Press; New York, NY: 1987. [Google Scholar]
- Neigel JE. Is F-ST obsolete? Conservation Genetics. 2002;3:167–173. [Google Scholar]
- Pardo LM, MacKay I, Oostra B, van Duijn CM, Aulchenko YS. The effect of genetic drift in a young genetically isolated population. Ann Human Gen. 2005;69:288–295. doi: 10.1046/j.1529-8817.2005.00162.x. [DOI] [PubMed] [Google Scholar]
- Piry S, Luikart G, Cornuet JM. BOTTLENECK: A computer program for detecting recent reductions in the effective population size using allele frequency data. J Hered. 1999;90:502–503. [Google Scholar]
- Polato NR, Concepcion GT, Toonen RJ, Baums IB. Isolation by distance across the Hawaiian Archipelago in the reef-building coral Porites lobata. Mol Ecol. doi: 10.1111/j.1365-294X.2010.04836.x. (in press) [DOI] [PubMed] [Google Scholar]
- Pritchard JK, Xiaoquan W, Falush D. Documentation for STRUCTURE software: Version 2.2. 2007 http://pritch.bsd.uchicago.edu/software/structure22/readme.pdf.
- Qiu B, Joyce TM. Interannual variability in the mid-latitude and low-latitude western North Pacific. J Phys Oceanogr. 1992;22:1062–1079. [Google Scholar]
- Randall JE. Zoogeography of shore fishes of the Indo-Pacific region. Zool Stud. 1998;37:227–268. [Google Scholar]
- Randall JE. Reef and Shore Fishes of the Hawaiian Islands. University of Hawaii Press; Honolulu: 2007. [Google Scholar]
- Raymond M, Rousset F. An exact test for population differentiation. Evolution. 1995;49:1280–1283. doi: 10.1111/j.1558-5646.1995.tb04456.x. [DOI] [PubMed] [Google Scholar]
- Reece JS, Bowen BW, Joshi K, Goz V, Larson L. Phylogeography of two moray eels indicates high dispersal throughout the Indo-Pacific. J Hered. 2010;101:391–402. doi: 10.1093/jhered/esq036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rocha LA, Rocha CR, Robertson DR, Bowen BW. Comparative phylogeography of Atlantic reef fishes indicates both origin and accumulation of diversity in the Caribbean. BMC Evol Biol. 2008;8:157. doi: 10.1186/1471-2148-8-157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rivera M, Andrews K, Kobayashi D, Wren J, Kelley C, Roderick G, Toonen RJ. Genetic analyses and simulations of larval dispersal reveal distinct populations and directional connectivity across the range of the Hawaiian Grouper (Epinephelus quernus) J Mar Bio. 2011:Article ID 765353. doi: 10.1155/2011/765353. [DOI] [Google Scholar]
- Rogers AR, Harpending H. Population-growth makes waves in the distribution of pairwise genetic-differences. Mol Biol Evol. 1992;9:552–569. doi: 10.1093/oxfordjournals.molbev.a040727. [DOI] [PubMed] [Google Scholar]
- RoyChoudhury A, Stephens M. Fast and accurate estimation of the population-scaled mutation rate, theta, from microsatellite genotype data. Genetics. 2007;176:1363–1366. doi: 10.1534/genetics.105.049080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rozas J, Sanchez-DelBarrio JC, Messeguer X, Rozas R. DnaSP, DNA polymorphism analyses by the coalescent and other methods. Bioinformatics. 2003;19:2496–2497. doi: 10.1093/bioinformatics/btg359. [DOI] [PubMed] [Google Scholar]
- Selkoe KA, Toonen RJ. Microsatellites for ecologists: a practical guide to using and evaluating microsatellite markers. Ecol Lett. 2006;9:615–629. doi: 10.1111/j.1461-0248.2006.00889.x. [DOI] [PubMed] [Google Scholar]
- Selkoe KA, Watson JR, White C, Ben Horin T, Iacchei M, Mitarai S, Siegel DA, Gaines SD, Toonen RJ. Taking the chaos out of genetic patchiness: seascape genetics reveals ecological and oceanographic drivers of genetic patterns in three temperate reef species. Mol Ecol. 2010;19:3708–3726. doi: 10.1111/j.1365-294X.2010.04658.x. [DOI] [PubMed] [Google Scholar]
- Seutin G, White BN, Boag PT. Preservation of avian blood and tissue samples for DNA analyses. Can J Zool. 1991;69:82–90. [Google Scholar]
- Skillings DJ, Bird CE, Toonen RJ. Gateways to Hawaii: Genetic population structure of the tropical sea cucumber Holothuria atra. J Mar Biol. 2011;2011:1–16. doi: 10.1155/2011/783030. [DOI] [Google Scholar]
- Slatkin M. Isolation by distance in equilibrium and nonequilibrium populations. Evolution. 1993;47:264–279. doi: 10.1111/j.1558-5646.1993.tb01215.x. [DOI] [PubMed] [Google Scholar]
- Sokal RR, Rohlf FJ. Taxonomic congruence in the Leptopodomorpha reexamined. Syst Zool. 1981;30:309–325. [Google Scholar]
- Song CB, Near TJ, Page JM. Phylogenetic relations among Percid fishes are inferred from mitochondrial cytochrome b DNA sequence data. Mol Phylog Evol. 1998;10:343–353. doi: 10.1006/mpev.1998.0542. [DOI] [PubMed] [Google Scholar]
- Sunnucks P, Hales DF. Numerous transposed sequences of mitochondrial cytochrome oxidase I-II in aphids of the genus Sitobion (Hemiptera: Aphididae) Mol Biol Evol. 1996;13:510–524. doi: 10.1093/oxfordjournals.molbev.a025612. [DOI] [PubMed] [Google Scholar]
- Taberlet P, Meyer A, Bouvert J. Unusually large mitochondrial variation in populations of the blue tit, Parus caeruleus. Mol Ecol. 1992;1:27–36. doi: 10.1111/j.1365-294x.1992.tb00152.x. [DOI] [PubMed] [Google Scholar]
- Timmers MA, Andrews KR, Bird CE, deMaintenon MJ, Brainard RE, Toonen RJ. Widespread dispersal of the crown-of-thorns sea star, Acanthaster planci, across the Hawaiian Archipelago and Johnston Atoll. J Mar Biol. 2011;2011:1–10. doi: 10.1155/2011934269. [DOI] [Google Scholar]
- Tissot BN, Hallacher LE. Effects of aquarium collectors on coral reef fishes in Kona, Hawaii. Con Bio. 2003;17:1759–1768. [Google Scholar]
- Tissot BN, Williams JW, Hallacher LE. Evaluating effectiveness of a marine protected area network in west Hawaii to increase productivity of an aquarium fishery. Pac Sci. 2004;58:175–188. [Google Scholar]
- Toonen RJ, Pawlik JR. Settlement of the gregarious tube worm Hydroides dianthus (Polychaeta: Serpulidae). I. Gregarious and nongregarious settlement. Mar Ecol Prog Ser. 2001;224:103–114. [Google Scholar]
- Toonen RJ, Andrews KR, Baums I, Bird CE, Concepcion GT, Daly-Engel TS, Eble JA, Faucci A, Gaither MR, Iacchei M, Puritz JB, Schultz JK, Skillings D, Timmers M, Bowen BW. Defining boundaries for ecosystem-based management: A multispecies case study of marine connectivity across the Hawaiian Archipelago. J Mar Biol. doi: 10.1155/2011/460173. (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ujiie Y, Ujiie H, Taira A, Nakamura T, Oguri K. Spatial and temporal variability of surface water in the Kuroshio source region, Pacific Ocean, over the past 21,000 years: evidence from planktonic foraminifera. Mar Micropaleontol. 2003;49:335–364. [Google Scholar]
- van Oosterhout CV, Hutchinson W, Wills D, Shipley P. MICRO-CHECKER: software for indentifying and correcting genotype errors in microsatellite data. Molecular ecology Notes. 2004;4:535–538. [Google Scholar]
- Walsh WJ. Patterns of recruitment and spawning in Hawaiian reef fishes. Environ Biol Fish. 1987;18:257–276. [Google Scholar]
- White C, Selkoe KA, Watson J, Siegel DA, Zacherl DC, Toonen RJ. Ocean currents help explain population genetic structure. Proc R Soc B. 2010;277:1685–1694. doi: 10.1098/rspb.2009.2214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williams ID, Walsh WJ, Claisse JT, Tissot BN, Stamoulis KA. Impacts of a Hawaiian protected area network on the abundance and fishery sustainability of the Yellow Tang, Zebrasoma flavescens. Biol Con. 2009;142:1066–1073. [Google Scholar]