Probabilistic cognition in two indigenous Mayan groups

Significance

Correct probabilistic evaluations are one of the hallmarks of rationality. Is the human ability to make them dependent on formal education, or does it emerge regardless of instruction and culture? This paper shows that preliterate and prenumerate Mayan adults are able to solve a variety of probabilistic problems. These individuals correctly use prior and posterior information, proportions and elementary combinatorial procedures to predict the occurrence of random outcomes. And they perform like Mayan school children and Western controls. The finding that adults with no formal education are able to make suitable predictions indicates that, regardless of schooling and culture, the human mind possesses a basic probabilistic knowledge.

Abstract

Is there a sense of chance shared by all individuals, regardless of their schooling or culture? To test whether the ability to make correct probabilistic evaluations depends on educational and cultural guidance, we investigated probabilistic cognition in preliterate and prenumerate Kaqchikel and K’iche’, two indigenous Mayan groups, living in remote areas of Guatemala. Although the tested individuals had no formal education, they performed correctly in tasks in which they had to consider prior and posterior information, proportions and combinations of possibilities. Their performance was indistinguishable from that of Mayan school children and Western controls. Our results provide evidence for the universal nature of probabilistic cognition.

He that will look into many parts of Asia and America, will find men reason there perhaps as acutely as himself, who yet never heard of a syllogism … God has not been so sparing to Men to make them barely two-legged creatures, and left to Aristotle to make them rational.

J. Locke (1)

The mathematics of probability provides rational procedures to deal with uncertainty. There is no consensus about the proper interpretation of the probability calculus (2, 3). Regardless of interpretations, however, the basic laws of probability rest on the same extensional considerations, notably, the principle that the probability of an event equals the sum of the probabilities of the various ways in which it can occur. Are these principles universal? Echoing the argument criticized by Locke that normative reasoning systems shape common reasoning, a classical view, based on the outmoded concept of a “primitive mind”, states that individuals living in traditional cultures are incapable of reasoning about probabilities (4, 5). Another view is that before the advent of the probability calculus there was no intuitive evaluation of chance, apart from predictions based on the frequencies of previously encountered events (6). An alternative theory is that individuals unfamiliar with the probability calculus sometimes violate its elementary rules (7). However, they possess a sense of chance that allows them to infer the probability of an event extensionally, namely, by considering the possible ways in which it may occur (8). Nonverbal creatures possess probabilistic intuitions, supporting the sense-of-chance view. Measures of looking time (9, 10) and choice behavior (11) suggest that preverbal infants and even nonhuman primates (12) form expectations of an event based on its possibilities. For example, given a container in which 3 yellow balls and 1 blue ball bounce, 12-mo-olds expect that one of the yellow balls, rather than the blue one, should exit.

The discovery of preverbal intuitions, however, does not answer the question of the universality of probabilistic cognition given that the ability to make correct probabilistic evaluations emerges only at a late stage of development (13). Indeed, before the age of 5–6 y, children do not make suitable predictions in tasks analogous to those that have documented infants’ intuitions, including simple tasks that do not require understanding of ratios. For example, given the above-described container, 3- and 4-y-olds answer randomly to the question: “Which sort of ball will exit the container?” (9, 14). Before the age of 5–6 y, children also fail more complex tasks in which they have to consider prior and posterior information (14) or combinations of possibilities (15). Where does older children’s ability to make correct probability judgments come from? Unfortunately, previous studies have tested only Western children who had received preschool or elementary school instruction. Western children are not explicitly trained in probability and combinatorics, at least in the initial school years. However, they are exposed early to educational practices, such as counting tasks, and cultural devices, such as sorting games, that may shape the emergence of probabilistic cognition. Therefore, it is unclear whether the ability to make correct probabilistic predictions emerges spontaneously in the course of development or whether it depends on exposure to educational or cultural guidance.

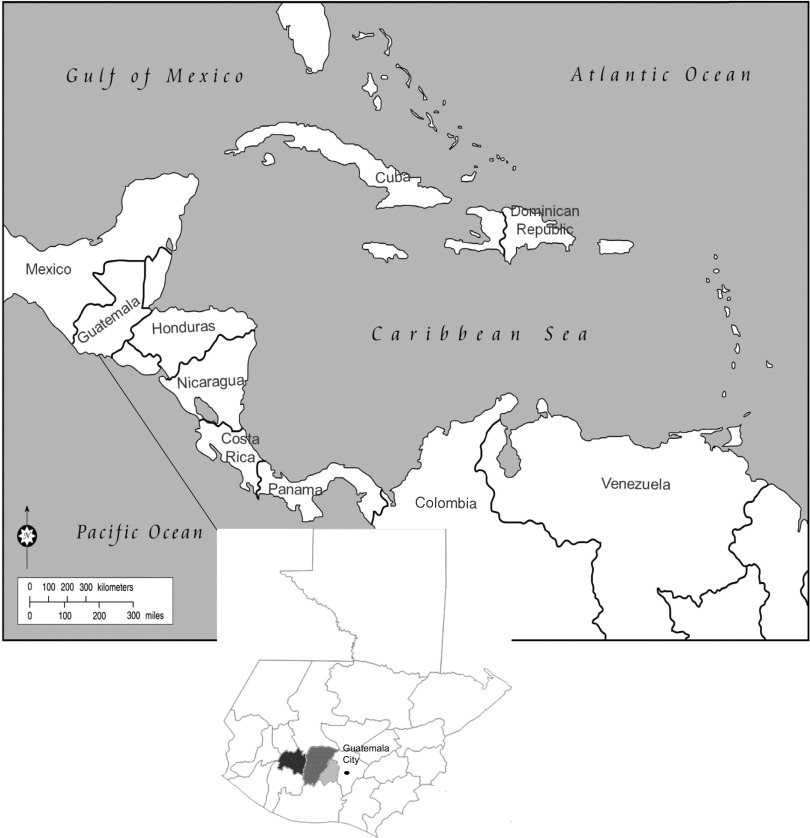
To answer this question, we studied probabilistic cognition in preliterate and prenumerate Kaqchikel and K’iche’, two groups of Maya Amerindians living in rural areas of Guatemala (Fig. 1). Men are mainly subsistence farmers and women do household maintenance work. One experimenter (L.F.) collected the reported evidence, testing a total of 188 Mayan participants, in field trips in 2012–2013 to various villages of Chimaltenango, Sacatepéquez, and Sololà departments of Guatemala. Several adults are bilingual in one Mayan language and in Spanish, and many children attend primary school, taught in Spanish. Do the advantages that bilingualism offers in some reasoning tasks (16) extend to probabilistic reasoning tasks? Do Mayan school children make better predictions than older but preliterate members of their culture? To address these questions, in each study, we tested three groups of Maya, each composed of 20 participants: monolingual (in K’iche’) adults, bilingual (in Kaqchikel and Spanish) adults, and bilingual (in Kaqchikel and Spanish) school children (in Study 1, 8-y-olds; in Study 2, 7-y-olds; in Study 3, 9-y-olds). In Study 1, we also tested eight adults bilingual in K’iche’ and Spanish. All of the adult participants were preliterate. They were recruited during the initial weeks of a national literacy program (17). In each study, we also tested 20 adult Italians. We used tasks that could probe the Maya’s mastering of various probabilistic abilities, including using posterior information (Study 1), reasoning about proportions (Study 2) and treating possibilities in a combinatorial way (Study 3). Although not exhaustive (e.g., we did not investigate the ability to combine probability and utility), this list of tasks taps into basic aspects of probabilistic cognition. In all tasks, participants bet on one of two possible random outcomes. If they were able to correctly make implicit probability estimations, they would prefer the more likely outcome.

Fig. 1.

Location of the three Guatemalan departments in which the studies were conducted, from left to right: Sololà, Chimaltenango and Sacatepéquez.

Study 1. Prior and Posterior Evaluation

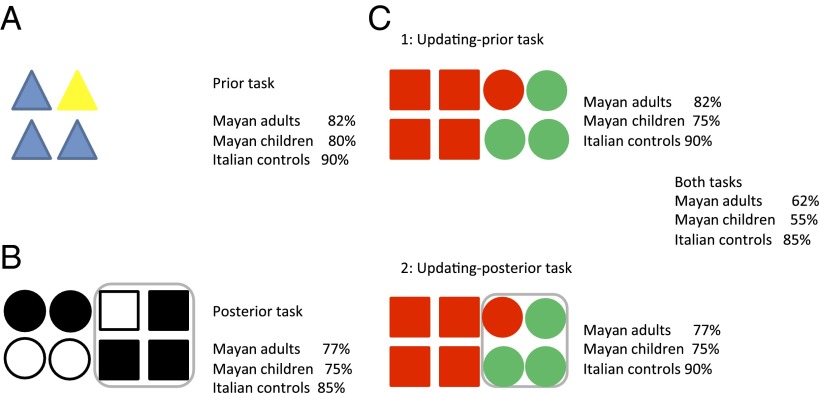
If preliterate and prenumerate Maya have a sense of chance, they should succeed in the probability problems that Western children solve by extensionally comparing the chances of two competing events, and without necessarily making a precise enumeration of the chances favoring each of them. In fact, the ability to make approximate comparisons of quantities has been documented in preliterate adults (18, 19). By contrast, if the ability to draw correct probabilistic inferences depends on formal education, then the Maya would fail. To test these diverging predictions, we used a series of three tasks (inspired by ref. 14). In an initial “prior task,” participants could make an optimal bet just on the basis of prior information: They were presented with a set of four chips of two different colors, and had to bet on the color of a randomly drawn chip (Fig. 2A). The odds were 3:1 in favor of the prevalent color. In each task, we considered as correct the bet on the more likely color. The Mayan groups did not differ reliably from each other (bilingual correct: 19 of 20; monolingual correct: 14 of 20), χ²_{(1 n = 40)} = 2.8, P = 0.10. Accordingly, in the following analyses, we collapsed their answers into one group. All groups of participants performed better than chance: Mayan adults (correct: 33 of 40), χ²_{(1 n = 40)} = 16.9, P = 0.0004; Mayan school children (correct: 16 of 20), χ²_{(1 n = 20)} = 7.2, P = 0.007; Italian controls (correct: 18 of 20), χ²_{(1 n = 20)} = 12.8, P = 0.0003. These responses seem to reflect a trend due to experience or maturation: Mayan children performed worse than Mayan adults who, in turn, performed worse than Italian controls. A Jonckheere’s test, however, did not reveal a reliable trend in the data, P = 0.39. This result indicates that preliterate Maya are able to use prior information to predict the occurrence of a random outcome. In two following tasks (presented in a counterbalanced order across participants), participants could make an optimal bet only by taking into account posterior information. If preliterate Maya possess an intuition of the principles that link prior and posterior probability, they should solve these tasks. In the “posterior task,” participants were presented with eight chips (four round chips and four square chips), five of which had a given color and three of which had another color (Fig. 2B). The experimenter randomly drew a chip, indicated its shape and participants bet on its color. The Mayan groups did not differ reliably from each other (bilingual correct: 15 of 20; monolingual correct: 16 of 20), χ²_{(1 n = 40)} = 0.14, P = 0.70. All groups performed better than chance: Mayan adults (correct: 31 of 40), χ²_{(1 n = 40)} = 12.1, P = 0.0005; Mayan school children (correct: 15 of 20), χ²_{(1 n = 20)} = 5.0, P = 0.025; Italian controls (correct: 17 of 20), χ²_{(1 n = 20)} = 9.8, P = 0.002. These data did not reflect a reliable trend: P = 0.44. The “updating task” was identical to the posterior one, except that participants were also asked for a prior bet: Before the experimenter drew a chip, participants bet on its color (Fig. 2C). The Mayan groups did not differ reliably from each other: mean number of correct bets out of two (prior and posterior), monolingual = 1.7, bilingual = 1.5, t(38) = 1.29, P = 0.2. In all groups, participants performed better than chance: Mayan adults, mean = 1.6, SD = 0.54, t(39) = 7.06, P < 0.0001, d = 1.12, Mayan school children, mean = 1.5, SD = 0.61, t(19) = 3.69, P = 0.002, d = 0.82, Italian controls, mean = 1.8, SD = 0.53, t(19) = 6.84, P < 0.0001, d = 1.53. A marginally reliable trend (Mayan children < Mayan adults < Italians, P = 0.06) indicated that updating performance was slightly better in older and more experienced individuals.* The request to make two consecutive bets on the same objects could have affected performance in the second bet (20). In fact, the second bet turned out to be as correct as the unique bet of the posterior task (77%, in both cases). Both the posterior and the updating tasks had two versions. In one version (confirmation), the posterior information about the chip’s shape increased the odds in favor of the initially prevalent color from 5:3 to 3:1. In another version (disconfirmation), the posterior information changed the odds from 5:3 in favor of the initially prevalent color to 1:3 against it. Had preliterate Mayan participants neglected the posterior information, they would have performed better in the confirmation than in the disconfirmation version. In fact, the responses of just two of them fit this pattern, those of another participant went against it (and the remainder were ties).^† In sum, preliterate Maya make optimal bets on the basis of prior information, and revise their bets in the light of new evidence.

Fig. 2.

Performance of Maya and Italian participants in tasks asking for a prior and/or posterior probability evaluation. In the prior task (A), participants had to bet on the color of a randomly drawn chip. In the posterior task (B), participants had to bet on the color of a randomly drawn chip whose shape was indicated by the experimenter. In the updating task (C), participants had to make both a prior and a posterior bet. The grey line indicates the possibilities compatible with the evidence, namely, the shape of the drawn chip: in B, the experimenter has drawn a square chip; in C, she has drawn a round chip. For each task, the figure reports the percentage of participants making the optimal bet.

Study 2. Quantity vs. Proportion

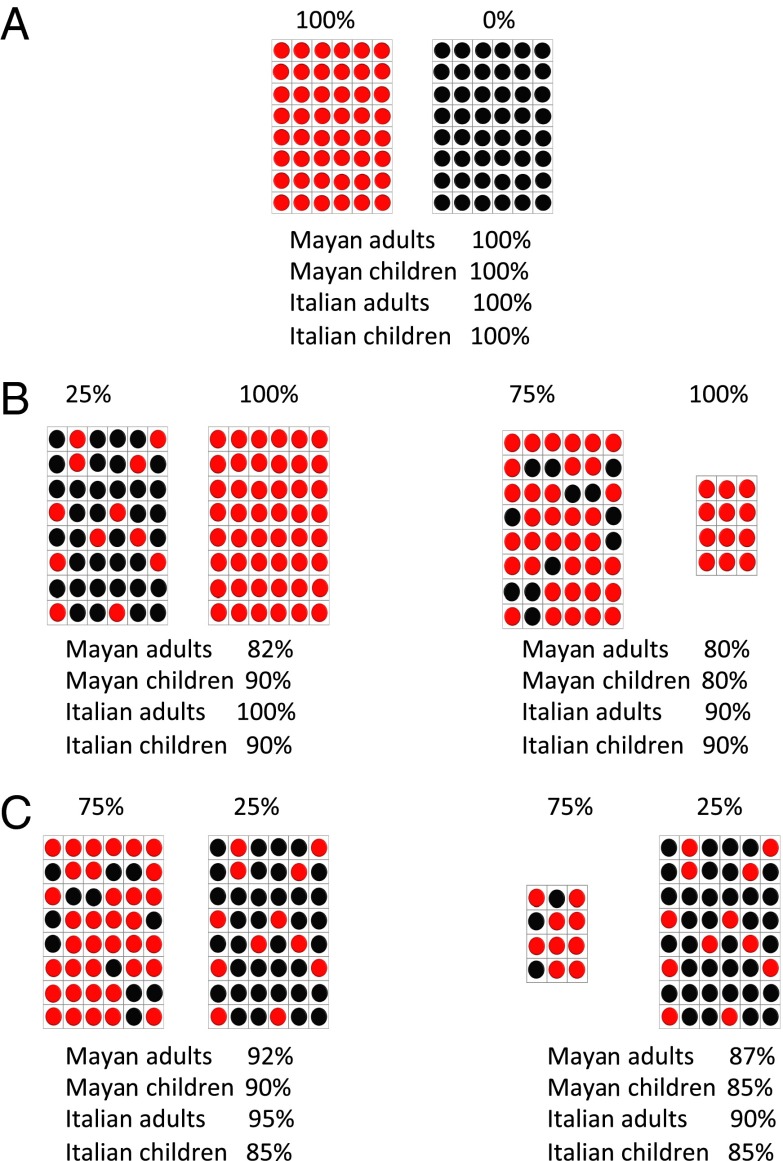
In principle, participants might solve the previous tasks by applying some superficial heuristic, rather than a proper chance evaluation. For example, they might bet on the more favorable outcome by considering the absolute number rather than the proportion of possibilities in its favor. To test whether preliterate participants succeed because they apply this “numerosity” heuristic (13), and extend our results, we used a second task [similar to 11] that would show more directly the use of probabilistic reasoning. In each trial, participants had to bet on which of two sets was more likely to yield a winning chip. The simplest trials did not ask for any estimation of proportions, given that one or both sets contained just winning chips (Fig. 3 A and B). Two other trials did ask for this estimation because both sets contained some winning chips (Fig. 3C). In one case, the favorable set contained a larger proportion as well as a greater number of winning chips. In the other case, it contained a larger proportion but not a greater number of winning chips. If preliterate Maya are able to compare the ratio of winning to nonwinning chips across sets, they should succeed in this crucial trial. Indeed, in each trial, all groups performed above chance level (as shown by binomial tests). Task A: all participants performed correctly, P = 0.0009. Task B-left panel: Mayan adults (correct: 33 of 40), P = 0.0002, Mayan school children (correct: 18 of 20), P = 0.0002, Italian adults (correct: 20 of 20), P = 0.0009. Task B-right panel: Mayan adults (correct: 32 of 40), and Mayan school children (correct: 16 of 20), P = 0.006, Italian adults (correct: 18 of 20), P = 0.0002. Task C-left panel: Mayan adults (correct: 37 of 40), P = 0.0009, Mayan school children (correct: 18 of 20), P = 0.0002, Italian adults (correct: 19 of 20), P = 0.0002. Task C-right panel: Mayan adults (correct: 35 of 40), P = 0.0004, Mayan school children (correct: 17 of 20), P = 0.002, Italian adults (correct: 18 of 20), P = 0.0002). In no trial the data reflected a reliable trend: Task B-left panel, Task B-left panel: P = 0.320. Task B-right panel: P = 0.48. Task C-left panel: P = 0.6. Task C-right panel: P = 0.63. These results suggest that preliterate individuals can base their predictions on proportional reasoning. Unlike Studies 1 and 3, we did not have the baseline data on Western children’s performance in these tasks. Thus, we tested 20 Italian 5–6 y-olds. They performed like participants in the other groups (see Fig. 3; Task B’s: P = 0.0002, in both tasks, correct: 18 of 20. Task C’s: P = 0.002, in both tasks, correct: 17 of 20). This result extends the recent evidence, published after we completed our work, that nonverbal creatures perform correctly in nonverbal tasks similar to those depicted in Fig. 3 (12, 21). Earlier studies reported that Western children failed problems akin to our crucial tasks. For example, 5-y-olds prefer to draw a token from a set containing 4 winning tokens and 4 losing token rather than from a set containing 2 winning tokens and 1 losing token (22). Compared with most previous problems, our tasks involved a larger number of tokens (e.g., 60 tokens in task C-right vs. 11 tokens in the above example), and a greater difference between proportions (e.g., 3:1 and 1:3 in task C-right vs. 2:1 and 4:4 in the above example). The combination of these factors may have encouraged approximate comparison over precise assessment of possibilities and, thus, yielded optimal choices (21).

Fig. 3.

Performance of Maya and Italian controls in tasks in which they had to bet on which of two sets was more likely to yield a red, winning token. The percentage of winning tokens is shown on the top of each set. In A and B, one or both sets contained just winning tokens. In C, both sets contained a proportion of winning tokens. In one task (left panel), the favorable set contained a larger proportion as well as a greater number of winning tokens. In the other task (right panel), it contained a larger proportion but not a greater number of winning tokens. The percentage of participants making the optimal bet is reported on the bottom of each task.

Study 3. Probability and Combinatorics

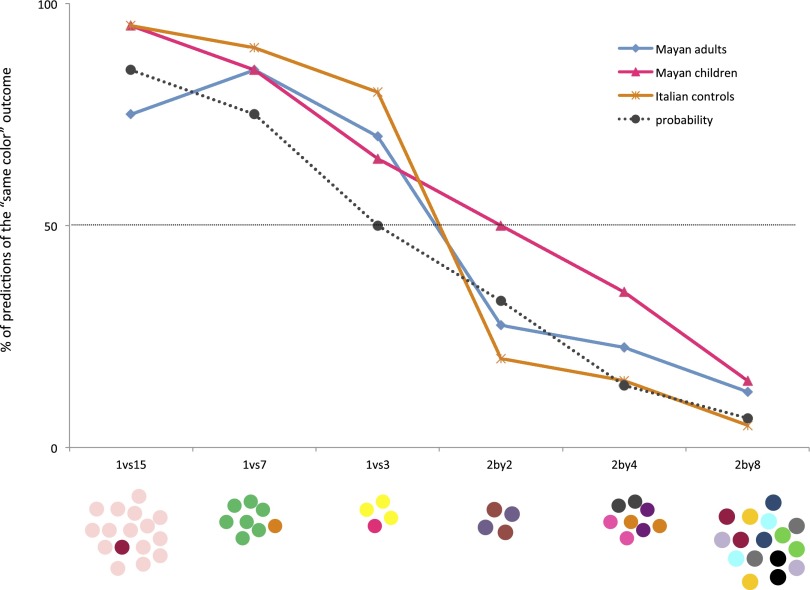
Finally, we investigated whether preliterate Maya are able to form appropriate expectations when they have to combine possibilities mentally. We used tasks that ask one to predict whether a given relation will occur between two randomly chosen tokens, and that Western children appear to solve from the age of about six (15). Participants were presented a set of chips. They had to bet on whether two randomly chosen chips would have the same color or two different colors (Fig. 4). To bet optimally, participants did not need to make a precise enumeration of all possibilities. In three tasks, there were k chips of the same color and one chip of a different color. Thus, when k > 3, participants could notice that each chip having the predominant color neighbored k − 1 same-colored chips and only 1 differently-colored chip. Accordingly, they could bet on the “same color” outcome. In three other tasks, there were k pairs of same-colored chips. Thus, participants could notice that each chip had just another chip of the same color and several [actually, 2(k − 1)] chips of different colors. Accordingly, they could bet on the “different color” outcome. As shown in Fig. 4, the rate of Maya’s bets on the same color relation follows the same tendency as the probability of such an outcome.^‡ For each participant, we computed an index Q of the quality of their prediction pattern, by normalizing the expected value of the number of correct bets (ref. 15; see also SI Study 3. Probability and Combinatorics). Q ranges from −1 (worse quality) to +1 (best quality). All groups performed above chance level: Monolingual Maya, mean Q = 0.37, SD = 0.53, t(19) = 3.07, P = 0.003, d = 0.69; Bilingual Maya, mean Q = 0.85, SD = 0.25, t(19) = 14.89, P < 0.0001, d = 3.33; Mayan school children, mean Q = 0.58, SD = 0.42, t(19) = 6.20, P < 0.0001, d = 1.39; Italian controls, mean Q = 0.81, SD = 0.38, t(19) = 9.56, P < 0.0001, d = 2.14. A reliable trend (Maya children < Maya adults < Italians, P = 0.03) indicated that performance increased with age and experience, suggesting that some probabilistic intuitions develop into adulthood (24). Unlike in Studies 1 and 2, adult bilingual Maya outperformed monolingual ones, t(38) = 3.67, P = 0.0007, d = 1.16. It is difficult to attribute this result to cultural factors, given that our bilingual and monolingual participants were equally preliterate, and lived in similar socio-economic conditions. Because Study 3 tasks involve mental manipulation of multiple possibilities, this result seems to support evidence for bilingual advantages in reasoning tasks of this sort (16). Despite differences in absolute performance levels, however, the above-chance performance of all groups points to a shared ability to treat possibilities in a combinatorial way.

Fig. 4.

Percentage of the “same color” predictions in six tasks in which participants had to bet on whether two randomly chosen tokens would have the same color or two different colors. The optimal bets consisted in predicting “same color” in the first two tasks and “different colors” in the last three tasks. In the third task, the two predictions had the same probability to be correct. The dotted line indicates the probability of the “same color” outcome.

Conclusion

To date, the question on whether culture shapes probabilistic cognition has been addressed only theoretically, applying defunct conceptions of “primitive mind” (4, 5). Our studies are, to our knowledge, the first to investigate probabilistic cognition empirically in preliterate individuals. The reported results provide evidence that the ability to make correct probabilistic evaluations emerges regardless of culture or instruction. Preliterate Maya solved problems in which they had to consider prior and posterior information, proportions and combinations of possibilities to predict the occurrence of random outcomes. And their performance was in most cases indistinguishable from that of Mayan school children and Western controls. Our results also shed some light on the question of the relation between normative and common reasoning. The probability calculus emerged only in the seventeenth century. Some theorists have used this evidence to deny the universal nature of probabilistic reasoning (6), or to argue that premodern time individuals lacked even the basic notions of probability, notably, the concept of evidential support, according to which one thing can indicate, contingently, the state of another thing (25). These arguments neglect the written traces that individuals living before the advent of the calculus were able to evaluate chances by reasoning extensionally. For example, medieval authors described dice games by relying on the principle that the expectation of a given outcome depends on the number of ways in which it can be obtained (26). Medieval authors could not even conceive a norm for measuring chance. However, they had some numerical knowledge to carry out a combinatorial analysis of the ways in which a sum could be produced. Our preliterate participants, by contrast, had not received any instruction on the symbolic numerical system. However, they made suitable predictions, indicating that a correct intuition of chance does not depend on the ability to evaluate probability numerically (8, 24). Moreover, our preliterate participants correctly used posterior evidence to update their decisions, suggesting that the basic concepts of evidence emerge even in cultures that do not prescribe norms for thinking about uncertainty. This finding seems to conflict with the evidence that literate Western adults often do not follow Bayes’ rule in their judgments of posterior probability (7). In fact, Western adults succeed in problems whose solution depends on a simple comparison of possibilities (8, 27–29). Western children (14) and preliterate Maya do the same. Like Western adults, they succeed by reasoning extensionally. [Notice that, unlike the problems typically used in Western adult literature, our tasks did not ask for a numerical judgment. However, they are closer to an ideal test of Bayesian reasoning than adult problems. Unlike the latter, in which participants do not revise any initial evaluation (6, 7, 27), in our updating tasks participants provide a prior answer and then a second one, in the light of posterior information.] In sum, regardless of culture and instruction, individuals share an intuitive comprehension of the basic principles that link prior and posterior probability.

Skeptics might argue that our results do not yield conclusions about probabilistic cognition because we used elementary tasks that asked for choices rather than probability judgments. This criticism rests on the implicit assumption that assigning a number on the [0,1] probability scale is the only way in which individuals express their expectations about uncertain events. This assumption conflicts with the normative and intuitively compelling principle that choices reveal the expectations of rational agents (2). More importantly, it leads to the paradoxical conclusion that individuals who are not able to compute a percentage or a fraction are not able to express their degree of belief in uncertain events. As for the elementary nature of our tasks, they were designed to reveal the existence of a sense of chance, not its limits. Using more complex tasks, one can easily document them. For example, in problems in which considering a sample of possibilities suffices to predict the occurrence of a relation, even preliterate Maya succeed. However, in problems asking to assess the exact number of the possibilities in which the relation holds, even literate Westerns fail (30). They fail even in problems that in principle could be solved by an extensional treatment of few possibilities. For example, they judge that getting “6–6” is as likely as getting “6–5” from a throw of two regular dice (31). Leibniz made the same biased judgment (32). Biases of this sort show that the application of extensional procedures does not guarantee correct evaluations. In some cases, the limited capacity of working memory and the difficulty of considering all relevant possibilities lead literate individuals to succumb to gross illusions in their reasoning through uncertainty (8, 33, 34). Not surprisingly, preliterate individuals exhibit similar errors in their superstitious practices (35).

In conclusion, our results extend previous evidence of probabilistic intuitions in infants and apes (9–12) and correct probabilistic judgments in Western 5- to 6-y-olds (13–15), by showing that adults who have not been exposed to any sort of formal education are able to make suitable predictions. Together, these findings indicate that, along with basic arithmetic (18, 19) and geometry (36), the human mind possesses a basic probabilistic knowledge.

Methods

The Ethics Committee of CERME (University Ca’ Foscari of Venice) approved the research. Verbal/written informed consent was obtained from the teachers/parents of the child participants tested in Guatemala and Italy. For further details on the methods, see Supporting Information.

Study 1. Prior and Posterior Evaluation.

Each participant received three tasks. In each task, the experimenter informed the participants that they could obtain a prize by playing with two differently colored puppets, each owning a set of chips of the same color. (With Mayan participants, we used the puppet procedure because it had proven successful with Western children (14). In Study 2, we used it only with Mayan and Italian children. Adults were simply informed that every time they got a red chip, they obtained the reward.) The experimenter labeled each puppet on the basis of its color. For instance, if the chips were yellow and blue, the experimenter named the yellow puppet ‘‘Mr. Yellow, the owner of the yellow chips,” and named the blue one ‘‘Mr. Blue, the owner of the Blue chips.’’ To test participants’ understanding of the instructions, the experimenter asked them to indicate one chip belonging to each puppet. If they failed, she corrected them. In posterior and updating tasks, the games concerned chips of different shapes. The experimenter indicated and named these shapes. To check whether participants had learned the names, they had to indicate a round chip and a square chip. If they failed, the experimenter corrected them. The experimenter put the chips in an opaque bag. As a mnemonic aid about the content of the bag, a cardboard depicting the chips was left in front of the participants. In each task, the experimenter randomly drew a chip, and asked participants to bet on its color.

In the prior task, the experimenter presented 4 triangular chips (2 cm per side) of blue and yellow color. One chip had one color (e.g., yellow), three chips the other one (e.g., blue). The experimenter said:

“I’m going to put all of the chips in this bag, but you can remember how they are because they are copied on this card [the experimenter indicated the card representing the four chips]. I will shake the bag and I will take a chip from it without looking. If the chip is . . . [the experimenter named one color], then Mr. . . . [the experimenter named and indicated the puppet of that color] wins a prize. If the chip is . . . [the experimenter named the other color], then Mr. . . . [the experimenter named and indicated the puppet of that color] wins a prize. You have to choose which puppet you would like to be to win the prize. Show me which puppet you would like to be.”

In the posterior task, the experimenter presented eight chips: four round chips (1.5 cm in diameter) and four square chips (2 cm per side), of black and white color or else of green and red color; five chips had one color (e.g., white) and three chips had the other one (e.g., black). The experimenter put the chips in a bag, randomly drew one of them and said:

“Ah, listen. I’m touching the chip that I have drawn and now I know something that might help you to win the game. I’m touching the chip that I have in my hand and I feel that it is . . . [the experimenter named a shape: either round or square]. Now, show me which puppet you would like to be.”

Unknown to the participants, the experimenter touched the chips and selected a chip having the shape determined by the task version. In the “confirmation” version, three out of four chips having the selected shape had the initially prevalent color. For example, consider a case in which most chips were white (i.e., five white vs. three black), and most round chips were equally white (i.e., three white vs. one black). Informing participants that the drawn chip was round, increased the odds in favor of the white color from 5:3 to 3:1. Therefore, the correct answer was to bet on the white puppet. In the “disconfirmation” version, only one out of four chips having the selected shape had the initially prevalent color. For example, consider a case in which most chips were white (i.e., five white vs. three black), but most round chips were black (i.e., three black vs. one white). Informing participants that the drawn chip was round, changed the odds from 5:3 in favor of the white color to 3:1 against it. Therefore, the correct answer was to bet on the black puppet.

In the updating task, the chips were the same as those used in the posterior task, except that they had different colors. For example, if the posterior task concerned black and white chips, the updating task concerned red and green chips. The updating task was composed of two subtasks: In the first one, the instructions were the same as those used in the prior task. In the second one, the instructions were the same as those used in the posterior task. Like the posterior task, the second subtask of the updating task occurred in a confirmation or a disconfirmation version.

Study 2. Quantity vs. Proportion.

Participants sat in front of a table on which there were two opaque boxes, placed at about 30 cm from each other, each measuring 30 × 15 × 10 cm, and each with a hole (10 cm in diameter) on the top. In front of each box, there was an opaque cup (12 cm in diameter, 10 cm in height). In each trial, two sets of red and black wooden chips (2 cm in diameter) were used. The experimenter said:

“Look at these two puppets [The experimenter presented two animal-toys of two different colors]. Which one do you prefer? [The participant selected a puppet] OK. You will play with it [The experimenter indicated the participant’s puppet]. You and your puppet will belong to the red team. This red sticker is for you and this one for the puppet [The experimenter distributed the stickers]. The other puppet belongs to the black team [The experimenter placed a black sticker on the other puppet]. Now, we will play a series of games with some red and some black chips. [The experimenter showed some chips]. The red chips make your red team win the game. The black chips make the black team win the game. Every time you find a red chip, your red team wins a sticker. Every time you find a black chip, the black puppet wins a sticker.”

To test participants’ understanding of the instructions, the experimenter asked them to name or point to the winning chip. If they failed, she corrected them. The experimenter went on:

“Look at these chips. [The experimenter indicated one group of chips] We will put them in this box. [The experimenter indicated one of the two boxes; then she encouraged the participant to help her in putting the chips in the mentioned box] To help you remembering the chips that we will put in the box, I have represented them here [The experimenter indicated a cardboard, 21 × 29 cm, which depicted the chips]. Look at these other chips. [The experimenter indicated the other group of chips] We put these chips in this box. [The experimenter indicated the other box and filled it with the new set of chips] To help you remembering the chips that we will put in the box, I have represented them here [The experimenter indicated another cardboard, 21 × 29 cm, which depicted the second set of chips]. Now, without looking, I take one chip from this box [The experimenter indicated one box] and one chip from this box [The experimenter indicated the other box]. And, without looking, I put them in these two cups [The experimenter took one chip from each box and placed it in the corresponding cup]. You have to choose a cup. Remember that, to win, you have to find a red chip. If you find a black chip, the black puppet wins [For adult participants: If you find a black chip, you do not win the prize]. Before making your choice, you may look at the two cardboards, which reminds you the content of each box. Thus, which cup do you choose to find a red chip?”

The participants made their choice, by pointing to one cup. The experimenter opened it and assigned the prize. The tasks were presented in the order indicated in Fig. 3.

Study 3. Probability and Combinatorics.

In each task, the experimenter used a different set of chips (measuring 2 cm in diameter). In three tasks, 1 chip of a given color and, respectively, 3, 7 and 15 chips of another color composed the set. We label the tasks 3 vs. 1, 7 vs. 1, and 15 vs. 1, respectively. In three other tasks, the set consisted of, respectively, 2, 4 and 8 pairs of twin-chips. Each twin-pair represented a different color. We label these tasks “2 by 2,” “4 by 2,” and “8 by 2,” respectively. Before the six experimental tasks, participants received a familiarization task. The experimenter presented four blue and four red chips. Participants had to indicate two chips of the same color, and then two chips of two different colors. If they failed, the experimenter corrected them. In each experimental task, the experimenter put the chips on a table, asked participants to examine them and then put them in an opaque bag. Participants had to draw two chips at the same time without looking inside the bag. As a mnemonic aid about the content of the bag, a cardboard depicting the chips was left in front of the participants. Before they drew the chips, the experimenter asked:

“Do you think you will draw two chips of the same color or two chips of two different colors? If your answer turns out to be right, you’ll win the prize.”

If participants’ bet turned out to be correct, they received the reward. The order of presentation of the six tasks was varied in such a way that each task was presented in all possible ranks to the same number of participants.