Significance
In response to a uniform stimulus, biochemical networks display a high degree of variability when assayed across many individual cells. However, due to their complexity, the relative contributions of different pathways to the overall network variability are hard to evaluate and control. Here we introduce a technique allowing for “noise mapping” to be performed within such networks. By experimentally assaying three distinct tumor necrosis factor (TNF) activated transcription factors within a mathematical framework, we show how noise is distributed in the TNF-induced network, in the presence or absence of feedback. This framework is readily scalable to allow the noise decomposition of larger and more complex signaling networks, permitting further investigations into the dependence of biological noise on signaling system architecture.
Keywords: signal transduction, intrinsic noise, extrinsic noise, analysis of variance, noise decomposition
Abstract
Experimental measurements of biochemical noise have primarily focused on sources of noise at the gene expression level due to limitations of existing noise decomposition techniques. Here, we introduce a mathematical framework that extends classical extrinsic–intrinsic noise analysis and enables mapping of noise within upstream signaling networks free of such restrictions. The framework applies to systems for which the responses of interest are linearly correlated on average, although the framework can be easily generalized to the nonlinear case. Interestingly, despite the high degree of complexity and nonlinearity of most mammalian signaling networks, three distinct tumor necrosis factor (TNF) signaling network branches displayed linearly correlated responses, in both wild-type and perturbed versions of the network, across multiple orders of magnitude of ligand concentration. Using the noise mapping analysis, we find that the c-Jun N-terminal kinase (JNK) pathway generates higher noise than the NF-κB pathway, whereas the activation of c-Jun adds a greater amount of noise than the activation of ATF-2. In addition, we find that the A20 protein can suppress noise in the activation of ATF-2 by separately inhibiting the TNF receptor complex and JNK pathway through a negative feedback mechanism. These results, easily scalable to larger and more complex networks, pave the way toward assessing how noise propagates through cellular signaling pathways and create a foundation on which we can further investigate the relationship between signaling system architecture and biological noise.
Cells transduce extracellular information through signal transduction pathways that often exhibit complex nonlinear behaviors. Commonly, receptor–ligand interactions initiate signals that diverge into parallel pathways and then converge onto common downstream elements. These branches can have different dose dependencies creating complicated dose–response characteristics, including biphasic properties (1–3). In such systems, the complexity of the network creates difficulty in identifying the sources of cell response variability, even if the topology is known. However, despite the challenges, characterizing the fidelity of biochemical networks could help identify new biochemical noise regulation mechanisms that would further our understanding of cellular decision-making processes (4). Therefore, although biological noise at the gene expression level is relatively well characterized (5–11), to fully understand the origins of cell decision heterogeneity we require novel experimental and mathematical methods to quantify signaling pathway noise.
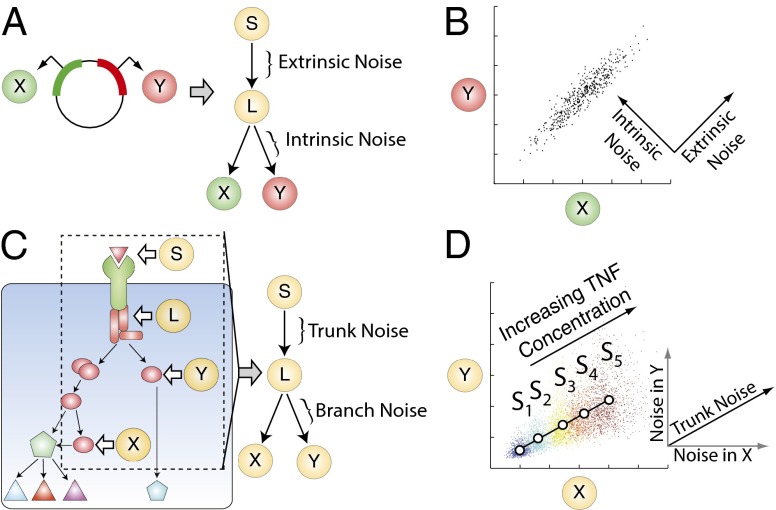
Prior efforts to understand biochemical noise have primarily focused on the utilization of the equivalent dual-reporter technique. This method involves the single-cell measurement of two distinguishable fluorescent reporter proteins under statistically equivalent conditions (e.g., identical promoters, equivalent integration sites, etc.; Fig. 1A) (8, 9, 12). The lack of correlation between reporter expression within a cell is thought to result from stochastic chemical kinetics that randomly and independently affect both reporters, and is referred to as intrinsic noise. The remaining reporter variability originates from the factors that simultaneously affect both reporters equally within an individual cell but vary from cell to cell, and is referred to as extrinsic noise. The extrinsic factors can include the expression levels of RNA polymerase, ribosome number, cell size, or cell cycle stage, all thought to affect both reporters similarly within a cell. The advantage of the equivalent dual-reporter method is the separation of intrinsic noise from extrinsic noise in an experimentally measurable way. This method has been extended to analyze signaling networks; however, it requires simultaneous measurement of two reporters per signaling node of interest (13). This can quickly become experimentally intractable as the system size increases.
Fig. 1.
(A) Schematic of the equivalent dual-reporter method. Two genes that encode for two distinguishable and statistically equivalent fluorescent reporters ( and ) can conceptually be reformulated as a four-node branch motif. can represent the cellular genetic background, can represent the overall activity of the gene expression machinery in a given cell, and and can represent the expression levels of the reporters. Thus, extrinsic noise is introduced in the segment , and intrinsic noise is introduced in the segments downstream of . (B) Simulated results for the reporters given in A. Each point corresponds to the expression level of both reporters in a single cell. Extrinsic noise causes points to spread out along the diagonal whereas intrinsic noise causes the points to additionally spread out in the direction orthogonal to this line. For an isotropic interpretation see Fig. S1. (C) A region of interest (ROI, dashed rectangle) for decomposition is selected from a larger complex intracellular signaling system. The components within the ROI can then be further simplified to a four-node motif comprising a ligand that binds to its native receptor, which sends a signal to a signaling intermediary, the receptor complex . The signal from then propagates down two parallel branches to the readouts and . We denote the factor that causes coordinated fluctuations in the reporters and as the trunk noise, whereas the noise uniquely contributed by each branch is termed the branch noise. (D) Simulated results for individual cells expressing the readouts ( and ) given in C under five input levels as denoted by the distinct colors. The means of the readout for each input level are indicated by the circles and fitted by regression to form a basis for decomposition. The trunk noise adds noise along the basis, and each branch noise will add noise parallel to its corresponding axis and orthogonal to the axis associated with the other branch.
Expanding on the success of the equivalent dual-reporter method, nonequivalent dual reporters have found success characterizing sources of cell-to-cell variability. For instance, by comparing a reporter in a signaling pathway of interest to a reporter of a constitutively expressed gene, one can separate pathway-specific noise from general gene expression noise (14, 15). Alternatively, multiple reporters placed within a serial gene expression network can facilitate decomposition of the noise propagation (6). More recently, a single-reporter variation of the original dual-reporter method enabled the decomposition of the intrinsic noise into memory and stochastic terms based upon their separate timescales (16). However, the methods described above frequently use custom-designed networks whose structure is known a priori, which allows for the construction of a specific mathematical framework. Thus, although dual-reporter methods and its variations have yielded important scientific insights, these methods routinely require reporter genes to be inserted into cells which can hamper efforts to rapidly characterize a variety of signaling networks. Furthermore, these reporter methods are limited to the analysis of biological noise at the gene expression level. Therefore, despite substantial advances in the characterization of gene expression noise, we still lack tools needed to understand noise in intracellular signaling.
Here, we present a mathematical generalization of the equivalent dual-reporter method that enables decomposition of signaling network noise using nonequivalent dual reporters. These reporters do not need to be genetically encoded, thus increasing the scope of systems that can be analyzed. Using this framework, we were able to quantify the relative noisiness of both the downstream mitogen activated protein kinase (MAPK) and NF-κB signaling pathways. We also show that this methodology can be used to identify previously unappreciated feedback mechanisms affecting both MAPK and NF-κB pathways. Overall, this methodology is revealing and experimentally facile to implement in a system where detailed knowledge of the topology is unavailable.
Mathematical Framework for Noise Decomposition Using Nonequivalent Dual Reporters
The method for noise decomposition proposed here can be understood as a generalization of the well-known extrinsic–intrinsic noise decomposition pioneered by Elowitz et al. (9). To demonstrate this relationship, we note that by conceptualizing the additive propagation of noise through the equivalent dual-reporter system, a four-node branch motif naturally emerges (Fig. 1A). The input node represents an external factor that modulates the activity of the entire motif. The intermediate node represents the noisy intracellular representation of . In turn, modulates the activity of and . For an equivalent reporter system, can represent the cellular genetic background, can represent the overall activity of the gene expression machinery in a given cell, and and are the expression levels of the reporter genes. In this case, extrinsic noise is introduced between and , and intrinsic noise is introduced downstream of . The mathematical expressions defining total, extrinsic, and intrinsic noise given by Elowitz et al. are shown in nonnormalized form in Eqs. 1–3 (9).
| [1] |
| [2] |
| [3] |
As illustrated in SI Text, the total noise is identical to the average variance of the reporters (Eq. 1), a sensible result when the reporters are equivalent. The collection of factors within a single cell that causes the two reporters to change in synchrony is defined as the extrinsic noise and is mathematically defined as the covariance between the reporters (Eq. 2). Because the two reporters are equivalent, and assuming that the reporters do not affect their common regulators (17), the remaining uncorrelated variation between the expression of the reporters in a given cell arises primarily from stochasticity. Mathematically, intrinsic noise can be defined as the difference between the total and extrinsic noise (Eq. 3). From these definitions, we can understand why extrinsic noise is typically depicted to be in the direction of the line and intrinsic noise is depicted in the direction orthogonal to this line (Fig. 1B; see Fig. S1 for an isotropic interpretation).
In the more general case where and are nonequivalent reporters, the assumptions supporting Eqs. 1–3 are no longer valid, and the framework must be reformulated for the more general nonequivalent case. For nonequivalent reporters, can represent an external stimulus (e.g., ligand concentration), can represent a signaling intermediate, and and can represent nonequivalent downstream signaling outputs (Fig. 1C). In this case, we refer to trunk noise as the noise introduced upstream of and branch noise as the noise introduced by a specific branch downstream of . We consider the additive contributions of trunk noise to be independent of the variability arising from the natural protein birth and decay processes (18). In the instance in which the trunk and branch noise are independent, additive, have zero mean, and and are linearly related to one another (but not necessarily along the line , we can show that the noise values are given by the following:
| [4] |
| [5] |
| [6] |
where represents the slope of the average relationship of versus (SI Text). Importantly, these results are independent of the distributions of , , and and do not make any assumptions as to whether the underlying processes are stationary or nonstationary.
Eq. 4 reveals that the trunk noise is proportional to the covariance term, thus it is mathematically analogous but not conceptually equivalent to extrinsic noise. Similar to the definition of intrinsic noise, the branch noise can then be calculated as the difference between the total noise specific to the branch and the trunk noise (Eqs. 5 and 6). Additionally, these equations show that the three noise components can be extracted from joint measurements of and without knowledge of , which may be experimentally inaccessible.
Graphically, this system can be depicted in – space as follows (Fig. 1D). In the total absence of noise, for a given input , the activity of and in all cells would be identical and map to a single point as shown. Experimentally, we can estimate this point by exposing many cells to the same stimulus and computing the average value of and . If were allowed to vary, then the locus of points would trace out a line defined by the changing stimulus. We refer to this line parameterized by as the geometrical basis for the noise decomposition and experimentally estimate it via reduced major axis regression.
For a given , by introducing only the trunk noise, the spread of activity of individual cells will lie along the basis line. Given that the noises in the two branches are mutually independent, each branch will contribute noise parallel to its respective axis and orthogonal to the axis associated with the other branch.
Finally, we observe that for a given level of , the graphical depiction in Fig. 1D simplifies to the case in Fig. 1B if the reporters are equivalent. In particular, for equivalent reporters so that the basis becomes , and the trunk noise along this line becomes the extrinsic noise (SI Text). Furthermore, we note that if we average the branch noise values, we will arrive at the definition of intrinsic noise as expected:
Thus, the equivalent reporter framework is a special case of the more general nonequivalent reporter framework. Next, we will show that these equations can be applied to a biological system that can provide insights into the nature of biological noise in signaling networks.
Pathway-Specific Noise in the Tumor Necrosis Factor Signaling Network
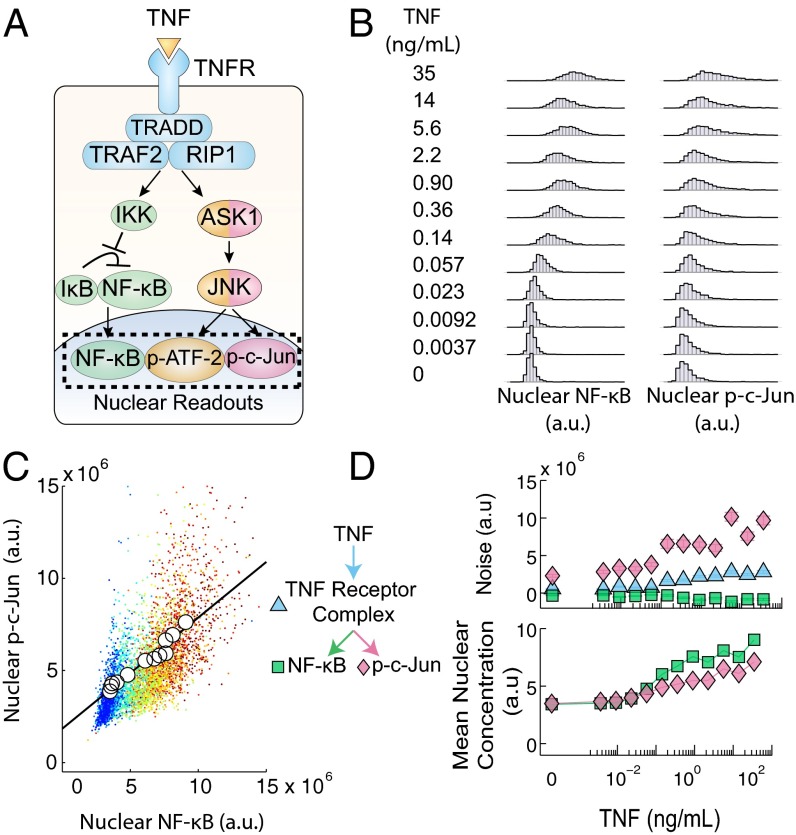
Using the above noise decomposition framework, we sought to quantify the noise contributed by the c-Jun and NF-κB pathways when activated by tumor necrosis factor (TNF), a model system for understanding signaling heterogeneity in mammalian cells (19–24), to understand noise propagation through this signaling network (Fig. 2A). We exposed mouse embryonic fibroblast cells to a wide range of TNF concentrations to elicit the full dynamic response of the transcription factors. For each TNF concentration, we measured the nuclear concentrations of the transcription factors in hundreds of individual cells using quantitative immunocytochemistry (immunofluorescence) (Fig. 2B). We find that the immunofluorescence signal has a strong correlation with the actual protein concentration (Fig. S2). We examined the responses at the 30-min time point, because the translocations of both transcription factors reach their maximum values at this time, indicating similar operational timescales (25).
Fig. 2.
(A) Schematic of the TNF–NF-κB–JNK signaling pathway. Briefly, TNF activates the TNF receptor which then activates both the NF-κB pathway and the JNK mediated pathway causing the nuclear translocation of the transcription factors NF-κB, p-c-Jun, and p-ATF-2. The single-cell nuclear concentrations of the transcription factors can then be quantified via immunofluorescence. (B) Distributions of NF-κB and p-c-Jun nuclear concentrations in response to TNF. The coordinated single-cell nuclear localizations of NF-κB and p-c-Jun were measured for their response to a 30-min exposure of TNF and used in calculations to decompose pathway noise. (C) Scatter plot of the data given in B. Individual points represent single cells and each color represents a unique TNF concentration as listed in B. Means at each TNF concentration are denoted by the circles and fit with linear regression to form a basis for noise decomposition. (D) The noise decomposition of the TNF–NF-κB–JNK pathway of the data given in B (Top) and the corresponding mean nuclear concentration of both transcription factors (Bottom). This figure is shown again as Fig. 3C.
In response to a stimulus, parallel signaling branches can have different dose dependencies leading to complex overall response characteristics, including biphasic qualities resulting in complex and highly nonlinear behavior (1–3). However, surprisingly, we find that NF-κB and p-c-Jun levels are proportional to each other over four orders of magnitude of TNF concentrations (Fig. S3A). Thus, even though the average NF-κB and p-c-Jun levels are nonlinear functions of TNF (Fig. 2D), they are linearly related (Fig. 2C).
We applied Eqs. 4–6 to decompose the observed noise into a common trunk noise and branch noises specific to the NF-κB and JNK pathways (Fig. 2D) and observed that for the NF-κB pathway, the trunk noise was slightly greater than NF-κB branch noise, whereas for the JNK pathway, the c-Jun branch noise was greater than the trunk noise. Therefore, although both responses are subject to the noise resulting from common upstream signaling components, the NF-κB pathway introduces less noise to the signaling output in comparison with the JNK pathway. We find that the inflection point in the dose–response of the trunk and c-Jun branch noise roughly mirrors the inflection point found in the dose–response of the p-c-Jun and NF-κB mean nuclear concentration. We further characterized the noise by calculating the square of the coefficient of variation, , for both branches and found that it was constant across TNF concentrations (Fig. S4). This result suggests that these branch noises could be log-normal or gamma distributed, a common characteristic of cellular protein distributions (18, 26, 27). Therefore, the notable similarity between the mean dose–response and branch noise is likely due to a general proportional scaling between the noise and mean protein abundance (28).
Noise Decomposition of the TNF Network
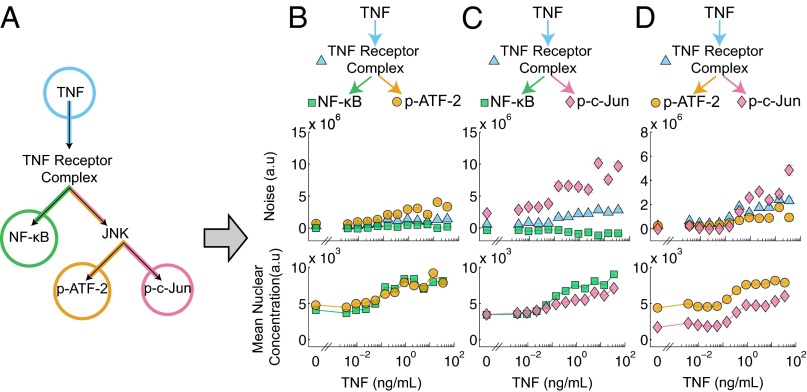
Next, we sought to demonstrate how our method could be extended to analyze larger and more complex signaling networks. Many signaling networks, including that of TNF, consist of multiple levels of branching. For instance, the TNF network branches into the NF-κB and JNK pathways, and the JNK pathway subsequently branches to activate two transcription factors: ATF-2 and c-Jun (Fig. 3A). To decompose the noise in this six-node system (Fig. 3A), we considered multiple four-node branch motifs embedded within the network (Fig. 3 B–D). We can decompose the noise of each motif in isolation but, because the three motifs have overlapping portions, we can assemble a more detailed noise map of the original network. To perform this decomposition, we measured, in parallel experiments, the joint pairwise TNF responses of NF-κB and p-ATF-2, NF-κB and p-c-Jun, and p-ATF-2 and p-c-Jun.
Fig. 3.
(A) Schematic illustrating the reduction of the TNF–NF-κB–JNK signaling pathway (Fig. 2A) into a six-node network which is then partitioned into three experimentally tractable four-node motifs (B–D) covering all possible transcription factor pairings. Each four-node motif consists of a TNF input, a signaling intermediary (either the TNF receptor complex or JNK), and two readouts of transcription factor activity. (B–D) The noise decomposition of the four-node motifs derived from A (Top) and the corresponding mean nuclear concentration of both transcription factors (Bottom). The JNK branch-specific noise is higher than both the NF-κB branch-specific noise and the TNF–TNFR trunk noise. Within the JNK pathway the c-Jun branch noise is greater than the ATF-2 branch noise at higher TNF concentrations. Fig. 3C is also presented as Fig. 2D.
First, we found that the results for the NF-κB/p-ATF-2 pair (Fig. 3B) were similar to that of the NF-κB/p-c-Jun pair analyzed earlier (Fig. 3C). Further quantitative analysis revealed that of the noise in the fully activated TNF–NF-κB pathway, ∼90% can be ascribed to the trunk portion shared with the TNF–JNK pathway, and the remaining ∼10% can be ascribed to the NF-κB–specific branch. In comparison, in the TNF–ATF-2 pathway, only ∼30% of the noise in the ATF-2 pathway originates from the trunk, and ∼70% of the noise arises from the remaining JNK pathway. Next, examining the results for the NF-κB/p-c-Jun pair (Fig. 3C), we observe that ∼80% of the p-c-Jun noise originates from the c-Jun-specific branch, suggesting that there may be slightly greater noise in the TNFR–c-Jun pathway than in the TNFR–ATF-2 pathway. Indeed, when we directly decomposed the p-ATF-2/p-c-Jun pair, we observed greater noise specific to the c-Jun pathway than compared with the ATF-2 pathway at higher concentrations of TNF (Fig. 3D).
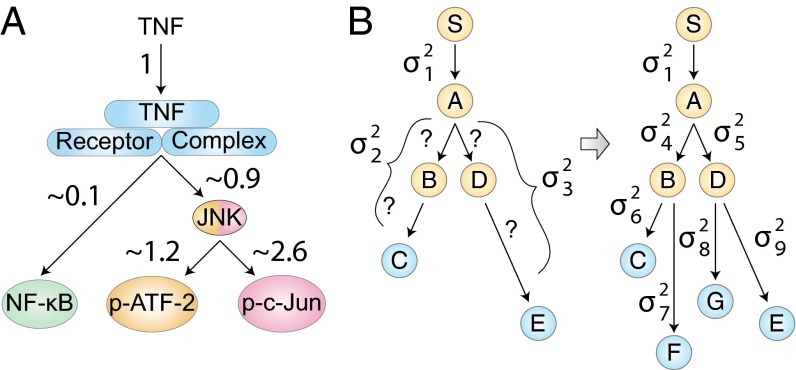
The pairwise analysis can be used to assign relative noise contributions to each part of the TNF signaling network (Fig. 4A). For instance, if as a reference we assign a noise value of 1 to the initial TNF–TNFR segment, then the noise value in the TNFR–NF-κB segment is ∼0.1 (SI Text). This is consistent with our above observation that the TNF–TNFR signaling segment contributes ∼90% of the total noise in the TNF–NF-κB pathway and the downstream NF-κB component contributes the remaining ∼10%. Similar calculations can be used to compute the relative noise contributions from the remaining segments (SI Text). This analysis yields the relative noise values shown in Fig. 4A. Interestingly, the total noise of the TNF–NF-κB pathway is ∼32% of the noise present in the TNF–ATF-2 pathway and 26% of the noise in the TNF–c-Jun pathway, indicating an asymmetry of pathway-specific noise between the JNK and NF-κB branches in TNF signal processing. This result corroborates our prior results, which demonstrated that the information carrying capacity of the NF-κB pathway is greater than that of the JNK pathway, with the capacity of both pathways influenced by a common TNF receptor-level bottleneck (21).
Fig. 4.
(A) TNF signaling network noise normalized to the noise that is contributed by the common TNF–TNFR segment, based upon the data in Fig. 3 B–D. The map demonstrates asymmetry in the amount of noise contributed by the NF-κB and JNK pathways and shows that the majority of noise in the JNK pathway is contributed downstream of the TNF receptor complex. (B) Illustration of a noise decomposition of a larger network. Given a hypothetical signaling network of six nodes and two readouts (C and E), only three noise values can be ascertained. With the addition of two new readouts (F and G), a more comprehensive noise decomposition map can be constructed that can guide further investigations.
Because of the inherent scalability, this noise decomposition methodology can be easily expanded to analyze the noise propagation through larger signaling networks. For example, given a hypothetical signaling network (Fig. 4B) and the two downstream readouts, and , we can provide only limited noise mapping: the noise contribution of the and pathway segments in addition to the trunk noise. However, with the addition of two more readouts ( and ), we can in principle resolve seven noise values and reconstruct a detailed noise decomposition of the entire network. Such a network noise map would allow one to further investigate portions of the network to find molecular mechanisms that regulate variability.
Impact of Feedback on Transcription Factor Variability
Negative feedback is a well-known mechanism that cells can use to modulate biochemical noise (29–31). To quantitatively demonstrate the effect of negative feedback on noise in TNF signaling, we performed a noise decomposition in wild-type cells and cells lacking A20, an enzyme up-regulated by NF-κB that is well-known to inhibit TNF-induced NF-κB activity by destabilizing the TNF receptor complex (32–35) (Fig. 5A). Destabilization of the receptor complex has also been reported to mitigate downstream JNK activation (36); however, this mechanism is still controversial (37, 38).
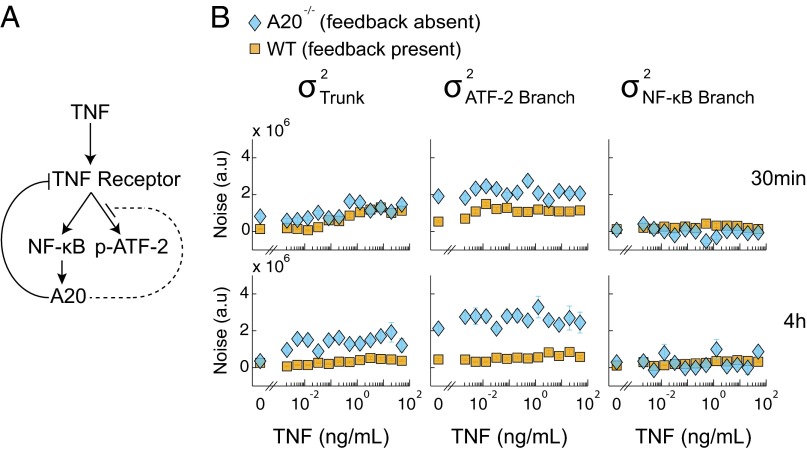
Fig. 5.
(A) Schematic of the A20 feedback loop. At 4 h, after up-regulation, A20 interferes with the functionality of the TNF receptor complex (solid line) and inhibits the activation of ATF-2 (dotted line). (B) Noise decomposition of the TNF–NF-κB–ATF-2 signaling pathway in WT and A20−/− cells at 30 min and 4 h. Absence of the A20 protein does not affect the noise in the NF-κB branch but causes an increase in the amount of noise in the trunk and ATF-2 branch at both 30 min and 4 h. This observation corroborates known information about the mechanisms of A20 regulation.
We also compared the noise decompositions at the 30-min and 4-h time point in these cells (Fig. 5B), as induced expression of A20 is negligible at the earlier time point but maximal by the latter time point (Fig. S5) (39, 40). Importantly, there exists a consistent linear relationship between NF-κB and p-ATF-2 across two time points and across both wild-type and A20−/− cells, enabling direct comparison of the noise decomposition results among all four conditions (Fig. S3B).
At the 30-min time point, we observed that the trunk noise was, on average, slightly greater in A20−/− cells than wild-type cells, whereas there was no difference in NF-κB–specific noise (Fig. 5B). The difference in trunk noise was greater at the 4-h time point, likely reflecting the difference between the effects of lower basally expressed A20 versus that of highly induced A20. These results corroborate the ability of A20 to regulate both NF-κB and JNK pathways at the receptor complex level. Unexpectedly, we also observed larger ATF-2 branch-specific noise in A20−/− cells compared with wild-type cells with the difference greater at the 4-h time point than at the 30-min time point. This result indicated that A20 can repress the JNK pathway independent from its effects on the TNF receptor complex. At the time that this prediction was made, there was no known direct inhibition of the JNK pathway by A20, but a later study by Won et al. verified that A20 directly represses ASK1, a kinase in the JNK pathway that has no known direct effects on the NF-κB pathway (38). We note that although negative feedback could potentially violate our assumption that the trunk and branch noise levels are independent, this experiment demonstrates that on a practical basis, our noise decomposition framework can yield sensible and even predictive results regarding the effects of negative feedback on signaling noise.
Discussion
By using the linear relationships between downstream effectors of the TNF pathway, we developed a mathematical and experimental framework that enables noise decomposition in intracellular signal transduction networks. This method distinguishes trunk from branch noise and can be derived as a natural extension of extrinsic–intrinsic noise analysis. In addition, although these results are independent of the underlying distributions, the methodology can still serve to characterize branch noise distributions. Corroborating previous results, we showed that there is a greater amount of noise present in the JNK branch than the NF-κB branch and that both branches are subject to a sizable contribution of noise from the TNF receptor complex. More detailed noise mapping of the JNK pathway revealed that within the JNK subnetwork, p-c-Jun is subject to greater noise than p-ATF-2.
Examining the impact of negative feedback on noise expression, we found further evidence that A20 is able to suppress variability at the level of the TNF receptor. We also unexpectedly discovered an additional mechanism of JNK noise suppression consistent with a recent observation of the direct inhibition of ASK1 by A20. Although negative feedback and reporter competition over common regulators can theoretically complicate the mathematical decomposition by allowing interactions between noise parameters (17), we nonetheless observed that the nonequivalent dual-reporter method can be robust to the presence of negative feedback and can provide a useful, and even predictive, first approximation. Furthermore, at a minimum, the noise analysis presented here can be used to characterize the noise and serve as a comparison against predictions developed by computational models.
Although this method requires a linear relationship between the reporters, we believe it does not tightly constrain the general applicability. In most biological signaling systems, nonlinear dose–responses align to allow for optimal information transfer which results in responses that are approximately linearly related to each other (31). Furthermore, we expect that in the case of nonlinear relationships between reporters, this method can be easily extended by replacing the slope parameter with the local slope without loss of general applicability. Indeed, the basis used for decomposition could be a curve, a two-dimensional surface, or higher-dimensional manifold depending on the number of responses of interest and their interrelationships.
We envision that this method and further generalizations could enable better measurements of noise which will clarify its molecular underpinnings and aid us in understanding the nature of variability within signaling pathways.
Materials and Methods
Cell Culture.
Wild-type and A20−/− 3T3-immortalized mouse embryonic fibroblasts (gift from A. Hoffmann, University of California, San Diego) were maintained in low-glucose DMEM (Invitrogen) supplemented with 10% calf bovine serum (American Type Culture Collection) and 10 U/mL each of penicillin and streptomycin (Invitrogen). P65-GFP cells (gift from M. Covert, Stanford University, Stanford, CA) were maintained in high-glucose DMEM (Invitrogen) supplemented with 10% FBS (American Type Culture Collection) and 10 U/mL each of penicillin and streptomycin (Invitrogen). Cells were seeded at a density of ∼150 cells per mm2 onto 15-mm-diameter circular coverslips (Fisher Scientific), coated with 0.1% gelatin (Sigma), placed in six well plates, and then serum starved in medium with reduced serum concentration (0.1%) overnight before experimentation.
Immunocytochemistry.
After exposure to murine TNF (Roche) at the specified concentrations and duration, the cells were washed three times with ice-cold PBS (Invitrogen) and fixed in 4% paraformaldehyde (Electron Microscopy Sciences) for 20 min. The cells were then permeabilized in 0.1% triton X-100 (Sigma) for 5 min and blocked in 10% goat serum (Invitrogen) for 60 min. Next, the cells were incubated in primary antibody solution. Primary antibody concentrations used were 1:100 rabbit anti-p65 antibody (Santa Cruz), 1:100 mouse anti-phospho-ATF-2 antibody (Santa Cruz), 1:100 mouse anti-phospho-c-Jun (Santa Cruz), and 1:100 rabbit anti-phospho-c-Jun (Cell Signaling).
Finally, the cells were incubated in a secondary antibody solution consisting of 1:200 Alexa Fluor 488-conjugated goat anti-rabbit and 1:200 Alexa Fluor 594-conjugated goat anti-mouse antibodies (Invitrogen) for 60 min and 2 µg/mL Hoechst-33258 (Sigma) for 60 min. All solutions were made in 10% goat serum (Invitrogen) in PBS, and cells were washed with PBS in between each step. To minimize experimentally induced variability and to enable quantitative comparisons across conditions, all concentrations of TNF and all cell lines were assayed at the same time using common reagents. Finally, the stained coverslips were mounted on glass microscope slides and imaged on an Axiovert 200M inverted epifluorescence microscope (Zeiss) equipped with Slidebook 4.2 (Intelligent Imaging Innovations). On average, over 350 cells were imaged per experimental condition.
Image and Data Analysis.
Image processing and data analysis were performed using MATLAB R2009a (MathWorks). Background correction, nucleus segmentation, and quantification of nuclear concentrations of NF-κB, phospho-ATF-2, and phospho-c-Jun were performed as described previously (21). Programs are available upon request. Top and bottom second percentiles of data were discarded to reduce the influence of outliers on the estimates of variance.
Supplementary Material
Acknowledgments
A.R. and R.C. were supported by National Institutes of Health Grants GM072024 and RR020839. R.C. was supported by the Medical Scientist Training Program at the Johns Hopkins University. A.L. acknowledges support from the Semiconductor Research Corporation SemiSynBio program.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1411932111/-/DCSupplemental.
References
- 1.Dyson S, Gurdon JB. The interpretation of position in a morphogen gradient as revealed by occupancy of activin receptors. Cell. 1998;93(4):557–568. doi: 10.1016/s0092-8674(00)81185-x. [DOI] [PubMed] [Google Scholar]
- 2.Chen SH, Masuno K, Cooper SB, Yamamoto KR. Incoherent feed-forward regulatory logic underpinning glucocorticoid receptor action. Proc Natl Acad Sci USA. 2013;110(5):1964–1969. doi: 10.1073/pnas.1216108110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Bronnikov GE, Zhang SJ, Cannon B, Nedergaard J. A dual component analysis explains the distinctive kinetics of cAMP accumulation in brown adipocytes. J Biol Chem. 1999;274(53):37770–37780. doi: 10.1074/jbc.274.53.37770. [DOI] [PubMed] [Google Scholar]
- 4.McCullagh E, et al. Not all quiet on the noise front. Nat Chem Biol. 2009;5(10):699–704. doi: 10.1038/nchembio.222. [DOI] [PubMed] [Google Scholar]
- 5.Raser JM, O’Shea EK. Noise in gene expression: Origins, consequences, and control. Science. 2005;309(5743):2010–2013. doi: 10.1126/science.1105891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Pedraza JM, van Oudenaarden A. Noise propagation in gene networks. Science. 2005;307(5717):1965–1969. doi: 10.1126/science.1109090. [DOI] [PubMed] [Google Scholar]
- 7.Ozbudak EM, Thattai M, Kurtser I, Grossman AD, van Oudenaarden A. Regulation of noise in the expression of a single gene. Nat Genet. 2002;31(1):69–73. doi: 10.1038/ng869. [DOI] [PubMed] [Google Scholar]
- 8.Raser JM, O’Shea EK. Control of stochasticity in eukaryotic gene expression. Science. 2004;304(5678):1811–1814. doi: 10.1126/science.1098641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Elowitz MB, Levine AJ, Siggia ED, Swain PS. Stochastic gene expression in a single cell. Science. 2002;297(5584):1183–1186. doi: 10.1126/science.1070919. [DOI] [PubMed] [Google Scholar]
- 10.Blake WJ, KÆrn M, Cantor CR, Collins JJ. Noise in eukaryotic gene expression. Nature. 2003;422(6932):633–637. doi: 10.1038/nature01546. [DOI] [PubMed] [Google Scholar]
- 11.Neildez-Nguyen TMA, et al. Epigenetic gene expression noise and phenotypic diversification of clonal cell populations. Differentiation. 2008;76(1):33–40. doi: 10.1111/j.1432-0436.2007.00219.x. [DOI] [PubMed] [Google Scholar]
- 12.Swain PS, Elowitz MB, Siggia ED. Intrinsic and extrinsic contributions to stochasticity in gene expression. Proc Natl Acad Sci USA. 2002;99(20):12795–12800. doi: 10.1073/pnas.162041399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Bowsher CG, Swain PS. Identifying sources of variation and the flow of information in biochemical networks. Proc Natl Acad Sci USA. 2012;109(20):E1320–E1328. doi: 10.1073/pnas.1119407109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Rinott R, Jaimovich A, Friedman N. Exploring transcription regulation through cell-to-cell variability. Proc Natl Acad Sci USA. 2011;108(15):6329–6334. doi: 10.1073/pnas.1013148108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Colman-Lerner A, et al. Regulated cell-to-cell variation in a cell-fate decision system. Nature. 2005;437(7059):699–706. doi: 10.1038/nature03998. [DOI] [PubMed] [Google Scholar]
- 16.Hensel Z, et al. Stochastic expression dynamics of a transcription factor revealed by single-molecule noise analysis. Nat Struct Mol Biol. 2012;19(8):797–802. doi: 10.1038/nsmb.2336. [DOI] [PubMed] [Google Scholar]
- 17.Stamatakis M, Adams RM, Balázsi G. A common repressor pool results in indeterminacy of extrinsic noise. Chaos. 2011;21(4):047523. doi: 10.1063/1.3658618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Friedman N, Cai L, Xie XS. Linking stochastic dynamics to population distribution: An analytical framework of gene expression. Phys Rev Lett. 2006;97(16):168302. doi: 10.1103/PhysRevLett.97.168302. [DOI] [PubMed] [Google Scholar]
- 19.Ashall L, et al. Pulsatile stimulation determines timing and specificity of NF-kappaB-dependent transcription. Science. 2009;324(5924):242–246. doi: 10.1126/science.1164860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Nelson DE, et al. Oscillations in NF-kappaB signaling control the dynamics of gene expression. Science. 2004;306(5696):704–708. doi: 10.1126/science.1099962. [DOI] [PubMed] [Google Scholar]
- 21.Cheong R, Rhee A, Wang CJ, Nemenman I, Levchenko A. Information transduction capacity of noisy biochemical signaling networks. Science. 2011;334(6054):354–358. doi: 10.1126/science.1204553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Tay S, et al. Single-cell NF-kappaB dynamics reveal digital activation and analogue information processing. Nature. 2010;466(7303):267–271. doi: 10.1038/nature09145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Lee TK, et al. A noisy paracrine signal determines the cellular NF-kappaB response to lipopolysaccharide. Sci Signal. 2009;2(93):ra65. doi: 10.1126/scisignal.2000599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Turner DA, et al. Physiological levels of TNFalpha stimulation induce stochastic dynamics of NF-kappaB responses in single living cells. J Cell Sci. 2010;123(Pt 16):2834–2843. doi: 10.1242/jcs.069641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Cheong R, Wang CJ, Levchenko A. High content cell screening in a microfluidic device. Mol Cell Proteomics. 2009;8(3):433–442. doi: 10.1074/mcp.M800291-MCP200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Cai L, Friedman N, Xie XS. Stochastic protein expression in individual cells at the single molecule level. Nature. 2006;440(7082):358–362. doi: 10.1038/nature04599. [DOI] [PubMed] [Google Scholar]
- 27.Cohen AA, et al. Protein dynamics in individual human cells: Experiment and theory. PLoS ONE. 2009;4(4):e4901. doi: 10.1371/journal.pone.0004901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Bar-Even A, et al. Noise in protein expression scales with natural protein abundance. Nat Genet. 2006;38(6):636–643. doi: 10.1038/ng1807. [DOI] [PubMed] [Google Scholar]
- 29.Nevozhay D, Adams RM, Murphy KF, Josic K, Balázsi G. Negative autoregulation linearizes the dose-response and suppresses the heterogeneity of gene expression. Proc Natl Acad Sci USA. 2009;106(13):5123–5128. doi: 10.1073/pnas.0809901106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Nevozhay D, Zal T, Balázsi G. Transferring a synthetic gene circuit from yeast to mammalian cells. Nat Commun. 2013;4:1451. doi: 10.1038/ncomms2471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Yu RC, et al. Negative feedback that improves information transmission in yeast signalling. Nature. 2008;456(7223):755–761. doi: 10.1038/nature07513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Heyninck K, Beyaert R. A20 inhibits NF-kappaB activation by dual ubiquitin-editing functions. Trends Biochem Sci. 2005;30(1):1–4. doi: 10.1016/j.tibs.2004.11.001. [DOI] [PubMed] [Google Scholar]
- 33.Coornaert B, Carpentier I, Beyaert R. A20: Central gatekeeper in inflammation and immunity. J Biol Chem. 2009;284(13):8217–8221. doi: 10.1074/jbc.R800032200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Vereecke L, Beyaert R, van Loo G. The ubiquitin-editing enzyme A20 (TNFAIP3) is a central regulator of immunopathology. Trends Immunol. 2009;30(8):383–391. doi: 10.1016/j.it.2009.05.007. [DOI] [PubMed] [Google Scholar]
- 35.Baer M, et al. Tumor necrosis factor alpha transcription in macrophages is attenuated by an autocrine factor that preferentially induces NF-kappaB p50. Mol Cell Biol. 1998;18(10):5678–5689. doi: 10.1128/mcb.18.10.5678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Devin A, Lin Y, Liu ZG. The role of the death-domain kinase RIP in tumour-necrosis-factor-induced activation of mitogen-activated protein kinases. EMBO Rep. 2003;4(6):623–627. doi: 10.1038/sj.embor.embor854. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Kelliher MA, et al. The death domain kinase RIP mediates the TNF-induced NF-kappaB signal. Immunity. 1998;8(3):297–303. doi: 10.1016/s1074-7613(00)80535-x. [DOI] [PubMed] [Google Scholar]
- 38.Won M, et al. Novel anti-apoptotic mechanism of A20 through targeting ASK1 to suppress TNF-induced JNK activation. Cell Death Differ. 2010;17(12):1830–1841. doi: 10.1038/cdd.2010.47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Werner SL, et al. Encoding NF-kappaB temporal control in response to TNF: Distinct roles for the negative regulators IkappaBalpha and A20. Genes Dev. 2008;22(15):2093–2101. doi: 10.1101/gad.1680708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Hoffmann A, Levchenko A, Scott ML, Baltimore D. The IkappaB-NF-kappaB signaling module: Temporal control and selective gene activation. Science. 2002;298(5596):1241–1245. doi: 10.1126/science.1071914. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.