Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2014 Oct 30;79(23):11370–11377. doi: 10.1021/jo5015728

Terminal Substituent Effects on the Reactivity, Thermodynamics, and Stereoselectivity of the 8π–6π Electrocyclization Cascades of 1,3,5,7-Tetraenes

Ashay Patel 1, K N Houk 1,*
PMCID: PMC4260667  PMID: 25358094

Abstract

graphic file with name jo-2014-015728_0013.jpg

M06-2X/6-31+G(d,p) computations are reported for the 8π–6π electrocyclization cascades of 1,3,5,7-tetraenes. The rate-determining step for these cascades is typically the second (6π) ring closure. According to experiment and theory, un- and monosubstituted tetraenes readily undergo 8π electrocyclic ring closure to form 1,3,5-cyclooctatrienes; however, the 6π electrocyclizations of these cyclooctatriene intermediates are slow and reversible, and mixtures of monocyclic and bicyclic products are formed. Computations indicate that di- and trisubstituted tetraenes undergo facile but less exergonic 8π electrocyclization due to a steric clash that destabilizes the 1,3,5-cyclooctatriene intermediates. Relief of this steric clash ensures the subsequent 6π ring closures of these intermediates are both kinetically facile and thermodynamically favorable, and only the bicyclic products are observed for the cascade reactions of naturally occurring tri- and tetrasubstituted tetraenes (in agreement with computations). The 6π electrocyclization step of these cascade electrocyclizations is also potentially diastereoselective, and di- and trisubstituted tetraenes often undergo cascade reactions with high diastereoselectivities. The exo mode of ring closure is favored for these 6π electrocyclizations due to a steric interaction that destabilizes the endo transition state. Thus, theory explains both the recalcitrance of the unsubstituted 1,3,5,7-octatetraene and 1-substituted tetraenes toward formation of the bicyclo[4.2.0]octa-2,4-diene products, as well as the ease and the stereoselectivity with which terminal di- and trisubstituted tetraenes are known to react biosynthetically.

Introduction

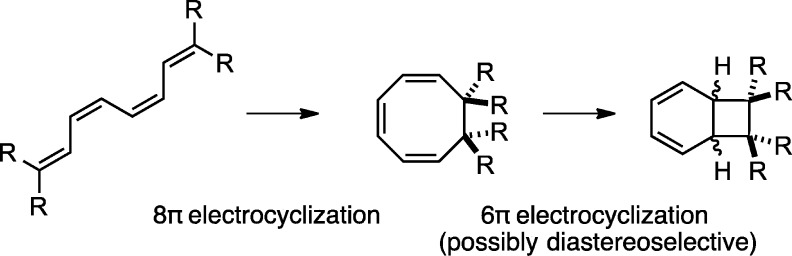
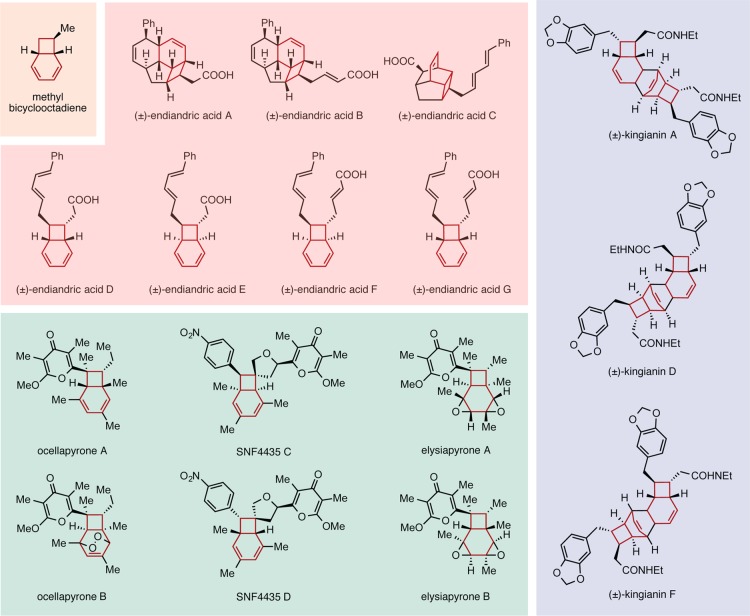
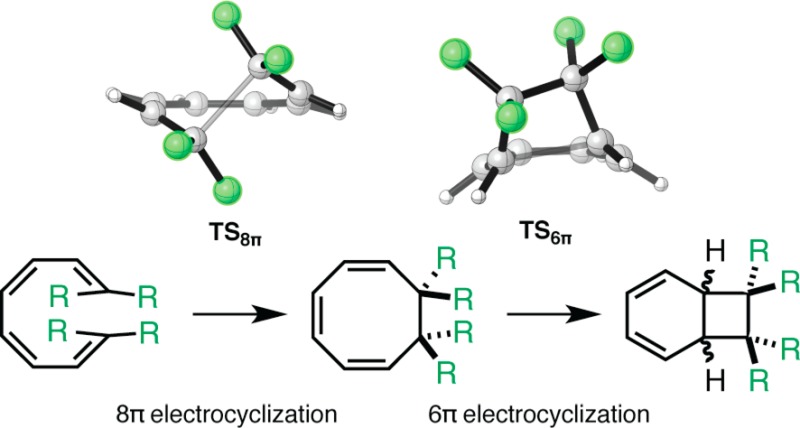
The 8π–6π electrocyclization cascade of the 1,3,5,7-tetraene shown in Scheme 1 is an important transformation in biosynthesis and chemical synthesis. A selection of natural products formed by such cascades is shown in Scheme 2. Black and colleagues’ original proposal1 that the endiandric acids are biosynthesized via nonenzymatic 8π–6π electrocyclizations prompted Nicolaou et al.2−5 to develop a biomimetic synthetic strategy to access members of this family of natural products. Their studies validated Black and co-workers’ biosynthetic proposal. Since the initial isolation of the endiandric acids, a number of additional metabolites arising from this pericyclic cascade have emerged (see Scheme 2).6−10 Subsequent biomimetic syntheses of those molecules by Trauner,11−14 Baldwin,15−19 Parker,20 and Sherburn21 have demonstrated the generality of this electrocyclization cascade. With the exception of the elysiapyrones,22 most of these natural products exist as racemates, suggesting that the cascade reactions can readily occur without catalysis by an enzyme.

Scheme 1. 8π–6π Electrocyclization.

Scheme 1

Open in a new tab

Scheme 2. Examples of Natural Products Formed by Biosynthetic and Biomimetic 8π–6π Electrocyclization Cascades.

Scheme 2

Open in a new tab

Terminal substitution of the tetraene reactants has been shown to strongly influence the chemistry of these 8π–6π electrocyclization cascades. These substituents affect, in particular, the kinetics, thermodynamics, and diastereoselectivity.23−27 Despite the importance of this electrocyclization cascade in biosynthesis and the attention it has received from the synthetic community, no systematic investigation of the influence of terminal subsititution on the cascade reaction has been reported. We performed a density functional theory (M06-2X) study to address this problem. The data from this study reveal that terminal substitution reduces the exothermicity of the 8π electrocyclization step of the cascade and that the second ring closure is both kinetically and thermodynamically more favorable. For those substrates that undergo 8π ring closure to form chiral 1,3,5-cyclooctatrienes, our work shows that the observed diastereoselectivity of the transannular 6π ring closure arises from the steric destabilization of the endo mode of 6π ring closure. We anticipate that these findings will inform the design of synthetic strategies for the stereoselective formation of new bicyclo[4.2.0]octa-2,4-diene scaffolds.

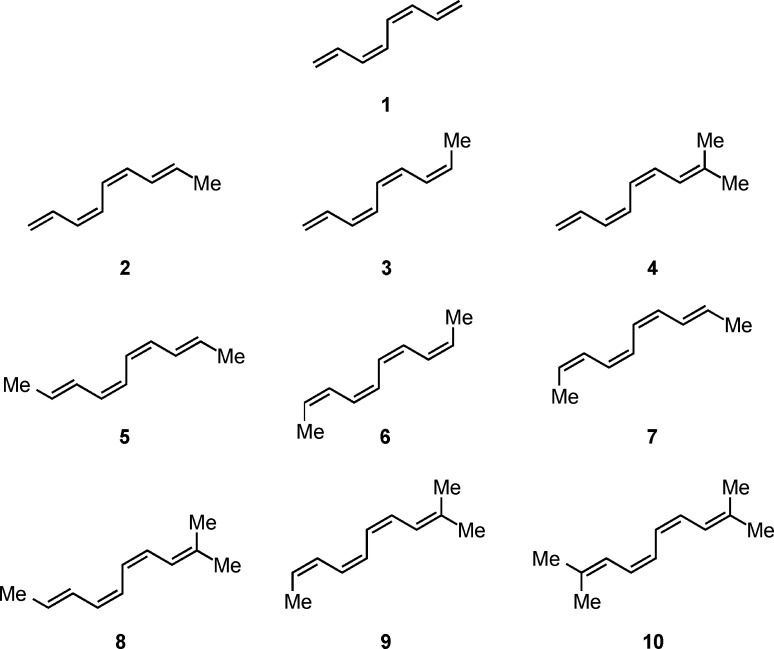
The tetraenes examined here are shown in Scheme 3. The kinetics and thermodynamics of the electrocyclic reactions of 1, 2, 5, 6, and 7 have been experimentally studied previously.24,28,29 Tetraenes 5 and 6 possess substitution patterns similar to those used in the synthesis of the endiandric acids and kinganian natural products, whereas trisubstituted tetraenes 8 and 9 resemble the starting materials used for the preparation of the pyrone-containing natural products (green box in Scheme 1).11−21 The electrocyclization cascades of 4 and 10 have not been studied experimentally, and metabolites arising from tetraenes possessing the same substitution patterns as 4 and 10 have not been isolated. The 8π ring closures of 4, 5, 6, and 10 yield achiral 1,3,5-cyclooctatrienes; thus, the 6π electrocycliczation of these cyclooctatrienes cannot be diastereoselective.

Scheme 3. Set of 1,3,5,7-Octatetraenes (1–10) Examined in This Study.

Scheme 3

Open in a new tab

Results and Discussion

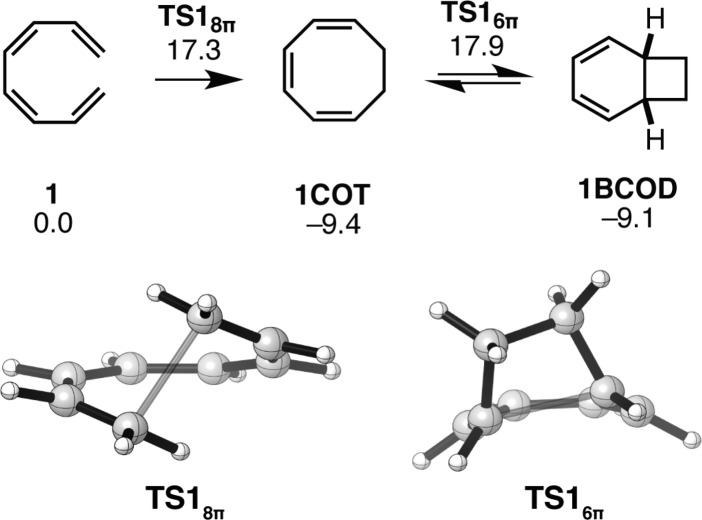
The energetics and the transition states for the 8π–6π electrocyclization cascade of 1 are shown in Figure 1. Goldfarb and Lindqvist reported that 1,3,5,7-octatetraene undergoes 8π ring closure with an activation enthalpy of about 17 kcal mol–1;28 Pohnert and Boland have expressed concern that this value may be an overestimate, as they have determined that the 8π electrocyclization of tetraene 2, which shows reactivity similar to that of substrate 1, has a ΔH⧧298.15 K of 13.6 kcal mol–1.29 Our computed ΔH⧧ value (ca. 14.5 kcal mol–1) is in closer agreement with Pohnert and Boland’s experimental data and constitutes a significant improvement in accuracy compared with previously reported Hartree–Fock or MP2 data.30 The half-life of the 8π ring closure is 0.5 s (ΔG⧧ = 17 kcal mol–1). The formation of 1,3,5-cyclooctatriene (1COT) is exergonic by 9 kcal mol–1.

Figure 1.

Figure 1

Open in a new tab

Gibbs free energy profile and transition structures for the 8π–6π ring closure cascade of unsubstituted tetraene 1. Structures and free energies (kcal mol–1) determined using the M06-2X/6-31+G(d,p) level of theory.

Experimentally, the thermal isomerization of 1 does not yield bicyclo[4.2.0]octa-2,4-diene (1BCOD) unless performed at elevated temperatures. Computations can explain this observation: The 8π and 6π electrocyclization transition states of 1 are nearly isoenergetic; however, the cyclooctatriene 1COT is significantly more stable than its tetraene precursor. It is for this reason that the rate-determining step for the cascade reaction of compound 1 is the 6π electrocyclization with a Gibbs free energy of activation of 27 kcal mol–1, corresponding to a reaction half-life of approximately 130 days at room temperature. The 8π product 1COT and the cascade product 1BCOD are isoenergetic and are predicted to be observed in almost equal amounts if the cascade reaction is under thermodynamic control.

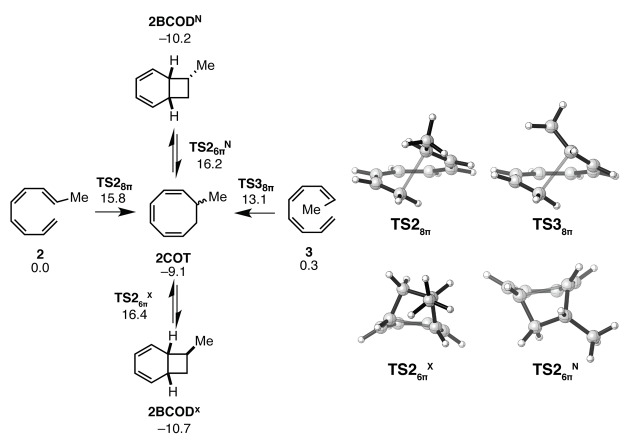
The energy profiles for the cascade reactions of the monosubstituted tetraenes 2 and 3 are qualitatively similar to that for 1; the initial 8π electrocyclizations are facile and exothermic, while the subsequent 6π ring closures are significantly more sluggish (see Figure 2 for ΔGrxn and ΔG⧧ values). The monosubstituted Z-tetraene 3 is approximately 100-fold more reactive (at room temperature) toward 8π ring closure than the E-tetraene 2. Presumably, the Z isomer is more reactive toward 8π ring closure due to greater strain relief that occurs upon pyramidalization of the substituted carbon at the transition state. The computed ΔH⧧ value of 13.6 kcal mol–1 for the 8π electrocyclization of 2 is in excellent agreement with the experimental ΔH⧧298.15K value of 13.4 kcal mol–1 as determined by Pohnert and Boland.29

Figure 2.

Figure 2

Open in a new tab

Gibbs free energy profile and transition structures for the 8π–6π ring closure cascade of monosubstituted tetraenes 2 and 3. Structures and free energies (kcal mol–1) determined using the M06-2X/6-31+G(d,p) level of theory.

Experimentally, only at high temperatures are 2BCODX and 2BCODN, the products of the 6π ring closure of intermediate 2COT, observed,29 and then only as minor products in relation to the cyclooctatriene 2COT. Our computations indicate that the bicyclic species 2BCODX and 2BCODN are slightly more stable than 2COT. This preference is small, and the deviation between theory and experiment is well within the computational error of our method. Because the 1,3,5-cyclooctatriene 2COT formed from 2 and 3 is chiral, the ensuing 6π ring closure produces diastereomeric products. According to computations, this ring closure is nonselective, in agreement with experiment. The exo and endo transition states TS26πX and TS26πN are shown in Figure 2. A single terminal methyl substituent alone does not exert a strong influence on the stereochemical course of the second ring closure because it can occupy a sterically uncongested position in both transition states.

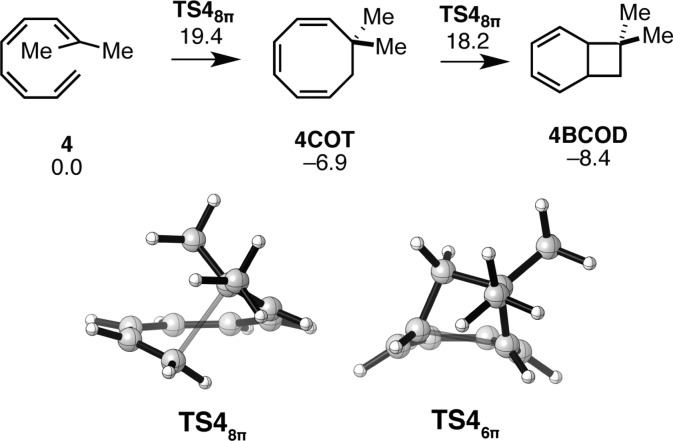
The reactivity of 4 resembles those of model substrates 1–3; because the 8π electrocyclization of 4 results in the formation of an achiral 1,3,5-cyclooctatriene (4COT) (Figure 3), the subsequent 6π electrocyclization cannot be stereoselective. The 8π ring closure of 4 is predicted to be a facile means of generating a quaternary center in a medium-sized ring.

Figure 3.

Figure 3

Open in a new tab

Gibbs free energy profile and transition structures for the 8π–6π ring closure cascade of gem-disubstituted tetraene 4. Structures and free energies (kcal mol–1) determined using the M06-2X/6-31+G(d,p) level of theory.

Huisgen and co-workers have studied the kinetics of the thermal isomerizations of tetraenes 5–7 experimentally.23−25 The computed data are shown in Figures 4 and 5. The reactions of substrates 5 and 6 correspond to reactions involved in the biosyntheses of the endiandric acid and kinginian families of natural products. The 8π electrocyclization of tetraene 5 proceeds with a ΔH⧧298.15K of 15.1 kcal mol–1,24 similar to the computed value of 14.4 kcal mol–1 (Figure 4). In the case of the 8π electrocyclization of 6, the computed value of ΔH⧧298.15K of 17.6 kcal mol–1 is at variance with the experimental value24 of 21.8 kcal mol–1 by approximately 4 kcal mol–1. The thermodynamic product of the 8π–6π electrocyclization of 5 and 6 is 5BCOD, although computations overestimate the stability of the bicyclic product.25

Figure 4.

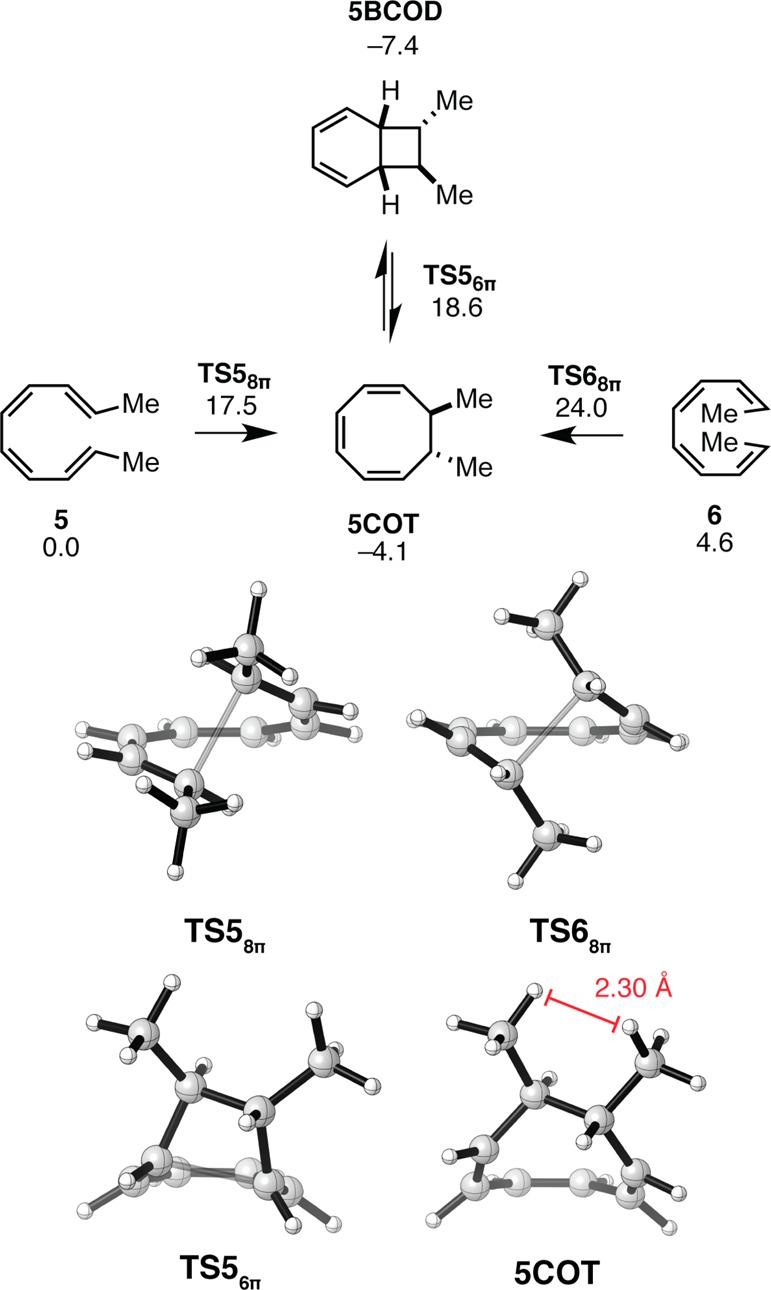
Figure 4

Open in a new tab

Gibbs free energy profile and transition structures for the 8π–6π ring closure cascade of disubstituted tetraenes 5 and 6. Structures and free energies (kcal mol–1) determined using the M06-2X/6-31+G(d,p) level of theory.

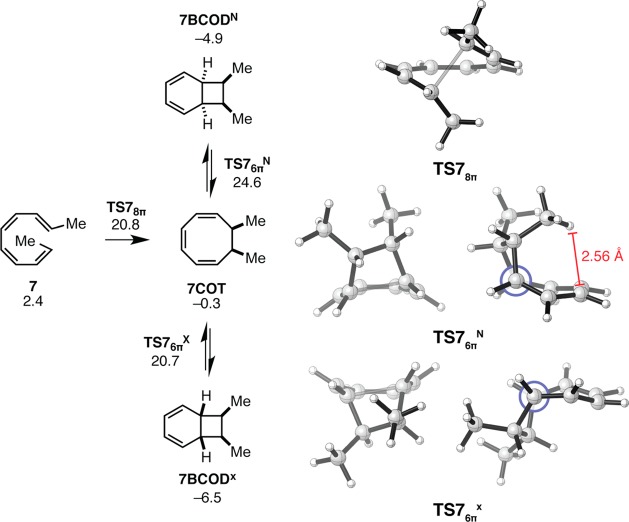
Figure 5.

Figure 5

Open in a new tab

Gibbs free energy profile and transition structures for the 8π–6π ring closure cascade of tetraene 7. Structures and free energies (kcal mol–1) determined using the M06-2X/6-31+G(d,p) level of theory. Both a front view and a side view (Newman projection along the forming bond also shown) of TS76πN and TS76πX are provided. Note the energies shown are relative to that of the most stable 1,8-dimethyl tetraene, 5.

The 8π ring closures of tetraenes 5 and 6 are approximately 5 kcal mol–1 less exergonic than those of 1–3 (ΔGrxn = −4 and −9 kcal mol–1, respectively) because the product 5COT is destabilized by steric repulsion between vicinal methyl groups at the 7 and 8 positions of the cyclooctatriene (shown in Figure 4, H–H distance of 2.30 Å). The ΔG⧧ of 6π electrocyclization of 5COT is 23 kcal mol–1, and 5BCOD is 3 kcal mol–1 more stable than its cyclooctatriene precursor. The increased reactivity of 5COT relative to 1COT (ΔΔG⧧6π = 4 kcal mol–1) and the increased stability of the bicyclo[4.2.0]octadiene resulting from the ring closure of 5COT is due to relief of the steric clash found in 5COT. Neither TS56π nor 5BCOD features a clash between the vicinal methyl groups. What prevents the C7 and C8 methyl substituents from clashing with one another in TS56π and 5BCOD? Formation of a strained four-membered ring leads to compression of the C5–C6–C7 and C1–C7–C6 angles from approximately 110° to 90°. Compression of these internal angles of the cyclobutane is accompanied by a widening of the external angles of the ring, which results in the positioning of the vicinal methyl groups far enough away from one another that they no longer clash.

The activation free energy (ca. 21 kcal mol–1) for the first step of the cascade process for the electrocyclization of 7 is similar to those of tetraenes 5 and 6, differing by only 4 and 2 kcal mol–1, respectively. The computed ΔH⧧298.15K for the conversion of 7 into 7COT is 1.4 kcal mol–1 lower than the experimental value of 17.8 kcal mol–1. The 8π electrocylic reaction of 7 is 1 kcal mol–1 less exergonic than those of 5 and 6. Like intermediate 5COT, 7COT is destabilized by steric repulsion between the C7 and C8 methyl groups. In fact, the steric clash between the syn-methyl groups of 7COT is more severe than the clash present in 5COT. As found for the 6π electrocyclization of 5COT, relief of steric strain explains the favorable kinetics and thermodynamics for the second ring closure.

According to computations, the second step of the cascade, the 6π electrocyclization, occurs with exclusive selectivity for the exo diastereomer, 7BCODX. The transition states for the 6π ring closure of 7COT are shown in Figure 5. A destabilizing steric clash in the endo transition state (TS76πN) is responsible for this preference. Natural products featuring a cis arrangement of the C7 and C8 substituents (as in 7BCODX) have not been reported.

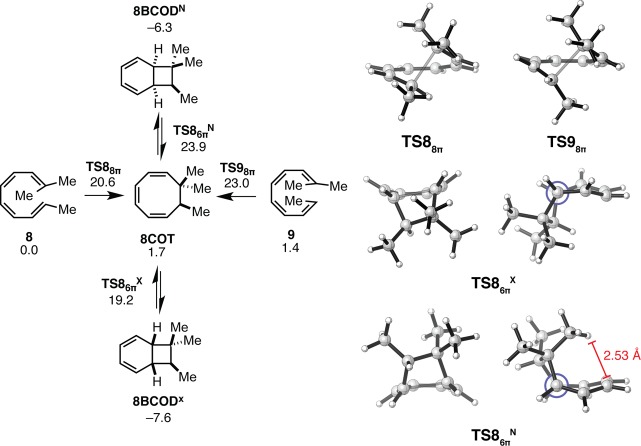
The 8π–6π electrocyclic reactions of trisubstituted tetraenes 8 and 9, which resemble reactions used by nature to synthesize the γ-pyrone-containing metabolites, are both facile and selective. Both electrocyclic reactions have similar ΔG⧧ values, and the rate-determining step of the cascades is now the 8π electrocyclization. The formation of 8BCOD is exergonic. Figure 6 shows the 8π and 6π electrocyclization transition states of substrates 8 and 9. The formation of the 8COT intermediate is endergonic by 2 kcal mol–1. Steric repulsion is more severe in 8COT than in 6COT or 7COT due to the presence of a third methyl substituent in 8COT, which introduces a second steric clash. Relief of both clashes by the geometric changes occurring during formation of the cyclobutane ring of 8BCOD explains the high reactivity of 8COT. The ring closure of intermediate 8COT is also highly diastereoselective (ΔΔG⧧ = 4.7 kcal mol–1), exclusively forming 8BCODX. In fact, our computations overestimate the diastereoselectivity of this ring closure on the basis of the biomimetic tandem electrocyclizations used to synthesize the elysiapyrones and SNF4435 C and D.11−13,15,16,18,20,22 Structural differences between the substrates studied computationally and those used by nature to construct these natural products, including the presence of additional substituents, may be responsible for this lack of quantitative agreement. Qualitatively, the diastereoselectivity of this ring closure can be rationalized using the same argument made to explain the selectivity of the 6π electrocyclization of the disubstituted cyclooctatriene 7COT. A steric effect destabilizes the endo transition state. This effect is responsible for increased closed-shell repulsion and geometric distortion of TS86πN.

Figure 6.

Figure 6

Open in a new tab

Gibbs free energy profile and transition structures for the 8π–6π ring closure cascade of trisubstituted tetraenes 8 and 9. Structures and free energies (kcal mol–1) determined using the M06-2X/6-31+G(d,p) level of theory. Both a front view and a side view (Newman projection) of TS86πN and TS86πX are provided.

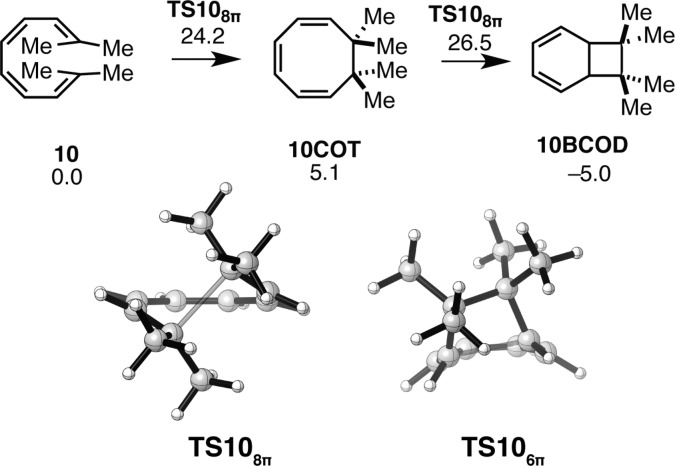
The reaction of the tetrasubstituted tetraene 10 has a ΔG⧧ = 24.2 kcal mol–1 (see Figure 7). Tetrasubstitution destabilizes the cyclooctatriene intermediate such that the initial 8π electrocyclization is endergonic. Thermodynamically, the formation of the bicyclic product 10BCOD remains favorable. Although tetrasubstituted tetraenes like 10 are not known in nature, these results suggest that the formation of two vicinal quaternary centers via an 8π–6π electrocyclization cascade is possible.

Figure 7.

Figure 7

Open in a new tab

Gibbs free energy profile and transition structures for the 8π–6π ring closure cascade of tetrasubstituted tetraene 10. Structures and free energies (kcal mol–1) determined using the M06-2X/6-31+G(d,p) level of theory.

Conclusions

Table 1 summarizes the results of our computational investigation of tetraenes 1–10. While 1–4 only undergo 8π electrocyclization, 5–10 readily undergo both steps of the 8π–6π electrocyclization cascade. Destabilization of the 1,3,5-cyclooctatriene intermediates by steric repulsion of vicinal groups at the 7 and 8 positions of cyclooctatrienes 5BCOD, 7BCOD, 8BCOD, and 10BCOD reduces the barriers of the 6π ring closures of these intermediates, explaining why the cascade reactions of 5–10 are so efficient. Tetraenes 7–9 yield chiral 1,3,5-cyclooctatrienes that are predicted to undergo highly diastereoselective 6π ring closures, favoring the formation of the exo mode of disrotatory ring closure. The diastereoselectivities in these cases are attributed to a destabilizing steric clash in the endo transition state. Lastly, by modeling the cascade electrocyclizations of tetraene 10, we demonstrate a potential means of generating vicinal quaternary centers in a single chemical step.

Table 1. Summary of M06-2X/6-31+G(d,p)-Computed Activation and Reaction Free Energies for Cascade Ring Closures of Tetraenes 1–10e.

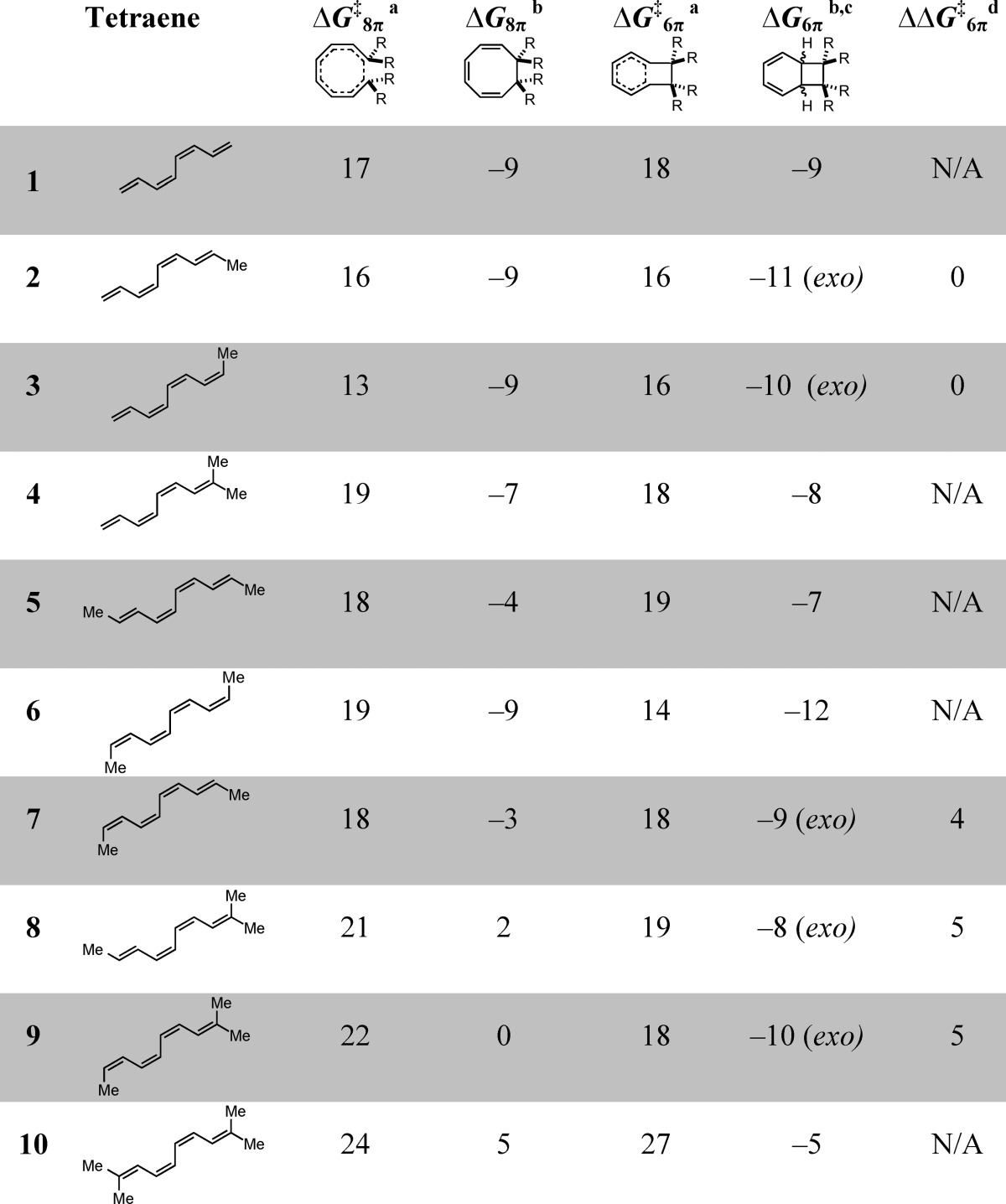
graphic file with name jo-2014-015728_0012.jpg

Open in a new tab
a

ΔG⧧8π and ΔG⧧6π are the free energies of activation for 8π and 6π ring closure of the indicated tetraene, respectively.

b

The reaction energies for the 8π and 6π electrocyclizations are, respectively, ΔG8π and ΔG6π.

c

The exo and endo designations indicate which of the two stereoproducts is more stable (where relevant).

d

Free energy difference between the endo and exo 6π ring closure transition states.

e

All Gibbs free energies are reported in kilocalories per mole and were calculated using the tetraene precursor as the point of reference.

Computational Methods

All computations were performed using Gaussian09 (revision D.01).31 Geometry optimizations and frequency calculations were carried out using the M06-2X32 metahybrid functional with the 6-31+G(d,p) basis set. The M06-2X functional was chosen for its accuracy in modeling main group chemistry.33 The B3LYP/6-31G(d) model chemistry was also tested; however, it was inferior in terms of accuracy to the M06-2X/6-31+G(d,p) level of theory. The details of the B3LYP/6-31G(d) computations are presented in the Supporting Information. The structures described herein are the lowest energy M06-2X/6-31+G(d,p)-optimized conformers. For the M06-2X/6-31+G(d,p) computations, a numerical integration grid consisting of 99 radial shells and 590 angular points per shell was employed. All stationary points were characterized as minima or transition states on the basis of normal vibrational mode analysis. Thermal corrections were computed from unscaled frequencies, assuming a standard state of 298.15 K and 1 atm. The vibrational partition functions used to calculate the entropic contributions of the Gibbs free energies were evaluated using Truhlar’s quasiharmonic approximation, in which all vibrational modes with frequencies below 100 cm–1 were raised to 100 cm–1 to reduce errors arising from the treatment of low modes as harmonic oscillations.34,35 The computed structures were rendered using the CYLview software.36 Gaussview37 and Avogadro38,39 were used to generate input geometries and visualize output structures.

Acknowledgments

We are grateful to the National Science Foundation (NSF) (Grants CHE 10509084 and CHE 1361104 to K.N.H.) for financial support of this research. A.P. thanks the Chemistry-Biology Interface Training Program (National Institutes of Health Grant T32 GM 008496) for support. Computations were performed using UCLA’s Hoffman2 cluster as well as the Extreme Science and Engineering Design Environment’s (Grant TG CHE 040013N) Gordon and Trestles supercomputers at the San Diego Supercomputing Center. We acknowledge Dr. Colin Lam for helpful discussions and his critical reading of this manuscript.

Supporting Information Available

Cartesian coordinates for all stationary points, electronic energies, zero-point energies (ZPEs), and thermal energy corrections of all reported structures, details regarding conformational analysis and the influence of non-alkyl substituents, and discussion of B3LYP/6-31G(d) computations. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States

Supplementary Material

jo5015728_si_001.pdf (597.4KB, pdf)

References

  1. Bandaranayake W. M.; Banfield J. E.; Black D. S. C. J. Chem. Soc., Chem. Commun. 1980, 902–903. [Google Scholar]
  2. Nicolaou K. C.; Zipkin R. E.; Petasis N. A. J. Am. Chem. Soc. 1982, 104, 5555–5557. [Google Scholar]
  3. Nicolaou K. C.; Zipkin R. E.; Petasis N. A. J. Am. Chem. Soc. 1982, 104, 5557–5558. [Google Scholar]
  4. Nicolaou K. C.; Petasis N. A.; Zipkin R. E. J. Am. Chem. Soc. 1982, 104, 5558–5560. [Google Scholar]
  5. Nicolaou K. C.; Petasis N. A.; Zipkin R. E. J. Am. Chem. Soc. 1982, 104, 5560–5562. [Google Scholar]
  6. Kurosawa K.; Takahashi K.; Tsuda E. J. Antibiot. 2001, 54, 541–547. [DOI] [PubMed] [Google Scholar]
  7. Takahashi K.; Tsuda E.; Kurosawa K. J. Antibiot. 2001, 54, 548–553. [DOI] [PubMed] [Google Scholar]
  8. Manzo E.; Ciavatta M. L.; Gavagnin M.; Mollo E.; Wahidulla S.; Cimino G. Tetrahedron Lett. 2005, 46, 465–468. [Google Scholar]
  9. Leverrier A.; Dau M. E. T. H.; Retailleau P.; Awang K.; Guéritte F.; Litaudon M. Org. Lett. 2010, 12, 3638–3641. [DOI] [PubMed] [Google Scholar]
  10. Leverrier A.; Awang K.; Guéritte F.; Litaudon M. Phytochemistry 2011, 72, 1443–1452. [DOI] [PubMed] [Google Scholar]
  11. Beaudry C. M.; Trauner D. Org. Lett. 2002, 4, 2221–2224. [DOI] [PubMed] [Google Scholar]
  12. Beaudry C. M.; Trauner D. Org. Lett. 2005, 7, 4475–4477. [DOI] [PubMed] [Google Scholar]
  13. Barbarow J. E.; Miller A. K.; Trauner D. Org. Lett. 2005, 7, 2901–2903. [DOI] [PubMed] [Google Scholar]
  14. Miller A. K.; Trauner D. Angew. Chem., Int. Ed. 2005, 44, 4602–4606. [DOI] [PubMed] [Google Scholar]
  15. Moses J. E.; Baldwin J. E.; Marquez R.; Adlington R. M. Org. Lett. 2002, 4, 3731–3743. [DOI] [PubMed] [Google Scholar]
  16. Jacobsen M. F.; Moses J. E.; Adlington R. M.; Baldwin J. E. Org. Lett. 2005, 7, 2473–2476. [DOI] [PubMed] [Google Scholar]
  17. Moses J. E.; Adlington R. M.; Rodriguez R.; Eade S. J.; Baldwin J. E. Chem. Commun. 2005, 1687–1689. [DOI] [PubMed] [Google Scholar]
  18. Jacobsen M. F.; Moses J. E.; Adlington R. M.; Baldwin J. E. Tetrahedron 2006, 62, 1675–1689. [Google Scholar]
  19. Eade S. J.; Walter M. W.; Byrne C.; Odell B.; Rodriguez R.; Baldwin J. E.; Adlington R. M.; Moses J. E. J. Org. Chem. 2008, 73, 4830–4839. [DOI] [PubMed] [Google Scholar]
  20. Parker K. A.; Lim Y.-H. J. Am. Chem. Soc. 2004, 126, 15968–15969. [DOI] [PubMed] [Google Scholar]
  21. Drew S. L.; Lawrence A. L.; Sherburn M. S. Angew. Chem., Int. Ed. 2013, 52, 4221–4224. [DOI] [PubMed] [Google Scholar]
  22. Cueto M.; D’Croz L.; Maté J. L.; San-Martín A.; Darias J. Org. Lett. 2005, 7, 415–418. [DOI] [PubMed] [Google Scholar]
  23. Huisgen R.; Dahmen A.; Huber H. J. Am. Chem. Soc. 1967, 89, 7130–7131. [Google Scholar]
  24. Huisgen R.; Dahmen A.; Huber H. Tetrahedron Lett. 1969, 10, 1461–1464. [Google Scholar]
  25. Dahmen A.; Huisgen R. Tetrahedron Lett. 1969, 10, 1465–1469. [Google Scholar]
  26. Marvell E. N.; Seubert J. J. Am. Chem. Soc. 1967, 89, 3377–3378. [Google Scholar]
  27. Marvell E. N.; Seubert J. Tetrahedron Lett. 1969, 10, 1333–1336. [Google Scholar]
  28. Goldfarb T. D.; Lindqvist L. J. Am. Chem. Soc. 1967, 89, 4588–4592. [Google Scholar]
  29. Pohnert G.; Boland W. Tetrahedron 1994, 50, 10235–10244. [Google Scholar]
  30. Thomas B. E. IV; Evanseck J. D.; Houk K. N. J. Am. Chem. Soc. 1993, 115, 4165–4169. [Google Scholar]
  31. Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Mennucci B.; Petersson G. A.; Nakatsuji H.; Caricato M.; Li X.; Hratchian H. P.; Izmaylov A. F.; Bloino J.; Zheng G.; Sonnenberg J. L.; Hada M.; Ehara M.; Toyota K.; Fukuda R.; Hasegawa J.; Ishida M.; Nakajima T.; Honda Y.; Kitao O.; Nakai H.; Vreven T.; J A Montgomery J.; Peralta J. E.; Ogliaro F.; Bearpark M.; Heyd J. J.; Brothers E.; Kudin K. N.; Staroverov V. N.; Kobayashi R.; Normand J.; Raghavachari K.; Rendell A.; Burant J. C.; Iyengar S. S.; Tomasi J.; Cossi M.; Rega N.; Millam J. M.; Klene M.; Knox J. E.; Cross J. B.; Bakken V.; Adamo C.; Jaramillo J.; Gomperts R.; Stratmann R. E.; Yazyev O.; Austin A. J.; Cammi R.; Pomelli C.; Ochterski J. W.; Martin R. L.; Morokuma K.; Zakrzewski V. G.; Voth G. A.; Salvador P.; Dannenberg J. J.; Dapprich S.; Daniels A. D.; Farka Ö.; Foresman J. B.; Ortiz J. V.; Cioslowski J.. Gaussian 09, revision D.01; Gaussian, Inc.: Wallingford, CT, 2014. [Google Scholar]
  32. Zhao Y.; Truhlar D. G. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar]
  33. Zhao Y.; Truhlar D. G. Acc. Chem. Res. 2008, 41, 157–167. [DOI] [PubMed] [Google Scholar]
  34. Zhao Y.; Truhlar D. G. Phys. Chem. Chem. Phys. 2008, 10, 2813–2818. [DOI] [PubMed] [Google Scholar]
  35. Ribeiro R. F.; Marenich A. V.; Cramer C. J.; Truhlar D. G. J. Phys. Chem. B 2011, 115, 14556–14562. [DOI] [PubMed] [Google Scholar]
  36. Legault C. Y.CYLview, version 1.0b; Université de Sherbrooke: Sherbrooke, Québec, Canada, 2009. [Google Scholar]
  37. Dennington R.; Keith T.; Millam J.. GaussView, version 5; Semichem Inc.: Shawnee Mission, KS, 2009. [Google Scholar]
  38. Avogadro: an open-source molecular builder and visualization tool, version 1.1.1. http://avogadro.openmolecules.net/, accessed December 12, 2013.
  39. Hanwell M. D.; Curtis D. E.; Lonie D. C.; Vandermeersch T.; Zurek E.; Hutchison G. R. J. Cheminf. 2012, 4, 17. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jo5015728_si_001.pdf (597.4KB, pdf)

Articles from The Journal of Organic Chemistry are provided here courtesy of American Chemical Society

RESOURCES