Relational Machine Learning for Electronic Health Record-Driven Phenotyping

Abstract

Objective

Electronic health records (EHR) offer medical and pharmacogenomics research unprecedented opportunities to identify and classify patients at risk. EHRs are collections of highly inter-dependent records that include biological, anatomical, physiological, and behavioral observations. They comprise a patient’s clinical phenome, where each patient has thousands of date-stamped records distributed across many relational tables. Development of EHR computer-based phenotyping algorithms require time and medical insight from clinical experts, who most often can only review a small patient subset representative of the total EHR records, to identify phenotype features. In this research we evaluate whether relational machine learning (ML) using Inductive Logic Programming (ILP) can contribute to addressing these issues as a viable approach for EHR-based phenotyping.

Methods

Two relational learning ILP approaches and three well-known WEKA (Waikato Environment for Knowledge Analysis) implementations of non-relational approaches (PART, J48, and JRIP) were used to develop models for nine phenotypes. International Classification of Diseases, Ninth Revision (ICD-9) coded EHR data were used to select training cohorts for the development of each phenotypic model. Accuracy, precision, recall, F-Measure, and Area Under the Receiver Operating Characteristic (AUROC) curve statistics were measured for each phenotypic model based on independent manually verified test cohorts. A two-sided binomial distribution test (sign test) compared the five ML approaches across phenotypes for statistical significance.

Results

We developed an approach to automatically label training examples using ICD-9 diagnosis codes for the ML approaches being evaluated. Nine phenotypic models for each MLapproach were evaluated, resulting in better overall model performance in AUROC using ILP when compared to PART (p=0.039), J48 (p=0.003) and JRIP (p=0.003).

Discussion

ILP has the potential to improve phenotyping by independently delivering clinically expert interpretable rules for phenotype definitions, or intuitive phenotypes to assist experts.

Conclusion

Relational learning using ILP offers a viable approach to EHR-driven phenotyping.

1. Introduction

Medical research attempts to identify and quantify relationships between exposures and outcomes. A critical step in this process is subject characterization or phenotyping [1–4]. Without rigorous phenotyping, these relationships cannot be properly assessed, leading to irreproducible study results and associations [1]. With the proliferation of electronic health records (EHRs), computerized phenotyping has become a popular and cost effective approach to identify research subjects [5]. The EHR contains highly inter-dependent biological, anatomical, physiological, and behavioral observations, as well as facts that represent a patient’s diagnosis and medical history. Typically, developing EHR-based phenotyping algorithms requires conducting multiple iterations of selecting patients from the EHR and then reviewing the selections to identify classification features that succinctly categorize them into study groups [6]. This process is time consuming [1] and relies on expert perceptions, intuition, and bias. Due to time limitations, experts carefully examine a small fraction of available EHR data for phenotype development. In addition, due to both the enormous volume of data found in the EHR and human bias, it is difficult for experts to uncover “hidden” relationships or “unseen” features relevant to a phenotype definition. The result is a serious temporal and informative bottleneck when constructing high quality research phenotypes.

The use of machine learning (ML) as an alternative EHR-driven phenotyping strategy has been limited [7–13]. Previous ML studies have applied a variety of standard approaches (e.g. SMO, Ripper, C4.5, Naïve Bayes, Random Forest via WEKA, Apriori, etc.) to coded EHR data in order to identify relevant clinical features or rules for phenotyping. All of these ML methods were propositional, that is, they used data that were placed into a single fixed length, flat feature table for analysis.

Data from EHRs pose significant challenges for such propositional ML and data mining approaches, as previously noted [14]. First, EHRs may include reports on thousands of different conditions across several years. Knowing which features to include in the final feature table and how they relate often requires clinical intuition and a considerable amount of time spent by experts (physicians). Second, EHR data are noisy. For example, in some cases diagnostic codes are assigned to explain that laboratory tests are being done to confirm or eliminate the coded diagnosis, rather than to indicate that the patient actually has the diagnosis. Third, EHR data are highly relational and multi-modal. Known flattening techniques, such as computing summary features or performing a database join operation, can usually result in loss of information [15]. For example, the Observational Medical Outcomes Partnership (OMOP) phenotypes lymphoma as either a temporal sequence initiated with a biopsy or related procedure, followed within 30 days by a 200–202 International Classification of Diseases, Ninth Revision (ICD-9) code, or a 200–202 ICD-9 code followed within 30 days by radiation or a chemotherapeutic treatment [16]. Verifying such a rule requires using data from three different tables and comparing the respective event times. Thus, a flat feature representation for learning ignores the structure of EHR data and, therefore, does not suitably model this complex task. Arguably, more advanced data structures such as trees, graphs, and propositional reasoners can handle the EHR data structure, but these approaches assume a noise free domain and cannot deal with missing or disparate data often present in the EHR [17,18].

Inductive logic programming (ILP), a subfield of relational machine learning, addresses the complexities of dealing with multi-relational EHR data [15] and has the potential to learn features without the existential perceptions of experts. ILP has been used in medical studies ranging from predictive screening for breast cancer [19,20] to predicting adverse drug events [14,21,22] or adverse clinical outcomes [23–25]. Unlike rule induction and other propositional machine learning algorithms that assume each example is a feature vector or a record, ILP algorithms work directly on data distributed over different EHR tables. The algorithmic details of leading ILP systems have been thoroughly described [26,27] and are summarized in the methods section.

To our knowledge, this represents the first use of ILP for phenotyping. The work of Dingcheng et al. in phenotyping type 2 diabetes [11] is similar to ours in that it also uses a rule-based data-mining approach (Apriori association rule learning algorithm) which shares the advantage of learning rules for phenotyping that are easily understood by human users. The primary difference between the two approaches is our use of ILP to directly learn from the extant tables of the EHR versus Apriori, which must learn from data conflated into a single table. This paper compares the use of ILP for phenotyping to other well-known propositional ML approaches.

As a final contribution, we introduce several novel techniques used to better automate the learning process and to improve model performance. These techniques fall into three categories: (1) selection of training set examples without expert (physician) involvement to provide supervision for the learning activities; (2) left-censoring of background data to identify subgroups of patients that have similar features denoting the phenotype; and (3) infusing borderline positive examples to improve rule prediction.

2. Methods

The Marshfield Clinic Research Foundation’s Institutional Review Board approved this study. The goal of our research was two-fold: (1) to evaluate the performance of ILP for EHR-driven phenotyping and compare it to other ML and data mining approaches; and (2) to develop methods that reduce expert (physician) time and enhance attribute awareness in the EHR-driven phenotyping process. The methods presented in this paper were applied to nine disease-based phenotypes to demonstrate the utility of the ILP approach.

2.1 Data source, study cohort, and phenotype selection

Marshfield Clinic’s internally developed CattailsMD EHR-Research Data Warehouse (RDW) was used as the source of data for this investigation. RDW data from 1979 through 2011, including diagnoses, procedures, laboratory results, observations, and medications for patients residing in a 22 ZIP Code area, were de-identified and made available for this study. The phenotypes used in this investigation were selected based on the availability of manually validated (case-control status) cohorts and include: acute myocardial infarction, acute liver failure, atrial fibrillation, cataract, congestive heart failure, dementia, type 2 diabetes, diabetic retinopathy and deep vein thrombosis [24,25,28]. The RDW was used to select training cohorts for each phenotype. These training cohorts were used to guide phenotype model development for all of the ML approaches. The manually validated cohorts (henceforth referred to as testing subjects or cohorts) were used to test the phenotype models by providing model performance comparison statistics. An overview of the study design is presented in Figure 1.

Figure 1.

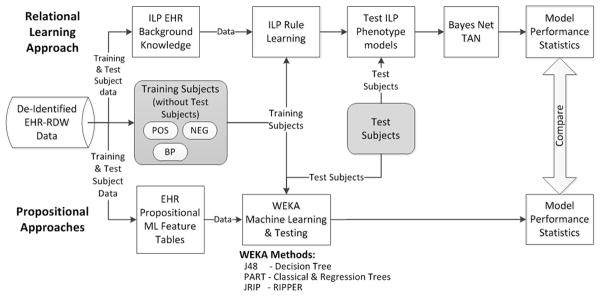
Overview of data preparation and analysis processes. Positive (POS), negative (NEG) and borderline positive (BP) training examples are selected using the electronic health record (EHR) data. Inductive logic programming (ILP) background knowledge (EHR data) and propositional machine learning (ML) feature tables are created and used by each of the respective ML methods. Manually verified test subject data is prepared similar to training data and is used to create performance statistics that are used to compare ML approaches..

2.2 Identification of training set examples

The ability to accurately identify training examples to guide a supervised machine learning task is critical. Several ML studies have used experts (physicians) to review medical records to classify patients into the positive (POS) (patients with a condition or exposure) and NEG (patients without the condition) example categories [7,9] or used pre-existing validated cohorts representing POS and NEG training examples. A secondary goal of this research was to develop methods that could reduce expert (physician) time required for EHR-driven phenotyping; thus, it would be optimal to develop an approach for selecting training examples that did not require physician input or pre-existing categorized training examples.

A recent study by Carroll et al. [7] evaluated support vector machines for phenotyping rheumatoid arthritis and demonstrated the utility of ICD-9 CM diagnostic codes when characterizing research subjects. This knowledge coupled with our past phenotyping experience [28] prompted the use of ICD-9 codes as a possible surrogate to identify potential positive (POS) training examples for model building. A sampling frame of patients with at least 15–20 ICD-9 codes spanning multiple days was used to define the surrogate POS cohort. From this cohort, we randomly selected a subset for model building (henceforth referred to as the POS training set). We required multiple ICD-9 codes based on the assumption that a patient who truly exhibits one of the phenotypes of interest will receive continuing care, in contrast with a patient who does not exhibit the phenotype but may have a small number of relevant ICD-9 codes in their record for administrative/billing reasons. A working cutoff for the number of codes was established as follows. The frequency distribution of patient numbers of ICD-9 codes was determined. Ranking patients from highest to lowest number of ICD-9 diagnoses, we targeted between 1000–1500 patients with highest ICD-9 counts to be labeled as POS, and similarly placed an upper limit on the training set size (refer to Table 1) to facilitate timely data transfers between the RDW and the machine learning environment.

Table 1.

Phenotypes and sampling frame

Phenotypes	ICD-9 Diagnosis Codes	Minimum # ICD-9 Codes used to select Training POS1	Pool of available POS1,2	# Training POS1,3	# Training NEG3,4	# Training Borderline Positives3
Acute Myocardial Infarction	410.*	20+	4364	1500	1500	460
Acute Liver Injury	277.4, 572.1–4, 573.1–4, 576.8, 782.4, 782.8, 790.40	15+	7393	314	314	314
Atrial Fibrillation	427.31	20+	6619	1000	1000	489
Cataracts	366.00–366.9 & 743.30 – 743.34	20+	19150	1000	1000	1000
Congestive Heart Failure	428*	20+	8280	1000	1000	750
Dementia	290.00, 290.10, 290.11, 290.12, 290.13, 290.3, 290.20, 290.0, 290.21, 291.2, 292.82, 294.1, 294.11, 294.10, 294.20, 294.21, 331.19, 331.82, 290.40, 290.41, 290.42, 290.43	20+	4139	1126	1126	657
Type 2 Diabetes	250.*	20+	10899	1500	1500	1000
Diabetic Retinopathy	362.01, 362.10, 362.12, 362.82, 362.84, 362.85, 362.07, 362.02, 362.03, 362.04, 362.05, 362.06	20+	2525	606	606	606
Deep Vein Thrombosis	453.*	20+	4140	1000	1000	658

^*include all decimal digits

¹POS indicates Positive examples

²Includes all patients with at least one ICD-9 diagnosis code.

³Randomly selected

⁴NEG indicates Negative examples

Note: Phenotype models were constructed for nine conditions. Training positive and borderline positive examples were identified using ICD-9 diagnosis codes. Negative training examples had no ICD-9 diagnosis code.

For each selected POS in our training set, we randomly selected a NEG (ICD-9 code of the phenotype was not present in patient’s medical history) from a pool of similar age and gender matched patients (Figure 2 provides overview of the sampling strategy). Patients with only a single diagnosis or multiple diagnoses on the same day were labeled as borderline positive examples (BPs). The use of these classifications will be described later. Refer to Table 1 for details on POS, NEG and BP numbers for each phenotype.

Figure 2.

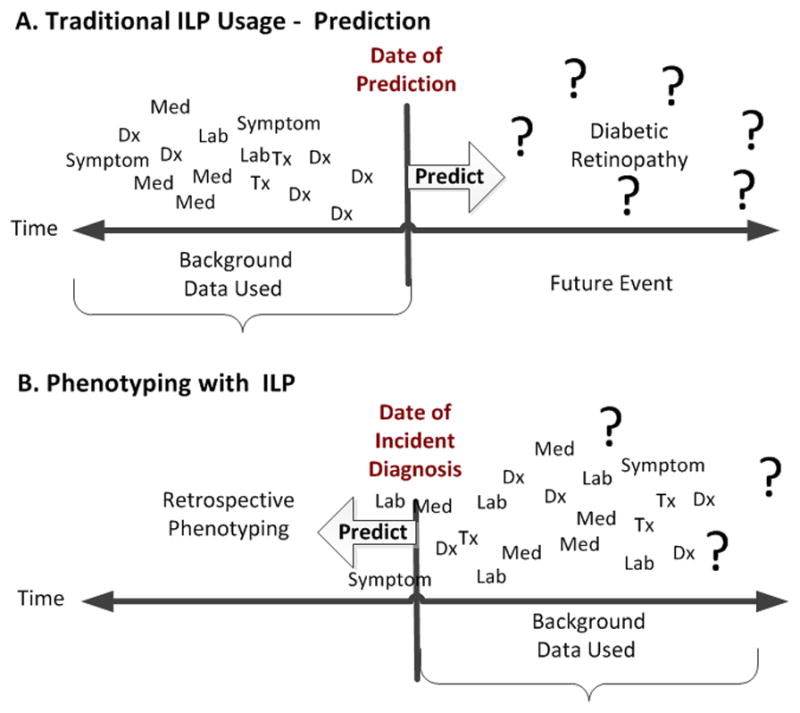
(A) Inductive logic programming (ILP) uses retrospective data to predict disease outcomes. (B) Phenotyping with ILP uses data collected after the incident date (of a condition), to predict features that a subgroup may be sharing that are representative of a phenotype.

2.3 Identification of testing set examples

Earlier in this discussion we indicated that we had access to manually validated phenotyped cohorts. We chose to use these cohorts for testing the performance of the phenotype models rather than for model training or development. Two testing cohorts (congestive heart failure [CHF] and acute liver injury [ALI]) were constructed in parallel to this investigation. A similar manual chart review and classification process was used for each phenotype to construct the testing cohorts. In general, trained research coordinators manually reviewed charts and classified a list of patients as either POS or NEG. A second research coordinator independently reviewed a sample of records completed by the first reviewer (usually a 5–10% sample or a fixed sample size for the larger cohorts) for quality assurance. A board-certified physician resolved disagreements or questions surrounding the classifications of subjects. For example, there were three noted disagreements in the ALI abstraction that were resolved in this manner.

2.4 Machine learning phenotyping approaches

2.4.1 ILP approach

ILP addresses the problem of learning (or inducing) first-order predicate calculus (FOPC) rules from a set of examples and a database that includes multiple relations (or tables). Most work in ILP limits itself to non-recursive Datalog [29], a subset of FOPC equivalent to relational algebra expressions or SQL queries, which differentiate positive examples (cases) from negative examples (control patients) given background knowledge (EHR data). A database with multiple tables is represented as an extensional Datalog program, with one predicate for each table and one fact for each tuple (record) in each table. The rules that we learn are equivalent to SQL queries; hence, a rule can be thought of as defining a new table and a set of rules as defining a new view of the database.

Our work used Muggleton’s Progol algorithm [30] as implemented in Srinivasan’s Aleph system [31]. Progol applies the idea that if a rule is useful, it must explain (or cover) at least one example. Thus, instead of blindly generating rules, Progol first looks in detail at one example, and it only constructs rules that are guaranteed to cover that example. The benefit of using this approach is that instead of having to generate rules for all conditions, drugs, or labs in the EHR, it can generate rules for a much smaller number of conditions.

The Aleph implementation uses the data connected to an example to construct rules. The head of the rule always refers to the patient. The body refers to facts for that specific patient. These “ground” rules are then generalized by introducing variables au lieu of individual patients or of specific time points. Shorter rules are constructed first. In this study, we used breadth-first search over a fast-growing search space, so the major limitation is the number of elements that we combine and still achieve acceptable performance. This is rarely more than 4. It is possible to explore longer rules, often up to 10 or more, by using greedy search or randomized search instead of a complete search.

In a nutshell, the Progol/Aleph algorithm: 1. Selects a positive example (referred to as a seed) not yet explained by any rule. In the EHR domain, the positive example is a patient that has the exposure or medical condition of interest. 2. Searches the database for data directly related to the example. In the case of an EHR, this means collecting all diagnoses, prescriptions, lab results, etc., for the example patient. 3. Generates rules based on the patient. The rule will be constructed from the events of the chosen patient’s history (referred to as clauses) generalized to explain other patients. This is achieved by replacing the references to the actual patient and temporal data with variables. The resulting rule (with variables) is applied to the training examples (both positive and negative) using the EHR data to identify patients that can be explained by the rule.4. In practice, ILP must deal with inconsistent and incomplete data; hence, it uses statistical criteria based on the number of positively and negatively explained examples to determine the quality of the rule. Two simple criteria that are often used to score rules are precision (the fraction of covered examples that are positive, also called the positive predictive value) or the number of positive examples minus the number of negative examples covered by the clause, known as coverage. 5. The procedure stops when it finds a good rule, and the examples explained by the new rule are removed. If no more examples remain, learning is complete. Otherwise, the process is repeated on the remaining examples. Appendix A provides a more detailed introduction on ILP to assist readers’ understanding.

2.4.1.1 Traditional ILP use

ILP usage in the medical domain has focused on predicting patient outcomes [14,19–22]. Supervision for the prediction task comes from positive examples (POS—patients with a medical outcome) and negative examples (NEG—patients without the medical outcome), given some common exposure. For example, to develop a model that will predict diabetic retinopathy (DR), given a patient has diabetes, the supervision comes in the form of POS (diabetic patients that have DR) and NEG (diabetic patients without DR). EHR data collected before the DR occurrence is used to build a model to predict whether a diabetic patient is at future risk for DR (refer to Figure 2A).

2.4.1.2 ILP for phenotyping

ILP applied to the phenotyping task uses a similar approach, but in a reversed manner. For example, when phenotyping we should not assume that we know all the clinical attributes that are needed to succinctly identify patients with a given phenotype (e.g., diabetes). Suppose we do not know in advance that diabetes is associated with elevated blood sugar. The POS and NEG cannot be selected as training examples based on elevated blood sugar, because it is not yet known that elevated blood sugar is an indicator for diabetes. Instead, the problem can be addressed by selecting training examples based on the desired phenotype or disease outcome (diabetes) and then running ILP with EHR data filtered by dates occurring on or after the first diagnosis (refer to Figure 2B). This seems counter-intuitive, because we are training on patients with data obtained after diabetes is diagnosed in order to identify the common features of the phenotype (diabetes). The features (or ILP rules) can then be applied to retrospective EHR data to select (or phenotype) unclassified patients. In addition, if we can identify diabetic patients based on similar medical features existing after the initial diagnosis, we may also be able to uncover unknown (unbiased) features that further define the phenotype.

2.4.1.3 Constructing background knowledge for ILP

Background knowledge (EHR data) for phenotyping was created by selecting coded ICD-9 diagnosis, medication, laboratory, procedure, and biometric observation measurement records from the EHR. A censor date, representing the initial diagnosis date of the phenotype, was determined for each POS and borderline positive (BP) example (BP will be explained in the following section). All EHR background knowledge records were labeled as before or after, based on the relationship of the event date (date of diagnosis, procedure, lab, or medication) to the censor date (refer to Figure 3). Before records were labeled if they occurred 5 years to 30 days before the censor date. We used 30 days before the censor date, because we did not want to include EHR facts that might be associated with diagnosing the phenotype condition. After records were labeled if they occurred in the period from less than 30 days before the censor date through 5 years after the censor date. EHR background knowledge records for each NEG were similarly labeled as before or after based on the censor date of the corresponding POS (since NEGs have no incident diagnosis date). All EHR background knowledge records were formatted for Aleph ILP system software. The detailed methods surrounding background file creation can be found in Appendix B-3. Appendix C provides detailed examples of diagnosis, lab, gender, drug, procedure, vitals and symptom record formatting for Aleph. To summarize, a “b” is attached to the beginning of the patient_id (first variable in the parentheses) to indicate a before record (i.e. vitals(‘b222aaa222’,68110,‘Blood Pressure Diastolic’,‘60’). There is no prefix used when formatting the after record (i.e. vitals(‘222aaa222’,78110,‘Blood Pressure Diastolic’,‘60’).

Figure 3.

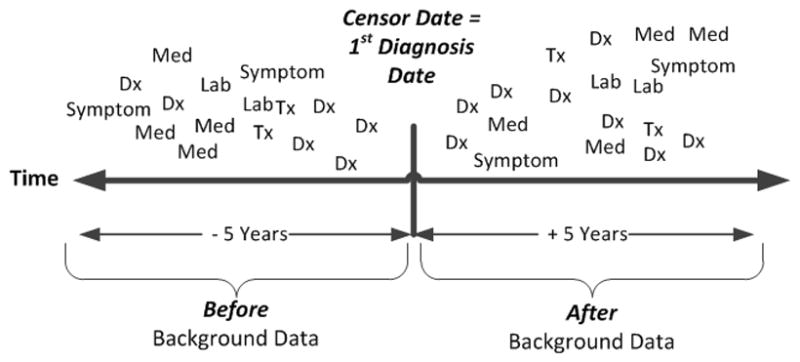
Censoring data to support inductive logic programming scoring functions.

2.4.1.4 ILP scoring functions

Scoring functions in Aleph and other ILP systems evaluate the quality of a rule and thus, are fundamental to the learning process. We tested two different scoring functions with Aleph [31]. The first scoring function follows standard ILP practice and was (POS_(after) − NEG_(after)), where POS_(after) denotes positive examples that use EHR data after the censor date and NEG_(after) denotes negative examples that use EHR data after the censor date (Figure 3). Simultaneously, we evaluated (POS_(after) − (NEG_(after) + POS_(before))), in which POS_(before) denotes positive examples that use EHR records before the censor date and POS_(after) and NEG_(after) are as in the previous example. Early on we found that diagnoses tended to “follow” patients over time. The scoring function mimics an epidemiology research method called Case-Crossover study design, where each case serves as its own control and allows for the detection of differences from one time period to another [32]. In our example, the later scoring function helps to identify differences in medical events between POS_(after) and POS_(before) time periods, thus highlighting new medical events that occurred after the initial diagnosis but not before. The cost function (POS_(after) − (NEG_(after) + POS_(before))) was found to improve model performance and accuracy over the initial scoring function. Henceforth, this function will be referred to as ILP-1.

From previous work, we found that using the ILP-1 scoring function tended to create rules that could differentiate the POS and NEGs based on ICD-9 codes relatively well, but often failed to provide more specific rules that could discriminate borderline POS and NEG examples. To further discriminate and improve the rules, we infused the NEGs with subjects that we considered borderline positives (BPs). BPs are examples of patients that have one relevant diagnosis code, but not two, or several diagnoses on the same day with no subsequent follow-up. BPs are problematic because subjects may (or may not) have the medical diagnosis. This is because ICD-9 diagnosis codes are sometimes used in clinical practice to justify laboratory tests or procedures rather than to define that a patient has the diagnosis. BPs likely include patients that do not have the phenotype condition and by adding them to the NEGs, we increase the precision of the learned rules. The scoring function used to support the infusion of BPs into the NEGs is: (POS_(after) − (NEG_(after) + POS_(before) + BPs_(after))). Henceforth, this function will be referred to as ILP+BP.

We used a 1:1 ratio of POS to NEG while building the phenotype model. Initially, we limited the number of POS and NEG to the maximum number of BPs available (this was done for ALI and diabetic retinopathy phenotypes). Later, after completing a sensitivity analysis to determine the optimal percent of BPs to add to the NEGs (e.g., 25%, 50%, 75%, or 100%), we increased POS and NEG training sets selection to accommodate the maximum subject limit between 3–4000. The number of BPs used in each study was determined by either the availability of BPs in the cohort, or the number of BPs could not exceed the number of NEG subjects in the training set. Refer to Table 1 for the exact number of diagnoses used to select training examples and the numbers of POS, NEG, and BPs present in each phenotype training set.

2.4.1.5 ILP configuration

ILP was adapted for phenotyping by adjusting Aleph parameters reflecting the following beliefs: (1) accepted rules should cover very few, ideally zero, negative examples; (2) rules that succeed on very few examples tend to over fit (a useful heuristic is that a rule is only acceptable when it covers at least 20 examples); and (3) search time heavily depends on the maximum number of rules that are considered for each seed. Because of the high run-time for relational learning and the large number of parameters, as well as to keep the process as simple and generalizable as possible, we did not tune, but rather chose a single set of parameter settings and applied them to all phenotypes. We were careful to avoid the pitfall of trying many combinations of parameter settings and then selecting the one that gives the best results on the test set. We instead chose to use the following settings which had shown good performance in previous applications: noise = 1, minpos = 80, minacc = 80, clauselength = 4, caching = false, i = 3, record = true and nodes = 1000000.

Using the cataract phenotype as an example, we have presented a detailed description of our methods in Appendix B and made available examples of record formats. Appendix C has examples of the scripts and configuration files (cat.b – file that contains the parameters for running Aleph and runAleph.sh – a script that initiates the Aleph phenotype model building session). Appendix D has examples of ILP rules created for the cataract phenotype using ILP-1 and ILP+BP ML approaches.

2.4.2 Propositional machine learning approaches

We selected two popular ML classifiers available in the widely used Waikato Environment for Knowledge Analysis (WEKA) software [34], after conducting a sensitivity analysis (using several ML classifiers), to determine the highest performing approaches based on area under the receivers operating characteristics curve (AUROC). Using atrial fibrillation as the phenotype, we compared: Random Forest (AUROC = 0.682), SMO (0.506), PART (0.772), and J48 (0.772). From this analysis, we selected J48 and PART for use in the ILP comparison. J48 is based on a Java implementation of the well-known decision tree classifier C4.5 [34] and PART, is the Java implementation of a rule based classifier based on Classical and Regression Tree [35]. We also selected JRIP, the WEKA implementation of the propositional rule learner Repeated Incremental Pruning to Produce Error Reduction (RIPPER) [36]. The RIPPER implementation is similar to ILP, except that it assumes that each example is a feature vector or record versus ILP algorithms work directly on data distributed over multiple tables.

2.4.2.1 Feature table creation

A feature table consisting of the same POS and NEG examples used in ILP phenotype model building was created and used by the propositional ML approaches for each phenotype. A record for each subject was constructed using information obtained from the EHR. Each unique occurrence of a diagnosis, laboratory result (categorized as ‘above’, ‘within’ or ‘below’ the normal range), medication, or procedure was identified as a feature. Frequencies of occurrence were calculated for each feature by subject. Because of the large size of the feature table, we only used features that were shared by more than 0.25% of the training subjects. In other words, features were included if more than two or three subjects (depending on phenotype) had the feature. The same features identified for the training sets were used as features for the validation/test examples. For details refer to Appendix B.7.

2.5 Analysis

Phenotyping model performance measurements were calculated using the number of correctly classified testing subjects. Contingency tables were used to calculate accuracy, precision, recall (the true positive rate, also called sensitivity), and F-Measure (defined as 2 x[(recall x precision)/(recall + precision)]) statistics for the ILP models. WEKA, version 3.6.9, automatically calculated those statistics along with Receiver Operator Characteristic (ROC) curves and area under the ROC curve (AUROC), for the propositional ML methods (J48, PART, and JRIP). To associate the probabilities of AUROC and construct ROC curves for the ILP models, we built a feature table using the ILP rules as features. A binary code indicating if a subject met (or not), the rule criteria was assigned for each feature by subject in the testing cohort. The Bayes Net-Tan classifier, as implemented in WEKA, was used to calculate AUROC using the ILP features (rules) for each phenotype model [37]. Such use of a Bayesian network to combine relational rules learned by ILP is a popular approach used in statistical relational learning to gain ROC curves and AUROC [15].

Significance testing using a two-sided sign test (binomial distribution test) at 95% confidence was used to evaluate model sensitivity when adding varying percentages of BPs (25%, 50%, 75%, and 100%) to NEGs in the ILP+BP scoring function. Discordant classifications of POS and NEG were obtained for each ILP approach comparison and then similar significance testing conducted.

To assess the difference in overall ML approach performance, we counted the number of wins for a ML approach across phenotypes and compared it to the number of wins for the comparison ML approach. Significance testing was done using a two-sided sign test (binomial distribution test) at 95% confidence, to evaluate a difference in overall model performance between any of the ILP-1, ILP+BP, PART, J48, and JRIP models.

3. Results

The sampling frame used for the selection of all phenotype training sets consisted of 113,493 subjects. Table 1 provides the number of POS, NEG, and BP training subjects randomly selected and used for the development of each phenotype model. Training set sizes for both POS and NEG examples ranged from 314 (acute liver injury) to 1500 (acute myocardial infarction and type 2 diabetes).

There was no significant difference detected in overall model performance when adjusting the BP percentages (between 25%, 50%, 75%, and 100%) for the ILP+BP scoring function. We found that adding BP examples to the scoring function yielded more descriptive rules for all phenotypes. For example, using atrial fibrillation, a single rule having the presence of ICD-9 code ‘427.31’ (atrial fibrillation) was learned by the ILP-1 approach. Using the ILP+BP with the addition of BPs at 50%, presented a total of 58 rules, which included a combination of diagnoses, labs, procedures, medications, and age. For consistency in reporting results, henceforth we will use ILP+BP with the contribution of 50% BPs.

Table 2 provides descriptive information on the phenotype testing cohorts. The POS and NEG testing cohorts tended to be older (>65 years of age) and similar with respect to years of follow-up and ICD-9 diagnosis counts.

Table 2.

Validation-testing sample characteristics

Phenotypes	Total Number		Female (%)	Mean Age3	Years Followup4 (StDev)		ICD-9 Diagnosis Count (StDev)
	POS1	NEG2			POS1	NEG2	POS1	NEG2
Acute Myocardial Infarction	363	158	199 (38.2%)	73.8	37.9 (9.7)	33.5 (12.2)	1848 (1475)	1384 (1304)
Acute Liver Injury	44	6	23(46%)	69.3	34.9 (10.6)	35.2 (10.0)	1880 (1568)	2550 (951)
Atrial Fibrillation	36	35	31 (44%)	79.8	29.2 (13.1)	31.7 (14.5)	1345 (811)	1468 (1100)
Cataracts	244	110	210 (59.32%)	75.2	39.7 (9.8)	37.9 (11.2)	1395 (1004)	864 (616)
CHF	60	36	51 (52%)	70	35.4 (10.0)	26.1 (13.8)	1614 (1184)	623 (647)
Dementia	303	70	203 (54.4%)	84	36.9 (11.3)	37.4 (8.64)	1579 (980)	1438 (1067)
Type 2 Diabetes	113	52	99 (60%)	67	36.3 (12.3)	34.0 (13.6)	1447 (781)	925 (781)
Diabetic Retinopathy	40	46	39 (45.4%)	71.6	35.1 (12.7)	37.9 (13.8)	2032 (1158)	1614 (1158)
Deep Vein Thrombosis	217	870	614 (56%)	76	38.3 (9.9)	38.9 (10.2)	1947 (1604)	1269 (836)

¹POS indicates Positive examples

²NEG indicates Negative examples

³Mean age calculated by (Year of data pull (2012) - Birth Year)

⁴Years Follow-up calculated by determining difference between first and last diagnosis date

Note: Phenotype models were validated using these validation cohorts.

Nine phenotypes were modeled with the performance measurements for each ML approach (ILP-1, ILP+BP, PART, J48, and JRIP) appearing in Table 3. Type 2 diabetes, diabetic retinopathy, and deep vein thrombosis phenotypic models consistently had high performance statistics (> 0.900 in all categories) across all ML approaches. Acute liver injury had the lowest performance measurements for all ML approaches. There was no significant difference in overall accuracy between ILP-1 and ILP+BP models, although ILP-1 performed significantly better than ILP+BP in detecting POS examples (p=0.0006), and ILP+BP performed significantly better than ILP-1 when detecting NEG examples (p=0.008). The addition of BP examples had the desired effect of increasing precision, but at the cost of decreased recall when comparing ILP-1 with ILP+BP.

Table 3.

Phenotype model validation results by phenotype

PHENOTYPE
	Acute Myocardial Infarction	Acute Liver Injury	Atrial Fibrillation	Cataracts	CHF	Dementia	Type 2 Diabetes	Diabetic Retinopathy	Deep Vein Thrombosis
Accuracy
ILP-11	0.800	0.600	0.775	0.890	0.865	0.810	0.939	0.977	0.980
ILP+BP2	0.810	0.640	0.732	0.898	0.885	0.810	0.945	0.988	0.965
PART3	0.775	0.660	0.775	0.879	0.875	0.850	0.945	0.988	0.949
J484	0.785	0.700	0.775	0.822	0.875	0.834	0.945	0.988	0.949
JRIP5	0.791	0.780	0.775	0.879	0.875	0.807	0.945	0.988	0.981
Precision
ILP-11	0.863	0.929	0.700	0.865	0.831	0.858	0.919	0.952	0.990
ILP+BP2	0.877	0.906	0.689	0.877	0.855	0.936	0.926	0.976	0.954
PART3	0.790	0.848	0.824	0.877	0.811	0.859	0.949	0.989	0.949
J484	0.797	0.829	0.824	0.819	0.881	0.850	0.949	0.989	0.949
JRIP5	0.869	0.902	0.700	0.904	0.853	0.917	0.926	0.976	0.990
Recall
ILP-11	0.850	0.591	0.972	0.996	0.980	0.858	1.000	1.000	0.910
ILP+BP2	0.850	0.659	0.860	0.992	0.980	0.822	1.000	1.000	0.870
PART3	0.755	0.660	0.775	0.879	0.875	0.850	0.945	0.988	0.949
J484	0.785	0.700	0.755	0.822	0.875	0.834	0.945	0.988	0.960
JRIP5	0.824	0.841	0.972	0.922	0.967	0.838	1.000	1.000	0.912
F-Measure
ILP-11	0.856	0.722	0.813	0.926	0.900	0.858	0.958	0.976	0.947
ILP+BP2	0.879	0.763	0.795	0.939	0.914	0.894	0.961	0.988	0.940
PART3	0.788	0.719	0.765	0.877	0.871	0.854	0.944	0.988	0.949
J484	0.789	0.747	0.765	0.820	0.871	0.840	0.944	0.988	0.960
JRIP5	0.794	0.798	0.765	0.878	0.871	0.818	0.944	0.988	0.980
AUROC10
ILP-1+BNT6	0.769	0.752	0.772	0.893	0.825	0.817	0.904	0.991	0.953
ILPBP+BNT7	0.831	0.701	0.774	0.873	0.914	0.831	0.957	0.990	0.971
PART3	0.788	0.716	0.772	0.842	0.844	0.798	0.913	0.989	0.947
J484	0.722	0.619	0.722	0.783	0.844	0.766	0.913	0.989	0.927
JRIP5	0.769	0.587	0.772	0.852	0.844	0.755	0.913	0.989	0.955

¹ILP-1: Inductive Logic Programming with using POS(after) − (NEG(after) + POS(before));

²ILP+BP: Inductive Logic Programming + Borderline Positives using POS(after) − (NEG(after) + POS(before) + FP(after));

³PART: Java implementation of a rule based classifier in WEKA;

⁴J48: Java implementation of C4.5 classifier available in WEKA;

⁵JRIP: Java implementation of RIPPER classifier available in WEKA;

⁶ILP-1+BNT: BayesNet-Tan using ILP Classification Rules;

⁸ILPFP+BNT: BayesNet-Tan using ILP+FP Classification Rules;

⁷ILPBP+BNT: BayesNet-Tan using ILP+FP Classification Rules;

¹⁰AUROC: Area Under Receiver Operating Characteristics Curve

Bolded numbers indicate highest score between phenotyping methods

Note: Phenotype model accuracy measurements were calculated for each scoring function by using the number of correctly classified positive and negative validation examples.

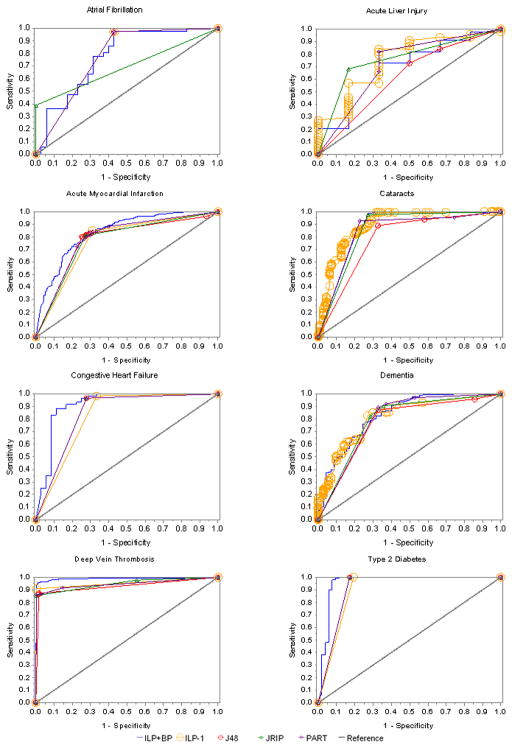
Figure 4 presents ROC curves for eight of the nine phenotypes. Shown on each plot are the ROC curves for each ML approach (ILP-1, ILP+BP, J48, PART, JRIP). The diabetic retinopathy ROC curves looked similar between all models and are not displayed because of space limitations. The pictured ROC curves suggest substantial improvement over chance assignment (indicated by the reference line), with generally similar results among approaches. ILP+BP appeared to outperform the other ML approaches for the congestive heart failure, deep vein thrombosis, and type 2 diabetes phenotypes. These plots combined with the summary statistics presented in Tables 3 and 4 provide an understanding of how the model results compare across phenotypes.

Figure 4.

A comparison between all machine learning approaches by phenotype using receiver operator characteristic (ROC) curves. The diabetes retinopathy ROC curves are not displayed because of the similarity between each machine learning approach. Overall, the pictured models were very similar with ILP+BP ROC showing the best results for congestive heart failure, deep vein thrombosis and type 2 diabetes.

Table 4.

Combined phenotype validation results

	ILP-11	ILP+BP2	PART3	J484	JRIP5
Accuracy	0.878	0.912	0.886	0.883	0.895
Precision	0.897	0.895	0.893	0.893	0.904
Recall	0.860	0.940	0.880	0.880	0.890
F-Measure	0.876	0.917	0.889	0.886	0.895

¹ILP-1: Inductive Logic Programming with using POS(after) − (NEG(after) + POS(before))

²ILP+BP: Inductive Logic Programming + Borderline Positives using POS(after) − (NEG(after) + POS(before) + FP(after))

³PART: Java implementation of a rule based classifier in WEKA

⁴J48: Java implementation of C4.5 classifier available in WEKA

⁵JRIP: Java implementation of RIPPER rule-based classifier available in WEKA

Note: The results from a binomial classification (counting # wins for each method by phenotype), then using a two-sided sign test (binomial distribution test) at 95% confidence to determine if there is a difference. There was a significant difference favoring ILP+BP when compared to PART (p=0.039), J48 (p=0.003) and JRIP (p=0.003) when evaluating AUROC. There was no significant difference when testing accuracy, precision, recall, and F-Measure.

An overall comparison of machine learning approaches is presented in Table 4. There was no significant difference in overall accuracy, precision, recall, or F-Measure between the ML approaches. When comparing AUROC for ILP+BP to PART, J48, and JRIP, ILP+BP performed significantly better than PART (p=0.039), J48 (p=0.003), and JRIP (p=0.003).

4. Discussion

In this study, we used a de-identified version of EHR coded data to construct phenotyping models for nine different phenotypes. All ML approaches used ICD-9-CM diagnostic codes to define training cases and controls (POS, NEG, and BP examples) for the supervised learning task. We developed ILP models (either ILP-1 or ILP+BP) that produced F-measure metrics for six of nine phenotypes that exceeded 0.900, which is comparable to other phenotyping investigations [38–41]. For example, the type 2 diabetes phenotype was also studied by Dingcheng et al. [11], where they reported an F-measure of 0.914; we achieved an F-measure of 0.958 (ILP-1) and 0.961 (ILP+BP), albeit on different validation data.

Several of the phenotypes selected for use in this research (type 2 diabetes, diabetic retinopathy, dementia, and cataracts), corresponded to phenotypes used by the Electronic Medical Records and Genomics (eMERGE) network [42] for genome-wide association studies [6,28,38]. The eMERGE phenotyping models used a variety of EHR data, were developed using a multi-disciplinary team approach, and each phenotyping model took many months to construct and validate. Our method used similar coded EHR data, required minimum effort from the multi-disciplinary team, and developed phenotype models in a few days; however, our development relied on testing cohorts. The ILP phenotyping models were comparable in precision (also referred to as positive predictive value) for three of the four phenotypes when compared to eMERGE network algorithms (refer to Table 5) [6,28,38]. We would expect similar precision rates between eMERGE-Marshfield and the ILP+BP approaches due to the overlap of patients in the testing cohorts and using similar EHR data. Possible reasons for the differences between eMERGE and ILP+BP precision could be sample differences and size. For example, the eMERGE cataract cohort had 4309 cataract cases used to calculate precision and our study had 244 cases (we selected a sample of the cases from the eMERGE cohort).

Table 5.

Comparison of eMERGE phenotyping model precision to ILP+BP

	eMERGE1	eMERGE at Marshfield	ILP+BP4
Cataract	0.960 – 0.977	0.9562	0.877
Dementia	0.730 – 0.897	0.8973	0.936
Type 2 Diabetes	0.982 – 1.000	0.9903	0.926
Diabetic Retinopathy	0.676 – 0.800	0.8003	0.976

¹eMERGE precision range taken from Table 3 in Newton et al [6]. The range represents multiple eMERGE institution precision estimates.

²Precision for Marshfield eMERGE cohort indicating the combined cohort precision definition in Peissig et al [28].

³eMERGE precision for Marshfield taken from Table 3 in Newton et al [6].

⁴LP+BP: Inductive Logic Programming + Borderline Positives taken from Table 3.

An advantage of using ILP is that the ILP rules reflect characteristics of patient subgroups for a phenotype. The ILP rules can be easily interpreted by a physician (or others) to identify relevant model features that not only identify patients, but also discriminate between patients that should or should not be classified as cases. In addition, ILP rules are learned from the EHR database. These rules are not based on human intuition or “filtered” because of preconceived opinions about a phenotype. To emphasize the later point, our physician author (MC) evaluated the ILP+BP rules for acute liver injury in Table 6 and questioned why high levels of “Differential Nucleated RBC” surfaced in Rule #35. After research, a mechanism for a sudden rise in nucleated red cells was found in the association with injury to hepatic and bone marrow sinusoidal endothelium as part of the fetal response to hypoxia or partial asphyxia [43]. This example provides some evidence that one’s existential biases can hide relevant information. This relevant information could be used to improve a phenotype model.

Table 6.

Top eight “scoring” inductive logic programming (ILP) rules for acute liver injury

Rule #	POS Cover1	NEG Cover2	ILP Rule	Probability3
30	95	0	diagnoses(A,B,C,‘790.4’,‘Elev Transaminase/Ldh’,D), lab(A,E,20719,‘Urea Nitrogen Bld’,F,‘Normal’), lab(A,E,20727,‘Alkaline Phosphatase (T-Alkp)’,G,‘High’).	1.00
35	52	0	has_tx(A,B,‘99232’,‘Sbsq Hospital Care/Day 25 Minutes’,C,D,E,F), lab(A,B,20816,‘Differential Nucleated RBC’,G,‘High’).	1.00
42	129	0	diagnoses(A,B,C,‘782.4’,‘Jaundice Nos’,D), lab(A,E,20727,‘Alkaline Phosphatase (T-Alkp)’,F,‘High’).	1.00
72	113	0	has_tx(A,B,‘99214’,‘Office Outpatient Visit 25 Minutes’,C,D,E,F), lab(A,G,20809,‘Differential Segment Neut- Segs’,H,‘Normal’), lab(A,G,20728,‘Bilirubin’,F,‘High’).	1.00
3	146	1	lab(A,B,20728,‘Bilirubin Total’,C,‘High’), lab(A,D,20900,‘Direct Bilirubin’,E,‘High’), lab(A,F,20857,‘Red Cell Distribute Width(RDW)’,G,‘High’).	0.99
51	142	1	lab(A,B,20900,‘Direct Bilirubin’,C,‘High’), lab(A,B,20719,‘Urea Nitrogen Bld’,D,‘Normal’), lab(A,B,20731,‘AST (GOT)’,E, ‘High’).	0.99
11	138	1	lab(A,B,20728,’Bilirubin Total’,C, ‘High’), lab(A,B,20809,‘Differential Segment Neut-Segs’,D,‘Normal’), lab(A,E,20282,‘Glucose’,F,‘High’).	0.99
60	137	1	lab(A,B,20715,‘Potassium (K)’,C,‘Normal’), lab(A,B,20727,‘Alkaline Phosphatase (T-Alkp)’,D,‘High’), lab(A,E,20901,‘Unconjugated Bilirubin’,F,‘High’).	0.99

¹Represents the number of positive examples covered by the rule.

²Represents the number of negative examples covered by the rule.

³Probability = POS examples/(POS examples + NEG examples).

Note: The ILP+BP rules can be easily interpreted by a human with little training. The “bold” lettered rules are indicative of “facts” related to or associated with acute liver injury. The highlighted ILP+BP rule (rule #35) represents a “fact” (Differential Nucleated RBC’ is ‘High’) that was unknown to a physician reviewer prior to this investigation. Fifty two POS subjects were classified in the training set using rule #35.

Initially, we used a simple scoring function that evaluated the differences between the POS and NEG examples using data captured after the initial diagnosis for both groups (POS_(after) − NEG_(after)). We then tried to improve model accuracy by adding the before data for POS patients and after data for the BP patients; the goal of these additions was to mute some of the features that were common between true positive and false positive examples, thus making the model more discriminatory. Given the high recall and precision of our method, in either case only a few EHR-driven models yielded substantially different classifications between the two approaches, making it difficult to demonstrate that there is a difference in model performance when adding the BP(_after) and POS(_before) data. We speculate that larger phenotype testing sets may allow one to see a difference if it exists. This could also be due to the nature of the phenotype being studied.

ILP provides a series of rules that identify patients with a given phenotype. Most of the rules include a diagnostic code (suspected because POS selection of training subjects was based on diagnostic codes) along with one or more other features. We noticed that in some situations, ILP would learn a rule that was too general and, thus, invite the identification of false positives. Future research is needed to examine grouping of rules and selection of subjects based on a combination of rule conditions, thereby combining the advantages of ILP and the general “rule-of-N” approach commonly used in phenotyping which states a unique event must be present on “N” days to determine a case/control.

This study has several limitations. First, the use of only structured or coded data found within the EHR for phenotyping [7,44]. Other studies have indicated that clinical narratives and images provide more specific information to refine phenotyping models [9,28,44]. We envision use of natural language processing and/or optical character recognition techniques as tools to increase the availability of EHR structured data and, thus, hypothesize that using such data will improve most ML phenotyping approach results as noted by Saria et al. [45]. Second, a single EHR and institution was used in this research, thus limiting the generalizability of the study results. We attempted to improve generalizability of this research by using multiple phenotypes representing both acute and chronic conditions. More research is needed to apply these approaches across several institutions and EHRs. Third, using 15–20 ICD-9 to identify POS examples can be problematic for some diseases/conditions. For example, a patient with 20+ deep vein thrombosis (DVT) ICD-9 codes may not have the same disease as a patient with only a single DVT code. More research is needed to investigate robust ways to identify POS examples for phenotype model building. Finally, we demonstrated ILP using relatively common diseases that were selected based on the availability of existing validation or testing cohorts. ILP did not perform well on acute conditions. For example, the performance measurements for acute liver injury were lower than many of the chronic diseases phenotypes presented in Table 3. More research is needed to evaluate ILP for acute, rare, and longitudinal phenotypes.

5. Conclusion

We believe that our research has the potential to address several challenges of using the EHR for phenotyping. First, we showed promising results for ILP as a viable EHR-based phenotyping approach. Second, we introduced novel filtering techniques and infused BPs into training sets to improve ILP, suggesting that this practice could be used to inform other ML approaches. Third, we showed that labeling examples as ‘positive’ based on having multiple occurrences of a diagnosis can potentially reduce the amount of expert time needed to create training sets for phenotyping. Finally, the human-interpretable phenotyping rules created from ILP could conceivably identify important clinical attributes missed by other methods, leading to refined phenotyping models.