Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2015 Dec 18.
Published in final edited form as: J Biomech. 2014 Oct 27;47(16):3868–3875. doi: 10.1016/j.jbiomech.2014.10.010

Mechanical Instability of Normal and Aneurysmal Arteries

Avione Y Lee 1,#, Arnav Sanyal 1,#, Yangming Xiao 1, Ramsey Shadfan 1, Hai-Chao Han 1
PMCID: PMC4261027  NIHMSID: NIHMS638521  PMID: 25458146

Abstract

Tortuous arteries associated with aneurysms have been observed in aged patients with atherosclerosis and hypertension. However, the underlying mechanism is poorly understood. The objective of this study was to determine the effect of aneurysms on arterial buckling instability and the effect of buckling on aneurysm wall stress. We investigated the mechanical buckling and post-buckling behavior of normal and aneurysmal carotid arteries and aorta’s using computational simulations and experimental measurements to elucidate the interrelationship between artery buckling and aneurysms. Buckling tests were done in porcine carotid arteries with small aneurysms created using elastase treatment. Parametric studies were done for model aneurysms with orthotropic nonlinear elastic walls using finite element simulations. Our results demonstrated that arteries buckled at a critical buckling pressure and the post-buckling deflection increased nonlinearly with increasing pressure. The presence of an aneurysm can reduce the critical buckling pressure of arteries, although the effect depends on the aneurysm’s dimensions. Buckled aneurysms demonstrated a higher peak wall stress compared to unbuckled aneurysms under the same lumen pressure. We conclude that aneurysmal arteries are vulnerable to mechanical buckling and mechanical buckling could lead to high stresses in the aneurysm wall. Buckling could be a possible mechanism for the development of tortuous aneurysmal arteries such as in the Loeys-Dietz syndrome.

Keywords: aneurysm, stability, tortuosity, critical buckling pressure, post-buckling, wall stress, deformation, aorta, artery

INTRODUCTION

Rupture of abdominal aortic aneurysms (AAA) is the thirteenth leading cause of death in the United States (Vorp 2007). Extensive biomechanical studies have shown that highly elevated local stress and weakened aneurysm wall make aneurysms vulnerable to rupture (Fillinger et al. 2002; Fillinger et al. 2003; Vorp 2007; Rodriguez et al. 2008).

Aneurysms are often associated with vessel tortuosity (Hatakeyama et al. 2001; Wolf et al. 2001; Fillinger et al. 2004; Vorp 2007). For example, in patients with Loeys-Dietz syndrome, the carotid and cerebral aneurysms tend to be tortuous (Loeys et al. 2006; Johnson et al. 2007). Around 10% of Loeys-Dietz syndrome patients also have abdominal aortic aneurysms, which may become tortuous as well (Wolf et al. 2001; Johnson et al. 2007). It has been suggested that artery tortuosity may lead to aneurysm formation (Deterling 1952; Arends et al. 2008) and aneurysmal tortuosity has been proposed as a risk factor for aneurysm rupture (Del Corso et al. 1998; Sacks et al. 1999; Fillinger et al. 2003; Pappu et al. 2008; Rodriguez et al. 2008; Georgakarakos et al. 2010). Therefore, it is important to better understand the relation between artery tortuosity and aneurysms.

Recent studies from our lab suggested that artery buckling, the loss of mechanical stability due to hypertension, decreased axial stretch ratio and elastin degradation in the wall, can lead to vessel tortuosity (Han 2007; Han 2009a; Lee et al. 2012; Han et al. 2013). However, the mechanical stability of aneurysmal arteries and the post-buckling behavior of normal and aneurysmal arteries have not been investigated. Therefore, the objective of this study was to investigate the buckling and post-buckling behavior of normal and aneurysmal arteries and the effects of buckling on the wall stress in aneurysmal arteries.

METHODS

The effects of aneurysms on arterial stability were evaluated by simulating the buckling and post-buckling behavior of normal and aneurysmal arteries using finite element analysis. Simulation results were compared with theoretical estimations and experimental measurements of porcine carotid arteries for validation.

Buckling analysis of normal arteries

Six cylindrical arterial wall models were created using Solidworks® (Dassault Systèmes, Waltham, MA) based on the specific dimensions of six normal porcine carotid arteries with diameters in the range of 4.5-7 mm and length in the range of 50-63 mm obtained in our previous study (Lee et al. 2012). The arterial wall was modeled as a homogenous, incompressible, orthotropic, nonlinear material with the Fung strain energy function of the form (Fung 1993):

w=b02eQ (1a)
Q=b1Eθ2+b2Ez2+b3Er2+2b4EθEz+2b5EzEr+2b6EθEr (1b)

where b1, b2, b3, b4, b5, b6, and b0 are material constants. Subscripts r, θ, z represents the radial, circumferential and axial directions, respectively, which have different mechanical stiffness (orthotropic). Although the material constants for these porcine carotid arteries were obtained in our previous study (Lee et al. 2012), they did not satisfy the convexity requirement of the strain energy density function for finite element analysis (Sacks and Sun 2005; Datir et al. 2011). Thus, we re-determined the material constants with the following restrictions to ensure convexity (Lee 2011; Lee et al. 2012):

bi>0,i=1,2,…6 (2a)
b1+b2>2b4;b2+b3>2b5;b3+b1>2b6; (2b)

The new set of convex material constants are listed in Table 1. Out of the six arteries, one artery (artery E6 in Table 1) was also treated with elastase over its entire length to obtain material constants of a weak arterial wall as described in our previous study (Lee et al. 2012).

Table 1.

Convex material constants of six normal porcine carotid arteries and one elastase-treated artery (refit of experimental data from (Lee et al. 2012)).

Artery ID b0 b1 b2 b3 b4 b5 b6
5 20.42 0.679 0.751 0.228 0.0519 0.033 0.051
6 18.14 0.470 0.460 0.150 0.090 0.060 0.030
7 33.04 0.461 0.588 0.266 0.123 0.083 0.087
8 13.35 0.827 0.547 0.613 0.018 0.072 0.027
9 16 0.820 0.771 0.509 0.116 0.092 0.046
E6 30.69 1.265 0.353 1.000 0.179 0.011 0.026
E6 treated 3.07 3.375 0.940 0.564 0.179 0.007 0.090
Open in a new tab

Note: “E6 treated” is the same artery as E6, but after elastase treatment to remove elastin in the wall (see (Lee et al. 2012) for details)

The buckling behavior of all arterial models was simulated using the commercial FEA package ABAQUS® (v6.10, Dassault Systèmes, Waltham, MA). The arterial models were meshed using hybrid, linear hexahedral elements. Since arteries are under significant longitudinal strain in vivo (Han and Fung 1995; Han et al. 2003), a designated axial displacement was first applied to all nodes at the distal end of the arteries to achieve the given stretch ratios. Then, a static internal pressure was applied to the lumen of the arterial models and the external pressure was set at zero. Both ends of the arteries were assumed as fixed with no lateral displacement or rotation, but were allowed to expand radially. A small initial bend of 1 degree along the central axis of the arteries was created as an imperfection to facilitate the buckling analysis. A series of different bend angle were used in a pilot study and the results showed that the variations in the small initial angle had no effect on the critical buckling pressure results (Datir et al. 2011; Lee 2011).

The maximum lateral deflection of the central axis of a model artery was determined by averaging the deflections of the two edges of the wall at the mid-point of the vessel and was plotted against the lumen pressure. The pressure at which the deflection starts to increase from baseline (zero) and reaches a small value of 0.5 mm was defined as the critical buckling pressure. This definition was consistent with the criteria used in our previous experimental studies on artery buckling (Lee et al. 2012; Liu and Han 2012). The critical buckling pressure was also determined from theoretical buckling equation for comparison (Han 2009a; Lee et al. 2012).

Buckling analysis of aneurysmal arteries

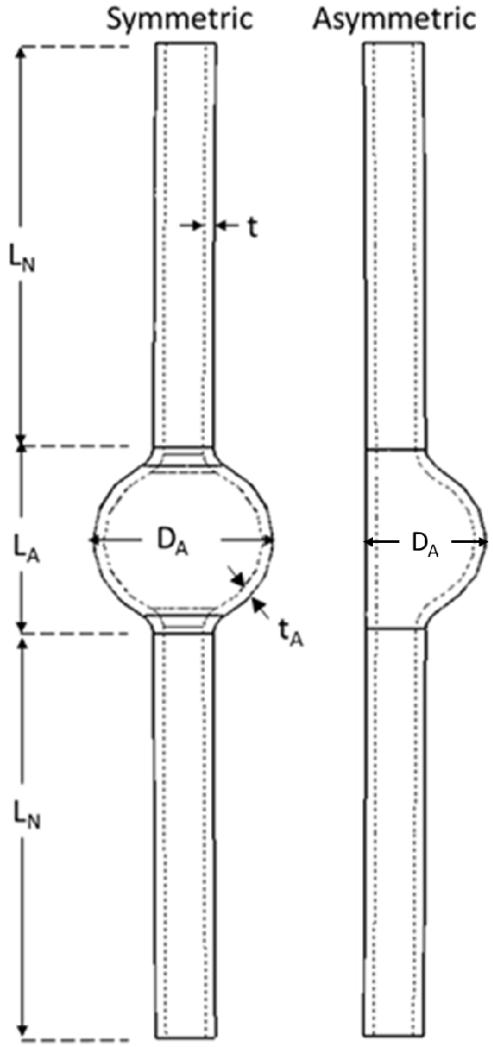
Aneurysmal arterial models were created by adding a spherically shaped dilation (fusiform aneurysm) at the middle segment of a normal cylindrical artery model (control). The control model was created with an outer diameter of 6 mm, wall thickness of 1 mm, and total length of 100 mm. Idealized symmetric aneurysms were drawn with various aneurysm diameter (DA), aneurysm length (LA), and aneurysm wall thickness tA while the total length of the vessels were kept at 100 mm (the neck lengths were determined by 2LN = total length L – aneurysm length LA accordingly) (Fig. 1) to investigate the effect of aneurysm dimensions (shape and size) on the critical buckling pressure and wall stress. The length and diameter of the aneurysm was varied in the range of 6-36 mm to determine the effect of different aneurysm sizes and shapes. Aneurysm wall thickness was assumed as either the same as the normal artery (1mm, uniform wall) or half the wall thickness of a normal artery (0.5 mm, thin wall). In addition, an asymmetric aneurysm model was created with dilation on one side of the vessel with an aneurysm length of 18mm, aneurysm diameter of 12mm and wall thickness of 1mm.

Fig. 1.

Fig. 1

Open in a new tab

Geometric models of symmetric (left) and asymmetric (right) shaped aneurysmal arteries. The aneurysm length, diameter, and thickness are denoted as LA, DA, and tA. The neck length of the vessel is 2LN.

The arterial and aneurysm wall were assumed to behave as a homogenous, incompressible, and orthotropic nonlinear material as described by Fung strain energy function with material constants given in Table 1. The aneurysm wall was assumed to have either the same material constants as the normal arterial wall (artery E6 in Table 1) or was assumed to have the material constants of the elastase-treated (weakened) arterial wall (artery “E6 treated” in Table 1) (Lee et al. 2012). This allowed us to compare normal and weakened aneurysmal walls.

To determine the effect of buckling on aneurysmal wall stress, we compared two models with identical aneurysms (LA=DA=18mm) but different neck lengths (a long neck with LN=41 mm and a short neck with LN=6 mm). By changing neck lengths, the two models had different critical buckling pressures, thus at physiological pressure, the aneurysm with the long neck buckled while the control one with the short neck remained un-buckled. The buckling behavior and aneurysm wall stress in the long and short models were determined for the set of six material constants for the normal arteries listed in Table 1.

Buckling analysis of tapered abdominal aorta with an aneurysm

To further illustrate the buckling behavior of abdominal aortic aneurysms, a model of a tapered abdominal aorta was created with a lumen diameter of 17 mm at the proximal end, 14 mm at the distal end, wall thickness of 1.5 mm and length of 123 mm. These dimensions were based on previously reported average measurements of human abdominal aortas (Fleischmann et al. 2001) and is a linear approximation of the actual changes in diameter and wall thickness along the aorta (Liu and Fung 1988; Han and Fung 1991). A fusiform aneurysm of 30 mm in diameter and 40 mm in length was created in the middle of the aorta. The wall thickness of the aneurysm was assumed to be either the same as the normal aorta (1.5 mm, uniform wall) or half the wall thickness of the normal aorta (0.75 mm, thin wall). Since human data is not available, the aorta wall was assumed to be of an orthotropic nonlinear material with Fung strain energy function with material constants of a porcine carotid artery (artery “E6” in Table 1). The aneurysm wall was assumed to have either the same material constants as the normal aorta wall or the material constants of the elastase-treated arterial wall (artery “E6 treated” in Table 1, weak wall) as specified.

Experimental measurement of post-buckling behavior of arteries

We measured the deflection from pre- to post-buckling of the set of six normal porcine carotid arteries listed in Table 1 using the method previously described (Martinez et al. 2010; Lee et al. 2012). Briefly, the displacements of the two edges of the arterial wall were determined from recorded buckling videos and photos using Image Pro Plus®. Then the maximum deflections of the central axis of the arteries were determined by averaging the displacements of the two edges of the wall measured at the middle points of the vessels. The experimental deflections were compared with the computational results.

Experimental measurement of critical buckling pressure of model aneurysmal arteries

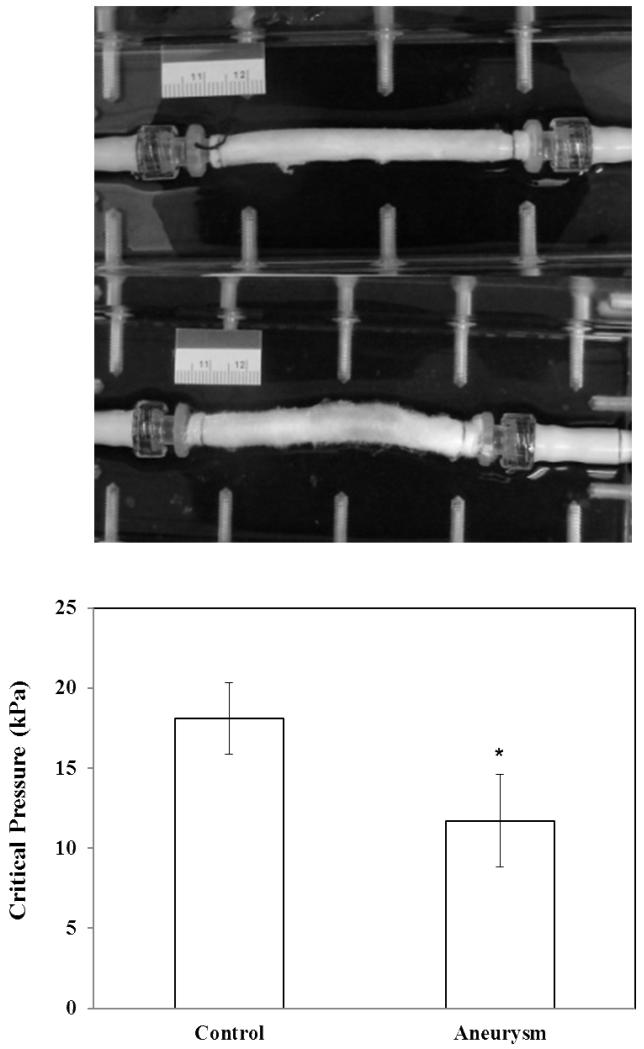
To validate aneurysm arterial simulations, we created small aneurysms in four porcine carotid arteries by using local elastase treatment. Briefly, porcine carotid arteries harvested from a slaughterhouse were mounted into a test box by tying them on to cannulae at both ends (Han 2007; Datir et al. 2011; Lee et al. 2012). Buckling tests were performed to determine the baseline critical buckling pressure as described previously. Then, the arteries were carefully removed, inverted and treated at the midsection with a cotton pad containing 0.5 ml of elastase at a concentration of 280 U/ml (Worthington, NJ) and incubated for two hours to create a focal aneurysm. The arteries were then carefully inverted back and re-mounted on to the test box at the same position. An aneurysm (locally enlarged diameter and wall thinning), was visually confirmed in the middle portion of the artery under lumen pressure (~50 mmHg). The buckling tests were repeated and the critical buckling pressures were measured as described previously. The critical buckling pressures of the normal and aneurysmal arteries were statistically compared using the paired student t-test.

RESULTS

Material constants of porcine carotid arteries

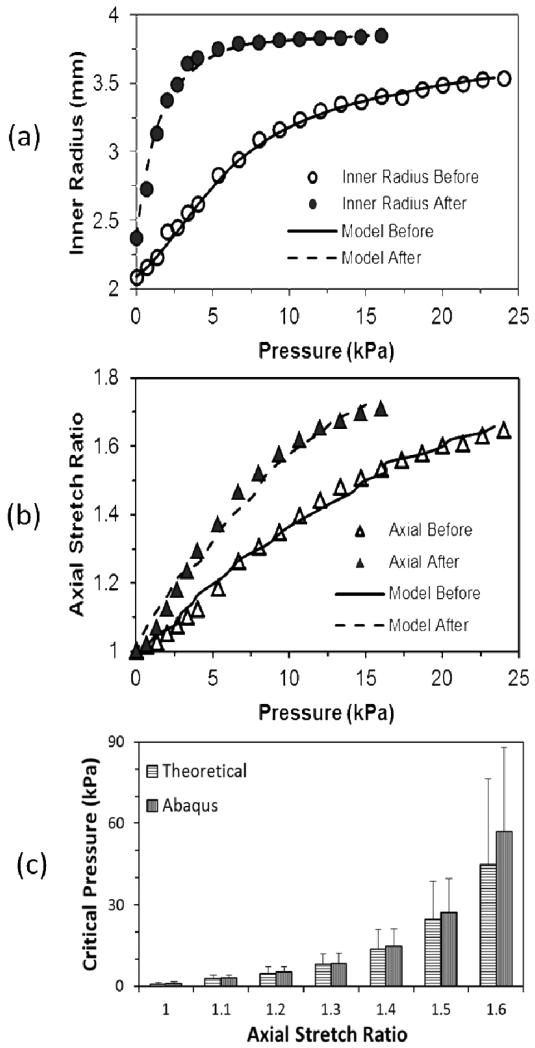
The convex material constants for the set of six normal porcine carotid arteries and one artery treated with elastase are given in Table 1. The pressure deformation curves obtained using the convex material constants fit the experimental data well (Fig. 2). The critical buckling pressures determined from the FEA simulations, using the convex material constants, also demonstrated good agreement with the critical buckling pressures (Fig. 2) determined from the theoretical buckling equation (Han 2009a; Lee et al. 2012) and these results validated the FEA results.

Fig. 2.

Fig. 2

Open in a new tab

Comparison of measured (a) circumferential deformation and (b) axial stretch of artery E6 before (solid line) and after (dashed line) elastase treatment and theoretical fitting results. Hollow and solid symbols are experimental data before and after elastase treatment. (c) Comparison of critical pressures (mean and standard deviation) obtained from FEA simulations and theoretical buckling equation for five normal arteries (artery 5-9, Table 1) at various axial stretch ratios.

Post-buckling deflection of normal arteries

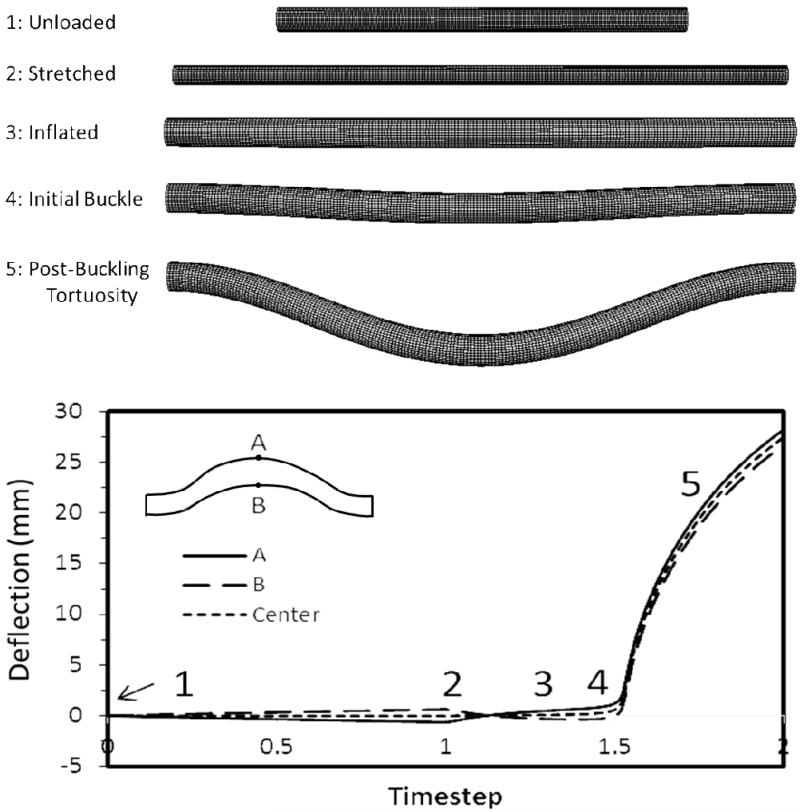
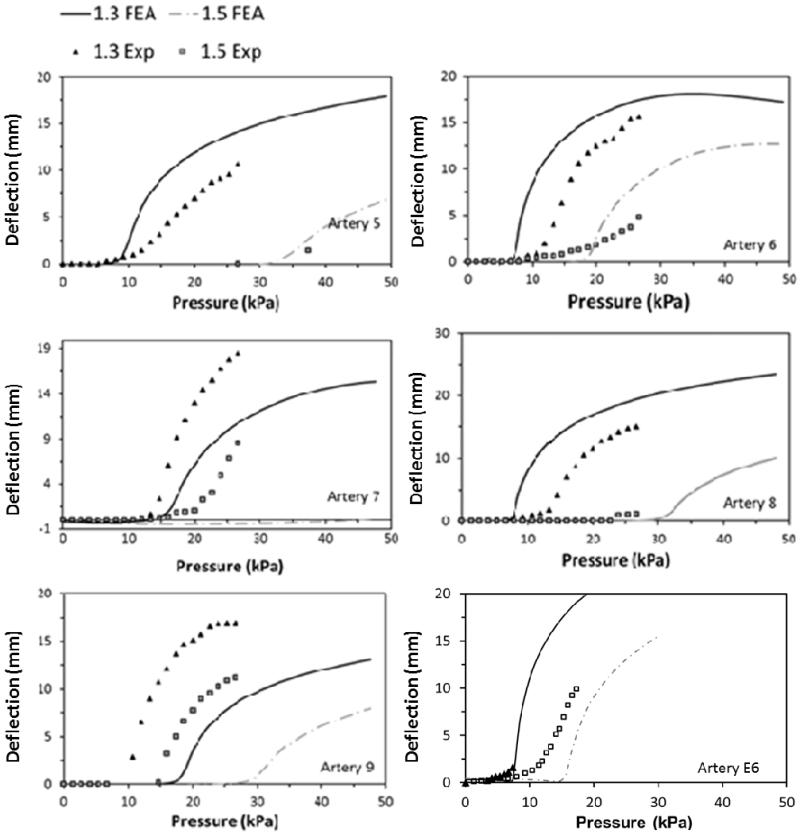
Our simulations captured the post buckling behavior of the arteries where a lateral deflection was initiated at a critical pressure and continued to increase post-buckling with increasing pressure (Fig. 3). Both FEA simulations and experimental measurements showed that arterial deflection increased nonlinearly with increasing lumen pressure beyond the critical buckling pressure. For the six normal arteries, the FEA simulations yielded similar post-buckling deflection curves compared to experimental measurements (Fig. 4), with slight shifts in the initiation points due to differences in critical buckling pressures.

Fig. 3.

Fig. 3

Open in a new tab

Deformation of an artery under increasing lumen pressure. Meshed vessels from top to bottom: under no load, axially stretched, inflated under a small pressure without buckling, slightly buckled, and post-buckling. Plot: Deflection of the two edges at the middle of the artery (points A & B) and the centerline (average of points A and B) plotted with the loading time steps.

Fig. 4.

Fig. 4

Open in a new tab

Comparison of the FEA predicted and experimentally measured post-buckling deflection curves of the six normal arteries (artery 5-9 & E6) at stretch ratios of 1.3 and 1.5.

Effect of aneurysm on critical buckling pressure and post-buckling deflection

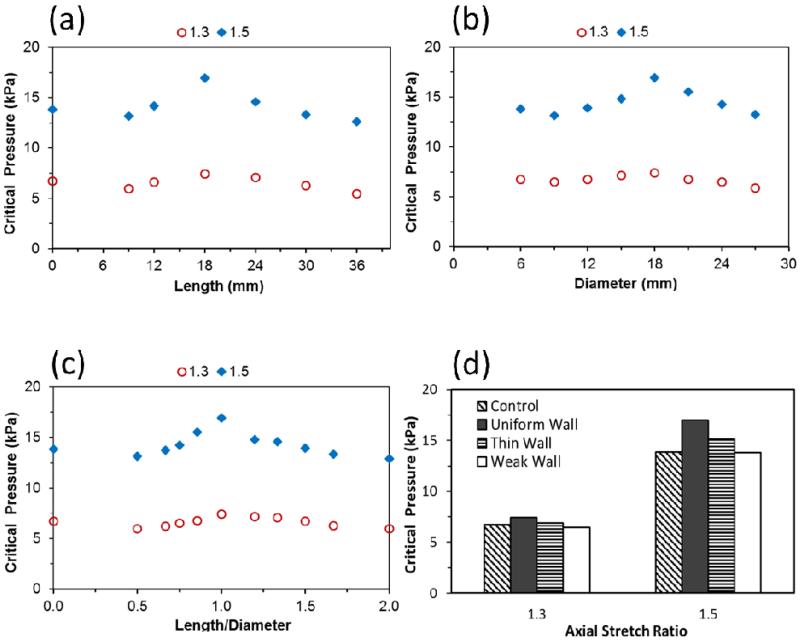
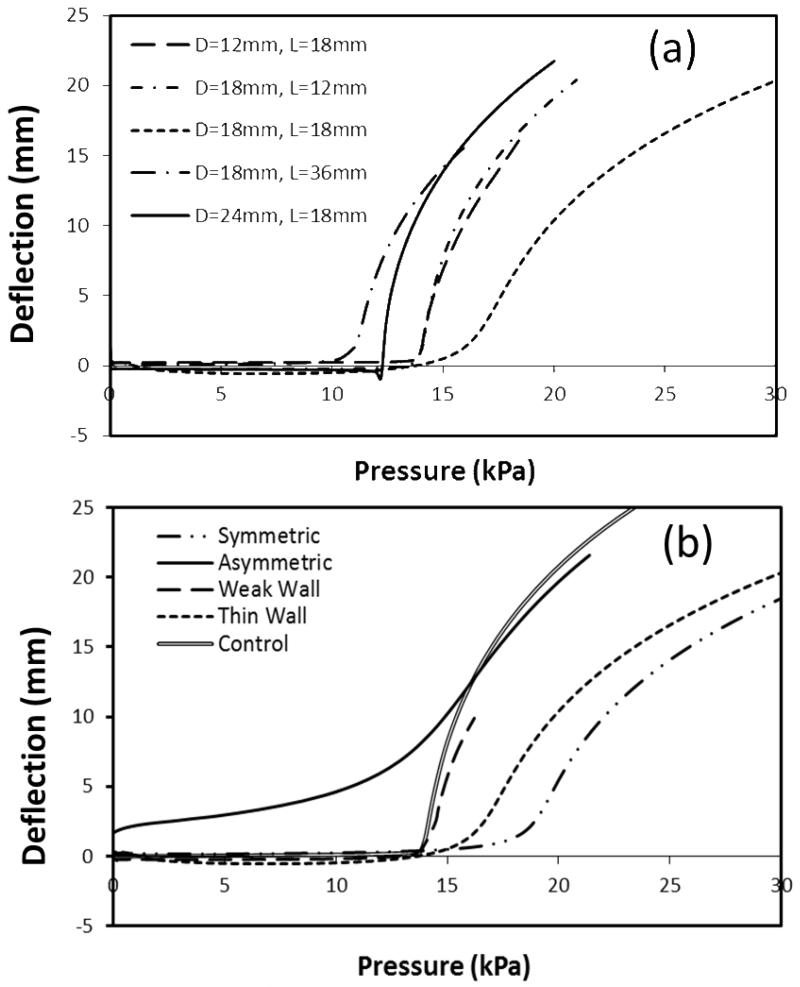
Experimental tests showed that porcine arteries with small aneurysms (after focal elastase treatment) buckled at a lower critical pressure compared to the controls (before elastase treatment) (Fig. 5). Further FEA simulations demonstrated that the dimensions (length and diameter) and shape (length-to-diameter ratio) of the aneurysms affected the critical buckling pressure (Fig. 6). The critical buckling pressure did not show a monotonic change with either aneurysm diameter or length (p>0.1, Fig. 6a, b). The shape of the aneurysm (length-to-diameter ratio, L/D) affected the critical buckling pressure such that an aneurysm with a spherical shape (L/D=1) had a higher critical buckling pressure than aneurysms with elliptical shapes (L/D≠1) (Fig. 6c). The critical buckling pressure of an aneurysmal artery was lower than that of a normal artery when the shape of the aneurysm is highly elliptical (L/D > 1.5 or L/D < 0.7 in Fig 6c). These results also explained the lower critical buckling pressure observed in the experimental tests on aneurysms (Figure 5) since these aneurysms had a large length-to-diameter ratio. The thin walled aneurysm and weakened aneurysm had lower critical buckling pressures compared to aneurysms with normal and uniform wall thicknesses (Fig. 6d). When the pressure increased beyond the critical buckling pressure, artery deflection increased nonlinearly. For arteries with aneurysms of different sizes and shapes, the deflection initiation points (at the critical buckling pressure) and the rate of increase of deflection were slightly different, but the trends were similar (Fig. 7). For severely asymmetric aneurysms with dilation on one side of the vessel (see Fig. 1), the deflection starts almost immediately after a pressure is applied and continues to increase with increasing lumen pressure. While the deflection accelerated at a certain pressure range, it was difficult to define a “critical buckling point” (Fig. 7b).

Fig. 5.

Fig. 5

Open in a new tab

Photographs: an artery at a lumen pressure of 80 mmHg during the buckling test (PBS) before (top) and after (bottom) focal elastase treatment at the middle portion of the segment. Bargraph: Comparison of the critical buckling pressure of arteries (mean ± SD, n=4) before and after elastase treatment. * p < 0.05.

Fig. 6.

Fig. 6

Open in a new tab

Effects of aneurysm size and shape on the critical buckling pressure. (a): Variation of critical buckling pressure with aneurysm length at a given diameter (DA=18 mm). (b): Variation of critical buckling pressure with aneurysm diameter at a given length (LA=18 mm). (c): Variation of critical buckling pressure with length/diameter ratio (L/D) of the aneurysm. The critical buckling pressure values are plotted at two levels of axial stretch ratios (1.3 and 1.5), assuming an aneurysm of uniform wall thickness (tA=1mm) and material constants of artery E6 (Table 1). Note L/D=0 represents the control without aneurysm. (d): Comparison of the critical buckling pressure of control (no aneurysm) and aneurysmal arteries with a uniform wall (tA=1mm), thin wall (tA=0.5mm) and weak wall (elastase treated). The aneurysm has dimensions of DA=LA=18 mm. All aneurysm walls were assumed to be of the same material constants as normal artery E6 (Table 1) except the “weak wall” case, which had the material constants of the elastase treated artery “E6 treated”.

Fig. 7.

Fig. 7

Open in a new tab

(a): Deflection versus pressure curve of aneurysmal arteries with various aneurysm shapes (different diameter and length) (b): Deflection versus pressure curve of control artery, asymmetric aneurysm and symmetric aneurysm with thick wall, thin wall and weak wall.

Effect of buckling on aneurysm wall stress

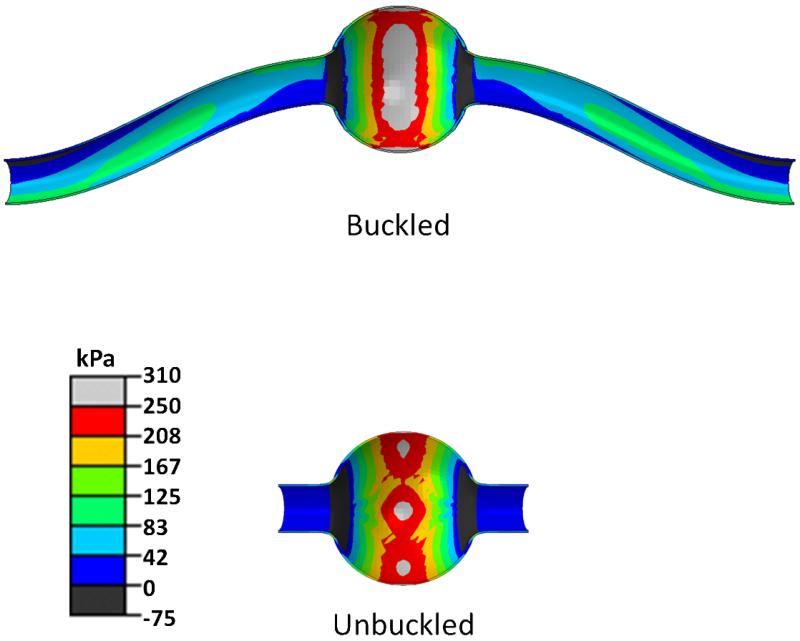
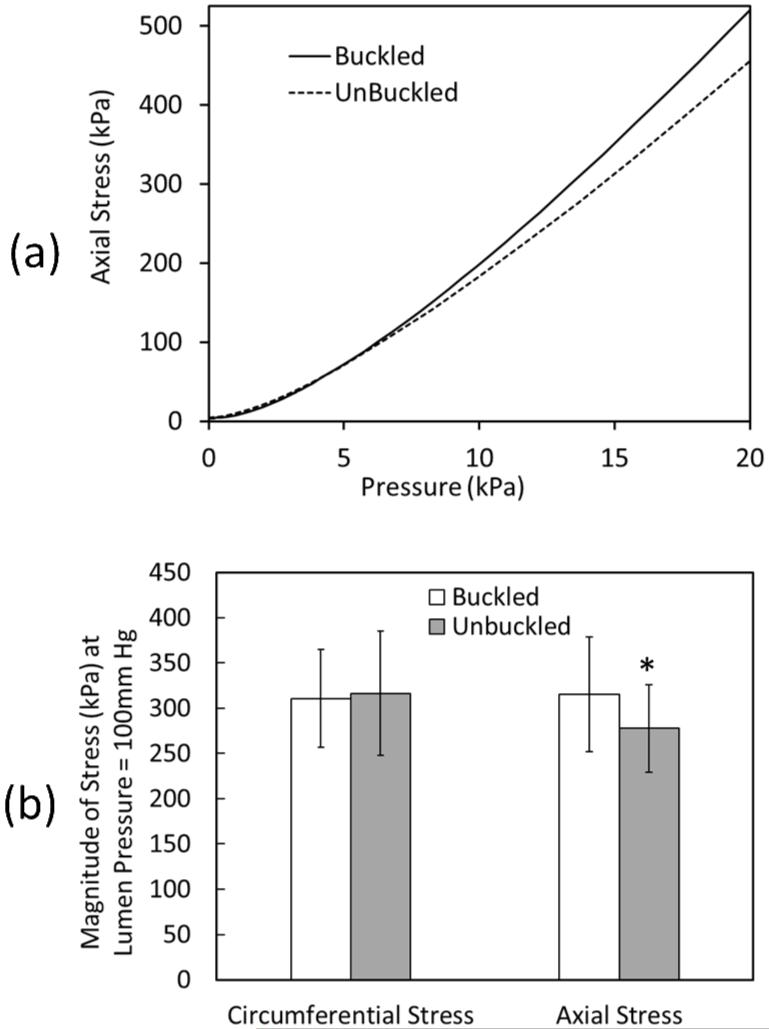
At a given pressure, buckled aneurysms demonstrated a larger area of increased stress compared to the control (un-buckled) aneurysms (Fig. 8). The peak axial stress was located at the tip of the aneurysm wall on the convex side of the buckled aneurysm. The stress in the buckled aneurysm increased much more significantly as the lumen pressure and severity of buckling (deflection) increased (Fig. 9a). Further analysis demonstrated that the peak axial stress (σzz) at 100 mmHg lumen pressure was significantly higher in buckled aneurysms than in unbuckled aneurysms (p=0.002), while the peak circumferential stress (σθθ) showed no statistical difference between the two groups (p=0.52) (Fig. 9b).

Fig. 8.

Fig. 8

Open in a new tab

Axial stress profile (kPa) in buckled and unbuckled symmetric spherical-shaped aneurysmal arteries under internal pressure. Both aneurysms are of the same dimensions (DA = 18mm, LA= 18mm and tA= 1 mm) and under the same pressure of ~100 mmHg (~13 kPa). The neck was cut short in the bottom model to avoid buckling.

Fig. 9.

Fig. 9

Open in a new tab

(a) Comparison of peak axial wall stress in a buckled and an unbuckled spherical-shaped aneurysmal artery (dimensions LA=DA=18mm) as a function of lumen pressure. (b) Comparison of the peak axial and circumferential stresses (mean ± standard deviation) for six arteries with an aneurysm (dimensions LA=DA=18mm) at 100mmHg lumen pressure for buckled and unbuckled conditions. The vessel dimensions and material constants were from Table 1. * p = 0.002

Buckling of tapered aneurysmal abdominal aorta

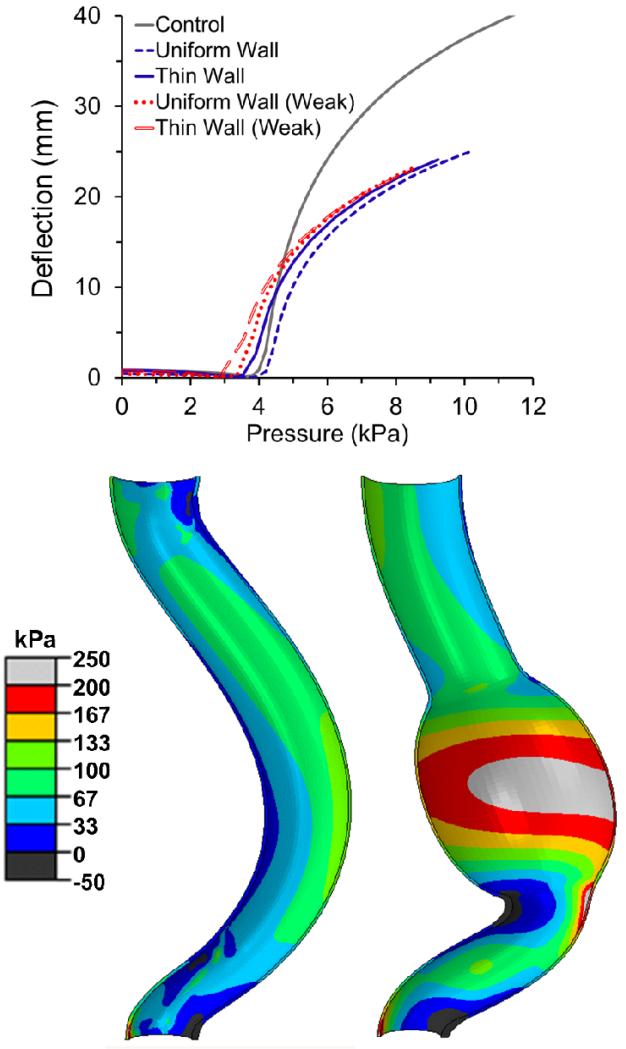
While the abdominal aorta with a thick uniform wall aneurysm (same wall thickness as the normal aorta) buckled at a higher critical buckling pressure compared to the normal control without an aneurysm, the aorta with a thin wall aneurysm and weak wall material aneurysms all had a lower pressure (Fig. 10). As the aneurysms commonly seen in humans are thinner and weaker than normal, these results indicate that aneurysms would reduce the stability of the human aorta. In addition, the presence of an aneurysm resulted in a higher lumen stress compared to the control aorta under the same lumen pressure (Fig. 10).

Fig. 10.

Fig. 10

Open in a new tab

Graph: Comparison of the deflection versus pressure curve of a tapered abdominal aorta model with and without an aneurysm (control). The aneurysm in the model was assumed to have either a uniform wall thickness (t=1.5mm) or a thin wall (t=0.75mm). The aneurysm wall was assumed to have an either normal or weak (elastase-treated) material property. Picture: Comparison of axial wall stress distribution in the lumen of the tapered aorta model without (left) and with an aneurysm (right) at a lumen pressure of 75mmHg and an axial stretch ratio of 1.3. See text for vessel dimensions.

DISCUSSION

In this study, we investigated the buckling and post-buckling behavior of normal and aneurysmal arteries with fusiform aneurysms. Our results demonstrated that the lateral deflection of arteries increased nonlinearly with increasing lumen pressure post-buckling. The presence of aneurysms could reduce the critical buckling pressure of arteries, and buckling resulted in higher axial stresses in the aneurysm wall. In addition, the shape of aneurysms affected the critical buckling pressure. For asymmetric aneurysms, the vessel deflection started at a very low pressure, increased slowly at low pressures, and then accelerated at higher pressures. Furthermore, the critical buckling pressure of normal arteries predicted by FEA match the theoretical predictions and the post-buckling deflections of normal arteries predicted by FEA simulations were in good agreement with the experimental results.

Mechanisms of mechanical instability of aneurysms

The effects of aneurysms on the arterial critical buckling pressure are multifaceted. First, the geometric changes, such as a thinner wall, axial asymmetry, and irregular shape can reduce the critical buckling pressure of aneurysmal arteries. Second, aneurysm wall properties are often different from normal arterial walls. Elastin degradation often occurs in an aneurysm wall and is believed to be a factor in the development of aneurysms (Dobrin and Canfield 1984; Dobrin et al. 1988; Vorp 2007) and tortuous arteries (Wagenseil et al. 2005; Wagenseil et al. 2007). Our previous theoretical and experimental work demonstrated that elastin degradation weakened the arterial wall and reduced the critical buckling pressure, making them prone to buckling (Han 2012; Lee et al. 2012). It has been also reported that the formation of an aneurysm may lead to an increase in the aortic length (Michineau et al. 2010), which could reduce the axial tension and axial stretch ratio in the aorta and thus reduce the critical buckling pressure. These effects combined together make aneurysmal arteries prone to buckling.

Effect of buckling on aneurysms

The deformation of aneurysmal arteries into tortuous shapes induces mechanical and hemodynamic changes in the aneurysms (Doyle et al. 2009; Datir et al. 2011; Han 2012). Previous studies have shown that aneurysm shape and size could significantly affect local stress concentrations in aneurysms (Kyriacou and Humphrey 1996; Fillinger et al. 2003; Challa and Han 2007). Buckling changes the shape and curvature of the aneurysmal wall surface which can lead to higher peak axial wall stresses and thus increase the risk of aneurysm rupture. Aneurysm asymmetry is another factor that is related to increased rupture risk (Fillinger et al. 2004; Doyle et al. 2009). Buckling deformation changes the blood flow in the aneurysm, which can alter the wall shear stress and affects intra-lumen thrombus distribution (Chesnutt and Han 2011; Chesnutt and Han 2013). While some of these changes are similar to normal arteries (Han 2012), they may be severe in aneurysms. Therefore, buckling could play an important role in aneurysm wall stress and rupture.

Clinical relevance

Aneurysmal arteries are often tortuous (Johnson et al. 2007) with AAAs estimated to be tortuous in over 80% of cases (Hatakeyama et al. 2001). Our results demonstrated that aneurysms could reduce the critical buckling pressure of the arteries, especially tapered arteries and can possibly make them more vulnerable to buckling and tortuosity. This new finding of reduced stability of aneurysmal arteries could be a possible mechanism for the development of tortuous aneurysmal arteries including those seen in patients with Loeys-Dietz syndrome (Loeys et al. 2006; Han 2012). Specifically, thin and weak aneurysms can reduce the critical pressure of the abdominal aorta greatly and thus make it vulnerable to buckling and tortuosity.

Tortuosity changes the curvature of aneurysm surfaces and thus the wall stress. Sacks et al demonstrated that removal of tortuosity would reduce surface curvature by nearly 30% (Sacks et al. 1999). Tortuous aneurysms also affect intraluminal blood flow and thrombosis formation (Sho et al. 2004; Tan et al. 2009). Peak wall stress in the presence of intraluminal thrombosis demonstrated a significant correlation with the degree of centerline tortuosity (Georgakarakos et al. 2010). Tortuosity is also proposed as a predictor of the expansion rate of the maximum transverse aneurysm diameter (Hatakeyama et al. 2001). Higher tortuosity levels have been associated with higher stress and a higher risk factor (Sacks et al. 1999; Hatakeyama et al. 2001; Pappu et al. 2008). A study also showed that over time the tortuosity of arteries increased and that these increases led to an increased rupture risk (Pappu et al. 2008). However, there has been a contradictory report that higher rupture risk is associated with no or mild tortuosity for diameter-matched aneurysms (Fillinger et al. 2004). One possible reason was considered to be due to the error from the 2D curvature measurement used. Further clinical data are needed to clarify this issue.

Limitations

There were a few limitations in this study. First, our simulations were limited to idealized aneurysm shapes. While these aneurysms were not actual patient specific aneurysms, they illustrated the effect of aneurysm buckling on their critical buckling pressure and wall stress. Further patient-specific analysis and the possible effects of other factors such as calcification and intralumenal thrombus on critical buckling pressure need to be studied in the future (Li et al. 2008; Wyss et al. 2011). Second, although arterial walls are anisotropic with a layered structure, we used a single layer anisotropic model in the analysis, representing the transmural average properties of the arterial wall. Similar models have been used widely for mechanical stress analysis of AAAs in other studies (Fillinger et al. 2003; Vorp 2007). Third, the boundary conditions were simplified in the simulations with the two ends of the artery assumed to be fixed with no surrounding tissue support (Han 2009a; Han 2009b). Finally, we examined only the instant effect of buckling on wall stress, further work is needed to study the effects of buckling on blood flow and long-term wall remodeling (Xiao et al. 2014; Zhang et al. 2014).

Significance

Our results demonstrated that aneurysms can reduce the mechanical stability of arteries and the mechanical instability affects the wall stress in aneurysms. These results provide insight into the underlying mechanism for the development and prevalence of tortuous aneurysmal arteries in humans. Mechanical buckling may play an important role in the development of tortuous aneurysms and increase their risk of rupture.

ACKNOWLEDGMENTS

This work was supported by CAREER award #0644646 from the National Science Foundation and grant HL095852 from the National Institutes of Health. It was also partially supported by HHSN 268201000036C (N01-HV-00244) for the NHLBI San Antonio Cardiovascular Proteomics Center. Avione Lee was partially supported by a MBRS-RISE pre-doctoral fellowship under grant GM60655 from NIH. We also thank the Computational Systems Biology Core funded by NIH (G12MD007591) for providing access to their computational facilities for the simulations.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

Conflict of interest

The authors have no conflict of interest.

References

  1. Arends J, Perkins KD, Zhang J, Polyakov I, Lee E. A new technique for the surgical creation of aneurysms in an in vivo tortuous vessel model to test neurovascular devices. J Invest Surg. 2008;21(1):39–45. doi: 10.1080/08941930701834189. [DOI] [PubMed] [Google Scholar]
  2. Challa V, Han HC. Spatial variations in wall thickness, material stiffness and initial shape affect wall stress and shape of intracranial aneurysms. Neurological Research. 2007;29(6):569–577. doi: 10.1179/016164107X164193. [DOI] [PubMed] [Google Scholar]
  3. Chesnutt JK, Han HC. Tortuosity triggers platelet activation and thrombus formation in microvessels. J Biomech Eng. 2011;133(12):121004. doi: 10.1115/1.4005478. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Chesnutt JKW, Han HC. Effect of red blood cells on platelet activation and thrombus formation in tortuous arterioles. Frontiers Bioeng Biotech. 2013;1(18):1–12. doi: 10.3389/fbioe.2013.00018. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Datir P, Lee AY, Lamm SD, Han HC. Effects of geometric variations on the buckling of arteries. Int J Appl Mech. 2011;3(2):385–406. doi: 10.1142/S1758825111001044. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Del Corso L, Moruzzo D, Conte B, Agelli M, Romanelli AM, Pastine F, Protti M, Pentimone F, Baggiani G. Tortuosity, kinking, and coiling of the carotid artery: expression of atherosclerosis or aging? Angiology. 1998;49(5):361–71. doi: 10.1177/000331979804900505. [DOI] [PubMed] [Google Scholar]
  7. Deterling RA. Tortuous right common carotid artery simulating aneurysm. Angiology. 1952;3(6):483–92. doi: 10.1177/000331975200300607. [DOI] [PubMed] [Google Scholar]
  8. Dobrin PB, Canfield TR. Elastase, collagenase, and the biaxial elastic properties of dog carotid artery. Am J Physiol. 1984;247(1 Pt 2):H124–31. doi: 10.1152/ajpheart.1984.247.1.H124. [DOI] [PubMed] [Google Scholar]
  9. Dobrin PB, Schwarcz TH, Baker WH. Mechanisms of arterial and aneurysmal tortuosity. Surgery. 1988;104(3):568–71. [PubMed] [Google Scholar]
  10. Doyle BJ, Callanan A, Burke PE, Grace PA, Walsh MT, Vorp DA, McGloughlin TM. Vessel asymmetry as an additional diagnostic tool in the assessment of abdominal aortic aneurysms. J Vasc Surg. 2009;49(2):443–54. doi: 10.1016/j.jvs.2008.08.064. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Fillinger MF, Marra SP, Raghavan ML, Kennedy FE. Prediction of rupture risk in abdominal aortic aneurysm during observation: Wall stress versus diameter. J Vasc Surg. 2003;37(4):724–732. doi: 10.1067/mva.2003.213. [DOI] [PubMed] [Google Scholar]
  12. Fillinger MF, Racusin J, Baker RK, Cronenwett JL, Teutelink A, Schermerhorn ML, Zwolak RM, Powell RJ, Walsh DB, Rzucidlo EM. Anatomic characteristics of ruptured abdominal aortic aneurysm on conventional CT scans: Implications for rupture risk. J Vasc Surg. 2004;39(6):1243–52. doi: 10.1016/j.jvs.2004.02.025. [DOI] [PubMed] [Google Scholar]
  13. Fillinger MF, Raghavan ML, Marra SP, Cronenwett JL, Kennedy FE. In vivo analysis of mechanical wall stress and abdominal aortic aneurysm rupture risk. J Vasc Surg. 2002;36(3):589–597. doi: 10.1067/mva.2002.125478. [DOI] [PubMed] [Google Scholar]
  14. Fleischmann D, Hastie TJ, Dannegger FC, Paik DS, Tillich M, Zarins CK, Rubin GD. Quantitative determination of age-related geometric changes in the normal abdominal aorta. J Vasc Surg. 2001;33(1):97–105. doi: 10.1067/mva.2001.109764. [DOI] [PubMed] [Google Scholar]
  15. Fung YC. Biomechanics: Mechanical Properties of Living Tissues. Springer Verlag; New YorK: 1993. [Google Scholar]
  16. Georgakarakos E, Ioannou CV, Kamarianakis Y, Papaharilaou Y, Kostas T, Manousaki E, Katsamouris AN. The role of geometric parameters in the prediction of abdominal aortic aneurysm wall stress. Eur J Vasc Endovasc Surg. 2010;39(1):42–8. doi: 10.1016/j.ejvs.2009.09.026. [DOI] [PubMed] [Google Scholar]
  17. Han HC. A biomechanical model of artery buckling. J Biomech. 2007;40(16):3672–8. doi: 10.1016/j.jbiomech.2007.06.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Han HC. Blood vessel buckling within soft surrounding tissue generates tortuosity. J Biomech. 2009a;42(16):2797–2801. doi: 10.1016/j.jbiomech.2009.07.033. [DOI] [PubMed] [Google Scholar]
  19. Han HC. The theoretical foundation for artery buckling under internal pressure. J Biomech Eng. 2009b;131(12):124501. doi: 10.1115/1.4000080. [DOI] [PubMed] [Google Scholar]
  20. Han HC. Twisted Blood Vessels: Symptoms, Etiology, and Biomechanical Mechanisms. J Vasc Res. 2012;49(3):185–197. doi: 10.1159/000335123. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Han HC, Chesnutt JK, Garcia JR, Liu Q, Wen Q. Artery buckling: new phenotypes, models, and applications. Ann Biomed Eng. 2013;41(7):1399–410. doi: 10.1007/s10439-012-0707-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Han HC, Fung YC. Species dependence of the zero-stress state of aorta: pig versus rat. J Biomech Eng. 1991;113(4):446–51. doi: 10.1115/1.2895425. [DOI] [PubMed] [Google Scholar]
  23. Han HC, Fung YC. Longitudinal strain of canine and porcine aortas. J Biomech. 1995;28(5):637–41. doi: 10.1016/0021-9290(94)00091-h. [DOI] [PubMed] [Google Scholar]
  24. Han HC, Ku DN, Vito RP. Arterial wall adaptation under elevated longitudinal stretch in organ culture. Ann Biomed Eng. 2003;31(4):403–11. doi: 10.1114/1.1561291. [DOI] [PubMed] [Google Scholar]
  25. Hatakeyama T, Shigematsu H, Muto T. Risk factors for rupture of abdominal aortic aneurysm based on three-dimensional study. J Vasc Surg. 2001;33(3):453–61. doi: 10.1067/mva.2001.111731. [DOI] [PubMed] [Google Scholar]
  26. Johnson PT, Chen JK, Loeys BL, Dietz HC, Fishman EK. Loeys-Dietz syndrome: MDCT angiography findings. AJR Am J Roentgenol. 2007;189(1):W29–35. doi: 10.2214/AJR.06.1316. [DOI] [PubMed] [Google Scholar]
  27. Kyriacou SK, Humphrey JD. Influence of size, shape and properties on the mechanics of axisymmetric saccular aneurysms. J Biomech. 1996;29(8):1015–22. doi: 10.1016/0021-9290(96)00010-3. [DOI] [PubMed] [Google Scholar]
  28. Lee AY. Biomedical Engineering. University of Texas at San Antonio; San Antonio, TX: 2011. Determining the Critical Buckling of Blood Vessels Through Modeling and In Vitro Experiments. PhD. [Google Scholar]
  29. Lee AY, Han B, Lamm SD, Fierro CA, Han HC. Effects of elastin degradation and surrounding matrix support on artery stability. Am J Physiol Heart Circ Physiol. 2012;302(4):H873–84. doi: 10.1152/ajpheart.00463.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Li ZY, J UK-I, Tang TY, Soh E, See TC, Gillard JH. Impact of calcification and intraluminal thrombus on the computed wall stresses of abdominal aortic aneurysm. J Vasc Surg. 2008;47(5):928–35. doi: 10.1016/j.jvs.2008.01.006. [DOI] [PubMed] [Google Scholar]
  31. Liu Q, Han HC. Mechanical buckling of artery under pulsatile pressure. J Biomech. 2012;45(7):1192–8. doi: 10.1016/j.jbiomech.2012.01.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Liu SQ, Fung YC. Zero-stress states of arteries. J Biomech Eng. 1988;110(1):82–4. doi: 10.1115/1.3108410. [DOI] [PubMed] [Google Scholar]
  33. Loeys BL, Schwarze U, Holm T, Callewaert BL, Thomas GH, Pannu H, De Backer JF, Oswald GL, Symoens S, Manouvrier S, Roberts AE, Faravelli F, Greco MA, Pyeritz RE, Milewicz DM, Coucke PJ, Cameron DE, Braverman AC, Byers PH, De Paepe AM, Dietz HC. Aneurysm syndromes caused by mutations in the TGF-beta receptor. N Engl J Med. 2006;355(8):788–98. doi: 10.1056/NEJMoa055695. [DOI] [PubMed] [Google Scholar]
  34. Martinez R, Fierro CA, Shireman PK, Han HC. Mechanical buckling of veins under internal pressure. Ann Biomed Eng. 2010;38(4):1345–53. doi: 10.1007/s10439-010-9929-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Michineau S, Dai J, Gervais M, Zidi M, Clowes AW, Becquemin JP, Michel JB, Allaire E. Aortic length changes during abdominal aortic aneurysm formation, expansion and stabilisation in a rat model. Eur J Vasc Endovasc Surg. 2010;40(4):468–74. doi: 10.1016/j.ejvs.2010.05.001. [DOI] [PubMed] [Google Scholar]
  36. Pappu S, Dardik A, Tagare H, Gusberg RJ. Beyond fusiform and saccular: a novel quantitative tortuosity index may help classify aneurysm shape and predict aneurysm rupture potential. Ann Vasc Surg. 2008;22(1):88–97. doi: 10.1016/j.avsg.2007.09.004. [DOI] [PubMed] [Google Scholar]
  37. Rodriguez JF, Ruiz C, Doblare M, Holzapfel GA. Mechanical stresses in abdominal aortic aneurysms: Influence of diameter, asymmetry, and material anisotropy. J Biomech Eng-Trans ASME. 2008;130(2) doi: 10.1115/1.2898830. [DOI] [PubMed] [Google Scholar]
  38. Sacks MS, Sun W. Finite element implementation of a generalized Fung-elastic constitutive model for planar soft tissues. Biomech Model Mechanobiol. 2005;4(2-3):190–199. doi: 10.1007/s10237-005-0075-x. [DOI] [PubMed] [Google Scholar]
  39. Sacks MS, Vorp DA, Raghavan ML, Federle MP, Webster MW. In vivo three-dimensional surface geometry of abdominal aortic aneurysms. Ann Biomed Eng. 1999;27(4):469–79. doi: 10.1114/1.202. [DOI] [PubMed] [Google Scholar]
  40. Sho E, Nanjo H, Sho M, Kobayashi M, Komatsu M, Kawamura K, Xu C, Zarins CK, Masuda H. Arterial enlargement, tortuosity, and intimal thickening in response to sequential exposure to high and low wall shear stress. J Vasc Surg. 2004;39(3):601–12. doi: 10.1016/j.jvs.2003.10.058. [DOI] [PubMed] [Google Scholar]
  41. Tan FPP, Torii R, Borghi A, Mohiaddin RH, Wood NB, Xu XY. Fluid-structure interaction analysis of wall stress and flow patterns in thoracic aorta aneurysm. Int J Appl Mech. 2009;1(1):179–199. [Google Scholar]
  42. Vorp DA. Biomechanics of abdominal aortic aneurysm. J Biomech. 2007;40(9):1887–1902. doi: 10.1016/j.jbiomech.2006.09.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Wagenseil JE, Knutsen RH, Li DY, Mecham RP. Elastin-insufficient mice show normal cardiovascular remodeling in 2K1C hypertension despite higher baseline pressure and unique cardiovascular architecture. Am J Physiol Heart Circ Physiol. 2007;293(1):H574–82. doi: 10.1152/ajpheart.00205.2007. [DOI] [PubMed] [Google Scholar]
  44. Wagenseil JE, Nerurkar NL, Knutsen RH, Okamoto RJ, Li DY, Mecham RP. Effects of elastin haploinsufficiency on the mechanical behavior of mouse arteries. Am J Physiol Heart Circ Physiol. 2005;289(3):H1209–17. doi: 10.1152/ajpheart.00046.2005. [DOI] [PubMed] [Google Scholar]
  45. Wolf YG, Tillich M, Lee WA, Rubin GD, Fogarty TJ, Zarins CK. Impact of aortoiliac tortuosity on endovascular repair of abdominal aortic aneurysms: evaluation of 3D computer-based assessment. J Vasc Surg. 2001;34(4):594–9. doi: 10.1067/mva.2001.118586. [DOI] [PubMed] [Google Scholar]
  46. Wyss TR, Dick F, Brown LC, Greenhalgh RM. The influence of thrombus, calcification, angulation, and tortuosity of attachment sites on the time to the first graft-related complication after endovascular aneurysm repair. J Vasc Surg. 2011;54(4):965–71. doi: 10.1016/j.jvs.2011.04.007. [DOI] [PubMed] [Google Scholar]
  47. Xiao Y, Hayman D, Khalafvand SS, Lindsey ML, Han HC. Artery Buckling Stimulates Cell Proliferation and NF-kappaB Signaling. Am J Physiol Heart Circ Physiol. 2014;307(4):H542–H551. doi: 10.1152/ajpheart.00079.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Zhang J, Liu Q, Han HC. An in vivo rat model of artery buckling for studying wall remodeling. Ann Biomed Eng. 2014;42(8):1658–67. doi: 10.1007/s10439-014-1017-5. [DOI] [PMC free article] [PubMed] [Google Scholar]

RESOURCES