The Effects of Data Sources, Cohort Selection, and Outcome Definition on a Predictive Model of Risk of Thirty-Day Hospital Readmissions

Abstract

Background

Hospital readmission risk prediction remains a motivated area of investigation and operations in light of the Hospital Readmissions Reduction Program through CMS. Multiple models of risk have been reported with variable discriminatory performances, and it remains unclear how design factors affect performance.

Objectives

To study the effects of varying three factors of model development in the prediction of risk based on health record data: 1) Reason for readmission (primary readmission diagnosis); 2) Available data and data types (e.g. visit history, laboratory results, etc); 3) Cohort selection.

Methods

Regularized regression (LASSO) to generate predictions of readmissions risk using prevalence sampling. Support Vector Machine (SVM) used for comparison in cohort selection testing. Calibration by model refitting to outcome prevalence.

Results

Predicting readmission risk across multiple reasons for readmission resulted in ROC areas ranging from 0.92 for readmission for congestive heart failure to 0.71 for syncope and 0.68 for all-cause readmission. Visit history and laboratory tests contributed the most predictive value; contributions varied by readmission diagnosis. Cohort definition affected performance for both parametric and nonparametric algorithms. Compared to all patients, limiting the cohort to patients whose index admission and readmission diagnoses matched resulted in a decrease in average ROC from 0.78 to 0.55 (difference in ROC 0.23, p value 0.01). Calibration plots demonstrate good calibration with low mean squared error.

Conclusion

Targeting reason for readmission in risk prediction impacted discriminatory performance. In general, laboratory data and visit history data contributed the most to prediction; data source contributions varied by reason for readmission. Cohort selection had a large impact on model performance, and these results demonstrate the difficulty of comparing results across different studies of predictive risk modeling.

1. Introduction¹

Clinical, legislative, and financial drivers have elevated the significance of hospital readmissions for the multidisciplinary care team and hospital administrators. The emphasis on readmissions as a reportable quality measure and as a source of potential reimbursement penalty through the Centers for Medicare and Medicaid Services (CMS) has been well-described.[1] Consensus is forming to support the need for patient-centered interventions across care settings to prevent readmissions for particular patients.[2, 3] The first step in the myriad of efforts to reduce readmissions remains identification of patients at high risk.[3]

The most comprehensive review of readmissions risk prediction models to date was published in 2011 by Kansagara et al.[4] Since then, thousands of new articles on the topic have been published. A simple OVID Medline search for “Patient readmission” in 2011 produced 5,476 hits,[4] while it yields 7,576 results at the start of 2014. Each model has the potential to be adapted by researchers and managers in new clinical settings, but to do so appropriately, it is critical to understand the sensitivity of such models to varying the way in which they are built and deployed. While researchers also must compare results across seemingly similar studies, it is poorly understood how different factors in model design affect performance. Thus, it remains unclear if comparisons are legitimate as studies may differ in a number of different aspects.

The goal of this study is to study the effect of three factors on prediction of hospital readmission risk. The first factor is the reason for readmission as defined by the primary readmission diagnosis. Early predictive models of readmissions focused on all-cause readmission and the most common diagnoses including congestive heart failure (CHF), acute myocardial infarction (acute MI), and chronic obstructive pulmonary disease (COPD), but the literature now spans multiple diagnoses and disciplines.[5–15] However, no studies have studied systematically the effects of changing readmission diagnoses being modeled while holding all else equal. This latter understanding will help interpret and compare studies of different diseases. Additionally, the ability to predict readmission as a simultaneous panel of cases may have clinical utility in that it may direct clinical interventions to causes deemed most likely for a particular patient by the predictive algorithm.

The second factor under study is data availability. Studies have included data types such as administrative and claims data, test results and clinical text.[4, 16–19] One study demonstrated that readmission rates and rates of unnecessary readmissions vary by method of chart review to tally readmissions and by altering the breadth of the definition of a readmission itself.[19] This work studies the effect of varying the features in the model across multiple readmission diagnoses holding all else unchanged. We attempt to elucidate the contributions of data types included for prediction in clinically meaningful bins: laboratory tests, visit utilization, demographics, clinical narrative. While it is clear that more data and more clinically deep data should be better, it remains unclear to what extent the selection of data type is dependent on how the problem is cast.

The third factor is the cohort that is selected for study. The challenge of generalizability to new cohorts is well known; in considering external validity of predictive models, cohort selection can impact discrimination and calibration.[20, 21] Prediction models generally take two forms: prediction of readmission for pre-selected cohorts such as known patients with chronic obstructive pulmonary disease, Medicare patients only, or those undergoing abdominal surgery[5, 16, 22–26]; or prediction of readmission for all patients to an institution or set of institutions. We hypothesize that this choice of cohort definition is a crucial one – that with the same input clinical data, the same prediction goal, and the same underlying population from which the cohort is selected, the criteria used to select the cohort can have large effects on the performance. This effect has not been quantified in the domain of readmissions risk to our knowledge, and there are implications to those seeking to use reported models in clinical practice. This research question has an important corollary implication: if performance is highly dependent on how the cohort is selected despite everything else being the same, then it demonstrates that comparing performance across studies must be difficult.

2 Materials and Methods

2.1 Dataset

A retrospective cohort of inpatient admissions at Columbia University Medical Center (CUMC) in New York City was identified from 2005–2009. These years were selected as the clinical data repository at the institution is replete with clinical and administrative data over this time period and because clinical workflows with respect to electronic health record data structures were fairly static over this time. One exception is an increase in adoption of electronic documentation over the study time period. 263,859 inpatient admissions were collected. Admissions for patients aged less than 18 years were excluded. Admissions within 30 days for ICD9 650.xx, “Normal delivery”, were also excluded as were admissions to the physical medicine and rehabilitation service, which are logged as separate admissions but represent planned transfers of care.

For each unique patient identifier, a single admission was selected randomly as the index admission. The study dataset comprised this index admission, data from previous admissions or other encounters within the past year, and data for any readmission within 30 days of discharge. When necessary for admissions in 2005, visit and diagnosis data from the preceding year were collected. Similarly, follow-up data regarding readmissions were collected when necessary for admissions in December 2009. Diagnostic, laboratory, and documentation data were accessed from the clinical data repository and preprocessed in Python in preparation for importing into the open-source language for statistical computing, R.[27] Characteristics of the training dataset and readmission prevalence stratified by readmission diagnosis are described in Tables 1 and 2.

Table 1.

Demographics and Utilization History Characteristics of Training Dataset (2005–2008)

Training Data Characteristics (Total Number of Patients=92,530)	Number of Patients	Percentage of Total Number of Patients
Age
18–45	26,239	28.4
45–65	32,144	34.7
>65	34,147	36.9
Sex
Male	43,964	47.5
Female	48,566	52.5
Insurance Status
Medicaid	12,152	13.1
Medicare	12,477	13.5
Admission Service Type
Internal Medicine	45,697	49.4
Surgery	13,887	15.0
Psychiatry	5,391	5.8
Neurology	4,380	4.7
Other	23,175	25.0
Discharge Status
To Home	72,749	78.6
To Skilled Nursing Facility	5,950	6.4
With Home Care Services	5,507	6.0
Other	8,324	9.0
Utilization Statistics
Number of ER Visits in Year Preceding Index Admission
0	69,778	75.4
1–4	20,861	22.5
>5	1,891	2.0
Number of Inpatient Visits in Year Preceding Index Admission
0	77,999	84.3
1–4	13,981	15.1
>5	550	0.6
Number of Outpatient Visits in Year Preceding Index Admission
0	57,592	62.2
1–4	19,629	21.2
5–10	7,559	8.2
>10	7,750	8.4

Table 2.

Prevalence of the Most Frequent Readmission Diagnoses in the Training Data (2005–2008)

Readmission Diagnosis	ICD9 Code	Number of Patients	Percentage of Total Number of Patients (Total N = 92,530)
All-cause readmission	Any diagnosis	6629	7.16
General Symptoms (most common reasons 780.2 syncope and 780.6 fever)	780.xx	567	0.61
Symptoms involving respiratory system and other chest symptoms (most common reason 786.5 chest pain)	786.xx	526	0.57
Chronic ischemic heart disease	414.xx	364	0.39
Other symptoms involving abdomen and pelvis (most common 789.0 abdominal pain)	789.xx	243	0.26
Complications peculiar to certain specified procedures (most common 996.6 infection due to internal prosthetic device and 996.8 complication of transplanted organ)	996.xx	243	0.26
Heart failure	428.xx	233	0.25
Episodic mood disorders	296.xx	172	0.19
Depressive disorder not elsewhere classified	311.xx	142	0.15
Symptoms involving digestive system	787.xx	121	0.13
Gastrointestinal hemorrhage	578.xx	111	0.12
Pneumonia, organism unspecified	486.xx	101	0.11
Cardiac dysrhythmias	427.xx	81	0.09
Other acute and subacute forms of ischemic heart disease	411.xx	61	0.07

2.2 Initial Feature Selection

Relevant features were selected in two phases. Initially, domain expert criteria were used to choose variables based on clinical importance. Then these preselected variables were used to create the dataset passed to L1-regularized logistic regression for further feature selection and modeling (see Section 2.4).[28, 29] The features can be divided into categories: demographics; utilization history; diagnostic; laboratory results; clinical narrative.

Demographics included age, ethnic codes, gender, and insurance status. Visit history data included utilization statistics at the Columbia University Medical Center for a twelvemonth period preceding each index admission. The numbers of inpatient admissions, emergency room visits, outpatient clinic visits, and prior thirty-day readmissions were tabulated. Clinic no-show data were not available in a systematically recorded form and, as such, were not included in visit history data for this study. Data for admissions to other hospitals were not available for the study period. The frequency of readmission to a different hospital in the geographic area for this study was not available. One published rate of readmission within 30 days to an alternative hospital from the hospital of index admission was 18%; outcomes in that Canadian study were worse in the cohort that was readmitted to an alternative hospital than compared to those admitted back to the original hospital.[30]

Diagnostic data comprised billing codes (ICD9) for any inpatient admissions that occurred for each patient in the past year. No billing codes were included for the index admission as these codes would not have been available on the day of admission. Granularity of diagnostic codes was addressed through binning. First, ICD9 codes were truncated to the whole number code without rounding. Codes were then binned into clinically meaningful categories to maximize information content while optimizing the number of variables necessary for the model. Each bin was a binary categorical variable indicating presence of a diagnostic code. For example, history of stroke was captured through binning ICD9 codes 430–438 in the diagnoses assigned to a prior visit.

Relevant laboratory tests on the day of admission were selected as features by study coauthors for perceived clinical relevance. Multiple instances of the same test were averaged. Few patient records included all laboratory values of interest on the day of admission. Missing data was handled with categorical variables added for each laboratory test to indicate whether a test was performed or not. Finally, laboratory tests were included as continuous variables of actual results, and categorical variables were added to indicate if the results were abnormally high or abnormally low based on laboratory reference ranges at the medical center. Missing continuous variables were handled with additional categorical variables marking their presence or absence and by setting the corresponding missing continuous values to zero.

Admission notes by physicians comprised the majority of electronic clinical documentation in the study period. Some notes were written on paper at the beginning of the study period prior to elimination of paper notes from the clinical workflow; these could not be included. Admission notes on the day of index admission were extracted via Python from the clinical data repository into a corpus of free text. The corpus was stemmed, text normalized, stop words removed, and terms left as unigrams.

Term frequency-inverse document frequency (TF-IDF) was then calculated for each term in a dictionary of terms identified in the literature in addition to those selected by study authors for perceived clinical relevance.[31] The value of TF-IDF is proportional to the number of times a word appears in a document divided by the frequency of the word in the corpus as a whole. These terms were subdivided into those focusing on: social and mental health determinants; other clinical and non-psychiatric factors. The “tm” package in R was used for all steps following corpus collection.[32] A categorical dummy variable was defined to indicate whether patient admissions were associated with electronic free text to handle missing data. Along with the dummy variable, a value of zero was entered for all continuous TF-IDF values for those records that did not have corresponding admission notes. Fifty three percent of the records in the dataset had at least one electronic admission note from 2005–2009.

Representative elements of each data source are described (Table 3) with the full feature set included in the Appendix.

Table 3.

Subset of Features Used in the Training of Regression Models (full feature set described in the Appendix)

Data Source Combinations for Training (total number of features in this category)	Example Features (Full list in Appendix)
Demographics (8)	Age (years); Gender; Ethnicity Codes; Visit History in the Preceding Year
Visit History (4)	# of thirty-day readmissions x 1 year # of inpatient admissions x 1 year # of outpatient visits x 1 year # of emergency room visits x 1 year
Laboratory Tests (100)	Hemoglobin; Blood Urea Nitrogen; Creatinine; Troponin; Blood Glucose
Prior ICD9 Codes (48)	Congestive Heart Failure; Diabetes Mellitus; Stroke; Dementia; Cirrhosis; Chronic Kidney Disease; Pain Syndrome
Social and Mental Health/Behavioral Factors (40)	Refuse(al,ing,ed); Homeless; Depress(ed/ion); Abuse; Dependence; Withdrawal
Other Keywords (52)	Fluid; Coumadin (warfarin); ESRD; Dialysis; Obes(e,ity); Frail(ty); Sep(sis/tic); Hemorrhag(e/ic)

2.3 Training, Validation, and Testing Data

The dataset was divided into a set of all index admissions (92,530 patients) from January 1, 2005, to December 31, 2008, used for training, and a testing set of admissions from January 1, 2009, to December 31, 2009. Bootstrapping on the entire dataset was used for internal validation and to generate confidence intervals around the ROC in each test; this method was chosen to minimize “replication instability” as compared to a traditional split-sample approach.[33] Temporal validation was selected as an intermediate to internal and external validation in testing as it is external in time and this generalization is important with the future intent to implement and evaluate prediction models prospectively.[34] Confidence intervals were obtained by calculating normal intervals with the ROCs of all bootstrap replicates.[35]

The class imbalance problem has been well described in the literature, and a number of methods to handle it have been reported.[36–38] Prevalence sampling, also called sub-sampling or undersampling, is one technique described to improve discriminatory performance in cases of class imbalance.[39, 40] The training dataset is built from all eligible cases combined with a subset of controls selected either randomly or via a chosen algorithm, e.g. nearest neighbors. Early experiments in this work included repeated model-building using all training cases matched to a number of randomly selected controls; the number of controls was varied to simulate differences in prevalence (10%, 20%, 50%, etc). The best discriminatory performance was achieved near 20% prevalence sampling in training; as a result, 20% prevalence sampling was used in all experiments described here.

Another commonly employed technique in situations of class imbalance in regression analyses is adding weights to observations for the minority class, in this case, patients that are readmitted. It retains the advantage that control data are not discarded and the disadvantage that it can be computationally more intensive as datasets are larger in size compared to sub-sampling. Observation weighting in regression was compared to 20% prevalence sampling. For each readmission diagnosis, a prevalence-adjusted weight was assigned to cases compared to controls. To mimic 20% prevalence sampling as closely as possible, cases were assigned weights of $\frac{0.2}{\mathit{Case}\mathit{Prevalence}}$ and controls a weight of 1, where Case Prevalence is the prevalence of readmission for each readmission diagnosis in Table 2.

The validation set for calibration was all of the data from 2005–2008.

2.4 Statistical Modeling

L1-Regularized logistic regression (LASSO: least absolute shrinkage and selection operator) was chosen for statistical modeling to prevent overfitting and to support parsimony in feature selection.[28, 29] Preliminary experiments testing ridge regression and the elastic net were performed, and performance was similar for all methods.[41–43] A brief comparison will be described in the Results of multiple values of α, a regularization parameter that controls the elastic net penalty and determines whether ridge regression (α = 0), LASSO (α = 1), or the elastic net (0 < α < 1) is implemented.[42, 44] Data were centered and scaled prior to regression.

A “grouping effect” for the elastic net in which “regression coefficients of a group of highly correlated variables tend to be equal” has been described for the elastic net penalty and does not occur with the LASSO penalty; a more complete discussion including mathematical justification of this effect is noted in Zou 2005.[42] It is relevant to this work in that we used a domain-knowledge driven, manual approach to excluding variables that might be highly correlated such as laboratory values of hemoglobin and hematocrit. Our approach discarded such duplicates on clinical grounds and was tractable because of the manageable number of features in this study. This approach cannot account for unexpected correlations that might be discovered in typical problems with larger numbers of features compared to small sample sizes.

LASSO regression is parametrized by a regularization parameter, here called λ, which sets the degree of penalty for including additional variables in the model. Formal feature selection was performed through 10-fold cross validation on training data to select λ. The optimal value of λ obtained through cross validation via standard squared error loss was then used to train the model on 20% prevalence sampled training data sets. Predictions were calculated on test sets and receiver-operating characteristics were obtained. LASSO regression was conducted through the “glmnet” and “caret” packages in R.[44, 45]

A comparison of regularized regression to a nonparametric learning algorithm – support vector machines (SVM) with a nonlinear kernel – was performed in the cohort selection experiment to compare sensitivity of regularized regression versus a nonparametric algorithm to different cohorts. The package “e1071” in R was used.[46]

This study was approved by the Institutional Review Board at the medical center.

3 Results

The testing set comprised 25,691 unique patient admissions in 2009.

3.1 Effect of Targeting Reason for Readmission on Model Performance

Predictive performance across all readmission diagnoses at 20% case prevalence demonstrated a range of performance from ROCs of 0.68 and 0.71 for all-cause readmission and readmission with primary complaints of syncope to 0.92 and 0.88 for congestive heart failure and post-transplant complications respectively. All discriminatory performance results by diagnosis are presented in Table 4 in section 3.2.

Table 4.

Highest discriminatory performance achieved by readmission diagnosis and data source combination; D-Demographics; L-Laboratory Tests; I-Prior ICD9 Codes; S-Social/Mental Health Keywords; O-Other Clinical Keywords; V-Visit Utilization History

Readmission Diagnosis	ICD9 Code	Data Source Combination	ROC (95% CI)
All-cause readmission	Any diagnosis	DVLI	0.68 (0.66–0.7)
General Symptoms (most common reasons 780.2 syncope and 780.6 fever)	780.xx	DVO	0.71 (0.68–0.75)
Symptoms involving respiratory system and other chest symptoms (most common reason 786.5 chest pain)	786.xx	DVLSOI	0.76 (0.72–0.8)
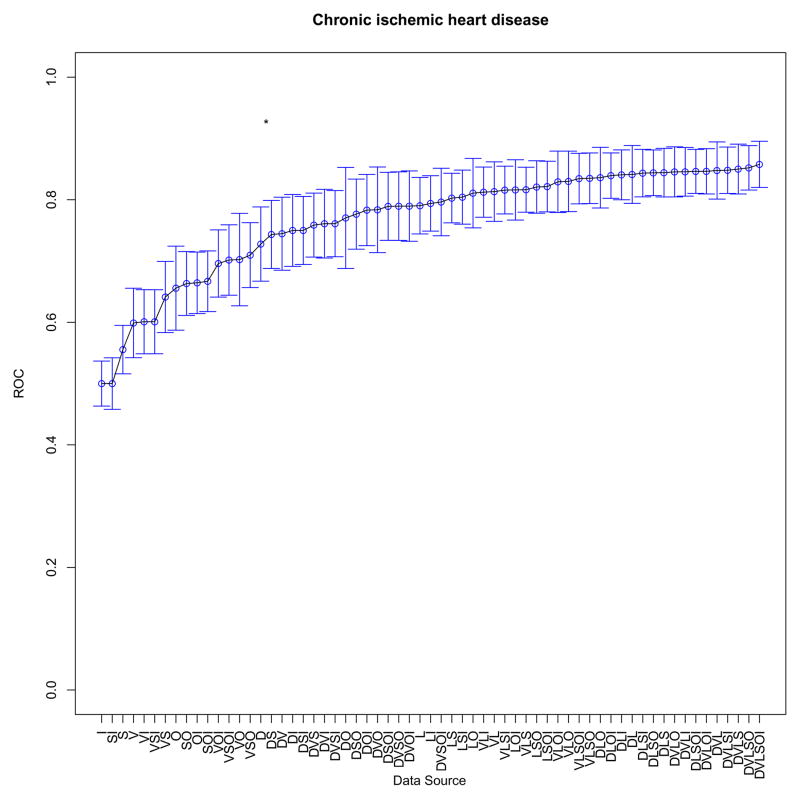
Chronic ischemic heart disease	414.xx	DVLSOI	0.86 (0.82–0.9)
Other symptoms involving abdomen and pelvis (most common 789.0 abdominal pain)	789.xx	DVLSO	0.75 (0.7–0.81)
Complications peculiar to certain specified procedures (most common 996.6 infection due to internal prosthetic device and 996.8 complication of transplanted organ)	996.xx	DVLOI	0.88 (0.82–0.94)
Heart failure	428.xx	VLSOI	0.92 (0.87–0.97)
Episodic mood disorders	296.xx	DLI	0.84 (0.76–0.93)
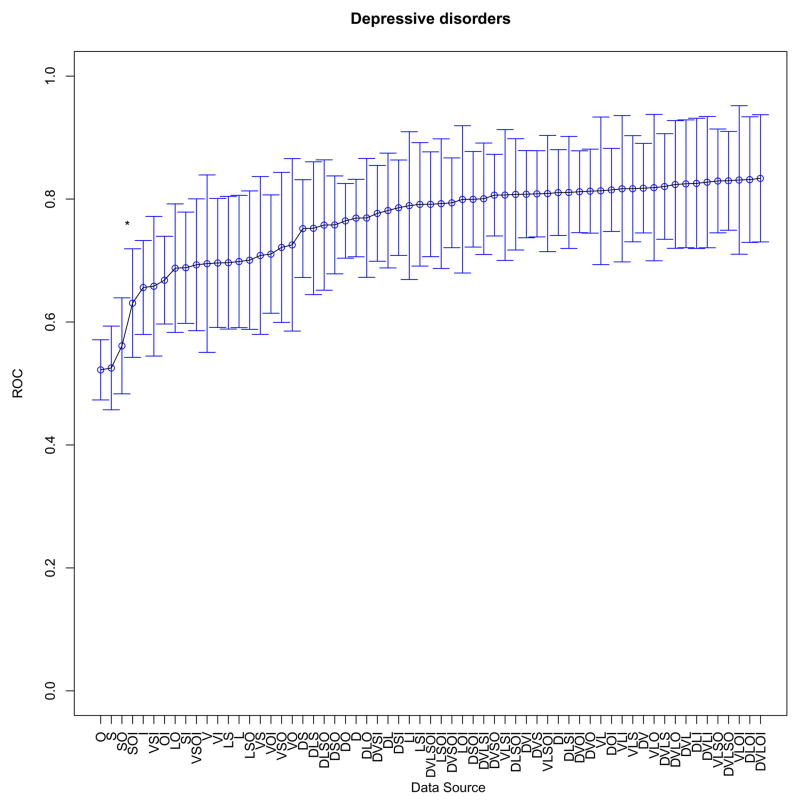
Depressive disorder not elsewhere classified	311.xx	DVLOI	0.83 (0.73–0.94)
Symptoms involving digestive system	787.xx	VLSOI	0.76 (0.64–0.88)
Gastrointestinal hemorrhage	578.xx	DLSI	0.84 (0.72–0.96)
Pneumonia, organism unspecified	486.xx	V	0.83 (0.74–0.92)
Cardiac dysrhythmias	427.xx	DO	0.76 (0.65–0.87)
Other acute and subacute forms of ischemic heart disease	411.xx	DVLSOI	0.71 (0.54–0.87)

Predictive performance for congestive heart failure was significantly higher than that for chest pain, syncope/fever, or abdominal pain after Bonferroni correction. Similar performance differences are noted for chronic ischemic heart disease compared to syncope/fever and for complications post-procedure compared to syncope/fever.

Predictive models across all readmission diagnoses except all-cause readmission were trained using identical datasets at 20% prevalence sampling for three values of the regularization parameter, α. Ridge, elastic net, and LASSO penalties were set at values of 0, 0.5, and 1, respectively, in the “glmnet” package in R.[44] The elastic net penalty is not restricted to a value of α of 0.5, but only this value is shown here for brevity. The mean discriminatory performances across all readmission diagnoses were 0.76, 0.77, and 0.77, for ridge, elastic net, and LASSO penalties respectively. Analysis of variance demonstrated no significant difference between these means [F(2, 972) = 1.34, p = 0.26].

To ensure discrimination was not hindered by sub-sampling compared to techniques such as observation weighting which do not discard control data, identical datasets were trained using both 20% prevalence sampling and by adding observation weights to all training data. These models were tested on identical test sets. The difference in discriminatory performance between sub-sampling and observation weights was not statistically significant (p 0.08) though there was a tendency to higher performance in 20% prevalence sampling.

3.2 Effect of Data Source on Model Performance

In each test, the six main types of data – demographic, visit history, laboratory testing, social/mental health keywords, other clinical keywords, and prior ICD9 diagnostic codes – were used to train models across all-cause and the thirteen specific diagnoses outlined above. Data sources were included both individually and in subsets.

A table organized by diagnosis shows the highest discriminatory performance by diagnosis across data source combinations; all combinations were tested but only one is shown (Table 4). The readmission diagnosis of pneumonia, for example, showed the best performance solely using data associated with visit history while other diagnoses performed best using all of the data types under study. As noted, the LASSO estimator has been preferred for its parsimony in feature selection. On average for all models described in this work, 52 features were selected in training out of 252 features total. One outlier included in this average was prediction of all-cause readmission in which 243 features were selected; of note, there was an order of magnitude more cases of readmission available in that model compared to other readmission diagnoses (Table 2).

At the individual model level, performance with each data source combination was then compared. One example comparing readmission for chronic ischemic heart disease with readmission for depression is shown (Figure 1a, b). When the difference between diagnostic tests was statistically significant (p value <0.05), the relevant segment is noted in each plot. In the case of chronic ischemic heart disease (ICD9 414.xx), the highest performance was achieved with all six data source types. In the case of readmission with a primary diagnosis of depression, however, predictive performance plateaus with the addition of visit history as a group of features to the model. Remaining plots are included in the Appendix.

Figure 1.

(a, b). Example contribution of data sources to prediction for two diagnoses (statistically significant differences between segments denoted by *); D-Demographics; L-Laboratory Tests; I-Prior ICD9 Codes; S-Social/Mental Health Keywords; O-Other Clinical Keywords; V-Visit Utilization History

To better understand the contributions of individual data types to prediction, two analyses were performed with respect to the presence or absence of a particular data type. The first analysis was the calculation of the ratio of discrimination across all readmission diagnoses for all data source combinations that included a particular data type compared to all combinations that excluded that same data type. The resulting ratio gives some sense of the relative contribution to discrimination of that data type. That ratio was converted to a percentage change in discrimination. Table 5 summarizes the change in discrimination with and without particular data types.

Table 5.

Change in discrimination with the data source present compared to its absence

Data source type	Change in discrimination with the data source present compared to its absence
Laboratory Results	+5%
Visit History	+5%
Demographics	+4%
Prior ICD9 Codes	+3%
Clinical Keywords	+2%
Social/Mental Health Keywords	Approximately no change*

^*No change when rounded to the nearest percentage

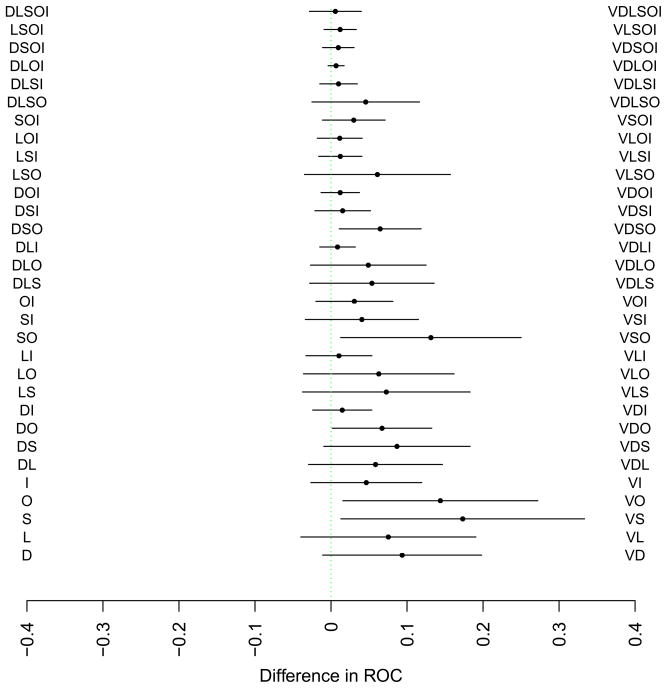
The second analysis examined specifically the increase in discrimination for each combination of data source types in the presence or absence of a data source. As an example, the presence of visit utilization was found to contribute significantly to predictive performance for multiple combinations of data types, and model performance suffered when visit utilization data were not included.

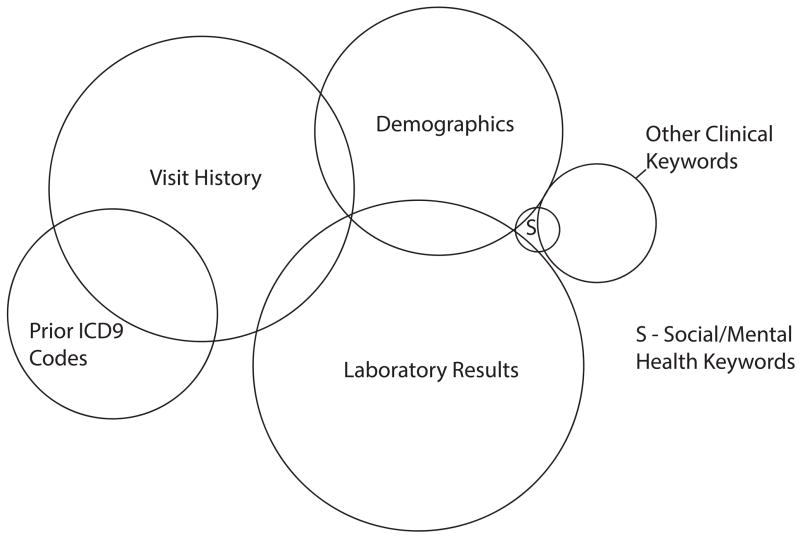
A multivariate linear model was then constructed with five features – binary variables recording the presence or absence of each data type in an experiment – and one outcome – the ROC for that experiment. Analysis of Variance (ANOVA) was performed to measure estimates of individual data types as well as first-order interactions between data types as Sum of Squares (SS). The respective SS were converted to circular area in a Venn diagram to represent visually the relationships between data types. Statistically significant first-order interactions between individual data types are quantified as overlap between elements in the Venn diagram (there was a small interaction between ICD9 code data and social keywords that could not be represented without introducing spurious overlap with other data types – one limitation of this visualization). There were no large interactions that were not statistically significant. The use of Venn diagrams in regression has been described though this use-case has not been described to our knowledge.[47, 48]

3.3 Effect of cohort selection on performance

We hypothesized that the reported ROC area would be highly sensitive to the definition of the cohort, rendering comparisons with previous studies difficult. To test this, we compared ROC areas for two cohorts: training and testing on all eligible patients versus training and testing on only those patients whose previous diagnosis matched the reason for readmission. We found that on average model performance for the diagnostic cohorts was generally inferior to that for the full training set.

The model predicting readmission from all index admissions (mean ROC 0.78) outperformed models trained on index diagnostic cohorts (mean ROC 0.55) by an average increase of 0.23 in ROC (p value 0.01). At the individual diagnosis level, the diagnosis-specific cohort underperformed the general cohort; the difference was statistically significant with respect to predicting readmission for chronic ischemic heart disease and for episodic mood disorders.

To understand whether a nonparametric algorithm might outperform regularized regression when trained on different cohorts, both SVM with a nonlinear kernel (radial) and the LASSO were trained on all readmission diagnoses in the manner described above. For SVM, training on all index admissions was associated with a mean discriminatory performance ROC of 0.74 compared to 0.54 in training on index diagnostic cohorts (p value < 10⁻⁹). Thus, the effect of varying cohorts in model training was consistent across these algorithms.

3.4 Calibration

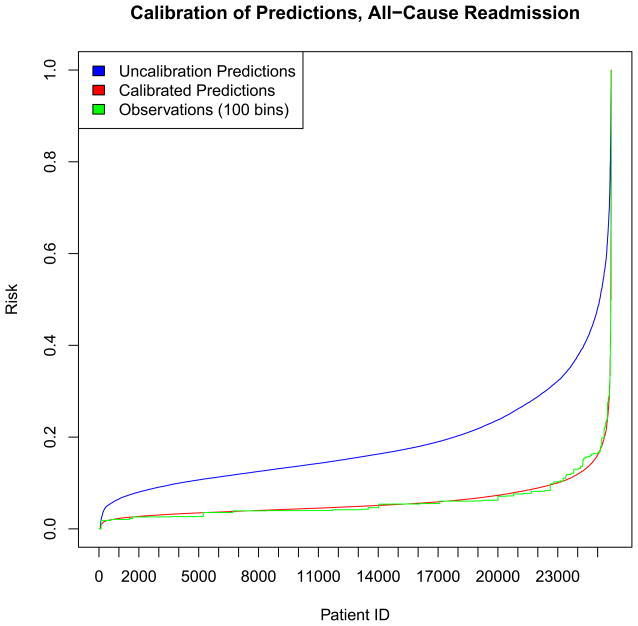
Calibration of predictions is a critical aspect of predictive modeling particularly in the setting of prevalence sampling. Discrimination is the ability of predictive models to separate data into classes, while calibration is the ability of the predictive model to make predictions that reflect the underlying probabilities in a population.[21] A well-calibrated model that predicts a 40% risk of readmission for one patient indicates that roughly 4 out of 10 similar patients would be readmitted.[21] Sub-sampling in this work was noted to improve discrimination, but the average prediction in the entire sample was calibrated to the prevalence of training – 20% – regardless of diagnosis of readmission. However, the actual prevalence of readmission for each diagnosis was never 20%; thus, sub-sampling improved discrimination but worsened calibration. A subsequent step is required to calibrate the model to reflect the underlying probability of readmission in each model.

A number of methods for calibration of clinical prediction models have been described.[21] In this work, experimental results were calibrated by model refitting. Regularized regression was performed at 20% prevalence sampling, and the model was then used to calculate uncalibrated predictions on the validation set. The log odds of those predictions were then passed through a sigmoid trained on the outcomes of the validation set – this has been called “logistic calibration”.[49, 50] As these outcomes reflect case prevalence, the resultant log odds were calibrated. A calibration plot is shown for all-cause readmission showing good calibration compared to observations (divided into one hundred bins). The mean squared errors for the uncalibrated and calibrated predictions were 0.022 and 7.5×10⁻⁴, respectively

4 Discussion

This study demonstrates the performance effects of varying three elements of a predictive model of readmissions: 1) Reason for readmission; 2) Included data types; 3) Cohort definition. The informatics findings from this work demonstrate that discriminatory performance is highly impacted by predicting reason for readmission rather than all-cause readmission alone, that cohort selection is critically important to measured performance, and that data types appear to have varying degrees of usefulness in prediction and that the contributions of data types depends on the cause of readmission being predicted.

A single model of all-cause readmission for all patients is no longer the standard in the literature or in practice. This work shows the degree to which specific causes of readmission can be modeled holding all else equal. The variation in discriminatory performance between different causes of readmission differed by over twenty percent. Patients are readmitted to hospitals for a number of reasons. The approach outlined in this work permitted the prediction of risks of readmission for a number of potential reasons for the same set of patients. In clinical practice, a predictive framework that generated risk predictions for the same patient across multiple possible reasons for readmission might yield insights into how to direct an intervention to lessen those risks. Additional research including evaluation in the clinical setting is required.

The variable impact of data sources on the clinical scenario – the readmission diagnosis itself – is clinically intuitive. A patient with severe congestive heart failure, for example, may have a number of measurable clinical tests that support the burden of disease – hyponatremia, an elevated B-type natriuretic peptide, elevated creatinine from concomitant renal failure, etc. Yet a patient with severe depression may have relatively unremarkable laboratory values while the elements of the history that capture the burden of psychiatric disease are contained instead in clinical notes by examining physicians. Social and mental health factors were not demonstrated to be as predictive as other data types in this study, but the heuristic approach to their inclusion coupled with the sporadic and inconsistent way in which social determinants of health are currently documented could be an important factor. Of note, the approach to grouping data features into groups of data sources was feasible because of the relatively small number of candidate features included in the study. For larger numbers of features (hundreds or thousands), scaling this approach would be difficult. Automatic methods to combine features into groups such as the “group lasso” have been described and should be considered in subsequent work.[51]

In a retrospective study, diagnostic billing codes are readily available and convenient. However, these codes are only assigned post-discharge. We implemented diagnostic codes solely prior to index admission in an effort to replicate realistic data that would be available prospectively. Billing systems have improved to permit physicians to assign codes at the time of note submission for billing; it is important to remember that a physician assigning codes to her own notes is not the same process as a biller assigning codes post-discharge. Each process results in ICD9 coding, but the biases inherent in each are not the same.

Free text narrative data was used to include social determinants of health and factors related to behavioral and mental health in addition to keywords related to diagnoses and disease burden. The relative simplicity of the approach to text mining outlined here could be readily applied to novel corpora; it relies only on electronic free text and open-source software tools.

The effect of cohort selection on discriminatory model performance suggests a single model for readmissions prediction in a clinical site may be insufficient. We report high ROCs (>0.9) in this study, but the effect is cohort-dependent. In a related experiment, we compared readmission prediction for patients older than seventy-five to patients of all ages. Prediction for all adult patients was higher than that for those seventy-five and older across all but two readmission diagnoses (pneumonia, symptoms involving digestive system). ROCs for all-cause readmission prediction in that example was 0.67 for all adults and 0.6 for adults older than seventy-five. That predictive power should be dependent on the cohort makes sense. For example, in the cohort of all patients, a heart failure readmission algorithm can surpass chance performance by simply selecting patients who had heart failure in the past; that cannot work if the cohort contains only patients with a history of heart failure. An important step in discriminating risk of readmission for a given disease is simply finding those patients with the disease in the first place.

The relationship of cohort selection and discriminatory performance makes it difficult to compare performance across studies: the cohorts must be the same. And, of course, it limits their generalizability and external validity. In recreating published work in a new clinical setting, attention must be paid to replicating the cohort as closely as possible to the original work. If this step is not taken, it will undermine any other efforts to achieve the same performance. As shown here, varying cohort selection alone reduced discrimination by nearly 25%.

Limitations of this study include generalizability from a single major academic medical center. This constraint is common to statistical models built using depth of data recorded in a mature clinical data repository. Breadth-approaches using large datasets of claims data pose a different set of advantages and disadvantages. Replicating this modeling attempt in another clinical site or multiple sites will be paramount. Another important limitation is the heuristic approach to initial feature selection. The balance between preselecting features based on perceived clinical importance versus permitting the model to see all available data must be considered in any large-scale modeling task. Outpatient medication use during the study period was not recorded in a structured way, so it was not included beyond the keyword approach outlined above. Clinical narrative was included, but less than one-third of patients had electronic admission notes during the study period. Today, every patient is required to have an electronic admission note at New York Presbyterian Hospital during the first day of admission.

Future research should include the application of this modeling approach on data beyond a single institution. Further work in modeling social determinants of health from electronic data may be valuable. Additional data such as structured medication data, radiology, electrocardiogram, or other diagnostic procedure results could be used to augment the model. Finally, actionability and preventability of risk factors must be considered to maximize impact of prediction on clinical outcomes. While predictive algorithms can achieve high performance as demonstrated here, an important open question remains whether clinicians and case-workers are interested in those necessary risk factors for prediction. A mass-customized model that predicts not only “readmission for congestive heart failure” but also “readmission because this patient forgets to take the evening dose of furosemide unless reminded by his grandson” would exceed utility as simply a method to target multidisciplinary attention to patients nebulously “at risk”.

5 Conclusions

Factors of model design have a large impact on predictive performance in the domain of readmission. High discriminatory performance can be achieved for specific causes of hospital readmission in a predictive model trained with L1-regularized logistic regression and multiple clinically relevant sources of data including laboratory test results and provider admission notes. Data types included in modeling have variable impact depending on the cause of readmission under consideration. Cohort selection has a notable impact on predictive performance and renders comparison of results across studies more difficult. Additionally, prevalence sampling or sub-sampling was shown to be as good as observation weighting in this study. One caveat is the impact of sub-sampling to mis-calibration; a method to recalibrate the resultant model was described. The LASSO performed as well as a nonparametric algorithm (SVM). Finally, in building predictive models using retrospective data, some censoring of data included in the model may be necessary. A model that relies heavily on claims data, for example, would have limited utility on the day of admission as those codes are only assigned after discharge.

Figure 2.

Contribution of Visit Utilization History to Model Performance; D-Demographics; L-Laboratory Tests; I-Prior ICD9 Codes; S-Social/Mental Health Keywords; O-Other Clinical Keywords; V-Visit Utilization History

Figure 3.

Venn diagram of data type contributions to predictive performance including first-order interactions; area of each circle correlates with size of contribution to prediction and overlap implies interaction between data types

Figure 4.

Calibration plot for all-cause readmission risk predictions

Highlights.

• Hospitals seek to predict readmissions, but there are many proposed models

• The study aims to show the impact of varying factors of model design on performance

• Targeting reason for readmission improves discrimination. ROCs range from 0.68–0.92

• Patient visit and laboratory results contribute most to prediction

• Performance is highly cohort-dependent. Comparing models across studies may be hard