Fast and Adaptive Detection of Pulmonary Nodules in Thoracic CT Images Using a Hierarchical Vector Quantization Scheme

Abstract

Computer-aided detection (CADe) of pulmonary nodules is critical to assisting radiologists in early identification of lung cancer from computed tomography (CT) scans. This paper proposes a novel CADe system based on a hierarchical vector quantization (VQ) scheme. Compared with the commonly-used simple thresholding approach, high-level VQ yields a more accurate segmentation of the lungs from the chest volume. In identifying initial nodule candidates (INCs) within the lungs, low-level VQ proves to be effective for INCs detection and segmentation, as well as computationally efficient compared to existing approaches. False-positive (FP) reduction is conducted via rule-based filtering operations in combination with a feature-based support vector machine classifier. The proposed system was validated on 205 patient cases from the publically available on-line LIDC (Lung Image Database Consortium) database, with each case having at least one juxta-pleural nodule annotation. Experimental results demonstrated that our CADe system obtained an overall sensitivity of 82.7% at a specificity of 4 FPs/scan, and 89.2% sensitivity at 4.14 FPs/scan for the classification of juxta-pleural INCs only. With respect to comparable CADe systems, the proposed system shows outperformance and demonstrates its potential for fast and adaptive detection of pulmonary nodules via CT imaging.

I. Introduction

According to the up-to-date statistics from American Cancer Society [1], lung cancer is the leading cause of cancer-related deaths with over 159,000 deaths estimated for the United States alone in 2013, and the overall 5-year survival rate for lung cancer is merely 16%. The survival rate increases to 52% if it is localized, and decreases to 4% if it has metastasized. Therefore, to detect lung cancer at earlier stages is of great importance [2], and computer-aided detection (CADe) in supplement to radiologists’ diagnosis has become a promising tool to serve such purposes [3].

While detection of pulmonary nodules has a crucial effect on the diagnosis of lung cancer, but the detection is a nontrivial task, not only because the density of pulmonary nodules varies in a wide range, but also because the nodule densities have low contrast against adjacent vessel segments and other lung tissues. Computed tomography (CT) has been shown as the most popular imaging modality for nodule detection [2], [4], because it has the ability to provide reliable image features for the detection of small nodules. The development of lung nodule CADe systems using CT imaging modality has made good progress over the past decade [5], [6]. Generally, such CADe systems consist of three stages: (1) image preprocessing, (2) initial nodule candidates (INCs) identification, and (3) false positive (FP) reduction of the INCs with preservation of the true positives (TPs).

In the preprocessing stage, the system aims to largely reduce the search space to the lungs, where a segmentation of the lungs from the entire chest volume is usually required. Because of the high image contrast between lung fields and the surrounding body tissue, image intensity-based simple thresholding is effective, and is currently the most commonly used technique for lung segmentation [7], [8]. However, the determination of an accurate threshold is greatly affected by image acquisition protocols, scanner types, as well as the inhomogeneity of intensities in the lung region, especially towards the segmentation of pathological lungs with severe pathologies [9], [10]. This work proposes an adaptive solution to mitigate the difficulty of threshold method in lung segmentation.

After defining the search space (i.e., the lung volume), INCs detection is the next step to build a CADe system. Various INCs detection techniques have been extensively studied in recent years, such as multiple thresholding [11], [12], nodule enhancement filtering [13], [14], mathematical morphology [15], [16], and genetic algorithm template matching [17], [18], among many others. The most commonly used multiple thresholding approach aims to find connected components of similar image gray-values. Though intensity-based thresholding methods are computationally cheaper than other pattern-recognition techniques for the detection of INCs, they also suffer considerable drawback. For example, it is difficult to adaptively and simultaneously determine the thresholds, because pulmonary nodules with a wide range of image intensity are embedded in an inhomogeneous parenchyma background. On the other hand, pattern-recognition techniques are complicated and usually computational intensive. This work proposes an efficient means which shares the adaptive natures of pattern-recognition techniques and the simplicity of intensity-based thresholding methods.

Sufficient detection power for nodule candidates is inevitably accompanied by many (obvious) FPs. A rule-based filtering operation [17], [19], [20] is often employed to cheaply and drastically reduce the number of obvious FPs, so that their influence on the computationally more expensive learning process can be eliminated. In general, FP reduction has been extensively studied using machine learning in the literature. Compared with unsupervised learning that aims to find hidden structures in unlabeled data, supervised learning, which aims to infer a function from labeled training data, is more frequently used to design a CADe system. The rules learned from the training dataset can be applied to the differentiation between nodules and non-nodules in the test dataset. A number of supervised FP reduction techniques have been reported for the characterization of INCs, such as linear discriminant analysis (LDA) [11], [17], artificial neural network (ANN) [16], [21]-[23], and support vector machine (SVM) [14], [19], [20]. The last step to complete a CADe system is to evaluate its performance for FP reduction. In this respect, receiver operating characteristic (ROC) analysis [24] has been widely acknowledged as a powerful tool to judge the performance of a classification system. This work takes the advantages of the rule-based filtering operation and the supervised learning for FP reduction and can be summarized below.

Inspired by our previous work [25], we have proposed a hierarchical vector quantization (VQ) approach to address the preprocessing and INCs detection issues in an adaptive manner, aiming to overcome the drawbacks of global thresholding methods. Compared with the existing approaches, the hierarchical VQ can be an alternative with either comparable detection performance and less computational cost, or comparable cost and better detection performance. To reduce FPs in the detected INCs, we make use of both rule-based filtering and supervised learning. Expert rules are learned from prior knowledge of true nodules annotated by the radiologists, while the classification rule for SVM is learned from two dimensional (2D) and 3D features extracted from the INCs.

The remainder of this paper is organized as follows: Section 2 describes the details of each module employed in the proposed CADe system. Section 3 reports the experimental outcomes on validating the proposed CADe system using the largest publicly available database built by the Lung Image Database Consortium and Image Database Resource Initiative (LIDC-IDRI). Section 4 discusses the experimental results, the advantages and disadvantages of the proposed CADe system, as well as the future work to improve the CADe system. The last section draws conclusions of this study.

II. Methods

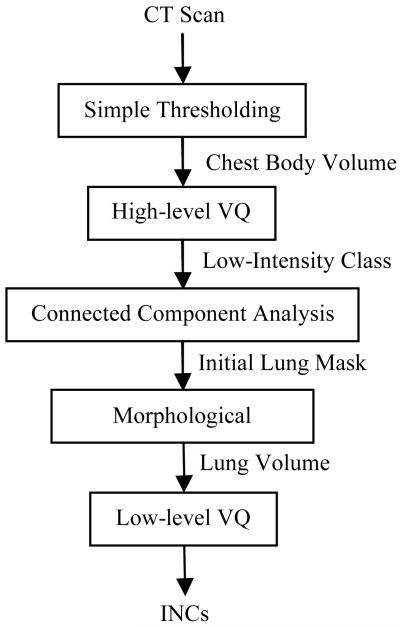
This section will provide details of the proposed CADe system for lung nodules. The top-level block diagram of the proposed CADe system is depicted in Fig. 1. In the preprocessor block, the chest volume is extracted from the field-of-view (FOV) of the image volume by simple thresholding (where the outside of the chest volume does not have anatomical structures). In the detector block, the two lungs are first separated from their surrounding anatomical structures via high level VQ and a connected component analysis. In order to include juxta-pleural nodules (i.e., nodules grow near, or originated from the parenchyma wall), the initial lung mask obtained by the above separation operation is refined by a morphological closing operation. Then low level VQ is employed to identify and segment the INCs within the extracted lung volume. In the classifier block, the obvious FPs are firstly excluded from the INCs via rule-based filtering operations, and then the SVM classifier is trained to further separate nodules from non-nodules based on the 2D and 3D features of the INCs. More details on the proposed CADe system are given by the following sections.

Fig. 1.

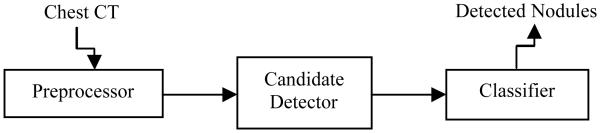
Top-level block diagram of the proposed CADe system for pulmonary nodules.

A. Self-adaptive VQ Algorithm for Image Segmentation

VQ was originally used for data compression in signal processing [26], and becomes popular in a variety of research fields such as speech recognition [27], face detection [28], image compression and classification [29], and image segmentation [25], [30], [31]. It allows for the modeling of probability density functions by the distribution of prototype vectors. The general VQ framework evolves two processes: (1) the training process which determines the set of codebook vector according to the probability of the input data; and (2) the encoding process which assigns input vectors to the codebook vectors. The well-known Linde-Buzo-Gray (LBG) algorithm has been widely used for the design of vector quantizer [26]. The algorithm aims to minimize the mean squared error and guarantees to converge to the local optimality. However, the following properties of the LBG algorithm limit its application in image segmentation: (1) it relies on the initial conditions, and (2) it requires an iterative procedure and long computation times. Hence in our previous work, the self-adaptive online VQ scheme [25] was proposed to speed up the vector quantizer, where the training and encoding processes are conducted in a parallel manner.

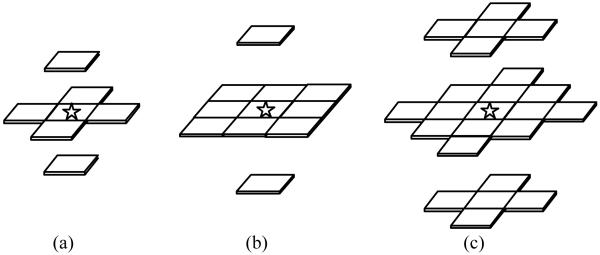
Medical image segmentation is the key step toward quantifying the shape and volume of different types of tissues in a given image modality, which are used for 3D display and feature analysis to facilitate diagnosis and therapy. The main idea of VQ for image segmentation is to classify voxels based on their local intensity distribution rather than voxel-based intensities. The local intensity distribution can be described by a vector of local intensities. Fig. 2 illustrates three typical configurations of the local intensity vector that can be used by the VQ algorithm, and in this study the 3D first order neighborhood was chosen to form the local intensity feature vector. Chest CT volume data consists of a very large number of body voxels, where each voxel has a local intensity vector. This requires intensive computing effort to process such a huge quantity of vectors. To greatly reduce the computational complexity, a feature extraction algorithm [32] can be applied in the local feature vector space. For each specific 3D volume, upon a linear Karhunen-Loéve (K-L) transformation of the local intensity vectors via the principal component analysis (PCA), we choose the first few principal components (PCs) that contribute at least 95% of the total variance for optimizing the dimension of the local vector space. Only the selected PCs will be retained to form the feature vector for VQ, and the remaining PCs with very little information will be neglected.

Fig. 2.

Three typical configurations of the local intensity vector: (a) the 3D first order neighborhood to form a 7D local intensity vector; (b) the 3D up-to-second order neighborhood to form a 11D local intensity vector; (c) the 3D up-to-third order neighborhood to form a 23D local intensity vector. The current voxel is marked by an asterisk.

VQ models the local statistics, analyzes group features and classifies each voxel in the dimension-reduced feature space. VQ scans from the first voxel to the last one in a contiguous manner. For a given volume of interest (VOI), there is only one class at the beginning (i.e., the current total number of classes K’ = 1) and its representative vector c₁ is the local feature vector of the first voxel. Since the initial value setup is data-oriented, the VQ algorithm is fully automatic. For each following voxel i, the squared Euclidean distance between its local feature vector ω_i and the representative vector c_k of every existing class k = 1, …, K’ is calculated by

$$d({\omega }_i,c_k)=\sum _{p=1}^p{({\omega }_{ip}-c_{kp})}^2$$ (1)

Here the local feature vector ω_i and each representative vector c_k are both of dimension P, which was previously determined by PCA. The finite set codebook CB = {c₁, c₂, …, c_K’} is then exhaustively searched for the nearest codevector c_min such that

$$d({\omega }_i,c_{\min })={\min }_{1\le k\le K^{\prime }}\left\{d\right({\omega }_i,c_k\left)\right\}$$ (2)

Let T denote the threshold for inter-cluster distance, so that if d(ω_i, c_min) > T, a new class K’ = K’ + 1 is generated subject to the constraint of maximum class number K. Otherwise, if d(ω_i, c_min) = d(ω_i, c_k) < T or K’ = K, the representative vector c_k of the current class k is updated after adding a new member x_i into the class k. After a whole scan of the VOI, the representative vector, prior probability, and covariance of each cluster are generated. Meanwhile, all voxels have been classified under the nearest neighbor rule, where the exhaustive search under condition of Eq. (2) ensures the optimal classification result. As described above, our VQ algorithm only depends on two parameters: K and T. The maximum class number K can be determined according to radiologists’ prior knowledge of how many major tissue types are perceived in the specific VOI. For instance in chest CT images, the lungs usually consist of four major tissue types: low and high frequency parenchyma, blood vessels, and nodules. And their average intensities increase from the lowest to the highest. To set an appropriate value for the classification threshold T is more crucial than the setting of K. If T is too large, only one class could be obtained. On the other hand, if T is too small, redundant classes might occur. According to extensive numerical experiments, a robust choice for T would be the maximum principle component variance of the local intensity vector series. In addition, to avoid the situation of resulting class number being less than the expected number of tissue types, the class separation threshold T may be tuned to be the second or third maximum principal component variance. Since the similarity threshold T is estimated from each CT scan, the algorithm is self-adaptive. The proposed VQ-based image segmentation algorithm is outlined as follows.

1. Perform PCA to obtain the K-L transformation matrix for the target VOI, determine the reduced dimension P for the local intensity vector space, and calculate the K-L transformed local intensity vector ω_i = {ω_i1, ω_i2, …, ω_iP} for each voxel i = 1, …, I.

2. Set the classification threshold T as the maximum principal component variance, and set a value for the maximum class number K based on prior anatomical knowledge.

3. i = 1, set the first voxel label ν₁ = 1, its local intensity vector ω₁ as the representative vector c₁ for the first class, n₁ = 1 as the number of voxels belonging to class 1, and K’ = 1 as the current number of classes.

4. i = i + 1, calculate the squared Euclidean distance d(ω_i, c_k) between the local intensity vector ω_i of the current voxel and the representative vector c_k for each existing class k = 1, …, K’.

5. Let d(ω_i, c_m) = min_1≤j≤K’{d(ω_i, c_j)}, if d(ω_i, c_m) < T or K’ = K, the label for the i-th voxel is ν_i = m. c_m is updated by c_m = (n_m*c_m + ω_i) / (n_m + 1), and n_m = n_m + 1. Otherwise, a new class K’ = K’ + 1 is generated with representative vector c_K’ = ω_i, and the current voxel is labeled as v_i = K’ s.t. K’ <= K.

6. Repeat from step 4 until i = I to complete a whole scan.

7. If K’ < K, repeat steps 1) to 6) for another whole scan while setting the classification threshold T to be the second or third maximum principal component variance until K’ = K.

In this paper, we mainly focus on demonstrating the merits of our hierarchical VQ scheme in the detection of INCs, from where a novel CADe system is proposed to efficiently detect pulmonary nodules. The detection is detailed below.

B. INCs Detection via a Hierarchical VQ Scheme

A very important but difficult task in the CADe of lung nodules is the detection of INCs, which aims to search for suspicious 3D objects as nodule candidates using specific strategies. This step is required to be characterized by a sensitivity that is as close to 100% as possible, in order to avoid setting a priori upper bound on the CADe system performance. Meanwhile, the INCs should minimize the number of FPs to ease the following FP reduction step. This section presents our hierarchical VQ scheme for automatic detection and segmentation of INCs. Due to the higher in-plane resolution, both the high level and low level VQ employ 3D first order neighbors of each voxel to form the local intensity vector.

1) Lung Segmentation by High Level VQ

First of all, since the chest CT images in the LIDC database were acquired under different scanning protocols, a standardization of CT intensities was carried out to preprocess our target datasets. Then by imposing an empirical threshold of −500 HU [11], [12] on the entire CT scan, we could separate the chest body volume from the surrounding materials, such as air, fastening belts, CT bed, and other background materials.

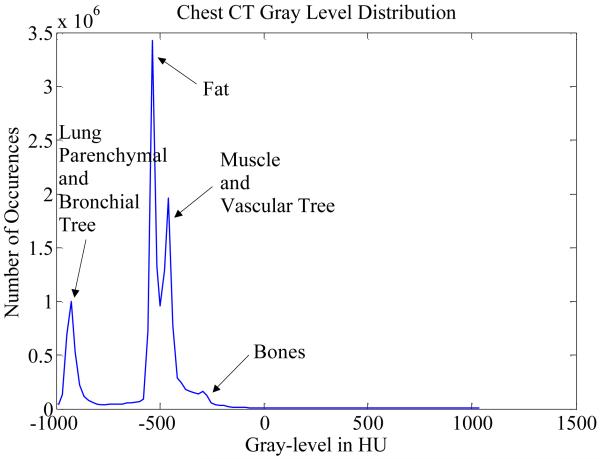
In order to ensure nodule detection being performed within the lung volume, the segmentation of lungs from the body volume is desired. Fig. 3 shows the histogram plot of the intensity of chest body volume from a typical lung CT scan, where we observe a clear separation of two major classes (i.e. the air tissue and other dense body tissue). Hence, it is reasonable to use the proposed high level VQ for body voxels with these two major classes for segmentation. Of note, “high level” in the context of this paper refers to the operation of segmenting lungs from the entire chest volume. Since the lung parenchyma and the air in other organs have similar image intensities, they were classified into the low-intensity class.

Fig. 3.

Image intensity or gray-level distribution of voxels in HU obtained from chest body volume of one CT scan of our datasets. Similar distributions can be obtained from other scans.

Most existing approaches utilize the outcome from simple thresholding to extract lungs from the chest volume. Though thresholding is computationally inexpensive, the associated side effect, called “salt and pepper” noise [33], diminishes the computational advantage. Furthermore, because of relatively high image contrast between pathologic abnormalities and normal lung parenchyma, it is known that the conventional thresholding methods fail to extract complete lungs from such scans [9]. The proposed high level VQ scheme can avoid the failure on lung boundary corrections, as shown by the rectangular regions marked in Fig. 4. Although both thresholding and VQ are intensity-based approaches, VQ classifies each voxel based on its local intensity features rather than the single voxel intensity used by simple thresholding. Moreover, most simple thresholding approaches set a uniform threshold for all CT scans, which is unrealistic, while the similarity threshold in VQ is adaptively determined for each scan. This makes VQ more robust to intensity inhomogeneity and image noise.

Fig. 4.

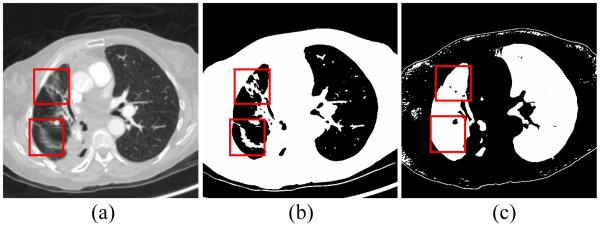
Comparison of simple thresholding and VQ for lung segmentation. Panel (a) shows a raw CT image with dense pathologies on the left lung lobe. Panel (b) illustrates the lung mask obtained by simple thresholding, and panel (c) is the lung mask obtained by the two-class high level VQ, which is robust to intensity inhomogeneity.

By the high level VQ scheme, the obtained initial lung mask corresponds to the largest and the second largest (if left and right lungs are disconnected due to pathologic abnormalities) connected components in the low-intensity class, where the holes inside the extracted lung mask are filled by a flood-fill operation. Furthermore, in order to include juxta-pleural nodules into consideration, a 3D morphological closing operation using a spherical structuring element of radius 15 mm is applied to close the boundary in the binary lung mask.

2) INCs Detection by Low Level VQ

After extraction of the lungs from the entire chest volume by using the high level VQ, the low level VQ aims to simultaneously detect and segment nodules from the much smaller lung volume or VOI. Hereby, “low level” also indicates the operation of VQ with a more diversified classification compared to the high level VQ. In contrast to the high-level classification in the first stage, the low-level VQ in the second stage becomes more challenging when it comes to the determination of an appropriate value for the maximum class number K.

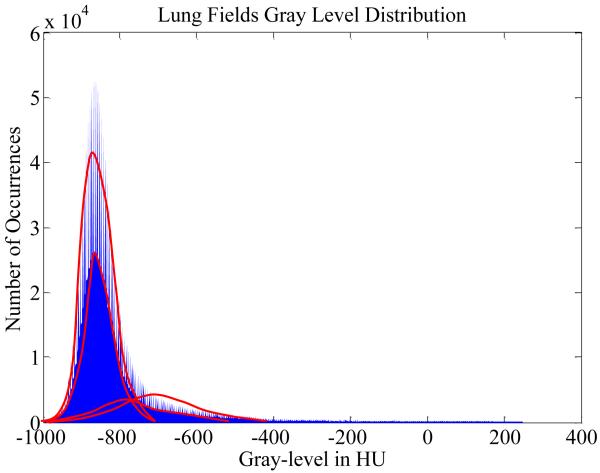
Fig. 5 shows the histogram plot of lung voxel intensities from one chest CT scan of the LIDC datasets. Recall the CT distribution of chest body volume in Fig. 3, Fig. 5 indeed depicts the distribution of the leftmost component in Fig. 3. Statistically, the observed distribution in Fig. 5 consists of both high frequency and low frequency parts. Each part is asymmetric and left skewed, which can be decomposed into two Gaussian components. Hence this intensity distribution can be eventually represented by four Gaussian mixtures in total. Based on physicians’ input, we interpret the four classes as low-frequency parenchyma, high-frequency parenchyma, blood vessels, and INCs.

Fig. 5.

Histogram of lung voxel intensities from one chest CT scan of the LIDC datasets. Each bar corresponds to the frequency of observing voxels having intensity within a specific range. Statistically, the observed distribution can be decomposed into four normal-tailed Gaussian mixtures as represented by the four bell-shaped curves.

To experimentally determine an appropriate value for the maximum class number K, we conducted repeated experiments of applying VQ to lung voxel classification with different K values. Consistent with our previous observation, we found that the four-class setting yielded the most stable segmentation result across different scans. Since the average intensity of lung nodules is relatively higher than the other three types of tissues, the class with the highest average intensity was extracted as the INCs class. The flowchart of the proposed hierarchical VQ scheme for INCs detection is illustrated through Fig. 6.

Fig. 6.

Flowchart of the proposed hierarchical VQ scheme for INCs detection.

C. False Positive Reduction from INCs

1) Rule-based Filtering Operations

It is challenging for any intensity-based detector to thoroughly separate nodules from attached structures due to their similar intensities, especially for the juxta-vascular nodules (the nodules attached to blood vessels). Since the thickness of blood vessels varies considerably (e.g., from small veins to large arteries), a 2D morphological opening disk with radius of 1 up to 5 pixels was adopted to detach vessels at different degrees. Of note, 2D rather than 3D opening operation is favored here because of the anisotropic nature of the LIDC data, where 2D operations have been found to outperform 3D operations for relatively thick-slice data [11]. Since vessels in lung parenchyma appear to have various radii, opening disks of different radii were adopted to treat varying levels of vessel attachment. In order to keep small nodules while removing attached vessels, the lower bound of opening disk radius was set to be the smallest - - one pixel. The upper bound of 5 pixels was experimentally determined by examining the sensitivity for annotated nodules in the LIDC training dataset.

The rule-based filtering operations were separately conducted for INCs obtained at each opening level, as well as for the original INCs without opening operation to preserve small solitary nodules. Therefore, there are four levels of INCs for rule-based filtering operations, and the final INCs to enter the SVM classification are formed by a logical union operation of the filtered INCs at all levels.

For each level of INCs, obvious FPs were first filtered out using the size rule on volume-equivalent diameter, which is calculated by

$$R_1=\left[\right(\#\text{of voxels}{}^{\ast }\text{voxel volume})∕(4\pi ∕3\left)\right)^(1∕3).$$ (3)

Because blood vessels are elongated in shape, we also established the elongation rule to exclude vessel-like structures with large elongation values. And the elongation in 3D space is defined by

$$R_2=\max (dx,dy,dz)∕\min (dx,dy,dz).$$ (4)

In addition, because pulmonary nodules are usually compact in shape, we define the following compactness rule:

$$R_3=\left(d{x}^{\ast }d{y}^{\ast }dz\right)∕\left\{\right[\max (dx,dy,dz)\left]^3\right\}.$$ (5)

In Eqs. (4) and (5), dx, dy, and dz are the maximal projection lengths (in mm) of an object along X, Y, and Z axes, respectively. Rules defined in Eqs. (4) and (5) together can capture the major shape characteristics of pulmonary nodules. In this study, the threshold values for R₁, R₂, and R₃ were determined experimentally. Given the true nodule (or TP) annotations in the LIDC database, we can compute the above three shape features for each true nodule. Then based on the range of each feature we can set a conservative threshold for each filtering rule. Combining these three expert rules, a

$$R_1<3.0\mid \mid R_1>30.0\mid \mid R_2>3.0\mid \mid R_3<0.1.$$ (6)

2) Feature-based SVM Classification

Our feature-based SVM classifier relies on a series of features extracted from each of the remaining INC after rule-based filtering operations. Table I lists the definitions of extracted features by four categories, including 10 geometric or shape features, 16 intensity features, 15 gradient features, and 8 Hessian eigenvalue based features. In the first three groups of features, both 2D and 3D features are extracted from each INC. It is noted that the step size difference along different dimensions is taken into account for the calculation of all related features. All 2D features are extracted from the largest area slice of INC segmentation, and the segmentation at maximum area slice is dilated for 5 layers to obtain the “outside” region where statistics features can be computed. For 3D features, the dilation is performed by enlarging the original segmentation using a spheroidal structuring element that has a radius of 5 pixels in the X-Y plane and extends by a single slice along each direction of the Z-axis.

TABLE I.

Overview of Features for SVM Classification

No.	Feature	Category
1	Area	2D geometric
2	Diameter (max dimension on largest area slice)	2D geometric
3	Eccentricity = ellipse foci / major axis length	2D geometric
4	Circularity = Area/[π(Diameter/2)^2]	2D geometric
5	Volume	3D geometric
6	Elongation = max(dx, dy, dz) / min(dx, dy, dz)	3D geometric
7	Compact1 = projection on x-y plane / (dx*dy)	3D geometric
8	Compact2 = (dx*dy*dz) / [max(dx, dy, dz)]^3	3D geometric
9-10	Mean and stdev of square compactness	3D geometric
11-16	Min, max, mean, stdev, skewness, and kurtosis	2D intensity
17-18	Inside vs. outside mean and stdev separation	2D intensity
19	Inside vs. outside contrast	2D intensity
20-23	Mean, stdev, skewness, and kurtosis	3D intensity
24-25	Inside vs. outside mean and stdev separation	3D intensity
26	Inside vs. outside contrast	3D intensity
27	XY gradient magnitude separation inside	2D gradient
28-29	Radial gradient mean and stdev inside	2D gradient
30-31	Radial gradient mean and stdev outside	2D gradient
32-33	Radial gradient mean and stdev separation	2D gradient
34-35	Mean and stdev of 3D gradient magnitude	3D gradient
36-37	Radial gradient mean and stdev inside	3D gradient
38-39	Radial gradient mean and stdev outside	3D gradient
40-41	Radial gradient mean and stdev separation	3D gradient
42-45	Min, max, mean and stdev of tubeness	3D Hessian
46-49	Min, max, mean and stdev of blobness	3D Hessian

Several of the features in Table I warrant some explanation. Specifically the square compactness is computed on the INC segmentation at each relevant CT section. The separation features (such as standard deviation separation) are computed using the difference of the inside and outside statistics divided by their sum. The inside and outside contrast is defined as the difference between the inside and outside means divided by the sum of the inside and outside standard deviations. For the gradient features, the XY gradient magnitude separation feature is defined as the mean separation between the magnitudes of gradients along the X- and Y-axis directions. Since pulmonary nodules usually have symmetric appearance, a radial gradient feature is also incorporated. It defines the projection of gradient magnitude on radial vector, and represents gradient strength along the radial direction. The 3D Hessian features are extracted from the Hessian matrix, which has been shown in the literature to be potentially useful to distinguish blob-like and tubular objects [13], [34]. Since the shape of most nodules is close to a blob and the shape of blood vessels are tubular, both tube-likeness and blob-likeness features [35] are employed for the differentiation of tubular and blob structures.

After extracting the above features from each remaining INC, a supervised learning strategy is carried out using the SVM classifier to further reduce FPs. The decision rule in our binary SVM classifier is whether the INC tends to be a TP or FP. The basic idea for SVM is to construct an optimal classification boundary that maximizes the inter-cluster distance. In this study, the LIBSVM [36] classifier with the commonly used radial-basis-function (RBF) kernel is employed.

Specifically, the remaining INCs after the rule-based filtering operations are randomly and equally split into two subsets with the same proportion of true nodules. Suppose the labeling information in subset 1 is known, a binary SVM classifier could be trained and applied for the classification of subset 2. Subsequently, subset 2 is switched to be the training set and subset 1 is treated as the testing set. This is indeed a two-fold cross validation. To alleviate the possible biases due to the selection of training and testing datasets, we repeated the random grouping process for sufficient times (e.g., 50). The overall detection accuracy can be summarized via ROC analysis over all SVM runs. By searching the optimal operating point on the averaged ROC curve, we can obtain the sensitivity and specificity of the CADe system, which are defined as follows

$$Sensitivity=\frac{TP}{TP+FN}$$ (7)

$$Specificity=\frac{TN}{TN+FP}$$ (8)

where TP represents the number of true positives, and FN, TN and FP denote the number of false negatives, true negatives and false positives, respectively.

III. Results

The proposed CADe system was validated on a subset of the largest publicly available database -- LIDC-IDRI [37]. A complete set of the annotated scans is available online at http://cancerimagingarchive.net. The LIDC-IDRI images were collected under different scanner manufacturers and models, variable spatial resolution and different X-ray imaging parameters (e.g. slice thicknesses: 0.45-5.0 mm; in-plane pixel size: 0.461-0.977 mm; total slice number: 96-605 slices; tube peak potential energies: 120-140 kV; and tube current: 40-627 mA).

As it is unclear how well most current CADe systems would perform for juxta-pleural nodules [38], in this study we aim to particularly emphasize the performance of our CADe system subject to the large presence of juxta-pleural nodules. The LIDC-IDRI database has 226 scans with at least one juxta-pleural nodule annotation. Among those scans, 21 were not included for the evaluation of our CAD system due to the following reasons. One scan shows a tube inside patient’s airway which leads to the leakage of lung volume by the connected component analysis. Four scans were excluded because of severe image streak artifacts induced by the failure of image reconstruction. There are two cases with incorrect radiologists’ annotation of VOI positions. The remaining 14 cases have at least one ground-glass opacity (GGO) nodule, which are not our consideration in this current study. Therefore a total of 205 chest CT scans in the LIDC database were utilized to evaluate the above presented CADe system.

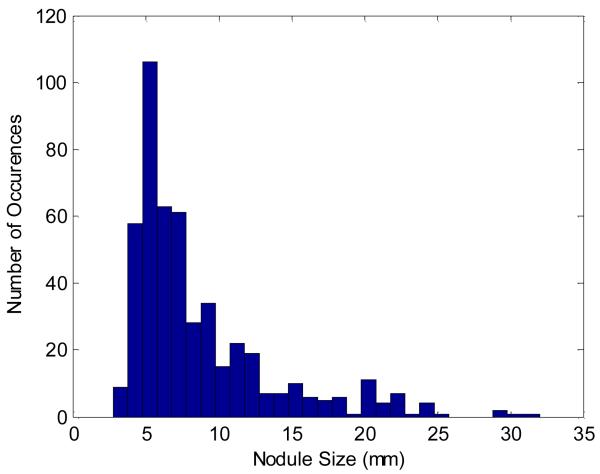
Fig. 7 shows the size distribution of the 490 nodules in the 205 considered datasets. These nodules were annotated with an agreement level of as low as one (i.e. each nodule was annotated by at least one out of the four radiologists). We can see that almost all of the nodules are within 3 ~ 30 mm in volume-equivalent diameter, and the majority are small nodules with a size of less than 10 mm. Each nodule’s relation with lung parenchyma was also summarized for the 205 considered datasets. Among all nodules, 99 are well-circumscribed, 68 are juxta-vascular, and 323 are juxta-pleural nodules. In terms of structural appearance, 283 are solid nodules while 207 are part-solid nodules.

Fig. 7.

The size (volume-equivalent diameter) distribution of the nodules in the 205 datasets of this study.

A. Evaluation of the PCA for Feature Extraction

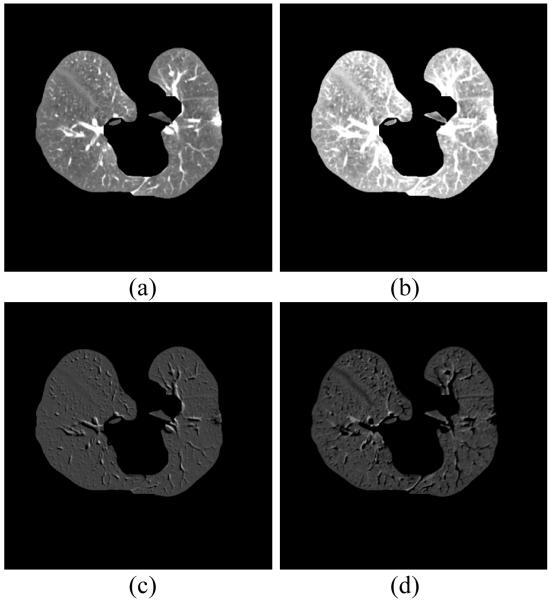
The purpose of local intensity feature extraction is to retain the major image information for reducing the computational burden. Fig. 8 shows an example of 3-component images, in the K-L domain selected by PCA, with a decreasing order of significance. It is clear that the first 3 PCs represent the dominant information. Those PCs beyond the third one contain even less information. PCA not only preserves the true image information, but also largely boosts the computational efficiency for our VQ algorithm.

Fig. 8.

The PCA selected component images in the K-L domain. (a) The original image; (b) The first PC; (c) The second PC; (d) The third PC.

B. INCs Detection and Segmentation Performance

At the prescreening stage, all of the 490 nodules from the target dataset of 205 chest CT scans were detected by the proposed hierarchical VQ approach. Hence the sensitivity for INCs detection is 100%, and the number of FPs is 1526 per scan.

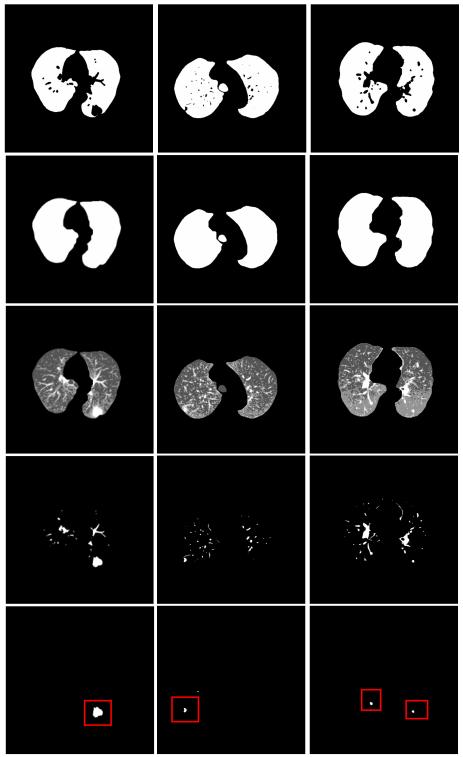
The rule-based filtering operations on the INCs preserved 475 of the nodules detected by VQ and brought the overall detection sensitivity to 96.9%. And the average number of FPs was significantly reduced from 1526 to 138.7 per scan, which corresponds to a FP reduction rate of more than 10 times. Three examples showing the performance of the hierarchical INCs detection approach followed by rule-based filtering operation are illustrated through Fig. 9. The leftmost image contains a huge juxta-pleural nodule. The second image shows an example of part-solid juxta-pleural nodule, while the last image contains a juxta-vascular nodule in the right lobe and a solitary nodule in the left lobe. The proposed scheme of hierarchical VQ followed by rule-based filtering operations is effective to detect all the TPs while substantially reducing the FPs in these three examples.

Fig. 9.

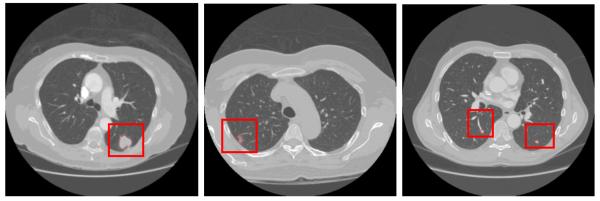
Examples on the performance of INCs detection and rule-based filtering operations. From top to bottom row: chest CT image; high-level VQ outcome; border-corrected lung mask; low-level VQ result; INCs from VQ detector; INCs after rule-based filtering operations.

C. Performance of FP Reduction by SVM Classification

After rule-based pruning of the obvious FPs, we further reduced the FPs via feature-based SVM classification. Two-fold cross validation was used to estimate the generalization capabilities of the SVM classifier. INCs were randomly and equally split into two folds, and each fold consisted of 237 true nodules and 14217 FPs. Each fold was used as the training set for once, and the other fold was treated as the testing set. This two-fold cross validation was repeated for 50 times to generate the averaged SVM classification results.

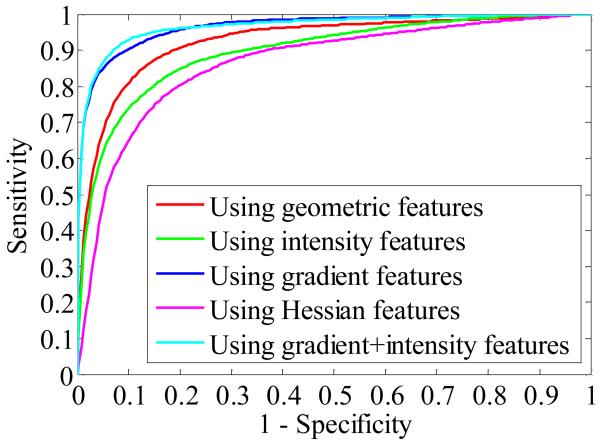
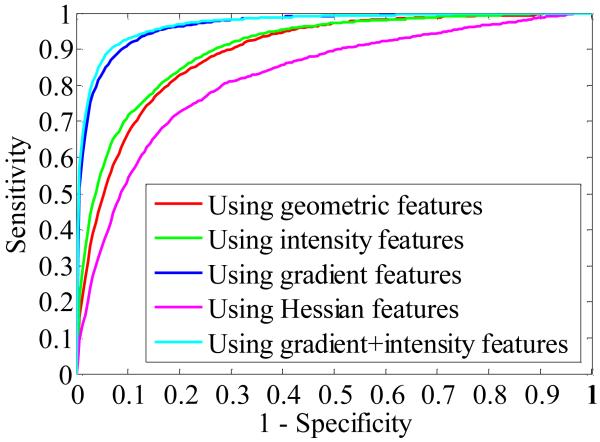
Table II shows the values of area under the ROC curve (AUC) in different feature spaces based on the 50 times average. For group-wise feature comparison, two-sample t-test was utilized to compare the mean of AUC value for different groups of features. Statistical analysis showed that the gradient features achieved a significantly higher AUC value than any of the other groups of features (one-sided p-value < 0.0001), and the geometric features is suboptimum, better than either of the intensity or Hessian features (one-sided p < 0.0001). The Hessian features alone yielded the least AUC value, significantly lower than the intensity features (one-sided p < 0.0001). According to the principle of forward feature selection, the next step is to compare the classifier performance by joining any of the other three groups of features with the gradient features selected in the previous step. The t-test showed that the AUC value in the “gradient + intensity” feature space was significantly higher (one-sided p < 0.0001) than the AUC value generated in either the “gradient + geometric” or the “gradient + Hessian” feature space. It also outperformed the previously selected gradient features (one-sided p < 0.0001). Furthermore, we compared the performance of the SVM classifier with the addition of either geometric or Hessian features to the “gradient + intensity” feature space. Statistical analyses showed the AUC mean with the addition of either geometric or Hessian features was, however, significantly lower than that for the previously selected “gradient + intensity” feature set (one-sided p < 0.05). Finally, all the four groups of features were combined together, but using all the extracted features still could not yield better performance than using only the “gradient + intensity” features (two-sided p = 0.5565).

TABLE II.

AUC Values for SVM Classification of INCs

Features	AUC mean	AUC stdev
Geometric Features	0.9257	0.0071
Intensity Features	0.8968	0.0104
Gradient Features	0.9656	0.0046
Hessian Features	0.8641	0.0115
Gradient + Geometric Features	0.9669	0.0055
Gradient + Intensity Features	0.9771	0.0041
Gradient + Hessian Features	0.9651	0.0050
Gradient + Intensity + Geometric	0.9743	0.0050
Gradient + Intensity + Hessian	0.9753	0.0047
All Features	0.9776	0.0044

Thus, the best feature subset for the SVM classifier is the combination of gradient and intensity features. Fig. 10 illustrates the averaged ROC curves calculated from different feature combinations. The optimal operating point for the best feature subset corresponds to a sensitivity of 92.7 % at a specificity level of 93.3%.

Fig. 10.

Averaged ROC curves showing CADe performance as a function of the step-wise selected features for the SVM classifier.

D. Performance on Detection of Juxtapleural Nodules

In particular, we conducted a further experiment to examine the performance of our CADe system to the detection of juxta-pleural nodules, where the SVM classifier was exclusively trained and applied to the juxta-pleural INCs. Technically, the corrected lung mask for each dataset is firstly eroded by 5 layers, and any INC with at least one voxel outside this eroded mask will be treated as a juxta-pleural candidate. The INCs that do not meet such criterion are categorized as internal candidates. The sensitivity and specificity of our CADe system before entering the SVM classifier could be summarized for the detection of juxta-pleural nodules exclusively. Among the 15 nodules that were mistakenly excluded by our filtering rules, 7 are juxta-pleural nodules. This indicates a sensitivity of 97.8% for the detection of 323 juxta-pleural nodules, and the number of FPs within juxta-pleural INCs was in average 53.8 per scan. Again, two-fold cross validation was used to evaluate the performance of the SVM classifier. Each fold consisted of 158 true nodules and 5512 FPs. This random cross-validation process was also repeated for 50 times to generate a series of AUC and ROC results.

The test AUC values of the SVM classification based on different features are summarized in Table III. For the group-wise feature comparison, the two-sample t-test indicated that the gradient features outperformed any of the other three groups of features (one-sided p < 0.0001). The intensity features were suboptimal, better than either of the geometric or Hessian features (one-sided p < 0.0001), while among the single-group features the Hessian features had the least contribution to the SVM classification. Upon forward selection of another group of features, the “gradient + intensity” features generated a significantly higher AUC value than the either of the “gradient + geometric” or “gradient + Hessian” features (one-sided p < 0.0001). There was also a significant increment of AUC value compared to that for the gradient features alone (one-sided p < 0.0001). In the next feature selection step, we added either geometric or Hessian features to the “gradient + intensity” feature space. The t-test showed there was no significant difference in AUC value by including the geometric features (two-sided p = 0.1396), and the AUC value after the inclusion of Hessian features was significantly lower (one-sided p = 0.0093). Finally, the AUC mean using all the extracted features was compared with that using the “gradient + intensity” features only. Two-sample t-test showed that AUC mean in the later feature set was, however, significantly higher than AUC mean of all features based classification at a significance level of 0.05 (one-sided p = 0.0417).

TABLE III.

AUC Values for SVM Classification of Juxta-pleural INCs

Features	AUC mean	AUC stdev
Geometric Features	0.8907	0.0099
Intensity Features	0.9031	0.0091
Gradient Features	0.9659	0.0050
Hessian Features	0.8225	0.0153
Gradient + Geometric Features	0.9651	0.0064
Gradient + Intensity Features	0.9703	0.0050
Gradient + Hessian Features	0.9621	0.0060
Gradient + Intensity + Geometric	0.9685	0.0065
Gradient + Intensity + Hessian	0.9677	0.0055
All Features	0.9684	0.0058

Hence, the optimal performance of the SVM classifier for the classification of juxta-pleural INCs could be achieved by using the gradient and intensity features only. The averaged ROC plot of Fig. 11 indicated that the optimal operating point in the “gradient + intensity” feature space corresponds to a sensitivity of 91.2% and a specificity of 92.3%.

Fig. 11.

Averaged ROC curves of the step-wise selected features for the SVM classification of juxta-pleural nodule candidates.

E. Comparison with Existing Methods

We compared the detection accuracy and speed of our CADe system with those of existing systems that also evaluated the LIDC-IDRI database. We selected five CADe systems that showed detection capability or reported detection speed. The detection of INCs in reference [22] was based on a multithreshold surface-triangulation approach, and the features used as input to their ANN classifier were volume, roundness, maximum density, mass, and principal moments of inertia. Reference [39] used a 2D filter to extract the seeds of INCs on each slice image, and then applied a SVM classifier with 6 complex features to reduce the FPs. Based on maximum intensity projection processing and Zernike moments, a feature extraction algorithm in reference [20] was employed to enhance the SVM for FP reduction. Reference [40] extracted the VOI by two segmentation algorithms of region growing and 3D active contour, while the following LDA classification employed three groups of features based on the gradient field, Hessian matrix, and the size and shape of the segmented object. Reference [23] proposed a fixed-topology ANN classifier based on 45 geometric, position, and intensity features.

Although the detection parameters and image datasets (number of cases, number of nodules, and agreement level of target nodules) employed in those methods are different, it is still meaningful to attempt making relative comparisons. Summary of comparison with the existing systems is shown in Table IV, where the ROC analysis results have been interpreted in terms of the free-response form. By considering the detection rate of 96.9% after our VQ and rule-based filtering operations, our proposed CADe system achieved an overall detection sensitivity of 82.7% at 4 FPs/scan. Consequently, our CADe system shows not only comparable detection performance but also less computational cost by using our fast hierarchical VQ approach. On average, the detection of INCs consumed about 20-25 seconds per case on a DELL Personal Computer with a processor speed of 2.26GHz. This is about 10 times faster than existing methods.

TABLE IV.

Performance Comparison of Proposed CADe System with Existing Systems using the LIDC-IDRI Database

CADe Systems	Number of cases	Number of nodules	Nodule size used	Agreement level	Average FPs/scan	Sensitivity (%)	Detection time (seconds)
Golosio et al [22]	84	148	>= 3 mm	1	4.0	45.0	-
Opfer and Wiemker [39]	-	127	>= 4 mm	1	4.0	76.0	180-300
Riccardi et al. [20]	154	387	-	1	4.0	49.0	-
Sahiner et al. [40]	48	73	3 - 36.4 mm	1	4.9	79.0	-
Tan et al. [23]	125	259	>= 3 mm	1	3.0	66.4	-
The proposed system	205	490	>= 3 mm	1	4.0	82.7	20 – 25

Moreover, we also compared the performance of our CADe system to three published systems that were devoted to the identification of juxta-pleural nodules. Reference [41] proposed a multiscale α-hull approach to identify juxta-pleural nodules by patching lung border concavities, and then fed the located nodules to an ANN classifier for FP reduction. In another study by [17], a conventional template matching approach was employed to detect nodules existing on the lung wall area, and only four features were used to eliminate FP findings. Reference [21] presented an approach to tackle the detection of internal and sub-pleural nodules, respectively, and both algorithms were finally combined as the assembled CADe system for evaluation. In their method [21], the INCs detection was based on a filter that enhanced spherical-shaped objects, and the FP reduction was carried out via a voxel-based neural network approach. Later on, reference [42] developed another CADe system particularly dedicated for pleural nodule identification using directional-gradient concentration method in combination with a morphological opening-based procedure. Each identified candidate was characterized by 12 morphological and textural features, which were analyzed by a rule-based filter and a neural classifier. Table V shows the summary of system performance comparison. Considering the detection rate of 97.8% for juxta-pleural nodules before SVM classification and an overall sensitivity of 89.2% for our CADe system at the optimal operating point after SVM classification, we would say our CADe system can outperform the existing systems for detection of juxta-pleural nodules. In terms of free-response ROC analysis, the corresponding specificity of our CADe system was 4.14 FPs per scan. Compared with the existing methods in Table V, our CADe system was evaluated via a larger dataset and, therefore, its favor performance is not only on the detection accuracy (including both sensitivity and specificity), but also on the statistical power.

TABLE V.

Comparison of Proposed CADe System with Existing Systems on Juxta-pleural Nodule Identification

CADe Systems	Number of cases	Number of nodules	Agreement level	Average FPs/scan	Sensitivity (%)
De Nunzio et al. [41]	57	78	-	-	66.5
Lee et al. [17]	20	24	-	14.15	71.0
Retico et al. [21]	39	27	2	10	74.0
Retico et al. [42]	42	25	2	6	72.0
The proposed system	205	323	1	4.14	89.2

IV. Discussions

As mentioned in Section 3, LIDC-IDRI images were collected from several different institutions. Consequently, the evaluation of such database was much more challenging than evaluation on images acquired from a single institution. Another challenge to the capability of our CADe system comes from the selection of target dataset. As we know, juxta-pleural nodules are usually semi-spherical or spiculate in shape, making them relatively difficult to detect. In addition, because they have similar intensities to the pleural wall, segmentation algorithms often fail in correcting the lung borders to include juxta-pleural nodules. Therefore, it is important to stress-test any CADe system in the presence of the irregularly-shaped juxta-pleural nodules. This study collected 205 chest CT scans with at least one juxta-pleural attachment to evaluate the proposed CADe system. For this regard, this study is unique.

The nodule size distribution in Fig. 7 shows the representativeness of the studied datasets, where about 74% of the nodules are less than 10 mm. This is clinically valuable in the sense that the detection of small nodules is crucial to detecting lung cancer at an early stage. Besides the substantial presence of small nodules, the consideration of nodules with the lowest agreement level also places a challenge to the detection power of our CADe system.

It is worth mentioning that the segmentation of challenging juxta-pleural nodules is critical, because failure to include such nodules makes it impossible for VQ to recover them in the later stages. Different from some previous works using 2D closing operation, we adopted the 3D morphological closing strategy to close the lung boundary. Fig. 12 portrays some examples of juxta-pleural nodules that were excluded by 2D closing operation but recovered by our 3D operation, which is more robust for lung border smoothing.

Fig. 12.

Examples of juxta-pleural nodules that were missed by 2D closing operation but recovered by 3D closing operation.

Though the proposed hierarchical VQ scheme was able to detect all non-GGO nodules in the studied datasets, more efforts are desired to deal with the associated large number of FPs. One possible solution is to merge clusters close to each other so that separated portions of a single object may be associated. Another solution is to incorporate more features into the feature vector for VQ, such as geometric features (e.g., shape index, curvedness) and texture features (e.g., local binary pattern, Haralick and Gabor features). By considering sophisticated features, FPs with low contrast to true nodules are expected to be identified by some unique feature characteristics other than just the image intensity. In addition, we also investigated the feasibility of boosting low level VQ for the detection of GGO nodules in LIDC database. Some of the GGO nodules may be recovered by increasing the maximum class number K, and by selecting two or more high-intensity classes as the INCs.

It has been widely acknowledged that the inclusion of rule-based filtering before the computationally expensive classification step will enhance the performance of CADe systems. Since intensity-based VQ could barely separate nodules from other attaching structures with similar intensities, preprocessing of the detected INCs is needed to handle the juxta-vascular nodules, which are otherwise prone to be excluded by expert rules. For computational simplicity, all the INCs are refined via morphological opening, because basic morphological operations are often effective for most juxta-vascular cases [15]. As a result, the detection rate after rule-based pruning retained at a relative high level of 96.9% as we desired and expected. The selection of appropriate radius for opening disk is critical to preserving TPs to the highest degree. Of note, certain nodules excluded by expert rules were irregularly-shaped nodules that could not be completely separated from attaching structures. Challenges also persist in determining the thresholds for expert rules. If too strict, it will lower the sensitivity of the CADe system. If too loose, too many FPs will render a difficulty to the following SVM classification. Replacing empirical filtering rules with semi-supervised learning is an ongoing topic for future research.

Both Table II and Table III demonstrate that among all single-group features of interest the gradient features contribute the most, which is consistent with our observation that most pulmonary nodules are symmetric in appearance while non-nodule structures are not. It is interesting to observe that the geometric features outperformed the intensity features for the classification of all INCs, but in contrast the intensity features are superior to the geometric features for the classification of juxta-pleural INCs only. This is reasonable because juxta-pleural nodules have a large variation in shape, and therefore shape-based features from the training set may not be representative for the testing dataset. It is also noted that the Hessian features show the lowest differentiation power among the four groups of features of interest. This may due to the fact that most tubular-like objects have already been excluded at the rule-based filtering stage, and thus the advantage of using Hessian eigenvalues to differentiate tubular from blob structures may be diminished.

Whereas the features incorporated in the SVM classifier has been commonly-used by published works on lung nodule detection, more sophisticated features such as texture features employed by our previous work for nodule diagnosis [43] can be incorporated to improve the performance of our CADe system.

V. Conclusion

In this paper, a novel CADe system was proposed for fast and adaptive detection of pulmonary nodules in chest CT scans. Based on our previous work of self-adaptive online VQ for image segmentation [25], we developed a hierarchical VQ scheme for INCs detection. The high level VQ proves to be feasible to replace the commonly-used simple thresholding scheme for extraction of the lungs in terms of higher accuracy, comparable processing time and automation level. The following low level VQ illustrates adequate detection power for non-GGO nodules, and is computationally more efficient than the state-of-the-art approaches. In this study, simple expert rules were firstly employed to exclude obvious FPs from being considered by the sophisticated feature-based SVM classifier, and further reduced the computational complexity. The SVM classification results indicated that gradient features contributed the most against any of the other three groups of features (geometric, intensity, and Hessian features). The forward feature selection strategy showed that the SVM classifier performed the best in the “gradient + intensity” feature space rather than in any other feature combination spaces. The optimal operating point of the SVM classifier for the best feature subset yielded a sensitivity of 92.7% and a specificity of 93.3%. In terms of the free-response ROC analysis, the proposed CADe system achieves an overall sensitivity of 82.7% at 4.0 FPs per scan. Compared with existing CADe systems evaluated on the same lung image LIDC database, our approach showed a comparable detection capability but a lower computational cost. In particular, we reported the performance of our system for the detection of juxta-pleural nodules. The outcome from our CADe system, with an overall sensitivity of 89.2% at a specificity level of 4.14 FPs/scan, is promising for tackling this challenging detection task. In a nutshell, the proposed hierarchical INCs detection approach is fast, adaptive and fully automatic. The presented CADe system yields comparable detection accuracy and more computational efficiency than existing systems, which demonstrates the feasibility of our CADe system for clinical utility.